Теоретические основы химической технологии, 2019, T. 53, № 2, стр. 131-137
Равновесие жидкость–жидкость в экстракционной системе на основе поливинилпирролидона-3500 и нитрата натрия
Ю. А. Заходяева 1, 2, *, Д. Г. Рудаков 1, В. О. Соловьев 2, А. А. Вошкин 1, 2, А. В. Тимошенко 1
1 МИРЭА – Российский технологический университет
Москва, Россия
2 Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: yz@igic.ras.ru
Поступила в редакцию 20.11.2018
После доработки 30.11.2018
Принята к публикации 26.11.2018
Аннотация
Изучено фазовое равновесие жидкость–жидкость для новой экстракционной системы, полученной на основе поливинилпирролидона-3500 и нитрата натрия при температурах 298.15, 313.15 и 333.15 K. Представлены как бинодальные данные, так и фазовые диаграммы с нанесенными на них нодами жидкость–жидкость. Проведено математическое моделирование фазового равновесия в данной системе. Подобраны новые параметры для уравнения UNIQUAC. Показано, что модель UNIQUAC может быть успешно использована для описания фазового равновесия в данной системе. Полученные результаты могут быть в дальнейшем использованы при разработке новых экстракционных процессов извлечения органических веществ.
ВВЕДЕНИЕ
Жидкостная экстракция широко используется в редкометальной и радиохимической промышленности, при производстве цветных и благородных металлов, для выделения органических кислот, а также в процессах очистки продуктов крекинга и риформинга нефтяных фракций от алифатических и ароматических соединений. В связи с этим интенсивно развиваются существующие процессы экстракции, а также активно ведется поиск новых методов экстракционного разделения и очистки, в том числе поиск новых экстракционных систем. Особый интерес представляют такие направления, как экстракционные системы на основе ионных жидкостей, которые успешно зарекомендовали себя для решения задач разделения неорганических [1–3] и органических веществ [4–9]. Двухфазные водные системы являются одними из перспективных направлений в настоящее время в разработке новых методов экстракционного разделения. Число работ, посвященных этой проблеме, заметно увеличивается в последние годы [10–14], что связано в том числе и с ужесточением требований к экологической безопасности химических производств, а также с ростом так называемых налогов на экологию. Двухфазные водные системы обладают рядом исключительных преимуществ по сравнению с классическими экстракционными системами, а именно: экологическая безопасность, пожарная безопасность, доступность. Ранее для разработки аналитических и радиохимических методов разделения и концентрирования веществ уже использовались двухфазные водные системы, также описано их применение в процессах утилизации химических элементов питания [13], для выделения органических кислот [14] и солей металлов. Кроме того, эти системы широко используются в биотехнологических процессах и в производстве фармацевтических препаратов [11]. Полученные ранее результаты [10, 12] позволяют предположить эффективность применения методов экстракции на основе двухфазных систем с водорастворимыми полимерами для очистки углеводородных фракций от серосодержащих соединений.
Системы на основе поливинилпирролидона (ПВП) можно рассматривать как одни из перспективных экстракционных систем, поскольку в последнее время появляется все большее количество работ, посвященных экстракционным системам, основанным именно на ПВП. Изучены свойства и фазовое равновесие систем на основе ПВП с разной молекулярной массой и различных солей: цитрата натрия [15], фосфата калия [16], сульфата натрия [17] и дигидрофосфата натрия [18]. В статье [19] изучено фазовое равновесие с пятью различными солями аммония, включая (NH4)2HPO4, (NH4)2SO4, (NH4)2CO3, (NH4)2C4H4O6 и (NH4)2HC6H5O7.
Информация о фазовом равновесии является фундаментальной для количественного описания процессов экстракции. Физико-химические взаимодействия, обусловливающие равновесие жидкость–жидкость в этих системах, основаны на термодинамических законах и могут быть представлены фазовыми диаграммами. Небольшое изменение давления оказывает незначительное воздействие на равновесие, но такие параметры, как температура и состав системы оказывают очень сильное влияние. Именно поэтому информация о фазовом равновесии для новых двухфазных водных систем крайне важна для последующей работы с ними.
В настоящей работе получены новые экспериментальные данные о фазовом равновесии в системе на основе ПВП-3500 и NaNO3 и выбрана модель UNIQUAC для описания фазового равновесия. Подобраны бинарные параметры уравнения UNIQUAC, а также оценены вандерваальсов объем и поверхность для молекул соли и полимера. Полученные результаты могут быть использованы в дальнейших исследованиях по созданию новых экстракционных процессов с использованием ПВП-3500, в том числе в процессах очистки легких углеводородных фракций от серосодержащих соединений.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
При проведении экспериментальных исследований были использованы следующие реактивы: поливинилпирролидон со средней молекулярной массой 3500 г/моль (производитель Acros Organics, чистота 99%), нитрат натрия (производитель Sigma-Aldrich, чистота ≥99.0%). Все реактивы были использованы без какой-либо дополнительной очистки.
Экспериментальное исследование фазовых равновесий в многокомпонентных системах проводили в стеклянной ячейке объемом 50 мл с использованием термостатированного шейкера (Enviro-Genie SI-1202, Scientific Industries, Inc., США) при варьируемой скорости вращения от 1 до 60 об/мин, где температура контролировалась в пределах ±0.2 К. Определение положения бинодальной кривой осуществлялось методом титрования до точки помутнения [20, 21]. Эксперименты проводили при температурах 298.15, 313.15 и 333.15 K. Бинодальная кривая определена точками помутнения путем добавления соли в раствор полимера с известной концентрацией полимера до тех пор, пока раствор не становился мутным, что указывало на образование двух несмешивающихся жидких фаз. В соответствии с количеством добавленной соли, пока наблюдалось помутнение, состав смеси для каждой точки на бинодальной кривой был рассчитан на основе масс каждого компонента в системе. Взвешивание осуществлялось на аналитических весах (Е10640, Ohaus, Швейцария) с точностью ±1 × 10–4 г. Для определения нод жидкость–жидкость были приготовлены системы с известным содержанием полимера, соли и воды, при котором соотношение объемов верхней (полимерной) и нижней (солевой) фаз было приблизительно 1 : 1. Образцы перемешивали в термостатированном шейкере в течение 30 мин и затем оставляли на 24 ч, что было достаточно для достижения равновесия.
Концентрацию нитрата натрия в верхней и нижней фазах определяли методом кондуктометрии (ОК 102/1, Radelkis, Венгрия). Для этого готовили серию калибровочных растворов нитрата натрия точной концентрации от 1 × 10–3 до 2.5 × × 10–2 мас. %, измеряли электропроводность приготовленных растворов при 298 K на кондуктометре (постоянная ячейки 0.68). По полученным данным строили градуировочный график в виде зависимости электропроводности от концентрации нитрата натрия. На участке от 0 до 50 мСм/см наблюдалась линейная зависимость, которая и была использована для дальнейшего определения содержания нитрата натрия в исследуемых равновесных фазах.
Концентрацию полимера в обеих фазах определяли путем измерения показателя преломления с помощью рефрактометра (Refracto 30P, Mettler Toledo, Швейцария). Погрешность измерения показателя преломления ±0.0001.
В соответствие с правилом аддитивности:
(1)
$n_{{\text{D}}}^{{{\text{MIX}}}} = a_{{}}^{{\text{P}}}{{w}^{{\text{P}}}} + a_{{}}^{{\text{S}}}{{w}^{{\text{S}}}} + n_{{\text{D}}}^{{\text{W}}},$причем
где nD – показатель преломления, w – массовая доля компонента.Следует отметить, что уравнение (1) справедливо только для разбавленных растворов. Поэтому, перед измерением показателя преломления было выполнено обязательное разбавление образцов. Затем были построены калибровочные графики для показателя преломления полимера в диапазоне его концентраций от 0 до 10 мас. % и для соли в диапазоне ее концентраций от 0 до 5 мас. %, по которым были определены значения констант aP и aS, для полимера и соли соответственно.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Полученные бинодальные данные для системы ПВП-3500–NaNO3–вода при 298.15, 313.15 и 333.15 K представлены в табл. 1.
Таблица 1.
Экспериментальные бинодальные данные для системы ПВП-3500– NaNO3–вода при 298.15, 313.15 и 333.15 K (составы в мас. %)
| T = 298.15 K | T = 313.15 K | T = 333.15 K | ||||||
|---|---|---|---|---|---|---|---|---|
| wP | wS | wW | wP | wS | wW | wP | wS | wW |
| 2.48 | 44.86 | 52.66 | 28.69 | 24.08 | 47.23 | 27.78 | 25.47 | 46.75 |
| 5.91 | 42.43 | 51.66 | 6.25 | 34.82 | 58.93 | 22.25 | 27.85 | 49.90 |
| 4.35 | 43.04 | 52.61 | 2.06 | 48.97 | 48.97 | 19.16 | 32.39 | 48.45 |
| 19.64 | 34.53 | 45.83 | 26.06 | 28.55 | 45.39 | 12.53 | 34.64 | 52.83 |
| 17.88 | 35.43 | 46.69 | 23.12 | 29.91 | 46.97 | 9.19 | 36.59 | 54.22 |
| 16.43 | 36.11 | 47.46 | 20.84 | 30.76 | 48.40 | 8.06 | 37.56 | 54.37 |
| 15.22 | 36.59 | 48.19 | 19.02 | 31.29 | 49.69 | 6.14 | 37.80 | 56.05 |
| 14.13 | 37.19 | 48.68 | 17.71 | 31.99 | 50.29 | 4.98 | 39.02 | 56.00 |
| 12.27 | 38.65 | 49.08 | 3.40 | 41.40 | 55.21 | 1.66 | 51.72 | 46.62 |
| 22.62 | 34.13 | 43.25 | 6.25 | 34.82 | 58.93 | 0.99 | 53.88 | 45.14 |
| 29.29 | 30.95 | 39.76 | 1.55 | 58.19 | 40.27 | 0.54 | 57.11 | 42.35 |
Данные о составах равновесных жидких фаз при 298.15, 313.15 и 333.15 K представлены в табл. 2. Все данные получены при давлении приблизительно 100 ± 1 кПа. Поскольку внешнее давление не оказывает значимого влияния на фазовое равновесие двух жидких фаз, специальных мер по его стабилизации не проводили. Область исследования фазового равновесия жидкость–жидкость в данной системе имеет максимально широкие границы, обусловленные одновременным наличием только двухфазной области жидкость–жидкость, при выходе за пределы которой либо образуется твердая фаза (выпадает осадок), либо формируется единственная жидкая фаза.
Таблица 2.
Равновесные данные для системы ПВП-3500–NaNO3–вода при 298.15, 313.15 и 333.15 K (составы в мас. %)
| № | Исходный состав | Верхняя фаза | Нижняя фаза | ||||||
|---|---|---|---|---|---|---|---|---|---|
| wP | wS | wW | wP | wS | wW | wP | wS | wW | |
| T = 298.15 K | |||||||||
| 1 | 15.30 | 37.84 | 46.86 | 22.62 | 34.13 | 43.25 | 10.38 | 40.04 | 49.57 |
| 2 | 16.56 | 37.88 | 45.56 | 32.98 | 29.83 | 37.19 | 3.17 | 44.34 | 52.48 |
| 3 | 17.00 | 37.57 | 45.43 | 35.00 | 29.03 | 35.98 | 3.01 | 44.70 | 52.29 |
| 4 | 17.50 | 36.99 | 45.51 | 29.06 | 31.44 | 39.50 | 7.08 | 42.15 | 50.77 |
| T = 313.15 K | |||||||||
| 1 | 14.00 | 40.00 | 46.00 | 18.68 | 33.40 | 47.92 | 5.58 | 41.19 | 53.24 |
| 2 | 15.00 | 37.00 | 48.00 | 21.10 | 32.30 | 46.60 | 4.90 | 42.50 | 52.60 |
| 3 | 13.00 | 39.00 | 48.00 | 25.40 | 30.64 | 43.96 | 4.70 | 44.88 | 50.42 |
| 4 | 17.00 | 37.57 | 45.43 | 27.50 | 29.83 | 42.67 | 3.50 | 47.57 | 48.93 |
| T = 333.15 K | |||||||||
| 1 | 20.00 | 35.00 | 45.00 | 26.43 | 29.09 | 44.48 | 1.66 | 51.72 | 46.62 |
| 2 | 20.59 | 35.29 | 44.12 | 28.14 | 29.00 | 42.86 | 0.99 | 53.88 | 45.14 |
| 3 | 22.00 | 37.00 | 41.00 | 31.60 | 28.02 | 40.39 | 0.54 | 57.11 | 42.35 |
| 4 | 17.00 | 40.00 | 43.00 | 29.70 | 28.50 | 41.80 | 0.91 | 55.00 | 44.09 |
Одними из параметров, которые необходимы для описания свойств данных систем, являются длина нод (tie-line length, TLL) и их наклон (slopes of the tie-line, STL). При постоянных давлении и температуре параметр TLL выражает разницу величин интенсивных термодинамических функциях между верхней и нижней фазами [22]. Обычно параметр TLL выражается как разность между концентрациями полимера и соли в фазах и, следовательно, может быть рассчитан по уравнению
(3)
${\text{TLL}} = {{\left[ {{{{\left( {w_{{\text{P}}}^{{\text{T}}}--w_{{\text{P}}}^{{\text{B}}}} \right)}}^{{\text{2}}}} + {{{\left( {w_{{\text{S}}}^{{\text{T}}}--w_{{\text{S}}}^{{\text{B}}}} \right)}}^{{\text{2}}}}} \right]}^{{0.{\text{5}}}}},$В свою очередь, влияние температуры на равновесие жидкость–жидкость может быть описано, в том числе, посредством параметра STL [23], который может быть рассчитан по уравнению
(4)
${\text{STL}} = {{\left( {w_{{\text{P}}}^{{\text{T}}}--w_{{\text{P}}}^{{\text{B}}}} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{\text{P}}}^{{\text{T}}}--w_{{\text{P}}}^{{\text{B}}}} \right)} {\left( {w_{{\text{S}}}^{{\text{T}}}--w_{{\text{S}}}^{{\text{B}}}} \right)}}} \right. \kern-0em} {\left( {w_{{\text{S}}}^{{\text{T}}}--w_{{\text{S}}}^{{\text{B}}}} \right)}},$Таблица 3.
Значения параметров TLL и STL для системы ПВП-3500–NaNO3–вода при 298.15, 313.15 и 333.15 K
| № | T = 298.15 K | T = 313.15 K | T = 333.15 K | |||
|---|---|---|---|---|---|---|
| TLL | STL | TLL | STL | TLL | STL | |
| 1 | 13.59 | –2.07 | 15.24 | –1.68 | 33.54 | –1.09 |
| 2 | 33.15 | –2.05 | 19.14 | –1.59 | 36.83 | –1.09 |
| 3 | 35.62 | –2.04 | 25.13 | –1.45 | 42.56 | –1.07 |
| 4 | 24.45 | –2.05 | 29.84 | –1.35 | 39.13 | –1.09 |
Видно, что длина нод (TLL) значительно увеличивается с ростом температуры, в то время как наклон нод (STL) уменьшается.
Согласованность полученных экспериментальных данных может быть проверена посредством методики Отмера–Тобиаса [24], основанной на эмпирическом уравнении
(5)
${\text{ln}}\left[ {{{\left( {{\text{1}}--w_{{\text{S}}}^{{\text{B}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\text{1}}--w_{{\text{S}}}^{{\text{B}}}} \right)} {w_{{\text{S}}}^{{\text{B}}}}}} \right. \kern-0em} {w_{{\text{S}}}^{{\text{B}}}}}} \right] = A + B{\text{ln}}[\left[ {{{\left( {{\text{1}}--w_{{\text{P}}}^{{\text{T}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\text{1}}--w_{{\text{P}}}^{{\text{T}}}} \right)} {w_{{\text{P}}}^{{\text{T}}}}}} \right. \kern-0em} {w_{{\text{P}}}^{{\text{T}}}}}} \right],$МОДЕЛИРОВАНИЕ ФАЗОВОГО РАВНОВЕСИЯ ЖИДКОСТЬ–ЖИДКОСТЬ
В целом существуют два основных подхода к математическому моделированию двухфазных водных систем типа водорастворимый полимер–соль–вода. 1Как правило, оба подхода используют концепцию локальных составов – уравнения NRTL, UNIQUAC и их модификации. Первый подход основан на “подробном” описании взаимодействия реальных частиц, имеющихся в растворе: катионов и анионов (учитывается реакция диссоциации) с молекулами воды и полимера. При этом молекула полимера представлена соответствующими сегментами с заданной структурой полимера в целом, возможен учет гидратации молекул. Главным недостатком этого подхода можно назвать большое количество используемых параметров модели и, как следствие, высокую размерность задачи, которая приводит к проблемам со сходимостью расчета.
Второй подход заключается в упрощенной схеме рассмотрения участвующих в фазовом равновесии компонентов – рассматриваются брутто-составы каждого из компонентов, без учета реально присутствующих в растворе частиц (например, вместо расчета концентраций катионов и анионов в каждой из фаз вычисляется концентрация соответствующей им соли, реакция диссоциации в таком случае не учитывается). Несмотря на значительные упрощения, именно такой метод используют большинство исследователей, поскольку он существенно снижает размерность задачи и благоприятствует сходимости расчета. Качество описания фазового равновесия при этом не ухудшается.
В данной работе проведено математическое моделирование фазового равновесия в системе ПВП-3500–NaNO3–вода по полученным нами экспериментальным данным с помощью модели локальных составов UNIQUAC [25] в программном комплексе Aspen Plus.
Параметры уравнения UNIQUAC aij, bij, cij, dij и eij подбираются регрессией экспериментальных данных для каждой бинарной пары. Вандерваальсов объем (R) и поверхность (Q) молекул оцениваются для каждого из компонентов отдельно по методу Бонди [26]. Сначала были оценены параметры R и Q для молекулы воды, затем для сегмента полимера и соли, они представлены в табл. 5.
Таблица 5.
Параметры R и Q для молекул компонентов смеси
| Компонент | R | Q |
|---|---|---|
| ПВП-3500 | 4.4998 | 3.856 |
| NaNO3 | 4.4998 | 3.856 |
| Вода | 1.4 | 0.92 |
Для подбора параметров aij, bij, cij, dij и eij был использован метод максимального правдоподобия, кроме этого, поскольку параметр eij, как правило, не оказывает существенного влияния на конечный результат, он был исключен из регрессии. Рассчитанные параметры уравнения UNIQUAC представлены в табл. 6.
Таблица 6.
Бинарные параметры уравнения UNIQUAC для системы ПВП-3500–NaNO3–вода
| Компонент i | Размерность | ПВП-3500 | ПВП-3500 | NaNO3 |
|---|---|---|---|---|
| Компонент j | NaNO3 | вода | вода | |
| aij | – | 0.5320 | 0.5751 | –0.1980 |
| aji | – | –2.9702 | –1.2686 | 0.0593 |
| bij | K | 550.716 | 37.935 | –39.618 |
| bji | K | –891.705 | –601.055 | 49.048 |
| cij | K | 0.05564 | 0.1145 | –0.0365 |
| cji | K | –0.5206 | –0.2012 | 0.0074 |
| dij | K | –0.00222 | 0.003397 | –0.00085 |
| dji | K | –0.00988 | –0.00207 | –0.00012 |
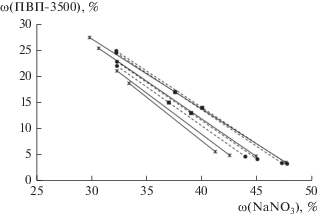
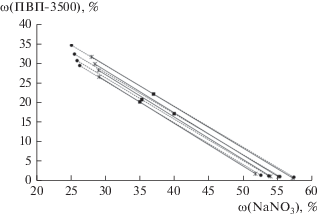
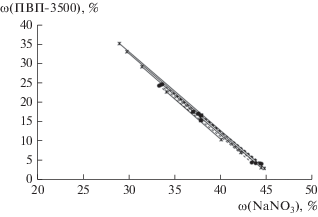
Далее, по модели UNIQUAC c подобранным параметрам были рассчитаны равновесные составы жидких фаз для каждой из трех температур 298.15, 313.15 и 333.15 K. Полученные результаты представлены на рис. 1–3, из которых видно, что область наличия двух жидких фаз достаточно узкая, особенно при 298 K, а это в свою очередь осложняет математическое описание.
Рис. 1.
Фазовая диаграмма для системы ПВП-3500–NaNO3–вода при 298.15 K (сплошная линия – эксперимент, пунктирная линия – расчетные данные).
ЗАКЛЮЧЕНИЕ
Предложена новая экстракционная система на основе поливинилпирролидона со средней молекулярной массой 3500 г/моль и нитрата натрия. Изучено фазовое равновесие жидкость–жидкость при трех температурах 298.15, 313.15 и 333.15 K. Посредством уравнения UNIQUAC проведено математическое моделирование фазового равновесия в данной системе, подобраны параметры уравнения UNIQUAC. Показана работоспособность предложенной данной данной для описания фазового равновесия в рассматриваемой системе. Полученные результаты могут быть использованы в дальнейших исследованиях по созданию новых экстракционных процессов с использованием поливинилпирролидона-3500, в том числе в процессах очистки легких углеводородных фракций от серосодержащих соединений.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 17-73-10486).
ОБОЗНАЧЕНИЯ
| A, B | параметры уравнения Отмера–Тобиаса |
| a, b, c, d, e | бинарные параметры уравнения UNIQUAC |
| Q | вандерваальсова поверхность |
| R | вандерваальсов объем |
| R2 | коэффициент регрессии |
| T | температура, K |
| w | концентрация, мас. % |
ИНДЕКСЫ
Список литературы
Вошкин А.А., Белова В.В., Холькин А.И. Экстракция железа(III) бинарными экстрагентами на основе четвертичных аммониевых оснований и органических кислот // Журн. неорг. химии. 2003. Т. 48. № 4. С. 699.
Белова В.В., Вошкин A.A., Егорова Н.С., Холькин А.И. Экстракция редкоземельных металлов из нитратных растворов бинарным экстрагентом на основе Cyanex 272 // Журн. неорг. химии. 2010. Т. 55. № 4. С. 679.
Егорова Н.С., Белова В.В., Вошкин А.А., Жилов В.И., Холькин А.И. Экстракция хлоридных солей лантаноидов бинарными экстрагентами на основе производных фосфиновых кислот // Журн. неорг. химии. 2005. Т. 50. № 11. С. 1902.
Królikowski M., Królikowska M., Wiśniewski C. Separation of aliphatic from aromatic hydrocarbons and sulphur compounds from fuel based on measurements of activity coefficients at infinite dilution for organic solutes and water in the ionic liquid N,N-diethyl-N-methyl-N-(2-methoxy-ethyl)ammonium bis(trifluoromethyl-sulfonyl)imide // The Journal of Chemical Thermodynamics. 2016. V. 103. P. 115.
Белова В.В., Куличенков С.А., Вошкин А.А. и др. Экстракция минеральных кислот динонилнафталинсульфонатом триоктилметиламмония // Журн. неорг. химии. 2007. Т. 52. № 3. С. 513.
Kholkin A.I., Belova V.V., Zakhodyaeva Y.A., Voshkin A.A. Solvent Extraction of Weak Acids in Binary Extractant Systems // Separation Science and Technology. 2013. V. 48. № 9. P. 1417.
Khol’kin A.I., Zakhodyaeva Yu.A., Voshkin A.A., Belova V.V. Interphase distribution of weak acids in systems with binary extractants // Theor. Found. Chem. Eng. 2013. V. 47. № 4. P. 453.
Zakhodyaeva Yu.A., Voshkin A.A., Belova V.V., Khol’kin A.I. Extraction of monocarboxylic acids by trioctylmethylammonium di(2-ethylhexyl)phosphate // Theor. Found. Chem. Eng. 2012. V. 46. № 4. P. 413.
Zakhodyaeva Yu.A., Voshkin A.A., Belova V.V., Khol’kin A.I. Extraction of monocarboxylic acids with binary extracting agents based on amines and quaternary ammonium bases // Theor. Found. Chem. Eng. 2011. V. 45. № 5. P. 739.
Kianpour E., Azizian S. Polyethylene glycol as a green solvent for effective extractive desulfurization of liquid fuel at ambient conditions // Fuel. 2014. V. 137. P. 36.
Mokhtari A., Shahriari S. Extraction of Cephalexin Using Aqueous Two-Phase Systems Composed of Cholinium Chloride and K3PO4 // J. Applied Chemical Research. 2017. V. 11. № 1. P. 21.
Chen Y., Song H., Meng H. et al. Polyethylene glycol oligomers as green and efficient extractant for extractive catalytic oxidative desulfurization of diesel // Fuel Processing Technology. 2017. V. 158. P. 20.
Zakhodyaeva Yu.A., Izyumova K.V., Solov’eva M.S., Voshkin A.A. Extraction separation of the components of leach liquors of batteries // Theor. Found. Chem. Eng. 2017. V. 51. № 5. P. 883.
Voshkin A.A., Zakhodyaeva Y.A., Zinov’eva I.V., Shkinev V.M. Interphase Distribution of Aromatic Acids in the Polyethylene Glycol–Sodium Sulfate–Water System // Theor. Found. Chem. Eng. 2018. V. 52. № 5. P. 890.
Pirdashti M., Movagharnejad K., Mobalegholeslam P. et al. Phase equilibrium and physical properties of aqueous mixtures of poly (vinyl pyrrolidone) with trisodium citrate, obtained experimentally and by simulation // J. Molecular Liquids. 2016. V. 223. P. 903.
Rahmani A., Rostami A.A., Pirdashti M., Mobalegholeslam P. Liquid-liquid equilibrium and physical properties of aqueous mixtures of poly(vinyl pyrrolidone) with potassium phosphate at different pH: Experiments and modeling // Korean J. Chem. Eng. 2017. V. 34. № 4. P. 1149.
Zafarani-Moattar M.T., Abdizadeh-Aliyar V. Thermodynamic studies on the complete phase diagram of the ternary aqueous system containing polyvinylpyrrolidone 3500 and sodium sulfate at different temperatures: Experiment and correlation // J. Chem. Thermodynamics. 2016. V. 98. P. 71.
Zafarani-Moattar M.T., Sadeghi R. Measurement and correlation of liquid–liquid equilibria of the aqueous two-phase system polyvinylpyrrolidone–sodium dihydrogen phosphate // Fluid Phase Equilibria. 2002. V. 203. P. 177.
Wang Y., Wu Y., Ni L. et al. Liquid−Liquid Equilibria of Polyvinylpyrrolidone + Several Ammonium Salts + Water Aqueous Two-Phase Systems: Experimental and Correlation // J. Chem. Eng. Data. 2012. V. 57. P. 3128.
Lemos L.R., Patrício P.R., Rodrigues G.D. et al. Liquid–liquid equilibrium of aqueous two-phase systems composed of poly(ethylene oxide) 1500 and different electrolytes ((NH4)2SO4, ZnSO4 and K2HPO4): Experimental and correlation // Fluid Phase Equilibria. 2011. V. 305. P. 19.
Martins J.P., Carvalho C.P., Silva L.H.M. et al. Liquid–Liquid Equilibria of an Aqueous Two-Phase System Containing Poly(ethylene) Glycol 1500 and Sulfate Salts at Different Temperatures // J. Chem. Eng. Data. 2008. V. 53. P. 238.
Silva L.H.M., Silva M.C.H., Francisco K.R. et al. PEO-$[{\text{M}}{{({\text{CN}})}_{5}}{\text{NO}}]_{x}^{ - }$ (M) Fe, Mn, or Cr) Interaction as a Driving Force in the Partitioning of the Pentacyanonitrosylmetallate Anion in ATPS: Strong Effect of the Central Atom // J. Phys. Chem. B. 2008. V. 112. P. 11669.
Martins J.P., Mageste A.B., Silva M.D.H. et al. Liquid–liquid equilibria of an aqueous two-phase system formed by a triblock copolymer and sodium salts at different temperatures // J. Chem. Eng. Data. 2009. V. 54. P. 2891.
Othmer D.F., Tobias P.E. Liquid-Liquid Extraction Data – The Line Correlation // Ind. Eng. Chem. 1942. V. 34. P. 693.
Abrams D.S., Prausnitz J.M. Statistical Thermodynamics of Liquid Mixtures: A New Expression for the Excess Gibbs Energy of Partly or Completely Miscible Systems // AIChE J. 1975. V. 21. № 1. P. 116.
Bondi A. Physical Properties of Molecular Crystals, Liquids and Gases. N.Y.: Wiley, 1960.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии