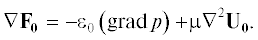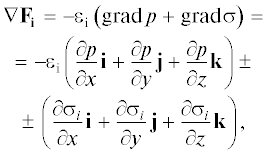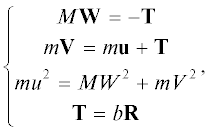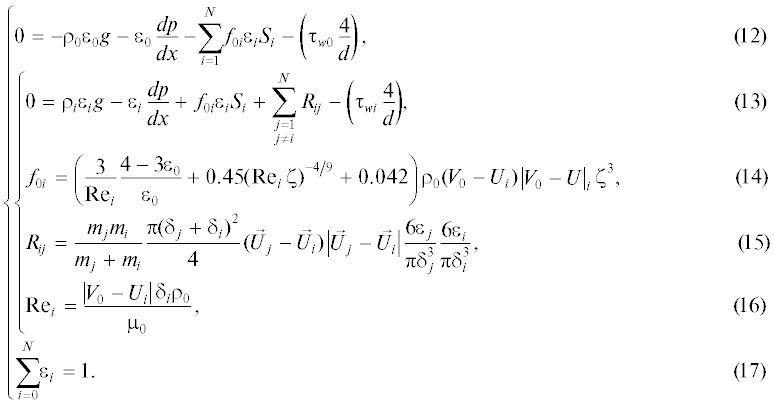Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 338-348

Математическое моделирование вертикального пневмотранспорта полидисперсного материала

А. Ю. Иваненко¹, М. А. Яблокова^1, *

¹ Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия

Поступила в редакцию 18.10.2017
После доработки 26.02.2018
Принята к публикации 23.05.2018

DOI: 10.1134/S0040357119020076

Аннотация

Предложена математическая модель вертикального пневмотранспорта полидисперсного сыпучего материала, основанная на теории взаимопроникающих континуумов и дополненная уравнениями межфракционного взаимодействия, учитывающими столкновения частиц различных фракций между собой. Показано, что силы межфракционного взаимодействия, обусловленные столкновением частиц, по численному значению вполне соизмеримы с силами межфазного взаимодействия частиц с газом. Для частиц мелких фракций столкновение с крупными частицами оказывает тормозящее действие, в то время как крупные частицы “подгоняются” мелкими. В целом это приводит к уменьшению разброса между скоростями движения частиц.

Ключевые слова: теория взаимопроникающих континуумов, вертикальный пневмотранспорт, полидисперсный материал, мелочь нефтяного кокса, математическая модель, гидродинамика

ВВЕДЕНИЕ

Одним из преимуществ пневматического транспорта, наряду с простотой эксплуатации и высоким уровнем автоматизации процесса, является возможность совместить процесс транспортирования с тепловой и массообменной обработкой сыпучего материала – подсушиванием, разогревом или охлаждением. Так, известны пневмотранспортные сушилки в биотехнологической промышленности, пневмотранспортные теплообменники в производстве цемента. В нефтеперерабатывающей промышленности подобным примером совмещения процесса транспортирования и тепловой обработки материала может служить пневмотранспортная система регенерации катализатора в установках каталитического крекинга. Для решения задачи формования коксовой мелочи также представляется рациональным совместить процесс нагревания частиц кокса с транспортированием в вертикальной трубе.

К сожалению, существующие распространенные методики расчета и моделирования пневматического транспорта оперируют со средним размером частиц дисперсной фазы, не учитывая ее полидисперсность. Когда речь идет о собственно транспортной задаче, подобное упрощение является вполне допустимым и позволяет получать решение с точностью, достаточной для инженерных расчетов. Если же речь идет о моделировании тепло- и массопереноса в полидисперсной системе со значительным разбросом размеров частиц, то очевидно, что результат будет сильно отличаться для частиц разного размера – как в силу различия в коэффициентах тепло- и массопередачи, так и вследствие различного времени пребывания в газовом потоке. Таким образом, встает вопрос разработки модели вертикального пневмотранспорта полидисперсного сыпучего материала.

Все многообразие разработанных к настоящему времени математических моделей различных типов гетерогенных потоков можно условно разбить на два больших класса. Модели первого класса (так называемые эйлерово-лагранжевые, траекторные, стохастические [1–3]) предполагают решение уравнений движения газовой фазы в обычной эйлеровой постановке, в то время как движение частиц описывается лагранжевыми уравнениями, которые интегрируются вдоль их траекторий.

Модели второго класса (эйлерово-эйлеровы, континуальные) описывают движение несущей газовой фазы и движение множества взвешенных частиц, основываясь на эйлеровом континуальном представлении.

Рассмотрим вкратце преимущества и ограничения эйлерово-эйлеровых и эйлерово-лагранжевых моделей описания движения потоков газа с твердыми частицами.

Преимуществом эйлерового подхода является использование похожих уравнений для описания движения газовой и дисперсной фаз. Это позволяет использовать большой опыт моделирования однофазных турбулентных течений и применять одни и те же численные методы решения всей системы уравнений. К недостаткам моделей этого типа можно отнести некоторую “потерю” информации о движении отдельных частиц, а также сложности в постановке граничных условий для дисперсной фазы на ограничивающих течение поверхностях.

Преимуществом лагранжевого подхода является получение детальной статистической информации о движении отдельных частиц в результате интегрирования уравнений движения (теплообмена) частиц в известном (предварительно рассчитанном) поле скоростей (температур) несущего газа.

Однако с увеличением концентрации дисперсной фазы возникают сложности в использовании этих уравнений. Можно выделить два обстоятельства. Во-первых, рост концентрации приводит к обратному влиянию частиц на параметры несущего газа, и расчеты приходится выполнять в несколько итераций, что осложняет вычислительную процедуру. Во-вторых, с увеличением концентрации возрастает вероятность столкновений частиц между собой, что приводит к необходимости вести расчет траекторий всех частиц, находящихся в данном объеме. Последнее обстоятельство приводит к совершенно непомерным требованиям к вычислительным ресурсам, как к объему оперативной памяти, так и к мощности вычислительной системы. Для мелкодисперсных частиц, концентрация которых в газовзвеси может достигать 10⁶–10⁸ м^–3, использование лагранжевых моделей становится абсолютно нереальным.

В силу последнего обстоятельства для построения математической модели пневмотранспорта полидисперсного материала была применена классическая эйлерово-эйлерова модель взаимопроникающих континуумов, дополненная уравнениями межфракционного взаимодействия, учитывающими столкновения частиц различных фракций между собой.

Данная работа посвящена построению математической модели движения полидисперсного материала в вертикальном потоке. Полученные значения параметров движения полидисперсного материала дают возможность перейти к расчетам тепло- и массообменных процессов при пневмотранспорте мелочи нефтяного кокса. Описание процессов массо- и теплообмена выходит за рамки настоящей статьи, полную модель пневмотранспорта с учетом тепломассообменных процессов авторы планируют опубликовать в отдельной работе.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЕРТИКАЛЬНОГО ПНЕВМОТРАНСПОРТА

Взаимопроникающие континуальные среды. При рассмотрении движения одиночных частиц в потоке сплошной среды принималось, что характеристики потока заданы, а частицы в силу их низкой концентрации не оказывают существенного воздействия на эти характеристики. Однако с увеличением концентрации частиц подобное упрощение становится уже невозможным, и приходится учитывать влияние взаимопроникающих фаз друг на друга.

При математическом моделировании многофазных течений для решения инженерных задач наибольшее распространение получила модель взаимопроникающих и взаимодействующих континуумов, изложенная в основополагающей работе Р.И. Нигматулина [4] и получившая развитие в последующих работах [5, 6]. Фазы, составляющие дисперсную смесь, как бы размазываются по объему, занятому смесью, но при этом каждая из них занимает лишь часть этого объема ε_i.

При математическом моделировании движения фаз и их компонентов во взаимопроникающих континуальных средах полагаются на главное допущение – размеры дисперсных частиц или неоднородностей должны быть во много раз меньше расстояний, на которых усредненные параметры фаз и их компонентов меняются существенно, т.е. размеры частиц и неоднородностей много меньше, например, чем диаметры каналов, по которым течет неоднородная среда.

Дифференциальные законы сохранения массы (1) и сохранения импульса (2) дисперсной смеси записываются для физически малого объема отдельно для каждой фазы.

В общем случае они имеют следующий вид:

(1)

$\frac{{\partial \left( {{{\rho }_{i}}{{\varepsilon }_{i}}} \right)}}{{\partial t}} + \nabla \left( {{{\rho }_{i}}{{\varepsilon }_{i}}{{V}_{i}}} \right) - \nabla {{D}_{i}}\nabla \left( {{{\rho }_{i}}{{\varepsilon }_{i}}} \right) - \mathop \sum \limits_{\begin{array}{*{20}{c}} {i = 0} \\ {j \ne i} \end{array}}^N {{J}_{{ji}}} = 0;$

(2)

${{\rho }_{i}}{{\varepsilon }_{i}}\frac{{d{{V}_{i}}}}{{dt}} = {{\rho }_{i}}{{\varepsilon }_{i}}g + \nabla {{F}_{i}} + \mathop \sum \limits_{\begin{array}{*{20}{c}} {i = 0} \\ {j \ne i} \end{array}}^N \left[ {{{R}_{{ji}}} + {{J}_{{ji}}}\left( {{{V}_{i}} - {{V}_{j}}} \right)} \right]\quad,$

где $i,j = 0 \ldots N;\,\,\,\,{{J}_{{ji}}} = - {{J}_{{ij}}};\,\,\,\,\quad{{R}_{{ji}}} = - {{R}_{{ij}}}.$

Индекс 0 всегда будем относить к сплошной фазе, индексы 1…N – к дисперсным фазам (фракциям частиц).

В уравнении сохранения массы (1): первое слагаемое – изменение во времени массы i-й фазы в выделенном объеме; второе слагаемое – перенос массы конвективным потоком; третье слагаемое – изменение массы за счет потока турбулентной диффузии, связанной с мелкомасштабным пульсационным движением фаз; D_i – в общем случае тензор коэффициентов турбулентной диффузии i-й фазы. В четвертом члене J_ji – характеризует поток массы из j-й фазы в i-ю и обратно за счет фазовых переходов. В общем случае перенос массы из одной фазы в другую может происходить не только вследствие физико-химических превращений (испарение, кипение, конденсация и т.п.), но и механическим путем (выпадение частиц на поверхности канала, унос капель с поверхности жидкой пленки и т.д.).

В уравнении переноса импульса (2): первое слагаемое характеризует массовые силы, действующие на i-ю фазу (g_i – вектор массовых сил). Во втором слагаемом F_i – тензор напряжений в i-й фазе.

В качестве условия совместного деформирования фаз используют условие одинаковости давления в фазах: p_i = p, где i = 1…N. В этом случае можно предположить, что поверхностные силы, действующие со стороны окружающей среды на выделенный объем смеси, воспринимаются только сплошной фазой, а воздействие на дисперсную фазу (фазы) со стороны сплошной среды определяется силой взаимодействия.

Тогда для сплошной фазы

В большинстве случаев вязкие напряжения в сплошной фазе пренебрежимо малы по сравнению с силами давления и силами межфазного взаимодействия. Тогда

$\nabla {{F}_{0}} = - {{\varepsilon }_{0}}\left( {\frac{{\partial p}}{{\partial x}}i + \frac{{dp}}{{dy}}j + \frac{{dp}}{{dz}}k} \right).$

Для дисперсных фаз

где σ_i – напряжения в плотном зернистом слое, Н/м²; в разреженных потоках σ_i = 0.

Четвертое слагаемое уравнения (2) описывает интенсивность обмена импульсом между фазами. R_ij – сила межфазного взаимодействия, отнесенная к единице объема смеси (Н/м³), возникающая из-за сил трения, сцепления между фазами. Второй член, стоящий в скобках, можно трактовать как реактивную силу; V_i, V_j – скорости массы, претерпевающей превращение j → i.

Силу межфазного взаимодействия между сплошной и дисперсными фазами можно представить в виде

(3)

${{{\mathbf{R}}}_{{0i}}} = {{\varepsilon }_{i}}{{{\mathbf{f}}}_{{0i}}}{{S}_{i}},$

где f_0i – удельная сила межфазного взаимодействия между частицами и газом, отнесенная к единице поверхности i-й фазы, Н/м²; S_i – удельная поверхность i-й фазы (поверхность фазы, отнесенная к ее объему), м²/м³.

В общем случае сила межфазного взаимодействия может складываться из силы вязкого трения, силы, связанной с воздействием присоединенных масс, силы Бассе, силы Магнуса [4–6] и т.д.:

(4)

$\begin{gathered} \quad{{f}_{{0i}}} = \left( {\frac{3}{{{\text{R}}{{{\text{e}}}_{i}}}}\frac{{4 - 3{{\varepsilon }_{0}}}}{{{{\varepsilon }_{0}}}} + 0.45{{{\left( {{\text{R}}{{{\text{e}}}_{i}}\zeta } \right)}}^{{{{ - 4} \mathord{\left/ {\vphantom {{ - 4} 9}} \right. \kern-0em} 9}}}} + 0.042} \right) \times \\ \times \,\,{{\rho }_{0}}\left( {{{V}_{0}} - {{U}_{i}}} \right)\left| {{{V}_{0}} - {{U}_{i}}} \right|{{\zeta }^{3}}, \\ \end{gathered} $

где

${\text{R}}{{{\text{e}}}_{i}} = \frac{{\left| {{{V}_{0}} - {{U}_{i}}} \right|{{\delta }_{i}}{{\rho }_{0}}}}{{{{\mu }_{0}}}};$

ζ – коэффициент извилистости каналов между частицами. Величина ζ зависит от формы частиц. Для шаров $\zeta \approx {{\varepsilon }_{0}} + 0.5\pi \left( {1 - \varepsilon } \right)$ [6].

Сила межфазного взаимодействия между частицами различных фракций определяется частотой столкновений между частицами [7]. Эта составляющая будет рассмотрена ниже.

Столкновение частиц и обмен импульсом. В восходящем потоке газовзвеси без поперечного сдвига со строго монодисперсными шарообразными частицами столкновений между ними, очевидно, не происходит. Если хотя бы одно из перечисленных условий не выполняется, траектории различных частиц могут пересекаться, что приводит к более или менее интенсивному межчастичному взаимодействию [7]. Крупные монодисперсные частицы, которые слабо увлекаются турбулентными пульсациями, тем не менее, вследствие столкновений приобретают заметное хаотическое движение и также интенсивно взаимодействуют между собой (это явление также называют псевдотурбулентностью [8, 9]). Особое значение взаимодействие частиц приобретает при полидисперсном составе дискретного компонента, поскольку осредненные аксиальные скорости частиц в потоке газовзвеси существенно зависят от их размера [8].

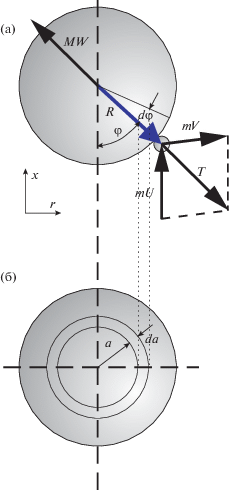
Рассмотрим одномерное движение двухфракционного материала с частицами размером δ_i и δ_j, причем δ_i > δ_j (см. рис. 1).

Рис. 1.

К выводу уравнений сохранения при столкновении двух частиц.

Система координат {x, r} – инерционная, движется равномерно и прямолинейно вдоль оси трубы со скоростью, равной скорости крупной фракции. Ось x – аксиальная, совпадает с осью трубы, ось r – радиальная. В этой системе координат скорости частиц крупной фракции равны нулю, а мелкие частицы набегают на крупные с относительной скоростью u = V₂ – V₁.

В общем случае характер движения частиц после соударения определяется механизмом их деформационного взаимодействия и будет различным для идеально упругих и для пластичных тел. В рассматриваемом случае частицы (коксовая мелочь) при столкновениях ведут себя подобно упругим телам (деформация наблюдается при очень больших скоростях, когда происходит разрушение самой структуры материала).

Уравнения сохранения импульса и кинетической энергии при упругом ударе (см. рис. 1а):

(5)

где $R$ – направляющий вектор единичной длины (b – размерный параметр):

$R = \left| {\begin{array}{*{20}{c}} { - {\text{cos}}\varphi } \\ {{\text{sin}}\varphi } \end{array}} \right|.$

Преобразуем уравнения (5) к виду

$\left\{ {\begin{array}{*{20}{c}} {W = - \frac{b}{M}R} \\ {V = u + \frac{b}{m}R} \\ {\frac{m}{M}{{u}^{2}} = {{W}^{2}} + \frac{m}{M}{{V}^{2}}} \end{array}} \right..$

Из первых двух уравнений сохранения импульса выразим (с учетом того, что u_r = 0)

$\begin{gathered} {{W}^{2}} = \frac{{{{b}^{2}}}}{{{{M}^{2}}}}\left( {R_{x}^{2} + R_{r}^{2}} \right) = \\ = \frac{{{{b}^{2}}}}{{{{M}^{2}}}}\left( {{\text{co}}{{{\text{s}}}^{2}}\varphi + {\text{si}}{{{\text{n}}}^{2}}\varphi } \right) = \frac{{{{b}^{2}}}}{{{{M}^{2}}}}, \\ \end{gathered} $

$\begin{gathered} {{V}^{2}} = {{\left( {{{u}_{x}} - \frac{b}{m}{\text{cos}}\varphi } \right)}^{2}} + {{\left( {\frac{b}{m}{\text{sin}}\varphi } \right)}^{2}} = \\ = u_{x}^{2} - \frac{{2b{{u}_{x}}}}{m}{\text{cos}}\varphi + \frac{{{{b}^{2}}}}{{{{m}^{2}}}} \\ \end{gathered} $

и подставим в третье уравнение системы (5) – уравнение сохранения энергии. Получим

$\frac{m}{M}u_{x}^{2} = \frac{{{{b}^{2}}}}{{{{M}^{2}}}} + \frac{m}{M}\left( {u_{x}^{2} - \frac{{2b{{u}_{x}}}}{m}{\text{cos}}\varphi + \frac{{{{b}^{2}}}}{{{{m}^{2}}}}} \right).$

После преобразования получаем уравнение относительно b:

$0 = {{b}^{2}}\left( {\frac{1}{{{{M}^{2}}}} + \frac{1}{{Mm}}} \right) - \frac{{2b{{u}_{x}}{\text{cos}}\varphi }}{M},$

откуда

$b = \frac{{2m{{u}_{x}}{\text{cos}}\varphi }}{{\left( {1 + \frac{m}{M}} \right)}}.$

Вертикальная и горизонтальная составляющие импульса обмена Т соответственно равны

${{T}_{x}} = - \frac{{2m{{u}_{x}}{\text{co}}{{{\text{s}}}^{2}}\varphi }}{{\left( {1 + \frac{m}{M}} \right)}},$

${{T}_{r}} = \frac{{2m{{u}_{x}}{\text{cos}}\varphi {\text{sin}}\varphi }}{{\left( {1 + \frac{m}{M}} \right)}}.$

Если m $ \ll $ M, то два последних уравнения можно упростить до

${{T}_{x}} = - 2m{{u}_{x}}{\text{co}}{{{\text{s}}}^{2}}\varphi ,$

${{T}_{r}} = 2m{{u}_{x}}{\text{cos}}\varphi {\text{sin}}\varphi .$

Принимая, что точка столкновения равновероятно распределена по площади миделева сечения крупной частицы, находим средневероятное значение для аксиальной и радиальной составляющих импульса, получаемого крупной частицей:

${{T}_{{mx}}} = \frac{{{{T}_{x}}\int\limits_0^R {2\pi ada} }}{{\pi {{R}^{2}}}},$

${{T}_{{mr}}} = \frac{{{{T}_{r}}\int\limits_0^R {2\pi ada} }}{{\pi {{R}^{2}}}},$

где a и da – линейные размеры, показанные на рис. 1б:

$a = R{\text{sin}}\varphi ,\,\,\,\,da = r{\text{cos}}\varphi d\varphi .$

После подстановки a и da в выражения для T_mx и T_mr и интегрирования получим

(6)

${{T}_{{mx}}} = \frac{{m{{u}_{x}}}}{{\left( {1 + \frac{m}{M}} \right)}},$

(7)

${{T}_{{mr}}} = \frac{\pi }{4}\frac{{m{{u}_{x}}}}{{\left( {1 + \frac{m}{M}} \right)}}\quad.$

Если m $ \ll $ M, то (6) и (7) можно упростить до

${{T}_{{mx}}} = m{{u}_{x}},$

${{T}_{{mr}}} = \frac{\pi }{4}m{{u}_{x}}.$

Здесь необходимо заметить, что для моделирования вертикального пневмотранспорта существенна лишь осевая составляющая импульса T_mx. Полученное выражение для T_mr − среднее значение модуля радиальной составляющей импульса. Очевидно, что в ограниченном стенками трубы объеме значение радиальной составляющей импульса T_mr, усредненной по всем частицам, равно нулю, т.е. перемещения частиц в радиальном направлении приводят лишь к усреднению полученного импульса между частицами одной фракции.

Частота соударений частиц. Количество соударений одной крупной частицы фракции i с мелкими частицами фракции j в единицу времени (частота столкновений) определяется соотношением

${{f}_{{cij}}} = {{E}_{{ij}}}\frac{{\pi {{{\left( {{{\delta }_{j}} + {{\delta }_{i}}} \right)}}^{2}}}}{4}\left| u \right|{{N}_{j}},$

где коэффициент Е_ij учитывает возможность искривления траекторий мелких частиц, увлекаемых потоком сплошной среды. Согласно работе [7], в общем случае Е зависит от числа Стокса Stk – критерия подобия, используемого в гидродинамике взвесей, который определяет соотношение между силами инерции частиц и силами вязкого трения в сплошной среде:

${\text{Stk}} = \frac{{\rho \delta _{j}^{2}u}}{{\mu {{\delta }_{i}}}}.$

Для потенциального обтекания (Re → ∞)

$E = {{\left[ {\frac{{{\text{Stk}}}}{{{\text{Stk}} + 0.25}}} \right]}^{2}}\,\,\,\,\left( {{\text{Stk}} > 0.04} \right).$

Для вязкого обтекания (Re $ \ll $ 1)

$E = {{\left[ {1 + 0.75\frac{{{ln\;}\left( {4{\text{Stk}}} \right)}}{{2{\text{Stk}} - 1.214}}} \right]}^{{ - 2}}}.$

При низких значениях Е редко достигается непосредственный контакт между частицами. При этом одни частицы влияют на движение других через сплошную среду. Это явление существенно для потоков с очень мелкими частицами.

Учет коэффициента Е важен при моделировании процессов, которые зависят от непосредственного контакта между частицами – таких как агломерация или коагуляция частиц и пр. Для моделирования же движения частиц дисперсной фазы, в общем, не играет роли, каким образом при их столкновениях происходит обмен импульсом – при непосредственном контакте или через газовую прослойку между ними. Поэтому в дальнейшем рассмотрении будем предполагать, что Е = 1.

Интервал между соударениями частиц фракции j с частицей фракции i

(8)

${{t}_{{mij}}} = \frac{1}{{{{f}_{{cij}}}}} = \frac{4}{{\pi {{{\left( {{{\delta }_{j}} + {{\delta }_{i}}} \right)}}^{2}}u{{N}_{j}}}}\quad.$

Удельная сила взаимодействия между фракциями. Сила, действующая на частицу i-го сорта, вызванная бомбардировкой мелкими частицами j-й фракции равна

${{F}_{{ji}}} = {{m}_{j}}\frac{{\pi {{{\left( {{{\delta }_{j}} + {{\delta }_{i}}} \right)}}^{2}}}}{{4\left( {1 + \frac{{{{m}_{j}}}}{{{{m}_{i}}}}} \right)}}{{\left| u \right|}^{2}}{{N}_{j}}.$

Здесь |u| – модуль относительной скорости частиц различных фракций.

Удельная сила взаимодействия между i-й и j-й фракциями равна

${{R}_{{ij}}} = {{m}_{j}}{{E}_{{ij}}}\frac{{\pi {{{\left( {{{\delta }_{j}} + {{\delta }_{i}}} \right)}}^{2}}}}{{4\left( {1 + \frac{{{{m}_{j}}}}{{{{m}_{i}}}}} \right)}}{{\left| u \right|}^{2}}{{N}_{j}}{{N}_{i}}.$

Счетная концентрация частиц i-й фракции равна

${{N}_{i}} = \frac{{6{{c}_{i}}{{M}_{{\text{s}}}}}}{{\pi \delta _{i}^{3}\rho }} = \frac{{6{{\varepsilon }_{i}}}}{{\pi \delta _{i}^{3}}}.$

Таким образом, удельную силу взаимодействия между фракциями можно выразить как

(9)

${{R}_{{ij}}} = \frac{{{{m}_{j}}{{m}_{i}}}}{{{{m}_{j}} + {{m}_{i}}}}\frac{{\pi {{{\left( {{{\delta }_{j}} + {{\delta }_{i}}} \right)}}^{2}}}}{4}{{\left| u \right|}^{2}}\frac{{6{{\varepsilon }_{j}}}}{{\pi \delta _{j}^{3}}}\frac{{6{{\varepsilon }_{i}}}}{{\pi \delta _{i}^{3}}}\quad.$

С учетом того, что m_jN_j = c_jM_s,

(10)

${{R}_{{ij}}} = {{E}_{{ij}}}\frac{{6{{{\left( {{{\delta }_{j}} + {{\delta }_{i}}} \right)}}^{2}}}}{{4\delta _{i}^{3}\left( {1 + \frac{{{{m}_{j}}}}{{{{m}_{i}}}}} \right)}}{{\left| U \right|}^{2}}{{c}_{j}}{{M}_{{\text{s}}}}.$

Для анализа переходных процессов введем понятие времени динамической релаксации частиц. Данную характеристику обозначим t_rl и представим в виде

(11)

${{t}_{{rl}}} = \frac{{{{\rho }_{i}}\delta _{i}^{2}}}{{18{{\mu }_{0}}}}.$

Время релаксации является характеристикой инерционности частицы и служит для оценки значимости переходных процессов. Как показали дальнейшие расчеты, для частиц коксовой мелочи характерные значения времени релаксации оказались довольно малы (10^–2–10^–6 с), тогда как среднее время пребывания дисперсной фазы в аппарате составило 0.5–5.0 с. Это позволяет принять следующие допущения:

1) поток газовзвеси считаем стационарным и установившимся, т.е. производными по времени в уравнениях (1) и (2) можно пренебречь;

2) характерное время процессов межфазного переноса (испарение влаги, выгорание летучих и т.п.) намного больше времени релаксации частиц, соответственно, можно пренебречь последними слагаемыми в уравнениях (1) и (2).

Разумеется, при испарении влаги из частиц кокса и охлаждении потока меняется плотность газа, его объемный расход и, соответственно, скорость. Но все эти изменения влияют на движение частиц опосредованно, через изменения параметров по высоте трубы, в каждом же сечении в каждый момент времени полагаем параметры неизменными и движение стационарным и установившимся.

Тогда, с учетом вышесказанного, движение многофазного вертикального потока можно описать следующей системой уравнений (индекс 0 относится к сплошной фазе – газу, индексы 1…N – к фракциям коксовых частиц):

В уравнениях (12)–(17) i = 1…N.

Если просуммировать уравнение (12) и уравнение (13) для всех i = 1…N, то с учетом зависимости (17) получим уравнение для расчета градиента давления в вертикальном потоке:

(18)

$\frac{{dp}}{{dx}} = - \left( {{{\rho }_{0}}{{\varepsilon }_{0}} + \mathop \sum \limits_{i = 1}^N {{\rho }_{i}}{{\varepsilon }_{i}}} \right)g - \left( {{grad\;}{{p}_{w}}} \right)\quad.$

Здесь ${grad\;}{{p}_{w}}\quad$ – потери на гидравлическое трение о стенки трубы при движении двухфазного полидисперсного потока, которые можно выразить через касательные напряжения на стенке трубы:

(19)

${grad\;}{{p}_{w}} = \left( {{{\tau }_{{w0}}} + \mathop \sum \limits_{I = 1}^N {{\tau }_{{wi}}}} \right)\frac{4}{d}\quad,$

где τ_w0 и τ_wi – касательные напряжения на стенке для сплошной и дисперсных фаз.

Одной из наиболее употребительных формул расчета удельных потерь давления является формула Гастерштадта [5, 6], которая для полидисперсного потока имеет следующий вид:

$\left( {{{\tau }_{0}} + \mathop \sum \limits_{i = 1}^N {{\tau }_{i}}} \right) = {{\tau }_{0}}\left( {1 + \mathop \sum \limits_{i = 1}^N {{c}_{i}}{{M}_{m}}{{K}_{i}}} \right).$

Здесь τ₀ – касательные напряжения на стенке трубы при движении чистого газа; K_i – коэффициент Гастерштадта, равный отношению λ_i/λ₀; λ₀ – коэффициент гидравлического трения чистого газа для гидравлически гладкой трубы; λ_i – коэффициент сопротивления для частиц; c_i – массовая доля i-й фракции; M_m – расходная концентрация, кг/кг.

Касательные напряжения на стенке трубы при движении чистого газа

${{\tau }_{0}} = {{\lambda }_{0}}\frac{{{{\rho }_{0}}V_{0}^{2}}}{8},$

где

${{\lambda }_{0}} = \frac{{0.316}}{{{\text{Re}}_{0}^{{0.25}}}},$

${\text{R}}{{{\text{e}}}_{0}} = \frac{{{{V}_{0}}d{{\rho }_{0}}}}{{{{\mu }_{0}}}}.$

Для вертикальных потоков коэффициент λ_i может быть найден из полуэмпирической зависимости

${{\lambda }_{i}} = 5.5{{\left( {1 - \frac{{{{\delta }_{i}}}}{d}} \right)}^{2}}\frac{1}{{{\text{Fr}}_{i}^{{0.65}}}},$

где критерий Фруда для частиц

${\text{F}}{{{\text{r}}}_{i}} = \frac{{U_{i}^{2}}}{{{{\delta }_{i}}g}}.$

Результаты численного решения модели пневматического вертикального транспорта полидисперсного сыпучего материала приведены далее.

ГИДРОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ ЗАДАЧИ О НАГРЕВАНИИ КОКСОВОЙ МЕЛОЧИ В ПОТОКЕ ДЫМОВЫХ ГАЗОВ

В качестве примера решения задачи вертикального пневмотранспорта полидисперсного сыпучего материала рассмотрим реальный случай нагревания отходов (мелочи) нефтяного кокса при подготовке их к формованию с целью утилизации. Коксовая мелочь нагревается смесью дымовых газов, отходящих из секции дожига печи прокалки товарного нефтяного кокса с температурой 1100–1300°С, и газов из котла-утилизатора с температурой 300°С. В зависимости от соотношения указанных газовых потоков температура газовой смеси может изменяться в пределах от 500 до 800°С.

Исходные данные для решения задачи были следующими. Массовый расход коксовой мелочи 10 т/ч = 2.778 кг/с. Массовый расход дымовых газов 101 940 кг/ч = 28.32 кг/с. Свойства дымовых газов при температурах 500–800°С принимали по данным справочников [10, 11]. Истинная плотность сырого нефтяного кокса 2090–2100 кг/м³. Влажность сырого нефтяного кокса 3–10%. Теплоемкость сырого нефтяного кокса в кДж/(кг К):

$С = 1.005 + 1.16 \times {{10}^{{--3}}}t + 8.6 \times {{10}^{{--7}}}{{t}^{2}},$

где t – температура, °С. Теплопроводность сырого нефтяного кокса: при температуре 200°С 0.212 Вт/(м К), при температуре 300°С 0.245 Вт/ (м К), при температуре 400°С 0.267 Вт/(м К). Начальная температура коксовой мелочи 20°С. Коксовую мелочь требуется нагреть до 350–400°С. Температура дымовых газов (после смешения с охлажденными газами, отходящими из котла-утилизатора) 500–800°С (в принципе, можно выбрать любую температуру в пределах от 500 до 800°С).

В табл. 1 приведены сведения о фракционном составе коксовой мелочи и ее аэродинамических характеристиках.

Таблица 1.

Фракционный состав коксовой мелочи и ее аэродинамические характеристики

Фракционный состав коксовой мелочи
δ, мм	0–0.16	0.16–0.50	0.50–1.0	1–3	3–5	5–8
c_i, мас. %	12.50	17.30	16.90	45.90	3.60	3.80
δ_m, мм	0.08	0.33	0.75	2	4	6.5
ρ, кг/м³	1810	1810	1810	1500	1350	1350
Аэродинамические характеристики
Ar	3.42	2.40 × 10²	2.81 × 10³	4.42 × 10⁴	3.18 × 10⁵	1.37 × 10⁶
Re	0.18	8.79	56.5	306.8	893	1900
V_vt, м/с	0.17	2.03	5.75	11.70	17.04	22.30
t_rl, с	4.66 × 10^–6	7.93 × 10^–5	4.10 × 10^–4	2.91 × 10^–3	1.16 × 10^–2	3.08 × 10^–2

Скорость витания частиц

${{V}_{{vt}}} = \frac{{\mu {\text{Re}}}}{{\delta {{\rho }_{0}}}},$

где $\quad{\text{Re}} = \frac{{{\text{Ar}}}}{{18 + 0.6\sqrt {{\text{Ar}}} }},$ ${\text{Ar}} = \frac{{g{{\delta }^{3}}}}{{{{\mu }^{2}}}}\Delta \rho {{\rho }_{0}}.$

Для самой крупной частицы (8 мм) ${{V}_{{vt}}}$ = 24.9 м/с.

Материальный и тепловой баланс. Расход газа определяем из теплового баланса нагревания коксовых частиц. Зададимся температурой дымовых газов на входе в пневмотранспортную трубу T_0.in = 750°С и на выходе из нее T_0.fin = 450°С. Примем начальную температуру кокса T_с.in = 20°С, конечную T_с.fin = 400°С. Теплоемкость сырого нефтяного кокса составляет 1.13 кДж/(кг К), влажность равна 10 мас. %. Массовый расход коксовой мелочи G = 2.778 кг/с. Скрытая теплота испарения Н_e = 2256 кДж/кг. Теплота на испарение влаги Q_e = 626.7 кВт. Теплота на нагревание кокса Q_h = 1192.8 кВт. Общие затраты теплоты в единицу времени Q_s = 1819.4 кВт. Требуемый массовый расход топочного газа G₀ = 5.096 кг/с = 18347 кг/ч. Требуемый объемный расход топочного газа ${{v}_{0}}$ = = 40147 м³/ч = 669 м³/мин = 11.2 м³/c.

Следует отметить, что решение задачи тепло- и массообмена между частицами и газом выходит за рамки настоящей статьи. Поэтому в первом приближении изменение температуры газа по высоте трубы предполагали изменяющимся по линейному закону, температуры газа на входе и выходе задавали, исходя из решения теплового баланса процесса. Свойства газа (плотность и вязкость) рассчитывали на каждом шаге, в соответствии с температурой в данном сечении. Также, с учетом того, что начальная влажность относительно невелика, изменением массы частиц в процессе сушки пренебрегали.

РЕШЕНИЕ ЗАДАЧИ ВЕРТИКАЛЬНОГО ПНЕВМОТРАНСПОРТА ПОЛИДИСПЕРСНОГО МАТЕРИАЛА

Система уравнений модели пневматического вертикального транспорта полидисперсного сыпучего материала (12)–(17) носит ярко выраженный нелинейный характер, поэтому ее решение проводилось численными методами.

В качестве исходных данных задавались: дисперсный состав частиц материала, в том числе и их свойства (плотность, теплоемкость, теплопроводность); свойства газа, приведенные к входным условиям; массовые расходы газа и материала; диаметр и высота трубы.

Также задавалась требуемая точность вычислений e = 10^–6 как условие завершения итерационного процесса.

Алгоритм разрешения уравнений (12)–(17) следующий.

1. На первом шаге после ввода исходных данных рассчитывались аэродинамические характеристики частиц – скорости витания и времена релаксации для каждой фракции. Найденные скорости витания принимались в качестве первого приближения для скоростей частиц относительно несущего потока.

2. Объемные доли каждой фракции в потоке определялись как

${{\varepsilon }_{i}} = \frac{{{{G}_{i}}{{c}_{i}}}}{{{{U}_{i}}{{\rho }_{i}}}}\frac{4}{{\pi {{d}^{2}}}}.$

3. Уточнялась истинная скорость газа

${{V}_{0}} = \frac{{{{G}_{0}}}}{{{{\rho }_{0}}\left( {1 - \sum {{\varepsilon }_{i}}} \right)}}\frac{4}{{\pi {{d}^{2}}}}.$

4. По уравнениям (13)–(15) рассчитывались удельная сила межфазного взаимодействия между частицами каждой фракции и газом f_0i, а также удельная сила взаимодействия между фракциями R_ij.

5. По уравнениям (18)–(19) рассчитывался градиент давления в газе.

6. Рассчитывались невязки ΔW₀ и ΔW_i правых частей уравнений (12) и (13) как

$\Delta {{W}_{0}} = - {{\rho }_{0}}{{\varepsilon }_{0}}g - {{\varepsilon }_{0}}\frac{{dP}}{{dx}} - \mathop \sum \limits_{i = 1}^N {{f}_{{0i}}}{{\varepsilon }_{i}}{{S}_{i}} - \left( {{{\tau }_{{w0}}}\frac{4}{d}} \right),$

$\Delta {{W}_{i}} = - {{\rho }_{i}}{{\varepsilon }_{i}}g - {{\varepsilon }_{i}}\frac{{dP}}{{dx}} + {{f}_{{0i}}}{{\varepsilon }_{i}}{{S}_{i}} + \mathop \sum \limits_{\begin{array}{*{20}{c}} {j = 1} \\ {j \ne i} \end{array}}^N {{R}_{{ij}}} - \left( {{{\tau }_{{wi}}}\frac{4}{d}} \right).$

7. Находились скорости частиц каждой фракции как

$U_{i}^{{iter + 1}} = U_{i}^{{iter}} + \omega \Delta {{W}_{i}},$

где ω – параметр релаксации итерационной процедуры, который принимался равным ω = 0.002–0.01.

8. Если не выполнялось хотя бы одно из условий: (ΔW₀ < e) или (ΔW_i < e), то совершалась следующая итерация с возвратом на шаг № 2.

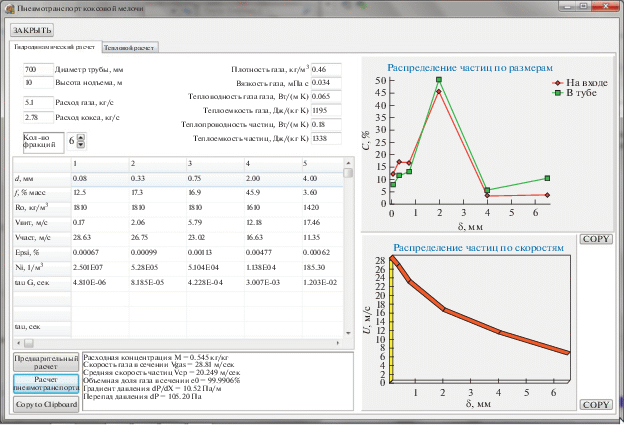
Для проведения расчетов по приведенному алгоритму была разработана программа на языке Delphi. Скриншот главного окна программы приведен на рис. 2. Результаты численного решения приведены в сводной табл. 2.

Рис. 2.

Главное окно программы расчета вертикального пневмотранспорта полидисперсного материала.

Таблица 2.

Сводная таблица результатов решения системы уравнений (12)–(17)

Характеристики			Номер фракции
Характеристики			1	2	3	4	5	6
Диаметр частиц		δ, мм	0.08	0.33	0.75	2	4	6.5
Фракционный состав		f, мас. %	12.5	17.3	16.9	45.9	3.6	3.8
Плотность частиц		ρ_o, кг/м³	1810	1810	1810	1610	1420	1350
Время релаксации		τ_rl, с	4.81 × 10^–6	8.19 × 10^–5	4.23 × 10^–4	3.01 × 10^–3	1.20 × 10^–2	3.18 × 10^–2
Удельная сила взаимодействия между фракциями	f_j, Н/м³	1	0.0000	–0.003	–0.0105	–0.0676	–0.0088	–0.0167
		2	0.0030	0.0000	–0.0107	–0.0888	–0.0116	–0.0222
		3	0.0105	0.0107	0.0000	–0.0532	–0.0091	–0.0189
		4	0.0676	0.0888	0.0532	0.0000	–0.0098	–0.0353
		5	0.0088	0.0116	0.0091	0.0098	0.0000	–0.0012
		6	0.0167	0.0222	0.0189	0.0353	0.0012	0.0000
Силы межфракционного взаимодействия при столкновении частиц		R_ij, Н/м³	–0.107	–0.130	–0.0599	0.1645	0.0381	0.0942
Межфазная сила		R_i0, Н/м³	0.1189	0.1894	0.2317	0.8324	0.0870	0.1477
Объемная доля		ε_i	0.0007	0.001	0.00113	0.00482	0.00062	0.00119
Скорость частиц		U, м/с	28.55	26.59	22.92	16.45	11.33	6.55

Главным итогом численного решения поставленной задачи явились найденные параметры пневмотранспорта коксовой мелочи:

расходная концентрация М = 0.545 кг/кг;

скорость газа в сечении V₀ = 28.81 м/с;

средняя скорость частиц V_m = 20.25 м/с;

объемная доля газа в сечении ε₀ = 99.99%;

градиент давления dp/dx = 10.52 Па/м;

перепад давления dp = 105.20 Па.

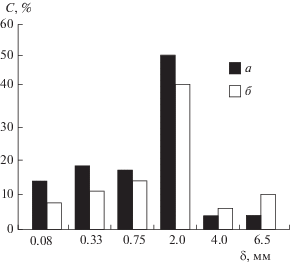
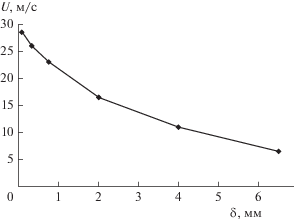
Фракционное распределение частиц по размерам на входе в трубу и в самой трубе показано на рис. 3. Распределение частиц по скоростям приведено на рис. 4.

Рис. 3.

Фракционное распределение частиц по размерам: а – на входе в трубу; б – в самой трубе.

Рис. 4.

Распределение частиц по скоростям.

Следует отметить, что рассчитанные значения времени релаксации для частиц оказались довольно малы, следовательно, область установившегося движения можно распространить на всю высоту пневмотранспортной трубы. Данный вывод справедлив в случае, если параметры газового потока являются неизменными (т.е. изменениями температуры и состава газа вследствие тепло- и массообмена с частицами пренебрегаем).

ЗАКЛЮЧЕНИЕ

Анализируя результаты расчетов, приведенные в табл. 2, можно сделать следующие выводы.

Вследствие различной скорости движения частиц разного размера, наблюдаемый фракционный состав материала в пневмотранспортной трубе отличается от заданного на входе (см. рис. 3) – относительное содержание крупных частиц увеличивается (крупные частицы дольше задерживаются в трубе), а относительное содержание мелких частиц уменьшается (мелкие частицы быстрее вылетают).

Столкновение между частицами различных фракций оказывает очень существенное влияние на движение отдельных фракций дисперсного материала. Как видно из табл. 2, силы межфракционного взаимодействия, обусловленные столкновением частиц (R_ij), по численному значению вполне соизмеримы с силами межфазного взаимодействия с газом (R_i0).

Для частиц мелких фракций столкновение с крупными частицами оказывает тормозящее действие (удельная сила R_ij имеет отрицательное значение), в то время как для крупных частиц сила R_ij по знаку совпадает с силами межфазного взаимодействия с газом (R_i0), т.е. крупные частицы “подгоняются” мелкими. В целом это приводит к уменьшению разброса между скоростями движения частиц.

Если просуммировать строку с силами межфракционного взаимодействия, то можно убедиться, что ΣR_ij = 0, т.е. межчастичные столкновения не влияют на движение всего материала в целом, приводя лишь к перераспределению кинетической энергии между отдельными фракциями.

Полученные значения параметров движения полидисперсного материала позволяют перейти к расчетам тепло- и массообменных процессов при пневмотранспорте коксовой мелочи.

ОБОЗНАЧЕНИЯ

a	линейный размер, м
b	размерный параметр, связывающий величину вектора импульса T и вектора R
c	массовая доля фракции
D	коэффициент турбулентной диффузии, м²/с
d	диаметр трубы, м
E	коэффициент, учитывающий возможность искривления траектории мелких частиц
e	требуемая точность вычислений
F	тензор напряжений, Па
f	удельная сила межфазного взаимодействия, Н/м²
G	массовый расход, кг/с
g	ускорение свободного падения, м/с²
H	теплота испарения, кДж/кг
i, j, k	единичные векторы по осям координат
K	коэффициент Гастерштадта
M	расходная концентрация, кг/кг; общая массовая концентрация дисперсной фазы, кг/м³; масса частицы крупной фракции, кг
m	масса частицы мелкой фракции, кг
N	номер фракции; счетная концентрация частиц фракции, 1/м³
p	давление, Па
Q	поток теплоты, кВт
R	направляющий единичный вектор, соединяющий центры частиц (направление обмена импульсом); сила межфазного взаимодействия, Н
r	радиальная координата, м
S	удельная поверхность фазы, м²/м³
T	импульс, которым обмениваются частицы, (кг м)/с
t	время, с; температура, °С
U	истинная скорость частицы, м/с
u	относительная скорость фаз, м/с
V	скорость, м/с
V, W	векторы скоростей частиц после столкновения, м/с
$v$	объемный расход, м³/с
x	осевая координата
Δ	невязка левой и правой частей уравнения
δ	размер частицы, м
ε	объемная доля фракции
λ	коэффициент гидравлического сопротивления, гидравлического трения
μ	динамическая вязкость, Па с
ζ	коэффициент извилистости каналов между частицами
ρ	плотность, кг/м³
σ	нормальные напряжения, Па
τ	касательные напряжения, Па
φ	угол наклона вектора T к вертикали
ω	параметр релаксации итерационной процедуры
Ar	число Архимеда
Fr	число Фруда
Re	число Рейнольдса
Stk	число Стокса

ИНДЕКСЫ

0	сплошная фаза
1	крупная дисперсная фаза
2	мелкая дисперсная фаза
c	кокс
e	испарение
fin	конечный
h	нагрев
i, j	номера фракций
in	начальный
m	средний
r	радиальная проекция вектора на оси координат
rl	релаксация
s	суммарный
vt	витание
w	стенка
x	осевая проекция вектора на оси координат

Список литературы

Ivanenko A.Yu., Yablokova M.A., Petrov S.I. Simulation of the separation of emulsified oil products from water in an apparatus with sinusoidal-profiled oleophilic plates // Theor. Found. Chem. Eng. 2010. V. 44. № 5. P. 729. [Иваненко А.Ю., Яблокова М.А., Петров С.И. Моделирование процесса выделения эмульгированных нефтепродуктов из воды в аппарате с олеофильными пластинами синусоидального профиля // Теорет. основы хим. технологии. 2010. Т. 44. № 5. С. 588.]
Senior R.C., Grace R.C. Integrated particle collision and turbulent diffusion model for dilute gas-solid suspensions // Powder Technology. 1998. V. 96. P. 48.
Huber N., Sommerfeld M. Modelling and numerical calculation of dilute-phase pneumatic conveying in pipe systems // Powder Technology. 1998. V. 99. P. 90.
Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987.
Новый справочник химика и технолога. Т. 6. Процессы и аппараты химических технологий. Ч. I / Под ред. Островского Г.М. СПб.: Профессионал, 2004.
Островский Г.М. Прикладная механика неоднородных сред. СПб.: Наука, 2000.
Вараксин А.Ю. Столкновения в потоках газа с твердыми частицами. М.: Физматлит, 2008.
Шрайбер А.А., Милютин В.Н., Яценко В.П. Гидромеханика двухкомпонентных потоков с твердым полидисперсным веществом. Киев: Наукова думка, 1980.
Eskin D., Leonenko Y., Vinogradov O. An engineering model of dilute polydisperse pneumatic conveying // Chem. Eng. Process. 2007. V. 46. P. 247.
Михеев М.А., Михеева И.М. Основы теплопередачи. М.: Энергия, 1977.
Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал