Теоретические основы химической технологии, 2019, T. 53, № 3, стр. 267-275
Моделирование процесса сорбции при очистке сточных вод от нефтепродуктов и тяжелых металлов
Е. С. Дремичева 1, *, А. Г. Лаптев 1
1 Казанский государственный энергетический университет
Казань, Россия
* E-mail: lenysha@mail.ru
Поступила в редакцию 18.10.2017
После доработки 24.10.2018
Принята к публикации 01.11.2018
Аннотация
Адсорбция в неподвижном слое широко применяется для очистки жидких смесей, в том числе промышленных сточных вод. В статье проведено моделирование адсорбционной очистки сточных вод от нефтепродуктов и тяжелых металлов при помощи торфа. Построена модель процесса, учитывающая продольное перемешивание жидкофазного потока, внешне- и внутридиффузионное сопротивление потока в гранулах сорбента, явления адсорбции на поверхности торфа. Представлены результаты экспериментальных исследований. Выявлен и объяснен эффект аномальной диффузии ионов тяжелых металлов в торфе. На основании проведенных исследований построены изотерма адсорбции нефтепродуктов из сточных вод, изменение коэффициента массопередачи от величины адсорбции. Экспериментально определено влияние на скорость ионного обмена химической кинетики. Обработка экспериментальных кривых поглощения ионов тяжелых металлов выполнена с применением уравнений диффузионной и химической кинетики. Сделаны выводы по полученным результатам.
ВВЕДЕНИЕ
Известно, что примесями, присутствующими в природных источниках водозабора промышленных предприятий и электростанций и оказывающими наиболее существенное влияние на работу оборудования, являются нефтепродукты и ионы тяжелых металлов (Fe3+, Cr6+, Cu2+ и Al3+). Растворенные и нерастворенные в воде нефтепродукты ухудшают работу механических фильтров в связи с образованием на внешней поверхности частиц масляной пленки. Это повышает нагрузку на фильтры, уменьшает время их полезной работы и создает дополнительные трудности при регенерации фильтрующего материала, так как удаление нефтепродуктов требует пропарки фильтров или промывки их горячей водой. Тяжелые металлы затрудняют работу ионообменных фильтров, предназначенных для удаления из воды катионов и анионов природного происхождения.
Одним из способов очистки как природных, так и сточных вод является метод сорбции. Этот метод характеризуется высокой степенью очистки, эксплуатационной надежностью, относительной простотой аппаратурного оформления и применяется, как правило, на завершающих стадиях очистки, обеспечивая глубокое, вплоть до следовых количеств, удаление примесей.
Свидетельством практической востребованности этого метода является стремительное развитие рынка промышленных сорбентов. За последнее время ассортимент продаваемых сорбентов вырос с 25 до более 200 наименований. Такой широкий спектр разнообразных по природе и качеству сорбентов свидетельствует с одной стороны о сложности адаптированного подбора сорбента, а с другой стороны позволяет производить индивидуальный его выбор в зависимости от природы удаляемых примесей, источника очищаемых вод, местных природных условий и возможностей предприятия в плане регенерации или утилизации отработанного сорбента [1, 2].
Целью данной работы является физическое моделирование процесса сорбции нефтепродуктов и ионов тяжелых металлов из водных растворов на природном материале.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Одной из важнейших эксплуатационных характеристик сорбентов является их селективность, поэтому одновременная очистка воды от нескольких различных по своей природе примесей одним и тем же сорбентом затруднительна. Перспективным направлением исследований в этой научной области может быть создание сорбционных композиций определенного состава, позволяющих удалять из воды различные по своей природе техногенные примеси. Подбор состава данных сорбентов производится на основании физического и математического моделирования процесса сорбции [3–5].
Комплексная очистка воды от нефтепродуктов и ионизированных примесей при помощи сорбционных композиций совмещает процессы хемосорбции и физической адсорбции нефтепродуктов.
Оба процесса являются сложными и многостадийными, поэтому их математическое описание выполнялось при условии отсутствия взаимного влияния этих процессов.
Предполагается равномерное распределение зерен сорбента для исключения пристеночных эффектов. Известно, что если диаметр аппарата на порядок больше диаметра зерен сорбента, влияние пристеночных эффектов незначительно. Поэтому рассмотрена одномерная задача адсорбции.
Физическая сорбция
Динамика процесса физической адсорбции описывается известной системой из трех уравнений: балансом адсорбированного вещества между твердой и жидкой фазами, кинетикой процесса переноса примеси из потока жидкости внутрь зерен адсорбента и изотермой адсорбции [6]:
(1)
$\frac{{\partial C}}{{\partial \tau }} + w\frac{{\partial C}}{{\partial x}} + \frac{{\partial y}}{{\partial \tau }}\frac{{1 - \varepsilon }}{\varepsilon } - D{\text{*}}\frac{{{{\partial }^{2}}C}}{{\partial {{x}^{2}}}} = 0,$Уравнение (1) – это уравнение конвективной диффузии с источниковым членом, которое описывает изменение концентрации в движущейся жидкой фазе (концентрация С изменяется как по координате x, вдоль которой движется жидкость, так и во времени τ). Первое слагаемое левой части уравнения выражает изменение концентрации C в точке фазы с координатой x во времени, второе слагаемое выражает изменение концентрации в этой точке фазы вследствие движения фазы, имеющей неоднородное концентрационное поле, третье слагаемое описывает массообмен между твердой и жидкой фазами (источниковый член уравнения конвективной диффузии, который при адсорбции отрицателен), а четвертое слагаемое – продольную диффузию.
Процесс одномерного перемещения вещества внутри твердого тела может быть описан дифференциальным уравнением массопроводности:
Коэффициент стесненной диффузии, или массопроводности, k не является постоянной величиной [7, 8].
Для выражения отношения интенсивности переноса вещества в ядре омывающей фазы к интенсивности переноса в твердом материале, где массообмен связан с массопроводностью, используют диффузионный критерий Био, а для изменения скорости потока вещества, перемещаемого массопроводностью в твердом теле, – диффузионный критерий Фурье.
Таким образом, для одномерного перемещения вещества по толщине зерна сорбента дифференциальное уравнение массопроводности имеет аналитическое решение в виде
(5)
${{\left( {y - {{y}_{е }}} \right)} \mathord{\left/ {\vphantom {{\left( {y - {{y}_{е }}} \right)} {\left( {{{у }_{0}} - {{у }_{е }}} \right)}}} \right. \kern-0em} {\left( {{{у }_{0}} - {{у }_{е }}} \right)}} = f\left( {Bi{\text{'}},Fo{\text{'}},{x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0em} \delta }} \right),$Ионный обмен
Реальные процессы ионного обмена в действительности представляют собой сложный многостадийный процесс, протекающий в гетерогенной системе твердая фаза сорбента – жидкий раствор, содержащий поглощаемое сорбентом вещество. Основным процессом, определяющим суммарную скорость ионообменного процесса, является диффузионный перенос целевого компонента внутри частиц смолы, в идеализированном случае считается, что конвективный перенос между основным потоком раствора и поверхностью гранул сорбента отсутствует.
Кинетика ионного обмена с учетом многостадийности и гетерогенности процесса, в идеализированном случае соответствует градиентному уравнению диффузионного типа [10, 11]:
(6)
${{\vec {j}}_{i}} = {{D}_{i}}\left( {1 + \frac{{d\ln {{\gamma }_{i}}}}{{d\ln {{C}_{i}}}}} \right)\left( {\operatorname{grad} {{C}_{i}} + \frac{{{{Z}_{i}}{{C}_{i}}F}}{{RT}}\operatorname{grad} \varphi } \right),$которое должно рассматриваться совместно с уравнениями сохранения массы компонента
и электрического заряда (для квазистационарного случая)
(8)
${\text{div}}\left( {{\text{grad}}\varphi } \right) = - {{4\pi {{\rho }_{{el}}}} \mathord{\left/ {\vphantom {{4\pi {{\rho }_{{el}}}} {{{\sigma }_{{el}}}}}} \right. \kern-0em} {{{\sigma }_{{el}}}}}.$Влияние на скорость ионного обмена химической кинетики определяется экспериментально. Многочисленные исследования различных авторов показали, что скорость ионного обмена определяется скоростью переноса массы, что позволяет считать ионообменные процессы аналогичными процессами адсорбции [11].
Для численного решения данных уравнений и нахождения неизвестных характеристик проведено два параллельных эксперимента по исследованию сорбционных свойств различных видов торфа из месторождений Татарстана, который предлагается использовать при разработке сорбционных композиций, по отношению к нефти и нефтепродуктам и тяжелым металлам [12, 13].
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Сорбция нефти и нефтепродуктов
Известно [14, 15], что природный торф обладает сорбционными свойствами по отношению к нефтепродуктам. Также торф обладает свойствами ионообменника, которые можно усилить путем химической обработки, удалив содержащуюся воду и водорастворимые примеси из природного торфа, снижающие его сорбционную емкость [16]. Таким образом, рациональным решением проблемы глубокой очистки сточных вод, содержащих нефтепродукты и тяжелые металлы, является использование торфа. Достоинством торфа как сорбента является дешевизна, доступность и возможность утилизации отработанного материала путем сжигания, что позволяет частично решить проблему надвигающегося энергетического кризиса.
Кроме того, использование одного и того же сорбента для очистки и нефтесодержащих сточных вод, и вод, содержащих тяжелые металлы, позволяет создать единую ресурсосберегающую систему его использования и утилизации.
Скорость достижения равновесия при сорбции, а также сорбционная емкость являются важнейшими характеристиками любого поглотителя и имеют как практическое, так и теоретическое значение. Из кинетической зависимости можно определить время, необходимое для установления равновесия в системе “сорбент–жидкая фазаˮ. Эта характеристика позволяет оценить возможность и целесообразность применения сорбента для решения практических задач.
Эксперимент проводился на модельной водонефтяной эмульсии. Для ее создания бралась вода и турбинное масло ТП-22С плотностью 0.9 г/см3. Концентрация турбинного масла в эмульсии составила 2 мг/дм3. Для проведения эксперимента в динамических условиях были приготовлены насыпные фильтры, представляющие собой колонку высотой 250 мм и диаметром 50 мм, наполненные торфом с размером гранул 0.5–1.0 мм и насыпной плотностью 0.505 г/см3. Высота плотно заполняющего колонку сорбента составляет 200 мм. Для пропускания через фильтр модельный раствор с тщательно перемешанной эмульсией при температуре 25°С отбирался в количестве 200 мл. Скорость пропуска раствора составила 2 мл/мин.
Определение содержания нефтепродуктов проводилось в соответствии со стандартной методикой. Метод заключается в экстракции эмульгированных и растворенных нефтепродуктов из воды четыреххлористым углеродом (ч. х. у.); отделение нефтепродуктов от сопутствующих органических соединений других классов в колонке, заполненной оксидом алюминия и измерение массовой концентрации нефтепродуктов методом ИК- спектрометрии [17]. Число измерений в эксперименте равно 3. Разброс значений относительно среднего не превышает 15%.
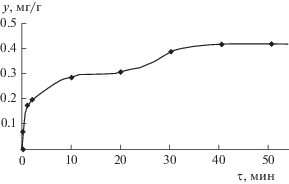
Результаты определения содержания нефтепродуктов в сточной воде в зависимости от времени приведены на рис. 1.
Из результатов проведенных исследований по оценке сорбционных свойств торфа относительно нефти видно, что к 15 мин контакта достигается псевдоравновесная концентрация, далее сорбция продолжается и приблизительно к 30 мин достигается истинная равновесная концентрация в фазах. Сопоставление литературных и полученных в работе данных позволило сделать следующий вывод: при основной сорбции, на временном участке от 2 до 15 мин, существенную роль играет внутренняя диффузия, обусловливающая проникновение сорбируемого вещества вглубь структуры сорбента в доступные по размерам поры, позволяющая нефтепродукту вновь сорбироваться на внешней поверхности сорбента. Поэтому одним из важных факторов, оказывающих влияние на процесс сорбции, является продолжительность контакта фаз.
Исследования равновесия адсорбции нефтепродуктов на торфе проводили методом переменных навесок и постоянной концентрации при 298 К.
По полученной кинетической кривой, приведенной на рис. 1, видно, что в данном случае имеет место аномальная (нефиковская) диффузия, протекающая по типу двухступенчатой сорбции, вызванная адсорбционным взаимодействием диффузанта при сложных изотермах сорбции (Ленгмюра, Фрейндлиха и др.) или химическим взаимодействием диффузанта с веществом [9, 18–20]. Аномальность процесса диффузии можно объяснить тем, что торф относится не к капиллярно-пористым материалам, как обычные технические адсорбенты, а к коллоидным капиллярно-пористым материалам. В нем содержится до 70% гуминовых веществ, которые представляют собой смесь природных высокополимеров с разными молекулярными массами. Сорбция низкомолекулярных веществ в полимерах происходит не только в порах, но и в матрице полимера с заполнением его микрополостей [8, 21].
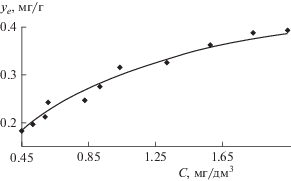
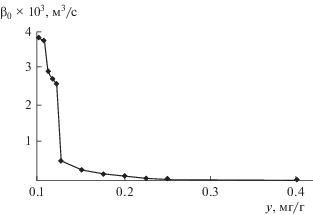
На основании полученных экспериментальных результатов по оценке равновесной зависимости была рассчитана и построена изотерма адсорбции (рис. 2), из которой можно определить основные сведения о сорбционных свойствах торфа и характере сорбции, а также оптимальные параметры промышленных установок очистки.
Анализ полученной изотермы сорбции показывает, что согласно классификации Гилльса данную кривую можно отнести к классу L-3 (изотермы Ленгмюра). Изотермы данного класса выгнуты относительно оси концентрации, что свидетельствует о сильной энергии адсорбции. Согласно кривой, адсорбция продолжается и после насыщения монослоя. В результате частицы сорбента, покрытые нефтепродуктом, способны образовывать агломераты. Кроме того, между сорбентом и нефтепродуктом существует вероятность незначительного протекания химических взаимодействий (хемосорбции).
Для решения уравнения (2) необходимо определение коэффициента массопередачи по твердой фазе, на который оказывают влияние природа сорбата и сорбента, пористость сорбента и степень заполнения его пор, он монотонно убывает при увеличении величины адсорбции, чем ниже концентрация примесей в воде, тем вероятнее попадание в очищенную воду только трудносорбируемых компонентов.
Общий коэффициент массопередачи β0 по твердой фазе определяется по зависимости
(9)
${1 \mathord{\left/ {\vphantom {1 {{{\beta }_{0}}}}} \right. \kern-0em} {{{\beta }_{0}}}} = {1 \mathord{\left/ {\vphantom {1 {{{\beta }_{ж }}}}} \right. \kern-0em} {{{\beta }_{ж }}}} + {1 \mathord{\left/ {\vphantom {1 {{{\beta }_{т }}}}} \right. \kern-0em} {{{\beta }_{т }}}},$Коэффициент массопередачи по твердой фазе в общем случае зависит от скорости движения жидкости относительно твердой фазы и от размера ее частиц. Для определения коэффициента массопереноса процесса сорбционной очистки в слое адсорбента в жидкой фазе необходимо оценить возможный гидродинамический режим. При переходе от ламинарного движения потока жидкости к турбулентному режиму величина βж растет, доля общего диффузионного сопротивления, приходящаяся на внешний массообмен, уменьшается. От величины адсорбции и начальной концентрации примеси в потоке жидкости коэффициент внешнего массообмена практически не зависит. Коэффициент же внутреннего массопереноса существенно зависит от величины адсорбции: с увеличением последнего значения βт резко уменьшаются и доля общего диффузионного сопротивления, приходящаяся на массоперенос в твердой фазе, возрастает.
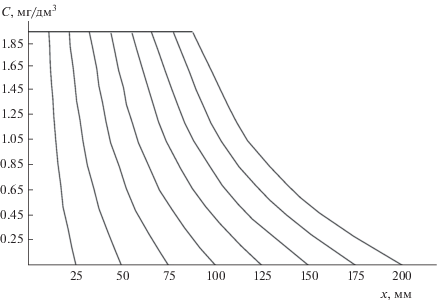
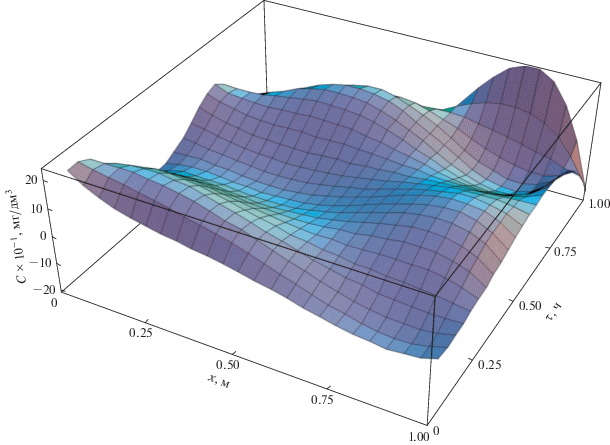
Решение уравнения диффузионной модели выглядит как $С \left( {x,\tau } \right)$ = $\sum\limits_{k = 0}^4 {\sum\limits_{j = 0}^4 {{{C}_{{k,j}}}{{x}^{k}}{{\tau }^{j}}} } $ и $y\left( {x,\tau } \right)$ = = $\int\limits_0^\tau {\beta \left( \tau \right)\left( {C\left( {x,\tau } \right) - {{C}_{e}}} \right)d\tau } $ и проводилось методом Галеркина, строя приближение в виде двумерного алгебраического многочлена 4-й степени по каждой переменой. Из решения уравнения диффузионной модели построены кривые распределения концентраций в слое сорбента, соответствующие времени наступления равновесия 30 мин (рис. 3), и зависимость концентрации от высоты слоя и времени контакта (рис. 4).
Из рис. 3 видно, что при прохождении “лобового” слоя в начальный период времени концентрация нефтепродуктов в потоке резко падает из-за поглощения его граничным слоем торфа. Далее вследствие непрерывного подвода концентрация нефтепродуктов в лобовом слое достигает равновесного значения и не изменяется на протяжении всего процесса. После насыщения лобового слоя адсорбция прекращается, и поток проходит этот участок без изменения концентрации. По окончании периода формирования фронта адсорбции (50 мм) начинается второй период. Концентрационный фронт перемещается с постоянной скоростью вдоль слоя. Отсюда находятся высоты работающего (80 мм) и неиспользованного слоев торфа (25 мм).
По экспериментальным данным равновесной зависимости и кривых распределения концентраций для каждого момента времени коэффициент массопередачи рассчитывается по уравнению (10), полученная зависимость представлена на рис. 5 [22]:
Сорбция ионов тяжелых металлов
Кинетику сорбции ионов тяжелых металлов изучали методом ограниченного объема [23]. Для этого навески торфа массой 10 г насыпались в конические колбы объемом в 500 мл, приливалось по 100 мл модельного монораствора и все перемешивалось непрерывно с помощью пропеллерной мешалки. Модельный раствор, содержащий ион железа(III), представляет собой раствор соли FeCl3 ⋅ 6H2O с концентрацией ионов Fe+3 10 мг/дм3 и рН 2.26. Модельный раствор, содержащий ион меди(II) с концентрацией ионов Cu+2 10 мг/дм3, готовился аналогичным способом из соли CuSO4 ⋅ · 5H2O, рН готового раствора составлял 4.6. После контакта с торфом рН растворов незначительно повысился. Растворы с сорбентами выдерживались от 0 до 60 мин с шагом 20 мин. Отбор пробы раствора и подготовка к анализу осуществлялись в соответствии с [24]. Очистка растворов от мелких частичек сорбента проводилась при помощи бумажных фильтров “синяя лента”. Остаточное содержание ионов железа(III) в фильтрате определялось фотоколориметрическим методом на фотоколориметре КФК-3. Содержание ионов железа(III) определялось с использованием сульфосалициловой кислоты, ионов меди – аммиачным способом [25].
Результаты эффективности сорбции при взаимодействии торфа с модельными смесями представлены на рис. 6.
Рис. 6.
Зависимость эффективности очистки от ионов железа(III) и меди(II) от времени взаимодействия с торфом: а – ионы Fe+3, б – ионы Cu+2.
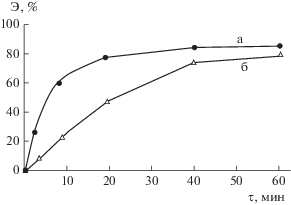
По полученным данным рассчитывали адсорбционную емкость торфа (величина сорбции). Кинетические исследования показывают, что процесс сорбции протекает достаточно быстро и практически заканчивается через 20 мин.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
С целью выяснения механизма процесса сорбции, выявления лимитирующих стадий процесса, что также может быть использовано для решения ряда практических вопросов по оптимизации ионообменных процессов, полученные кинетические кривые были обработаны с помощью уравнений диффузионной и химической кинетики.
Для внешнедиффузионных процессов кинетическая кривая должна быть линейной [26], если ее представить в координатах –ln(Ae – Aτ) от τ (рис. 7а). Кривые сорбции ионов меди во всей зависимости от времени и для ионов железа на начальном этапе описываются прямыми, следовательно, диффузия в пленке раствора вносит вклад в общую скорость процесса. При дальнейшем контакте кривые сорбции ионов железа искривляются. Согласно литературным данным [27], это свидетельствует о том, что диффузия в зерне сорбента контролирует общую скорость процесса.
Рис. 7.
Анаморфозы кинетических кривых в моделях псевдопервого (а) и псевдовторого (б) порядка: 1 – ионы Fe+3, 2 – ионы Cu+2.
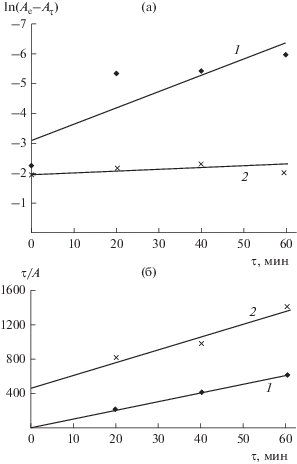
В случае химического взаимодействия торфа с ионами тяжелых металлов (реакции ионного обмена) вклад в кинетику может вносить стадия собственно химической реакции между сорбируемым ионом и функциональными группами поглотителя. Поэтому для выявления вклада химической стадии при описании сорбционного процесса использовались модели псевдопервого и псевдовторого порядка [27].
Линейные формы этих моделей представлены уравнениями (11) и (12) соответственно:
(12)
${\tau \mathord{\left/ {\vphantom {\tau {{{A}_{\tau }}}}} \right. \kern-0em} {{{A}_{\tau }}}} = \frac{1}{{{{k}_{2}}A_{e}^{2}}} + \frac{1}{{{{A}_{e}}}}\tau ,$Следует отметить, что уравнение модели псевдопервого порядка идентично уравнению пленочной диффузии. Однако в случае диффузии в пленке скорость процесса зависит от размера частиц сорбента и толщины пленки. Если же вклад вносит химическая реакция, то скорость сорбции зависит только от концентрации ионов и температуры. Таким образом, в случае модели псевдопервого порядка сорбции предшествует диффузия. Лимитирующей стадией как в псевдопервом, так и в псевдовтором порядке реакции является химическая реакция ионного обмена. В этом случае предполагается, что реакция между сорбатом и функциональной группой сорбента является реакций второго порядка, и они взаимодействуют между собой в соотношении 1 : 1 [27, 28].
На рис. 7 представлены анаморфозы кинетических кривых в моделях псевдопервого и псевдовторого порядка.
Для установления модели, оптимально описывающей сорбцию меди и железа на торфе, сравнивались коэффициенты корреляции для каждого иона.
Установлено, что сорбция ионов меди наилучшим образом описывается моделью псевдопервого порядка, т.е. сорбции ионов предшествует диффузия, а сорбция ионов железа – моделью псевдовторого порядка, и между сорбатом и функциональной группой сорбента происходит химическая реакция.
Таким образом, кинетические кривые сорбционного извлечения ионов железа и меди линеаризируются в координатах ln(A) от τ, что дает хорошую основу для моделирования кинетики сорбции. Полученные новые данные о кинетике сорбции позволяют расширить область представлений о механизме взаимодействия торфа с ионами тяжелых металлов, а именно меди(II) и железа(III). Значения кинетических параметров процесса указывают на возможность разделения ионов торфом [29].
ЗАКЛЮЧЕНИЕ
На основе полученных равновесных и кинетических характеристик исследованных адсорбционных процессов при решении конкретной практической задачи может быть рассчитано время защитного действия сорбентов в зависимости от высоты слоя фильтрующего материала, площади свободной поверхности композиции и скорости фильтрования.
Проведенные исследования показали, что одновременное удаление из воды техногенных примесей (нефтепродуктов и ионов тяжелых металлов) может быть успешно реализовано на стадии предварительной очистки на механических фильтрах, загруженных торфом.
Предлагаемая система глубокой очистки воды является технологией двойного назначения, предназначенная для подготовки природных вод и глубокой очистки сточных вод тепловых станций с перспективой увеличения доли оборотных и замкнутых систем, что способствует повышению в этой области эффективности водопользования и, соответственно, ресурсо- и энергосбережению. Ее реализация позволит уменьшить техногенную нагрузку промышленных предприятий, в том числе объектов ТЭК, на окружающую среду и повысить эффективность использования природных вод.
Работа выполнена в рамках базовой части государственного задания в сфере научной деятельности (№ 13.6384.2017/БЧ).
ОБОЗНАЧЕНИЯ
| A | количество сорбированного иона металла на единицу массы сорбента, мг/г |
| $Bi{\text{'}}$ | диффузионный критерий Био |
| С | концентрация примеси в сточной воде, мг/дм3 |
| ${{\left( {y - {{y}_{е }}} \right)} \mathord{\left/ {\vphantom {{\left( {y - {{y}_{е }}} \right)} {\left( {{{у }_{0}} - {{у }_{е }}} \right)}}} \right. \kern-0em} {\left( {{{у }_{0}} - {{у }_{е }}} \right)}}$ | безразмерная концентрация распределяемого вещества в твердой фазе |
| D | коэффициент диффузии, м2/с |
| F | постоянная Фарадея, F = = 96485 Кл/моль |
| $Fo{\text{'}}$ | диффузионный критерий Фурье |
| j | плотность потока массы, кг/(м2 с) |
| K | коэффициент стесненной диффузии, или массопроводности, м2/с |
| k | константа скорости сорбции |
| w | линейная скорость, м/с |
| х | координата, м |
| ${x \mathord{\left/ {\vphantom {x \delta }} \right. \kern-0em} \delta }$ | безразмерная координата точки, в которой концентрация равна С |
| y | количество примеси, поглощаемое единицей объема адсорбента, мг/г |
| Z | заряд обменивающегося иона |
| β | коэффициент массопередачи адсорбируемой примеси, м3/с |
| δ | определяющий размер твердого тела, м |
| γ | коэффициент активности |
| ε | доля свободного объема |
| τ | время, мин |
| ρ | плотность электрических зарядов, Кл/м2 |
| φ | электростатический потенциал, В |
| σ | диэлектрическая постоянная среды, Ф/м |
ИНДЕКСЫ
Список литературы
Климов Е.С., Бузаева М.В. Природные сорбенты и комплексоны в очистке сточных вод. Ульяновск: УлГТУ, 2011.
Bandura L., Woszuk A., Kołody’nska D., Wojciech F. Application of Mineral Sorbents for Removal of Petroleum Substances: A Review // Minerals. 2017. V. 7. № 3. P. 37.
Келбалиев Г.И., Расулов С.Р., Рзаев А.Г., Сулейманов Г.З., Мустафаева Г.Р. Моделирование фильтрации нефтей в пористой среде и технология жидкофазной экстракции асфальтенов // Теорет. основы хим. технологии. 2016. Т. 50. № 6. С. 673.
Polka M., Kukfisz B., Wysocki P., Polakovic P., Kvarcak M. Efficiency analysis of the sorbents used to adsorb the vapors of petroleum products during rescue and firefighting actions // Przemysl Chemiczny. 2015. V. 94. № 3. P. 331.
Мясников С.К., Тихонов А.Ю., Чипрякова А.П., Кулов Н.Н. Очистка воды от ионов тяжелых металлов в совмещенном сорбционно-кристаллизационном процессе с использованием активированных глин // Теорет. основы хим. технологии. 2016. Т. 50. № 4. С. 376. [Myasnikov S.K., Tikhonov A.Yu., Chipryakova A.P., Kulov N.N. Removal of heavy metal ions from water by an combined sorption–crystallization process using activated clays // Theor. Found. Chem. Eng. 2016. V. 50. № 4. P. 366.]
Сергеева Е.С., Лаптедульче Н.К. Разработка подходов к моделированию процессов очистки нефтесодержащих вод в динамических условиях природными сорбентами // Энергосбережение и водоподготовка. 2009. № 4. С. 9.
Плановский А.Н., Николаев П.И. Процессы и аппараты химической и нефтехимической технологии. Учебник для вузов. 3-е изд., перераб. и доп. М.: Химия, 1987.
Рудобашта С.П. Массоперенос в системах с твердой фазой. М.: Химия, 1980.
Ишанходжаева М.М. Физическая химия. Часть I. Диффузия в системах твердой фазой. СПб.: СПбГТУРП, 2012.
Архангельский Л.К., Белинская Ф.А., Волжинский А.И. и др. Иониты в химической технологии / Под ред. Никольского Б.П., Романкова П.Г. Л.: Химия, 1982.
Романков П.Г., Фролов В.Ф. Массообменные процессы химической технологии (системы с дисперсной твердой фазой). Л.: Химия, 1990.
Дремичева Е.С., Лаптедульче Н.К. Торф как сорбент для очистки промышленных сточных вод // Вода: химия и экология. 2015. № 8. С. 57.
Дремичева Е.С., Лаптедульче Н.К. Перспективы применения торфа для очистки промышленных сточных вод // Водоочистка. 2015. № 1. С. 20.
Белькевич П.И., Чистова Л.Р., Рогач Л.М., Соколова Т.В. Сорбционные свойства гранулированного торфа // Химия твердого топлива. 1984. № 5. С. 35.
Лаптедульче Н.К., Дремичева Е.С. Сравнительная оценка эффективности сорбционной очистки сточных вод от тяжелых металлов // Вода: химия и экология. 2014. № 12. С. 81.
Афанасьев А.Е., Ефремов А.С. Влияние структурообразования на плотность жидкости коллоидных капиллярно-пористых тел // Теорет. основы хим. технологии. 2011. Т. 45. № 1. С. 119. [Afanas’ev A.E., Efremov A.S. Effect of structuring on the density of the liquid in colloidal capillary porous bodies // Theor. Found. Chem. Eng. 2011. V. 45. № 1. P. 120.]
ГОСТ Р 51797-2001. Содержание нефтепродуктов в природных и сточных водах.
Pomerantsev A.L. Phenomenological modeling of anomalous diffusion in polymers // J. Appl. Polym. Sci. 2005. V. 96. № 4. P. 1102.
Брюханов В.В., Самусев И.Г., Иванов А.М., Мыслицкая Н.А. Аномальная диффузия наночастиц в воде вблизи пористой поверхности // Журнал физической химии. 2008. Т. 82. № 2. С. 326.
Нафадзокова Л.Х., Козлов Г.В., Лигидов М.Х., Пахомов С.И. Странная (аномальная) диффузия как способ управления кинетикой химических реакций // Известия высших учебных заведений. Серия: Химия и химическая технология. 2008. Т. 51. № 9. С. 79.
Роджерс К. В кн.: Проблемы физики и химии твердого состояния органических соединений. М.: Мир, 1968.
Лаптев А.Г., Сергеева Е.С. Физическое и математическое моделирование сорбционных свойств торфа для очистки воды от нефтепродуктов // Вода: химия и экология. 2008. № 3. С. 14.
Салдадзе К.М., Копылова-Валова В.Д. Комплексообразующие иониты (комплекситы). М.: Химия, 1980.
ПНД Ф 12.15.1-08 “Методические указания по отбору проб для анализа сточных вод”. Утверждено ФГУ “Федеральный центр анализа и оценки техногенного воздействия” 18.04.2008. М., 2015.
Лурье Ю.Ю. Унифицированные методы анализа. Изд. 2-е испр. М.: Химия, 1973.
Гельферих Ф. Иониты (основы ионного обмена). М.: Изд-во иностр. лит., 1962.
Ho Y.S., Ng J.C.Y., McKay G. Kinetics of pollutant sorption by biosorbents: review // Separ. Purif. Methods. 2000. V. 29. № 2. P. 189.
Неудачина Л.К., Петрова Ю.С., Засухин А.С., Осипова В.А., Горбунова Е.М., Ларина Т.Ю. Кинетика сорбции ионов тяжелых металлов пиридилэтилированным аминопропилполисилоксаном // Аналитика и контроль. 2011. Т. 15. № 1. С. 87.
Дремичева Е.С. Изучение кинетики сорбции на торфе ионов железа(III) и меди(II) из сточных вод // Вестник Московского университета. Серия 2: Химия. 2017. Т. 58. № 4. С. 204. [Dremicheva E.S. Studying the Sorption Kinetics on Peat Ions of Iron(III) and Copper(II) from Wastewater // Moscow University Chemistry Bulletin. 2017. V. 72. № 4. P. 196.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии