Теоретические основы химической технологии, 2019, T. 53, № 4, стр. 458-467

Гидратообразование в пористой среде при инжекции жидкого диоксида углерода с учетом его кипения

М. К. Хасанов^*

Стерлитамакский филиал Башкирского государственного университета
Стерлитамак, Россия

Поступила в редакцию 27.01.2017
После доработки 31.03.2017
Принята к публикации 12.04.2017

DOI: 10.1134/S0040357119030059

Аннотация

Исследуются особенности образования газогидрата при инжекции жидкого диоксида углерода в насыщенную метаном и водой пористую среду с учетом кипения двуокиси углерода. Установлено, что образование газогидрата диоксида углерода может происходить как на фронтальной границе, так и в протяженной области. Показано, что кипение диоксида углерода и соответствующее охлаждения пласта способствует образованию его газогидрата на фронтальной поверхности. Построены кривые, разделяющие разные режимы, в зависимости от давления инжекции, начального давления и проницаемости пласта.

Ключевые слова: пористая среда, газовые гидраты, фильтрация, диоксид углерода

ВВЕДЕНИЕ

В настоящее время одним из направлений решения проблемы быстрого роста концентрации углекислого газа в атмосфере (вследствие его роли в парниковом эффекте) видится подземная утилизация выработанного промышленными объектами диоксида углерода [1–5]. Для минимизации риска выхода утилизируемых выбросов из коллекторов на поверхность рядом авторов была предложена идея подземной утилизации диоксида углерода в газогидратном состоянии [6, 7]. Учитывая эффект самоконсервации газогидратов и их способность связывать огромное количество газа в небольшом объеме, хранение парниковых газов в газогидратном состоянии представляется достаточно безопасным и надежным способом их утилизации. Подходящими геологическими объектами для захоронения диоксида углерода в газогидратном состоянии могут быть, в том числе отработанные газовые коллекторы, частично насыщенные водой [6, 7].

Математические модели инжекции газа в пористую среду, насыщенную газом и водой, представлены, например, в работах [8–11]. В этих работах исследуется только одно фазовое превращение – образование газогидрата. Математическая модель образования газогидрата CO₂ при инжекции жидкого диоксида углерода в пористую среду, частично насыщенную водой и метаном, сформулирована в работе [12]. Хотя в этой работе математическая модель также учитывает только одно фазовое превращение (гидратообразование), но в ней было показано, что такая модель в ряде случаев приводит к термодинамическому противоречию и поэтому требует учета кипения диоксида углерода.

В настоящей работе в отличие от [12] исследуется математическая модель образования гидрата CO₂ при инжекции жидкого диоксида углерода с учетом его кипения.

ПОСТАНОВКА ЗАДАЧИ

На рис. 1 представлена фазовая диаграмма, на которой отражены условия существования гидратов диоксида углерода и метана [13]. На этой диаграмме кривые 1 и 2 определяют линии трехфазного равновесия “диоксид углерода–вода–гидрат СО₂” и “метан–вода–гидрат СН₄” соответственно, а кривая 3 – линию двухфазного равновесия “жидкость–пар” для диоксида углерода.

Рис. 1.

Фазовая диаграмма для систем “CO₂–H₂O” и “CH₄–H₂O”. Кривые 1 и 2 – линии трехфазного равновесия “СО₂–вода–гидрат СО₂” и “СН₄–вода–гидрат СН₄” соответственно; кривая 3 – линия двухфазного равновесия "жидкость–пар” для диоксида углерода.

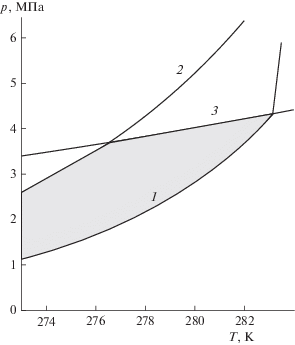
Пусть пласт (занимающий полупространство x > 0) в начальный момент насыщен водой с исходной насыщенностью ${{S}_{{{\text{v}}0}}}$ и метаном, начальные температура T₀ и давление p₀ которых на фазовой диаграмме лежат между кривыми 1 и 3, а также ниже кривой 2. Данная термодинамическая область на рис. 1 закрашена и соответствует существованию метана и воды в свободном (не газогидратном) состоянии, а также условиям существования диоксида углерода в газообразном состоянии и его газогидрата. Положим, что через границу (x = 0) пласта закачивается диоксид углерода, давление p_w и температура T_w которого соответствуют условиям существования диоксида углерода в жидком состоянии (лежат выше кривой 3). Будем полагать, что инжекция жидкого диоксида углерода сопровождается его вскипанием и дальнейшим образованием его газогидрата из углекислого газа и воды.

Как показывают лабораторные эксперименты, образование частиц гидрата сопровождается неравновесными процессами, связанными с диффузией гидратообразующего газа к поверхности контакта “вода–гидрат” через пленки гидрата. Экспериментальные значения времени кинетики гидратообразования в пористых средах сильно зависят от характерных размеров пор, но в среднем составляют порядка несколько часов. Так в работе [14], в которой исследовалось образование и разложение гидрата CO₂ в пористой среде с размерами зерен 110 мкм, данное время составило порядка одного часа. Эти характерные времена, как правило, очень малы по сравнению со временем распространения диоксида углерода в протяженном природном пласте. В этой связи в рассматриваемой задаче процесс гидратообразования лимитируется не кинетическими механизмами, а скоростью фильтрационного массопереноса в пористой среде.

В рассматриваемой задаче будем пренебрегать диффузионным перемешиванием углекислого газа и метана, т.к. вследствие непрерывной закачки диоксида углерода в пласт, интенсивность массопереноса, обусловленного фильтрацией в проницаемой пористой среде, значительно превышает интенсивность массопереноса обусловленного диффузией. Кроме того, фронт вытеснения метана диоксидом углерода можно считать устойчивым вследствие ламинарного характера течений в пористых средах, а также большей по сравнению с метаном вязкостью углекислого газа.

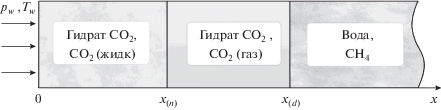
Поскольку в рассматриваемой задаче как параметры на левой границе, так и начальное состояние пласта соответствуют условиям образования газогидрата диоксида углерода, то аналогично работе [11] можно полагать, что образование газогидрата CO₂ происходит на границе вытеснения метана углекислым газом. Следовательно, в рассматриваемом случае в пласте образуются три характерные области. В первой (ближней) области поры насыщены жидким диоксидом углерода и газогидратом CO₂, во второй (промежуточной) области присутствуют углекислый газ и газогидрат CO₂, а в третьей (дальней) области поры насыщены метаном и водой (рис. 2). Соответственно существуют две подвижные межфазные поверхности: между первой и второй областями, на которой происходит кипение диоксида углерода, а также между второй и третьей областями, где образуется газогидрат CO₂ из углекислого газа и воды.

Рис. 2.

Схематическое расположение зон в пласте.

ОСНОВНЫЕ УРАВНЕНИЯ

Для описания процессов тепломассопереноса при закачке диоксида углерода в пористый пласт примем следующие допущения. Скелет пористой среды, вода и гидрат несжимаемы, пористость постоянна, метан и углекислый газ являются калорически совершенными газами, а жидкий диоксид углерода – упругой слабосжимаемой жидкостью, вода неподвижна (т.к. рассматривается случай, когда величина исходной водонасыщенности не превышает 0.2).

Система основных уравнений, описывающая в одномерном случае процессы фильтрации и теплопереноса в пористой среде, представляет собой законы сохранения масс и энергии, закон Дарси и уравнение состояния [8–12]:

(1)

$\begin{gathered} \frac{\partial }{{\partial t}}\left( {{{\rho }_{i}}\phi {{S}_{i}}} \right) + \frac{\partial }{{\partial x}}\left( {{{\rho }_{i}}\phi {{S}_{i}}{{\upsilon }_{i}}} \right) = 0,\,\,\,\,(i = l,c,{\text{m}}) \\ \frac{\partial }{{\partial t}}\left( {\rho C{{T}_{i}}} \right) + {{\rho }_{i}}{{C}_{i}}\phi {{S}_{i}}{{\upsilon }_{i}}\frac{{\partial {{T}_{i}}}}{{\partial x}} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial {{T}_{i}}}}{{\partial x}}} \right), \\ \phi {{S}_{i}}{{\upsilon }_{i}} = - \frac{{{{k}_{i}}}}{{{{\mu }_{i}}}}\frac{{\partial {{p}_{i}}}}{{\partial x}},\,\,\,\,{{\rho }_{l}} = {{\rho }_{{0l}}}\left( {1 + \beta ({{p}_{l}} - {{p}_{0}})} \right), \\ {{\rho }_{c}} = {{{{p}_{c}}} \mathord{\left/ {\vphantom {{{{p}_{c}}} {{{R}_{{{\text{g}}c}}}{{T}_{c}}}}} \right. \kern-0em} {{{R}_{{{\text{g}}c}}}{{T}_{c}}}},\,\,\,\,\,{{\rho }_{{\text{m}}}} = {{{{p}_{{\text{m}}}}} \mathord{\left/ {\vphantom {{{{p}_{{\text{m}}}}} {{{R}_{{{\text{gm}}}}}{{T}_{{\text{m}}}}}}} \right. \kern-0em} {{{R}_{{{\text{gm}}}}}{{T}_{{\text{m}}}}}}. \\ \end{gathered} $

Здесь нижние индексы i = l, c, m относятся к жидкому диоксиду углерода, углекислому газу и метану соответственно; t – время; x – координата; $\phi $ – пористость; S_i, ρ_i, ${{\upsilon }_{i}},$ k_i, С_i и μ_i – насыщенность пор, плотность, скорость, фазовая проницаемость, удельная массовая теплоемкость и динамическая вязкость подвижного флюида соответственно; R_gc и R_gm – газовые постоянные углекислого газа и метана; p – давление; T – температура; β – коэффициент объемного сжатия жидкой двуокиси углерода; ρ_0l – истинная плотность жидкой двуокиси углерода, соответствующая давлению p₀; ρС и λ – удельная объемная теплоемкость и коэффициент теплопроводности системы. Так как основной вклад в значения ρС и λ вносят соответствующие параметры скелета пористой среды, то будем считать их постоянными величинами.

Фазовую проницаемость подвижного флюида k_i будем считать линейной функцией его насыщенности S_i:

${{k}_{i}} = {{k}_{0}}{{S}_{i}}\,\,\,\,(i = l,c,{\text{m}}),$

где k₀ – абсолютная проницаемость пласта.

Условия баланса массы диоксида углерода и тепла на границе между первой и второй областями (фронте кипения) имеют вид:

$\phi {{\rho }_{l}}{{S}_{l}}{\text{(}}{{\upsilon }_{l}} - {{\dot {x}}_{{(n)}}}{\text{)}} = \phi {{\rho }_{c}}{{S}_{c}}{\text{(}}{{\upsilon }_{c}} - {{\dot {x}}_{{(n)}}}{\text{),}}$

$\lambda \frac{{\partial {{T}_{c}}}}{{\partial x}} - \lambda \frac{{\partial {{T}_{l}}}}{{\partial x}} = \phi {{\rho }_{l}}{{S}_{l}}{{L}_{l}}({{\upsilon }_{l}} - {{\dot {x}}_{{{\text{(}}n{\text{)}}}}}).$

Здесь L_l – удельная массовая теплота парообразования CO₂; ${{\dot {x}}_{{(n)}}}$ – скорость движения границы кипения CO₂. Температура и давление на этой границе полагаются непрерывными. Здесь и далее индекс n в скобках относится к параметрам на границе между первой и второй областями.

Последние уравнения с учетом закона Дарси и уравнения состояния можно записать следующим образом:

(2)

$\begin{gathered} - \frac{{{{\rho }_{{0l}}}{{k}_{l}}}}{{{{\mu }_{l}}}}\frac{{\partial {{p}_{l}}}}{{\partial x}} + \frac{{{{k}_{c}}}}{{2{{\mu }_{c}}{{R}_{{{\text{g}}c}}}{{T}_{0}}}}\frac{{\partial p_{c}^{2}}}{{\partial x}} = \\ = \phi \left( {1 - {{S}_{h}}} \right){{\rho }_{{0l}}}\left( {1 + \beta ({{p}_{{(n)}}} - {{p}_{0}}) - \frac{{{{p}_{{(n)}}}}}{{{{\rho }_{{0l}}}{{R}_{{{\text{g}}c}}}{{T}_{0}}}}} \right){{{\dot {x}}}_{{(n)}}}, \\ \lambda \frac{{\partial {{T}_{c}}}}{{\partial x}} - \lambda \frac{{\partial {{T}_{l}}}}{{\partial x}} = {{\rho }_{{0l}}}\left( {1 + \beta ({{p}_{{(n)}}} - {{p}_{0}})} \right) \times \\ \times \,\,{{L}_{l}}\left( { - \frac{{{{k}_{l}}}}{{{{\mu }_{l}}}}\frac{{\partial {{p}_{l}}}}{{\partial x}} - \phi \left( {1 - {{S}_{h}}} \right){{{\dot {x}}}_{{{\text{(}}n{\text{)}}}}}} \right). \\ \end{gathered} $

Кроме того, зависимость между давлением и температурой на границе кипения в случае небольших перепадов температуры можно представить в виде аппроксимации кривой Клаузиуса–Клапейрона [15]:

(3)

${{p}_{{(n)}}} = {{p}_{{c0}}}\exp \left( {\frac{\theta }{{{{T}_{{c0}}}}} - \frac{\theta }{{{{T}_{{(n)}}}}}} \right),$

где p_c0 – равновесное давление кипения, соответствующее температуре T_c0, θ – эмпирический параметр.

Поскольку, как было указано выше, в рассматриваемой задаче можно пренебречь перемешиванием газов и считать устойчивым фронт вытеснения метана углекислым газом, то с учетом образования гидрата углекислого газа условия баланса массы углекислого газа и метана на границе между второй и третьей областями имеют вид:

$\phi {{\rho }_{c}}{{S}_{c}}({{\upsilon }_{c}} - {{\dot {x}}_{{(d)}}}) = \phi {{\rho }_{h}}{{S}_{h}}G{{\dot {x}}_{{(d)}}},$

$\phi {{\rho }_{{\text{m}}}}{{S}_{{\text{m}}}}({{\upsilon }_{{\text{m}}}} - {{\dot {x}}_{{(d)}}}) = 0,$

где ${{\rho }_{h}},$ S_h – плотность и насыщенность газогидрата, G – относительная массовая концентрация диоксида углерода в его газогидрате; ${{\dot {x}}_{{(d)}}}$ – скорость движения границы гидратообразования. Здесь и далее нижний индекс d относится к параметрам на границе между второй и третьей областями.

С учетом последней системы уравнений и закона Дарси, условия баланса массы и тепла на границе между второй и третьей областями можно записать следующим образом:

(4)

$\begin{gathered} - \frac{{{{k}_{c}}}}{{{{\mu }_{c}}}}\frac{{\partial {{p}_{c}}}}{{\partial x}} = \phi \left( {\frac{{{{\rho }_{h}}}}{{{{\rho }_{c}}}}{{S}_{h}}G + {{S}_{c}}} \right){{{\dot {x}}}_{{(d)}}}, \\ - \frac{{{{k}_{{\text{m}}}}}}{{{{\mu }_{{\text{m}}}}}}\frac{{\partial {{p}_{{\text{m}}}}}}{{\partial x}} = \phi {{S}_{{\text{m}}}}{{{\dot {x}}}_{{(d)}}}, \\ \phi {{S}_{h}}{{\rho }_{h}}(1 - G){{{\dot {x}}}_{{(d)}}} = \phi {{S}_{{\text{v}}}}{{\rho }_{{\text{v}}}}{{{\dot {x}}}_{{(d)}}}, \\ \lambda \frac{{\partial {{T}_{c}}}}{{\partial x}} - \lambda \frac{{\partial {{T}_{{\text{m}}}}}}{{\partial x}} = \phi {{\rho }_{h}}{{L}_{h}}{{S}_{h}}{{{\dot {x}}}_{{(d)}}}. \\ \end{gathered} $

Здесь L_h – удельная массовая теплота образования газогидрата диоксида углерода, ${{\rho }_{{\text{v}}}}$ и S_v – плотность и насыщенность пор для воды. Температура и давление на границе гидратообразования полагаются непрерывными.

Насыщенность пористой среды водой в третьей области равна исходной водонасыщенности пласта S_v0. Тогда на основе третьего уравнения системы (4) можно найти величину гидратонасыщенности S_h в первой и второй областях:

${{S}_{h}} = \frac{{{{\rho }_{{\text{v}}}}{{S}_{{{\text{v0}}}}}}}{{{{\rho }_{h}}\left( {1 - G} \right)}}.$

Тогда насыщенность пор диоксидом углерода в первой и второй областях равна:

${{S}_{l}} = {{S}_{c}} = 1 - \frac{{{{\rho }_{{\text{v}}}}{{S}_{{{\text{v0}}}}}}}{{{{\rho }_{h}}\left( {1 - G} \right)}}.$

Начальные и граничные условия рассматриваемой задачи имеют вид:

$x = 0\,:\,\,\,\,\,T = {{T}_{w}},\,\,\,\,p = {{p}_{w}}\,\,\,\,(t > 0).$

На основе уравнений системы (1), уравнения пьезопроводности и температуропроводности для каждой из областей запишутся в виде:

(5)

$\begin{gathered} \frac{{\partial {{p}_{{(1)}}}}}{{\partial t}} = \frac{{{{k}_{l}}}}{{{{\mu }_{l}}\phi \beta {{S}_{l}}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial {{p}_{{(1)}}}}}{{\partial x}}} \right), \\ \frac{{\partial {{T}_{{(1)}}}}}{{\partial t}} = {{\chi }^{{(T)}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial {{T}_{{(1)}}}}}{{\partial x}}} \right) + {{\chi }^{{(T)}}}\frac{{{{\rho }_{0}}_{l}{{C}_{l}}{{k}_{l}}}}{{\lambda {{\mu }_{l}}}}\frac{{\partial {{p}_{{(1)}}}}}{{\partial x}}\frac{{\partial {{T}_{{(1)}}}}}{{\partial x}}, \\ \end{gathered} $

(6)

$\begin{gathered} \frac{{\partial p_{{(2)}}^{2}}}{{\partial t}} = \frac{{{{k}_{c}}{{p}_{0}}}}{{{{\mu }_{c}}\phi {{S}_{c}}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial p_{{(2)}}^{2}}}{{\partial x}}} \right), \\ \frac{{\partial {{T}_{{(2)}}}}}{{\partial t}} = {{\chi }^{{(T)}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial {{T}_{{(2)}}}}}{{\partial x}}} \right) + {{\chi }^{{(T)}}}\frac{{{{С }_{c}}{{k}_{c}}}}{{2\lambda {{R}_{{{\text{g}}c}}}{{T}_{0}}{{\mu }_{c}}}}\frac{{\partial p_{{(2)}}^{2}}}{{\partial x}}\frac{{\partial {{T}_{{(2)}}}}}{{\partial x}}, \\ \end{gathered} $

(7)

$\begin{gathered} \frac{{\partial p_{{(3)}}^{2}}}{{\partial t}} = \frac{{{{k}_{{\text{m}}}}{{p}_{0}}}}{{{{\mu }_{{\text{m}}}}\phi {{S}_{{\text{m}}}}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial p_{{(3)}}^{2}}}{{\partial x}}} \right), \\ \frac{{\partial {{T}_{{(3)}}}}}{{\partial t}} = {{\chi }^{{(T)}}}\frac{\partial }{{\partial x}}\left( {\frac{{\partial {{T}_{{(3)}}}}}{{\partial x}}} \right) + {{\chi }^{{(T)}}}\frac{{{{С }_{{\text{m}}}}{{k}_{{\text{m}}}}}}{{2\lambda {{R}_{{{\text{gm}}}}}{{T}_{0}}{{\mu }_{{\text{m}}}}}}\frac{{\partial p_{{(3)}}^{2}}}{{\partial x}}\frac{{\partial {{T}_{{(3)}}}}}{{\partial x}}, \\ \end{gathered} $

где ${{\chi }^{{(T)}}} = {\lambda \mathord{\left/ {\vphantom {\lambda {\rho С }}} \right. \kern-0em} {\rho С }}$ – коэффициент температуропроводности пласта; индексы j = 1, 2, 3 относятся к параметрам первой, второй и третьей областей соответственно.

Отметим, что при записи уравнения пьезопроводности для первой области учтено, что $\beta (p - {{p}_{0}})$ $ \ll $ 1, а при записи данного уравнения для второй и третьей областей использована линеаризация Лейбензона [16]. Кроме того, поскольку в рассматриваемой задаче перепады температур в пласте незначительны (ΔT $ \ll $ T₀), то аналогично работам [8–12] в уравнении пьезопроводности отброшено слагаемое, отвечающее за переменность температуры.

АВТОМОДЕЛЬНОЕ РЕШЕНИЕ

Введем автомодельную переменную: ξ = = ${x \mathord{\left/ {\vphantom {x {\sqrt {{{\chi }^{{(T)}}}t} }}} \right. \kern-0em} {\sqrt {{{\chi }^{{(T)}}}t} }}.$ Для этой переменной уравнения пьезопроводности и температуропроводности (5)–(7) в каждой области примут вид:

(8)

$\begin{gathered} - \xi \frac{{d{{p}_{{(1)}}}}}{{d\xi }} = 2{{\eta }_{{(1)}}}\frac{d}{{d\xi }}\left( {\frac{{d{{p}_{{(1)}}}}}{{d\xi }}} \right), \\ - \xi \frac{{d{{T}_{{(i)}}}}}{{d\xi }} = {{{\rm X}}_{{(1)}}}\frac{{d{{p}_{{(1)}}}}}{{d\xi }}\frac{{d{{T}_{{(i)}}}}}{{d\xi }} + 2\frac{d}{{d\xi }}\left( {\frac{{d{{T}_{{(i)}}}}}{{d\xi }}} \right), \\ \end{gathered} $

(9)

$\begin{gathered} - \xi \frac{{dp_{{(2)}}^{2}}}{{d\xi }} = 2{{\eta }_{{(2)}}}\frac{d}{{d\xi }}\left( {\frac{{dp_{{(2)}}^{2}}}{{d\xi }}} \right), \\ - \xi \frac{{d{{T}_{{(2)}}}}}{{d\xi }} = {{{\rm X}}_{{(2)}}}\frac{{dp_{{(2)}}^{2}}}{{d\xi }}\frac{{d{{T}_{{(2)}}}}}{{d\xi }} + 2\frac{d}{{d\xi }}\left( {\frac{{d{{T}_{{(2)}}}}}{{d\xi }}} \right), \\ \end{gathered} $

(10)

$\begin{gathered} - \xi \frac{{dp_{{(3)}}^{2}}}{{d\xi }} = 2{{\eta }_{{(3)}}}\frac{d}{{d\xi }}\left( {\frac{{dp_{{(3)}}^{2}}}{{d\xi }}} \right), \\ - \xi \frac{{d{{T}_{{(3)}}}}}{{d\xi }} = {{{\rm X}}_{{(3)}}}\frac{{dp_{{(3)}}^{2}}}{{d\xi }}\frac{{d{{T}_{{(3)}}}}}{{d\xi }} + 2\frac{d}{{d\xi }}\left( {\frac{{d{{T}_{{(3)}}}}}{{d\xi }}} \right), \\ \end{gathered} $

где ${{\eta }_{{(1)}}} = \frac{{{{k}_{l}}}}{{{{\mu }_{l}}\phi \beta {{S}_{l}}{{\chi }^{{(T)}}}}},$ ${{\eta }_{{(2)}}} = \frac{{{{k}_{c}}{{p}_{0}}}}{{{{\mu }_{c}}\phi {{S}_{c}}{{\chi }^{{(T)}}}}},$ ${{\eta }_{{(3)}}}$ = = $\frac{{{{k}_{{\text{m}}}}{{p}_{0}}}}{{{{\mu }_{{\text{m}}}}\phi {{S}_{{\text{m}}}}{{\chi }^{{(T)}}}}},$ ${{{\rm X}}_{{(1)}}}$ = $\frac{{2{{\rho }_{0}}_{l}{{C}_{l}}{{k}_{l}}}}{{\lambda {{\mu }_{l}}}},$ ${{{\rm X}}_{{(2)}}} = \frac{{{{С }_{c}}{{k}_{c}}}}{{\lambda {{R}_{{{\text{g}}c}}}{{T}_{0}}{{\mu }_{c}}}},$ ${{{\rm X}}_{{(3)}}} = \frac{{{{С }_{{\text{m}}}}{{k}_{{\text{m}}}}}}{{\lambda {{R}_{{{\text{gm}}}}}{{T}_{0}}{{\mu }_{{\text{m}}}}}}.$

После интегрирования (8)–(10) решения для распределения давления и температуры в каждой из областей могут быть записаны в виде:

(11)

$\begin{gathered} {{p}_{{(1)}}} = {{p}_{{(n)}}} + \frac{{\left( {{{p}_{w}} - {{p}_{{(n)}}}} \right)\int\limits_\xi ^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(1)}}}}}} \right)} d\xi }}{{\int\limits_0^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(1)}}}}}} \right)} d\xi }}, \\ {{T}_{{(1)}}} = {{T}_{{(n)}}} + \frac{{\left( {{{T}_{w}} - {{T}_{{(n)}}}} \right)\int\limits_\xi ^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(1)}}}{{p}_{{(1)}}}} \right)} d\xi }}{{\int\limits_0^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(1)}}}{{p}_{{(1)}}}} \right)} d\xi }}, \\ 0 < \xi < {{\xi }_{{(n)}}}, \\ \end{gathered} $

(12)

$\begin{gathered} p_{{(2)}}^{2} = p_{{(d)}}^{2} + \frac{{\left( {p_{{(n)}}^{2} - p_{{(d)}}^{2}} \right)\int\limits_\xi ^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(2)}}}}}} \right)} d\xi }}{{\int\limits_{{{\xi }_{{(n)}}}}^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(2)}}}}}} \right)} d\xi }}, \\ {{T}_{{(2)}}} = {{T}_{{(d)}}} + \frac{{\left( {{{T}_{{(n)}}} - {{T}_{{(d)}}}} \right)\int\limits_\xi ^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(2)}}}p_{{(2)}}^{2}} \right)} d\xi }}{{\int\limits_{{{\xi }_{{(n)}}}}^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(2)}}}p_{{(2)}}^{2}} \right)} d\xi }}, \\ \end{gathered} $

(13)

$\begin{gathered} p_{{(3)}}^{2} = p_{0}^{2} + \left( {p_{{(d)}}^{2} - p_{0}^{2}} \right)\frac{{\int\limits_\xi ^\infty {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(3)}}}}}} \right)} d\xi }}{{\int\limits_{{{\xi }_{{(d)}}}}^\infty {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(3)}}}}}} \right)} d\xi }}, \\ {{T}_{{(3)}}} = {{T}_{0}} + \frac{{\left( {{{T}_{{(d)}}} - {{T}_{0}}} \right)\int\limits_\xi ^\infty {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(3)}}}p_{{(3)}}^{2}} \right)} d\xi }}{{\int\limits_{{{\xi }_{{(d)}}}}^\infty {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(3)}}}p_{{(3)}}^{2}} \right)} d\xi }}, \\ {{\xi }_{{(d)}}} < \xi < \infty . \\ \end{gathered} $

На основе соотношений (2), (3) и с учетом решений (11), (12) получим уравнения для определения координаты фронта кипения ${{\xi }_{{(n)}}}$ и значений параметров на нем:

(14)

$\frac{{{{\rho }_{{0l}}}{{k}_{l}}}}{{{{\mu }_{l}}}}\frac{{\left( {{{p}_{w}} - {{p}_{{(n)}}}} \right)\exp \left( { - \frac{{\xi _{{(n)}}^{2}}}{{4{{\eta }_{{(1)}}}}}} \right)}}{{\int\limits_0^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(1)}}}}}} \right)} d\xi }} + \,\,\frac{{{{k}_{c}}}}{{2{{\mu }_{c}}{{R}_{{gc}}}{{T}_{0}}}}\frac{{\left( {p_{{(d)}}^{2} - p_{{(n)}}^{2}} \right)\exp \left( { - \frac{{\xi _{{(n)}}^{2}}}{{4{{\eta }_{{(2)}}}}}} \right)}}{{\int\limits_{{{\xi }_{{(n)}}}}^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(2)}}}}}} \right)} d\xi }} = {{A}_{{(1)}}}\left( {1 + \beta ({{p}_{{(n)}}} - {{p}_{0}}) - \frac{{{{p}_{{(n)}}}}}{{{{\rho }_{{0l}}}{{R}_{{{\text{g}}c}}}{{T}_{0}}}}} \right){{\xi }_{{(n)}}},$

(15)

$\begin{gathered} \lambda \frac{{\left( {{{T}_{{(d)}}} - {{T}_{{(n)}}}} \right)\exp \left( { - \frac{{\xi _{{(n)}}^{2}}}{4} - {{{\rm X}}_{{(2)}}}p_{{(n)}}^{2}} \right)}}{{\int\limits_{{{\xi }_{{(n)}}}}^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(2)}}}p_{{(2)}}^{2}} \right)} d\xi }} - \,\,\lambda \frac{{\left( {{{T}_{{(n)}}} - {{T}_{w}}} \right)\exp \left( { - \frac{{\xi _{{(n)}}^{2}}}{4} - {{{\rm X}}_{{(1)}}}{{p}_{{(n)}}}} \right)}}{{\int\limits_0^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(1)}}}{{p}_{{(1)}}}} \right)} d\xi }} + \,\,\frac{{{{k}_{l}}}}{{{{\mu }_{l}}}}{{\rho }_{{0l}}}{{L}_{l}}\frac{{\left( {{{p}_{{(n)}}} - {{p}_{w}}} \right)\exp \left( { - \frac{{\xi _{{(n)}}^{2}}}{{4{{\eta }_{{\left( 1 \right)}}}}}} \right)}}{{\int\limits_0^{{{\xi }_{{(n)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{\left( 1 \right)}}}}}} \right)d\xi } }} = \\ = - {{B}_{{(1)}}}\left( {1 + \beta ({{p}_{{(n)}}} - {{p}_{0}})} \right){{\xi }_{{(n)}}}, \\ \end{gathered} $

${{T}_{{(n)}}} = {{T}_{{c0}}}\frac{1}{{1 - \frac{{{{T}_{{c0}}}}}{\theta }\ln \left( {\frac{{{{p}_{{(n)}}}}}{{{{p}_{{c0}}}}}} \right)}},$

где ${{A}_{{(1)}}} = \frac{1}{2}{{\chi }^{{(T)}}}\phi \left( {1 - {{S}_{h}}} \right){{\rho }_{{0l}}},$ ${{B}_{{(1)}}} = \frac{{\phi {{\rho }_{{0l}}}\left( {1 - {{S}_{h}}} \right)\lambda {{L}_{l}}}}{{2\rho C}}.$

Аналогично на основе соотношений (4) с учетом решений (12) и (13) получим систему уравнений для определения координаты фронта образования гидрата углекислого газа ${{\xi }_{{(d)}}}$ и значений параметров на нем:

(17)

$\frac{{\left( {p_{{(n)}}^{2} - p_{{(d)}}^{2}} \right)\exp \left( { - \frac{{\xi _{{(d)}}^{2}}}{{4{{\eta }_{{(2)}}}}}} \right)}}{{\int\limits_{{{\xi }_{{(n)}}}}^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(2)}}}}}} \right)} d\xi }} = {{A}_{{(2)}}}{{p}_{{(d)}}}{{\xi }_{{(d)}}},$

(18)

$\frac{{\left( {p_{{(d)}}^{2} - p_{0}^{2}} \right)\exp \left( { - \frac{{\xi _{{(d)}}^{2}}}{{4{{\eta }_{{(3)}}}}}} \right)}}{{\int\limits_{{{\xi }_{{(d)}}}}^\infty {\exp \left( { - \frac{{{{\xi }^{2}}}}{{4{{\eta }_{{(3)}}}}}} \right)} d\xi }} = {{A}_{{(3)}}}{{p}_{{(d)}}}{{\xi }_{{(d)}}},$

(19)

$\begin{gathered} \frac{{\left( {{{T}_{{(d)}}} - {{T}_{{(n)}}}} \right)\exp \left( { - \frac{{\xi _{{(d)}}^{2}}}{4} - {{{\rm X}}_{{(2)}}}p_{{(d)}}^{2}} \right)}}{{\int\limits_{{{\xi }_{{(n)}}}}^{{{\xi }_{{(d)}}}} {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(2)}}}p_{{(2)}}^{2}} \right)} d\xi }} - \hfill \\ - \,\,\frac{{\left( {{{T}_{0}} - {{T}_{{(d)}}}} \right)\exp \left( { - \frac{{\xi _{{(d)}}^{2}}}{4} - {{{\rm X}}_{{(3)}}}p_{{(d)}}^{2}} \right)}}{{\int\limits_{{{\xi }_{{(d)}}}}^\infty {\exp \left( { - \frac{{{{\xi }^{2}}}}{4} - {{{\rm X}}_{{(3)}}}p_{{(3)}}^{2}} \right)} d\xi }} = {{B}_{{(2)}}}{{\xi }_{{(d)}}}, \hfill \\ \end{gathered} $

где ${{A}_{{(2)}}} = \frac{{\phi {{\mu }_{c}}{{\chi }^{{(T)}}}}}{{{{k}_{c}}}}\left( {\frac{{{{\rho }_{h}}G{{S}_{h}}}}{{{{\rho }_{{0c}}}}} + 1 - {{S}_{h}}} \right),$ ${{A}_{{(3)}}}$ = $\frac{{\phi {{\mu }_{{\text{m}}}}{{\chi }^{{(T)}}}}}{{{{k}_{{\text{m}}}}}}$ × × (1 – S_v0), ${{B}_{{(2)}}}$ = $\frac{{\phi {{\rho }_{h}}{{L}_{h}}{{S}_{h}}}}{{2\rho C}}.$

Система граничных уравнений (14)–(19) в работе решена следующим образом. Вначале задается нулевое приближение искомых величин на фронте кипения. Далее, решая квадратное уравнение (17), находим величину p_(d) (как функцию ${{\xi }_{{(d)}}}$), подставляя которую в уравнение (18) получим трансцендентное уравнение для нахождения ${{\xi }_{{(d)}}}.$ Решив данное уравнение (методом половинного деления), определим величину ${{\xi }_{{(d)}}}$ (и соответственно p_(d)), а затем из (19) определяем T_(d). Далее, решая квадратное уравнение (14), находим новое приближение величины p_(n) (как функцию ${{\xi }_{{(n)}}}$) и подставляя ее в (16) новое приближение величины T_(n) (как функцию ${{\xi }_{{(n)}}}$). Подставляя найденные значения p_(n) и T_(n) в уравнение (15) получим трансцендентное уравнение для нахождения ${{\xi }_{{(n)}}}.$ Решая данное уравнение (методом половинного деления), определяем новое приближение величины ${{\xi }_{{(n)}}}$ (и соответственно p_(n) и T_(n)). В результате циклического повторения описанной итерационной процедуры получаем последовательность приближенных значений, которая сходится к искомым значениям граничных параметров.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

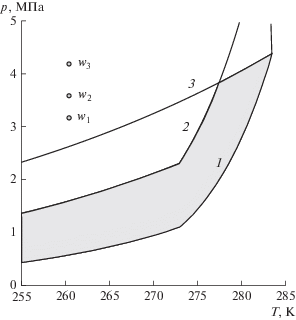
На основе уравнений (11)–(19) были проведены расчеты для случая закачки двуокиси углерода с температурой T_w = 260 К и трех разных значениях давления инжекции p_w = 3.2 (а), 3.6 (б), 4.2 (в) МПа. Данные значения давления и температуры соответствуют существованию диоксида углерода в жидком состоянии (рис. 3).

Рис. 3.

Фазовая диаграмма для систем “CO₂–H₂O” и “CH₄–H₂O”. Точки w₁, w₂ и w₃ соответствуют параметрам инжектируемого диоксида углерода, а закрашенная область соответствует рассматриваемой в модели термодинамической области исходных параметров пласта.

Здесь и далее (если не оговорено иное) для параметров, характеризующих систему, приняты следующие значения: $\phi $ = 0.1, S_v0 = 0.2, p₀ = 3.0 МПа, T_w = = 260 К, T₀ = 279 К, k = 5 × 10^–16 м², G = 0.28, λ = = 2 Вт/(м К), ρC = 2 × 10⁶ Дж/(К кг), ρ_h = 1100 кг/м³, ρ_v = 1000 кг/м³, ρ_0l = 890 кг/м³, C_l = 2800 Дж/(К кг), C_c = 800 Дж/(К кг), C_m = 1560 Дж/(К кг), R_gc = = 189 Дж/(К кг), R_gm =520 Дж/(К кг), μ_l = 1 × × 10^–4 Па с, μ_c = 1.3 × 10^–5 Па с, μ_m = 1 × 10^–5 Па с, L_h = 4 × 10⁵ Дж/кг, L_l = 2.25 × 10⁵ Дж/кг, $\theta $ = 1610 К, T_c0 = 274 К, p_c0 = 3.56 МПа.

Вычисленные распределения температуры и давления приведены на рис. 4. Штриховая линия показывает равновесную температуру разложения гидрата углекислого газа, соответствующую вычисленному распределению давления.

Рис. 4.

Распределение температуры и давления при давлении инжекции p_w = 3.2 (а), 3.6 (б) и 4.2 (в) МПа. Штриховая линия – равновесная температура разложения гидрата диоксида углерода.

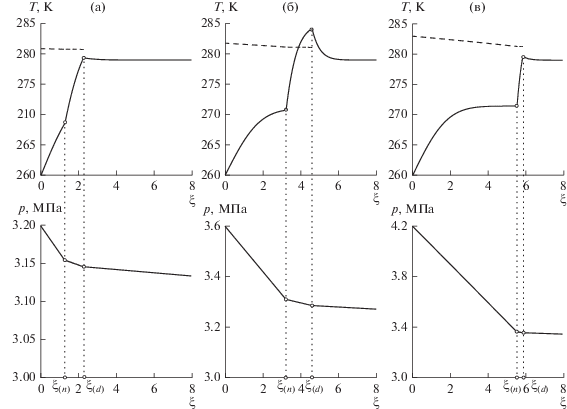
Процесс гидратообразования сопровождается выделением скрытой теплоты фазовых переходов. В этой связи температура в областях, насыщенных гидратом диоксида углерода, может подняться до значений, вызывающих его диссоциацию. Рисунок показывает, что при небольшом значении давлении инжекции диоксида углерода p_w = 3.2 МПа (случай a) температура пласта в областях, насыщенных гидратом, ниже равновесной температуры его диссоциации. Это обусловлено тем, что в этом случае газогидратная зона расположена очень близко к холодной левой границе пласта, что обеспечивает эффективный отвод через эту границу тепла, выделяющегося при гидратообразовании.

При более высоком давлении инжекции диоксида углерода p_w = 3.6 МПа (случай б) расчетная температура пласта на некотором участке области, насыщенной гидратом (непосредственно за фронтом гидратообразования), поднимается выше равновесной температуры его разложения (в рамках рассматриваемой модели с фронтальной границей образования газогидрата). Это обусловлено тем, что в этом случае фронт гидратообразования расположен уже достаточно далеко от холодной левой границы пласта, что снижает эффективность отвода через эту границу тепла, выделяющегося на фронте образования газогидрата углекислого газа. В этом случае модель с фронтальной границей образования газогидрата не дает адекватного описания процесса и поэтому необходимо рассматривать образование гидрата углекислого газа в протяженной (объемной) области.

При еще более высоком давлении инжекции диоксида углерода p_w = 4.2 МПа (случай в) температура пласта за фронтом гидратообразования снова опускается ниже равновесной температуры его диссоциации. Это обусловлено тем, что согласно рис. 4в в этом случае фронт гидратообразования расположен очень близко к фронту кипения. А поскольку кипение сопровождается поглощением скрытой теплоты парообразования, то это приводит к охлаждению участков пласта, расположенных около фронта кипения. Следовательно, в этом случае (как и при параметрах, соответствующих рис. 4а) модель с фронтальной границей гидратообразования дает адекватное математическое описание процесса.

На рис. 5 приведены зависимости автомодельных координат и температур границ кипения (кривые 1) и гидратообразования (кривые 2) от давления инжекции при k₀ = 5 × 10^–16 м² (а) и k₀ = = 3 × 10^–16 м² (б). Штриховая линия показывает равновесную температуру разложения гидрата диоксида углерода, соответствующую давлению на фронте гидратообразования. Рисунок 5а иллюстрирует превышение температуры на фронте образования газогидрата CO₂ над температурой его диссоциации (т.е. возможность существования режима с протяженной областью гидратообразования) лишь в определенном диапазоне значений давления инжекции. Согласно рис. 5б при достаточно низком значении проницаемости температура на фронте гидратообразования не поднимается выше равновесной температуры диссоциации газогидрата CO₂ (что соответствует режиму с фронтальным гидратообразованием) при любых значениях давления инжекции. Это обусловлено тем, что в низкопроницаемых пластах скорость фильтрации диоксида углерода очень низка и сравнима со скоростью распространения температурного фронта охлаждения от холодной левой границы пласта. Поэтому вследствие эффективного охлаждения от левой границы температура в зоне образования газогидрата CO₂ не поднимается выше температуры его диссоциации.

Рис. 5.

Зависимость автомодельных координат и температур границ кипения (1) и гидратообразования (2) от давления инжекции диоксида углерода при k₀ = 5 × 10^–16 м² (а) и 3 × 10^–16 м² (б). Штриховая линия – равновесная температура разложения гидрата диоксида углерода, соответствующая давлению на фронте гидратообразования.

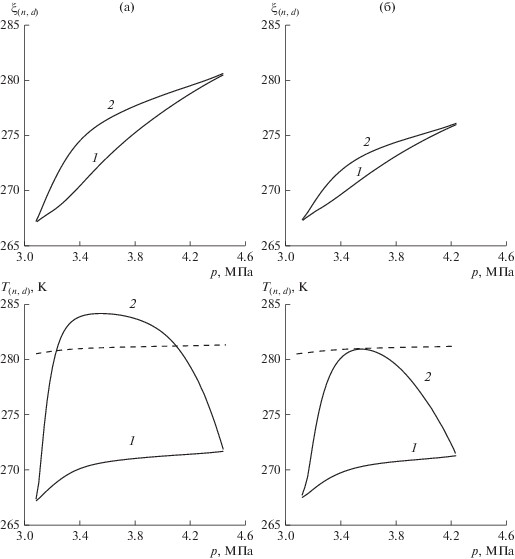
Также согласно рис. 5 при очень низких или очень высоких значениях давления инжекции наблюдается выравнивание координат фронтов, т.е. вырождение промежуточной области (зоны кипения диоксида углерода). Следовательно, режим с кипением диоксида углерода реализуется лишь в определенном диапазоне давлений. Существование верхней границы данного диапазона обусловлено тем, что кипение диоксида углерода требует достаточно низких значений давления. Существование нижней границы указанного диапазона обусловлено тем, что для кипения диоксида углерода необходимы достаточно высокие значения температуры. Действительно, при низких значениях давления инжекции скорость распространения диоксида углерода достаточно мала и сравнима со скоростью распространения температурного фронта охлаждения от холодной левой границы пласта. Следовательно, в этом случае температура области, насыщенной диоксидом углерода, не поднимается выше температуры его кипения.

Также согласно рис. 5 диапазон существования решений с кипением диоксида углерода сужается с уменьшением проницаемости, т.е. режим с вскипанием CO₂ характерен для высокопроницаемых пластов. Это обусловлено тем, что снижение проницаемости уменьшает скорость фильтрации и соответственно вызывает смещение зоны, насыщенной диоксидом углерода, ближе к холодной левой границе пласта, где термобарические условия способствуют существованию CO₂ в жидком состоянии.

Таким образом, согласно рис. 5 возможны качественно различные режима протекания рассматриваемого процесса: с фронтальным или протяженным гидратообразованием, а также с кипением и без кипения диоксида углерода. На рис. 6 приведены зависимости предельных давлений инжекции, разделяющих режимы с фронтальным и протяженным гидратообразованием (кривая 1), а также режимы с кипением и без кипения диоксида углерода (кривая 2), от проницаемости (а) при p₀ = 3 МПа и от начального давления (б) при k₀ = = 5 × 10^–16 м². Данные кривые разделяют плоскости параметров “давление инжекции–проницаемость”, а также “давление инжекции–начальное давление” на три области. Область I соответствует существованию решений с объемным гидратообразованием и кипением. Данный режим характерен для высокопроницаемых пластов с низким начальным давлением. В области II расположены решения с кипением и фронтальным гидратообразованием. Область III соответствует существованию решений с фронтальным гидратообразованием и без кипения. Данный режим характерен для низкопроницаемых пластов с высоким начальным давлением. Зависимость, полученная на рис. 6а, обусловлена, как было указано выше, смещением зоны, насыщенной диоксидом углерода, с понижением проницаемости ближе к холодной левой границе пласта. Поэтому уменьшение проницаемости способствует отсутствию кипения, а также способствует полному переходу воды в гидрат на фронтальной поверхности. Зависимость предельных давлений инжекции, разделяющих разные режимы, от начального давления, представленная на рис. 6б, может быть объяснена следующими факторами. Повышение начального давления способствует существованию диоксида углерода в жидком состоянии. При фиксированном давлении инжекции увеличение начального давления снижает перепад давлений в пласте, а значит, уменьшает скорость распространения диоксида углерода и удаленность насыщенной им зоны от холодной левой границы пласта. В этом случае вследствие эффективного охлаждения от левой границы пласта температура в зоне образования газогидрата CO₂ не поднимается выше температуры его диссоциации.

Рис. 6.

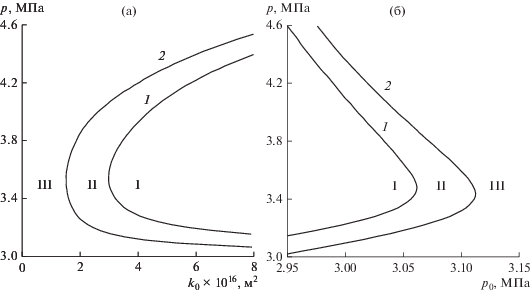
Зависимость предельных давлений инжекции, разделяющих режимы с фронтальным и протяженным гидратообразованием (1), а также режимы с кипением и без кипения диоксида углерода (2), от проницаемости (а) при p₀ = 3 МПа и от начального давления (б) при k₀ = 5 × 10^–16 м². I – режим с объемным гидратообразованием и кипением; II – режим с фронтальным гидратообразованием и кипением; III – режим без кипения.

ЗАКЛЮЧЕНИЕ

Исследована математическая модель образования газогидрата углекислого газа на фронтальной границе при инжекции жидкого диоксида углерода, сопровождающейся его кипением. Показано, что процессу полного переходa воды в газогидрат на фронтальной границе препятствует выделение тепла при гидратообразовании и способствует поглощение тепла при кипении диоксида углерода. Показано, что при достаточно близком расположении фронтов кипения и гидратообразования в пласте режим с фронтальной границей гидратообразования реализуется даже при интенсивной инжекции диоксида углерода. Установлено, что существует некоторое предельное значение проницаемости, ниже которого режим с фронтальной границей гидратообразования реализуется при любых значениях давления инжекции. На плоскости параметров “давление инжекции–проницаемость”, а также “давление инжекции–начальное давление” выделены три области, соответствующие качественно различным режимам протекания процесса.

ОБОЗНАЧЕНИЯ

C	удельная массовая теплоемкость, Дж/(К кг)
G	относительное массовое содержание газа в газогидрате
L	удельная теплота фазового перехода, Дж/кг
R	газовая постоянная, Дж/(К кг)
S	насыщенность
T	температура, К
k	коэффициент проницаемости, м²
p	давление, Па
t	время, с
x	координата, м
β	коэффициент объемного сжатия жидкой двуокиси углерода
θ	эмпирический параметр, К
$\lambda $	коэффициент теплопроводности, Вт/(м К)
$\mu $	коэффициент динамической вязкости, Па с
$\xi $	безразмерная автомодельная переменная
$\rho $	плотность, кг/м³
$\upsilon $	скорость, м/с
$\phi $	коэффициент пористости пласта

ИНДЕКСЫ

0	начальное состояние
c	углекислый газ
d	границa между второй и третьей областями
g	газовая фаза
h	газогидрат
j	номер области
l	жидкий диоксид углерода
m	метан
n	границa между первой и второй областями
v	вода
w	левая граница пласта

Список литературы

Jadhawar P., Mohammadi A., Yang J., Tohidi B. Subsurface carbon dioxide storage through clathrate hydrate formation // Advances in the Geological Storage of Carbon Dioxide. 2006. P. 111.
Benson S.M, Cole D.R. CO₂ sequestration in deep sedimentary formations // Elements. 2008. V. 4. P. 325.
Oldenburg C.M., Pruess R., Benson S.M. Process modeling of CO₂ injection into natural gas reservoirs for carbon sequestration and enhanced gas recovery // Energy and Fuel. 2001. V. 15. P. 293.
Advances in the geological storage of carbon dioxide. NATO Sci. Ser. / Ed. by Lombardi S., Altunina L.K., Beaubien S.E. Berlin, Springer Publ., 2006.
Metz B., Davidson O., de Coninck H.C., Loos M., Meyer L.A. IPCC special report on carbon dioxide capture and storage. Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press. 2005.
Duchkov A.D., Sokolova L.S., Ayunov D.E., Permyakov M.E. Assesment of potential of west siberian permafrost for the carbon dioxide storage // Earth’s Cryosphere. 2009. V. 13. № 4. P. 62. [Дучков А.Д., Соколова Л.С., Аюнов Д.Е., Пермяков М.Е. Оценка возможности захоронения углекислого газа в криолитозоне Западной Сибири // Криосфера Земли. 2009. Т. 13. № 4. С. 62.]
Chuvilin E.M., Guryeva O.M. Experimental investigation of CO₂ gas hydrate formation in porous media of frozen and freezing sediments // Earth’s Cryosphere. 2009. V. 13. № 3. P. 70. [Чувилин Е.М., Гурьева О.М. Экспериментальное изучение образования гидратов СО₂ в поровом пространстве промерзающих и мерзлых пород // Криосфера Земли. 2009. Т. 13. № 3. С. 70.]
Khasanov M.K., Gimaltdinov I.K., Stolpovsky M.V. Specific features of the formation of gas hydrates during the injection of a cold gas into a porous medium saturated with a gas and water // Theor. Found. Chem. Eng. 2010. V. 44. №. 4. P. 424. [Хасанов М.К., Гималтдинов И.К., Столповский М.В. Особенности образования газогидратов при нагнетании холодного газа в пористую среду, насыщенную газом и водой // Теорет. основы хим. технологии. 2010. Т. 44. № 4. С. 442.]
Shagapov V.Sh., Musakaev N.G., Khasanov M.K. Formation of gas hydrates in a porous medium during an injection of cold gas // Int. J. Heat Mass Transfer. 2015. V. 84. P. 1030.
Khasanov M.K. Investigation of regimes of gas hydrate formation in a porous medium, partially saturated with ice // Thermophysics and Aeromechanics. 2015. V. 22. № 2. P. 255. [Хасанов М.К. Исследование режимов образования газогидратов в пористой среде, частично насыщенной льдом // Теплофизика и аэромеханика. 2015. Т. 22. № 2. С. 255.]
Tsypkin G.G. Formation of carbon dioxide hydrate at the injection of carbon dioxide into a depleted hydrocarbon field // Fluid Dynamics. 2014. V. 49. № 6. P. 789. [Цыпкин Г.Г. Образование гидрата углекислого газа при его инжекции в истощенное месторождение углеводородов // Изв. РАН. Механика жидкости и газа. 2014. № 6. С. 101.]
Tsypkin G.G. Formation of hydrate in injection of liquid carbon dioxide into a reservoir saturated with methane and water // Fluid Dynamics. 2016. V. 51. № 5. P. 672. [Цыпкин Г.Г. Образование гидрата при инжекции жидкой двуокиси углерода в пласт, насыщенный метаном и водой // Изв. РАН. Механика жидкости и газа. 2016. № 5. С. 99.]
Истомин В.А., Якушев В.С. Газовые гидраты в природных условиях. М.: Недра, 1992.
Yang M., Song Y., Zhao Y., Liu Y., Jiang L., Li Q. MRI measurements of CO₂ hydrate dissociation rate in a porous medium // Magn. Reson. Imaging. 2011. V. 29. P. 1007.
Цыпкин Г.Г. Течения с фазовыми переходами в пористых средах. М.: Физматлит, 2009.
Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика. М.: Недра, 1993.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал