Теоретические основы химической технологии, 2019, T. 53, № 6, стр. 622-633
Гидродинамика и массообмен на вихревой ступени при барботаже
Н. А. Войнов a, *, А. С. Фролов a, А. В. Богаткова a, Д. А. Земцов a, О. П. Жукова a
a Сибирский государственный университет науки и технологий им. академика М.Ф. Решетнёва
Красноярск, Россия
* E-mail: n.a.voynov@mail.ru
Поступила в редакцию 16.03.2019
После доработки 01.06.2019
Принята к публикации 10.06.2019
Аннотация
Разработаны и исследованы вихревые контактные устройства для ввода газа, позволяющие увеличить нагрузки по газу и жидкости на ступени в сравнении с клапанными и колпачковыми устройствами, снизить флуктуации газожидкостной среды на поверхности жидкости, повысить эффективность разделения. На основании экспериментальных исследований и численного моделирования установлена схема движения жидкости и газа на ступени, рассчитаны профили их скорости при барботаже. Определены параметры ступени: гидравлическое сопротивление, газосодержание, среднеповерхностный диаметр пузырьков, межфазная поверхность, эффективность, коэффициенты массоотдачи. Представлены зависимости для их расчета. Разработана конструкция вихревой ступени для исчерпывающей ректификационной колонны, обеспечивающая при факторе скорости до 3 Па0.5 и плотности орошения 78 м3/(ч м2) снижение металлоемкости в 1.5 раза в сравнении со стандартной колпачковой тарелкой и увеличение эффективности.
ВВЕДЕНИЕ
Контактные массообменные ступени большой производительности по газу (пару) и жидкости востребованы при проведении процессов абсорбции, ректификации, аэрации [1, 2].
Одним из направлений совершенствования конструкций массообменных аппаратов является использование вихревых ступеней, которые могут эффективно работать на загрязненных средах при больших нагрузках по газу и жидкости, позволяют обеспечить требуемую межфазную поверхность, снизить металлоемкость.
Известны различные типы центробежных тарелок [3–8], которые можно разделить на вихревые ступени, вихревые камеры и прямоточно-вихревые устройства. Конструкции ступеней [9, 10], выполненных на основе прямоточно-вихревых контактных устройств, обладают большой пропускной способностью по газу вследствие установки сепараторов и обеспечения тем самым высокой скорости газовой фазы по сечению колонны. Однако из-за большой металлоемкости, низкой производительности по жидкости, а также отсутствия перемешивания рабочей смеси между контактными элементами на ступени они не нашли широкого применения в промышленности.
Конструкции тарелок на основе вихревой камеры или ступени [11, 12], на которых газожидкостная смесь совершает вращательное движение на поверхности цилиндрических перегородок или вставок, не обеспечивают достаточную эффективность при высокой нагрузке по жидкости и в основном востребованы для создания укрепляющих ректификационных колонн. В этой связи целесообразнее использовать вихревые ступени в режиме барботажа. Однако их внедрение сдерживается вследствие не достаточной изученности гидродинамики и массообмена.
Целью работы является определение путем экспериментальных исследований и математического моделирования параметров вихревой ступени для нужд конструирования и прототипирования газожидкостных аппаратов.
МЕТОДИЧЕСКАЯ ЧАСТЬ
Типы исследованных контактных устройств ступеней, выполненные по 3D-модели технологией послойной печати, представлены на рис. 1, а их конструктивные параметры – в табл. 1.
Таблица 1.
Параметры контактных устройств (завихрителей) (dout,din – наружный и внутренний диаметры завихрителя, h – высота канала, b, b1 – ширина канала, n – количество каналов)
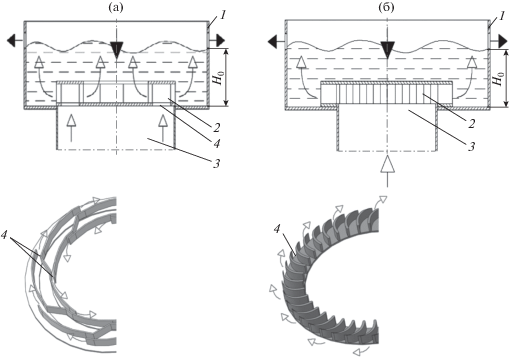
Схема потоков жидкости и газа на контактной ступени с кольцевыми каналами представлена на рис. 2а, с тангенциальными каналами – на рис. 2б.
Рис. 2.
Схемы потоков на контактной ступени: (а) – с кольцевыми каналами завихрителя; (б)
– с тангенциальными каналами; 1 – царга, 2 – завихритель, 3 – газовый патрубок, 4 – каналы для входа газа;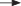 
– жидкость; 
– газ.
Диаметр царги 1 (рис. 2) изменялся от 0.18 до 0.38 м. При использовании барботера, вместо контактных устройств, диаметр царги составил 0.3–0.52 м, диаметр отверстий в барботере 1.5–5.0 мм, количество отверстий 12–68.
Расход воздуха варьировался от 10 до 100 м3/ч и измерялся нормальной диафрагмой. Гидравлическое сопротивление ступени определялось дифференциальным манометром. Среднерасходная и угловая скорости газожидкостного потока определялись при помощи ввода маркера в жидкость на расстоянии 10 мм от стенки ступени, его перемещение фиксировалось видеосъемкой с последующей обработкой данных [13].
Величина коэффициента гидравлического сопротивления сухой ступени определялась по зависимости
(1)
$\xi = {{2\Delta Р} \mathord{\left/ {\vphantom {{2\Delta Р} {{{\rho }_{G}}{{u}_{G}}^{2}}}} \right. \kern-0em} {{{\rho }_{G}}{{u}_{G}}^{2}}},~$Величина газосодержания в слое жидкости определялась объемным методом согласно
где H0 – высота слоя жидкости на ступени, м; HG–L – высота газожидкостного слоя, м.Среднеповерхностный диаметр пузырька определялся при помощи фотосъемки согласно [13, 14]
где ni – количество пузырей определенного размера; dbi – диаметр пузыря, м.Размер пузырей рассчитывался по зависимости [15]
(4)
${{d}_{b}} = 3.48 \times {{\left( {\frac{{{{\sigma }^{3}}}}{{{{\xi }^{3}}\rho _{L}^{3}\varepsilon _{G}^{2}}}} \right)}^{{\frac{1}{5}}}}.$Межфазная поверхность определялась как
(5)
$a = {{6\varphi } \mathord{\left/ {\vphantom {{6\varphi } {{{d}_{b}}}}} \right. \kern-0em} {{{d}_{b}}}}.$Массообмен на ступени изучался на примере абсорбции водой кислорода воздуха. Расход воды с пониженным содержанием кислорода варьировался от 0.1 до 3.0 м3/ч. Начальная концентрация кислорода в воде составляла 0.15 × 10–3 кг/м3. Концентрация кислорода в воде определялась датчиком полярографического типа.
Коэффициенты массоотдачи, полученные экспериментально при температурах 18–30°С, приводились к температуре 20°С.
Интенсивность массоотдачи определялась по зависимости [11]
Диссипация энергии εG (Вт/кг), вводимой струями воздуха в рабочий объем царги, рассчитывалась по формуле [15, 16]
(7)
${{\varepsilon }_{G}} = {{{{Е}_{G}}} \mathord{\left/ {\vphantom {{{{Е}_{G}}} M}} \right. \kern-0em} M},$внутренняя энергия ЕG рассчитывалась согласно
Энергия входного потока газа
(9)
${{Е}_{{G{\text{in}}}}} = {{Q}_{G}}{{\rho }_{G}}\frac{{u_{G}^{2}}}{2} + {{Q}_{G}}{{\rho }_{L}}Hg,$энергия выходного потока газа
Эффективность ступени рассчитывалась по зависимости [11]
Для изучения гидродинамических параметров на ступени и получения полей скоростей жидкой и газовой фаз был применен метод численного моделирования в программе COMSOL Multiphysics, которая является интерактивной средой, основанной на дифференциальных уравнениях в частных производных [17]. Расчеты проводили по модели турбулентности k–ε совместно с моделью пузырькового течения Шварца–Тернера, описывающей перемещение в воде воздушных пузырьков со средним диаметром 1–10 мм [18]. Указанная модель является упрощением двухжидкостной модели, рассматривающей две фазы как взаимопроникающую среду. Уравнения неразрывности и баланса импульса описывают динамику каждой из фаз при следующих допущениях: плотность газа незначительна по сравнению с плотностью жидкости, движение пузырьков газа относительно жидкости определяется балансом сил вязкого сопротивления и давления, две фазы имеют одинаковое поле давлений. Программное обеспечение пакета поддерживает конечно-элементную технологию совместно с адаптивным построением сетки и контролем ошибок. В построении расчетной сетки были использованы треугольные элементы со стандартной сеткой типа Normal, обеспечивающей разбиение на элементы и увеличение их количества в зоне взаимодействия газа и жидкости.
В параметрах решателя, отвечающих за точность (Relative tolerance), было выбрано значение 0.001.
В начальных условиях расчета задавались начальная скорость газовой фазы uG0 = 0.2–0.8 м/с, диаметр пузырьков 5–10 мм, высота слоя жидкости на тарелке – H0 = 0.1 м. Физические свойства жидкости (воды) и газовой фазы (воздуха) принимались при температуре 20оС.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Результаты численного моделирования. Расчетное газосодержание в жидкости на ступени представлено на рис. 3а. Из рисунка видно, что в поверхностном слое жидкости образуется газожидкостный слой величиной dG–L, размер которого зависит от скорости газовой фазы в канале и диаметра ступени. Распределению доли пузырьков газа в жидкости способствует циркуляционное движение слоев жидкости на ступени, что подтверждает анализ профилей скоростей жидкости на ступени (рис. 3б). Циркуляционное движение газожидкостной смеси наблюдается в объемах жидкости между стенкой ступени и каналом для выхода газа, а также в объеме между соседними каналами (рис. 3, позиция 2) для выхода газовой фазы. В исследованном диапазоне начальных скоростей газовой фазы наибольшая скорость движения жидкости uLz = 0.5–0.9 м/c наблюдается в месте ее контакта с восходящим потоком газовой фазы в осевом направлении z, а также в поверхностных слоях жидкости на ступени в направлении оси x.
Рис. 3.
Изменение газосодержания в жидкости (а) и скорости жидкости (б) по высоте ступени, рассчитанные при H0 = 0.05 м, S = 0.1 м, dout = 0.2 м, t = 5 с, uG0= 0.8 м/c, db = 10 мм: 1 – царга; 2 – канал выхода газовой фазы.
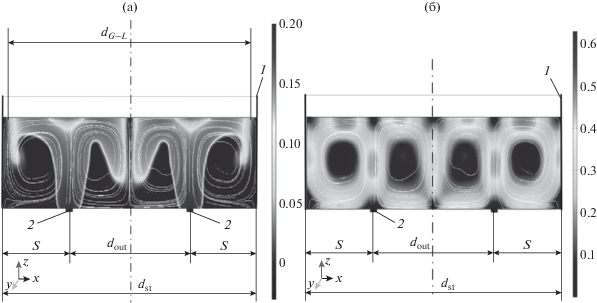
Анализ профилей скорости газа позволяет заключить, что c увеличением размера пузырька скорость uGz возрастает. Так, при заданном диаметре пузырька 10 мм она составила 0.85–0.95 м/с, а для пузырьков диаметром 5 мм – 0.6–0.7 м/с.
Исходя из полученной расчетом скорости жидкости на ступени, диаметр пузырьков газа, увлекаемых потоком газожидкостной среды, может достигать 8 мм [19].
Как установлено, при увеличении расстояния S от стенки царги до канала для выхода газовой фазы происходит снижение циркуляции жидкости на ступени. Например, при S = 0.1 м максимальная скорость составила 0.48 м/c, а при величине 0.2 м – 0.24 м/c.
Полученные при моделировании данные распределения потоков подтверждаются экспериментальными наблюдениями и анализом режимов движения жидкости на ступени. Как установлено, при сравнительно небольших расходах газа на ступени наблюдается струйный режим взаимодействия фаз, при котором наблюдается восходящее движение струй газа и отдельных больших пузырьков с флуктуацией объемов газожидкостной смеси на поверхности жидкости (рис. 4а). Такой режим работы наблюдался нами также при работе колпачковых и клапанных устройств при больших нагрузках по газу.
Рис. 4.
Структура газожидкостной смеси на вихревой ступени: (а) – струйный режим; (б) – барботажный режим; (в) – барботажно-кольцевой режим.
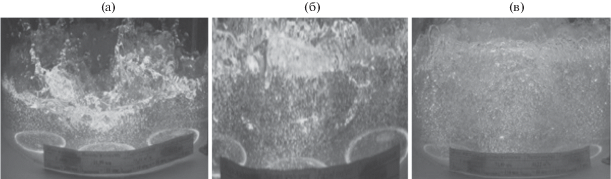
С увеличением расхода струи газа смыкаются, образуя восходящий газожидкостный поток диаметром dG–L, вырывающийся на 20–50 мм над поверхностью жидкости. Как установлено экспериментально, с увеличением расхода газа, высоты слоя жидкости на ступени и диаметра завихрителя величина dG–L возрастает (рис. 5), что согласуется с данными, полученными при численном моделировании.
Рис. 5.
Изменение диаметра газожидкостного слоя на поверхности жидкости в зависимости от расхода газа для различных типов завихрителей при dst = 0.38 м. Экспериментальные точки 1–2 – завихритель № 5: 1 – H0 = 0.057 м; 2 – H0 = 0.076 м; 3–5 – завихритель № 3: 3 – H0 = 0.057 м; 4 – H0 = 0.076 м; 5 – H0 = 0.095 м; 6–8 – завихритель № 6: 6 – H0 = 0.057 м; 7 – H0 = = 0.076 м; 8 – H0 = 0.095 м.
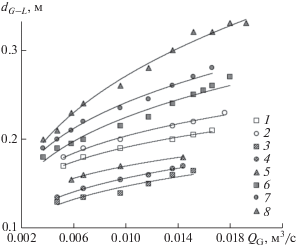
При дальнейшем увеличении расхода газа возникает барботажно-кольцевой режим (рис. 4в), при котором достигается наибольшая величина dG–L и, вследствие циркуляции жидкости на ступени, снижаются флуктуации газожидкостной фазы на поверхности жидкости.
При более высоких нагрузках по газу образуется кольцевой режим течения, характеристики которого рассмотрены нами ранее в работах [11–13].
Экспериментальные значения скорости жидкости, перемещающейся у стенки царги к полотну тарелки в зависимости от скорости газа в завихрителе при вариации его диаметра, представлены на рис. 6а. Величина скорости возрастала с увеличением расхода газа и диаметра завихрителя и при S = 0.1 м составила uLz = 0.3–0.5 м/c, а при S = 0.125 м – 0.2–0.35 м/c, что согласуется с данными моделирования (рис. 3) и подтверждает наличие циркуляции жидкости на ступени. Экспериментально определенные значения скорости жидкости на вихревой ступени сопоставимы с расчетными скоростями по модели при начальной скорости газовой фазы uG0 = 0.2–0.4 м/c и прочих равных условиях.
Рис. 6.
Зависимость линейной (а) и угловой (б) скорости жидкости от скорости газа в каналах завихрителя при dst = 0.38 м, H0 = 0.1 м. Экспериментальные точки 1–2: 1 – dout = 0.184 м, завихритель № 5; 2 – dout = 0.130 м, завихритель № 3.
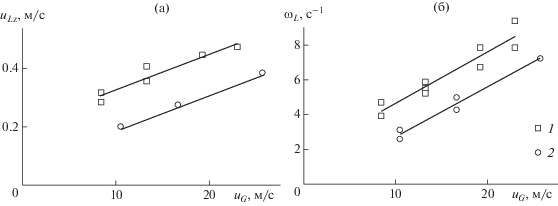
При скорости газа в каналах завихрителя менее 10 м/c наблюдается вращательно-поступательное движение только нижних слоев жидкости на ступени. При увеличении расхода газа наблюдается вращение всего объема газожидкостной смеси с угловой скоростью 3–10 с–1, что способствует формированию газожидкостной среды на ступени.
Исходя из полученных экспериментальных и расчетных данных, движение газожидкостной смеси на ступени можно представить следующим образом: струи газа, вышедшие из каналов завихрителя, имея большой скоростной напор (в отличие от колпачковых и клапанных контактных устройств), внедряются в жидкость и формируют область пузырькового течения. Восходящий газовый поток увлекает за собой жидкость, образуя циркуляционные контуры газожидкостной смеси в объеме жидкости. При этом происходит захват пузырьков газа циркулирующей жидкостью, этому способствует также вращательно-поступательное движение жидкости, в результате образуется развитая межфазная поверхность (рис. 4в). С увеличением расстояния от завихрителя до стенки царги скорость циркулирующей жидкости и величина dG–L на поверхности жидкости снижаются.
Таким образом, при конструировании промышленных ступеней на основе численного моделирования, изменяя конструктивные и технологические параметры завихрителя, можно определить условия, обеспечивающие циркуляцию жидкости на ступени.
Гидродинамические параметры ступени. Как установлено экспериментально (точки 1 и 2, рис. 7а), сопротивление вихревой ступени, на которой установлен завихритель с кольцевыми каналами (рис. 1в–1д), в 1.5 раза ниже, чем сопротивление вихревой ступени с тангенциальными каналами (рис. 1а, 1б).
Рис. 7.
Изменение коэффициента сопротивления сухой вихревой ступени (а) от параметра ${\text{R}}{{{\text{e}}}^{{ - 0.28~}}}{{\left( {\frac{h}{b}} \right)}^{{ - 0.25}}}$ и общего сопротивления ступени от расхода газа (б): (а) – экспериментальные точки 1–3: 1 – завихритель № 1; 2 – завихритель № 2; 3 – завихритель № 5; (б) – экспериментальные точки 1–4 для завихрителя № 6: 1 – H0 = 0.057 м; 2 – H0 = 0.076 м; 3 – H0 = 0.095 м; 4 – H0 = 0.114 м. Пунктирная линия – сопротивление сухой тарелки.
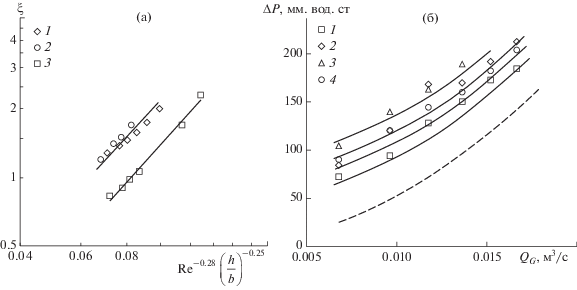
Коэффициент гидравлического сопротивления сухой вихревой ступени подчиняется зависимости [20]
где Re = (ubρ)/µ – число Рейнольдса газа, А = 21 для завихрителей № 1–2, для завихрителей № 5 с кольцевыми каналами А = 13.2.Общее гидравлическое сопротивление ступени (сплошные линии на рис. 7б) с кольцевыми каналами подчиняется зависимости
(14)
$\Delta {{P}_{{}}} = \left( {\left( {\xi \frac{{{{\rho }_{G}}u_{G}^{2}}}{2}} \right) + \left( {{{\rho }_{L}}(1 - \varphi )gH} \right)} \right).$При конструировании контактных устройств для определения размеров каналов завихрителя № 6, размещенных с внутренней и наружной стороны, необходимо, задавшись общим сопротивлением ступени и расходом газа, решить совместно уравнения (13) и (14).
Межфазная поверхность. Экспериментальные данные зависимости газосодержания φ от диссипации энергии, полученные нами ранее [21], представлены на рис. 8а. С увеличением диссипации энергии до 1.5 Вт/кг величина φ возрастает, однако дальнейший ее рост на величину газосодержания практически не влияет. Как установлено, влиянием количества каналов завихрителя на газосодержание можно пренебречь при n ≥ 8. При пропускании воздуха через барботер, установленный на ступени, величина газосодержания составила 0.1–0.15 (точки на рис. 8 не показаны).
Рис. 8.
Изменение газосодержания (а) и среднеповерхностного диаметра пузырька газа (б) от диссипации энергии при dst = 0.38 м: (а) – экспериментальные точки 1–12: 1 – завихритель № 1, H0 = 0.05–0.1 м; 2–7 – завихритель № 3–5, H0 = 0.05–0.16 м; 8, 9 – данные [12], завихритель № 2, n = 8, H0 = 0.045–0.078 м; 10–12 –данные [12], завихритель № 2, n = 4, H0 = 0.045–0.078 м; (б) – экспериментальные точки 1–9: 1–3 – завихритель № 2, n = 8, H0 = 0.05–0.16 м; 4–9 – завихритель № 3–5 при H0 = 0.05–0.16 м. Пунктирная линия – расчет по (4).
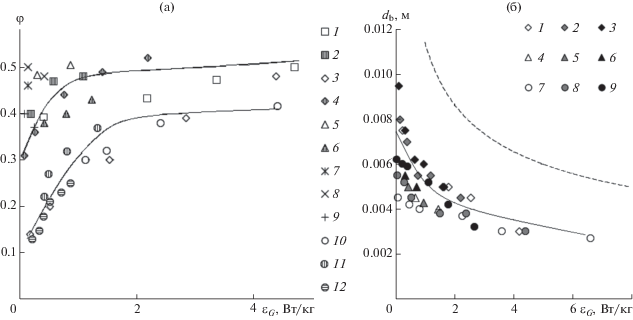
Экспериментальные значения среднеповерхностного диаметра пузырька представлены на рис. 8б, их величина составила 3–10 мм и существенно не зависела от типа завихрителя.
Зависимость диаметра пузырька, рассчитанного по уравнению (4), полученному в предположении о дроблении струй газа турбулентностью, от диссипации энергии представлена на рис. 8б пунктирной линией. Расчетный диаметр пузырька имеет примерно вдвое большую величину в сравнении с экспериментально полученными значениями. Можно предположить, что формирование пузырьков в объеме жидкости происходит не только за счет турбулентного дробления струй газа, но и за счет контакта с циркулирующей жидкостью.
Значения межфазной поверхности, рассчитанные по уравнению (5), с учетом экспериментальных данных рис. 8, представлены на рис. 9, где точки 1–7 получены при пропускании воздуха через барботер, размещенный на ступени, а точки 8–10 – при установке завихрителей № 2, 3 и 6.
Рис. 9.
Зависимость межфазной поверхности от диссипации энергии газа. Экспериментальные точки 1–7 при установке трубчатого барботера диаметром 20 мм: 1 – dst = 0.3 м, H/dst = 0.8, dop = 1.5 мм, n = 12; 2 – dst = 0.52 м, H/dst = 0.54, dop = 5 мм, n =17; 3 – dst = 0.52 м, H/dst = 0.27, dop = 5 мм, n =17; 4 – dst = 0.5 м, H/dst = 1.4, dop = 5 мм, n = 17; 5 – dst = 0.5 м, H/dst = 1.12 , dop = 5 мм, n = 17; 6 – dst = 0.52 м, H/dst = 0.54, dop = 2 мм, n = 68; 7 – dst = 0.52 м, H/dst = 0.27, dop = 2 мм, n = 68. Экспериментальные точки 8–10 согласно данным, представленным на рис. 11: 8 – завихритель № 6, 9 – завихритель № 2 при n = 4, 10 – завихритель № 3.
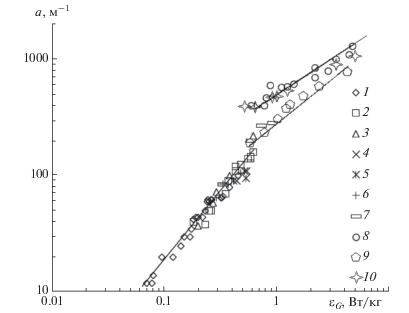
Величина межфазной поверхности на вихревой ступени с кольцевыми каналами (точки 8, рис. 9) превосходит аналогичные характеристики ступени с тангенциальными завихрителями при n = 4 (точки 9, рис. 9) и барботера, установленного в качестве контактного устройства на ступени (точки 1–7, рис. 9).
Массоотдача на вихревой ступени. С увеличением скорости в каналах завихрителя и снижением расхода жидкости эффективность ступени возрастает (рис. 10а). Значения эффективности стандартного колпачкового устройства диаметром 80 мм (точки 6, рис. 10а) составили меньшую величину в сравнении с вихревой ступенью.
Рис. 10.
Зависимость эффективности ступени от соотношения расходов (а) и скорости газа в каналах завихрителя (б) при H0 = 0.1 м: (а) – экспериментальные точки 1–6 при uG = 20–50 м/с: 1 – завихритель № 6; 2 – завихритель № 5; 3 – завихритель № 1; 4 – завихритель № 2; 5 – завихритель № 3; 6 – колпачковое устройство; (б) – экспериментальные точки 1–5 при QL = (2.75–7.25) × 10–4 м3/с: 1 – завихритель № 6; 2 – завихритель № 5; 3 – завихритель № 1; 4 – завихритель № 2; 5 – завихритель № 3.
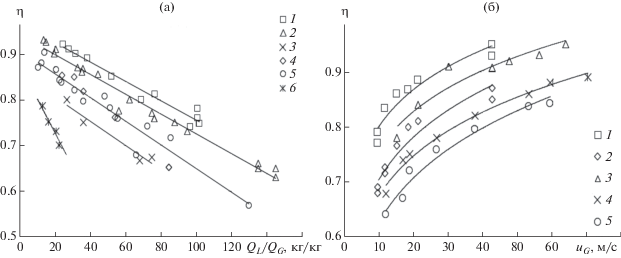
Наибольшая эффективность на ступени достигается при использовании завихрителя с кольцевыми каналами № 6. Согласно данным, представленным на рис. 11, максимальная величина объемного коэффициента массоотдачи достигается при установке на ступени контактного устройства № 6 с кольцевыми каналами, вследствие достижения наибольшей межфазной поверхности. У других типов завихрителей, вследствие меньшей величины аэрированной зоны dG–L, межфазная поверхность меньше.
Рис. 11.
Изменение объемного коэффициента массоотдачи от соотношения потоков (а) и параметра εG0.6a0.8 (б): (а) – экспериментальные точки 1–6: 1 – завихритель № 6; 2 – завихритель № 5; 3 – завихритель № 1; 4 – завихритель № 2; 5 – завихритель № 3; 6 – колпачковое усройство; (б) – экспериментальные точки 1–11: 1–6 – данные с рис. 9; 7 – завихритель № 6; 8 – завихритель № 5; 9 – завихритель № 1; 10 – завихритель № 2; 11 – завихритель № 3.
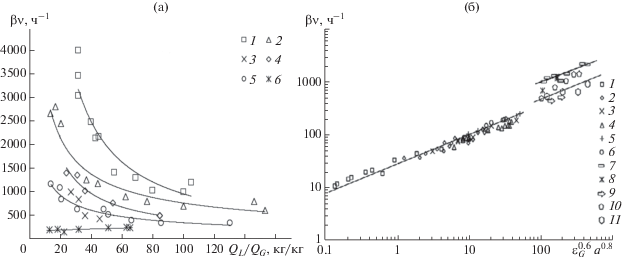
Обработка массива экспериментальных данных (рис. 11б) позволила получить зависимость объемного коэффициента массоотдачи (ч–1) при абсорбции кислорода из воздуха в виде
При наличии в емкости барботера А = 30, а для вихревой ступени с завихрителем № 6 А = 136, так как в этом случае величина dG–L максимальна.
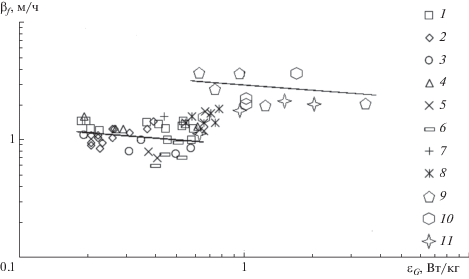
Это выражение с относительной погрешностью 25% обобщает полученный массив экспериментальных данных при плотности орошения 0.9–26 м3/(м2 ч). Величина поверхностного коэффициента массоотдачи, для данных рис. 11, представлена на рис. 12 и достигала порядка (0.5–0.8) ×10–3 м/с.
Рис. 12.
Зависимость поверхностного коэффициента массоотдачи от диссипации энергии газа. Экспериментальные точки 1–8 при пропускании воздуха через барботер (по данным рис. 9). Экспериментальные точки 9–11: 9 – завихритель № 6; 10 – завихритель № 1; 11 – завихритель № 2 при n = 8.
На основании полученных данных разработана конструкция вихревой ступени исчерпывающей ректификационной бражной колонны (рис. 13). Ступень рассчитана по данным [2] при расходе питания 80 и 120 м3/ч, которым соответствуют расходы пара соответственно 2.84 и 4.2 кг/c при средней плотности паров 1 кг/м3.
Рис. 13.
Ступень ректификационной исчерпывающей колонны с вихревыми контактными устройствами с кольцевыми каналами: 1 – царга, 2 – переток, 3 – полотно тарелки, 4 – завихритель, 5 – каналы для входа газа.
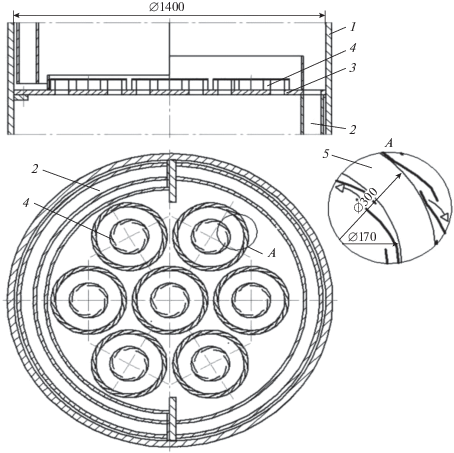
Внутренний диаметр ректификационной исчерпывающей колонны составил 1.4 м. Количество наружных каналов в контактном устройстве – 15, количество внутренних каналов – 10. Высота каналов при расходе пара 2.84 кг/с – 0.05 м, ширина канала – 0.01 м. При расходе пара 4.2 кг/c соответственно 0.075–0.01 м.
Живое сечение колонны с семью контактными элементами при dout = 0.300 м, din = 0.170 м составило 12%. Фактор скорости 1.84 и 2.72 Па0.5. Плотность орошения 52 и 78 м3/(ч м2) соответственно.
Масса ступени с 7 вихревыми контактными устройствами – 60 кг, тогда как масса стандартной колпачковой колонны [22] равна 90 кг. С учетом данных, представленных на рис. 10, при факторе скорости 1.84–2.72 Па0.5 эффективность ступени ориентировочно составила 0.85–0.95, что в сравнении с данными [23–25] позволяет обеспечить больший диапазон устойчивой работы колонны в сравнении с колпачковой и клапанной ступенями.
ЗАКЛЮЧЕНИЕ
Численное моделирование в COMSOL Multiphysics с помощью модели турбулентности k–ε совместно с моделью пузырькового течения позволило установить наличие циркуляционного движения жидкости на ступени, определить профили скоростей фаз, получить величину начальной скорости газовой фазы uG0, при которой достигается согласование экспериментальных и расчетных значений скорости жидкости uLz.
Обеспечение циркуляции жидкости на ступени со скоростью 0.2–0.5 м/c и ее вращение позволяет увлекать в объем жидкости на ступени пузырьки газа размером до 8 мм, что способствует увеличению межфазной поверхности по сравнению с барботированием жидкости.
Вихревое контактное устройство с кольцевыми каналами в барботажно-кольцевом режиме позволяет снизить флуктуации газожидкостной среды на поверхности жидкости, увеличить межфазную поверхность до 2 × 103 м–1 и достигнуть величины поверхностного коэффициента массоотдачи порядка (0.5–0.8) × 10–3 м/с.
Разработана укрепляющая ректификационная колонна с вихревыми контактными устройствами, обеспечивающая эффективность 0.85–0.95 при факторе скорости 1.84 и 2.72 Па0.5 и плотности орошения 52 и 78 м3/(ч м2). При этом ее металлоемкость в 1.5 раза ниже по сравнению со стандартной колпачковой тарелкой.
ОБОЗНАЧЕНИЯ
| А | коэффициент |
| а | межфазная поверхность, м–1 |
| b | ширина канала, м |
| С | концентрация, кг/м3 |
| D | коэффициент диффузии, м2/с |
| d | диаметр, м |
| Е | поток энергии, Вт |
| g | ускорение свободного падения, м/с2 |
| H | высота слоя жидкости на ступени, м |
| h | высота каналов в завихрителе, м |
| M | масса жидкости на ступени, кг |
| n | количество, шт. |
| Р | гидравлическое сопротивление, Па |
| Q | расход, м3/с |
| s | расстояние, м |
| t | время, с |
| u | скорость, м/с |
| V | объем жидкости, м3 |
| β | коэффициент массопередачи, с–1 |
| ε | диссипация энергии, Вт/кг |
| η | эффективность ступени |
| μ | коэффициент динамический вязкости, Па с |
| ξ | коэффициент сопротивления сухой ступени |
| ρ | плотность, кг/м3 |
| σ | коэффициент поверхностного натяжения воды, Н/м |
| φ | газосодержание |
| Re = = (ubρ)/µ | число Рейнольдса газа |
ИНДЕКСЫ
Список литературы
Ахметов С.А., Сериков Т.П., Кузеев И.Р., Баязитов М.И. Технология и оборудование процессов переработки нефти и газа: учебное пособие. СПб.: Недра, 2006.
Войнов Н.А., Жукова О.П., Воронин С.М. Результаты внедрения и исследования контактных ступеней бражных колонн // Изв. высш. учебн. завед. Лесн. ж. 2011. № 4. P. 93.
Naziri N., Zadghaffari R., Naziri H. CFD Simulation and Experimental Study of New Developed Centrifugal Trays // Int. J. Chem. Eng. Appl. 2012. V. 3. № 3. P. 201.
Belov S.A. Orazova M.A. Centrifugal Trays. Design of Decks for Strength and Rigidity // Chem. Technol. Fuels Oils. 2006. V. 42. № 5. P. 374.
Lebedev Yu.N. Mass-exchange units. High-performance centrifugal trays // Chem. Technol. Fuels Oils. 2004. V. 40. № 1. P. 55.
Lebedev Yu.N., Chekmenev V.G., Danilov D.Yu. Testing new centrifugal trays with liquid recirculation // Chem. Technol. Fuels Oils. 2010. V. 46. № 4. P. 262.
Wilkinson P., Vos E., Konijn G., Kooijman H., Mosca G., Tonon L. Distillation trays that operate beyond the limits of gravity by using centrifugal separation // Chem. Eng. Res. Des. 2007. V. 85. P. 130.
Yang Q., Mosca G., Roza M. Characteristics of Trays Using Inertial Separation Technology // Chin. J. Chem. Eng. 2010. V. 18. № 6. P. 954.
Николаев Н.А., Жаворонков Н.М., Малюсов В.А. Расчет ректификационных колонн с прямоточно-вихревыми контактными устройствами // Теор. осн. хим. технол. 1974. Т. 8. № 6. С. 853.
Савельев Н.И., Войнов Н.А., Николаев Н.А. Закономерности массопереноса в прямоточных пленочных контактных устройствах при ректификации бинарных смесей // Теор. осн. хим. технол. 1983. Т. 17. № 2. С. 254.
Voinov N.A., Zhukova O.P., Lednik S.A., Nikolaev N.A. Mass transfer in gas-liquid layer on vortex contact stages // Theor. Found. Chem. Eng. 2013. V. 47. № 1. P. 55. [Войнов Н.А., Жукова О.П., Ледник С.А., Николаев Н.А. Массоотдача в газожидкостном слое на вихревых ступенях // Теор. осн. хим. технол. 2013. Т. 47. № 1. С. 62.]
Войнов Н.А., Ледник С.А. Гидродинамика и массообмен на ступени с профилированными тангенциальными каналами // Хим. пром-сть. 2011. Т. 88. № 5. С. 250.
Voinov N.A., Zhukova O. P., Nikolaev N.A. Hydrodynamics of the vortex stage with tangential swirlers // Theor. Found. Chem. Eng. 2010. V. 44. № 2. P. 213. [Войнов Н.А., Жукова О.П., Николаев Н.А. Гидродинамика вихревой ступени с тангенциальными завихрителями // Теор. осн. хим. технол. 2010. Т. 44. № 2. С. 225.]
Shahbazi B., Rezai B., Chehreh Chelgani S., Koleini S.M.J., Noaparast M. Estimation of diameter and surface area flux of bubbles based on operational gas dispersion parameters by using regression and ANFIS // Int. J. Min. Sci. Technol. 2013. № 23. P. 343.
Островский Г.М. Прикладная механика неоднородных сред. СПб.: Наука, 2000.
Лаптева Е.А., Лаптев А.Г. Прикладные аспекты явлений переноса в аппаратах химической технологии и теплоэнергетики (гидродинамика и тепломассообмен). Казань: Печать-Сервиз XXI века, 2015.
Abd Al K.M. CFD simulation of bubbly flow through a bubble column // Int. J. Sci. Eng. Res. 2014. V. 5. № 4. P. 904.
Schwarz M.P., Turner W.J., Applicability of the Standard k–ε Turbulence Model to Gas-stirred Baths // Appl. Math. Modell. 1988. V. 12. P. 273.
Процессы и аппараты химической технологии. Явления переноса, макрокинетика, подобие, моделирование, проектирование. В 5 т. Т. 2. Механические и гидромеханические процессы / Под ред. Кутепова А.М. М.: Логос, 2002.
Voinov N.A., Zemtsov D.A., Zhukova O.P., Bogatkova A.V. Hydraulic Resistance of Tangential Swirlers // Chem. Pet. Eng. 2019. V. 55. № 1–2. P. 51. [Войнов Н.А., Земцов Д.А., Жукова О.П., Богаткова А.В. Гидравлическое сопротивление тангенциальных завихрителей // Хим. нефтегазов. машиностр. 2019. № 1. С. 31.]
Voinov N.A., Zhukova O.P., Konovalov N.M., Hydrodynamics and Heat Transfer during Boiling in a Rotating Gas–Liquid Layer // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 987. [Войнов Н.А., Жукова О.П., Коновалов Н.М. Гидродинамика и теплоотдача при кипении во вращающемся газожидкостном слое // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 689.]
Дытнерский Ю.И. Процессы и аппараты химической технологии. В 2-х томах. М.: Химия, 1991.
Лаптев А.Г., Фарахов М.И., Минеев Н.Г. Основы расчета и модернизация тепломассообменных установок в нефтехимии. Монография. Казань: Казан. гос. энерг. унив., 2010.
Поникаров И.И., Гайнулин М.Г. Машины и аппараты химических производств и нефтегазопереработки. Учебник. М.: Альфа-М, 2006.
Тимонин А.С., Балдин Б.Г., Борщев В.Я., Гусев Ю.И. и др. Машины и аппараты химических производств. Учебник для вузов. Калуга: Ноосфера, 2014.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии
Пн.-пт.: 10.00-19.00