1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 1, 2020

Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 114-124

Термокапиллярная конвекция вертикально завихренной жидкости

Н. В. Бурмашева a, *, Е. Ю. Просвиряков a, **

a Институт машиноведения УрО РАН
г. Екатеринбург, Россия

* E-mail: nat_burm@mail.ru
** E-mail: evgen_pros@mail.ru

Поступила в редакцию 11.12.2018
После доработки 15.06.2019
Принята к публикации 18.06.2019

Полный текст (PDF)

Аннотация

Представлено новое точное решение уравнений Обербека–Буссинеска для описания установившейся конвекции Марангони вертикально завихренной жидкости в сдвиговом потоке вязкой несжимаемой жидкости. Подробно исследовано поле скоростей неоднородного вихревого течения жидкости. Показано существование застойных точек при течении жидкости, количество которых может равняться пяти. Наличие застойных точек приводит к образованию противотечений с очень сложной топологией, напоминающей ячеистую структуру течения. При течении жидкости касательные напряжения не являются постоянной величиной. Они также стратифицируются на зоны растягивающих и сжимающих напряжений. Из-за структуры точного решения компоненты завихренности с точностью до диссипативного коэффициента совпадают с выражениями для касательных напряжений, что означает наличие нескольких вихрей в жидкости, которые вращаются в противоположные стороны. Аналогичные исследования полиномиальных точных решений для температуры и давления позволили определить количество областей стратификации соответствующих полей.

Ключевые слова: сдвиговые течения, точные решения, переопределенная система, противотечение, усиление скоростей, вертикальная компонента завихренности, конвекция Марангони

ВВЕДЕНИЕ

Течение несжимаемых жидкостей в природных, химических, технологических процессах, как правило, происходит в неоднородных тепловых полях, которые индуцируют конвекцию [1–4]. Естественная конвекция обусловлена расширением жидкости при нагреве, что влечет появление силы Архимеда, или действием капиллярных сил на межфазной свободной границе слоя жидкости, зависящих от температуры [1–4].

Начиная с экспериментальных работ Бенара [5–7] было показано, что важную роль в конвекции играет зависимость коэффициента поверхностного натяжения от температуры, поэтому одно из первых точных решений уравнений естественной конвекции было получено Р.В. Бирихом для описания стационарной конвекции Марангони в однонаправленном слоистом потоке вязкой несжимаемой жидкости [8, 9]. Конвективное движение жидкости, описанное в [8, 9], индуцируется заданием постоянного продольного градиента температуры на обеих границах слоя жидкости. Точное решение Бириха неоднократно открывалось заново авторами статей [10, 11].

К настоящему времени известно использование класса Бириха и его модификаций для исследований концентрационной конвекции [12, 13], для описания механизмов термодиффузии в многокомпонентных жидкостях [14–17], системах газ–жидкость [18–23] и для исследования теплообмена при действии вибраций на поток жидкости [24–27]. Довольно подробно исследованы группы преобразования уравнений Обербека–Буссинеска, позволяющих “размножать” точное решение Бириха на случай нестационарных движений жидкостей [28–32]. Стоит отметить, что значительное число исследований связано с устойчивостью течений Бириха, позволяющих моделировать сложные гидродинамические эффекты в водоемах [33–35].

В статьях [12, 28–32, 36–41] были построены более широкие классы точных решений типа Бириха для уравнений конвекции, позволяющие исследовать течения жидкости при линейном распределении горизонтальных градиентов температуры и обнаруживать новые физические эффекты. Данный класс решений применялся для исследования конвекции в сдвиговых потоках вращающейся жидкости [41–48]. В [49–52] были приведены точные решения уравнений Навье–Стокса и уравнений Обербека–Буссинеска, являющиеся примером течений жидкости с вертикальной закруткой при отсутствии вращения. В настоящей статье изучается возможность применения такого решения для описания конвекции Марангони в вертикально завихренной вязкой несжимаемой жидкости.

ПОСТАНОВКА КРАЕВОЙ ЗАДАЧИ

Конвективные сдвиговые (слоистые) течения вязкой несжимаемой жидкости принято описывать различными по физической трактовке модификациями системы уравнений Навье–Стокса [1–4, 15, 19, 21, 44, 52]. В данной статье исследуются крупномасштабные стационарные слоистые течения вязкой несжимаемой жидкости в бесконечном горизонтальном слое жидкости, у которых поперечная компонента вектора скорости полагается равной нулю. В этом случае система уравнений тепловой конвекции в приближении Буссинеска [12, 29, 31, 33, 34, 44, 52] принимает вид

(1)
$\begin{gathered} {{V}_{x}}\frac{{\partial {{V}_{x}}}}{{\partial x}} + {{V}_{y}}\frac{{\partial {{V}_{x}}}}{{\partial y}} = \nu \Delta {{V}_{x}} - \frac{{\partial P}}{{\partial x}}, \\ {{V}_{x}}\frac{{\partial {{V}_{y}}}}{{\partial x}} + {{V}_{y}}\frac{{\partial {{V}_{y}}}}{{\partial y}} = \nu \Delta {{V}_{y}} - \frac{{\partial P}}{{\partial y}}, \\ \frac{{\partial P}}{{\partial z}} = g\beta T,\,\,\,\,{{V}_{x}}\frac{{\partial T}}{{\partial x}} + {{V}_{y}}\frac{{\partial T}}{{\partial y}} = \chi \Delta T, \\ \frac{{\partial {{V}_{x}}}}{{\partial x}} + \frac{{\partial {{V}_{y}}}}{{\partial y}} = 0. \\ \end{gathered} $

Здесь ${{V}_{x}}\left( {x,y,z} \right),$ ${{V}_{y}}\left( {x,y,z} \right)$ – компоненты вектора скорости; $P\left( {x,y,z} \right)$ – отклонение давления от гидростатического, деленное на среднюю плотность жидкости; $T\left( {x,y,z} \right)$ – отклонение температуры от отсчетного значения; $\nu $, $\chi $ – кинематическая (молекулярная) вязкость жидкости и ее температуропроводность; $\Delta $ – трехмерный оператор Лапласа [1, 2].

Система (1) является переопределенной. Точное решение системы (1) будем искать в виде [30, 48, 49, 51–56]

(2)
$\begin{gathered} {{V}_{x}} = U\left( z \right) + yu\left( z \right),\,\,\,\,{{V}_{y}} = V\left( z \right), \\ T = {{T}_{0}}\left( z \right) + {{T}_{1}}\left( z \right)x + {{T}_{2}}\left( z \right)y, \\ P = {{P}_{0}}\left( z \right) + {{P}_{1}}\left( z \right)x + {{P}_{2}}\left( z \right)y. \\ \end{gathered} $

Точное решение (2) позволяет описывать вертикально завихренную жидкость вне поля силы Кориолиса [48, 49, 51, 52].

Подстановка класса (2) в систему (1) приводит последнюю к системе обыкновенных дифференциальных уравнений [30, 53–55]

(3)

Здесь и далее штрихом обозначена производная по вертикальной координате z. Уравнения системы (3) интегрируются в том порядке, в котором они выписаны.

Полагаем, что нижняя поверхность ($z = 0$) бесконечного слоя жидкости является абсолютно твердой, верхняя поверхность ($z = h$) – свободной и недеформируемой [12, 30, 31, 48, 49, 51, 52]. На верхней границе слоя $z = h$ действуют термокапиллярные силы, генерирующие конвективные течения вертикально завихренной жидкости [1, 2, 12, 29, 31]:

$\eta V_{x}^{'} = - \sigma \frac{{\partial T}}{{\partial x}},\,\,\,\,\eta V_{y}^{'} = - \sigma \frac{{\partial T}}{{\partial y}}.$

На обеих границах слоя жидкости заданы тепловые возмущения:

$T\left( {x,y,0} \right) = By,\,\,\,\,T\left( {x,y,h} \right) = \vartheta + Cx.$

Задание нулевой температуры на нижней границе $z = 0$ означает, что это значение принято за отсчетную конфигурацию. Верхнюю границу слоя считаем базовым уровнем отсчета давления. Полагаем, что задано однородное давление, совпадающее с атмосферным давлением, и по аналогии с заданием температуры принято за нуль:

$P\left( {x,y,h} \right) = 0.$

Нижняя граница бесконечного слоя жидкости может перемещаться согласно следующему закону [48, 49, 51]:

${{V}_{x}} = W\cos \alpha + \Omega y,\,\,\,\,{{V}_{y}} = W\sin \alpha .$

Отметим, что последние формулы характеризуют неоднородное параболическое распределение скоростей.

С учетом структуры класса (2) окончательно приходим к системе краевых условий на нижней границе:

(4)
$\begin{gathered} u\left( 0 \right) = \Omega ,\,\,\,\,{{T}_{0}}\left( 0 \right) = 0,\,\,\,\,{{T}_{1}}\left( 0 \right) = 0, \\ {{T}_{2}}\left( 0 \right) = B,\,\,\,\,U\left( 0 \right) = W\cos \alpha ,\,\,\,\,V\left( 0 \right) = W\sin \alpha . \\ \end{gathered} $

На верхней границе заданы следующие гидродинамические поля:

(5)
$\begin{gathered} u{\kern 1pt} '\left( h \right) = 0,\,\,\,\,{{T}_{0}}\left( h \right) = \vartheta ,\,\,\,\,{{T}_{1}}\left( h \right) = C,\,\,\,\,{{T}_{2}}\left( h \right) = 0, \\ {{P}_{0}}\left( h \right) = 0,\,\,\,\,{{P}_{1}}\left( h \right) = 0,\,\,\,\,{{P}_{2}}\left( h \right) = 0, \\ \eta U{\kern 1pt} '\left( h \right) = - \sigma {{T}_{1}}\left( h \right),\,\,\,\,\eta V{\kern 1pt} '\left( h \right) = - \sigma {{T}_{2}}\left( h \right). \\ \end{gathered} $

Точное полиномиальное решение $1$краевой задачи (3)–(5) имеет вид

$\begin{gathered} u = \Omega ;\,\,\,\,{{T}_{1}} = \frac{{Cz}}{h};\,\,\,\,{{T}_{2}} = B + \frac{{Bz}}{h} + \frac{{\Omega Cz}}{{3!h\chi }}\left[ {{{z}^{2}} - {{h}^{2}}} \right]; \\ {{P}_{1}} = \frac{{g\beta C}}{{2h}}\left[ {{{z}^{2}} - {{h}^{2}}} \right];\,\,\,\,{{P}_{2}} = - \frac{{g\beta B}}{{2h}}{{\left( {z - h} \right)}^{2}} + \\ + \,\,\frac{{g\beta C\Omega }}{{24h\chi }}{{\left( {{{z}^{2}} - {{h}^{2}}} \right)}^{2}};\,\,\,\,U = W\cos \alpha + \\ \end{gathered} $
(6)
$\begin{gathered} + \,\,\frac{{g\beta Cz}}{{4!h\nu }}\left( {{{z}^{3}} - 6{{h}^{2}}z + 8{{h}^{3}}} \right) - \frac{{g\beta B\Omega z}}{{6!h{{\nu }^{2}}}} \times \\ \times \,\,\left( {{{z}^{5}} - 6h{{z}^{4}} + 15{{h}^{2}}{{z}^{3}} - 20{{h}^{3}}{{z}^{2}} + 24{{h}^{5}}} \right) + \\ + \,\,\frac{{g\beta C{{\Omega }^{2}}z}}{{3 \times 8!h{{\nu }^{2}}\chi }}(3{{z}^{7}} - 28{{h}^{2}}{{z}^{5}} + 210{{h}^{4}}{{z}^{3}} - \\ \end{gathered} $
$\begin{gathered} - \,\,448{{h}^{5}}{{z}^{2}} + 648{{h}^{7}}) - \frac{{C\sigma z}}{\eta } + \frac{{\Omega W\sin \alpha }}{{2\nu }}\left( {z - 2h} \right)z; \\ V = W\sin \alpha - \frac{{g\beta Bz}}{{4!h\nu }}\left( {{{z}^{3}} - 4h{{z}^{2}} + 6{{h}^{2}}z - 4{{h}^{3}}} \right) + \\ + \,\,\frac{{g\beta C\Omega z}}{{6!h\nu \chi }}\left( {{{z}^{5}} - 5{{h}^{2}}{{z}^{3}} + 15{{h}^{4}}z - 16{{h}^{5}}} \right). \\ \end{gathered} $

Выражения для фоновой температуры и фонового давления определяются полиномами одиннадцатой и двенадцатой степени соответственно. Они здесь не приводятся из-за громоздкой записи формул.

Точное решение (6) описывает течения, обобщающие классическое течение Куэтта [57]. Если в формулах (6) положить $\Omega = 0$ и $W = 0,$ то поле скоростей было исследовано в [12, 29, 31]. Отметим, что установившаяся конвекция Марангони вертикально завихренной жидкости может наблюдаться только при согласованном задании силовых и кинематических характеристик на обеих границах слоя жидкости. Это наблюдение особенно важно при конструировании аппаратов химической технологии, поскольку при движении границ слоя жидкости приходится учитывать новые эффекты, связанные с возникновением вертикальной закрутки в жидкости, для описания термокапиллярной конвекции.

ИЗОТЕРМИЧЕСКОЕ ТЕЧЕНИЕ

Для лучшего понимания влияния термокапиллярного эффекта и силы Архимеда на структуру течения рассмотрим изотермическое течение (6) вязкой несжимаемой жидкости:

(7)
$\begin{gathered} u = 1;\,\,\,\,U = \frac{{2\operatorname{Re} \cos \alpha }}{{{\text{Ta}}}} + \frac{{{{\delta }^{2}}\operatorname{Re} \sin \alpha }}{2}Z\left( {Z - 2} \right); \\ V = \frac{{2\operatorname{Re} \sin \alpha }}{{{\text{Ta}}}}, \\ \end{gathered} $
где $Z = \frac{z}{h} \in [0,1]$ – безразмерная вертикальная координата; $\delta = \frac{h}{l};$ $h$ – толщина слоя жидкости, $l$ – характерный масштаб течения по горизонтали, $\operatorname{Re} = \frac{{Wl}}{\nu }$ – число Рейнольдса, ${\text{Ta}}\,{\text{ = }}\,\,\frac{{2\Omega {{l}^{2}}}}{\nu }$ – модифицированное число Тейлора [59]. Здесь и далее скорости, записанные в безразмерном виде, будут обозначаться теми же символами, что и размерные компоненты поля скоростей.

Изотермическое решение (7) в силу системы (3) является изобарическим [48, 49]. Анализ точного решения (7) показывает, что расслоение поля скоростей может быть обусловлено только фоновым течением, определяемым скоростью U. Скорость $U$ может принимать нулевое значение, если выполняется неравенство

$\cos \alpha \left( {4\cos \alpha - {\text{sin}}\alpha {\text{Ta}}{{\delta }^{2}}} \right) < 0.$

Из последнего неравенства следует, что противотечения в жидкости в сечении $Y = 0$ относительно скорости $U$, существуют при любом значении угла $\alpha \ne \left\{ {0;\frac{\pi }{2};\pi ;\frac{{3\pi }}{2}} \right\}$ с согласованным заданием вертикальной закрутки. При $\alpha = 0$ и $\alpha = \pi $ точное решение (7) описывает однонаправленное течение жидкости с постоянной скоростью $U = \pm \frac{{2\operatorname{Re} }}{{{\text{Ta}}}}.$

Дальнейшее взаимодействие разнонаправленных потоков будет осуществляться в области, заданной неравенством

$\left( {\frac{{2\operatorname{Re} \cos \alpha }}{{{\text{Ta}}}} + Y} \right)\left( {\frac{{2\operatorname{Re} \cos \alpha }}{{{\text{Ta}}}} - \frac{{{{\delta }^{2}}\operatorname{Re} \sin \alpha }}{2} + Y} \right) < 0,$
где $Y = {y \mathord{\left/ {\vphantom {y l}} \right. \kern-0em} l}$ – безразмерная горизонтальная координата.

Противотечения (7) с одной застойной точкой наблюдаются при постоянном распределении вертикальной компоненты завихренности по толщине слоя при отсутствии вращения жидкости. Этот результат соотносится с крупномасштабными течениями, у которых вертикальная компонента завихренности жидкости распределена линейно вне поля силы Кориолиса [48, 49, 51], и классическим спиральным течением Экмана [58]. Таким образом, появление дополнительных застойных точек при учете вертикальной закрутки в жидкости может быть обусловлено только тепловыми факторами [52].

КОНВЕКТИВНОЕ ТЕЧЕНИЕ

Запишем точное решение (6) в безразмерном виде

(8)
$\begin{gathered} U = \frac{{{{\delta }^{3}}{\text{Gr}}}}{{12{\text{Ta}}}}Z\left( {{{Z}^{3}} - 6Z + 8} \right) - \\ - \,\,\frac{{b{{\delta }^{5}}{\text{Gr}}}}{{6!}}Z\left( {{{Z}^{5}} - 6{{Z}^{4}} + 15{{Z}^{3}} - 20{{Z}^{2}} + 24} \right) - \\ - \,\,\frac{{2\delta {\text{Mg}}}}{{\Pr {\text{Ta}}}}Z + \frac{{{{\delta }^{7}}{\text{PeTa}}}}{{2 \times 3 \times 8!}}Z(3{{Z}^{7}} - 28{{Z}^{5}} + 210{{Z}^{3}} - \\ - \,\,448{{Z}^{2}} + 648) + \frac{{{{\delta }^{2}}\operatorname{Re} \sin \alpha }}{2}Z\left( {Z - 2} \right) + \\ + \,\,\frac{{2\operatorname{Re} \cos \alpha }}{{{\text{Ta}}}} = \frac{{{{\delta }^{3}}{\text{Gr}}}}{{12{\text{Ta}}}}{{g}_{1}}\left( Z \right) - \frac{{b{{\delta }^{5}}{\text{Gr}}}}{{6!}}{{g}_{2}}\left( Z \right) - \\ - \,\,\frac{{2\delta {\text{Mg}}}}{{\Pr {\text{Ta}}}}Z + \frac{{{{\delta }^{7}}{\text{PeTa}}}}{{2 \times 3 \times 8!}}{{g}_{3}}\left( Z \right) + \\ + \,\,\frac{{{{\delta }^{2}}\operatorname{Re} \sin \alpha }}{2}{{g}_{4}}\left( Z \right) + \frac{{2\operatorname{Re} \cos \alpha }}{{{\text{Ta}}}}. \\ \end{gathered} $
(9)
$\begin{gathered} V = - \frac{{b{\text{Gr}}{{\delta }^{3}}}}{{{\text{12Ta}}}}Z\left( {Z - 2} \right)\left( {{{Z}^{2}} - 2Z + 2} \right) + \\ + \,\,\frac{{{{\delta }^{5}}{\text{Pe}}}}{{6!}}Z\left( {{{Z}^{5}} - 5{{Z}^{3}} + 15Z - 16} \right) + \frac{{2\operatorname{Re} \sin \alpha }}{{{\text{Ta}}}} = \\ = - \frac{{b{\text{Gr}}{{\delta }^{3}}}}{{{\text{12Ta}}}}{{f}_{1}}\left( Z \right) + \frac{{{{\delta }^{5}}{\text{Pe}}}}{{6!}}{{f}_{2}}\left( Z \right) + \frac{{2\operatorname{Re} \sin \alpha }}{{{\text{Ta}}}}, \\ u = 1. \\ \end{gathered} $

Здесь $\Pr = \frac{\nu }{\chi },$ ${\text{Gr}} = \frac{{Cg\beta {{l}^{4}}}}{{{{\nu }^{2}}}},$ ${\text{Pe}} = {\text{PrGr}}$ – числа Прандтля, Грасгофа и Пекле соответственно, ${\text{Mg}} = \frac{{C\sigma {{l}^{2}}}}{{\eta \chi }}$ – модифицированное число Марангони [12, 31], $b = {B \mathord{\left/ {\vphantom {B C}} \right. \kern-0em} C}$ – безразмерный параметр.

По сравнению с изотермическим случаем (7) точное решение (8)–(9) в случае задания горизонтальных градиентов температуры на обеих границах является суперпозицией большего числа вторичных течений, обусловленных различными способами переноса тепла в жидкости.

Проанализируем получившееся поле скоростей (8)–(9). Начнем со скорости $V$ (9). В данном частном случае нагрева к изотермическому решению (7) добавляются еще два потока: течение $ - \frac{{b{\text{Gr}}{{\delta }^{3}}}}{{{\text{12Ta}}}}{{f}_{1}}(Z),$ отвечающее за конвективное перемешивание за счет силы Архимеда и учета вертикальной завихренности в жидкости, и течение $\frac{{{{\delta }^{5}}{\text{Pe}}}}{{6!}}{{f}_{2}}(Z),$ учитывающее молекулярный перенос тепла в естественной конвекции. Соотношение значений коэффициентов, стоящих перед соответствующими полиномами, влияет на вклад каждого течения в результирующее поле скоростей.

Профили течений ${{f}_{1}}\left( Z \right)$ и ${{f}_{2}}\left( Z \right)$ являются строго монотонными по толщине слоя. Добавление любого из этих двух потоков к изотермическому решению может привести к существенному изменению топологии течения и к появлению застойной точки.

Изучим структуру конвективного течения вязкой несжимаемой жидкости для некоторых предельных случаев. Если устремить число Прандтля ${\text{Pr}} \to {\text{0,}}$ то из (9) следует, что скорость $V$ будет определяться выражением

$V = - \frac{{b{\text{Gr}}{{\delta }^{3}}}}{{{\text{12Ta}}}}{{f}_{1}}\left( Z \right) + \frac{{2\operatorname{Re} \sin \alpha }}{{{\text{Ta}}}}.$

В этом случае единственная застойная точка может появиться только при выполнении неравенства, связывающего краевые условия и безразмерные управляющие параметры задачи:

$\operatorname{Re} \sin \alpha \left( {b{\text{Gr}}{{\delta }^{3}} + 24\operatorname{Re} \sin \alpha } \right) < 0.$

Если рассмотреть аналогично случай ${\text{Ta}} \to \infty ,$ то из (9) следует, что дополнительная застойная точка в этом случае не появится. Однако, ввиду нелинейности течений, описываемых полиномами ${{f}_{1}}\left( Z \right)$ и ${{f}_{2}}\left( Z \right)$, наложение этих течений одного на другое может привести к еще большему изменению характера монотонности суммарного течения. При этом вне зависимости от значений коэффициентов, стоящих перед полиномами ${{f}_{1}}\left( Z \right)$ и ${{f}_{2}}\left( Z \right),$ на нижней границе слоя суперпозиция этих двух течений удовлетворяет условию прилипания в направлении оси $OY$. Но итоговая скорость $V$(9) в общем случае этому условию не удовлетворяет.

Исследование локализации корней многочлена $V$(9) на интервале $\left( {0;1} \right)$ показывает, что скорость ${{V}_{Y}}$ может принимать нулевые значения не более чем в двух точках. Противотечения в жидкости могут сопровождаться усилением скоростей относительно заданных возмущений на верхней границе (рис. 1). Аналогично можно подобрать управляющие параметры краевой задачи таким образом, что усиление скоростей будет наблюдаться относительно заданного неоднородного поля скоростей на нижней границе.

Рис. 1.

Профили скоростей $U$(сплошная линия) и $V$(пунктирная линия) в предельных случаях с максимальным числом застойных точек.

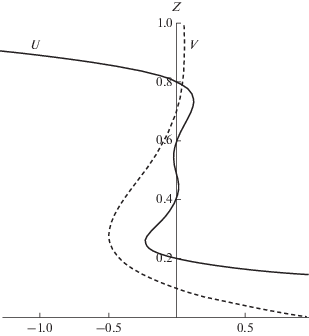
При наличии двух застойных точек в жидкости формируются локализованные зоны вблизи обеих границ слоя жидкости. Таким образом, точное решение (9), описывающее скорость ${{V}_{Y}}$, позволяет регистрировать при неоднородном распределении температуры противотечения в жидкости, сопровождающиеся погранслойными придонным и приповерхностным течениями.

В отличие от классического течения Куэтта касательное напряжение

(10)
$\begin{gathered} {{\tau }_{{YZ}}} = {{\tau }_{{ZY}}} = kV{\kern 1pt} ' = k\frac{{{{\delta }^{5}}{\text{Pe}}}}{{120}}{{\left( {Z - 1} \right)}^{3}} \times \\ \times \,\,\left\{ {{{Z}^{2}} + 3Z + \frac{{8{{\delta }^{2}}{\text{Ta}}\Pr - 120b}}{{3{{\delta }^{2}}{\text{Ta}}\Pr }}} \right\} \\ \end{gathered} $

не является знакопостоянной функцией. Здесь $k > 0$ – безразмерный диссипативный коэффициент.

Касательное напряжение (10) может расслаиваться на зоны растягивающих и сжимающих напряжений. Кроме того, может существовать в жидкости слой за исключением верхней границы $Z = 1,$ где касательное напряжение ${{\tau }_{{YZ}}}$ становится равным нулю. Отметим, что равенство нулю касательного напряжения на нижней границе слоя жидкости возможно при выполнении соотношения $b = \frac{{{{\delta }^{2}}{\text{Ta}}\Pr }}{{15}}.$

Кроме того, выражение (10) с точностью до множителя $k$ описывает распределение компоненты завихренности: ${{\Omega }_{X}} = - V{\kern 1pt} '.$ Таким образом, движение жидкости вдоль оси $OY$ может сопровождаться двумя вихрями, вращающимися в противоположные стороны. Направление вращения вихрей согласуется со знаком выражения $\frac{{{\text{Pe}}\left( {15b - {{\delta }^{2}}{\text{Ta}}\Pr } \right)}}{{3{{\delta }^{2}}{\text{Ta}}}}.$ В том случае если $\frac{{{\text{Pe}}\left( {15b - {{\delta }^{2}}{\text{Ta}}\Pr } \right)}}{{3{{\delta }^{{\text{2}}}}{\text{Ta}}}} < 0,$ то горизонтальный вихрь ${{\Omega }_{X}},$ формирующийся около нижней границы, вращается против часовой стрелки.

Проанализируем теперь течение жидкости вдоль оси $OX$. Из точного решения видно (8), что однородная составляющая $U$ компоненты вектора скорости ${{V}_{X}}$ представляет собой сумму шести течений различной природы. К составляющим $\frac{{{{\delta }^{2}}\operatorname{Re} \sin \alpha }}{2}{{g}_{4}}\left( Z \right)$ и $\frac{{2\operatorname{Re} \cos \alpha }}{{{\text{Ta}}}}$ изотермического течения вертикально завихренной жидкости, входящим в точное решение (7), добавляются следующие потоки: течение $\frac{{{{\delta }^{3}}{\text{Gr}}}}{{12{\text{Ta}}}}{{g}_{1}}\left( Z \right),$ порождаемое гравитационной конвекцией; течение $ - \frac{{b{{\delta }^{5}}{\text{Gr}}}}{{6!}}{{g}_{2}}\left( Z \right),$ отвечающее за конвективное перемешивание под действием силы Архимеда; течение $\frac{{{{\delta }^{7}}{\text{PeTa}}}}{{2 \times 3 \times 8!}}{{g}_{3}}\left( Z \right),$ вызванное молекулярными переносами тепла, и течение $ - \frac{{2\delta {\text{Mg}}}}{{\Pr {\text{Ta}}}}Z,$ индуцированное конвективными эффектами в результате действия термокапиллярных механизмов. Чем больше коэффициент, стоящий при соответствующем полиноме, тем большее влияние оказывает данное течение на суммарное движение в рассматриваемом слое жидкости. Взаимодействие тепловых потоков с фоновым изотермическим течением приводит к появлению дополнительных застойных точек.

Скорость $U$ (8) описывается полиномом восьмого порядка, однако, число застойных точек в слое $\left( {0;1} \right)$ не превосходит пяти (рис. 1). Наличие большого числа застойных точек позволяет рассматривать точное решение (6) или (8)–(9) для локального описания спиральных течений. Годографы, построенные при $Y = 0,$ иллюстрируют спиралевидную и петлеобразную форму траекторий жидких частиц, которая имеет место для конвективного течения Экмана [58]. Напомним, что в данной статье рассматривается течение вертикально завихренной жидкости без учета поля силы Кориолиса, поэтому приведенные в статье точные решения могут быть полезными для решения проблемы генерации конвективного динамо [60–62].

Исследование касательного напряжения τXZ = = τZX = $k\left( {U + y} \right){\kern 1pt} ' = kU{\kern 1pt} '$ проводится аналогично анализу касательного напряжения ${{\tau }_{{YZ}}}$. В этом случае компонента завихренности ${{\Omega }_{Y}}$ совпадает с выражением для напряжения ${{\tau }_{{XZ}}}$ (с точностью до постоянного множителя k). Число зон расслоения касательного напряжения не превосходит пяти. Соответственно, в направлении оси $OY$ могут образовываться до пяти вихрей. Несмотря на то, что обе компоненты завихренности ${{\Omega }_{X}},$ ${{\Omega }_{Y}}$ могут становиться нулевыми, движение жидкости будет только вихревым без вырождения в потенциальное течение.

Таким образом, всего возможно восемнадцать сценариев поведения вихревого течения жидкости. На рис. 2 представлены примеры с различным числом зон, образующихся внутри слоя, в случае наличия двух застойных точек у скорости V. Даже для однонаправленного потока жидкости, параллельном оси $OX$ (однородного течения), в результирующем сдвиговом течении формируются противотечения. Данный эффект обусловлен нелинейным взаимодействием потоков в рассматриваемой краевой задаче (3)–(5). Очевидно, что число зон, на которые разбивается слой жидкости, увеличивается по мере роста числа застойных точек у компоненты $U$поля скорости.

Рис. 2.

Линии тока поля скорости в случае двух застойных точек у скорости $V$: (а) – у скорости $U$ четыре застойные точки; (б) – у скорости $U$ пять застойных точек.

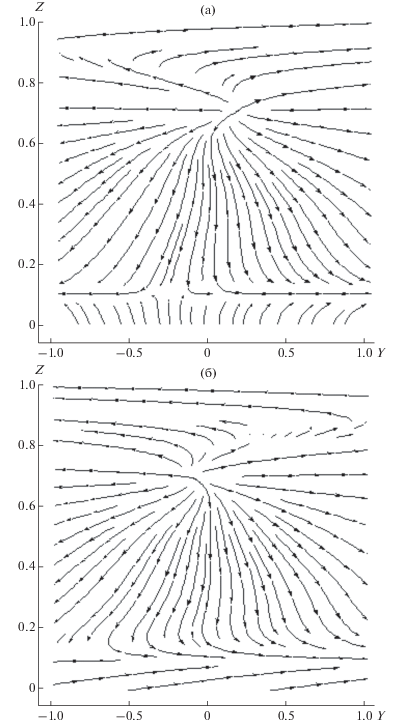
Аналогичная тенденция усложнения топологии течения наблюдается и в случаях, когда у скорости $V$либо нет застойных точек, либо одна застойная точка.

АНАЛИЗ ПОЛЯ ТЕМПЕРАТУРЫ

Топологические характеристики поля температуры T зависят от свойств горизонтальных (продольных) градиентов ${{T}_{1}}$, ${{T}_{2}}$ и фоновой температуры ${{T}_{0}}.$ Поскольку в качестве отсчетной температуры выбрано нулевое значение, заданное на нижней границе, то качественный вид температурного поля определяется расположением его нулевых точек.

Продольный градиент ${{T}_{1}} = CZ$ является монотонным и принимает значения одного знака, а значит, поле ${{T}_{1}}x$ не имеет точек расслоения. Из представления горизонтального градиента ${{T}_{2}}$ в мультипликативном виде

${{T}_{2}} = \left( {1 - Z} \right)\left( {B - \frac{{\Omega С{{h}^{2}}}}{{6\chi }}Z\left( {Z + 1} \right)} \right)$

следует, что соответствующее температурное поле ${{T}_{2}}y$ допускает стратификацию только в одной точке при выполнении условия:

$0 < \frac{B}{{\Omega С}} < \frac{{{{h}^{2}}}}{{3\chi }}.$

Фоновая температура ${{T}_{0}}$ формируется в результате взаимодействия нескольких составляющих, вызванных различными факторами: неоднородным нагревом (охлаждением) границ слоя, учетом термокапиллярного эффекта, неоднородным движением твердой нижней границы.

В случае однородного поля скорости ($\Omega = 0$) фоновая температура ${{T}_{0}}$ описывается следующим полиномом:

(11)
$\begin{gathered} {{T}_{0}} = \vartheta Z + \frac{{W{{h}^{2}}C\cos \alpha }}{{6\chi }}{{Z}^{3}} + Z\left( {1 - Z} \right) \times \\ \times \,\,\left\{ { - \frac{{5g\beta {{h}^{5}}{{B}^{2}}}}{{7!\nu \chi }}\left[ {{{Z}^{5}} - 6{{Z}^{4}} + 15{{Z}^{3}} - 20{{Z}^{2}} + 8Z + 8} \right] - } \right. \\ - \,\,\frac{{g\beta {{h}^{5}}{{C}^{2}}}}{{7!\nu \chi }}\left[ {5{{Z}^{5}} + 5{{Z}^{4}} - 58{{Z}^{3}} + 82{{Z}^{2}} + 82Z + 82} \right] - \\ \left. { - \,\,\frac{{W{{h}^{2}}Bsin\alpha }}{{6\chi }}\left( {2 - Z} \right) + \frac{{\sigma {{C}^{2}}{{h}^{3}}}}{{12\eta \chi }}\left( {{{Z}^{2}} + Z + 1} \right)} \right\}. \\ \end{gathered} $

Если положить в формуле (11) $W = 0$ (т.е. считать, что нижняя граница слоя неподвижна), то полученное в этом случае температурное поле ${{T}_{0}}$ будет определяться взаимодействием четырех составляющих:

(12)
$\begin{gathered} {{T}_{0}} = \vartheta Z + Z\left( {1 - Z} \right)\left\{ { - \frac{{5g\beta {{h}^{5}}{{B}^{2}}}}{{7!\nu \chi }} \times } \right. \\ \times \,\,\,\,\left[ {{{Z}^{5}} - 6{{Z}^{4}} + 15{{Z}^{3}} - 20{{Z}^{2}} + 8Z + 8} \right] - \\ - \,\,\frac{{g\beta {{h}^{5}}{{C}^{2}}}}{{7!\nu \chi }}[5{{Z}^{5}} + 5{{Z}^{4}} - 58{{Z}^{3}} + 82{{Z}^{2}} + \\ + \,\,82Z + 82] + \left. {\frac{{\sigma {{C}^{2}}{{h}^{3}}}}{{12\eta \chi }}\left( {{{Z}^{2}} + Z + 1} \right)} \right\}. \\ \end{gathered} $

В выражении (12) первые три слагаемых описывают влияние естественной конвекции. Последняя составляющая обусловлена заданием термокапиллярных сил на межфазной границе слоя жидкости. Отметим, что для формирования температурного поля ${{T}_{0}}$ (12) существенным является только величина горизонтальных градиентов B и C, а не их знак. Если положить горизонтальный температурный градиент $C = 0,$ то выражение (12) преобразуется к виду

(13)
$\begin{gathered} {{T}_{0}} = Z\left\{ {\vartheta - \frac{{5g\beta {{h}^{5}}{{B}^{2}}}}{{7!\nu \chi }}\left( {1 - Z} \right)} \right. \times \\ \left. {\frac{{^{{}}}}{{}} \times \,\,\left[ {{{Z}^{5}} - 6{{Z}^{4}} + 15{{Z}^{3}} - 20{{Z}^{2}} + 8Z + 8} \right]} \right\}. \\ \end{gathered} $.

Свойства решения (13) определяются свойствами полинома

$f\left( Z \right) = \left( {1 - Z} \right)\left[ {{{Z}^{5}} - 6{{Z}^{4}} + 15{{Z}^{3}} - 20{{Z}^{2}} + 8Z + 8} \right],$

который не имеет точек экстремума на интервале $\left( {0;1} \right).$ Следовательно, температура ${{T}_{0}}$ в рассматриваемом частном случае может иметь только одну нулевую точку, если выполняется неравенство

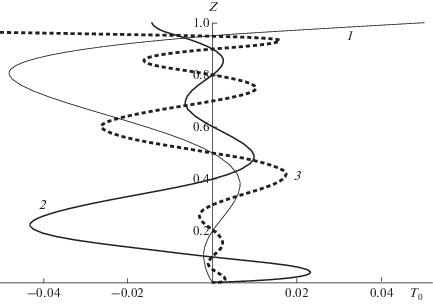
$0 < \vartheta < \frac{{{\text{40}}g\beta {{h}^{5}}{{B}^{2}}}}{{7!\nu \chi }}.$

На основе исследования свойств полинома (13) в случае, когда температурный градиент $C \ne 0$, можно утверждать, что фоновая температура имеет не более трех нулей внутри рассматриваемого слоя жидкости (рис. 3, кривая 1).

Рис. 3.

Профили фоновой температуры ${{T}_{0}}$.

Отметим, что фоновая температура ${{T}_{0}},$ представленная на рис. 3, имеет явную локализацию вблизи верхней границы $Z = 1$ слоя жидкости. Таким образом, в жидкости реализуется термоклин.

Сравнение выражений (11) и (12) показывает, что в случае суперпозиции поступательного и вращательного движений нижней границы ($W \ne 0$) вклад в формирование температуры вносят еще два слагаемых. В результате чего число нулей фоновой температуры, определяемой выражением (11), не превосходит пяти (рис. 3, кривая 2).

Анализ поведения фоновой температуры ${{T}_{0}}$ в общем случае (с учетом вертикальной компоненты завихренности) позволяет сделать вывод о том, что при определенном сочетании управляющих параметров у температуры ${{T}_{0}}$ может быть до девяти нулевых точек (рис. 3, кривая 3), что соответствует десяти зонам стратификации температурного поля. Таким образом, наличие вертикального вихря в жидкости увеличивает количество зон стратификации фоновой температуры.

При рассмотрении итогового температурного поля T, полученного суперпозицией тепловых полей ${{T}_{1}}x,$ ${{T}_{2}}y$ и ${{T}_{0}},$ было установлено, что количество зон стратификации сохраняется вблизи оси $Oz$. При увеличении значений $x$ и $y$ происходит доминирование тепловых полей, обусловленных наличием горизонтальных градиентов, и уменьшается число зон стратификации. Это ведет к выравниванию температуры по поперечной координате и ее локализации вблизи границ слоя жидкости.

Отметим также, что для поля давления $P$ справедливы те же закономерности относительно характера распределения изолиний и изменения числа нулевых точек поля при изменении сечения, что были описаны выше для температурного поля T.

ЗАКЛЮЧЕНИЕ

В настоящей работе найдено и изучено новое точное уравнений Обербека–Буссинеска, описывающее термокапиллярное конвективное течение вертикально завихренной вязкой несжимаемой жидкости. Постоянная вертикальная закрутка в жидкости индуцируется не вращением жидкости, а рассмотрением неоднородного поля скоростей, позволяющего описать движение границы слоя суперпозицией поступательного и вращательных движений. Учет конвекции Марангони приводит к увеличению числа противотечений в слое вертикально завихренной жидкости. Примечательно, что в силу структуры течения касательные напряжения с точностью до коэффициента совпадают с горизонтальными вихрями. Данные силовые поля конвекции Марангони также стратифицируются по толщине слоя жидкости. Проанализирована структура полей температуры и давления. Показано, что полученное новое точное решение системы Обербека–Буссинеска описывает течение вязкой несжимаемой жидкости с десятью зонами стратификации. Это позволяет наблюдать термоклин вблизи границ слоя, сопровождающийся немонотонным распределением температуры между локализованными зонами нагрева (охлаждения) жидкости. Аналогичное исследование проведено для давления.

ОБОЗНАЧЕНИЯ

$A$, $B$, $C$, $D$ горизонтальные градиенты температуры T, К/м
$h$ толщина слоя жидкости, м
$k$ безразмерный диссипативный коэффициент
$l$ характерный горизонтальный размер слоя жидкости, м
$P$ отклонение давления от гидростатического, деленное на среднюю плотность жидкости, м2/с2
$T$ отклонение температуры от отсчетного значения, К
$U$, $V$, $u$, ${{T}_{0}}$, ${{T}_{1}}$, ${{T}_{2}}$, ${{P}_{0}}$, ${{P}_{1}}$, ${{P}_{2}}$ функции, входящие в класс решений (2)
${{V}_{x}}$, ${{V}_{y}}$ компоненты вектора скорости течения жидкости, м/с
${{V}_{X}}$, ${{V}_{Y}}$ безразмерные компоненты вектора скорости течения жидкости
W значение скорости на нижней границе, м/с
$X$, $Y$,$Z$ безразмерные координаты
$x$, $y$, $z$ декартовы координаты, м
$\alpha $ угол, характеризующий преобразование поворота вектора скорости на нижней границе, рад
$\beta $ коэффициент температурного расширения, 1/К
$\delta $ безразмерный показатель геометрической анизотропии
$\eta $ динамическая вязкость, кг/(м с)
$\vartheta $ значение однородной составляющей температуры на верхней границе слоя, К
$\nu $ кинематическая (молекулярная) вязкость жидкости, м2/с
$\sigma $ температурный коэффициент поверхностного натяжения жидкости, Н/(м К)
${{\tau }_{{XZ}}}$, ${{\tau }_{{YZ}}}$, ${{\tau }_{{ZX}}}$, ${{\tau }_{{ZY}}}$ безразмерные компоненты тензора напряжений
$\chi $ температуропроводность вязкой жидкости, м2/с
$\Omega $ градиент скорости ${{V}_{x}}$, 1/с
${{\Omega }_{X}}$, ${{\Omega }_{Y}}$ безразмерные компоненты псевдовектора вихря
${\text{Gr}}$ число Грасгофа
${\text{Mg}}$ число Марангони
${\text{Pe}}$ число Пекле
$\Pr $ число Прандтля
$\operatorname{Re} $ число Рейнольдса
$Ta$ модифицированное число Тейлора

Список литературы

  1. Гершуни Г.З., Жуховицкий Е.М. Конвективная неустойчивость несжимаемой жидкости. М.: Наука, 1972.

  2. Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика. М.: Квантум, 1996.

  3. Гетлинг А.В. Конвекция Рэлея–Бенара. Структура и динамика. М.: Эдиаториал УРСС, 1999.

  4. Chandrasekhar S. Hydrodynamic and hydromagnetic stability. Oxford: Clarendon, 1961.

  5. Benard H. Les tourbillons cellulaires dans une nappe liquide propageant de la chaleur par convection, en regime permanent. These. Paris: Gauthier–Villars, 1901.

  6. Benard H. Etude experimentale des courants de convection dans une nappe liquide. Regime permanent: tourbillons cellulaires // J. Phys. Theor. Appl. 1900. V. 9. № 1. P. 513.

  7. Benard H. Les tourbillons cellulaires dans une nappe liquide propageant de la chaleur par convection, en regime permanent // Annales de chimie et de physique. 1901. V. 23. P. 62.

  8. Остроумов Г.А. Свободная конвекция в условиях внутренней задачи. М.: Гос. изд-во технико-теоретической литературы, 1952.

  9. Бирих Р.В. О термокапилярной конвекции в горизонтальном слое жидкости // Прикл. мех. тех. физ. 1966. № 3. С. 69. [Birikh R.V. Thermocapillary convection in a horizontal layer of liquid // J. Appl. Mech. Tech. Phys. 1966. V. 7. № 3. P. 43.]

  10. Ortiz-P’erez A.S., D’avalos-Orozco L.A. Convection in a horizontal fluid layer under an inclined temperature gradient // Phys. Fluids. 2011. V. 28. № 3. P. 084107.

  11. Smith M.K., Davis S.H. Instabilities of dynamic thermocapillary liquid layers. Pt. 1. Convective instabilities // J. Fluid Mech. 1983. V. 132. P. 119.

  12. Князев Д.В. Плоские течения вязкой бинарной жидкости между подвижными твердыми границами // Прикл. мех. тех. физ. 2011. Т. 52. № 2. С. 66. [Knyazev D.V. Two-dimensional flows of a viscous binary fluid between moving solid boundaries // J. Appl. Mech. Tech. Phys. 2011. V. 52. № 2. P. 212.]

  13. Аристов С.Н., Просвиряков Е.Ю., Спевак Л.Ф. Нестационарная слоистая тепловая и концентрационная конвекция Марангони вязкой несжимаемой жидкости // Вычисл. мех. сплошных сред. 2015. Т. 8. № 4. С. 445. [Aristov S.N., Prosviryakov E.Y., Spevak L.F. Nonstationary laminar thermal and solutal Marangoni convection of a viscous fluid // Comput. Continuum Mech. 2015. V. 8. № 4. P. 445.]

  14. Goncharova O.N., Kabov O.A. Investigation of the two-layer fluid flows with evaporation at interface on the basis of the exact solutions of the 3D problems of convection // J. Phys.: Conf. Ser. 2016. V. 754. № 3. P. 032008–1.

  15. Napolitano L.G. Plane Marangoni–Poiseuille flow of two immiscible fluids // Acta Astronaut. 1980. V. 7. № 4. P. 461.

  16. Рыжков И.И. Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость. Новосибирск: СО РАН, 2013.

  17. Ryzhkov I.I. The extended Graetz problem with specified heat flux for multicomponent fluids with the Soret and Dufour effects // Int. J. Heat Mass Transfer. 2013. V. 66. P. 461.

  18. Шлиомис М.И., Якушин В.И. Конвекция в двухслойной бинарной системе с испарением // Уч. зап. Перм. гос. унив. Сер. гидродин. 1972. № 4. С. 129.

  19. Ryzhkov I.I., Shevtsova V. Thermocapillary instabilities in liquid columns under co- and counter-current gas flow // Int. J. Heat Mass Transfer. 2012. V. 55. № 4. P. 1236.

  20. Андреев В.К., Бекежанова В.Б. Устойчивость неизотермических жидкостей (обзор) // Прикл. мех. тех. физ. 2013. № 2. С. 3. [Andreev V.K., Bekezhanova V.B. Stability of non-isothermal fluids (Review) // J. Appl. Mech. Tech. Phys. 2013. V. 54. № 2. P. 171.]

  21. Гончарова О.Н., Кабов О.А. Гравитационно-термокапиллярная конвекция жидкости в горизонтальном слое при спутном потоке газа // Докл. Акад. наук. 2009. Т. 426. № 2. С. 183.

  22. Бекежанова В.Б., Гончарова О.Н. Задачи испарительной конвекции (обзор) // Прикл. мат. мех. 2018. Т. 82. № 2. С. 219.

  23. Бекежанова В.Б., Гончарова О.Н., Резанова Е.В., Шефер И.А. Устойчивость двухслойных течений жидкости с испарением на границе раздела // Изв. Акад. наук. Мех. жидк. газа. 2017. № 2. С. 23. [Bekezhanova V.B., Shefer I.A., Goncharova O.N., Rezanova E.B. Stability of two-layer fluid flows with evaporation at the interface // Fluid Dyn. 2017. V. 52. № 2. P. 189.]

  24. Fedyushkin A., Bourago N., Polezhaev V., Zharikov E. The influence of vibration on hydrodynamics and heat–mass transfer during crystal growth // J. Cryst. Growth. 2005. V. 275. № 1–2. P. e1557.

  25. Gershuni G.Z., Lubimov D.V. Thermal vibrational convection. New York: Wiley, 1998.

  26. Рыжков И.И., Степанова И.В. Групповые свойства и точные решения модели вибрационной конвекции бинарной смеси // Прикл. мех. тех. физ. 2011. Т. 52. № 4. С. 72. [Ryzhkov I.I., Stepanova I.V. Group properties and exact solutions of equations for vibrational convection of a binary mixture // J. Appl. Mech. Tech. Phys. 2011. V. 52. № 4. P. 560.]

  27. Брацун Д.А., Мошева Е.А. Особенности формирования волн плотности в двухслойной системе смешивающихся реагирующих жидкостей // Вычисл. мех. сплошных сред. 2018. Т. 11. № 3. С. 302. [Bratsun D.A., Mosheva E.A. Peculiar properties of density wave formation in a two-layer system of reacting miscible liquids // Comput. Continuum Mech. 2018. V. 11. № 3. P. 302.]

  28. Пухначев В.В. Нестационарные аналоги решения Бириха // Изв. Алтай. гос. унив. 2011. Т. 69. № 1–2. С. 62.

  29. Бирих Р.В., Пухначёв В.В. Осевое конвективное течение во вращающейся трубе с продольным градиентом температуры // Докл. Акад. наук. 2011. Т. 436. № 3. С. 323. [Birikh R.V., Pukhnachev V.V. An axial convective flow in a rotating tube with a longitudinal temperature gradient // Dokl. Phys. 2011. V. 56. № 1. P. 47.]

  30. Аристов С.Н., Просвиряков Е.Ю. О слоистых течениях плоской свободной конвекции // Нелинейная дин. 2013. Т. 9. № 4. С. 651. [Aristov S.N., Prosviryakov E.Y. On laminar flows of planar free convection // Russ. J. Nonlinear Dyn. 2013. V. 9. № 4. P. 651.]

  31. Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теор. осн. хим. технол. 2016. Т. 50. № 3. С. 294. [Aristov S.N., Prosviryakov E.Y. A new class of exact solutions for three-dimensional thermal diffusion equations // Theor. Found. Chem. Eng. 2016. V. 50. № 3. P. 286.]

  32. Аристов С. Н., Просвиряков Е.Ю., Спевак Л.Ф. Нестационарная конвекция Бенара–Марангони слоистых течений вязкой несжимаемой жидкости // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 137. [Aristov S.N., Prosviryakov E.Y., Spevak L.F. Unsteady-state Bénard–Marangoni convection in layered viscous incompressible flows // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 132.]

  33. Бекежанова В.Б. Неустойчивость двухслойной системы при наличии объемных источников тепла // Вычисл. технол. 2008. Т. 13. № 4. С. 24.

  34. Бурмашева Н.В., Просвиряков Е.Ю. Крупномасштабная слоистая стационарная конвекция вязкой несжимаемой жидкости под действием касательных напряжений на верхней границе. Исследование поля скоростей // Вестн. Самар. гос. тех. унив. Сер. физ.-мат. науки. 2017. Т. 21. № 1. С. 180.

  35. Бурмашева Н.В., Просвиряков Е.Ю. Крупномасштабная слоистая стационарная конвекция вязкой несжимаемой жидкости под действием касательных напряжений на верхней границе. Исследование полей температуры и давления // Вестн. Самар. гос. тех. унив. Сер. физ.-мат. науки. 2017. Т. 21. № 4. С. 736.

  36. Goncharova O.N., Kabov O.A., Pukhnachov V.V. Solutions of special type describing the three dimensional thermocapillary flows with an interface // Int. J. Heat Mass Transfer. 2012. V. 55. № 4. P. 715.

  37. Andreev V.K., Gaponenko Yu.A., Goncharova O.N., Pukhnachov V.V. Mathematical models of convection (De Gruyter Studies in Mathematical Physics). Berlin: De Gruyter, 2012.

  38. Margerit J., Colinet P., Lebon G., Iorio C.S., Legros J.C. Interfacial nonequilibrium and Benard–Marangoni instability of a liquid-vapor system // Phys. Rev. E. 2003. V. 68. P. 041601-1.

  39. Андреев В.К. Решения Бириха уравнений конвекции и некоторые его обобщения. Препринт № 1–10. Красноярск: ИВМ СО РАН, 2010.

  40. Шварц К.Г. Плоскопараллельное адвективное течение в горизонтальном слое несжимаемой жидкости с твердыми границами // Изв. Акад. наук. Мех. жидк. газа. 2014. № 4. С. 26. [Schwarz K.G. Plane-parallel advective flow in a horizontal incompressible fluid layer with rigid boundaries // Fluid Dyn. 2014. № 4. P. 438.]

  41. Аристов С.Н., Шварц К.Г. Вихревые течения адвективной природы во вращающемся слое жидкости. Пермь: Перм. ун-т, 2006.

  42. Вяткин А.А., Иванова А.А., Козлов В.Г., Сабиров Р.Р. Конвекция тепловыделяющей жидкости во вращающемся горизонтальном цилиндре // Изв. Акад. наук. Мех. жидк. газа. 2014. № 1. С. 21. [Vyatkin A.A., Ivanova A.A., Kozlov V.G., Sabirov R.R. Convection of a heat-generating fluid in a rotating horizontal cylinder // Fluid Dyn. 2014. V. 49. № 1. P. 17.]

  43. Kozlov V., Vjatkin A., Sabirov S. Convection of liquid with internal heat release in a rotating container // Acta Astronaut. 2013. V. 89. P. 99.

  44. Козлов В.Г. Вибрационная тепловая конвекция во вращающихся полостях // Изв. Акад. наук. Мех. жидк. газа. 2004. №1. С. 5. [Kozlov V.G. Thermal vibrational convection in rotating cavities // Fluid Dyn. 2004. V. 39. № 1. P. 3.]

  45. Горшков А.В., Просвиряков Е.Ю. Конвективное слоистое течение Экмана вязкой несжимаемой жидкости // Изв. Акад. наук. Физ. атмос. океана. 2018. Т. 54. № 2. С. 213. [Gorshkov A.V., Prosviryakov E.Y. Ekman Convective Layer Flow of a Viscous Incompressible Fluid // Izv., Atmos. Ocean. Phys. 2018. V. 54. № 2. P. 189.]

  46. Аристов С.Н., Шварц К.Г. Адвективное течение во вращающейся жидкой пленке // Прикл. мех. тех. физ. 2016. № 1. С. 216. [Aristov S.N., Shvarts K.G. Advective flow in a rotating liquid film // J. Appl. Mech. Tech. Phys. 2016. V. 57. № 1. P. 188.]

  47. Аристов С.Н., Мясников В.П. Нестационарные трехмерные структуры в приповерхностном слое океана // Докл. Акад. наук. 1996. Т. 349. № 4. С. 457. [Aristov S.N., Myasnikov V.P. Time-dependent three-dimensional structures in the near-surface layer of the ocean // Dokl. Phys. 1996. V. 41. № 8. P. 358.]

  48. Aristov, S.N., Nycander J. Convective flow in baroclinic vortices // J. Phys. Oceanogr. 1994. V. 24. № 9. P. 1841.

  49. Аристов С.Н., Просвиряков Е.Ю. Неоднородные течения Куэтта // Нелинейная дин. 2014. Т. 10. № 2. С. 177. [Aristov S.N., Prosviryakov E.Y. Inhomogeneous Couette flow // Russ. J. Nonlinear Dyn. 2014. V. 10. № 2. P. 177.]

  50. Просвиряков Е.Ю., Спевак Л.Ф. Пространственно неоднородные слоистые течения вязкой несжимаемой жидкости // Теор. осн. хим. технол. 2018. Т. 52. № 5. С. 483.

  51. Брутян М.А., Крапивский П.Л. Точное решение уравнений Навье–Стокса, описывающее эволюцию вихревой структуры в обобщенном сдвиговом течении // Ж. вычисл. мат. мат. физ. 1992. Т. 32. № 2. С. 326. [Brutyan M.A., Krapivskii P.L. The exact solution of the Navier-Stokes equations for the evolution of the vortex structure in a generalized shear flow // Comput. Math. Math. Phys. 1992. V. 32. № 2. P. 270.]

  52. Аристов С.Н. Просвиряков Е.Ю. Нестационарные слоистые течения завихренной жидкости // Изв. Акад. наук. Мех. жидк. газа. 2016. № 2. С. 25. [Aristov S.N., Prosviryakov E.Y. Unsteady layered vortical fluid flows // Fluid Dyn. 2016. V. 51. № 2. P. 148.]

  53. Аристов С.Н., Князев Д.Е., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных // Теор. осн. хим. технол. 2009. Т. 43. № 5. С. 547. [Aristov S.N., Knyazev D.V., Polyanin A.D. Exact solutions of the Navier-Stokes equations with the linear dependence of velocity components on two space variables // Theor. Found. Chem. Eng. 2009. V. 43. № 5. P. 642.]

  54. Полянин А.Д, Аристов С.Н. Новый метод построения точных решений трехмерных уравнений Навье–Стокса и Эйлера // Теор. осн. хим. технол. 2011. Т. 45. № 6. С. 696. [Polyanin A.D., Aristov S.N. A new method for constructing exact solutions to three-dimensional Navier–Stokes and Euler equations // Theor. Found. Chem. Eng. 2009. V. 45. № 6. P. 885.]

  55. Aristov S.N., Polyanin A.D. New Classes of Exact Solutions and Some Transformations of the Navier–Stokes Equations // Russ. J. Math. Phys. 2010. V. 17. № 1. P. 1.

  56. Polyanin A.D. Exact solutions to new classes of reaction-diffusion equations containing delay and arbitrary functions // Theor. Found. Chem. Eng. 2015. V. 49. № 2. P. 169. [Полянин А.Д. Точные решения новых классов реакционно-диффузионных уравнений, содержащих запаздывание и произвольные функции // Теор. осн. хим. технол. 2015. Т. 49. № 2. С. 175.]

  57. Couette M. Etudes sur le frottement des liquides // Ann. Chim. Phys. 1890. V. 21. P. 433.

  58. Ekman V.W. On the Influence of the Earth’s Rotation on Ocean-Currents // Ark. Mat. Astron. Fys. 1905. V. 2. № 11. P. 1.

  59. Mehdizadeh A., Oberlack M. Analytical and numerical investigations of laminar and turbulent Poiseuille–Ekman flow at different rotation rates // Phys. Fluids. 2010. V. 22. P. 105104.

  60. Копп М.И., Тур А.В., Яновский В.В. Нелинейное вихревое динамо во вращающейся стратифицированной влажной атмосфере // Ж. эксп. теор. физ. 2017. Т. 151. № 6. С. 1179. [Kopp M.I., Yanovsky V.V., Tur A.V. Nonlinear vortex dynamo in a rotating stratified moist atmosphere // J. Exp. Theor. Phys. 2017. V. 124. № 6. P. 1010.]

  61. Moffatt H.K. Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. Part 1. Fundamentals // J. Fluid Mech. 1985. V. 159. P. 359.

  62. Moffatt H.K. Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. Part 2. Stability considerations // J. Fluid Mech. 1986. V. 166. P. 359.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал