Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 38-44

Многокомпонентная неизотермическая диффузия при термическом разложении диспергированной аммиачной селитры

М. Г. Давидханова^a, *, Е. П. Моргунова^a, А. В. Беспалов^a

^a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

Поступила в редакцию 15.06.2019
После доработки 25.07.2019
Принята к публикации 28.09.2019

DOI: 10.31857/S0040357120010054

Аннотация

Проведен анализ частного случая протекания гетерогенного химического процесса, сопровождающегося многокомпонентной неизотермической диффузией, – термического разложения диспергированного расплава аммиачной селитры для производства закиси азота. На основе расчета по разработанной математической модели даны рекомендации по организации процесса в реакторе.

Ключевые слова: аммиачная селитра, медицинская закись азота, гетерогенный химический процесс, многокомпонентная неизотермическая диффузия, термическое разложение, диспергированный поток

ВВЕДЕНИЕ

Среди реализуемых в промышленности процессов производства закиси азота высокой чистоты, – медицинской закиси азота (МЗА), широкое распространение получил способ термического разложения слоя плава 92–96% раствора NH₄NO₃ в полом цилиндрическом реакторе с электрообогревом [1, 2] при температуре 270–280°C. Это экзотермический процесс и, вследствие того, что продукты образуются в газовой (паровой) фазе, взрывоопасный.

Разложение аммиачной селитры с преимущественным образованием закиси азота протекает в интервале температур 225–278°С по реакции

(1)

${\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{{\text{3}}}} = {{{\text{N}}}_{{\text{2}}}}{\text{O}} + 2{{{\text{H}}}_{{\text{2}}}}{\text{O}} + 36.9{\text{ кДж}}.$

Кроме этой основной реакции, в указанном интервале температур протекает ряд побочных реакций с образованием элементарного азота, моно-, ди- и триоксида азота, аммиака и азотной кислоты. Оптимальный температурный диапазон процесса разложения с максимальным выходом закиси азота составляет 265–278°С. При температуре ниже 265°С и выше 278°С увеличивается скорость побочных реакций и уменьшается выход закиси азота. При температуре 180°С идет главным образом реакция диссоциации аммиачной селитры с образованием аммиака и азотной кислоты:

(2)

${\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{3}} = {\text{N}}{{{\text{H}}}_{{\text{3}}}} + {\text{HN}}{{{\text{O}}}_{3}} - 174.7{\text{ кДж}}.$

Начиная с температуры 230°С разложение аммиачной селитры ускоряется. При температуре выше 278°С значительно возрастает выход элементарного азота и окислов азота по реакциям

(3)

$2{\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{3}} = {{{\text{N}}}_{2}} + 2{\text{NO}} + 4{{{\text{H}}}_{{\text{2}}}}{\text{O}} + 57\,\,{\text{кДж}},$

(4)

$2{\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{3}} = 2{{{\text{N}}}_{2}} + 4{{{\text{H}}}_{{\text{2}}}}{\text{O}} + {{{\text{O}}}_{2}} + 239.4\,\,{\text{кДж}},$

(5)

$4{\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{3}} = 3{{{\text{N}}}_{2}} + 2{\text{N}}{{{\text{O}}}_{2}} + 8{{{\text{H}}}_{{\text{2}}}}{\text{O}} + 140\,\,{\text{кДж}},$

(6)

$3{\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{3}} = 2{{{\text{N}}}_{2}} + {{{\text{N}}}_{{\text{2}}}}{{{\text{O}}}_{3}} + 6{{{\text{H}}}_{{\text{2}}}}{\text{O}} + 113\,\,{\text{кДж}}.$

При соприкосновении расплава аммиачной селитры со стенками реактора протекает побочная реакция

(7)

$5{\text{N}}{{{\text{H}}}_{{\text{4}}}}{\text{N}}{{{\text{O}}}_{3}} = 2{\text{HN}}{{{\text{O}}}_{3}} + 4{{{\text{N}}}_{2}} + 9{{{\text{H}}}_{{\text{2}}}}{\text{O}} + 157\,\,{\text{кДж}}.$

Исходя из целей применения, к качеству продукционной МЗА действуют фармакопейные требования, что обусловливает многостадийную и энергоемкую очистку сырого газового продукта. Основные недостатки существующей технологии МЗА, которую можно охарактеризовать как энерго- и ресурсоемкий процесс: высокое содержание неконденсирующихся примесей в продукте; большое содержание аммиачной селитры и кислых примесей в сточных водах; наличие сублимата в газе-сырце; большой расход аммиачной селитры; высокая энергоемкость процесса; многостадийная система очистки продукта от конденсирующихся примесей; неконтролируемые потери закиси азота на стадии очистки от неконденсирующихся примесей; сложная система обеспечения взрывобезопасности технологического процесса.

При решении задачи усовершенствования процесса термического разложения аммиачной селитры и повышения его селективности по N₂O в первую очередь необходимо добиться изотермичности, уменьшения времени пребывания газообразных продуктов реакции в высокотемпературной зоне реактора и исключить соприкосновение плава NH₄NO₃ со стенками реактора во избежание протекания побочных реакций (2)–(7). Эти требования выполнимы при осуществлении процесса термического разложения расплава аммиачной селитры в диспергированном потоке в изотермическом реакционном объеме. При этом можно избежать перегрева плава селитры, уменьшить долю свободного объема в реакторе и свести до минимума контактирование селитры со стенками реактора. В [3] предложена конструкция реактора-разлагателя для непрерывного процесса получения закиси азота с разбрызгиванием расплава NH₄NO₃.

Цель настоящей работы – анализ тепловых явлений при термическом разложении в диспергированном потоке расплава аммиачной селитры с целью получения закиси азота и определение основных технологических параметров: степень диспергирования (размер капель расплава аммиачной селитры) и конструктивные размеры реактора-разлагателя на основе ранее разработанной математической модели [4].

АНАЛИЗ ТЕПЛОВЫХ ЯВЛЕНИЙ ПРИ ТЕРМИЧЕСКОМ РАЗЛОЖЕНИИ КАПЛИ РАСПЛАВА АММИАЧНОЙ СЕЛИТРЫ

Процесс разложения аммиачной селитры с образованием закиси азота протекает при 543 К, и разность температур между поверхностью капли и объемом газа составляет не более пяти градусов [5].

Молекулярные массы продуктов разложения N₂O и H₂O составляют соответственно 44 и 18. Из этих данных получим значение термодиффузионного коэффициента k_T = 0.018, что свидетельствует о пренебрежимо малом эффекте термодиффузии (Δx = 0.00016).

Рассмотрим прогрев частицы конденсированного вещества – капли – без изменения ее размера. Полный тепловой поток q есть поток тепла, передаваемый излучением и контактом с другими телами – т.е. капля прогревается за счет выделяющегося на ее поверхности тепла. Изменение температуры в капле описывается уравнением

(8)

${{C}_{k}}\frac{{\partial T}}{{\partial t}} = {{\lambda }_{k}}\left( {\frac{{{{\partial }^{2}}{{T}_{k}}}}{{\partial {{r}^{2}}}} + \frac{2}{r}\frac{{\partial {{T}_{k}}}}{{\partial r}}} \right);$

граничные условия:

(9)

${\text{при}}\,\,r = 0\,\,\frac{{\partial {{T}_{k}}}}{{\partial t}} = 0,\,\,{\text{при}}\,\,r = {{r}_{k}}\,\,{{\lambda }_{k}}\frac{{\partial {{T}_{k}}}}{{\partial r}} = q.$

Введем безразмерные радиусы:

${{\rho }_{k}} = \frac{{{{r}_{k}}}}{{{{R}_{0}}}};\,\,\,\rho = \frac{r}{{{{r}_{k}}}}.$

Приведем уравнения (8) и (9) к виду

(10)

$\frac{{\partial T}}{{\partial t}} = A\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{\rho }^{2}}}} + \frac{2}{\rho }\frac{{\partial T}}{{\partial \rho }}} \right),$

при t = 0 T = T_нач; ρ_k =1;

при ρ = 0 $\frac{{\partial T}}{{\partial \rho }} = 0;$ при ρ = 1 T_П ≡ T;

(11)

$\frac{{\partial T}}{{\partial \rho }} = Bk({{T}_{{\text{п}}}}) - D(T - {{T}_{0}}).$

Здесь

(12)

$\begin{gathered} A = \frac{{{{Q}_{p}}{{\rho }^{2}}}}{{3{{\lambda }_{k}}{{R}_{0}}}}; \\ B = \frac{{{{Q}_{p}}{{R}_{0}}^{2}}}{{3{{\lambda }_{k}}}} - \frac{{\nu {{C}_{p}}{{R}_{0}}^{2}}}{{3{{\lambda }_{k}}}}\left( {{{T}_{0}} - T{\kern 1pt} *} \right); \\ D = \frac{{\alpha {{R}_{0}}}}{{{{\lambda }_{k}}}}. \\ \end{gathered} $

Значения параметров для шарообразной капли плава аммиачной селитры: A = 0.5; В = 140; D = 0.05.

Проведенный в [6] анализ влияния размера частицы и скорости реакции на прогрев показал, что скорость реакции незначительно сказывается на разности температур поверхности и центра частицы. При увеличении скорости реакции в пять раз температура частицы стремительно возрастает – реакция переходит в тепловой взрыв. Увеличение диаметра, естественно, увеличивает время прогрева частицы. Таким образом, процесс внутри частицы малого размера (1–2 мм) можно считать изотермическим.

Перенос в пограничном слое совместно с явлениями прогрева частицы и уменьшением ее размера вследствие разложения – это сложная многопараметрическая система, и ее анализ возможен только с применением численного эксперимента. Оценим сначала вклад составляющих процесса для условий термического разложения капли аммиачной селитры.

Термическое разложение аммиачной селитры – это необратимая экзотермическая гетерогенная реакция, идущая на поверхности раздела фаз, тепловой эффект реакции Q_P = 36.9 кДж/моль. Скорость разложения аммиачной селитры, которая постоянна во времени и не зависит от концентрации исходного реагента [7], можно представить в виде w = k(T), что определяет протекание реакции по нулевому порядку, где k = 2.3 × × 10^–4 с^–1 при 270°С [7].

Для дальнейшего анализа процесса термического разложения селитры необходимо уточнить размерность и значение скорости реакции. В [7] константа скорости рассчитана из уравнения $k = \frac{1}{t}ln\frac{{{{V}_{f}}}}{{{{V}_{f}} - {{V}_{t}}}}$, где ${{V}_{f}}$ – конечный объем продуктов (газа) на единицу массы NH₄NO₃,_{V_t –_{текущий объем продуктов (газа) в момент времени t. ${{V}_{f}}{\text{ и }}{{V}_{f}}$ рассчитываются из стехиометрического соотношения исходного компонента (селитры) и
газообразных продуктов реакции.}}

Если начальное количество селитры N₀ (моль) и за время реакции t ее осталось N (моль), то $\frac{{{{V}_{f}}}}{{{{V}_{f}} - {{V}_{t}}}}$ = $\frac{{{{N}_{0}}}}{{{{N}_{0}} - ({{N}_{0}} - N)}}$ = $\frac{{{{N}_{0}}}}{N}$, из чего получаем $k = \frac{1}{t}\ln \frac{{{{N}_{0}}}}{N}.$ Дифференцируя по времени, получим скорость разложения N молей селитры, моль/с:

(13)

$\frac{{dN}}{{dt}} = kN.$

Из вида уравнения (13) следует, что реакция разложения происходит во всем объеме конденсированного вещества.

Количество селитры в единице объема конденсированного вещества ${{N}_{0}} = \frac{\rho }{M},$ где молекулярная масса селитры М=80; плотность расплава селитры ρ = 1.4 г/см³, N₀ = 1.75 × 10^–2 г-моль/см³. Скорость разложения 1 см³ расплава селитры при 270°С $w = \frac{k}{{{{N}_{0}}}} = \frac{{2.3 \times {{{10}}^{{ - 4}}}}}{{1.75 \times {{{10}}^{{ - 2}}}}}$ ≈ 1.3 × 10^–2 моль/(с см³). Газообразные продукты разложения удаляются с поверхности капли, и при дальнейшем рассмотрении скорость разложения относим к единице поверхности ${{w}_{s}}$ шара с радиусом ${{R}_{{\text{c}}}}$:

(14)

${{w}_{S}} = w\frac{{\frac{4}{3}\pi R_{{\text{c}}}^{3}}}{{4\pi R_{{\text{c}}}^{2}}} = w\frac{{{{R}_{{\text{c}}}}}}{3}.$

Уравнение (14) указывает на экспоненциальное уменьшение количества конденсированного компонента со временем. Скорость разложения экспоненциально уменьшается со временем только при расходовании большей части вещества, что связано не только с реакцией разложения, но и с испарением. Упругость паров NH₄NO₃ над расплавом (давление диссоциации) при 270°С Р_нас = 0.12 ат. Содержание паров в единице объема ${{N}_{{0,{\Pi {\rm A}{\rm P}}}}}$ ≈ 5.4 × 10^–6 моль/см³.

Мольное содержание селитры в газовой фазе на 4 порядка меньше, чем в конденсированной фазе, поэтому вкладом разложения в парах в общей скорости разложения можно пренебречь. Но расходование конденсированного компонента на испарение может сказаться на кинетике превращения капель расплава [7].

Вид кинетического уравнения указывает на то, что реакция разложения протекает в объеме, и скорость реакции относится к единице объема плава. Термическое разложение аммиачной селитры – реакция объемная, но выделение газообразных продуктов реакции происходит с поверхности конденсированного вещества. Поэтому скорость реакции в уравнении математического описания процесса определим как

(15)

$r = \frac{{{{R}_{{\text{c}}}}}}{3}k\left( T \right).$

Полагаем, что выделение энергии – тепловой эффект реакции разложения – также сосредоточено на поверхности капли. Поэтому при дальнейшем рассмотрении процесса будем принимать поверхностное выделение теплоты реакции и использовать соотношение (15).

Разложение селитры происходит в объем, заполненный продуктами разложения. Градиент концентраций между поверхностью и объемом отсутствует, массоперенос от поверхности в объем происходит за счет выделения продуктов разложения, и поток от поверхности равен скорости реакции. Возможно возникновение градиента концентраций вследствие термодиффузии:

(16)

$\frac{{dx}}{{d\xi }} = \frac{{{{k}_{{\text{T}}}}}}{T}\frac{{dT}}{{d\xi }}.$

Коэффициент термодиффузии для стехиометрической смеси закиси азота и воды имеет вид

${{k}_{{\text{T}}}} = x(1 - x)\frac{{{{M}_{1}}{{M}_{2}}}}{{{{\nu }_{1}}{{M}_{1}} + {{\nu }_{2}}{{M}_{2}}}}(2 - m) = 0.018.$

При температуре 270°С

$\frac{{dx}}{{d\xi }} \approx \frac{{dT}}{{d\xi }} \times 3 \times {{10}^{{ - 5}}}.$

При градиенте температур до 100°C градиент концентрации компонента не будет превышать 0.003 (т.е. не более 1% от содержания компонента). По условиям проведения термического разложения плава аммиачной селитры допустимый градиент температуры должен быть не более 10°C. Очевидно, что вклад термодиффузионного эффекта в массоперенос пренебрежимо мал.

Тогда вследствие жестких требований к условиям образования закиси азота при термическом разложении плава аммиачной селитры модель процесса в пограничном слое может быть существенно упрощена. Скорость образования продуктов равна скорости разложения селитры. Градиентом концентраций компонентов между поверхностью и объемом, а также термодиффузионным потоком можно пренебречь. Поэтому далее при разложении аммиачной селитры можно рассматривать только тепловые явления.

Если учитывать прогрев по глубине капли, то изменение температуры в капле описывается уравнением теплопроводности

(17)

${{\lambda }_{{\text{c}}}}\left( {\frac{{{{\partial }^{2}}{{T}_{{\text{c}}}}}}{{\partial {{R}^{2}}}} + \frac{2}{R}\frac{{\partial {{T}_{{\text{c}}}}}}{{\partial R}}} \right) = {{C}_{{\text{c}}}}\frac{{\partial {{T}_{{\text{c}}}}}}{{\partial t}}.$

Граничные условия:

(18)

${\text{при}}\,\,R = 0{\kern 1pt} :\,\,\frac{{\partial {{T}_{{\text{c}}}}}}{{\partial R}} = 0$

(19)

$\begin{gathered} {\text{при}}\,\,R = {{R}_{0}} = \frac{{{{d}_{{\text{к}}}}}}{2}{\kern 1pt} :\,\,\,{{\lambda }_{{\text{c}}}}\frac{{\partial {{T}_{{\text{с}}}}}}{{\partial R}} = q, \\ {\text{при}}\,\,t = 0{\kern 1pt} :\,\,T(R) = {{T}_{{{\text{нач}}}}}. \\ \end{gathered} $

Полный тепловой поток q есть поток тепла, передаваемый излучением и контактом с другими телами. Здесь роль “другого тела” играет внутренняя часть капли плава, т.е. сама капля плава, которая прогревается за счет тепла, выделяющегося на ее поверхности.

Теплообмен между поверхностью и объемом описывается уравнением

(20)

$\begin{gathered} q + \alpha \left( {{{T}_{{\text{п}}}} - {{T}_{0}}} \right) = \\ = \,\,\left[ {{{Q}_{P}}(T*) - {{{\bar {C}}}_{P}}(T - T*)} \right]r({{T}_{{\text{п}}}}) - \\ - \,\,\nu {{C}_{{\text{г}}}}r({{T}_{{\text{п}}}})({{T}_{{\text{п}}}} - T*). \\ \end{gathered} $

Изменение размера капли вследствие ее разложения

(21)

$\frac{{d{{R}_{{\text{c}}}}}}{{dt}} = \frac{{r({{T}_{{\text{П}}}})}}{{{{n}_{0}}}}$

при $t = 0{\kern 1pt} :{\text{ }}{{R}_{{\text{c}}}} = {{R}_{0}}$ – первоначальный размер капли.

Вводя безразмерные радиусы ${{\rho }_{{\text{c}}}} = \frac{{{{R}_{{\text{c}}}}}}{{{{R}_{0}}}}$ и $\rho = \frac{R}{{{{R}_{{\text{c}}}}}}$, приведем уравнения (19), (20) и (21) к виду

(22)

$\frac{{\partial T}}{{\partial t}} = \frac{A}{{\rho _{{\text{c}}}^{2}}}\left( {\frac{{{{\partial }^{2}}T}}{{\partial {{\rho }^{2}}}} + \frac{2}{\rho }\frac{{\partial T}}{{\partial \rho }}} \right),$

(23)

$\begin{gathered} {\text{при}}\,\,\,t = 0{\kern 1pt} :T = {{T}_{{{\text{нач}}}}}\,\,{{\rho }_{{\text{c}}}} = 1, \hfill \\ {\text{при}}\,\,\,\rho = 0{\kern 1pt} :\,\,\frac{{\partial T}}{{\partial \rho }} = 0; \hfill \\ {\text{при}}\,\,\,\rho = 1{\kern 1pt} :\,\,{{T}_{{\text{п}}}} \equiv T, \hfill \\ \end{gathered} $

(24)

$\frac{{\partial T}}{{\partial \rho }} = B\rho _{{\text{c}}}^{2}k(T) - D{{\rho }_{{\text{c}}}}(T - {{T}_{0}}),$

(25)

$\frac{{d{{\rho }_{{\text{c}}}}}}{{dt}} = - k(T)\frac{{{{\rho }_{{\text{c}}}}}}{{3{{n}_{0}}}},$

где

(26)

$\begin{gathered} A = \frac{{{{\lambda }_{{\text{c}}}}}}{{{{C}_{{\text{c}}}}R_{0}^{2}}};\,\,\,B = \frac{{R_{0}^{2}}}{{3{{\lambda }_{{\text{c}}}}}}\left[ {{{Q}_{P}} - \nu {{C}_{P}}({{T}_{0}} - T)} \right]; \\ D = \frac{{\alpha {{R}_{0}}}}{{{{\lambda }_{{\text{c}}}}}}. \\ \end{gathered} $

Значения параметров (26) при температуре 543 К для капли плава диаметром 1 мм: A = 0.82; B = 140; D = 0.05.

Рассмотрим прогрев капли плава селитры без изменения ее размера. Результаты некоторых компьютерных расчетов представлены на рис. 1 и 2 .

Рис. 1.

Изменение во времени температуры центра капли Т_ц и разности температур между центром и поверхностью Т_ц–Т_п. Начальная температура капли и температура газа 543 К. Диаметр капли 1 (1) и 2 (2) мм.

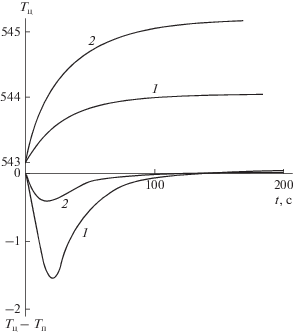
Рис. 2.

Изменение во времени температуры центра капли Т_ц. Температура газа 540 К. Диаметр капли 1 (4), 2 (1–3) и 4 (5) мм: 1 – прогрев и протекание реакции, 2 – изотермичность процесса по сечению капли, 3 – прогрев без реакции.

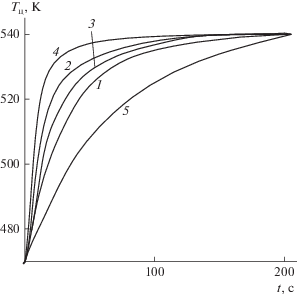
Рисунок 1 показывает изменение температуры центра капли (верхняя часть графика) и разность температур между центром капли и поверхностью (нижняя часть рисунка). Видно, что в результате протекания экзотермической реакции происходит небольшой (до 2°C) разогрев капли.

На короткое время возникает разность температур между центром капли и поверхностью, причем она меньше изменения температуры капли. За время нагрева капли температура по ее глубине выравнивается.

Эти данные получены при равных температурах окружающего газа Т₀ и поверхности капли Т_п (543°С). Разогрев капли вследствие протекания экзотермической реакции составляет около 2°C для d_к = 2 мм и 1°C для капли диаметром d_к = 1 мм. В последнем случае разность температур между центром капли и поверхностью составляет менее 0.2 градуса, т.е. процесс внутри частицы можно считать изотермическим.

Такие же характеристики времени прогрева капли наблюдаются при прогреве капли от более низких температур (рис. 2).

Если считать прогрев по всей глубине капли изотермическим (кривая 2 на рис. 2), то динамика прогрева капли совпадает с динамикой прогрева за счет теплопроводности плава (кривая 1 на рис. 2). Практически совпадают кривые прогрева капли с реакцией (кривая 1) и прямого прогрева (кривая 3): реакция незначительно сказывается на изменении температуры капли.

Естественно, что капля большего размера прогревается медленнее (для капли диаметром 4 мм – кривая 5 на рис. 2).

Рассмотрим процесс разложения капли безотносительно ее положения в реакторе. Степень превращения шарообразной капли ${{X}_{{\text{T}}}} = 1 - \rho _{{\text{c}}}^{3}.$

Хотя реакция термического разложения нитрата аммония имеет нулевой порядок по веществу, количество разложившегося вещества и, следовательно, количество газообразных продуктов зависит от общего количества конденсированного вещества. Для разложения селитры время половинного разложения (аналог – “период полураспада”) составляет около 1500 с.

Зависимости изменения Х_Т и ρ со временем показаны на рис. 3, и они одинаковы для частиц разного размера. Совершенно незначительное различие вызвано разной температурой процесса из-за разного разогрева частиц разного размера.

Рис. 3.

Изменение во времени относительного размера капли ρ и степени превращения капли Х_Т при температуре 543 К.

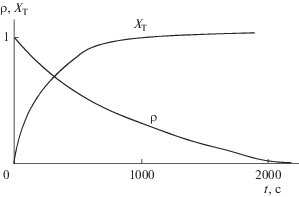
Характерное время изменения размера частицы более чем на порядок превышает время прогрева частицы. Поэтому термическое разложение капли аммиачной селитры можно рассматривать как изотермический процесс, протекающий при температуре окружающего газового потока.

При разбрызгивании капли плава в аппарате падают под действием силы тяжести. Движение падающей частицы описывается уравнением [8]

(27)

$\begin{gathered} \frac{{dv}}{{dt}} = \zeta {{\rho }_{{\text{г}}}}\frac{{w{{{(v - u)}}^{2}}}}{2} + g; \\ w = \frac{1}{{{{\rho }_{{\text{c}}}}}}\frac{{{{S}_{{\text{м}}}}}}{{{{{\text{V}}}_{{\text{c}}}}}}, \\ \end{gathered} $

где ${{S}_{{\text{м}}}} = \pi {\text{ }}R_{{\text{c}}}^{2}$ – площадь миделевого сечения, ${{V}_{{\text{c}}}} = \frac{{4\pi }}{3}R_{{\text{c}}}^{3}$ – объем капли.

Газ в реакторе-разлагателе можно считать неподвижным: при объеме отходящего из промышленного реактора газового продукта его скорость составляет менее 2 см/с. В работе [9] коэффициент сопротивления cреды для 2 ≤ Re ≤ 500 определен как ζ = 18.5Re^–0.6.

Расчет показал, что время падения капли с высоты 2 м составляет менее 1 с. За это время заметного уменьшения размера капли вследствие разложения не произойдет. При этом капля совершает падение в среде, насыщенной продуктами разложения и испарения селитры, и поддерживает насыщение среды.

Рассмотрим прогрев падающей капли. Как показано выше, можно принять каплю изотермичной по объему, тогда изменение температуры капли описывается уравнением

(28)

${{V}_{{\text{c}}}}{{C}_{{\text{c}}}}\frac{{dT}}{{dt}} = \alpha {{S}_{{\text{c}}}}({{T}_{0}} - T).$

Для одиночной сферической частицы [10] Nu = 2 + + 0.5Re^0.5; Nu = 2αr_c/λ_c. Решение уравнений (27), (28) показано на рис. 4.

Рис. 4.

Изменение во времени температуры Т и пройденного расстояния l падающей капли размером 1 (1) и 2 (2) мм. Т₀ – температура газа.

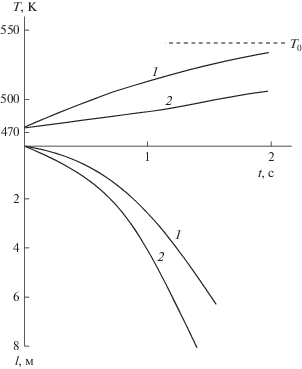
Капля диаметром 1 мм за время падения, равное 1 с, в реакторе высотой 2 м не успевает прогреться более чем на 50°C. Более крупные капли прогреваются еще медленнее.

Из полученных результатов численного анализа математической модели термического разложения капли плава аммиачной селитры следует, что процесс по глубине капли можно считать изотермическим. Вследствие быстрого прогрева капли можно принять, что реакция разложения протекает при температуре окружающего газового потока.

Процесс разложения протекает в узком температурном интервале (несколько градусов). Это позволяет определить теплоту реакции Q_P при температуре поверхности капли $(T\,* = {{T}_{\Pi }})$ и принять ее не зависящей от температуры. Обоснованы возможности допущения квазистационарности распределения температуры в пограничном слое относительно изменения температуры капли и изотермичности последней.

Поэтому процесс разложения расплава аммиачной селитры в капле с достаточной для практических целей точностью можно описать системой уравнений (29)–(30):

− изменение температуры капли

(29)

$\frac{{{{r}_{{\text{c}}}}}}{3}{{C}_{{\text{c}}}}\frac{{dT}}{{dt}} = {{Q}_{P}}r(T) - \alpha ({{T}_{0}} - T)$

при $t = 0{\kern 1pt} :{\text{ }}T = {{T}_{{\text{H}}}}$;

− изменение размера капли селитры

(30)

$\frac{{d{{r}_{{\text{c}}}}}}{{dt}} = \frac{M}{{{{\rho }_{{\text{c}}}}}}\frac{{{{r}_{c}}}}{3}k(T)$

при $t = 0{\kern 1pt} :{{r}_{{\text{c}}}} = {{R}_{0}}$;

− скорость образования i-го продукта реакции (на единицу объема плава)

(31)

${{w}_{i}} = {{\nu }_{i}}k(T).$

ЗАКЛЮЧЕНИЕ

Получено и обосновано упрощенное математическое описание процесса термического разложения капли расплава аммиачной селитры. Результаты математического моделирования позволяют обосновать промышленный способ получения медицинской закиси азота термическим разложением расплава аммиачной селитры в диспергированном потоке и предложить практические рекомендации по конструкции реактора- разлагателя:

перед диспергированием потока необходим предварительный подогрев подаваемого расплава селитры, для этого диспергирующее устройство должно располагаться в обогреваемой зоне реактора;

целесообразно процесс проводить на каплях диаметром 1 мм (и не более 2 мм);

высота реакционной зоны определяется временем прогрева капли: при диаметре 1 мм капля пролетает в падении свыше 6 м.

ОБОЗНАЧЕНИЯ

C_k	удельная массовая теплоемкость конденсированного компонента
c	концентрация, моль/м^3t
D	коэффициент диффузии, см²/с
d_к	диаметр капли, м
$g$	ускорение свободного падения, 9.8 м²/с
P	давление, Па
Q_P	тепловой эффект реакции, кДж/моль
R	универсальная газовая постоянная, Дж/(моль К)
R_c	текущий радиус капли
S_c	площадь наружной поверхности капли
T	температура, К
T_k	температура частицы конденсированного компонента, K
Т_нач	начальная температура капли
T_c	температура внутри капли
t	время, с
u	скорость движения газового потока
V_c	объем частицы
$v$	скорость движения капли
w	скорость термического разложения
α	коэффициент теплообмена между каплей и газом
ζ	коэффициент сопротивления среды
λ_c	коэффициент теплопроводности расплава аммиачной селитры
${{\nu }_{i}}$	стехиометрический коэффициент
ρ	безразмерный радиус
${{\rho }_{{\text{г}}}}$	Плотность газа
${{\rho }_{{\text{c}}}}$	плотность капли селитры
Nu	число Нуссельта
Pe	число Пекле
Re	число Рейнольдса

ИНДЕКСЫ

i, j	номера компонентов
k	конденсированный компонент
г	газ
пс	пограничный слой
с	аммиачная селитра

Список литературы

Косяков Н.Е., Криштопа П.П., Белев И.А. Способ получения закиси азота. А.с. 1675202 SU // Б.И. 1991. № 33.
Мазниченко С.В., Подерягин Н.В., Шутенко Л.И., Енин Л.Ф., Белецкая С.Э., Киселев В.К. Способ получения закиси азота и разлагатель плава аммиачной селитры для ее образования. Патент UА 2146646. 2000.
Březina J., Pěgřimoč B., Jaša B. Reaktor pro kontinuálni výrobu kysličnfku dushnėgo. Patent ČSSR 221216. 1986.
Davidkhanova M.G., Bespalov A.V., Morgunova E.P. Mathematical Modeling of Multicomponent Nonisotherhermic Diffusion in the Process of the Thermal Decomposition of Ammonium Nitrate Melt in a Dispersed Flow // Theor. Found. Chem. Eng. 2018. V. 52. № 2. P. 157. [Давидханова М.Г., Беспалов А.В., Моргунова Е.П. Математическое моделирование многокомпонентной неизотермической диффузии в процессе термического разложения расплава нитрата аммония в диспергированном потоке // Теор. осн. хим. технол. 2018. Т. 52. № 2. С. 131.]
Франк-Каменецкий Д.А. Диффузия и теплопередача в химической кинетике. М.: Наука, 1987.
Бесков В.С., Давидханова М.Г. Многокомпонентная неизотермическая диффузия в гетерогенном процессе разложения конденсированного вещества // Промышленная химия и катализ. Сб. науч. тр. РХТУ им. Д.И. Менделеева. Вып. 185. М.: РХТУ им. Д.И. Менделеева, 2012. С. 16.
Brower K.R., Oxley J.C., Tewari M. Evidence for Homolytic Decomposition of Ammonium Nitrate at High Temperature // J. Phys. Chem. 1989. V. 93. P. 4029.
Вайнберг А.М., Мукосей В.И., Бесков В.С. Математическое моделирование процесса грануляции из расплавов и его применение при проектировании грануляционных башен // Применение мат. методов и вычисл. техники при проектировании. Труды ГИАП. Вып. 40. М.: ГИАП, 1976. С. 48.
Лева Н.А. Псевдоожижение. М.: Госоптотехиздат, 1961.
Аэров М.Э., Тодес О.М. Гидравлические и тепловые основы работы аппаратов со стационарным и кипящим зернистым слоем. Л.: Химия, 1968.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал