1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 1, 2020

Теоретические основы химической технологии, 2020, T. 54, № 1, стр. 52-61

Десублимация UF6 в емкостях с вертикальным оребрением

А. А. Орлов a, А. Ф. Цимбалюк a, Р. В. Малюгин b, *

a Томский политехнический университет
Томск, Россия

b ТО СургутНИПИнефть ПАО Сургутнефтегаз
Тюмень, Россия

* E-mail: malyugin@tpu.ru

Поступила в редакцию 05.11.2018
После доработки 27.08.2019
Принята к публикации 12.09.2019

Полный текст (PDF)

Аннотация

Описана разработанная и программно реализованная упрощенная трехмерная математическая модель нестационарного процесса десублимации UF6 в вертикальные погружные емкости с вертикальным оребрением. С помощью численного моделирования проведено исследование закономерностей процесса десублимации UF6. Приведены результаты расчетов средней производительности емкостей с вертикальным оребрением объемом 1.0–4.0 м3 при изменении давления в коллекторе, температуры хладагента и геометрии емкостей. Показано, что увеличение количества ребер и изменение режима тепло- и массообмена позволяет существенно увеличить среднюю производительность емкостей с вертикальным оребрением и уменьшить время их заполнения.

Ключевые слова: гексафторид урана, десублимация, математическое моделирование, газовая динамика, задача Стефана, процессы тепло- и массопереноса

ВВЕДЕНИЕ

В последнее время на предприятиях России по обогащению урана происходит модернизация разделительного оборудования, которая сопровождается увеличением их разделительных мощностей и нагрузки на цеха конденсационно-испарительных установок, в которых происходит десублимация UF6. В связи с этим приобрели актуальность работы направленные на исследование и интенсификацию процесса десублимации UF6, проектирование коллекторов десублимации UF6 повышенной производительности и совершенствование конструкций емкостей.

Наиболее перспективным способом решения подобного рода задач является использование математического моделирования нестационарных процессов тепло- и массообмена, протекающих при десублимации UF6, поскольку экспериментальный подход дорог и занимает много времени [1–7].

В настоящее время на предприятиях по обогащению урана для десублимации UF6 в основном используются вертикальные погружные емкости, а также горизонтальные емкости и аппараты с тепловым сбросом совместно с вертикальными погружными емкостями [1]. Эти емкости имеют гладкие внутренние стенки, вертикальное или горизонтальное оребрение внутренних стенок. Внутреннее оребрение емкостей используется для повышения их производительности и уменьшения времени заполнения, поскольку увеличивает площадь теплообменной поверхности. Кроме того, емкости имеют различный объем, геометрические размеры (в том числе ребер) и диаметр входного патрубка [1–5, 8, 9].

Ранее нами была разработана двухмерная математическая модель нестационарного процесса десублимации UF6 в вертикальные погружные емкости с гладкими внутренними стенками и горизонтальным оребрением, которая в отличие от известных математических моделей [2, 5, 10, 11] не использует эмпирические данные и учитывает движение газообразного UF6 внутри емкости, десублимацию UF6 на торцевых стенках емкости, эллиптичность этих стенок, а также нестационарность процессов тепло- и массообмена.

Показано, что эта модель адекватно описывает процесс десублимации UF6 в указанных емкостях. С ее помощью проведены исследования динамики заполнения емкостей различного объема с гладкими внутренними стенками газообразным UF6 при изменении температуры хладагента и отношения высоты емкостей к их радиусу, а также влияния диаметра центрального отверстия горизонтальных ребер в емкости объемом 6×10–2 м3 на ее среднюю производительность [12, 13].

Установлено, что при увеличении отношения высоты емкостей H объемом 1.0, 2.0, 3.0 и 4.0 м3 с гладкими внутренними стенками к их радиусу R до предельных значений средняя производительность увеличивается на 23.5, 14.3, 8.9 и 3.8% соответственно [13]. Полученные расчетные значения средней производительности, времени заполнения емкостей и площади их теплообменной поверхности представлены в табл. 1.

Таблица 1.  

Параметры работы емкостей с гладкими внутренними стенками при исходной геометрии и при предельном отношении H/R

V, м3 Исходная геометрия Предельные значения Δq, % ΔS, % Δτ, %
H/R q, г/с S, м2 τ, ч H/R q, г/с S, м2 τ, ч
1.0 3.51 3.38 5.08 289.7 8.45 4.18 6.10 268.2 23.55 20.08 7.42
2.0 3.82 5.16 8.22 380.4 6.99 5.91 9.52 333.5 14.32 15.81 12.33
3.0 3.47 6.63 10.56 444.8 5.74 7.22 11.86 409.3 8.91 12.31 7.98
4.0 3.71 7.92 12.97 497 4.64 8.22 13.64 479.1 3.83 5.17 5.17

Полученные результаты показывают возможность существенного повышения эффективности процесса десублимации UF6 за счет изменения конструкции вертикальных погружных емкостей, поэтому представляет интерес провести аналогичные исследования в емкостях с вертикальным оребрением.

Для исследования процесса десублимации UF6 в емкостях с вертикальным оребрением двухмерная математическая модель непригодна, так как объект исследования является трехмерным, поэтому она была нами усовершенствована.

В данной статье приведено описание разработанной и программно реализованной упрощенной трехмерной математической модели нестационарного процесса десублимации UF6 в вертикальных погружных емкостях, результаты исследования влияния отношения высоты емкостей к их радиусу и конфигурации ребер на среднюю производительность емкостей с вертикальным оребрением различного объема.

ОБЪЕКТ ИССЛЕДОВАНИЯ

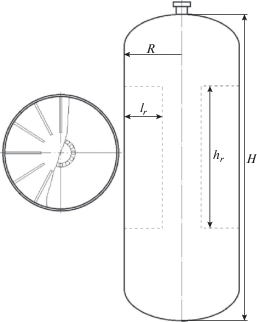
В качестве объекта исследования выступала вертикальная погружная емкость с вертикальным оребрением, представленная на рис. 1, изготовленная из стали марки 16ГС. Ребра располагаются осесимметрично на одинаковом расстоянии от нижней и верхней торцевых стенок емкости. Геометрические размеры емкости и ребер могут меняться.

Рис. 1.

Вертикальная погружная емкость с вертикальным оребрением.

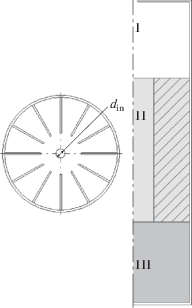
Объем емкости разбивали на несколько подобластей, каждую из которых рассматривали отдельно [14–16]. Схема разбиения емкости на подобласти представлена на рис. 2. Подобласть I соответствует объему емкости между ее верхней торцевой стенкой и верхним краем вертикального ребра. Подобласть II – объему емкости с оребрением. Подобласть III – объему между нижним краем вертикального ребра и донной торцевой стенкой емкости. В каждой подобласти находили совместное (с учетом соседних подобластей) решение уравнений тепло- и массообмена.

Рис. 2.

Схема разбиения емкости с вертикальным оребрением на подобласти (заштрихованная область соответствует вертикальному ребру). Обозначения разъяснены в тексте.

ОПИСАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Принятые допущения. При построении математической модели нестационарного процесса десублимации UF6 приняты следующие допущения [12, 13, 17]:

1. Процесс десублимации UF6 происходит только на боковой и донной частях емкости. Верхняя часть емкости с патрубком выступает из термостата, заполненного хладагентом, и не участвует в теплообмене.

2. Температуру внешних поверхностей боковой и донной стенок емкости считали постоянной и равной температуре хладагента. Температура внешней поверхности верхней части емкости равна температуре воздуха.

3. Процесс десублимации UF6 определяется теплоотводом через стенку емкости и слой десублимата. Все тепло, выделяющееся при фазовом переходе, отводится хладагентом.

4. Температура фазового перехода UF6 равна равновесной температуре и определяется по давлению газообразного UF6 над слоем десублимата.

5. Изменение энтальпии газообразного UF6 при охлаждении до температуры фазового перехода пренебрежимо мало по сравнению с теплотой десублимации.

6. Выполняется гипотеза локального термодинамического равновесия в пределах каждой из фаз.

7. Происходит только поверхностная десублимация UF6 на боковой и донной стенках емкости. Десублимация в объеме газообразного UF6 отсутствует.

8. Химические реакции в рассматриваемой системе не протекают.

9. Ударно-волновые процессы при протекании процесса десублимации UF6 отсутствуют, поэтому для решения задачи Римана о распаде произвольного разрыва использовалось акустическое приближение [18].

Уравнения газовой динамики. Подобласти I и III разбивали равномерными сетками, на которых решали систему уравнений газовой динамики в цилиндрической системе координат:

(1)
$\begin{gathered} \frac{\partial }{{\partial t}}\iint\limits_S {r\rho dzdr} + \oint\limits_\Gamma {r\left( {\rho udr - \rho vdz} \right)} = \iint\limits_S {r\dot {m}dzdr}, \\ \frac{\partial }{{\partial t}}\iint\limits_S {r\rho udzdr} + \oint\limits_\Gamma {r\left[ {\left( {\rho {{v}^{2}} - P} \right)dr - \rho uvdz} \right]} = 0, \\ \frac{\partial }{{\partial t}}\iint\limits_S {r\rho vdzdr} + \oint\limits_\Gamma {r\left[ {\rho uvdr - \left( {\rho {{v}^{2}} + P} \right)dz} \right]} = \\ = \iint\limits_S {Pdzdr} + \frac{\partial }{{\partial t}}\iint\limits_S {r\rho gdzdr}, \\ \frac{\partial }{{\partial t}}\iint\limits_S {rEdzdr} + \oint\limits_\Gamma {r\left[ {\left( {E + P} \right)vdr - \left( {E + P} \right)udz} \right]} = \\ = \iint\limits_S {re\dot {m}dzdr}. \\ \end{gathered} $

В подобласти II параметры течения газообразного UF6 рассматривались в сечениях верхнего и нижнего торцов вертикальных ребер, образуемых радиальной и азимутальной осями. Изменение расчетных параметров газообразного UF6 между этими сечениями по аксиальной координате считали линейным, что делало рассматриваемую расчетную область псевдотрехмерной. Система уравнений газовой динамики в этом случае выглядела следующим образом:

(2)
$\begin{gathered} \frac{\partial }{{\partial t}}\iint\limits_S {r\rho drd\varphi } + \oint\limits_\Gamma {r\left( {\rho udr - \rho vd\varphi } \right)} = \iint\limits_S {r\dot {m}drd\varphi }, \\ \frac{\partial }{{\partial t}}\iint\limits_S {r\rho udrd\varphi } + \oint\limits_\Gamma {r\left[ {\left( {\rho {{v}^{2}} - P} \right)dr - \rho uvd\varphi } \right]} = 0, \\ \frac{\partial }{{\partial t}}\iint\limits_S {r\rho vdrd\varphi } + \oint\limits_\Gamma {r\left[ {\rho uvdr - \left( {\rho {{v}^{2}} + P} \right)d\varphi } \right]} = 0, \\ \frac{\partial }{{\partial t}}\iint\limits_S {rEdrd\varphi } + \oint\limits_\Gamma {r\left[ {\left( {E + P} \right)vdr - \left( {E + P} \right)ud\varphi } \right]} = \\ = \iint\limits_S {re\dot {m}drd\varphi }. \\ \end{gathered} $

Системы уравнений газовой динамики (1) и (2) решали с использованием алгоритма SIMPLE [19–22] на геометрически адаптивной разностной сетке [23–29], используемой для учета движения фронта фазового перехода UF6.

В качестве граничных условий на входе емкости задавали давление и температуру торможения. На оси симметрии емкости – условия симметрии. Считали, что на боковой и донной поверхностях емкости скорости движения газообразного UF6 равны стефановскому потоку, который определяется при решении задачи Стефана и зависит от скорости движения фронта фазового перехода. На верхней стенке емкости выполняется условие теплоизоляции.

Уравнения теплопроводности. Процесс теплообмена газообразного UF6 с хладагентом через боковую стенку емкости и слой образованного на ней десублимата описывали уравнениями теплопроводности в одномерном приближении. Для стенки емкости:

(3)
$r{{\rho }_{P}}{{c}_{P}}\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial r}}\left( {{{\lambda }_{P}}r\frac{{\partial T}}{{\partial r}}} \right).$

Для учета движения фронта фазового перехода в слое десублимата вводили нормированную координату $\psi = {r \mathord{\left/ {\vphantom {r {{{r}_{w}}}}} \right. \kern-0em} {{{r}_{w}}}}$:

(4)
$\begin{gathered} \psi {{r}_{w}}{{c}_{U}}{{\rho }_{U}}\frac{{\partial T}}{{\partial t}} + {{v}_{w}}\left( \tau \right)\psi {{c}_{U}}{{\rho }_{U}}\frac{{\partial T}}{{\partial \psi }} = \\ = \frac{\partial }{{\partial \psi }}\left( {\frac{{{{\lambda }_{U}}}}{{{{r}_{w}}}}\frac{{\partial T}}{{\partial \psi }}} \right). \\ \end{gathered} $

Тепловые процессы в вертикальных ребрах рассматривали с использованием вспомогательной декартовой системы координат x, y, z. Ось x направлена вдоль ребра от стенки емкости к оси симметрии, ось y перпендикулярна плоскости ребра, а ось z в основной и вспомогательной системах координат совпадает и направлена вертикально вниз. Трехмерное уравнение теплопроводности для вертикального ребра емкости записали в виде

(5)
$\frac{{\partial {{\rho }_{P}}{{с}_{P}}T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {{{\lambda }_{P}}\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{{\lambda }_{P}}\frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{{\lambda }_{P}}\frac{{\partial T}}{{\partial z}}} \right).$

Поверхность раздела фаз газообразного и твердого UF6 не линейна. Для ее построения использовали принцип Гюйгенса [30]. Вспомогательную систему координат приводили к безразмерному виду [31, 32]:

$x,y,z \Rightarrow \xi ,\eta ,\zeta ,$
$\begin{gathered} x = {{x}_{w}}\left( t \right)\xi ,\,\,\,\,\frac{{\partial x}}{{\partial t}} = \frac{{\partial \phi }}{{\partial t}} = \frac{{\partial {{x}_{w}}\left( t \right)}}{{\partial t}}\xi = {{v}_{w}}\left( t \right)\xi , \\ \frac{{\partial \phi }}{{\partial \xi }} = {{x}_{w}}\left( t \right), \\ y = {{y}_{w}}\left( t \right)\eta ,\,\,\,\,\frac{{\partial y}}{{\partial t}} = \frac{{\partial \phi }}{{\partial t}} = \frac{{\partial {{y}_{w}}\left( t \right)}}{{\partial t}}\eta = {{u}_{w}}\left( t \right)\eta , \\ \frac{{\partial \phi }}{{\partial \eta }} = {{y}_{w}}\left( t \right), \\ z = {{z}_{w}}\left( t \right)\zeta ,\,\,\,\,\frac{{\partial z}}{{\partial t}} = \frac{{\partial \phi }}{{\partial t}} = \frac{{\partial {{z}_{w}}\left( t \right)}}{{\partial t}}\zeta = {{w}_{w}}\left( t \right)\zeta , \\ \frac{{\partial \phi }}{{\partial \zeta }} = {{z}_{w}}\left( t \right), \\ \end{gathered} $
$\begin{gathered} \frac{\partial }{{\partial x}} = \frac{1}{{{{x}_{w}}\left( t \right)}}\frac{\partial }{{\partial \xi }},\,\,\,\,\frac{\partial }{{\partial y}} = \frac{1}{{{{y}_{w}}\left( t \right)}}\frac{\partial }{{\partial \eta }},\,\,\,\,\frac{\partial }{{\partial z}} = \frac{1}{{{{z}_{w}}\left( t \right)}}\frac{\partial }{{\partial \zeta }}, \\ \frac{\partial }{{\partial t}} = \frac{\partial }{{\partial t}} + \frac{{{{v}_{w}}\left( t \right)\xi }}{{{{x}_{w}}\left( t \right)}}\frac{\partial }{{\partial \xi }} + \frac{{{{u}_{w}}\left( t \right)\eta }}{{{{y}_{w}}\left( t \right)}}\frac{\partial }{{\partial \eta }} + \frac{{{{w}_{w}}\left( t \right)\zeta }}{{{{z}_{w}}\left( t \right)}}\frac{\partial }{{\partial \zeta }}. \\ \end{gathered} $

Таким образом, уравнение теплопроводности для слоя десублимата на вертикальном ребре емкости записали в следующем виде:

(6)
$\begin{gathered} {{\rho }_{U}}{{c}_{U}}\frac{{\partial T}}{{\partial t}} + \frac{{{{v}_{w}}\left( t \right){{\rho }_{U}}{{c}_{U}}\xi }}{{{{x}_{w}}\left( t \right)}}\frac{{\partial T}}{{\partial \xi }} + \frac{{{{u}_{w}}\left( t \right)\rho {{c}_{U}}\eta }}{{{{y}_{w}}\left( t \right)}}\frac{{\partial T}}{{\partial \eta }} + \\ + \,\,\frac{{{{w}_{w}}\left( t \right){{\rho }_{U}}{{c}_{U}}\zeta }}{{{{z}_{w}}\left( t \right)}}\frac{{\partial T}}{{\partial \zeta }} = \frac{1}{{{{x}_{w}}\left( t \right)}}\frac{\partial }{{\partial \xi }}\left( {\frac{{{{\lambda }_{U}}}}{{{{x}_{w}}\left( t \right)}}\frac{{\partial T}}{{\partial \xi }}} \right) + \\ + \,\,\frac{1}{{{{y}_{w}}\left( t \right)}}\frac{\partial }{{\partial \eta }}\left( {\frac{{{{\lambda }_{U}}}}{{{{y}_{w}}\left( t \right)}}\frac{{\partial T}}{{\partial \eta }}} \right) + \frac{1}{{{{z}_{w}}\left( t \right)}}\frac{\partial }{{\partial \zeta }}\left( {\frac{{{{\lambda }_{U}}}}{{{{z}_{w}}\left( t \right)}}\frac{{\partial T}}{{\partial \zeta }}} \right). \\ \end{gathered} $

Для определения скорости движения поверхности фазового перехода в качестве граничного условия использовали уравнение Стефана:

(7)
${{v}_{w}}\left( \tau \right){{\rho }_{U}}{{L}_{{UF}}} = {{\left. {{{\lambda }_{{UF}}}\frac{{\partial T}}{{\partial n}}} \right|}_{{r = {{r}_{w}}}}}.$

Температуру газообразного UF6, контактирующего с теплообменной поверхностью, определяли с использованием известной зависимости [33]

$\begin{gathered} {{P}_{{UF}}} = 133.322\exp \left( { - 132.869 - \frac{{344490}}{{T_{{UF}}^{2}}}} \right. + \\ \left. { + \,\,\frac{{707.31}}{{{{T}_{{UF}}}}} + 26.436\ln {{T}_{{UF}}} - 0.038674{{T}_{{UF}}}} \right). \\ \end{gathered} $

Разработанная упрощенная трехмерная математическая модель нестационарного процесса десублимации UF6 в вертикальные погружные емкости была программно реализована на языке FORTRAN-90 в среде Microsoft Developer Visual Studio [34].

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ И ИХ ОБСУЖДЕНИЕ

Факторы, способные влиять на эффективность процесса десублимации UF6 условно разделили на два типа: 1) параметры, задающие режим процесса десублимации (рабочее давление в коллекторе и температура хладагента), 2) геометрия емкости (отношение высоты емкости к ее радиусу, количество, размеры и расположение ребер в емкости).

Исследование влияния давления в коллекторе и температуры хладагента на среднюю производительность емкостей объемом 1.0, 2.0, 3.0 и 4.0 м3 при их заполнении до 70% свободного объема десублимированным UF6 проводили при температуре газообразного UF6 30°С, давлении в емкостях в начальный момент заполнения 4 мм рт. ст., изменении рабочего давления в коллекторе с 60 до 80 мм рт. ст., температуры хладагента с минус 15°С до минус 25°С. Количество вертикальных ребер во всех емкостях составляло 12 штук, толщина ребер – 5 × 10–3 м. Толщина стенок емкостей – 8 × 10–3 м. Геометрические размеры емкостей и ребер представлены в табл. 2.

Таблица 2.  

Геометрические размеры емкостей и ребер

V, м3 H/R Sr, м2 hr, м lr, м
1.0 3.51 0.48 0.95 0.25
2.0 3.82 0.97 1.6 0.3
3.0 3.47 1.45 1.8 0.4
4.0 3.71 2.6 2.13 0.45

При проведении расчетов емкости с эллиптичными торцевыми стенками представляли в виде эквивалентных емкостей упрощенной цилиндрической геометрии с плоскими торцевыми стенками с такой же площадью поверхности теплообмена, как у емкостей с эллиптичными стенками.

На рис. 3 представлена расчетная зависимость изменения средней производительности емкости с вертикальным оребрением объемом 1.0 м3 от давления в коллекторе при различной температуре хладагента.

Рис. 3.

Зависимость средней производительности емкости с вертикальным оребрением объемом 1.0 м3 от давления в коллекторе при температуре хладагента: 1 – минус 15°С, 2 – минус 20°С, 3 – минус 25°С.

Из рис. 3 видно, что средняя производительность данной емкости меняется линейно при увеличении давления в коллекторе и различных температурах хладагента. Максимальное значение средней производительности наблюдается при давлении в коллекторе 80 мм рт. ст. и температуре хладагента минус 25°С. Аналогичные зависимости получены для емкостей другого объема (табл. 3).

Таблица 3.  

Средняя производительность емкостей различного объема при изменении давления в коллекторе и температуры хладагента

P, мм рт. ст. Th, °С Средняя производительность емкостей q, г/с
V = 2.0 м3 V = 3.0 м3 V = 4.0 м3
60 –15 6.16 9.19 12.04
–20 7.13 10.61 13.92
–25 8.08 12.04 15.78
70 –15 6.58 9.80 12.85
–20 7.54 11.23 14.71
–25 8.49 12.65 16.57
80 –15 6.94 10.34 13.58
–20 7.9 11.76 15.41
–25 8.85 13.35 17.26

Расчеты показали, что увеличение давления в коллекторе с 60 до 80 мм рт. ст. и понижение температуры хладагента от минус 15°С до минус 25°С позволяет повысить среднюю производительность емкостей объемом: 1.0 м3 на 43.8%, 2.0 м3 на 43.6%, 3.0 м3 на 45.3%, 4.0 м3 на 43.3%.

Дальнейшее увеличение давления в коллекторе (выше 80 мм рт. ст.) нецелесообразно, так как может привести к десублимации газообразного UF6 в его трубах. Для предотвращения этого потребуется осуществлять подогрев труб коллектора, что усложнит технологию и увеличит ее себестоимость. Понижение температуры хладагента (CaCl2) ниже минус 25°С также не желательно, поскольку это приведет к значительному увеличению его вязкости [35].

Исследование влияния геометрии емкостей на эффективность их работы проводилось при давлении в емкости в начальный момент заполнения 4 мм рт. ст., давлении в коллекторе 80 мм рт. ст., температуре хладагента минус 25°C, температуре газообразного UF6 30°C. Все емкости имели 12 вертикальных ребер.

Для оценки влияния геометрии вертикальных ребер на среднюю производительность емкостей был проведен расчет заполнения емкостей объемом 1.0–4.0 м3 при изменении толщины ребер 1.0 × 10–3–9.0 × 10–3 м (шаг расчета составлял 1.0 × × 10–3 м), а также при изменении ширины и длины ребер с сохранением постоянной площади их теплообменной поверхности. Шаг расчета при изменении ширины ребер составлял 2.5 × 10–2 м.

Результаты расчетов представлены на рис. 4 и 5 и в табл. 4.

Рис. 4.

Зависимость средней производительности емкостей от толщины вертикальных ребер для V = 4.0 (1), 3.0 (2), 2.0 (3) и 1.0 (4) м3.

Рис. 5.

Зависимость средней производительности емкости объемом 1.0 м3 от ширины вертикальных ребер.

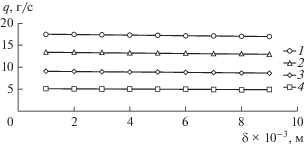
Таблица 4.  

Размеры вертикальных ребер

V, м3 lmin, м hmax, м q(lmin), г/с lmax, м hmin, м q(lmax), г/с Δq, %
1.0 0.15 1.57 3.55 0.3 0.79 4.94 39.28
2.0 0.25 1.92 7.81 0.375 1.28 9.06 16.02
3.0 0.325 2.21 11.8 0.475 1.51 13.26 12.41
4.0 0.375 2.56 15.71 0.5 1.95 17.07 8.64

Из рис. 4 видно, что уменьшение толщины вертикальных ребер на 1.0 × 10–3 м приводит к линейному возрастанию средней производительности емкостей примерно на 0.4–0.6%. Как видим, уменьшение толщины ребер не приводит к существенному росту средней производительности емкостей.

Из рис. 5 видно, что увеличение ширины вертикальных ребер приводит к нелинейному росту средней производительности емкости объемом 1.0 м3. Аналогичные зависимости получены для емкостей другого объема. Из данных табл. 4 следует, что увеличение ширины ребер приводит к существенному росту средней производительности емкостей. Причем, чем меньше объем емкости, тем больше становится ее средняя производительность при увеличении ширины ребер. С другой стороны расчеты показали, что при ширине ребра больше lmax происходит “перемерзание” (образование перемычки из десублимата) между вертикальными ребрами в центральной части емкостей, что снижает эффективность их работы.

Данную закономерность можно объяснить следующим: При заполнении емкостей происходит нарастание слоя десублимированного UF6 на их боковых стенках и вертикальных ребрах. После того, как толщина слоя десублимата на стенке станет равна ширине ребер емкость с вертикальным оребрением начинает работать как безреберная, т.е. менее эффективно. Поэтому увеличение ширины вертикальных ребер приводит к тому, что оребрение участвует в теплообмене дольше и за счет этого их средняя производительность увеличивается.

Исследование зависимости средней производительности емкостей от количества вертикальных ребер проводилось при изменении числа ребер от 4 до 20. Толщина ребра в расчетах составляла 5 × 10–3 м. Результаты расчетов представлены на рис. 6.

Рис. 6.

Зависимость средней производительности емкостей от количества вертикальных ребер для V = 4.0 (1), 3.0 (2), 2.0 (3) и 1.0 (4) м3.

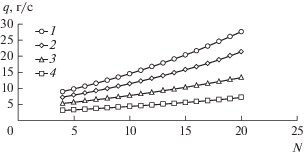
Из рис. 6 видно, что средняя производительность емкостей при увеличении количества ребер увеличивается.

Показано, что увеличение количества ребер с 12 до 20 позволяет повысить среднюю производительность емкостей и сократить время их заполнения до 70% свободного объема (табл. 5). При этом свободный объем емкостей уменьшается на 1.0 × 10–2–3.8 × 10–2 м3, а затраты металла на их изготовление увеличиваются на 0.4–0.8%.

Таблица 5.  

Средняя производительность и время заполнения емкостей при изменении количества ребер

V, м3 12 ребер 20 ребер Δq, % Δτ, %
q, г/с τ, ч q, г/с τ, ч
1.0 4.97 211.61 7.03 135.2 41.5 29.35
2.0 8.85 215.6 13.45 141.91 51.9 34.18
3.0 13.17 218.36 21.14 135.95 60.6 37.74
4.0 16.83 228.65 27.88 138 65.7 39.65

Необходимо учитывать, что при увеличении длины ребер и их количества происходит увеличение площади контакта ребер со стенкой емкости, что способствует возрастанию термических напряжений возникающих в стенке емкости. Известно, что плотность твердого UF6 при повышении температуры снижается, а коэффициент его линейного расширения примерно в 30 раз больше, чем у металла емкости [5]. Поэтому существенное повышение температуры окружающей среды в летний период может привести к деформации стенок емкостей и нарушению их герметичности. При наличии деформации емкостей их дальнейшая эксплуатация станет невозможной.

Затем было исследовано влияние на среднюю производительность отношения высоты емкостей к их радиусу (H/R). В расчетах емкости имели 12 вертикальных ребер толщиной 5 × 10–3 м, площадь поверхности ребер была постоянной за счет изменения их ширины и длины.

Введено ограничение по высоте емкостей Hmax = = 3.0 м в связи с тем, что высота железнодорожных вагонов для их перевозки ограничена. Вопрос устойчивости емкостей при их транспортировке не рассматривался.

Результаты расчетов представлены на рис. 7–9. Черной точкой на графиках отмечены предельные значения отношения H/R для емкостей.

Рис. 7.

Зависимость средней производительности емкостей с вертикальным оребрением от отношения H/R для V = 4.0 (1), 3.0 (2), 2.0 (3) и 1.0 (4) м3.

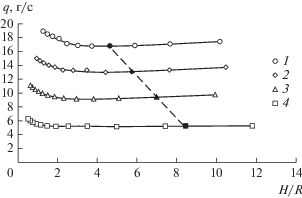
Рис. 8.

Зависимость времени заполнения емкостей с вертикальным оребрением от отношения H/R для V = = 4.0 (1), 3.0 (2), 2.0 (3) и 1.0 (4) м3.

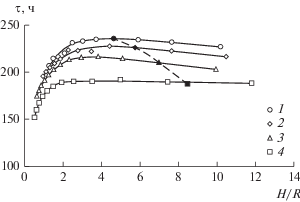
Рис. 9.

Зависимость площади теплообменной поверхности емкостей с вертикальным оребрением от отношения H/R для V = 4.0 (1), 3.0 (2), 2.0 (3) и 1.0 (4) м3.

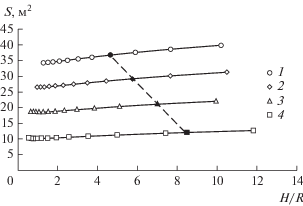
Из рис. 7–9 видно, что зависимости q(H/R), τ(H/R) и S(H/R) имеют перегиб (минимум либо максимум). Увеличение отношения H/R до предельных значений приводит к небольшому уменьшению времени заполнения емкостей десублимированным UF6, а также к незначительному увеличению средней производительности емкостей и площади их теплообменной поверхности (табл. 6). Это связано с тем, что площадь теплообменной поверхности вертикальных ребер существенно больше площади теплообменной поверхности стенок емкости, поэтому изменение отношения H/R приводит к меньшему изменению средней производительности по сравнению с емкостями с гладкими внутренними стенками (см. табл. 1 и 6).

Таблица 6.  

Значения параметров работы емкостей с вертикальным оребрением при исходной геометрии и при предельном отношении H/R

V, м3 Исходная геометрия Предельные значения Δq, % ΔS, % Δ τ, %
H/R q, г/с S, м2 τ, ч H/R q, г/с S, м2 τ, ч
1.0 3.51 5.20 10.91 191 8.45 5.28 12.12 187 1.54 11.09 2.09
2.0 3.82 9.10 19.81 216 6.99 9.37 21.15 210 2.97 6.76 2.78
3.0 3.47 13.05 27.97 226 5.74 13.23 29.27 223 1.38 4.65 1.32
4.0 3.71 16.77 36.18 235 4.64 16.96 36.85 234.8 1.13 1.85 0.08

ЗАКЛЮЧЕНИЕ

Разработана и программно реализована упрощенная трехмерная математическая модель нестационарного процесса десублимации газообразного UF6 в вертикальные погружные емкости с вертикальным оребрением.

В результате проведенных численных исследований процесса десублимации в емкостях объемом 1.0–4.0 м3 с вертикальным оребрением показано, что увеличение давления в коллекторе с 60 до 80 мм рт. ст. и понижение температуры хладагента от минус 15°С до минус 25°С позволяет повысить среднюю производительность емкостей объемом 1.0–4.0 м3 с вертикальным оребрением примерно на 43.3–45.3%, а увеличение количества ребер с 12 до 20 штук – на 41.5–65.7%. Уменьшение толщины ребер на 1.0 × 10–3 м повышает эффективность работы емкостей на 0.4–0.6%. Увеличение ширины вертикальных ребер в 1.33–2.0 раза при сохранении постоянной площади их теплообменной поверхности приводит к увеличению средней производительности емкостей объемом 1.0–4.0 м3 на 8.6–39.3% соответственно. Увеличение отношения высоты емкостей к их радиусу до предельного значения позволяет повысить их среднюю производительность на 1.13–2.97%.

Таким образом, установлено, что увеличение количества ребер и изменение режима тепло- и массообмена позволяет существенно увеличить среднюю производительность емкостей с вертикальным оребрением и уменьшить время их заполнения.

ОБОЗНАЧЕНИЯ

c теплоемкость, Дж/кг К
d диаметр, м
E полная энергия, Дж
e удельная внутренняя энергия, Дж/кг
g ускорение свободного падения, м/с2
H высота емкости, м
h длина вертикального ребра, м
L теплота фазового перехода, Дж/кг
l ширина вертикального ребра, м
m масса газообразного UF6, кг
N количество вертикальных ребер в емкости
n нормаль к поверхности фазового перехода
P давление, Па
q средняя производительность емкости, г/с
Δq увеличение средней производительности емкости, %
R радиус емкости, м
r, φ, z основная цилиндрическая система координат, начало которой находится на оси симметрии входного отверстия
S площадь теплообменной поверхности, м2
ΔS увеличение площади теплообменной поверхности емкости, %
T температура, К
t время, с
u, w, $v$ проекции вектора скорости, м/с
V объем емкости, м3
x, y, z вспомогательная декартовая система координат для вертикального оребрения
δ толщина вертикального ребра, м
λ коэффициент теплопроводности, Дж/(с м К)
ξ, η, ζ вспомогательная безразмерная декартовая системы координат для слоя десублимата на вертикальных ребрах
ρ плотность газа, кг/м3
τ время заполнения емкости, ч
Δτ уменьшение времени заполнения емкости, %
ψ безразмерная координата для уравнения теплопроводности в слое десублимата на боковой стенке емкости

ИНДЕКСЫ

h хладагент
in входное отверстие
P стенка емкости
r вертикальное ребро
U твердый UF6
UF газообразный UF6
w граница раздела фаз

Список литературы

  1. Orlov A.A., Tsimbalyuk A.F., Malyugin R.V. Desublimation for purification and transporting UF6: process description and modeling // Sep. Purif. Rev. 2017. V. 46. № 1. P. 81.

  2. Vilnina A.V., Diadik V.F., Bajdali S.A., Livencov S.N. Experimental study of the duration desublimation cycle of cooling // Bull. Tomsk Polytech. Univ. 2009. V. 315. № 2. P. 91. [Вильнина А.В., Дядик В.Ф., Байдали С.А., Ливенцов С.Н. Экспериментальное исследование процесса десублимации от длительности цикла захолаживания // Изв. Томск. политех. унив. 2009. Т. 315. № 2. С. 91.]

  3. Белозеров Б.П., Русаков И.Ю., Андреев Г.Г., Жиганов А.Н., Кобзарь Ю.Ф. Анализ процесса и аппаратуры для десублимации гексафторида урана и других летучих фторидов // Цветн. мет. 2012. № 1. С. 58.

  4. Раев В.В., Сапрыгин А.В., Цедилкин А.П., Новокшонов К.В. Определение коэффициента теплопроводности твердой фазы гексафторида урана // Фундам. пробл. соврем. материаловед. 2011. Т. 8. № 4. С. 125.

  5. Vilnina A.V., Livencov S.N. Adaptive algorithm node management uranium hexafluoride desublimation // Bull. Tomsk Polytech. Univ. 2008. V. 312. № 5. P. 133. [Вильнина А.В., Ливенцов С.Н. Адаптивный алгоритм управления узлом десублимации гексафторида урана // Изв. Томск. политех. унив. 2008. Т. 312. № 5. С. 133.]

  6. Gubanov S.M., Krainov A.Yu., Mazur R.L. Theoretical and experimental modeling of the cooling of uranium hexafluoride vapor desublimation tanks // Theor. Found. Chem. Eng. 2016. V. 50. № 5. P. 766. [Губанов С.М., Крайнов А.Ю., Мазур Р.Л. Теоретическое и экспериментальное моделирование охлаждения емкостей для десублимации паров гексафторида урана // Теор. осн. хим. технол. 2016. Т. 50. № 5. С. 589.]

  7. Gubanov S.M., Krainov A.Yu., Mazur R.L., Durnovtsev M.I. Theoretical modeling of cooling of containers for the desublimation of hydrogen fluoride vapors // Theor. Found. Chem. Eng. 2017. V. 51. № 3. P. 352. [Губанов С.М., Крайнов А.Ю., Мазур Р.Л., Дурновцев М.И. Теоретическое моделирование охлаждения емкостей для десублимации паров фтористого водорода // Теор. осн. хим. технол. 2017. Т. 51. № 3. С. 343.]

  8. Edwards C.E., Oliever A.J. Uranium processing: A review current methods and technology // JOM. 2000. V. 52. P. 12.

  9. Morel B., Duperret B. Uranium and fluorine cycle in the nuclear industry // J. Fluorine Chem. 2009. V. 130. P. 7.

  10. Smolkin P.A., Buynovskiy A.S., Lazarchuk V.V., Matveev A.A., Sofronov V.L. Mathematical model of desublimation process of volatile metal fluorides // Bull. Tomsk Polytech. Univ. 2007. V. 310. № 3. P. 69. [Смолкин П.А., Буйновский А.С., Лазарчук В.В., Матвеев А.А., Софронов В.Л., Брендаков В.Н. Математическая модель для определения тепловых условий процесса десублимации летучих фторидов металлов // Изв. Томск. политех. унив. 2007. Т. 310. № 3. С. 80.]

  11. Smolkin P.A., Buynovskiy A.S., Lazarchuk V.V., Matveev A.A., Sofronov V.L., Brendakov V.L. Mathematical model of determining heat condition in desublimation process of volatile metal fluorides // Bull. Tomsk Polytech. Univ. 2007. V. 310. № 3. P. 77. [Смолкин П.А., Буйновский А.С., Лазарчук В.В., Матвеев А.А., Софронов В.Л. Математическая модель процесса десублимации летучих фторидов металлов // Изв. Томск. политех. унив. 2007. Т. 310. № 3. С. 77.]

  12. Orlov A.A., Tsimbalyuk A.F., Malyugin R.V., Glazunov A.A. Dynamics of UF6 desublimation with the influence of tank geometry for various coolant temperature // MATEC Web Conf. 2016. V. 72. Article number 01079.

  13. Orlov A.A., Tsimbalyuk A.F., Malyugin R.V., Leontieva D.A., Kotelnikova A.A. Effect of tank geometry on its average performance // AIP Conf. Proc. 2018. V. 1938. Article number 020009.

  14. Byun D.Y., Baek S.W., Kim M.Y. Investigation of radiative heat transfer in complex geometries using blocked-off, multiblock, and embedded boundary treatments // Numer. Heat Transfer, Part A. 2003. V. 43. P. 807.

  15. Chai J.C., Moder J.P. Spatial-multiblock procedure heat transfer // Numer. Heat Transfer, Part B. 1997. V. 31. P. 277.

  16. Orlov A.A., Tsimbalyuk A.F., Malyugin R.V. Mathematical modeling of process of obtaining the solid uranium hexafluoride // Key Eng. Mater. 2016. V. 683. P. 533.

  17. Consalvi J.I., Porterie B., Loraund J.C. A blocked-off-region strategy to compute fire-spread scenarios involving internal flammable targets // Numer. Heat Transfer, Part B. 2005. V. 47. P. 419.

  18. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н. Численное решение многомерных задач газовой динамики. М.: Наука, 1976.

  19. Patankar S.V. Numerical Heat Transfer and Fluid Flow. Washington, DC: Hemisphere, 1980.

  20. Hu M.-H., Wu J.-S., Chen Y.-S. Development of a parallelized 2D/2D-axisymmetric Navier-Stokes equation solver for all-speed gas flows // Comput. Fluids. 2011. V. 45. № 1. P. 241.

  21. Corcione M., Cianfrini M., Quintino A. Enhanced natural convection heat transfer of nanofluids in enclosures with two adjacent walls heated and the two opposite walls cooled // Int. J. Heat Mass Transfer. 2015. V. 88. P. 902.

  22. Mamourian M., Milani Shirvan K., Ellahi R., Rahimi A.B. Optimization of mixed convection heat transfer with entropy generation in a wavy surface square lid-driven cavity by means of Taguchi approach // Int. J. Heat Mass Transfer. 2016. V. 102. P. 544.

  23. Esfahani J.A., Akbarzadeh M., Rashidi S., Rosen M.A., Ellahi R. Influences of wavy wall and nanoparticles on entropy generation over heat exchanger plat // Int. J. Heat Mass Transfer. 2017. V. 109. P. 1162.

  24. Ciofalo M., Arini A., Liberto M.D. On the influence of gravitational and centrifugal buoyancy on laminar flow and heat transfer in curved pipes and coils // Int. J. Heat Mass Transfer. 2014. V. 82. P. 123.

  25. Mazhukin V.I., Shapranov A.V., Perezhigin V.E., Koroleva O.N., Mazhukin A.V. Kinetic melting and crystallization stages of strongly superheated and supercooled metals // Math. Models Comput. Simul. 2017. V. 9. № 4. P. 448. [Мажукин В.И., Шапранов А.В., Пережигин В.Е., Королёва О.Н., Мажукин А.В. Кинетические стадии плавления и кристаллизации сильно перегретых и переохлажденных металлов // Мат. модел. 2016. Т. 28. № 12. С. 83.]

  26. Mazhukin V.I., Shapranov A.V., Samokhin A.A., Ivochkin A.Yu. Modeling of explosive boiling of a thin film during homogeneous subnanosecond heating // Math. Models Comput. Simul. 2014. V. 6. № 5. P. 542. [Мажукин В.И., Шапранов А.В., Самохин А.А., Ивочкин А.Ю. Моделирование взрывного вскипания тонкой пленки при однородном субнаносекундном нагреве // Мат. модел. 2014. Т. 26. № 3. С. 125.]

  27. Isaev S.A., Schelchkov A.V., Leontiev A.I., Gortyshov Yu F., Baranov P.A., Popov I.A. Vortex heat transfer enhancement in the narrow plane-parallel channel with the oval-trench dimple of fixed depth and spot area // Int. J. Heat Mass Transfer. 2017. V. 109. P. 40.

  28. Breslavskii P.V., Mazhukin V.I. Dynamic adaptation method in gasdynamic simulations with nonlinear heat conduction // Comput. Math. Math. Phys. 2008. V. 48. № 11. P. 2102. [Бреславский П.В., Мажукин В.И. Метод динамической адаптации в задачах газовой динамики с нелинейной теплопроводностью // Ж. вычисл. мат. мат. физ. 2008. Т. 48. № 11. С. 2067.]

  29. Mazhukin V.I., Samokhin A.A., Demin M.M., Shap-ranov A.V. Explosive boiling of meyals upon irradiation by a nanosecond laser pulse // Quantum Electron. 2014. V. 44. № 4. P. 283.

  30. Сивухин В.Д. Общий курс физики. Оптика. М.: Наука, 1980.

  31. Kofanov A.V., Liseikin V.D. Grid construction for discretely defined configuration // Comput. Math. Math. Phys. 2013. V. 53. № 6. P. 938. [Кофанов А.В., Лисейкин В.Д. Построение сеток для конфигураций, заданных дискретно // Ж. вычисл. мат. мат. физ. 2013. Т. 53. № 6. С. 938.]

  32. Kofanov A.V., Liseikin V.D., Rychkov A.D. Application of the spherical metric tensor to grid adaptation and the solution of applied problems // Comput. Math. Math. Phys. 2012. V. 52. № 4. P. 653. [Кофанов А.В., Лисейкин В.Д., Рычков А.Д. Применение шарового метрического тензора для адаптации сеток и решения прикладных задач // Ж. вычисл. мат. мат. физ. 2012. Т. 52. № 4. С. 653.]

  33. Katz J.J., Rabinowiych E. The Chemistry of Uranium. Part I. The Element, Its Binary and Related Compounds. New York: McGraw-Hill, 1961.

  34. Орлов А.А., Цимбалюк А.Ф., Малюгин Р.В. Расчет динамики заполнения вертикальных погружных емкостей при десублимации в них гексафторида урана. Свидетельство о государственной регистрации программы для ЭВМ № 2016616566 от 15.06.2016.

  35. Grigoras C.G., Muntianu G., Gavrila L. Mathematical modelling of CaCl2 aqueous solutions thermophysical properties // Sci. Study Res.: Chem. Chem. Eng., Biotechnol., Food Ind. (Univ. Bacau). 2016. V. 17. № 4. P. 417.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал