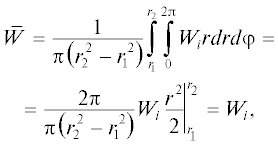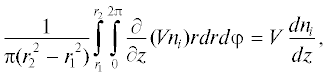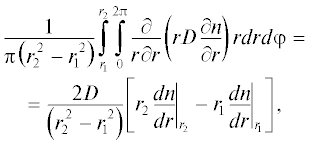1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 54, № 3, 2020

Теоретические основы химической технологии, 2020, T. 54, № 3, стр. 370-375

Конструкция реактора диэлектрического барьерного разряда и моделирование процессов очистки водных растворов

Е. С. Бобкова *

Российский государственный университет нефти и газа (национальный исследовательский университет) им. И.М. Губкина
Москва, Россия

* E-mail: lenabobkova777@gmail.com

Поступила в редакцию 11.12.2018
После доработки 18.01.2019
Принята к публикации 08.02.2019

Полный текст (PDF)

Аннотация

Рассматривается конструкция установки диэлектрического барьерного разряда атмосферного давления для очистки воды от органических загрязнений. Приводится конструкция реактора, последовательность расчета основных физических параметров барьерного разряда в кислороде и методика определения химического состава водного раствора, содержащего органический загрязнитель (на примере формальдегида).

Ключевые слова: диэлектрический барьерный разряд, обработка растворов, деструкция органических соединений, плазменные технологии очистки воды, разряд, плазмохимические реакторы

ВВЕДЕНИЕ

Большое количество работ, определяющих приоритетные направления инженерных научных исследований, связаны с созданием и реализацией новых ресурсосберегающих экологически безопасных производств. Разработка и применение современных технологий и методов моделирования для проектирования химико-технологических процессов необходимы для обеспечения безопасности и охраны окружающей среды [1]. Исследования возможности применения неравновесной плазмы атмосферного давления, создаваемой с помощью газовых разрядов в водных растворах, подчеркивают увеличивающийся интерес к данной области. Одна из причин этого заключается в новых возможностях, которые открывают эти разряды для практического использования. Одним из перспективных направлений использования разрядов в жидкостях является их применение для деструкции органических загрязнений, содержащихся в сточных водах. Рациональная организация таких технологий невозможна без знания кинетики и механизмов процессов, приводящих к образованию химически активных частиц, как в самой плазме, так и в растворе, находящемся в контакте с ней [2]. Интерес для разработки процессов снижения химического загрязнения природных вод заключается в возможности использования безреагентной деструкции [3] органических соединений в жидкой фазе в условиях неравновесной плазмы. Недостаточность сведений по этому вопросу определяет цели и задачи данной работы.

Наиболее распространенным в лабораторной и технической практике способом генерации состояния плазмы является газовый разряд – прохождение тока через среду под действием высокого внешнего напряжения. Для обработки водных растворов используют исключительно разряды атмосферного давления. Зона разряда (плазмы) непосредственно контактирует с обрабатываемым раствором. Первичным процессом, определяющим существование плазмы, является ионизация молекул или атомов плазмообразующего газа ударами электронов, ускоренных под действием внешнего электрического поля. Гибель заряженных частиц происходит как путем их диффузии к границам разрядной зоны (раствор), так и при совместной рекомбинации электронов и положительных ионов в объеме плазмы [4].

В настоящее время для воздействия на водные растворы разработано несколько типов плазмохимических реакторов, которые отличаются как видом разряда, так и конструкцией, например: разряд постоянного тока над поверхностью раствора [5], разряд скользящей дуги [6], разряд импульсной стримерной короны над раствором и в растворе [7], диэлектрический барьерный разряд (ДБР) [8], контактный тлеющий разряд [9], диафрагменный и капиллярный разряды [10].

АНАЛИЗ УСТАНОВКИ ДБР ДЛЯ ОЧИСТКИ ВОДНЫХ РАСТВОРОВ

Водные растворы органических веществ (фенола, формальдегида, карбоновых кислот) подвергали плазменному воздействию в проточном реакторе диэлектрического барьерного разряда.

Описание установки. В экспериментах использовали установку, изображенную на рис. 1.

Рис. 1.

Схема экспериментальной установки ДБР: 1, 3 – вход и выход плазмообразующего газа (O2); 2 – внешний электрод (фольга); 4, 11 – вход и выход водного раствора; 5 – диэлектрический барьер из пирекса rвнут = 9 мм, rвнеш = 11 мм; 6 – высоковольтный зонд; 7 – источник высокого напряжения; 8 – двухканальный цифровой осциллограф; 9 – пористый гидрофильный материал толщиной 1 мм; 10 – внутренний электрод rэ = 4 мм; 12 – резистор (100 Ом).

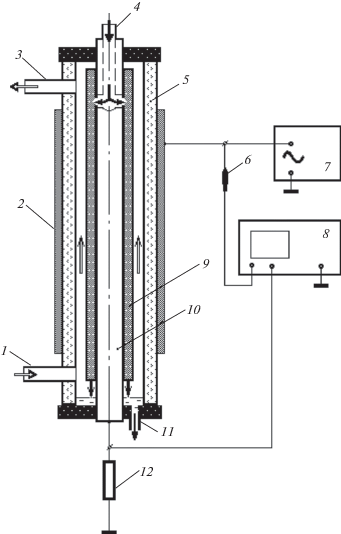
Разряд создавался в реакторе коаксиального типа длиной активной зоны 12 см путем приложения высокого напряжения (до 20 кВ) промышленной частоты (50 Гц). Полное падение напряжения измерялось высоковольтным зондом (2000 : 1), а разрядный ток определялся по падению напряжения на резисторе (100 Ом), включенным между внешним электродом и землей. Обе волновые формы регистрировались цифровым двухканальным осциллографом GW Instek GDS-2052 (Тайвань). Внутренний электрод из алюминиевого сплава был покрыт гидрофильной пористой тканью толщиной ~1 мм, по которой в пленочном режиме стекал обрабатываемый раствор. Объемный расход раствора регулировался, а его время контакта (τк) с зоной разряда изменялось примерно от 2 до 12 с. Величина τк рассчитывалась по соотношению

${{\tau }_{{\text{к}}}} = \frac{{\pi DhL}}{Q},$
где D – диаметр покрытия из ткани, h – толщина пленки раствора, Q – объемный расход раствора.

Толщина пленки раствора определялась по выражению, справедливому для ламинарного потока в поле силы тяжести [11]

$h = {{\left( {\frac{{3\nu }}{g}\frac{Q}{{\pi D}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$
где ν – кинематическая вязкость, g – гравитационная постоянная.

Кинематическая вязкость воды может быть рассчитана по соотношению

$\nu (T) = \frac{{1.78 \times {{{10}}^{{ - 6}}}}}{{1 + 0.0337(T - 273) + 0.000221{{{(T - 273)}}^{2}}}}.$

Плазмообразующим газом был технический кислород (99.8%), расход которого составлял 3.4 см3/с. После достижения стационарного состояния пробы раствора, обработанного разрядом, подвергались химическому анализу.

Моделирование процессов, протекающих в жидкой фазе ДБР. Поле концентраций i-го компонента в стационарном цилиндрически-симметричном потоке описывается системой уравнений

(1)
$\begin{gathered} \frac{\partial }{{\partial z}}\left[ {{{D}_{i}}\frac{{\partial {{n}_{i}}}}{{\partial z}}} \right] + \frac{1}{r}\frac{\partial }{{dr}}\left[ {r{{D}_{i}}\frac{{\partial {{n}_{i}}}}{{\partial r}}} \right] - \frac{\partial }{{\partial z}}(V{{n}_{i}}) + \\ + \,\,\sum\limits_k {W_{{ko}}^{i} - } \sum\limits_m {W_{{mг}}^{i} = 0} , \\ \end{gathered} $
где суммирование для i-го компонента ведется по k – процессам образования и m – процессам гибели, ni – концентрация i-го компонента, Di – его коэффициент диффузии, r – текущий радиус, z – продольная координата вдоль разряда, V – скорость потока жидкости, см/с, $W_{{k{\text{o}}}}^{i}$ – скорость образования i-го компонента в k-й реакции, $W_{{m{\text{г}}}}^{i}$ – скорость гибели i-го компонента в m-й реакции.

Оценим порядки величин слагаемых в (1). Первый член дает характерное время диффузии в продольном направлении τD ≈ L2/Di. Типичные значения коэффициентов диффузии (D) органических соединений в воде составляют ~10–5 см2/с [12]. При длине зоны разряда $L$ =12 см это дает τD = 105 с. Максимальное время контакта раствора с зоной разряда (3-й член) τк ≈ L/V = 12 c. Следовательно, член, описывающий диффузию в продольном направлении, пренебрежимо мал по сравнению с членом, описывающим конвективный перенос. Характерное время диффузии в радиальном направлении (2-й член) равен τDr ≈ h2/D, что дает при типичной толщине слоя раствора h ≈ ≈ 1.6 × 10–3 см время τDr ≈ 1.6 с. Поэтому диффузия должна выровнять концентрации по слою раствора.

Поскольку экспериментально измеряются средние по сечению слоя раствора концентрации, усредним (1) по сечению слоя раствора:

(2)
(3)
(4)
где r2 = 5 мм и r1 = 4 мм – наружный и внутренний радиусы слоя раствора.

Слагаемое (4) описывает потоки частиц данного сорта, выходящие через границы слоя раствора. Эти потоки могут быть записаны в виде

$ - D{{\left. {\frac{{dn}}{{dr}}} \right|}_{{{{r}_{2}}}}} = {{\left. {\frac{1}{4}V\gamma n} \right|}_{{{{r}_{2}}}}}$

и

${{\left. { - D\frac{{dn}}{{dr}}} \right|}_{{{{r}_{1}}}}} = {{\left. {\frac{1}{4}V\gamma n} \right|}_{{{{r}_{1}}}}}.$

В этих выражениях $\frac{1}{4}V\gamma $ – тепловой поток на соответствующей границе, $V = \sqrt {\frac{{8kT}}{{\pi m}}} $ – средняя тепловая скорость молекул, γ – вероятность перехода в другую фазу, ${{\left. n \right|}_{{{{r}_{2}}}}}$ и ${{\left. n \right|}_{{{{r}_{1}}}}}$ – концентрации в растворе на расстоянии длины свободного пробега от границ. Поскольку профиль концентраций почти плоский, то концентрации на границе практически равны объемным. С учетом этих соотношений (4) запишется как

$\frac{V}{{2\left( {r_{2}^{2} - r_{1}^{2}} \right)}}\left( {{{r}_{1}}{{\gamma }_{1}} - {{r}_{2}}{{\gamma }_{2}}} \right)n.$

В этом выражении величина, стоящая в скобках, есть эффективная константа скорости (частота), т.е. процессы массообмена можно формально описывать как реакцию 1-го кинетического порядка.

Таким образом, для стационарных условий система (1) запишется как

(5)
$V\frac{{d{{n}_{i}}}}{{dz}} = \sum\limits_k {\bar {W}_{{k{\text{o}}}}^{i}} - \sum\limits_m {\bar {W}_{{m{\text{г}}}}^{i}} .$

Поскольку раствор является сильно разбавленным, а степень разложения воды мала, то V есть линейная скорость движения воды, определяемая по ее расходу.

Вводя новую безразмерную переменную x = = z/L и время контакта раствора с зоной разряда τж ≈ L/Vж, уравнение (5) преобразуется к виду

(6)
$\frac{{d{{n}_{i}}}}{{dx}} = {{\tau }_{{\text{ж}}}}\left[ {\sum\limits_k {W_{{k{\text{o}}}}^{i}} - \sum\limits_m {W_{{m{\text{г}}}}^{i}} } \right].$

Система уравнений (6) является системой обыкновенных дифференциальных уравнений.

Электрические параметры ДБР. Диэлектрический барьерный разряд, работающий на переменном токе, представляет собой реактивную нагрузку. На опыте измеряется полное напряжение, приложенное к этой нагрузке, тогда как для анализа кинетики процессов, протекающих в разряде, необходимо знать электрическое поле, приложенное непосредственно к газовому зазору. Для этого проанализируем структуру эквивалентной цепи разряда.

Разрядное устройство (рис. 1) состоит из трех последовательно включенных цилиндрических конденсаторов, образованных пирексовой трубкой (С1), газовым зазором (С2) и слоем раствора (С3) соответственно. Эти емкости определяются соотношением

$C = \frac{{2\pi {{\varepsilon }_{1}}{{\varepsilon }_{0}}L}}{{\ln \left( {{{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}}} \right)}},$
где ε1 – относительная диэлектрическая проницаемость материала конденсатора, ε0 = 8.85 × × 10–12 Ф/м – диэлектрическая проницаемость вакуума, $L$ = 0.12 м – длина конденсатора, r1 и r2 – радиусы внутренней и внешней обкладок каждого конденсатора. Относительные диэлектрические постоянные для пирекса, кислорода и воды составляют 4.5, 1 и 81 соответственно.

Расчет дает С1 = 0.151 × 10–9 Ф, С2 = 0.962 × 10–11 Ф и С3 = 0.458 × 10–8 Ф. Эти значения дают следующие величины емкостных сопротивлений для частоты 50 Гц: ${{R}_{{{{C}_{1}}}}}{\text{ = }}{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\left( {{\text{2}}f{{C}_{1}}} \right)}}} \right. \kern-0em} {\left( {{\text{2}}f{{C}_{1}}} \right)}}$ = 2.11 × 107 Ом; ${{R}_{{{{C}_{2}}}}}$ = = 3.30 × 108 Ом; ${{R}_{{{{C}_{3}}}}}$ = 6.95 × 105 Ом.

Рассчитаем активные сопротивления трубки из пирекса и слоя воды. Для цилиндрической геометрии сопротивление равно

$R = \frac{\rho }{{2\pi L}}\int\limits_{{{r}_{2}}}^{{{r}_{1}}} {\frac{{dr}}{r}} = \frac{\rho }{{2\pi L}}\ln ({{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} {{{r}_{2}}}}} \right. \kern-0em} {{{r}_{2}}}}),$
где $\rho $ = 1015 Ом см и $\rho $ = 106 Ом см – удельные сопротивления пирекса и дистиллированной воды соответственно. Расчет дает для пирекса $R$ = 2.7 × × 1012 Ом и $R$ = 1.6 × 103 Ом. Среднее активное сопротивление цепи можно рассчитать как ${{R}_{D}} = \bar {U}{\text{/}}\bar {I},$ где $\bar {U}$ и $\bar {I}$ – среднеквадратичные значения тока и напряжения. При $\bar {U} \approx 10$ кВ величина тока $\bar {I} \approx 0.5$ мА, что дает $R$ ≈ 2 × 107 Ом. Сравнивая полученные сопротивления, видно, что эквивалентная цепь разряда представляет собой емкостное сопротивление диэлектрического барьера (пирекса) и активного сопротивления разряда, включенных последовательно. Поэтому приложенное напряжение Uappl можно записать как
${{U}_{{appl}}}(t) = {{U}_{p}}(t) + \frac{1}{{{{C}_{1}}}}\int\limits_0^t {I(t)dt} ,$
где первое слагаемое в правой части Up – падение напряжения на разряде, а второе – падение напряжения на емкостном сопротивлении диэлектрического барьера.

По этим данным рассчитывалась мощность, вложенная в разряд за период: $W = \frac{1}{T}\int\limits_0^T {{{U}_{р}}Idt} $ и среднеквадратичное приложенное напряжение: $\bar {U} = \sqrt {\frac{1}{T}\int\limits_0^T {{{U}_{р}}{{U}_{р}}dt} } .$

Расчеты параметров плазмы проводились для средних по газовому промежутку 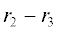(${{r}_{3}}$ = 9 мм) величин. Распределение электрического поля дается выражением $E = \frac{{{{U}_{р}}}}{{r\ln ({{{{r}_{2}}} \mathord{\left/ {\vphantom {{{{r}_{2}}} {{{r}_{3}}}}} \right. \kern-0em} {{{r}_{3}}}})}}.$ Среднее значение поля: $\bar {E} = \frac{1}{{{{r}_{2}} - {{r}_{3}}}}\int\limits_{r3}^{r2} {Edr} .$ Откуда получаем

$\bar {E} = \frac{{{{U}_{р}}}}{{{{r}_{2}} - {{r}_{3}}}}.$

Радиус $\bar {R}$, при котором это поле реализуется, равен $\bar {R} = \frac{{{{r}_{2}} - {{r}_{3}}}}{{\ln ({{{{r}_{2}}} \mathord{\left/ {\vphantom {{{{r}_{2}}} {{{r}_{3}}}}} \right. \kern-0em} {{{r}_{3}}}})}}.$ Для наших условий $\bar {R} = 0.65$ см, а $\bar {E} = 2.22{{U}_{р}}$ В/см. По среднему радиусу рассчитывались плотность тока и концентрация электронов. Для определения по этим данным величины приведенной напряженности электрического поля E/N необходимы сведения о газовой температуре. Согласно результатам работы [8], эти температуры не превосходят 305 К. Это значение использовалось для расчета полной концентрации частиц N из уравнения p = NkT.

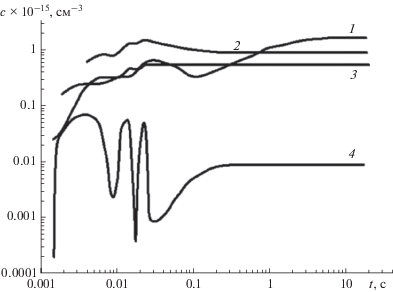
Кинетические процессы в ДБР. Процессы, происходящие вследствие прямого электронного удара, являются первичными в образовании активных частиц. Константы скоростей реакций рассчитываются с учетом ФРЭЭ, полученной из решения уравнения Больцмана в двучленном приближении Кинетическая схема реакций, описывающая процессы, происходящие в плазме атмосферного давления в кислороде, включает 20 компонент кислородной плазмы и 105 реакций [13]. Расчеты показывают, что основными частицами плазмы являются O3, O2(a1Δg), H2O2 и OH-группа (расположены в порядке убывания концентраций), которые участвуют в процессе окисления органических соединений в воде (рис. 2).

Рис. 2.

Концентрации основных компонент кислородной плазмы в ДБР как функции времени: 1 – O3, 2 – O2(a1Δg), 3 – H2O2, 4 – OH. Пример расчета кинетических уравнений и уравнения Больцмана для разряда в кислороде. $\bar {U}$ = 6235 В, $\bar {I}$ = 0.279 мА. Содержание паров воды 5%.

Для очистки водных растворов от, например, формальдегида система обыкновенных дифференциальных уравнений типа (6) для всех 20 компонент кислородной плазмы дополняется аналогичными уравнениями для процессов разложения формальдегида: 9 реакций и 6 компонент [13]. Эволюция процесса разложения формальдегида приведена на рис. 3.

Рис. 3.

Концентрация формальдегида (1) и степень его разложения (2) как функции времени контакта раствора с зоной разряда. Точки – эксперимент, линии – расчет.

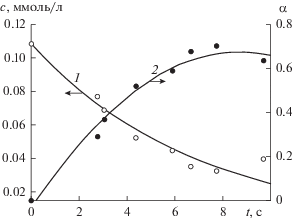
Увеличение мощности, вкладываемой в разряд, приводит к росту степени разложения всех исследованных соединений. Эффективность разложения зависит от начальной концентрации вещества. Результаты расчетов хорошо согласуются с опытами. Степень очистки водного раствора с формальдегидом в зависимости от условий составляет от 80 до 99%.

Аналогичный подход может быть применен к описанию процессов очистки водных растворов от органических загрязнителей: фенолов, карбоновых кислот, синтетических поверхностно-активных веществ [14, 15].

ЗАКЛЮЧЕНИЕ

Предложенная конструкция реактора ДБР и методика моделирования могут быть использованы для очистки сточных вод от органических соединений, процессов водоподготовки, а также для оптимизации параметров ДБР реакторов.

Список литературы

  1. Ziyatdinov N.N. Modeling and Optimization of Chemical Engineering Processes and Systems // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 889. [Зиятдинов Н.Н. Моделирование и оптимизация химико-технологических процессов и систем // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 613.]

  2. Шутов Д.А., Рыбкин В.В. Электрические разряды атмосферного давления как инструмент химической активации водных растворов // Тез. докл. Всеросс. (с междунар. участием) конф. “Физика низкотемпературной плазмы – ФНТП-2017”. Казань: Отечество, 2017. С. 214.

  3. Макальский Л.М., Цеханович О.М. Применение лавиностримерного разряда для очистки сточных вод // Вестн. Волгогр. гос. унив. Сер. 11. Естеств. науки. 2017. Т. 7. № 2. С. 12.

  4. Bruggeman P., Leys C. Non-thermal plasmas in and in contact with liquids // J. Phys. D: Appl. Phys. 2009. V. 42. Article number 053001.

  5. Mezei P., Cserfalvi T. Electrolyte cathode atmospheric glow discharges for direct solution analysis // Appl. Spectrosc. Rev. 2007. V. 42. № 6. P. 573.

  6. Burlica R., Kirkpatrick M., Finney W., Clark R., Locke B. Organic dye removal from aqueous solution by glidarc discharges // J. Electrost. 2004. V. 62. № 4. P. 309.

  7. Malik A., Schoenbach K. New approach for sustaining energetic, efficient and scalable non-equilibrium plasma in water vapours at atmospheric pressure // J. Phys. D: Appl. Phys. 2012. V. 45. № 13. Article number 132001.

  8. Bubnov A.G., Grinevich V.I., Maslova O.N., Rybkin V.V. Application of barrier discharge to the treatment of water from phenol: reactor thermal characteristics // Theor. Found. Chem. Eng. 2007. V. 41. № 4. P. 396. [Бубнов А.Г., Гриневич В.И., Маслова О.Н., Рыбкин В.В. Применение барьерного разряда для очистки воды от фенола: температурные характеристики реактора // Теор. осн. хим. технол. 2007. Т. 41. № 4. С. 420.]

  9. Singh R., Gangal U., Sen-Gupta S. Effects of alkaline ferrocyanide on non-faradaic yields of anodic contact glow discharge electrolysis: determination of the primary yield of OH-radicals // Plasma Chem. Plasma Process. 2012. V. 33. № 3. P. 609.

  10. Захаров А.Г., Максимов А.И., Титова Ю.В. Физико-химические свойства плазменно-растворных систем и возможности их технологических применений // Усп. хим. 2007. Т. 76. № 3. С. 37.

  11. Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena. N.Y.: Wiley, 2007.

  12. Reid R.C., Prausnitz J.M., Sherwood T.K. The Properties of Gases and Liquids. N.Y.: McGraw-Hill, 1977.

  13. Бобкова Е.С. Научные основы низкотемпературных плазменных процессов разложения органических соединений, растворенных в воде. Дис. … докт. хим. наук. Иваново: Ивановский государственный химико-технологический университет, 2015.

  14. Bobkova E.S., Isakina A.A., Shishkina A.I., Kuznets N., Morev A.M. Features of phenol degradation in aqueous solution in dielectric-barrier discharge in oxygen // High Energy Chem. 2015. V. 49. № 1. P. 68. [Бобкова Е.С., Исакина А.А., Шишкина А.И., Кузнец Н., Морев А.М. Особенности деструкции фенола в водном растворе в диэлектрическом барьерном разряде в атмосфере кислорода // Хим. выс. энерг. 2015. Т. 49. № 1. С. 71.]

  15. Бобкова Е.С. Плазменная очистка сточных вод, содержащих поверхностно-активные вещества // Вода: хим. экол. 2017. № 9. С. 37.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал