Теоретические основы химической технологии, 2020, T. 54, № 4, стр. 480-495
Апробация математической модели радиационного теплообмена многоатомных газов в установках вакуумного дегидрирования углеводородов
А. А. Назаров a, *, С. И. Поникаров a
a Казанский национальный исследовательский технологический университет
Казань, Россия
* E-mail: 2901015@gmail.com
Поступила в редакцию 22.04.2019
После доработки 06.12.2019
Принята к публикации 31.01.2020
Аннотация
Рассмотрены экспериментальные и численные исследования процессов газодинамики, теплообмена, в особенности радиационного теплообмена, протекающих в установках вакуумного дегидрирования углеводородного сырья для многоатомных газов, проведено сравнение результатов экспериментов и численных исследований. Рассмотрена математическая модель процессов газодинамики, теплообмена, в особенности радиационного теплообмена, протекающих как в экспериментальной установке, так и в установках вакуумного дегидрирования углеводородного сырья в целом, приведено описание численного моделирования данных процессов в программном комплексе ANSYS CFX. Приведены результаты, полученные в ходе экспериментального и численного исследований, их сравнение. Получено экспериментальное подтверждение правильного описания математической моделью газодинамических и теплообменных процессов, в особенности процессов радиационного теплообмена, протекающих в экспериментальной установке вакуумного дегидрирования для многоатомных газов.
ВВЕДЕНИЕ
Огромный ряд процессов глубокой переработки углеводородного сырья сводится в основном к дегидрированию углеводородов. По состоянию на 2017 год в химической промышленностью РФ с применением процессов дегидрирования углеводородного сырья произведено 2 859 501 т этилена, 1 476 608 т пропилена, 1 200 000 т изопрена, 500 000 т бутадиена, 691 748 т стирола. Как видно из вышеприведенных цифр, дегидрированием произведено свыше 8 млн т продукции за 2017 год только в РФ. В настоящее время все реакции дегидрирования проводятся при больших температурах на катализаторах в присутствии водяного пара, применение которого позволяет за счет разбавления смеси значительно снизить парциальное давление исходных продуктов и снизить необходимую температуру в реакционной зоне, что ведет к предотвращению термической деструкции исходных веществ и продуктов реакций, а также приводит к увеличению степени конверсии исходного сырья [1]. По средним оценкам в России для производства 1 кг стирола необходимо 3–10 кг водяного пара, 1 кг изопрена – 7–10 кг пара, 1 кг бутадиена – 10–20 кг пара, что означает, что для годового производства всей продукции, полученной дегидрированием в 2017 году было использовано по средним оценкам свыше 80 млн т водяного пара. Важной особенностью применения водяного пара является то, что на выходе из реактора водяной пар следует сконденсировать, а конденсат содержит в себе остатки непрореагировавших исходных веществ и продуктов, конденсат невозможно подавать на рецикл и необходимо утилизировать. Из вышесказанного можно сделать вывод, что применение водяного пара в реакциях дегидрирования в промышленности несет собой существенные затрата, значительно увеличивает себестоимость целевых продуктов и сложность технологического оформления производства.
Проведение реакций дегидрирования углеводородного сырья под вакуумом позволяет исключить применение водяного пара и сопутствующего дорогостоящего теплотехнического оборудования из технологической линии, а также значительно увеличить степень конверсии исходных веществ в целевые продукты, что приведет к значительному снижению себестоимости целевых продуктов реакций дегидрирования углеводородного сырья на объектах нефтехимических и нефтеперерабатывающих производств более чем на 23%.
В настоящее время реакции дегидрирования проводятся в присутствии водяного пара с незначительным снижением полного давления в реакторах, в зарубежных и отечественных источниках открытой печати и информации также отсутствуют какие-либо сведения об экспериментальных исследованиях полного исключения водяного пара из реакционной зоны и проведение реакций дегидрирования углеводородного сырья под вакуумом. Подобные эксперименты не описаны в литературе.
Авторами была создана экспериментальная установка для проведения исследований процессов дегидрирования углеводородов под вакуумом, что позволит понизить давление исходных продуктов без применения подачи водяного пара и, в свою очередь, исключить из технологической цепочки дорогостоящее и сложное теплотехническое оборудование, снизив стоимость производства, а также увеличить степень конверсии исходного сырья в конечный продукт [2].
В связи с многогранностью физико-химических процессов, протекающих при дегидрировании углеводородного сырья под вакуумом, сложностью технологического оформления экспериментальной установки, а также сложностью реакционного процесса, было принято решение о проведении последовательных серий экспериментальных исследований для подтверждения адекватности попутно разрабатываемой математической модели дегидрирования углеводородного сырья под вакуумом.
В предыдущих работах авторов статьи [3, 4] приведены результаты экспериментальных и численных исследований газодинамических и теплообменных процессов, протекающих в установке вакуумного дегидрирования углеводородов, с использованием воздуха в качестве рабочего тела, состоящего преимущественно из двухатомных газов, практически не участвующих в радиационном теплообмене в реакционной зоне установок вакуумного дегидрирования, также приведено экспериментальное подтверждение правильности описания разработанной математической моделью вышеуказанных процессов путем сравнения результатов экспериментальных и численных исследований, проведенных в программном комплексе ANSYS CFX.
Поскольку в реакционной зоне установок вакуумного дегидрирования одновременно присутствует множество многотомных газов при больших температурах, а обертоны и составные частоты основных колебаний молекул многоатомных газов имеют значительную интенсивность в средней ИК-области (2.5–50 мкм), то значительный вклад в теплообменные процессы, протекающие внутри установок вакуумного дегидрирования, обусловлен процессами радиационного теплообмена. Поэтому перед дальнейшими исследованиями процессов химической кинетики дегидрирования углеводородов под вакуумом возникает необходимость экспериментального подтверждения правильности описания разработанной математической моделью процессов радиационного теплообмена с использованием многоатомных газов.
В зарубежных и отечественных источниках открытой печати и информации отсутствуют экспериментальные и численные работы в области исследования газодинамических и теплообменных процессов, протекающих в установках дегидрирования углеводородов при значительном понижении давления и в отсутствии водяного пара. Существующие научные работы акцентированы в области процессов химической кинетики при атмосферном давлении или при незначительном понижении давления в реакционной зоне, а также в области применения различных катализаторов.
В связи с вышеизложенным целью данной работы является экспериментальное подтверждение правильности описания разработанной математической моделью газодинамических и теплообменных процессов (с учетом физических параметров газовой и твердой фаз (катализатора), зависимых от температуры и определяемых в процессе численного решения в каждой ячейке расчетной области) [3, 4], в особенности процессов радиационного теплообмена, протекающих в установке вакуумного дегидрирования углеводородов путем сравнения с результатами численных исследований, проведенных в программном комплексе ANSYS CFX с применением углекислого газа в качестве рабочего тела. В дальнейшем это позволит усложнить математическую модель процессами химической кинетики дегидрирования углеводородов, протекающих со значительным поглощением тепла в реакционной зоне, скорость и направление которых зависят от температуры и давления и в конечном итоге определяют степень конверсии и селективность процессов дегидрирования.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Описание установки. На рис. 1 представлена экспериментальная установка.
Рис. 1.
Схема экспериментальной установки исследования вакуумного дегидрирования углеводородного сырья: 1 – баллон с исходным сырьем; 2 – баллон с инертным газом; 3 – счетчик газовый; 4 – вакуумный натекатель; 5 – греющая камера; 6 – дополнительный патрубок; 7 – показывающий вакуумметр; 8 – реакционная камера; 9, 10, 11, 12 – термопары; 13 – теплообменник; 14 – показывающий вакуумметр; 15, 16 – патрубки теплообменника для холодного теплоносителя; 17 – конденсатосборник № 1; 18 – вентиль на входе в вакуум насос; 19 – вакуум насос; 20 – показывающий вакуумметр/термопара; 21 – конденсатосборник № 2; 22 – вентиль; 23 – вентиль пробоотборной линии; 24 –вакуум насос; 25 – вентиль пробоотборной линии; 26 – вентиль пробоотборной линии; 27 – вентиль пробоотборной линии; 28 – конденсатосборник № 3; 29 – показывающий вакуумметр; 30 – вентиль; 31 – вентиль; 32 – теплоизоляция; 33 – саркофаг.
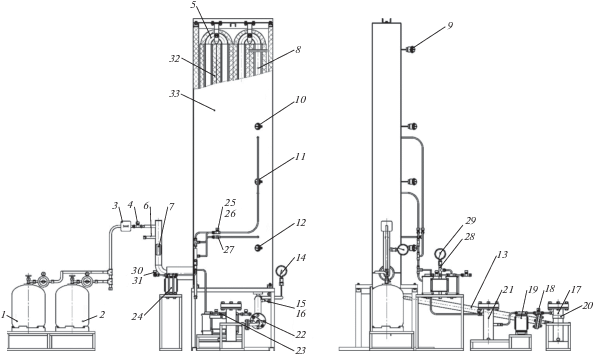
Исходное углеводородное сырье поступает из баллона 1, через электронный газовый счетчик 3 и вакуумный натекатель 4 в греющую камеру 5. Баллон 2 содержит инертный газ, предназначенный для регенерации катализатора. Греющая камера 5 представляет собой зигзагообразную систему труб. Нагрев установки осуществляется с помощью нихромовой проволоки, спирально обмотанной вокруг нагревательных труб, защищенной от прямого контакта с металлом керамическими бусами. На входе в греющую камеру установлен показывающий вакуумметр 7.
После греющей камеры нагретое сырье поступает в реакционную камеру 8, представляющую собой вертикальный трубный реактор, и проходит через 1.2–1.4 метровый слой размещенного внутри катализатора. Используется железокалиевый цериевый катализатора КД–1 производства ОАО “Синтез-Каучук” цилиндрической формы (диаметр цилиндра 3.0–4.5 мм, длина гранул – 3.0–20.0 мм), насыпной плотностью – 1.2–1.7 г/см3, состоящий из: оксида железа – 53.5–81.3 мас. %, оксида калия – 12.0–19.0 мас. %, оксида церия – 1.2–5.0 мас. %, оксида кальция – 2.0–8.0 мас. %, оксида магния – 1.0–7.0 мас. %, оксида алюминия 0.5–2.0 мас. %, оксида молибдена – 1.0–3.0 мас. %, оксида кремния – 1.0–2.5 мас. %.
При этом применение водяного пара исключается, а снижение парциального давления в реакционной зоне достигается за счет создания вакуума. Длина реакционной камеры спроектирована из условия максимально допустимого времени пребывания исходных веществ и продуктов реакции в реакционной зоне, исключающего термическую деструкцию исходных веществ и продуктов реакции. Поскольку исследуемые реакции протекают с поглощением тепла, нагрев реакционной камеры для поддержания необходимой температуры в реакционной зоне осуществляется с помощью нихромовой проволоки аналогичным образом.
Температура ядра газового потока на выходе из греющей камеры измеряется при помощи термопары 9, а в реакционной камере – с помощью аналогичных термопар 10, 11 и 12.
После прохождения слоя катализатора продукты реакции и непрореагировавшая часть исходного сырья поступают в теплообменник 13. На входе в теплообменник после реакционной камеры в U-образном отводе установлен показывающий вакуумметр 14. Холодным теплоносителем является водопроводная вода. После теплообменника продукты реакции поступают в конденсатосборник № 1 17, после которого установлен безмасляный мембранный вакуум насос 19. После вакуумного насоса 19 продукты реакции поступают в кондесаторосборник № 2 21. На выходе из конденсатосборника № 2 установлен двойник, к которому присоединены многооборотные вентили 22 и 23, позволяющие целенаправленно ориентировать направление потока продуктов реакции.
Отбор проб в исследованиях процессов химической кинетики происходит за счет создания в пробоотборной вакуумной линии более низкого давления при помощи вакуум-насоса 24. Отбор проб производится на четырех различных участках основной вакуумной линии в реакционной камере: в трех местах присоединения пробоотборных трубопроводов по высоте реакционной камеры, а также после полного прохождения исходным газом реакционной камеры. Пробы отбираются на выходе из вакуум-насоса 24.
Поскольку нагрев установки осуществляется до температур порядка 600°С, применяется тепловая изоляция греющей и реакционной камер. В качестве изоляционного материала используются теплоизоляционные маты из базальтового волокна 32. Реакционная и нагревательная камеры помещены в прямоугольный саркофаг 33, выполненный из оцинкованных листов металла.
Экспериментальные исследования проводят в диапазоне давлений 10–30 кПа на выходе из реакционной камеры и диапазоне температур 300–550°С в ядре потока в реакционной камере. В качестве рабочего тела, поступающего в установку, применяется углекислый газ. Каждый эксперимент проводится 3 раза при тех же условиях [5, 6].
Результаты экспериментальных исследований представлены в табл. 1 и 2. Относительная полная погрешность измерений давлений не превышает 18%, температур в ядре потока – 3%.
Таблица 1.
Результаты экспериментальных и численных исследований (полученные значения давлений на входе и выходе из экспериментальной установки)
| № серии эксперимента | Давление на входе в установку | Давление на выходе из установки | |||||
|---|---|---|---|---|---|---|---|
| Pвх, кПа | полн. погр., кПа | отн. погр., % | Pвых, кПа | полн. погр., кПа | отн. погр., % | ||
| 1 | Эксп. значения | 32.00 | 1.83 | 5.73 | 29.33 | 1.72 | 5.87 |
| Численные значение | 31.41 | – | – | 29.28 | – | – | |
| 2 | Эксп. значения | 20.17 | 1.94 | 9.64 | 18.17 | 1.72 | 9.48 |
| Численные значение | 19.26 | – | – | 18.15 | – | – | |
| 3 | Эксп. значения | 13.00 | 1.83 | 14.10 | 11.33 | 1.94 | 17.16 |
| Численные значение | 11.60 | – | – | 11.33 | – | – | |
| 4 | Эксп. значения | 30.67 | 1.94 | 6.34 | 27.50 | 1.83 | 6.67 |
| Численные значение | 30.03 | – | – | 27.44 | – | – | |
| 5 | Эксп. значения | 20.67 | 1.94 | 9.41 | 18.17 | 1.94 | 10.70 |
| Численные значение | 19.45 | – | – | 18.15 | – | – | |
| 6 | Эксп. значения | 12.17 | 1.72 | 14.16 | 10.33 | 1.72 | 16.67 |
| Численные значение | 10.68 | – | – | 10.33 | – | – | |
Таблица 2.
Результаты экспериментальных и численных исследований (полученные значения температуры в ядре течения газа внутри экспериментальной установки в контрольных измерительных точках)
| № серии эксперимента | Температура в ядре потока в контрольных измерительных точках | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Т1, °С | oтн. погр., % | Т2, °С | oтн. погр., % | Т3, °С | oтн. погр., % | Т4, °С | oтн. погр., % | ||
| 1 | Эксп. значения | 340.7 | 2.84 | 338.0 | 2.92 | 409.7 | 2.76 | 427.3 | 2.41 |
| Численные значение | 343.4 | – | 342.0 | – | 406.5 | – | 419.4 | – | |
| 2 | Эксп. значения | 351.3 | 2.77 | 341.3 | 2.96 | 414.3 | 2.79 | 431.3 | 2.86 |
| Численные значение | 345.4 | – | 345.6 | – | 410.7 | – | 422.3 | – | |
| 3 | Эксп. значения | 355.3 | 2.94 | 352.7 | 2.96 | 426.0 | 2.78 | 435.7 | 2.23 |
| Численные значение | 349.3 | – | 347.1 | – | 416.1 | – | 426.9 | – | |
| 4 | Эксп. значения | 503.7 | 2.91 | 459.7 | 2.97 | 514.3 | 2.91 | 547.7 | 2.74 |
| Численные значение | 497.0 | – | 450.1 | – | 501.0 | – | 535.2 | – | |
| 5 | Эксп. значения | 509.3 | 2.93 | 462.7 | 2.96 | 519.3 | 2.89 | 553.7 | 2.64 |
| Численные значение | 500.6 | – | 458.5 | – | 510.0 | – | 540.5 | – | |
| 6 | Эксп. значения | 503.3 | 2.69 | 478.3 | 2.52 | 531.7 | 2.67 | 555.3 | 2.75 |
| Численные значение | 495.1 | – | 469.0 | – | 523.0 | – | 541.8 | – | |
ТЕОРЕТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА И ЧИСЛЕННОЕ МОДЕЛИРОВНИЕ
Численные исследование газодинамических и теплообменных процессов, в особенности процессов радиационного теплообмена, протекающих в экспериментальной установке вакуумного дегидрирования, проводятся с использованием нижеописанной математической модели в программном комплексе вычислительной гидрогазодинамики ANSYS CFX.
Математическая модель. Математическая модель, описывающая газодинамические и теплообменные процессы, протекающие в экспериментальной установке дегидрирования углеводородов, подробно описана в предыдущих работах авторов [7, 8].
Математическая модель состоит из основных уравнений гидрогазодинамики: уравнения неразрывности, уравнения сохранение импульса, общего уравнения энергии. В модели вводится допущение об идеальном газе, поэтому плотность рассчитывается исходя из уравнения идеального газа, теплоемкость при постоянном давлении зависит от температуры. Для описания состояния многокомпонентной газовой смеси, скалярные уравнения переноса решаются для скорости, давления, температуры и других величин многокомпонентного потока. В модели вводится предположение, что компоненты образуют идеальную смесь, на основании этого предположения определяются следующие свойства газовой смеси: ламинарная вязкость, удельная теплоемкость при постоянном объеме, удельная теплоемкость при постоянном давлении и теплопроводность. Уравнение сохранения энергии для многокомпонентного потока включает только основные скалярные компоненты. Потери импульса через изотропную пористую среду записывают с использованием коэффициентов проницаемости и потерь [9, 10].
Ниже описан блок математической модели, описывающий радиационный теплообмен, протекающий в установках вакуумного дегидрирования. Источником уравнений (1)–(5), указанных ниже, является сопроводительная техническая документация ANSYS CFX [11].
Для описания процессов радиационного теплообмена в модели решается уравнение переноса излучения. При моделировании используется условие когерентности и независимости от времени процессов излучения. Подобное ограничение дает очень хорошие приближение для моделирования технологических процессов, поскольку временная шкала для перехода процессов излучения в стационарный режим очень короткая, а температуры относительно низки.
Основное уравнение спектрального лучистого переноса:
(1)
$\begin{gathered} \frac{{d{{{\text{I}}}_{{\text{v}}}}\left( {{\mathbf{r}},{\mathbf{s}}} \right)}}{{ds}}{\text{\;}} = {\text{\;}}\left( { - \left( {{{K}_{{a{\text{v}}}}}{\text{\;}} + {\text{\;}}{{K}_{{s{\text{v}}}}}} \right){{{\text{I}}}_{{\text{v}}}}\left( {{\mathbf{r}},{\mathbf{s}}} \right) + \frac{{}}{{}}~} \right. \\ \left. { + \,\,~{{K}_{{a{\text{v}}}}}{{{\text{I}}}_{{\text{b}}}}\left( {{\text{v}},T} \right)\,\,~ + \,\,~\frac{{{{K}_{{s{\text{v}}}}}}}{{4\pi }}\int\limits_{4\pi } {d{{{\text{I}}}_{{\text{v}}}}} \left( {{\mathbf{r}},{\mathbf{s}}{\kern 1pt} '} \right)\Phi \left( {{\mathbf{ss}}{\kern 1pt} '} \right)d{\Omega }{\kern 1pt} {\text{'}}~\,\, + \,~\,{{{\text{S}}}_{{\text{R}}}}} \right), \\ \end{gathered} $Уравнение спектрального лучистого переноса является интегрально-дифференциальным уравнением 1-го порядка для Iv в заданном направлении излучения s. Для решения этого уравнения в пределах расчетной области требуется граничное условие для спектральной интенсивности излучения Iv. В качестве граничного условия используется, поддерживаемое в ANSYS CFX, условие диффузионно-излучающих и диффузионно-отражающих непрозрачных границ:
(2)
$\begin{gathered} {{{\text{I}}}_{\nu }}\left( {{\mathbf{r}},{\mathbf{s}}} \right) = \,\,~{{\varepsilon }_{\nu }}\left( {\mathbf{r}} \right){{{\text{I}}}_{{\text{b}}}}\left( {\nu ,T} \right) + \\ + \,\,~\frac{{\rho \left( r \right)}}{\pi }~\int\limits_{{\mathbf{n}}*{\mathbf{s}}{\kern 1pt} ' < 0} {{{{\text{I}}}_{{\text{v}}}}\left( {{\mathbf{r}},{\mathbf{s}}{\kern 1pt} '} \right)} \left| {{\mathbf{n}}*{\mathbf{s}}{\kern 1pt} '} \right|d\Omega {\kern 1pt} ', \\ \end{gathered} $Поскольку в вышеописанных уравнениях переменные зависят от 3 пространственных координат, 2 локальных направлений и частоты, решение уравнения спектрального лучистого переноса требует значительных временных затрат. По этой причине вводятся дополнительные аппроксимации: аппроксимация Росселанда для зависимостей переменных от направлений и аппроксимация взвешенной суммы серых газов в качестве спектральных приближений.
В модели применяются аппроксимации Росселанда для уравнения спектрального лучистого переноса. Вводится новый диффузионный член в уравнение переноса энергии.
Полный удельный радиационный поток тепла в оптически толстой и линейно анизотропной рассеивающей среде записывается следующим образом:
(3)
${{q}_{r}} = {\text{\;}} - \int\limits_0^\infty {\frac{4}{{3\beta - A{{K}_{s}}}}} {\text{\;}}\nabla {{E}_{{{\text{bv}}}}}~d\nu ,$При использовании аппроксимации Росселанда удельные тепловые потоки за счет теплопроводности и радиационного теплообмена в уравнение переноса энергии комбинируются следующим образом:
где qс – удельный тепловой поток теплопроводностью; qr – удельный тепловой поток излучением; λ – коэффициент теплопроводности; kr – полная радиационная проводимость.Полная радиационная проводимость определяется по следующей формуле:
где σ – константа Стефана–Больцмана.Помимо вышеописанного, в качестве спектральных приближений в модель вводится аппроксимация взвешенной суммы серых газов.
Численное моделирование. Компьютерная трехмерная твердотельная модель строится по исходным размерам экспериментальной установки, показанной на рис. 1, впоследствии импортируется в модуль программного комплекса ANSYS Meshing для создания расчетной области (сетки). Расчетная область представляет структурированную преимущественно гексаэдрическую сетку с незначительным количеством тетраэдрических, призматических и пирамидальных элементов. Общее количество элементов составляет 309 767. Максимальный линейный размер элемента составляет 4 мм, минимальный – 2.5 мм. Значение максимального линейного размера элементов расчетной области снижалось с последующим численным перерасчетом до тех пор, пока результаты численного расчета не стали изменяться не более чем до 3 значащей цифры. Подробное описание построения расчетной области экспериментальной установки приведено в предыдущих работах авторов [3, 4].
В препроцессоре ANSYS CFX задаются следующие основные параметры.
Принимается ламинарная модель движения газовой смеси.
Средние скорости газовой фазы в численных расчетах описываемых экспериментов в слое катализатора составляют 1.597–3.195 м/c, внутри установки – 1.597–6.389 м/c. Числа Рейнольдса для движения потока в греющей и реакционной камерах до попадания на слой катализатора находятся в диапазоне 229–401, что свидетельствует о чистом ламинарном режиме течения. Модифицированные числа Рейнольдса в пористом слое катализатора составляют 46–72, что свидетельствует о нижней границе переходного режима течения в пористом слое (10–2000). В результате попутного численного моделирования процессов с применением ламинарной и турбулентной моделей движения потока в экспериментальной установке, а также сравнения полученных результатов, было установлено, что получаемые в результате решения поля скоростей, давлений, температур и прочих физических параметров существенно не отличаются, что можно объяснить преобладанием ламинарного режима течения в большей части установки, а также движением потока в нижней части переходного режима в пористом слое катализатора. В связи с вышеуказанным для численного моделирования процессов, протекающих в установке вакуумного дегидрирования, принимается ламинарная модель течения газов, в связи с лучшей предсказательностью и меньшими требованиям к вычислительным мощностям, что позволяет при той же вычислительной мощности производить расчет на значительно более мелкой расчетной сетке с увеличением точности расчета.
Для экспериментальной проверки численной модели многокомпонентной газовой смеси и последующего еe использования для моделирования процессов химической кинетики, поступающая в установку газовая среда (углекислый газ) определяется как газовоздушная смесь, аналогичным способом из предыдущих численных исследований авторов [3, 4], с массовыми долями: азота – 0.0, кислорода – 0.0, аргона – 0.0, углекислого газа – 100.0 мас. %.
Исходя из предположения об идеальной смеси, используется закон Рауля, рассчитываются следующие свойства газовой смеси: удельная теплоемкость, динамическая вязкость, теплопроводность, показатель преломления, показатель поглощения, показатель рассеяния. Для составляющих газов удельная теплоемкость, энтальпия и энтропия определяются с использованием полиномов NASA SP–273, коэффициенты принимаются равными стандартным коэффициентам из базы данных ANSYS.
Для составляющих газов динамическая вязкость и теплопроводность определяется по формуле Сазерленда.
В экспериментальных исследованиях процессов дегидрирования углеводородов под вакуумом применяется цилиндрический железокалиевый цериевый катализатор, который моделируется в ANSYS CFX как пористое тело, молярная масса катализатора задается равной 117.64 кг/кмоль, плотность катализатора – 2196.42 кг/м3.
Поскольку в дальнейшем данная математическая модель будет использована для моделирования процессов химической кинетики реакций дегидрирования углеводородов, идущих со значительным поглощением тепла, то при численном решении значения удельной теплоeмкости газовой фазы, удельной теплоемкости и теплопроводности катализатора, описанные ниже, задаются зависимыми от температуры, а их значения определяются в процессе численного решения в каждой ячейке расчетной области. Данные физические параметры вводятся в препроцессор ANSYS CFX в виде зависимых от температуры пользовательских функций, которые получают интерполяцией на основе табличных значений этих параметров для температур 400 и 600°С.
Значения теплоемкости и теплопроводности катализатора (пористого тела) определяются, как указано выше, в процессе расчета путем простой интерполяции теплоемкостей и теплопроводностей по основному компоненту катализатора (оксид железа) на основе табличных данных для вышеуказанного диапазона температур.
Пористый слой катализатора моделируется не путем создания сложной расчетной сетки гранул катализатора (в общем случае практически нерешаемой и требующей значительных вычислительных мощностей), а путем использования встроенной в ANSYS CFX модели пористого тела, которая предполагает предварительное указание значений пористости слоя, коэффициента проницаемости, коэффициента инерционных потерь, удельную площадь межфазной поверхности и коэффициент теплопередачи между жидкой и твердой фазами.
Пористость катализатора определялась экспериментальным путем и составляет 64.8%. Удельная площадь межфазной поверхности катализатора определялась экспериментальным путем и составляет 697.05 1/м.
Поскольку в дальнейшем данная математическая модель будет использована для моделирования процессов химической кинетики, идущих со значительным поглощением тепла, коэффициент теплопередачи между газом и твердой фазой задается не произвольным числом, а вычисляется в каждой ячейке расчетной области в процессе расчета c использованием пользовательской функции непосредственно в препроцессоре ANSYS CFX. Коэффициент теплопередачи между газовой и твердой фазой определяется через число Нуссельта, диаметр эквивалентной сферы гранул катализатора, равный 0.00635 м, и теплопроводность газового потока в данной ячейке. В свою очередь, число Нуссельта, используемое в расчете коэффициента теплопередачи, определяется в каждой ячейке расчетной области через значения чисел Рейнольдса и Прандтля.
Коэффициент проницаемости и коэффициент инерционных потерь в пористом слое находятся из уравнения Эргуна, которое применяется при расчете гидродинамики в задачах с течением однофазной жидкости в неподвижных слоях с определенной пористостью и плотностью упаковки частиц. Коэффициент проницаемости составляет 5.127 × 10–7 м2, коэффициент инерционных потерь составляет 19 998.86 1/м.
Для составляющих смесь газов радиационные свойства принимаются следующими: показатель преломления принимается равным 1, показатель поглощения определяется из закона Бугера–Ламберта–Бера и усредненных показателей абсорбции поперечного сечения по всему спектру для компонентов газовой смеси, которые определяются при помощи периодически обновляемой базы данных HITRAN, показатель рассеяния принимается равным 0 [12, 13].
Радиационные свойства катализатора принимаются равными радиационным свойствам основного компонента катализатора (оксид железа). Показатель преломления оксида железа принимается усредненным по диапазону длин волн 0.74–50 мкм инфракрасного излучения на основе табличных данных и составляет 2.42. Показатели поглощения и рассеяния находятся аналогичным образом и составляют 5.36 × 106 и 610.24 × 106 м–1 соответственно.
В качестве граничных условий задаются: массовый расход газового потока на входе в установку, давление на выходе из установки, температуры труб греющих камер и реакционной камеры в виде температурного градиента, полученного путем прямого измерения температур стенок труб в контрольных точках в ходе эксперимента согласно рис. 2, адиабатические граничные условия на участках соединяющих вышеуказанные участки установки (колена, изгибы), условие симметрии на поверхности, образованной поперечным симметричным срезом экспериментальной установки. Количественные значения вышеуказанных граничных условий задаются по экспериментальным данным.
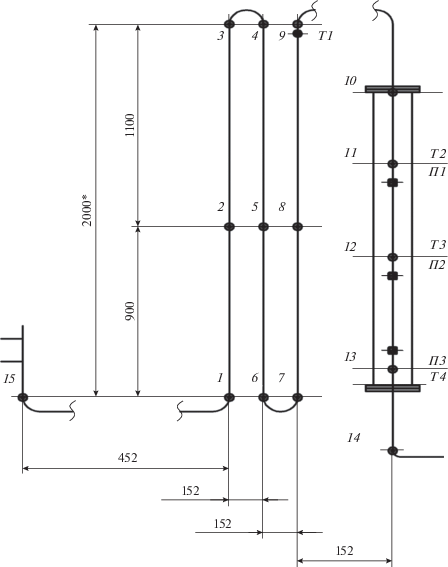
Рис. 2.
Схема размещения точек измерения температуры стенок установки и температур в ядре газового потока на выходе из греющей камеры и в реакционной камере: 1–9 – точки замера температуры на стенке греющей камеры; 10–13 – точки замера температуры на стенке реакционной камеры; 14 – точка замера температуры стенки на выходе из реакционной камеры; 15 – точка замера температуры стенки на входе в греющую камеру; Т1–Т4 – температуры в ядре потока, измеренные термопарами; П1–П3 – точки врезки пробоотборных линий.
Для выполнения условий сходимости численное решение в программном модуле Ansys CFX Solver проводилось без ограничения максимального количества итераций и ограничивалось следующими условиями: среднеквадратичное нормированное значения невязок решаемых уравнений не превышают значения 0.0001, глобальные дисбалансы для гидродинамических уравнений не превышают значения 0.01 (1%).
Результаты численных исследований представлены в табл. 1 и 2.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Полученные в ходе эксперимента данные были использованы для сравнения с данными, полученными в ходе численных исследований в программном комплексе ANSYS CFX. В табл. 1 и 2 представлены основные данные, полученные в ходе натурных и численных экспериментов.
На рис. 3–5 представлены поля давления, скорости и температуры в плоскости симметрии экспериментальной установки, полученные в ходе серии численных экспериментов № 1 (табл. 1, 2).
Рис. 3.
Поле давления в плоскости симметрии экспериментальной установки, полученное в ходе серии численных экспериментов № 1.
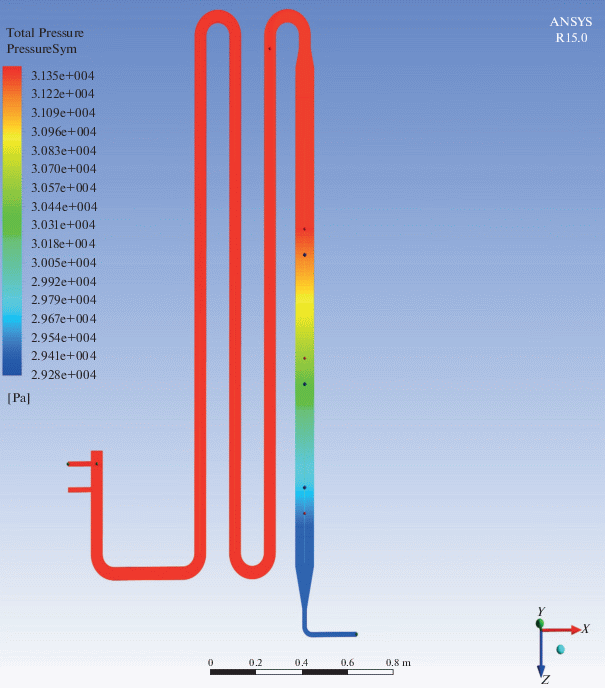
Рис. 4.
Поле скорости в плоскости симметрии экспериментальной установки, полученное в ходе серии численных экспериментов № 1.

Рис. 5.
Поле температуры в плоскости симметрии экспериментальной установки, полученное в ходе серии численных экспериментов № 1.

Как видно из полученных результатов, значения температур в ядре потока и давлений на входе в установку, полученных при численных исследованиях в ANSYS CFX, укладываются в доверительные интервалы экспериментальных значений (в пределах полной экспериментальной погрешности измерений указанных значений).
Таким образом, в результате проведенной работы получена математическая модель, адекватно описывающая газодинамические, теплообменные процессы и процессы радиационного теплообмена, протекающие в установках вакуумного дегидрирования углеводородов, для многоатомных газов.
По результатам численных и натурных экспериментов на рис. 6–8 видно, что средняя скорость газовой фазы в слое катализатора составляет 1.597–3.195 м/c, внутри установки – 1.597–6.389 м/c. Профиль скорости на соединительных участках (колена, изгибы) неравномерный со смещением в сторону большего радиуса, при поступлении газового потока в первую прямолинейную трубу греющей камеры происходит стабилизация профиля на участке до 4–6 диаметров трубы, во вторую трубу – на участке до 4–7 диаметров, в третью – на участке до 6–10 диаметров, на всем остальном протяжении труб греющей камеры профиль скорости равномерный ламинарный, при поступлении газового потока в прямолинейную трубу реакционной камеры профиль скорости стабилизируется на участке до 4–6 диаметров трубы, по всей длине пористого слоя катализатора профиль скорости равномерный ламинарный. Гидравлическое сопротивление экспериментальной установки в исследуемых диапазонах составляет в среднем 1.5–2.7 кПа.
Рис. 6.
Векторное представление поля скорости в плоскости симметрии экспериментальной установки, полученное в ходе серии численных экспериментов № 1.
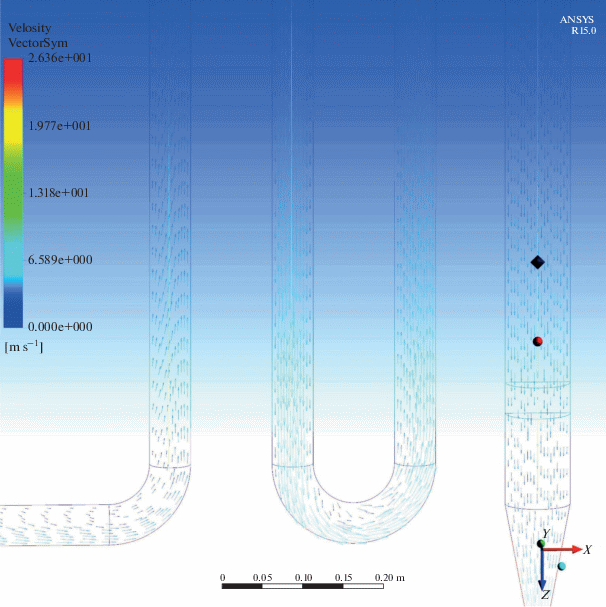
Рис. 7.
Векторное представление поля скорости в плоскости симметрии экспериментальной установки, полученное в ходе серии численных экспериментов № 1.
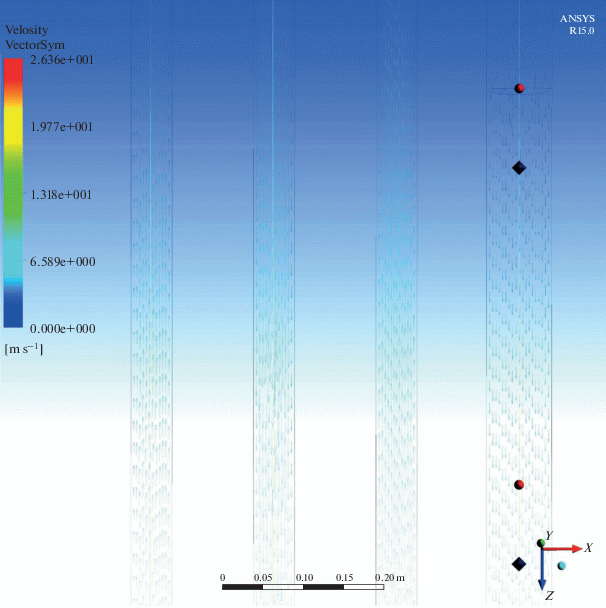
Рис. 8.
Векторное представление поля скорости в плоскости симметрии экспериментальной установки, полученное в ходе серии численных экспериментов № 1.
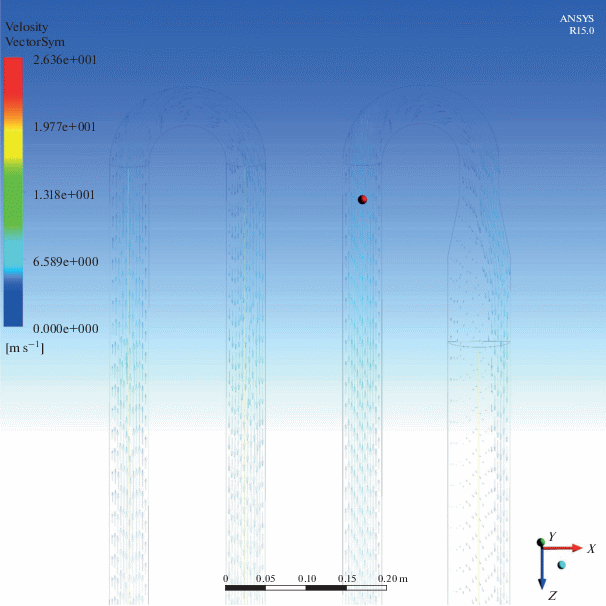
При понижении давления внутри установки и прочих равных условиях происходит рост температуры в ядре потока по ходу движения газового потока в реакционной зоне, понижение давления на 10 кПа в исследуемом диапазоне давлений внутри установки (10–30 кПа) приводит к росту температуры в реакционной зоне в среднем на 4–13°С.
В результате попутного численного моделирования вышеуказанных процессов с применением ламинарной и турбулентной моделей движения потока в экспериментальной установке (описание сопутствующих численных расчетов аналогичных описанным выше опущено в целях экономии места), а также сравнения полученных результатов, было установлено, что получаемые в результате решения поля скоростей, давлений, температур и прочих физических параметров существенно не отличаются, что можно объяснить преобладанием ламинарного режима течения в большей части установки.
В связи с вышеуказанным, для численного моделирования газодинамических и теплообменных процессов, включая процессы радиационного теплообмена, протекающих в установке вакуумного дегидрирования, рекомендуется применять ламинарную модель течения газовой фазы по причине меньших требований к вычислительным мощностям, что позволит при той же вычислительной мощности производить последующие численные расчеты, учитывающие химическую кинетику, на значительно более мелкой расчетной сетке с увеличением точности расчета.
ЗАКЛЮЧЕНИЕ
В настоящей работе проведены экспериментальные исследования газодинамических и теплообменных процессов, в особенности процессов радиационного теплообмена, протекающих в установке вакуумного дегидрирования углеводородов, с применением углекислого газа в качестве рабочего тела.
Проведены численные исследования с применением математической модели, описывающей газодинамические и теплообменные процессы, протекающие в установках вакуумного дегидрирования, в программном комплексе ANSYS CFX.
Поскольку в дальнейшем описанная математическая модель будет использована для моделирования химической кинетики процессов дегидрирования углеводородов, идущих со значительным поглощением тепла, значительная часть физических параметров, входящих в математическую модель, таких как удельные теплоемкости и теплопроводности газовой фазы и твердой фазы (катализатора), динамическая вязкость газовой фазы, задаются зависимыми от температуры с использованием формулы Сазерленда для динамической вязкости и теплопроводности газовой фазы и путем интерполяции на основе табличных значений для теплоемкости газовой фазы, теплоемкости и теплопроводности твердой фазы (катализатор) соответственно. Вышеуказанные значения определяются в процессе численного решения в каждой ячейке расчетной области в зависимости от температуры.
Получены убедительные данные, подтверждающие правильность описания математической моделью исследуемых процессов для многоатомных газов, в особенности процессов радиационного теплообмена.
По результатам численных и натурных экспериментов установлено преобладание ламинарного режима течения в большей части установки. В дальнейшем рекомендуется применять ламинарную модель течения газовой фазы по причине меньших требований к вычислительным мощностям, что позволит при той же вычислительной мощности производить последующие численные расчеты, учитывающие химическую кинетику, на значительно более мелкой расчетной сетке с увеличением точности расчета.
Установлено, что при снижении давления внутри установки и прочих равных условиях происходит рост температуры в ядре потока по ходу движения газового потока в реакционной зоне.
Подтверждение экспериментальными исследованиями математической модели, описывающей газодинамические и теплообменные процессы, протекающие внутри установок вакуумного дегидрирования, с использованием в качестве рабочего тела смеси преимущественно двухатомных газов [3, 4], а также подтверждение правильности описания процессов радиационного теплообмена, протекающих внутри установки, с использованием в качестве рабочего тела многоатомного газа (углекислого газа в данной работе), позволяет в дальнейшем использовать данную математическую модель для адекватного описания процессов химической кинетики, протекающих в установках дегидрирования углеводородов под вакуумом, представляющими собой преимущественно эндотермические реакции, скорость которых существенно зависит от температуры и давления в реакционной зоне и существенно влияет в конечном итоге на селективность и степень конверсии реакций дегидрирования углеводородов в промышленных реакторах проточного типа.
ОБОЗНАЧЕНИЯ
| A | линейный коэффициент анизотропии |
| Ebv | энергетический спектр, излучаемый абсолютно черным телом |
| Ib | интенсивность излучения абсолютно черного тела, Вт/м2 |
| Iv | спектральная интенсивность излучения, Вт/м2 |
| Ka | показатель поглощения, 1/м |
| Ks | показатель рассеяния, 1/м |
| kr | коэффициент полной радиационной проводимости, Вт/(м К) |
| n | показатель преломления |
| qс | удельный тепловой поток теплопроводностью, Вт |
| qr | удельный тепловой поток излучением, Вт |
| r | вектор положения площадки |
| SR | источник интенсивности излучения |
| s | вектор направления излучения |
| T | температура, °К |
| β | коэффициент экстинкции (сумма показателей поглощения и рассеяния), 1/м |
| ${{\varepsilon }_{\nu }}$ | спектральный коэффициент излучения (степень черноты) |
| λ | теплопроводность, Вт/(м К) |
| ν | частота, Гц |
| ρ | плотность, кг/м3 |
| σ | константа Стефана-Больцмана |
| Ф | фазовая функция рассеивания |
| Ω | телесный угол, ср |
Список литературы
Назаров А.А. Вакуумное дегидрирование // Хим. нефтегазов. машиностр. 2012. № 2. С. 25.
Первов Д.Н., Назаров А.А., Поникаров С.И. Экспериментальная установка исследования процессов дегидрирования углеводородного сырья под вакуумом // Вестн. Казан. технол. унив. 2015. Т. 18. № 19. С. 64.
Nazarov A.A., Ponikarov S.I. Gas-Dynamic and Heat-Exchange Processes in a Facility for the Vacuum Dehydrogenation of Hydrocarbons // Theor. Found. Chem. Eng. 2019. V. 53. № 4 P. 515. [Назаров А.А., Поникаров С.И. Газодинамические и теплообменные процессы в установке вакуумного дегидрирования углеводородов // Теор. осн. хим. технол. 2019. Т. 53. № 4. С. 416.]
Назаров А.А., Поникаров С.И., Петлин К.А. Численное исследование газодинамических и теплообменных процессов и апробация математической модели путем сравнения с экспериментальными данными // Вестн. Казан. технол. унив. 2018. Т. 21. № 11. С. 157.
Назаров А.А., Матвеев В.П., Поникаров С.И., Петлин К.А. Вакуумное дегидрирование углеводородного сырья в химической и нефтехимической промышленности // Вестн. Казан. технол. унив. 2018. Т. 21. № 4. С. 107.
Первов Д.Н., Назаров А.А., Поникаров С.И. Методика проведение эксперимента на экспериментальной установке дегидрирования углеводородов под вакуумом // Вестн. Казан. технол. унив. 2015. Т. 18. № 20. С. 220.
Akhmadiev A.L., Matveev V.P., Nazarov A.A., Giniyatulin A.I. A mathematical model of heating of a reaction mixture in the process of vacuum dehydrogenation of hydrocarbons // Chem. Pet. Eng. 2013. V. 48. № 9–10. P. 618. [Ахмадиев А.Л., Матвеев В.П., Назаров А.А., Гиниатулин А.И. Математическая модель нагрева реакционной смеси в процессе вакуумного дегидрирования углеводородов // Хим. нефтегазов. машиностр. 2012. № 10. С. 22.]
Назаров А.А., Поникаров С.И., Петлин К.А. Математическая модель газодинамических и теплообменных процессов вакуумного дегидрирования углеводородов // Вестн. Казан. технол. унив. 2018. Т. 21. № 10. С. 153.
Telyakov E.Sh., Osipova L.E., Ponikarov A.S. Kinetics of nonequimolar mass transfer in multicomponent gas (vapor)–liquid systems // Theor. Found. Chem. Eng. 2018. V. 52. № 1. P. 11. [Теляков Э.Ш., Осипова Л.Э., Поникаров А.С. Кинетика неэквимолярного массопереноса в многокомпонентных системах газ (пар)-жидкость // Теор. осн. хим. технол. 2018. Т. 52. № 1. С. 13.]
Moskalev L.N., Ponikarov S.I. Application of a contact vortex condenser to absorb methanol from a contact gas // Theor. Found. Chem. Eng. 2016. V. 50. № 2. Р. 194. [Москалев Л.Н., Поникаров С.И. Применение контактного конденсатора вихревого типа при поглощении метанола из контактного газа // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 200.]
ANSYS CFX-Solver Theory Guide. 2013 ANSYS CFX Release 15.0 Canonsburg, 2013.
Magaril Ya.F., Nazarov A.A., Shpaner Ya.S., Gimranov R.G. Special torch heads // Chem. Pet. Eng. 2009. V. 45. № 1–2. P. 13. [Магарил Я.Ф., Назаров А.А., Шпанер Я.С., Гимранов Р.Г. Факельные установки. Специальные оголовки факельных установок // Хим. нефтегазов. машиностр. 2009. № 1. С. 17.]
Panchenko V.I., Magaril Y.F., Nazarov A.A., Shpaner Y.S. Gimranov R.G. Aerodynamic gas gates for flare units // Chem. Pet. Eng. 2009. V. 45. № 5–6. P. 278. [Магарил Я.Ф., Назаров А.А., Шпанер Я.С., Гимранов Р.Г., Панченко В.И. Аэродинамические газовые затворы для факельных установок // Хим. нефтегазов. машиностр. 2009. № 5. С. 14.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


