Теоретические основы химической технологии, 2020, T. 54, № 5, стр. 572-583
Моделирование оптимального управления нелинейным объектом
Ю. В. Шариков a, *, И. В. Ткачев a, Н. В. Снегирев a
a Санкт-Петербургский горный университет
Санкт-Петербург, Россия
* E-mail: yvshar@mail.ru
Поступила в редакцию 19.02.2020
После доработки 02.04.2020
Принята к публикации 15.05.2020
Аннотация
Рассматривается система усовершенствованного управления процессом каталитического риформинга на основе математической модели процесса. Цель данной работы – продемонстрировать осуществимость адаптивной системы оптимального управления с предсказывающей моделью в контуре управления. Показана целесообразность применения рассматриваемой системы управления.
ВВЕДЕНИЕ
Интенсификация реакторного узла каталитического риформинга путем улучшения системы управления – наиболее интересный способ повышения эффективности установки с точки зрения экономики и экологии. Каталитический риформинг – это химический процесс, используемый для превращения нафты, в частности низкооктанового прямогонного лигроина в высокооктановый бензин. Помимо производства высокооктанового бензина, каталитический риформинг также является основным источником ароматических соединений, используемых в нефтехимической промышленности [1]. Каталитический риформинг сегодня подробно исследован [2], но нестационарность процесса не позволяет прийти к общей конструкции математической модели, которая одновременно удовлетворяет детализации, точности и быстроте расчета модели.
В течение последних двух десятилетий ученые и производственники приложили большие усилия для разработки и применения методов нелинейного управления по предсказывающей модели. Значительные результаты были получены, но исследование управления по предсказывающей модели, представляющее наибольший интерес, является сложной задачей. Хотя линейное управление по предсказывающей модели действительно имеет хорошо разработанные методологии для получения желаемой эффективности управления при удовлетворении требования стабильности, методы нелинейного управления по предсказывающей модели не имеют такой общей и зрелой конструкции [3, 4].
Управление в режиме реального времени, основанное на оптимизации моделей нелинейного динамического процесса, привлекает все большее внимание в течение последних десятилетий, например, в химической технике [5]. Среди преимуществ этого подхода – гибкость при создании объективной обобщенной модели процесса и возможность быстрого реагирования на возмущения. Причиной такого ускорения является тот факт, что при использовании прогнозирующей модели реакция на возмущение появляется через время, равное времени решения уравнений модели. Это время на несколько порядков отличается от времени прохождения возмущения по объекту. Это приводит к значительному ускорению выработки компенсирующего возмущения. Ускорение определяется соотношением между временем решения модели и временем запаздывания нелинейного объекта с распределенными параметрами. Одной из важных особенностей является наличие надежных и эффективных алгоритмов численного оптимального управления [6].
Прогнозирующий контроль линейной модели давно имеет репутацию мощного инструмента для управления промышленными процессами управления [5, 7, 8]. В схеме прогнозирующего управления модель используется для прогнозирования будущего поведения системы как при известных, так и при неизвестных входных возмущениях. Точность предсказания модели напрямую определяет качество и эффективность закона управления и является основным направлением в ходе реализации. Построение модели может основываться на фундаментальных принципах и на эмпирических данных, либо на комбинации обоих подходов.
Обычно оптимизацию в реальном времени связывают с методами максимизации экономической прибыли [9]. Большинство из систем оптимального управления основаны на нелинейных моделях устойчивого состояния системы процессов в сочетании со сверкой данных на сходимость или оценкой параметров для обновления ключевых параметров, таких как состав питания и эффективность процесса. В непрерывном процессе достигать максимальной экономической выгоды при сохранении желаемого качества продукта значительно сложнее в динамической среде с установившимися условиями [10]. Идентификация математической модели процесса по многим переменным помогает в этом [11]. Решение об идентификации принимается в том случае, когда разница между результатами моделирования и измерения выходных переменных превышает экспериментальную ошибку при определении выходных переменных. Для повышения точности модели в процессе идентификации участвуют свойства нескольких внутренних состояний и принимаются как контролируемые возмущения [12]. Химический реактор моделируется с использованием обыкновенных дифференциальных уравнений, или дифференциальных уравнений в частных производных, которые описывают изменения состава, температуры и давления вдоль трубчатого реактора [13].
В статье описан подход к разработке модели системы управления с математической моделью в контуре управления, демонстрирующий возможность достаточно точного описания сложного технологического процесса. Целью работы является интенсификация технологического процесса путем применения усовершенствованной системы управления.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Алгоритм управления. Нелинейное управление по прогнозирующей модели, схематично приведенное на рис. 1, основано на идее трехуровневой иерархии распределенной системы управления [14]. Верхний уровень – это базы данных и математические модели, выполняющие роль интерфейса к технологическому процессу на промышленном персональном компьютере. Второй уровень – преобразователи сигналов и регуляторы, работающие в связке с промышленным компьютером. Третий уровень – исполнительные устройства.
Рис. 1.
Функциональная схема системы оптимального управления с математической моделью в контуре управления: Xin(t) – вектор-функция входных переменных; ContrOb – объект управления; Yout(t) – вектор-функция выходных переменных; InputAn – анализатор входных переменных; OutAn – анализатор выходных переменных; ComD – вычислительное устройство; ModId – идентификатор модели; ContrD – устройство управления. Сплошная стрелка – материальный поток, пунктирная стрелка – сигнал.
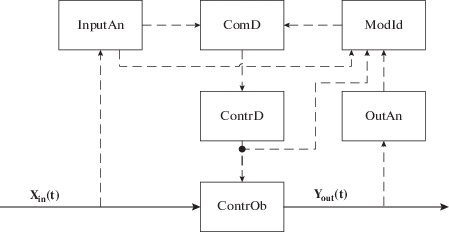
Аналоговые входные данные Xin(t) поступают на InputAn. Анализатор входных переменных преобразует аналоговый сигнал в цифровой. Цифровой сигнал поступает в ComD и в идентификатор модели ModId. Вычислительное устройство ComD рассчитывает оптимальное управление для текущего состояния реального объекта по текущим коэффициентам, полученным от идентификатора модели. Результаты расчета вычислительного устройства поступают в устройство управления ContrD и в идентификатор модели, откуда генерируется аналоговый компенсационный сигнал на реальный объект ContrOb. Алгоритм адаптации имитационной модели к объекту управления реализован в идентификаторе модели. Выходные аналоговые данные Yout(t) поступают на OutAn, где анализатор выходных переменных преобразует аналоговый сигнал в цифровой. Откуда цифровой сигнал поступает в идентификатор модели с заданными границами сходимости. В случае потери адекватности модель адаптируется к объекту управления через минимизацию функции ошибки. Решается обратная задача по коррекции внутренних параметров модели. Затем обновленные коэффициенты математической модели поступают на вычислительное устройство.
Математическая модель. Математическое описание сложных технологических процессов нефтегазоперерабатывающей отрасли по принципу черного ящика не дает информации о текущем состоянии территориально распределенных процессов с распределенными параметрами и требует большого объема данных, обработанных во всем диапазоне работы нестационарного моделируемого объекта. Модели, созданные по принципу белого ящика, опираются на фундаментальные законы химической кинетики и термодинамики и могут быть усложнены до необходимого уровня имитации технологического процесса, а также способны обеспечивать оператора данными в реальном времени по состоянию переменных, не измеряемых автоматически в условиях завода. Это делает их ценным источником оперативной информации для человека и надежной основой для усовершенствованного управления.
Многие попытки также предпринимаются для достижения гармоничного баланса между простотой и детализацией модели каталитического риформинга. Следует отметить, что простая модель с небольшим количеством групп может быть не в состоянии представить желаемую ситуацию, тем не менее, выбор сложной модели не выгоден, потому что для определения параметров модели требуется огромное количество экспериментальной информации, которая является трудоемкой и ресурсозатратной задачей [15]. Таким образом, подходящей моделью является та, которая, несмотря на простоту, способна правильно прогнозировать состояние технологического процесса.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Математическая модель процесса каталитического риформинга. В основу используемой модели положена схема реакций групповых превращений, приведенная на рис. 2.
Рис. 2.
Схема реакций образования бензола: ACP6 – алкилциклопентаны; ACH6 – алкилциклогексаны; A6 – ароматика; IP6 – изопарафины; NP6 – парафины.
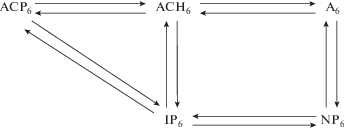
С помощью обыкновенных дифференциальных уравнений по схеме групповых превращений компонентов с промежуточным подогревом реакционной смеси описана модель с радиальным вводом реагентов в адиабатические реакторы идеального вытеснения с неподвижным слоем катализатора. Дифференциальные уравнения решаются конечно-разностным методом.
Массовый баланс:
где Ci – молярная концентрация i-го компонента смеси, моль/м3; r – радиус слоя катализатора, м; u – линейная скорость реакционной смеси в реакторе, м/с; vij – стехиометрический коэффициент i-го вещества в j-й реакции; wi – скорость образования i-го вещества, моль/(с м3); ρ – плотность газовой смеси, кг/м3; G – массовый расход, кг/с; S – площадь поперечного сечения для радиального ввода реагентов, м2; l – длина слоя катализатора в реакторе, м.Тепловой баланс [1] рассчитывается по уравнению (4) на основе тепловых эффектов реакций в табл. 1:
(4)
$\frac{{dT}}{{dr}} = \frac{{S\sum\limits_{i = 1}^{{\text{NR}}} {({{w}_{i}})( - \Delta {{H}_{j}})} }}{{\sum\limits_{i = 1}^{{\text{NC}}} {{{Q}_{i}}C{{p}_{i}}} }},$(5)
$C{{p}_{i}} = {{{\text{A}}}_{i}} + {{{\text{B}}}_{i}}T{\text{ }} + {{{\text{D}}}_{i}}{{T}^{2}} + {{{\text{E}}}_{i}}{{T}^{3}},$Таблица 1.
Тепловые эффекты реакций
| Реакция | ∆Н, кДж/моль |
|---|---|
| Дегидрирование нафтеновых | +221 |
| Изомеризация парафиновых | –4.6 |
| Изомеризация нафтеновых | –15.6 |
| Гидрокрекинг нафтеновых (размыкание кольца) | –43.9 |
| Гидрокрекинг парафиновых | –56.4 |
| Дегидроциклизация парафиновых | +200 |
Перепад давления в реакторе рассчитывается по уравнению (6):
(6)
$\begin{gathered} \frac{{dP}}{{dl}} = 1.75 \times {{10}^{{ - 5}}}\frac{{(1 - {\varepsilon })}}{{{{{\varepsilon }}^{3}}}}\frac{{{{u}^{2}}}}{{{\rho }{{d}_{{\text{p}}}}g}} + \\ + \,\,1.5 \times {{10}^{{ - 3}}}\frac{{{{{(1 - {\varepsilon })}}^{2}}}}{{{{{\varepsilon }}^{3}}}}\frac{{u{\mu }}}{{{\rho }d_{p}^{2}g}}, \\ \end{gathered} $(7)
$\begin{gathered} \varepsilon = \chi \left( {0.38{\text{ }} + {\text{ }}0.73 \times _{{_{{}}}}^{{^{{}}}}} \right. \\ \times \,\,\left. {\left( {{{\left( {1{\text{ }} + {\text{ }}{{{\left( {{{{{d}_{{ap}}}} \mathord{\left/ {\vphantom {{{{d}_{{ap}}}} {{{d}_{p}}}}} \right. \kern-0em} {{{d}_{p}}}}--{\text{ }}2} \right)}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {1{\text{ }} + {\text{ }}{{{\left( {{{{{d}_{{ap}}}} \mathord{\left/ {\vphantom {{{{d}_{{ap}}}} {{{d}_{p}}}}} \right. \kern-0em} {{{d}_{p}}}}--{\text{ }}2} \right)}}^{2}}} \right)} {{{{\left( {{{{{d}_{{ap}}}} \mathord{\left/ {\vphantom {{{{d}_{{ap}}}} {{{d}_{p}}}}} \right. \kern-0em} {{{d}_{p}}}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {{{{{d}_{{ap}}}} \mathord{\left/ {\vphantom {{{{d}_{{ap}}}} {{{d}_{p}}}}} \right. \kern-0em} {{{d}_{p}}}}} \right)}}^{2}}}}} \right)} \right), \\ \end{gathered} $(9)
$\chi = {{\Delta m} \mathord{\left/ {\vphantom {{\Delta m} {{{m}_{{{\text{max}}}}}}}} \right. \kern-0em} {{{m}_{{{\text{max}}}}}}},$На перепад давления в реакторе влияет несколько факторов, поэтому диаметр катализатора в модели является варьируемым параметром в соответствие с процессом коксообразования для уточнения перепада давления из-за механического износа катализатора. Процесс коксообразования и другие факторы вносят долю неопределенности в поведение такой динамической системы как каталитический риформинг, что со временем снижает точность прогноза и может привести к потере адекватности математической модели. Для корректной работы модели варьируются ее внутренние параметры, представленные в табл. 2.
Таблица 2.
Диапазон изменения параметров модели реакций риформинга, описанных с помощью псевдокомпонентов
| j | Реакция | PFRi | |
|---|---|---|---|
| kj, моль/(м3 с) | k0j, моль/(м3 с) | ||
| kj0 | |||
| 1 | ACH6 ↔ A6 + 3H2 | 14.3–21.7 | 13.5–20.4 |
| 2 | ACH7 ↔ A7 + 3H2 | 14.2–21.7 | 13.4–20.4 |
| 3 | NP6 ↔ IP6 | 14.9–16.7 | 16.7–18.6 |
| 4 | NP7 ↔ IP7 | 14.9–16.7 | 16.9–18.7 |
| 5 | ACP6 ↔ ACH6 | 14.7–18.9 | 13.5–17.7 |
| 6 | ACP7 ↔ ACH7 | 14.6–18.6 | 14.3–18.1 |
| 7 | ACP6 + H2 ↔ IP6 | 12.3–15.3 | 9.9–12.9 |
| 8 | ACP7 + H2 ↔ IP7 | 12.1–16.9 | 10.2–14.5 |
| 9 | NP6 + 5H2 → 6CH4 | 13.2–20.4 | – |
| 10 | NP7 + 6H2 → 7CH4 | 13.6–23.7 | – |
| 11 | NP6 ↔ A6 + 4H2 | 15.3–16.4 | 14.8–15.8 |
| 12 | NP7 ↔ A7 + 4H2 | 15.9–17.8 | 14.6–16.5 |
| 13 | 4NP6 → Ck + 3CH4 + 5H2 | 0.2–0.8 | – |
| 14 | 4NP7 → Ck + 6CH4 + 9H2 | 0.2–0.8 | – |
| 15 | 4IP6 → Ck + 3CH4 + 5H2 | 0.1–0.6 | – |
| 16 | 4IP7 → Ck + 6CH4 + 9H2 | 0.1–0.6 | – |
| 17 | 4A6 + 3H2 → Ck + 2CH4 | 0.1–0.6 | – |
| 18 | 4A7 + 7H2 → Ck + 6CH4 | 0.1–0.6 | – |
| 19 | NP6 → OC6 + H2 | 3.9–11 | – |
| 20 | IP7 + A7 → Unws | 10.2–14.7 | – |
Приращение компонентов по слою катализатора в радиальном направлении [16] от стенок реактора к центральной трубе описывается уравнениями (10)–(24):
(10)
$\frac{{d{{C}_{{{\text{AC}}{{{\text{H}}}_{6}}}}}}}{{dr}} = \frac{{\left( {\left( { - {{k}_{1}}[{\text{AC}}{{{\text{H}}}_{6}}] + {{k}_{{01}}}[{{{\text{A}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right) + \left( {{{k}_{5}}[{\text{AC}}{{{\text{P}}}_{6}}] - {{k}_{{05}}}[{\text{AC}}{{{\text{H}}}_{6}}]} \right)} \right)}}{u},$(11)
$\frac{{d{{C}_{{{\text{AC}}{{{\text{H}}}_{7}}}}}}}{{dr}} = \frac{{\left( {\left( { - {{k}_{2}}[{\text{AC}}{{{\text{H}}}_{7}}] + {{k}_{{02}}}[{{{\text{A}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right) + \left( {{{k}_{6}}[{\text{AC}}{{{\text{P}}}_{7}}] - {{k}_{{06}}}[{\text{AC}}{{{\text{H}}}_{7}}]} \right)} \right)}}{u},$(12)
$\frac{{d{{C}_{{{\text{AC}}{{{\text{P}}}_{6}}}}}}}{{dr}} = \,\,~\frac{{\left( { - {{k}_{5}}[{\text{AC}}{{{\text{P}}}_{6}}] + {{k}_{{05}}}[{\text{AC}}{{{\text{H}}}_{6}}]} \right) + \left( {0.5\left( { - {{k}_{7}}[{\text{AC}}{{{\text{P}}}_{6}}][{{{\text{H}}}_{2}}] + {{k}_{{07}}}[{\text{I}}{{{\text{P}}}_{6}}]} \right)} \right)}}{u},$(13)
$\frac{{d{{C}_{{{\text{AC}}{{{\text{P}}}_{7}}}}}}}{{dr}} = \frac{{\left( {\left( { - {{k}_{6}}[{\text{AC}}{{{\text{P}}}_{7}}] + {{k}_{{07}}}[{\text{AC}}{{{\text{H}}}_{7}}]} \right) + \left( {0.5\left( { - {{k}_{8}}[{\text{AC}}{{{\text{P}}}_{7}}][{{{\text{H}}}_{2}}] + {{k}_{{08}}}[{\text{I}}{{{\text{P}}}_{7}}]} \right)} \right)} \right)}}{u},$(14)
$\frac{{d{{C}_{{{{{\text{A}}}_{6}}}}}}}{{dr}} = \frac{{\left( {0.25\left( {{{k}_{1}}[{\text{AC}}{{{\text{H}}}_{6}}] - {{k}_{{01}}}[{{{\text{A}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + \left( {0.2\left( {{{k}_{{11}}}[{\text{N}}{{{\text{P}}}_{6}}] - {{k}_{{011}}}[{{{\text{A}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{4}}} \right)} \right) + \left( {\frac{4}{7}\left( { - {{k}_{{17}}}[{{{\text{A}}}_{6}}]{{{\kern 1pt} }^{4}}{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right)}}{u},$(15)
$\begin{gathered} \frac{{d{{C}_{{{{{\text{A}}}_{7}}}}}}}{{dr}} = \frac{{\left( {0.25\left( {{{k}_{2}}[{\text{AC}}{{{\text{H}}}_{7}}] - {{k}_{{02}}}[{{{\text{A}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + \left( {0.2\left( {{{k}_{{12}}}[{\text{N}}{{{\text{P}}}_{7}}] - {{k}_{{012}}}[{{{\text{A}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{4}}} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {\frac{4}{{11}}\left( { - {{k}_{{18}}}{{{[{{{\text{A}}}_{7}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{7}}} \right)} \right) + \left( {0.5\left( { - {{k}_{{20}}}[{\text{I}}{{{\text{P}}}_{7}}][{{{\text{A}}}_{7}}]} \right)} \right)}}{{}}, \\ \end{gathered} $(16)
$\begin{gathered} \frac{{d{{C}_{{{\text{C}}{{{\text{H}}}_{4}}}}}}}{{dr}} = \frac{{\left( {6\left( {{{k}_{9}}[{\text{N}}{{{\text{P}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{5}}} \right)} \right) + \left( {7\left( {{{k}_{{10}}}[{\text{N}}{{{\text{P}}}_{7}}]{{{[{{H}_{2}}]}}^{6}}} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {\frac{3}{9}\left( {{{k}_{{13}}}{{{[{\text{N}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right) + \left( {\frac{6}{{16}}\left( {{{k}_{{14}}}{{{[{\text{N}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {\frac{3}{9}\left( {{{k}_{{15}}}{{{[{\text{I}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right)}}{{}} \\ \frac{{ + \,\,\left( {\frac{6}{{16}}\left( {{{k}_{{16}}}{{{[{\text{I}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {\frac{2}{3}\left( {{{k}_{{17}}}{{{[{{{\text{A}}}_{6}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + \left( {\frac{6}{7}\left( {{{k}_{{18}}}{{{[{{{\text{A}}}_{7}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{7}}} \right)} \right)}}{{}}, \\ \end{gathered} $(17)
$\begin{gathered} \frac{{d{{C}_{{{{{\text{H}}}_{2}}}}}}}{{dr}} = \frac{{\left( {0.75\left( {{{k}_{1}}[{\text{AC}}{{{\text{H}}}_{6}}] - {{k}_{{01}}}[{{{\text{A}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {0.75\left( {{{k}_{2}}[{\text{AC}}{{{\text{H}}}_{7}}] - {{k}_{{02}}}[{{{\text{A}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {0.5\left( { - {{k}_{7}}[{\text{AC}}{{{\text{P}}}_{6}}][{{{\text{H}}}_{2}}] + {{k}_{{07}}}[{\text{I}}{{{\text{P}}}_{6}}]} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {0.5\left( { - {{k}_{8}}[{\text{AC}}{{{\text{P}}}_{7}}][{{{\text{H}}}_{2}}] + {{k}_{{08}}}[{\text{I}}{{{\text{P}}}_{7}}]} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {\frac{5}{6}\left( { - {{k}_{9}}[{\text{N}}{{{\text{P}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{5}}} \right)} \right) + \left( {\frac{6}{7}\left( { - {{k}_{{10}}}[{\text{N}}{{{\text{P}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{6}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {0.8\left( {{{k}_{{11}}}[{\text{N}}{{{\text{P}}}_{6}}] - {{k}_{{011}}}[{{{\text{A}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{4}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {0.8\left( {{{k}_{{12}}}[{\text{N}}{{{\text{P}}}_{7}}] - {{k}_{{012}}}[{{{\text{A}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{4}}} \right)} \right) + }}{{}} \\ \frac{{~ + \,\,\left( {\frac{5}{9}\left( {{{k}_{{13}}}{{{[{\text{N}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right) + \left( {\frac{9}{{16}}\left( {{{k}_{{14}}}{{{[{\text{N}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {\frac{5}{9}\left( {{{k}_{{15}}}{{{[{\text{I}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {\frac{9}{{16}}\left( {{{k}_{{16}}}{{{[{\text{I}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {\frac{3}{7}\left( { - {{k}_{{17}}}{{{[{{{\text{A}}}_{6}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {\frac{7}{{11}}\left( { - {{k}_{{18}}}{{{[{{{\text{A}}}_{7}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{7}}} \right)} \right) + \left( {0.5\left( {{{k}_{{19}}}[{\text{N}}{{{\text{P}}}_{6}}]} \right)} \right)}}{{}}, \\ \end{gathered} $(18)
$\begin{gathered} \frac{{d{{C}_{{{\text{I}}{{{\text{P}}}_{6}}}}}}}{{dr}} = \frac{{\left( {{{k}_{3}}[{\text{N}}{{{\text{P}}}_{6}}] - {{k}_{{03}}}[{\text{I}}{{{\text{P}}}_{6}}]} \right) + }}{u} \\ \frac{{ + \,\,\left( {\left( {{{k}_{7}}[{\text{AC}}{{{\text{P}}}_{6}}][{{{\text{H}}}_{2}}] - {{k}_{{07}}}[{\text{I}}{{{\text{P}}}_{6}}]} \right)} \right) + \left( {4\left( { - {{k}_{{15}}}{{{[{\text{I}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right)}}{{}}, \\ \end{gathered} $(19)
$\begin{gathered} \frac{{d{{C}_{{{\text{I}}{{{\text{P}}}_{7}}}}}}}{{dr}} = \\ = \,\,\frac{{\left( {{{k}_{4}}[{\text{N}}{{{\text{P}}}_{7}}] - {{k}_{{04}}}[{\text{I}}{{{\text{P}}}_{7}}]} \right) + \left( {\left( {{{k}_{8}}[{\text{AC}}{{{\text{P}}}_{7}}][{{{\text{H}}}_{2}}] - {{k}_{{08}}}[{\text{I}}{{{\text{P}}}_{7}}]} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {4\left( { - {{k}_{{16}}}{{{[{\text{I}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {0.5\left( { - {{k}_{{20}}}[{\text{I}}{{{\text{P}}}_{7}}][{{{\text{A}}}_{7}}]} \right)} \right)}}{{}}, \\ \end{gathered} $(20)
$\begin{gathered} \frac{{d{{C}_{{{\text{Ck}}}}}}}{{dr}} = \\ = \frac{{\left( {\frac{1}{9}\left( {{{k}_{{13}}}{{{[{\text{N}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right) + \left( {\frac{1}{{16}}\left( {{{k}_{{14}}}{{{[{\text{N}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {\frac{1}{9}\left( {{{k}_{{15}}}{{{[{\text{I}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {\frac{1}{{16}}\left( {{{k}_{{16}}}{{{[{\text{I}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right) + \left( {\frac{1}{3}\left( {{{k}_{{17}}}{{{[{{{\text{A}}}_{6}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{3}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {\frac{1}{6}\left( {{{k}_{{18}}}{{{[{{{\text{A}}}_{7}}]}}^{4}}{{{[{{{\text{H}}}_{2}}]}}^{7}}} \right)} \right)}}{{}}, \\ \end{gathered} $(21)
$\begin{gathered} \frac{{d{{C}_{{{\text{N}}{{{\text{P}}}_{6}}}}}}}{{dr}} = \frac{{\left( { - {{k}_{3}}[{\text{N}}{{{\text{P}}}_{6}}] + {{k}_{{03}}}[{\text{I}}{{{\text{P}}}_{6}}]} \right) + \left( {\frac{1}{6}\left( { - {{k}_{9}}[{\text{N}}{{{\text{P}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{5}}} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {\left( { - {{k}_{{11}}}[{\text{N}}{{{\text{P}}}_{6}}] + {{k}_{{011}}}[{{{\text{A}}}_{6}}]{{{[{{{\text{H}}}_{2}}]}}^{4}}} \right)} \right) + }}{{}} \\ \frac{{ + \,\,\left( {4\left( { - {{k}_{{13}}}{{{[{\text{N}}{{{\text{P}}}_{6}}]}}^{4}}} \right)} \right) + \left( {\left( { - {{k}_{{19}}}[{\text{N}}{{{\text{P}}}_{6}}]} \right)} \right)}}{{}}, \\ \end{gathered} $(22)
$\begin{gathered} \frac{{d{{C}_{{{\text{N}}{{{\text{P}}}_{7}}}}}}}{{dr}} = \\ = \,\,\frac{{\left( { - {{k}_{4}}[{\text{N}}{{{\text{P}}}_{7}}] + {{k}_{{04}}}[{\text{I}}{{{\text{P}}}_{7}}]} \right) + \left( {\frac{1}{7}\left( { - {{k}_{{10}}}[{\text{N}}{{{\text{P}}}_{7}}]{{{[{{{\text{H}}}_{2}}]}}^{6}}} \right)} \right) + }}{u} \\ \frac{{ + \,\,\left( {\left( { - {{k}_{{12}}}[{\text{N}}{{{\text{P}}}_{7}}]} \right)} \right) + \left( {4\left( { - {{k}_{{14}}}{{{[{\text{N}}{{{\text{P}}}_{7}}]}}^{4}}} \right)} \right)}}{{}}, \\ \end{gathered} $(23)
$\frac{{d{{C}_{{{\text{O}}{{{\text{C}}}_{6}}}}}}}{{dr}} = \frac{{0.5\left( {{{k}_{{19}}}[{\text{N}}{{{\text{P}}}_{6}}]} \right)}}{u},$(24)
$\frac{{d{{C}_{{{\text{Unws}}}}}}}{{dr}} = \frac{{\left( {{{k}_{{20}}}[{\text{I}}{{{\text{P}}}_{7}}][{{{\text{A}}}_{7}}]} \right)}}{u},$Приращение компонентов рассчитывается по закону действующих масс, константы скорости химических реакций по уравнению Аррениуса
где k0j – константы скорости j-й обратной реакции, моль/(м3 с); kj0 – предэкспоненциальный множитель; kj – константа скорости j-й прямой реакции, моль/(м3 с).Каталитический риформинг территориально распределенный процесс поэтому требуется ввести локальные обозначения в соответствие с локацией объекта, приведенные на рис. 3.
Рис. 3.
Схема реакторного блока каталитического риформинга: 1 – сырье (стабильный гидрогенизат); 2–4 – газосырьевая смесь; 5 – нестабильный катализат; 6 – водородсодержащий газ; 7 – топливный газ; P – насос; M – смеситель сырья и водородсодержащего газа; HE – трубчатый теплообменник; F1–F3 – многосекционная печь; V1–V3 – исполнительные устройства, регулирующие клапаны; Spl – ветвитель потока теплоносителя; PFRi – i-й реактор идеального вытеснения; AC – аппарат воздушного охлаждения; S – сепаратор; C – коллектор; 10, 20, 30 – регуляторы в контуре управления входной температурой в соответствующий реактор; 40 – регулятор в контуре управления качеством продукта реакторного блока. Сплошная стрелка – материальный поток, пунктирная стрелка – сигнал.
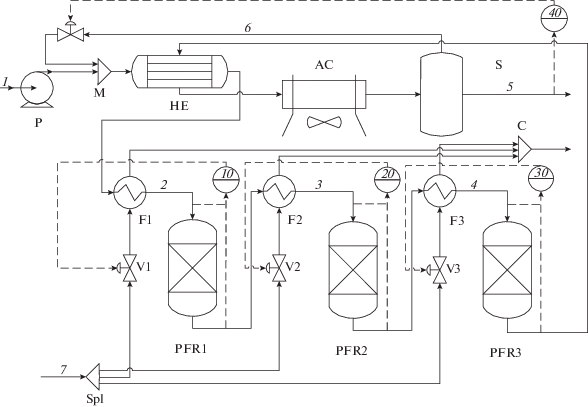
Изменение скорости реакционной смеси выражается через геометрию слоя катализатора, представленную в табл. 3, в направлении движения реакционной смеси на установке типа ЛГ – 35 – 11/300 – 95 в соответствие с технологическими параметрами процесса в табл. 4. Индексы переменных табл. 4 образованы от обозначений на рис. 3.
Таблица 3.
Геометрия катализатора в реакторах каталитического риформинга
| NR | PFR1 | PFR2 | PFR3 |
|---|---|---|---|
| l, м | 2.2 | 4.5 | 7.9 |
| dap, м | 2.6 | 2.6 | 2.6 |
| dp, м | 1.5 × 10–3–3.5 × 10–3 | 1.5 × 10–3–3.5 × 10–3 | 1.5 × 10–3–3.5 × 10–3 |
Таблица 4.
Технологические параметры процесса
| Наименование переменной | Допустимые пределы параметра |
|---|---|
| F1, м3/ч | 35–60 |
| T2, K | 743–803 |
| P2, Па | 2.2 × 106–2.5 × 106 |
| ∆PPFR1, Па | 0–2 × 105 |
| ∆TPFR1, K | ≤ 70 |
| T3, K | 743–803 |
| P3, Па | 2.2 × 106–2.5 × 106 |
| ∆PPFR2, Па | 0–2 × 105 |
| ∆TPFR2, K | ≤ 40 |
| T4, K | 743–803 |
| P4, Па | 2.2 × 106–2.5 × 106 |
| ∆PPFR3, Па | 0–2 × 105 |
| ∆TPFR3, K | ±14 |
| F6, м3/ч | 50 × 10–3–110 × 10–3 |
| F6 : F1, м3/м3 | 1500 × 10–6–1800 × 10–6 |
На примере точки динамической системы в табл. 5 показано, что модель адекватна и обладает необходимой точностью прогноза.
Таблица 5.
Сравнение расчетных значений и данных Атырауского НПЗ
| ωi, % | Сырье | Катализат | ∆ | |
|---|---|---|---|---|
| Завод | Модель | |||
| ωn | 35.92 | 12.34 | 11.92 | –0.42 |
| ωa | 9.35 | 43.14 | 43.73 | 0.59 |
| ωp | 53.23 | 43.21 | 42.91 | –0.30 |
Идентификация и адаптация. Обычно процесс каталитического риформинга протекает в статическом режиме с переходными процессами и его классифицируют как динамический, нелинейный, детерминированный и непрерывный. Нестационарность процесса возникает из-за наличия неопределенности, выражающейся, например, через процесс коксообразования.
Статическая модель каталитического риформинга не способна охватить ряд факторов, такие как: человеческий фактор; механический износ катализатора; переходные режимы работы установки; влияние влаги в катализаторе; снижение кислотной функции из-за дихлорирования катализатора; отравление катализатора каталитическими ядами; внешние воздействия.
Изменение активности катализатора приводит к изменению технологических величин, которые косвенно характеризуют состояние нестационарной части процесса. По ряду таких факторов система управления со временем может перестать интенсифицировать работу установки поэтому применяется идентификация и адаптация математической модели.
Для идентификации математической модели блока реакторов каталитического риформинга применяется следующая функция рассогласования [17]:
(26)
$\begin{gathered} \phi ({\mathbf{K}}) = \frac{1}{m}\sum\limits_{n = 1}^m {\left[ {{{\eta }_{Y}}{{{\left( {\frac{{Y_{n}^{{ct}} - Y_{n}^{e}}}{{Y_{n}^{e}}}} \right)}}^{2}}} \right.} + \\ \left. { + \,\,{{\eta }_{\omega }}\sum\limits_{i = 1}^{NR} {{{{\left( {\frac{{\omega _{{n,i}}^{{ct}} - \omega _{{n,i}}^{e}}}{{\omega _{{n,i}}^{e}}}} \right)}}^{2}} + {{\eta }_{{T{\kern 1pt} \_}}}\sum\limits_{i = 1}^{NR} {{{{\left( {\frac{{T{\kern 1pt} \__{{n,i}}^{{ct}}{\kern 1pt} {\kern 1pt} - T{\kern 1pt} \__{{n,i}}^{e}}}{{T{\kern 1pt} \__{{n,i}}^{e}}}} \right)}}^{2}}} } } \right], \\ \end{gathered} $где ϕ – целевая функция; K – массив векторов коэффициентов, корректирующих математическую модель; m – число экспериментальных данных; n – номер эксперимента; ηY – коэффициент значимости выхода катализата; $Y_{n}^{{ct}}$, $Y_{n}^{e}$ – расчетное и экспериментальное значение выхода катализата, кг/кг; ηω – коэффициент значимости массовых долей углеводородов; NR – число реакторов; i – номер реактора; $\omega _{{n,i}}^{{ct}}$, $\omega _{{n,i}}^{e}$ – расчетное и экспериментальное значение массовых долей групп компонентов в продукте каждого реактора, мас. %; ηT_ – коэффициент значимости выходных температур; $T\__{{n,i}}^{{ct}}$, $T\__{{n,i}}^{e}$ – расчетное и экспериментальное значение температур на выходе каждого реактора, К.
В случае рассогласования прогноза модели и соответствующих измеренных выходных координат объекта управления минимизируется функция ошибок методом последовательного квадратичного программирования с ограничениями параметров, представленных в табл. 2.
Оптимальное управление. Целью управления процессом является получение на выходе продукта с заданным качеством. В ходе экспериментов со статической моделью процесса было выяснено, что наибольшее влияние на целевые показатели оказывает температура на входе в реактор, так как суммарный тепловой эффект реакций отрицательный. Поэтому в качестве основного канала управления в реакторном блоке каталитического риформинга рассматривается компенсация возмущений путем изменения температуры сырья на входе каждого реактора. Расход водородсодержащего газа практически линейно влияет на выход катализата и обратно влияет на октановое число продукта. Следовательно, повышение одного из целевых показателей за счет изменения расхода водородсодержащего газа снизит значение второго показателя.
Выход и октановое число катализата являются технико-экономическими показателями работы установки риформинга поэтому они приняты как целевые показатели при оптимальном управлении. Для разработки математической модели на основе массового и энергетического балансов и других корреляций применяются следующие допущения: по причине высокой температуры процесса применим закон об идеальном газе; для описания гетерогенного каталитического процесса в системе газ–твердое используется квазигомогенная модель; приращение компонентов по объему катализатора происходит по закону действующих масс; константы скоростей химических реакций зависят от температуры реакционной смеси по закону Аррениуса; на основе уравнения состояния идеального газа рассчитывается плотность реакционной смеси; реакционная смесь движется в поршневом режиме течения; нестационарность процесса со временем приводит к изменению констант скоростей реакций путем коррекции предэкспоненциальных множителей; рассмотрены адиабатические условия процесса в реакторах, на ход процесса влияют только внутренние воздействия; псевдокомпоненты характеризует группу близких по свойствам и молярной массе веществ.
Предполагается, что принятые допущения оказывают незначительное влияние на целевые показатели процесса – выход катализата в уравнении (27) и октановое число в уравнении (28):
(27)
$Y = {{{{G}_{С}}} \mathord{\left/ {\vphantom {{{{G}_{С}}} {{{G}_{1}}}}} \right. \kern-0em} {{{G}_{1}}}},$(28)
${\text{ON}} = \sum {{{\text{b}}}_{i}}{{\omega }_{i}}--{{{\text{b}}}_{{\text{o}}}}\omega _{{\text{a}}}^{2},$Задачу оптимизации можно сформулировать как: максимизация выхода целевого продукта при установленном октановом числе в уравнении (29); максимизация показателя октанового числа целевого продукта при установленном выходе катализата в уравнении (30):
при ограничениях параметров, указанных в табл. 4 для каждого реактора.
Поставленные задачи решаются с помощью метода последовательного квадратичного программирования, так как этот метод и его модификации хорошо зарекомендовали себя в системах оптимального управления [3]. Выбор задачи управления рассматривается как возможность целеполагания в соответствие с меняющимися целями установки каталитического риформинга со временем.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
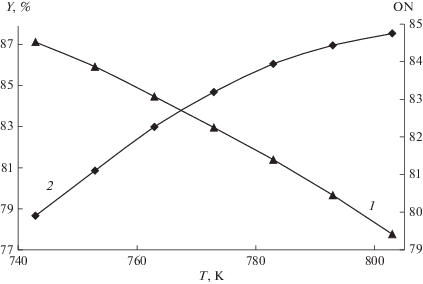
В промышленной практике оптимальная работа непрерывных процессов обычно рассматривается через иерархию управления, включающую различные уровни. В таком случае оптимизация в реальном времени вычисляет оптимальную рабочую точку на основе нелинейной статической модели технологического процесса. Количественная и качественная характеристики катализата в зависимости от температуры приведены на рис. 4 на примере нескольких рабочих точек.
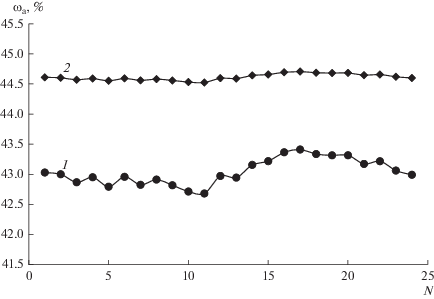
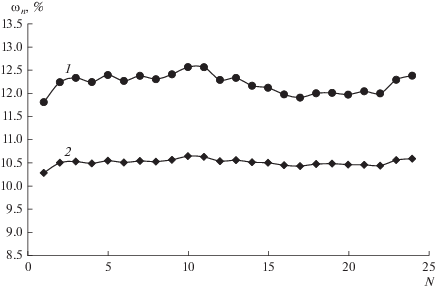
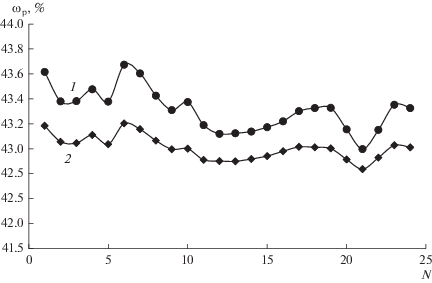
На рис. 5–7 представлены графики сравнения расчетных значений и реальных данных по выходам ароматики, нафтенов и парафинов при максимизации октанового числа.
На рисунках сравнения показана разница управления реального объекта и оптимального управления по прогнозирующей модели технологического процесса на примере основных групп соединений продуктового потока каталитического риформинга. Рисунки показывают, что оптимальное управление позволяет снизить запас по качеству продукта за счет снижения амплитуды колебания выходных координат процесса относительно границы спецификации показателя качества продукта, заданной для объекта управления в соответствие с текущими потребностями предприятия. Таким образом можно сказать, что при оптимальном управлении вырабатывается более точное компенсирующее воздействие на входящее возмущение. Результаты моделирования усовершенствованной системы управления показывают, что оптимальное управление с прогнозирующей моделью интенсифицирует процесс реакторного узла каталитического риформинга.
ЗАКЛЮЧЕНИЕ
Путем анализа имитационной модели в контуре управления системы оптимального управления по прогнозирующей модели сложного объекта показана возможность оптимального управления поведением технологического процесса на основе технико-экономических показателей.
Применяя оптимальное управление на основе прогнозирующей модели, система управления стабилизирует технологический процесс лучше, чем это делает оператор без усовершенствованной системы управления и автоматически смещает технологический режим в оптимальную рабочую точку согласно заданному критерию оптимизации.
ОБОЗНАЧЕНИЯ
| Ci | молярная концентрация i-го компонента смеси, моль/м3 |
| Cpi | молярная удельная теплоемкость i-го компонента смеси, Дж/(моль К) |
| dap | внутренний диаметр аппарата, м |
| dp | диаметр частиц катализатора, м |
| Ea | энергия активации, Дж/моль |
| Fi | объемный расход i-го потока, м3/ч |
| Gi | массовый расход i-го потока, кг/с |
| GС | массовый расход катализата, кг/с |
| g | ускорение свободного падения, м/с2 |
| ΔHj | тепловой эффект j-й реакции, Дж/моль |
| k0j | константы скорости j-й обратной реакции, моль/(м3 с) |
| kj | константа скорости j-й прямой реакции, моль/(м3 с) |
| l | длина слоя катализатора в реакторе, м |
| N | номер точки динамической системы |
| ON | октановое число |
| P | давление в системе, Па |
| P2, P3, P4 | давление на входе каждого реактора, Па |
| ∆PPFRi | перепад давления в i-м реакторе, Па |
| Qi | молярный расход i-го компонента смеси, моль/с |
| R | универсальная газовая постоянная, Дж/(моль К) |
| r | радиус слоя катализатора, м |
| S | площадь поперечного сечения для радиального ввода реагентов, м2 |
| T | температура реакционной смеси, K |
| T_ | температуры на выходе каждого реактора, К |
| T2, T3, T4 | температура на входе в каждый реактор, К |
| ∆TPFRi | перепад температуры в i-м реакторе, К |
| u | линейная скорость реакционной смеси в реакторе, м/с |
| wi | скорость образования i-го вещества, моль/(с м3) |
| Y | выход катализата, % |
| µ | динамическая вязкость смеси, Па с |
| ρ | плотность газовой смеси, кг/м3 |
| ωa | массовая доля ароматики в катализате, мас. % |
| ωi | массовая доля i-й группы компонентов в катализате, мас. % |
| ωn | массовая доля нафтенов в катализате, мас. % |
| ωp | массовая доля парафинов в катализате, мас. % |
ИНДЕКСЫ
Список литературы
Ancheyta J. Modeling and Simulation of Catalytic Reactors for Petroleum Refining. New York: Wiley, 2011.
Rahimpour M.R., Jafari M., Iranshahi D. Progress in catalytic naphtha reforming process: A review // Appl. Energy. 2013. V. 109. P. 79.
Agachi P.S. Advanced Process Engineering Control. Berlin: Walter De Gruyter, 2017.
Grüne L., Pannek J. Nonlinear Model Predictive Control Theory and Algorithms. Cham: Springer, 2017.
García C.E., Prett D.M., Morari M. Model predictive control: Theory and practice—A survey // Automatica. 1989. V. 25. № 3 . P. 335.
Diehl M. et al. Real-time optimization and nonlinear model predictive control of processes governed by differential-algebraic equations // J. Process Control. 2002. V. 12. № 4. P. 577.
Morari M., Lee H.J. Model predictive control: past, present and future // Comput. Chem. Eng. 1999. V. 23. № 4–5. P. 667.
Qin S.J., Badgwell T.A. A survey of industrial model predictive control technology // Control Eng. Pract. 2002. V. 11. P. 733.
De Souza G., Odloak D., Zanin A.C. Real time optimization (RTO) with model predictive control (MPC) // Comput. Chem. Eng. 2010. V. 34. № 12. P. 1999.
Engell S. Feedback control for optimal process operation // J. Process Control. 2007. V. 17. № 3. P. 203.
Sotomayor O.A.Z., Park S.W., Garcia C. Multivariable identification of an activated sludge process with subspace-based algorithms // Control Eng. Pract. 2003. V. 11. № 8 P. 961.
Chandra S.T., Nordin S., Karsiti M.N. System identification of an interacting series process for real-time model predictive control // Proceedings of the American Control Conference. 2009. P. 4384.
Froment G.F., Bischoff K.B., Wilde J. Chemical Reactor Analysis and Design. New York: Wiley, 2010.
Li S., Zheng Y. Distributed Model Predictive Control for Plant-Wide Systems. Singapore: Wiley, 2015.
Кафаров В.В. Методы кибернетики в химии и химической технологии. М.: Химия, 1976.
Ткачев И.В., Шариков Ю.В., Снегирев Н.В. Моделирование системы управления процессами реакторного блока каталитического риформинга. Программа для ЭВМ. 2019614794 РФ. 2019.
Войтенко И.В. Адаптивная оптимизация процесса каталитического риформинга на основе технико-экологических критериев // Автом., телемех. связь нефт. пром-сти. 1998. № 12. С. 11.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии