Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 747-757
Оценка множественности стационарных состояний ферментативного процесса получения молочной кислоты по заданной концентрации компонента, воспроизводящего основной субстрат
Ю. Л. Гордеева a, *, Л. В. Равичев b, Е. Л. Гордеева b
a Московская государственная академия ветеринарной медицины и биотехнологии им. К.И. Скрябина
Москва, Россия
b Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: l.s.gordeev@yandex.ru
Поступила в редакцию 02.07.2020
После доработки 06.07.2020
Принята к публикации 10.07.2020
Аннотация
Приведена расчетная схема оценки технологических показателей непрерывной ферментации молочной кислоты при заданной концентрации компонента, воспроизводящего основной субстрат. Расчетная схема включает предварительный анализ, основной анализ и численный пример реализации расчета. В предварительном анализе приведены соотношения для оценки граничных показателей, формирующих область значений последних, реально обеспечивающих заданное значение концентрации компонента, воспроизводящего основной субстрат (M0, г/л). Отмечены координаты точки максимальной продуктивности и особых точек. Иллюстрация положения указанных координат воспроизведена на портрете зависимости M0 от величины протока D для величины продуктивности QP = 6 г/(л ч). На этом же портрете отмечены части I, II и III раздельно, для которых сформированы расчетные соотношения. Схема формирования расчетных соотношений представлена раздельно для каждой из частей. Границы частей определены соотношениями (22)–(24). Для координат особых точек, для точки экстремума QP и для каждой из частей сформированы множества по заданному значения M0: для части I – множество Мн1, для части II – множества Мн1* и Мн2*, для части III – множества Мн1**, Мн2** и Мн3**. Теоретические соотношения использованы для численной оценки показателей множеств. Показано, что диапазон задания M0 наиболее широк для части I, в то время как диапазон для величины протока D наибольший для части III. Численные оценки в сравнительном варианте для множеств частей II и III показали, что конечные концентрации компонентов при одинаковых начальных условиях отличаются по значениям M0 и S. Последнее дает возможность оценить дальнейшую переработку результатов синтеза (выделение молочной кислоты, утилизация и использование непревращенных компонентов, выделение побочного продукта).
ВВЕДЕНИЕ
Особенностью процесса непрерывной ферментации молочной кислоты является то, что при использовании одних и тех же компонентов различные их количества на входе в аппарат могут обеспечивать одно и то же значение основного показателя – продуктивности по молочной кислоте QP, г/(л ч). Аналогичное условие может реализоваться с использованием различных значений величины протока D, ч–1.
Таким образом, технологическое обеспечение процесса определяется тремя входными показателями – величиной протока через ферментер (D, ч–1); величиной концентрации основного субстрата в поступающем потоке (S0, г/л) (под основным субстратом понимается субстрат, непосредственно потребляемый микроорганизмами; для многих микроорганизмов часто основным субстратом является глюкоза [1]); величиной концентрации компонента сырья (M0, г/л), воспроизводящего основной субстрат в процессе ферментации. Так, в работе [2] этим компонентом является мальтоза, при деградации которой воспроизводится основной субстрат. В работе [3] дополнительное количество субстрата образуется деградацией крахмала. Общее количество субстрата, потребляемого микроорганизмами, складывается из двух составляющих – часть от основного субстрата и часть от компонента, воспроизводящего субстрат.
Ниже приведем уравнения математической модели [4].
Уравнения обобщенной математической модели:
(1)
$\left\{ \begin{gathered} - DX + \mu X = 0 \hfill \\ \left( {\alpha \mu + \beta } \right)X - DP = 0 \hfill \\ \left( {{{\alpha }_{B}}\mu + {{\beta }_{B}}} \right)X - DB = 0 \hfill \\ D\left( {{{S}_{0}} - S} \right) - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\mu X + {{k}_{M}}M = 0 \hfill \\ D\left( {{{M}_{0}} - M} \right) - {{k}_{M}}M = 0 \hfill \\ \mu = {{\mu }_{{\max }}}{{\left( {1 - \frac{X}{{{{X}_{{\max }}}}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{P}{{{{P}_{{\max }}}}}} \right)}^{{{{n}_{2}}}}}\frac{S}{{{{K}_{m}} + S + {{{{S}^{2}}} \mathord{\left/ {\vphantom {{{{S}^{2}}} {{{K}_{i}}}}} \right. \kern-0em} {{{K}_{i}}}}}} \hfill \\ \end{gathered} \right..$В приложении (формулы (П.1)−(П.4)) приведены соотношения, полученные преобразованием системы (1).
Последовательность теоретического анализа формирования множественности в реализации технологического процесса состоит из трех ступеней. На первой ступени множественность рассматривается по величине протока, на второй – по концентрации основного субстрата. В настоящем сообщении множественность рассматривается по величине концентрации компонента, воспроизводящего основной субстрат в процессе синтеза.
Ниже выполнен анализ по оценке множественности, когда задана концентрация M0, г/л компонента, воспроизводящего основной субстрат, т.е. в рассмотрении задается концентрация M0, г/л и оцениваются значения D, ч–1 и S0, г/л, обеспечивающие ${{Q}_{P}} \leqslant \max {{Q}_{P}}$.
Для решения поставленной задачи требуется выполнение предварительных расчетов, суть которых заключается в возможности получения соотношений, обеспечивающих реальное осуществление процесса. Таким образом, дальнейший анализ базируется на уравнениях математической модели (1).
ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
Целью предварительного анализа является получение характеристики объекта, для которого будет оцениваться множественность.
Задачей технологического процесса является получение показателей, обеспечивающих заданное значение продуктивности по целевому продукту QP, г/(л ч) – молочной кислоте. При этом возможен вариант получения максимальной продуктивности – maxQP или продуктивности меньше максимальной. В последнем случае возможна экономия сырьевых материалов или лучшие условия выделения целевого продукта и др.
Первая задача, которая решается при получении характеристик объекта, есть задача оценки maxQP и определение величины протока Dopt, обеспечивающего maxQP.
Максимальное значение QP вычисляется с использованием соотношения (П.1), т.е. вычисляется значение Dopt, обеспечивающее maxQP в уравнении
(2)
${{\left( {\frac{{{{K}_{i}}}}{2}} \right)}^{2}}{{\left[ {A\left( D \right)\frac{{{{\mu }_{{{\text{max}}}}}}}{D} - 1} \right]}^{2}} - {{K}_{m}}{{K}_{i}} = 0.$Численное решение (2) дает значения
Для maxQP и Dopt вычисляется $S_{{{\text{opt}}}}^{'}$ с использованием (П.3).
Получаем
(4)
$\begin{gathered} S_{{{\text{opt}}}}^{'} = S_{1}^{'}\left( {{{D}^{{{\text{opt}}}}}} \right) = S_{2}^{'}\left( {{{D}^{{{\text{opt}}}}}} \right) = \\ = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{\text{max}}{{Q}_{P}}}}{{\left( {\alpha {{D}^{{{\text{opt}}}}} + \beta } \right)}} + {{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}. \\ \end{gathered} $Используя $S_{{{\text{opt}}}}^{'}$, Dopt, по (П.2) получаем (при S0 = 0)
(5)
$M_{0}^{{{\text{opt}}}} = \frac{{{{D}^{{{\text{opt}}}}} + {{k}_{M}}}}{{{{k}_{M}}}}S_{{{\text{opt}}}}^{'}.$Максимальное значение QP обозначим особой точкой 5. Координаты этой точки $\left\{ {M_{0}^{{{\text{opt}}}},{{D}^{{{\text{opt}}}}}} \right\}$.
Следующая задача заключается в получении оценок при условии
Для QP по условию (6) также решается уравнение (2). Получаем два значения D1 и D2 (значения D не могут быть меньше D1 и не могут быть больше D2 по условиям (П.3)).
Для D1 и D2 вычисляются значения $S{\kern 1pt} '\left( {{{D}_{1}}} \right)$ и $S{\kern 1pt} '\left( {{{D}_{2}}} \right)$, используя (П.3):
(7)
$\begin{gathered} S{\kern 1pt} '\left( {{{D}_{1}}} \right) = S_{1}^{'}\left( {{{D}_{1}}} \right) = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha {{D}_{1}} + \beta } \right)}} + \\ + \,\,{{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = S_{2}^{'}\left( {{{D}_{1}}} \right), \\ \end{gathered} $(8)
$\begin{gathered} S{\kern 1pt} '\left( {{{D}_{2}}} \right) = S_{1}^{'}\left( {{{D}_{2}}} \right) = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha {{D}_{2}} + \beta } \right)}} + \\ + \,\,{{\left( {{{K}_{m}}{{K}_{i}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = S_{2}^{'}\left( {{{D}_{2}}} \right) \\ \end{gathered} $По $S{\kern 1pt} '\left( {{{D}_{1}}} \right)$, $S{\kern 1pt} '\left( {{{D}_{2}}} \right)$, D1, D2 по (П.2) вычислены координаты точек 1 и 2 (точки 1 и 2 назовем особыми) при S0 = 0.
Для точки 1:
(9)
${{M}_{0}}\left( {{{D}_{1}}} \right) = \frac{{{{D}_{1}} + {{k}_{M}}}}{{{{k}_{M}}}}S{\kern 1pt} '\left( {{{D}_{1}}} \right).$Для точки 2:
(10)
${{M}_{0}}\left( {{{D}_{2}}} \right) = \frac{{{{D}_{2}} + {{k}_{M}}}}{{{{k}_{M}}}}S{\kern 1pt} '\left( {{{D}_{2}}} \right).$Таким образом, координатами для точек 1 и 2 будут:
особая точка 1:
особая точка 2:
Координаты особых точек 1 и 2 определяют область значений D при QP < maxQP:
Далее вычисляются координаты еще двух особых точек 3 и 4.
Особая точка 3 представляет максимальное значение M0 для условий (6), точка 4 – минимальное значение M0 для условий (6).
Обозначив максимальное значение M0 в виде M0(D3), вычисляем значение D3:
(14)
${{M}_{0}}\left( {{{D}_{3}}} \right) = \mathop {\max }\limits_D \frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{1}^{'}\left( D \right),$$S_{1}^{'}\left( D \right)$ по (П.3), т.е. определяется D3 по условию максимума (14).
По полученному D3 вычисляется M0(D3):
(15)
${{M}_{0}}\left( {{{D}_{3}}} \right) = \frac{{{{D}_{3}} + {{k}_{M}}}}{{{{k}_{M}}}}S_{1}^{'}\left( {{{D}_{3}}} \right).$Обозначив минимальное значение M0 в виде M0(D4), вычисляем значение D4:
(16)
${{M}_{0}}\left( {{{D}_{4}}} \right) = \mathop {\min }\limits_D \frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{2}^{'}\left( D \right),$$S_{2}^{'}\left( D \right)$ по (П.3), т.е. определяется D4 по условию минимума (16).
По полученному D4 вычисляется M0(D4):
(17)
${{M}_{0}}\left( {{{D}_{4}}} \right) = \frac{{{{D}_{4}} + {{k}_{M}}}}{{{{k}_{M}}}}S_{2}^{'}\left( {{{D}_{4}}} \right).$В результате получили координаты точек экстремума и особых точек, ограничивающие значения M0 в технологическом процессе для условия (6):
(18)
$\left. \begin{gathered} {\text{особая}}\,\,{\text{точка}}\,\,1:\left\{ {{{M}_{0}}\left( {{{D}_{1}}} \right),\;{{D}_{1}}} \right\} \hfill \\ {\text{особая}}\,\,{\text{точка}}\,\,2:\left\{ {{{M}_{0}}\left( {{{D}_{2}}} \right),\;{{D}_{2}}} \right\} \hfill \\ {\text{особая}}\,\,{\text{точка}}\,\,3:\left\{ {{{M}_{0}}\left( {{{D}_{3}}} \right),\;{{D}_{3}}} \right\} \hfill \\ {\text{особая}}\,\,{\text{точка}}\,\,4:\left\{ {{{M}_{0}}\left( {{{D}_{4}}} \right),\;{{D}_{4}}} \right\} \hfill \\ {\text{особая}}\,\,{\text{точка}}\,\,5:\left\{ {{{M}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right),\;{{D}^{{{\text{opt}}}}}} \right\} \hfill \\ \end{gathered} \right\}.$Отметим (по (П.3)) следующее:
Ниже приведем числовой расчет с использованием констант базового варианта для системы (1) (табл. 1), определяющий область существования технологических показателей для QP = 6 г/(л ч).
Таблица 1.
Численные значения констант для базового варианта
| Km, г/л | Ki, г/л | µmax, ч–1 | Xmax, г/л | Pmax, г/л | n1 | n2 | YX/S, г/г | kM, ч–1 | α, г/г | β, ч–1 | αB, г/г | βB, ч–1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.2 | 164 | 0.48 | 30 | 98.0 | 0.5 | 0.5 | 0.4 | 0.035 | 2.2 | 0.02 | 1.1 | 0.01 |
По решению уравнения (2) получены следующие значения для оптимальной точки: maxQP = = 8.1718 г/(л ч), Dopt = 0.205 ч–1, $S_{{{\text{opt}}}}^{'} = 57.4$ г/л; ${{M}_{0}}\left( {{{D}^{{{\text{opt}}}}}} \right) = 393.6$ г/л.
Для вычисления координат особых точек 1–4 использовано следующее условие:
По решению уравнения (2) с использованием (П.1) вычисляют D1 и D2 при QP = 6 г/(л ч). Получили
Таким образом, область значений D ограничена
Для значений D1 и D2 вычисляются значения $S_{1}^{'}\left( {{{D}_{1}}} \right)$, $S_{1}^{'}\left( {{{D}_{2}}} \right)$ по (П.3). Получили
Вычисляются координаты особых точек 1 и 2 по (9) и (10). Получили
Вычисляются значения D3 по (14) и D4 по (16). Получили
Для значений D3 и D4 вычисляются значения $S_{1}^{'}\left( {{{D}_{3}}} \right)$ и $S_{2}^{'}\left( {{{D}_{4}}} \right)$ по (П.3). Получили
Вычисляются координаты особых точек 3 и 4 по (15) и (17) при S0 = 0. Получили
Численные значения координат:
(19)
$\left. \begin{gathered} {\text{точка экстремума: }}\left\{ {{\text{393}}{\text{.6 }}{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {\text{л}}}} \right. \kern-0em} {\text{л}}}{\text{; 0}}{\text{.205 }}{{{\text{ч}}}^{{ - {\text{1}}}}}} \right\}{\text{ }} \hfill \\ {\text{особая точка 1: }}\left\{ {{\text{295}}{\text{.28 }}{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {\text{л}}}} \right. \kern-0em} {\text{л}}}{\text{; 0}}{\text{.09818 }}{{{\text{ч}}}^{{ - {\text{1}}}}}} \right\} \hfill \\ {\text{особая точка }}2:\left\{ {{\text{349}}{\text{.16 }}{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {\text{л}}}} \right. \kern-0em} {\text{л}}}{\text{; 0}}{\text{.3107 }}{{{\text{ч}}}^{{ - {\text{1}}}}}} \right\} \hfill \\ {\text{особая точка }}3:\left\{ {{\text{773}}{\text{.1 }}{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {\text{л}}}} \right. \kern-0em} {\text{л}}}{\text{; 0}}{\text{.18 }}{{{\text{ч}}}^{{ - {\text{1}}}}}} \right\} \hfill \\ {\text{особая точка }}4:\left\{ {{\text{234}}{\text{.96 }}{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {\text{л}}}} \right. \kern-0em} {\text{л}}}{\text{; 0}}{\text{.18 }}{{{\text{ч}}}^{{ - {\text{1}}}}}} \right\} \hfill \\ {\text{особая точка 5}}:\left\{ {{\text{393}}{\text{.6 }}{{\text{г}} \mathord{\left/ {\vphantom {{\text{г}} {\text{л}}}} \right. \kern-0em} {\text{л}}}{\text{; 0}}{\text{.205 }}{{{\text{ч}}}^{{ - {\text{1}}}}}} \right\} \hfill \\ \end{gathered} \right\}.$В соответствии с целью предварительного анализа координаты особых точек являются ограничительными характеристиками для оценки множественности стационарных состояний по заданному значению M0. Эти характеристики получены по условию S0 = 0, т.е. фактически для технологической схемы, в которой не содержится основной субстрат.
В более общем варианте технология реализуется, когда сырье содержит и основной субстрат с концентрацией S0 и компонент сырья с концентрацией M0, воспроизводящий основной субстрат в процессе синтеза.
Далее приведем расчетные соотношения, обеспечивающие показатели точки экстремума и особые точки для условия содержания в сырье основного субстрата, и компонента, воспроизводящего основной субстрат. Сразу отметим, что уже здесь формируется множество технологических решений.
Для каждой из этих точек формируется множество технологических показателей S0 и M0 по соотношениям, представленным в табл. 2.
Таблица 2.
Расчетные соотношения для вычисления $S_{0}^{i}$ и $M_{0}^{i}$
| Обозначения | Расчетные соотношения | |
| Dk, ч–1; ${{S'}_{k}}$, г/л | $M_{0}^{i} = \frac{{{{n}_{k}} - i}}{{{{n}_{k}}}}\frac{{{{D}_{k}} + {{k}_{M}}}}{{{{k}_{M}}}}S_{k}^{'}$ (20) | |
| Координаты точек | ||
| k = 0.0 | Точка экстремума D0 = Dopt; $S_{0}^{'} = S{\kern 1pt} '\left( {{{D}^{{{\text{opt}}}}}} \right)$ |
$S_{0}^{i} = \frac{i}{{{{n}_{k}}}}S_{k}^{'}$ (21) |
| k = 1.0 | Особая точка 1 D1, $S_{1}^{'} = S{\kern 1pt} '\left( {{{D}_{1}}} \right)$ |
nk > 0 – задает пользователь для каждой точки; i = 0.0–nk |
| k = 2.0 | Особая точка 2 D2, $S_{2}^{'} = S{\kern 1pt} '\left( {{{D}_{2}}} \right)$ |
|
| k = 3.0 | Особая точка 3 D3, $S_{3}^{'} = S{\kern 1pt} '\left( {{{D}_{3}}} \right)$ |
|
| k = 4.0 | Особая точка 4 D4, $S_{4}^{'} = S{\kern 1pt} '\left( {{{D}_{4}}} \right)$ |
|
Приведем результаты численного расчета множеств $\left\{ {S_{0}^{i},\;M_{0}^{i}} \right\}$ для точки экстремума и особых точек, используя вышеуказанные координаты (19).
Исходные данные:
1. Для всех точек мощность множеств принята одинаковой (nk = 4.0) и равной 5 (i = 0.0; 1.0; 2.0; 3.0; 4.0).
2. Координаты точек в соответствии с табл. 2:
В табл. 3 приведены результаты расчетов $S_{0}^{i}$, $M_{0}^{i}$ для вышеприведенных условий. Таким образом, для каждой точки получили множество $\left\{ {S_{0}^{i},M_{0}^{i}} \right\}$ при nk = 4.0 (5 вариантов). Множеств может быть сколько угодно в зависимости от принятых nkи i. Понятно, здесь M0 произвольно не может быть задано, так как требуется обеспечить значения координат особых точек и точки экстремума.
Таблица 3.
Результаты расчетов элементов множеств $M_{0}^{i}$ и $S_{0}^{i}$ для точки экстремума и особых точек
| № п/п |
i | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|
| 1 | Точка экстремума |
$M_{0}^{0} = 393.6$$S_{0}^{0} = 0.0$ | $M_{0}^{1} = 295.2$$S_{0}^{1} = 14.35$ | $M_{0}^{2} = 196.8$$S_{0}^{2} = 28.7$ | $M_{0}^{3} = 98.4$$S_{0}^{3} = 43.05$ | $M_{0}^{4} = 0.0$$S_{0}^{4} = 57.4$ |
| 2 | Особая точка 1 | $M_{0}^{0} = 295.28$$S_{0}^{0} = 0.0$ | $M_{0}^{1} = 221.46$$S_{0}^{1} = 19.4$ | $M_{0}^{2} = 147.64$$S_{0}^{2} = 38.8$ | $M_{0}^{3} = 73.82$$S_{0}^{3} = 58.2$ | $M_{0}^{4} = 0.0$$S_{0}^{4} = 77.6$ |
| 3 | Особая точка 2 | $M_{0}^{0} = 349.16$$S_{0}^{0} = 0.0$ | $M_{0}^{1} = 251.87$$S_{0}^{1} = 8.83$ | $M_{0}^{2} = 174.58$$S_{0}^{2} = 17.67$ | $M_{0}^{3} = 87.29$$S_{0}^{3} = 26.51$ | $M_{0}^{4} = 0.0$$S_{0}^{4} = 35.35$ |
| 4 | Особая точка 3 | $M_{0}^{0} = 773.1$$S_{0}^{0} = 0.0$ | $M_{0}^{1} = 579.81$$S_{0}^{1} = 31.46$ | $M_{0}^{2} = 386.54$$S_{0}^{2} = 62.93$ | $M_{0}^{3} = 193.27$$S_{0}^{3} = 94.39$ | $M_{0}^{4} = 0.0$$S_{0}^{4} = 125.85$ |
| 5 | Особая точка 4 | $M_{0}^{0} = 234.96$$S_{0}^{0} = 0.0$ | $M_{0}^{1} = 176.22$$S_{0}^{1} = 9.56$ | $M_{0}^{2} = 117.48$$S_{0}^{2} = 19.125$ | $M_{0}^{3} = 39.79$$S_{0}^{3} = 28.69$ | $M_{0}^{4} = 0.0$$S_{0}^{4} = 38.25$ |
Далее рассматривается более общая задача, когда задается M0 для условий, отличных от рассмотренных выше. Эта задача решается в разделе “Основной анализ”.
ОСНОВНОЙ АНАЛИЗ
Целью основного анализа является получение расчетных соотношений для вычисления технологических показателей S0, M0, D и, соответственно, остальных показателей процесса P, X, S, M, B по заданному значению M0. Анализ ориентирован на условие: QP < maxQP, т.е. значение продуктивности по молочной кислоте ниже значения максимальной продуктивности при одинаковых условиях. Если значение M0 задается по координатам точки экстремума и особых точек, то для этих условия S0 = 0 и показатели процесса вычисляются по (П.4). В дальнейшем этот вариант не рассматривается, так как был рассмотрен ранее.
По результатам предварительного анализа область значений M0 разделяется на три части:
(22)
${\text{Часть}}\,\,{\text{I}}:{{M}_{0}}\left( {{{D}_{2}}} \right) \leqslant {{M}_{0}} \leqslant {{M}_{0}}\left( {{{D}_{3}}} \right),$(23)
${\text{Часть}}\,\,{\text{II}}:{{M}_{0}}\left( {{{D}_{1}}} \right) \leqslant {{M}_{0}} \leqslant {{M}_{0}}\left( {{{D}_{2}}} \right),$(24)
${\text{Часть}}\,\,{\text{III}}:{{M}_{0}}\left( {{{D}_{4}}} \right) \leqslant {{M}_{0}} \leqslant {{M}_{0}}\left( {{{D}_{1}}} \right).$Значения D1–D4 определены в предварительном анализе. Задаваемое значение M0 должно удовлетворять неравенствам (22)–(24) по каждой части.
Формирование множеств $\left\{ {S_{0}^{i},{{D}^{i}}} \right\}$ по заданному значению M0 реализуется для каждой из частей отдельно.
Часть I. По части I рассматривается последовательность формирования множества $\left\{ {S_{0}^{i},{{D}^{i}}} \right\}$ для заданного значения M0 по неравенству (22).
1.1. Вычисляются значения $D_{1}^{1}$ и $D_{1}^{2}$ (при S0 = 0) по уравнению
используя (П.3) и (П.2). M0 задано по (22).
Значения $D_{1}^{1}$ и $D_{1}^{2}$ удовлетворяют неравенствам
1.2. Вычисляется шаг h по D от $D_{1}^{1}$ до $D_{1}^{2}$:
где n1 – произвольное положительное число.1.3. Вычисляется значение ${{D}^{i}}$, используя шаг h:
где i = 0 – n1.1.4. Соотношение (27) преобразуется по (26):
1.5. Для каждого значения ${{D}^{i}}$ вычисляется $S_{0}^{i}$ по формуле
В результате получили множество Мн1: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ для заданного M0. Результирующие формулы приведены в табл. 4 (часть I, Мн1). Остальные показатели процесса вычисляются по П. 4 для каждого номера i, используя M0, $S_{0}^{i}$, ${{D}^{i}}$.
Таблица 4.
Расчетные соотношения для вычисления множеств при заданном M0
| Часть I | Часть II | |
|---|---|---|
| ${{M}_{0}}\left( {{{D}_{2}}} \right) < {{M}_{0}} < {{M}_{0}}\left( {{{D}_{3}}} \right)$ | ${{M}_{0}}\left( {{{D}_{1}}} \right) < {{M}_{0}} < {{M}_{0}}\left( {{{D}_{2}}} \right)$ | |
| $D_{1}^{1}$ и $D_{1}^{2}$ по решению $\frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{1}^{'}\left( D \right) - {{M}_{0}} = 0$ $D_{1}^{1} < {{D}_{3}}$, $D_{1}^{2} > {{D}_{3}}$ |
$D_{2}^{1}$ по решению $\frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{1}^{'}\left( D \right) - {{M}_{0}} = 0$ $D_{2}^{2}$ по решению $\frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{2}^{'}\left( D \right) - {{M}_{0}} = 0$ $D_{2}^{1} < {{D}_{3}}$; $D_{2}^{2} > {{D}_{4}}$; $S_{1}^{'}\left( D \right)$ по (П.3); $S_{2}^{'}\left( D \right)$ по (П.3) |
|
| Мн1: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ | Мн1*: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ | Мн2*:$\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ |
| ${{D}^{i}} = D_{1}^{1} + \frac{i}{{{{n}_{1}}}}\left( {D_{1}^{2} - D_{1}^{1}} \right)$ ${{n}_{1}} > 0$; $i = 0 \div {{n}_{1}}$ |
${{D}^{i}} = D_{2}^{1} + \frac{i}{{n_{2}^{1}}}\left( {{{D}_{2}} - D_{2}^{1}} \right)$ $n_{2}^{1} > 0$; $i = 0 \div n_{2}^{1}$ |
${{D}^{i}} = D_{2}^{2} + \frac{i}{{n_{2}^{2}}}\left( {{{D}_{2}} - D_{2}^{2}} \right)$ $n_{2}^{2} > 0$; $i = 0{\kern 1pt} - {\kern 1pt} n_{2}^{2}$ |
| $S_{0}^{i} = S_{1}^{'}({{D}^{i}}) - \frac{{{{k}_{M}}}}{{{{D}^{i}} + {{k}_{M}}}}{{M}_{0}}$ $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) |
$S_{0}^{i} = S_{1}^{'}({{D}^{i}}) - \frac{{{{k}_{M}}}}{{{{D}^{i}} + {{k}_{M}}}}{{M}_{0}}$ $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) |
$S_{0}^{i} = S_{2}^{'}({{D}^{i}}) - \frac{{{{k}_{M}}}}{{{{D}^{i}} + {{k}_{M}}}}{{M}_{0}}$ $S_{2}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) |
| Часть III | ||
| ${{M}_{0}}\left( {{{D}_{4}}} \right) < {{M}_{0}} < {{M}_{0}}\left( {{{D}_{1}}} \right)$ | ||
| $D_{3}^{1}$ и $D_{3}^{2}$ по решению $\frac{{D + {{k}_{M}}}}{{{{k}_{M}}}}S_{2}^{'}\left( D \right) - {{M}_{0}} = 0$, где $S_{2}^{'}\left( D \right)$ по (П.3); $D_{3}^{1} < {{D}_{4}}$, $D_{3}^{2} > {{D}_{4}}$ | ||
| Мн1**: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ | Мн1**: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ | Мн2**: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ |
| ${{D}^{i}} = {{D}_{1}} + \frac{i}{{n_{3}^{1}}}\left( {{{D}_{2}} - {{D}_{1}}} \right)$ $n_{3}^{1} > 0$; $i = 0{\kern 1pt} - {\kern 1pt} n_{3}^{1}$ |
${{D}^{i}} = {{D}_{1}} + \frac{i}{{n_{3}^{2}}}\left( {D_{3}^{1} - {{D}_{1}}} \right)$ $n_{3}^{2} > 0$; $i = 0{\kern 1pt} - {\kern 1pt} n_{3}^{2}$ |
${{D}^{i}} = D_{3}^{2} + \frac{i}{{n_{3}^{3}}}\left( {{{D}_{2}} - D_{3}^{2}} \right)$ $n_{3}^{3} > 0$; $i = 0{\kern 1pt} - {\kern 1pt} n_{3}^{3}$ |
| $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) | $S_{2}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) | $S_{2}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) |
| $S_{0}^{i} = S_{1}^{'}({{D}^{i}}) - \frac{{{{k}_{M}}}}{{{{D}^{i}} + {{k}_{M}}}}{{M}_{0}}$, где $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) | $S_{0}^{i} = S_{2}^{'}({{D}^{i}}) - \frac{{{{k}_{M}}}}{{{{D}^{i}} + {{k}_{M}}}}{{M}_{0}}$, где $S_{2}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) | $S_{0}^{i} = S_{2}^{'}({{D}^{i}}) - \frac{{{{k}_{M}}}}{{{{D}^{i}} + {{k}_{M}}}}{{M}_{0}}$, где $S_{2}^{'}\left( {{{D}^{i}}} \right)$ по (П.3) |
Часть II. Особенностью для части II является возможность формирования двух множеств Мн1* и Мн2* для одного и того же значения M0 по (23).
2.1. Для обоих множеств общим является вычисление $D_{2}^{1}$ и $D_{2}^{2}$.
Вычисляется $D_{2}^{1}$ (при S0 = 0) по уравнению
используя (П.3) и (П.2); M0 задано по (23). Получили $D_{2}^{1} < {{D}_{3}}$.
Вычисляется $D_{2}^{2}$ (при S0 = 0) по уравнению
используя (П.3) и (П.2); M0 задано по (23). Получили $D_{2}^{2} < {{D}_{4}}$.
Последовательность формирования множеств аналогична последовательности Мн1 части I (здесь не приводится). Результирующие формулы приведены в табл. 4 (часть II, Мн1* и Мн2*). Остальные показатели процесса вычисляются по (П.4) для каждого i.
Часть III. Особенностью части III является возможность формирования трех множеств Мн1**, Мн2** и Мн3** для одного и того же значения M0 по (24).
3.1. Для всех трех множеств общим является вычисление $D_{3}^{1}$ и $D_{3}^{2}$.
Вычисляются $D_{3}^{1}$ и $D_{3}^{2}$ (при S0 = 0) по уравнению
используя (П.3) и (П.2); M0 задано по (24). Получили $D_{3}^{1} < {{D}_{4}}$ и $D_{3}^{2} > {{D}_{4}}$.
Последовательность формирования множеств аналогична последовательности Мн1 части I (так же, как и для части II здесь не приводится). Результирующие формулы приведены в табл. 4 (часть III, Мн1**, Мн2** и Мн3**). Остальные показатели процесса вычисляются по (П.4) для каждого i.
Ниже приведены результаты числового расчета показателей технологического процесса, полученные по соотношениям табл. 4 с использованием формул (П.4) для констант табл. 1.
ЧИСЛЕННЫЙ РАСЧЕТ
Расчет выполнен для всех трех частей по формулам табл. 4 с указанием вида множества. В расчете использованы значения констант базового варианта (табл. 1) для системы (1), а также данные предварительного анализа.
На рис. 1 показан портрет зависимости M0 от D с ограничениями по их значениям для QP = 6.0 г/(л ч).
Рис. 1.
Портрет M0 от D при QP = 6.0 г/(л ч): 1–4 – положения особых точек; 5 – положение точки экстремума.
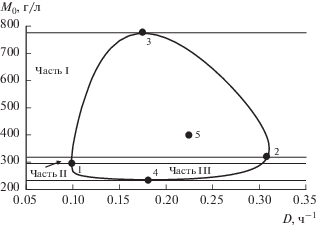
Портрет воспроизводит положение особых точек и точки экстремума. На портрете отмечены границы частей I, II и III в соответствии с (22)–(24).
Расчет по части I. В расчете использованы формулы табл. 4, часть I, множество Мн1.
1. Принимается значение M0 согласно (22), где M0(D2) = 349.16 г/л, M0(D3) = 773.1 г/л. Значение M0 принято равным 670 г/л.
2. Вычисляются значения $D_{1}^{1}$ и $D_{1}^{2}$. Для вычисления $D_{1}^{1}$ и $D_{1}^{2}$ значение $S_{1}^{'}\left( D \right)$ по (П.3). Получено $D_{1}^{1} = 0.13$ ч–1, $D_{1}^{2} = 0.241$ ч–1. Для вычисления ${{D}^{i}}$ принято значение n1 = 5.545, значения i = 0.0; 1.0; 2.0; 3.0; 4.0; 5.0; 5.545.
3. Вычисляются значения $S_{0}^{i}$, где $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3).
4. Результаты вычислений по пунктам 2 и 3 приведены в табл. 5.
Таблица 5.
Значения элементов множества Мн1
| i | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 5.545 |
| ${{D}^{i}}$ | 0.13 | 0.15 | 0.17 | 0.19 | 0.21 | 0.23 | 0.2409 |
| $S_{1}^{'}\left( {{{D}^{i}}} \right)$ | 142.13 | 141.16 | 131.89 | 119.37 | 105.82 | 92.24 | 85.00 |
| $S_{0}^{i}\left( {{{D}^{i}}} \right)$ | 0.0 | 14.4 | 17.5 | 15.15 | 10.1 | 3.75 | 0.0 |
Таким образом, для M0 = 670 г/л получили множество Мн1 из семи пар значений $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$. Количество пар может быть иным в зависимости от заданных значений i по условию i = 0 – n1 и заданных значений n1. В данном случае пользователь может сделать выбор из семи вариантов. Остальные показатели процесса для каждого из вариантов вычисляются по (П.4).
Так, если принят вариант для i = 2.0, технологические показатели по (П.4) будут следующими: S0 = 17.5 г/л; M0 = 670 г/л; D = 0.17 ч–1; P = 35.29 г/л; X = 15.22 г/л; S = 93.82 г/л; M = 555.61 г/л; B = = 17.637 г/л.
Расчет по части I завершен.
Расчет по части II. Как уже отмечалось ранее (табл. 4), в части II формируются два множества Мн1* и Мн2*. В расчете использованы формулы табл. 4 для Мн1* и Мн2* соответственно. Общим для обоих множеств являются пункты 1 и 2.
1. Принимается значение M0 согласно (23), где M0(D1) = 295.28 г/л, M0(D2) = 349.16 г/л. Значение M0 принято равным 321.2 г/л.
2. Вычисляется значение $D_{2}^{1}$, где ${{S'}_{1}}\left( D \right)$ по (П.3). Получено $D_{2}^{1} = 0.09865$ ч–1. Вычисляется значение $D_{2}^{2}$, где $S_{2}^{'}\left( D \right)$ по (П.3). Получено $D_{2}^{2} = 0.3091$ ч–1.
Для множества Мн1*
3. Вычисляются значения ${{D}^{i}}$ и $S_{0}^{i}$. Для вычисления ${{D}^{i}}$ принято значение $n_{2}^{1} = 10.0625$; значения i приведены в табл. 6.
Для вычисления $S_{0}^{i}$ значения $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3).
4. Результаты вычислений по пунктам 2 и 3 приведены в табл. 6.
Таким образом, для M0 = 321.2 г/л получили множество Мн1* значений $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$. Количество пар может быть иным в зависимости от заданных значений i по условию $i = 0.0{\kern 1pt} - {\kern 1pt} n_{2}^{1}$ и заданных значений $n_{2}^{1}$. Остальные показатели процесса для каждого из вариантов вычисляются по (П.4).
Для множества Мн2*
3а. Вычисляются значения ${{D}^{i}}$ и $S_{0}^{i}$. Для вычисления ${{D}^{i}}$ принято значение $n_{2}^{2} = 1.6$; значения i приведены в табл. 6.
Таблица 6.
К формированию множеств Мн1* и Мн2*
| Мн1* | i | 0.0 | 0.5675 | 1.0675 | … | 10.5225 | 10.5425 | 10.5625 | 10.5825 | 10.6025 |
| ${{D}^{i}}$ | 0.09865 | 0.11 | 0.12 | … | 0.3091 | 0.3095 | 0.3099 | 0.3103 | 0.3107 | |
| $S_{1}^{'}\left( {{{D}^{i}}} \right)$ | 84.092 | 122.03 | 136.14 | … | 38.937 | 38.408 | 37.807 | 37.069 | 35.35 | |
| $S_{0}^{i}$ | 0.0 | 44.55 | 63.63 | … | 6.266 | 5.80 | 5.212 | 4.512 | 2.83 | |
| Мн2* | i | 0.0 | 0.4 | 0.8 | 1.2 | 1.6 | ||||
| ${{D}^{i}}$ | 0.3091 | 0.3095 | 0.3099 | 0.3103 | 0.3107 | |||||
| $S_{2}^{'}\left( {{{D}^{i}}} \right)$ | 32.688 | 32.973 | 33.35 | 33.863 | 35.35 | |||||
| $S_{0}^{i}$ | 0.0 | 0.34 | 0.755 | 1.308 | 2.831 |
Для вычисления $S_{0}^{i}$ значения $S_{2}^{'}\left( {{{D}^{i}}} \right)$ по (П.3).
4а. Результаты вычислений по п. 3а приведены в табл. 6.
Таким образом, для M0 = 321.2 г/л получили множество Мн2* значений $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$. Количество пар может быть иным в зависимости от заданных значений i по условию $i = 0.0{\kern 1pt} - {\kern 1pt} n_{2}^{2}$ и заданных значений $n_{2}^{2}$. Остальные показатели процесса для каждого из вариантов вычисляются по (П.4).
Следует отметить, что значения i для Мн1* и Мн2* выбирались таким образом, чтобы последние пять значений ${{D}^{i}}$ для Мн1* были такими же, как пять значений для Мн2*. Это позволяет сравнивать решения по показателям процесса для одинакового значения M0 и ${{D}^{i}}$.
Расчет по части III. Как уже отмечалось ранее (табл. 4), в части III формируются три множества Мн1**, Мн2**, Мн3**. В расчете использовались формулы табл. 4 для Мн1**, Мн2** и Мн3**. Общими для всех множеств являются пункты 1 и 2.
1. Принимается значение M0 согласно (24), где M0(D4) = 234.96 г/л, M0(D1) = 295.28 г/л. Значение M0 принято равным 239.0 г/л.
2. Вычисляется значение $D_{3}^{1}$ и $D_{3}^{2}$ где ${{S'}_{2}}\left( D \right)$ по (П.3). Получено $D_{3}^{1} = 0.1387$ ч–1; $D_{3}^{2} = 0.2285$ ч–1.
Для множества Мн1**
Для множества Мн1** область значений D от D1 = 0.09818 ч–1 до D2 = 0.3107 ч–1; значение $S_{1}^{'}$ вычисляется по (П.3).
3. Вычисляются значения ${{D}^{i}}$и $S_{0}^{i}$. Для вычисления ${{D}^{i}}$ принято значение $n_{3}^{1} = 10.6$; значения i приведены в табл. 7.
Таблица 7.
Результаты вычисления элементов множеств Мн1**, Мн2**, Мн3**
| Мн1** | Мн2** | ||||
|---|---|---|---|---|---|
| i | ${{D}^{i}}$ | $S_{1}^{'}$ | $S_{0}^{i}$ | $S_{2}^{'}$ | $S_{0}^{i}$ |
| 0.0 | 0.09818 | 77.6 | 14.79 | 77.6 | 14.79 |
| 0.506 | 0.1083 | 118.43 | 60.06 | 61.342 | 2.968 |
| 1.011 | 0.1184 | 134.54 | 80.01 | 55.906 | 1.375 |
| 1.521 | 0.1286 | 141.64 | 90.51 | 51.64 | 0.509 |
| 2.026 | 0.1387 | 143.26 | 95.11 | 48.16 | 0.0 |
| 4.091 | 0.18 | 125.85 | 86.94 | ||
| Мн3** | |||||
| $S_{2}^{'}$ | $S_{0}^{i}$ | ||||
| 6.516 | 0.2285 | 93.252 | 61.506 | 31.745 | 0.0 |
| 7.541 | 0.249 | 79.683 | 50.228 | 30.112 | 0.658 |
| 8.571 | 0.2696 | 66.497 | 39.035 | 29.147 | 1.684 |
| 9.596 | 0.2901 | 53.534 | 27.809 | 29.19 | 3.46 |
| 10.6 | 0.3107 | 35.35 | 11.15 | 35.35 | 11.15 |
Для вычисления $S_{0}^{i}$ значения $S_{1}^{'}\left( {{{D}^{i}}} \right)$ по (П.3).
4. Результаты вычислений по пп. 2 и 3 приведены в табл. 7.
Таким образом, для M0 = 239.0 г/л получено множество Мн1** значений $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$. Количество пар может быть иным в зависимости от заданных значений i по условию $i = 0.0{\kern 1pt} - {\kern 1pt} n_{3}^{1}$ и заданных значений $n_{3}^{1}$. Остальные показатели процесса для каждого из вариантов вычисляются по (П.4).
Пояснение. Из табл. 7 видно, что область значений ${{D}^{i}}$ для Мн1** ограничена значениями D от D1 = 0.09818 ч–1 до D2 = 0.3107 ч–1. В целом выбор $n_{3}^{1}$ и значений $i = 0.0{\kern 1pt} - {\kern 1pt} n_{3}^{1}$ является произвольным, в данном расчете он не является случайным. Так, первые пять значений ${{D}^{i}}$ в табл. 7 подобраны так, чтобы покрыть область значений D для множества Мн2**, последние пять – чтобы покрыть область значений D для множества Мн3**.
| Для множества Мн2** | Для множества Мн3** |
| Область значений D от
D1 = 0.09818 ч–1 до $D_{3}^{1} = 0.1387$ ч–1. Значения ${{D}^{i}}$ принимались равными ${{D}^{i}}$ в первых пяти вариантах для множества Мн1** (табл. 8). Значения $S_{0}^{i}$ вычислялись по формуле табл. 4, где ${{S'}_{2}}\left( {{{D}^{i}}} \right)$ по (П.3). Результаты расчетов приведены в табл. 8. Таким образом, сформировано множество Мн2**: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ для M0 = 239.0 г/л. |
Область значений D от $D_{3}^{2} = 0.2285$ ч–1 до 0.3107 ч–1. Значения ${{D}^{i}}$ принимались равными ${{D}^{i}}$ в последних пяти вариантах для множества Мн1** (табл. 8). Значения $S_{0}^{i}$ вычислялись по формуле табл. 4, где ${{S'}_{2}}\left( {{{D}^{i}}} \right)$ по (П.3). Результаты расчетов приведены в табл. 8. Таким образом, сформировано множество Мн3**: $\left\{ {S_{0}^{i},\;{{D}^{i}}} \right\}$ для M0 = 239.0 г/л. |
ЗАКЛЮЧЕНИЕ
В заключении приведены для сравнения результаты рассчитанных показателей процесса по двум множествам части II для одинаковых исходных условий и для трех множеств части III. По части I множество единственное. Расчеты выполнялись с использованием соотношений (П.4).
По части II в табл. 8 приведены расчеты показателей множеств Мн1* и Мн2* для начальных условий M0 = 321.2 г/л и ${{D}^{i}} = 0.3099$ ч–1. Значение ${{D}^{i}}$ использовалось по табл. 6. Выбор начальных условий производился произвольно.
Таблица 8.
Технологические показатели по Мн1* и Мн2* для начальных условий M0 = 321.2 г/л и Di = 0.3099 ч–1
| Множество | M0, г/л | Di, ч–1 | P, г/л | X, г/л | M, г/л | B, г/л | S0, г/л | S, г/л |
|---|---|---|---|---|---|---|---|---|
| Мн1* | 321.2 | 0.3099 | 19.36 | 4.55 | 288.6 | 9.68 | 5.23 | 16.45 |
| Мн2* | 321.2 | 0.3099 | 19.36 | 4.55 | 288.6 | 9.68 | 0.755 | 11.975 |
Фактическое различие в показателях процесса отмечается только по значениям S0 и S.
По части III приведены две таблицы (табл. 9 и 10). В табл. 9 сравнивались данные множеств Мн1** и Мн2**, в табл. 10 – данные множеств Мн1** и Мн3**.
Таблица 9.
Технологические показатели для Мн1** и Мн2** для начальных условий M0 = 239 г/л и Di= 0.1286 ч–1
| Множество | M0, г/л | D, ч–1 | P, г/л | X, г/л | M, г/л | B, г/л | S0, г/л | S, г/л |
|---|---|---|---|---|---|---|---|---|
| Мн1** | 239.0 | 0.1286 | 46.656 | 19.807 | 187.87 | 23.328 | 90.51 | 92.122 |
| Мн2** | 239.0 | 0.1286 | 46.656 | 19.807 | 187.87 | 23.328 | 0.509 | 2.121 |
Таблица 10.
Технологические показатели для Мн1** и Мн3** для начальных условий M0 = 239 г/л и Di = 0.2696 ч–1
| Множество | M0, г/л | D, ч–1 | P, г/л | X, г/л | M, г/л | B, г/л | S0, г/л | S, г/л |
| Мн1** | 239.0 | 0.2696 | 22.255 | 9.786 | 211.537 | 1.127 | 39.034 | 42.031 |
| Мн2** | 239.0 | 0.2696 | 22.255 | 9.786 | 211.537 | 1.127 | 1.684 | 4.681 |
Начальные условия для обеих таблиц принимались по данным табл. 7. Значения начальных условий приведены в заглавии таблиц.
Для части III (табл. 9 и 10) различие в технологических показателях для множеств Мн1** и Мн2** и для множеств Мн1** и Мн3** наблюдается также только в двух позициях: S0 и S. Остальные позиции полностью совпадают.
Настоящая публикация завершает теоретический анализ оценки множественности стационарных состояний технологического процесса ферментативного получения молочной кислоты. Получены все расчетные соотношения для оценки показателей множественности по заданной концентрации компонента сырья, воспроизводящего основной субстрат.
Таким образом, созданы предпосылки для практической разработки технологических процессов, ориентированных на обеспечение требуемой продуктивности по основному продукту – молочной кислоте. Разработанные соотношения послужат основой практической реализации технологии.
Исследование выполнено при финансовой поддержке РХТУ им. Д.И. Менделеева.
ПРИЛОЖЕНИЕ
(П.1)
$A\left( D \right) = {{\left( {1 - \frac{{{{Q}_{P}}}}{{{{X}_{{\max }}}\left( {\alpha D + \beta } \right)}}} \right)}^{{{{n}_{1}}}}}{{\left( {1 - \frac{{{{Q}_{P}}}}{{{{P}_{{\max }}}D}}} \right)}^{{{{n}_{2}}}}}.$(П.3)
$\begin{gathered} S_{{1,2}}^{'} = \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{{{{Q}_{P}}}}{{\left( {\alpha D + \beta } \right)}} + \frac{{{{K}_{i}}}}{2}\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right] \pm \\ \pm \,\,\sqrt {{{{\left( {\frac{{{{K}_{i}}}}{2}} \right)}}^{2}}{{{\left[ {A\left( D \right)\frac{{{{\mu }_{{\max }}}}}{D} - 1} \right]}}^{2}} - {{K}_{m}}{{K}_{i}}} . \\ \end{gathered} $(П.4)
$\left\{ \begin{gathered} P = \frac{{{{Q}_{P}}}}{D};\,\,\,\,X = \frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}}; \hfill \\ B = \left( {{{\alpha }_{B}} + {{{{\beta }_{B}}} \mathord{\left/ {\vphantom {{{{\beta }_{B}}} D}} \right. \kern-0em} D}} \right)\frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}} \hfill \\ S = {{S}_{0}} + \frac{{{{k}_{M}}{{M}_{0}}}}{{D + {{k}_{M}}}} - \frac{1}{{{{Y}_{{{X \mathord{\left/ {\vphantom {X S}} \right. \kern-0em} S}}}}}}\frac{P}{{\alpha + {\beta \mathord{\left/ {\vphantom {\beta D}} \right. \kern-0em} D}}};\,\,\,M = \frac{{D{{M}_{0}}}}{{D + {{k}_{M}}}}. \hfill \\ \end{gathered} \right.$ОБОЗНАЧЕНИЯ
| B | концентрация суммарного количества побочных продуктов, г/л |
| D | величина протока, ч–1 |
| Ki | константа ингибирования, г/л |
| Km | константа насыщения субстрата, г/л |
| kM | константа, определяющая количество воспроизведенного субстрата, ч–1 |
| M | концентрация сырья, дополнительно воспроизводящего субстрат, г/л |
| P | концентрация продукта, г/л |
| QP | продуктивность, г/(л ч) |
| S | концентрация субстрата, г/л |
| X | концентрация биомассы, г/л |
| YX/S | стехиометрический коэффициент, г/г |
| α, αB, β, βB | константы |
| µ | удельная скорость роста микроорганизмов, ч–1 |
ИНДЕКСЫ
Список литературы
Hofvendahl K., Hahn-Hägerdal B. Factors affecting the fermentative lactic acid production from renewable resources // Enzyme Microb. Technol. 2000. V. 26. P. 87.
Gonzalez K., Tebbani S., Lopes F., Thorigné A., Givry S., Dumur D., Pareau D. Modeling the continuous lactic acid production process from wheat flour // Appl. Microbiol. Biotechnol. 2016. V. 100. № 1. P. 147.
Åkerberg C., Hofvendahl K., Zacchi G., Hahn-Hӓgerdal B. Modelling the influence of pH, temperature, glucose and lactic acid concentrations on the kinetics of lactic acid production by Lactococcus lactis ssp. lactis ATCC 19435 in whole-wheat flour // Appl. Microbiol. Biotechnol. 1998. V. 49. № 6. P. 682.
Gordeeva Yu.L., Borodkin A.G., Gordeeva E.L. Estimating the Technological Characteristics of Lactic Acid Production by Continuous Fermentation: Optimal Conditions // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 216. [Гордеева Ю.Л., Бородкин А.Г., Гордеева Е.Л. Технологические показатели непрерывного процесса ферментативного получения молочной кислоты. Оптимальные условия // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 91.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


