Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 663-667
Оценка величины коэффициента разделения изотопов кислорода в водных солевых растворах
В. С. Покальчук a, Э. П. Магомедбеков a, *, И. Л. Растунова a, А. Ю. Чеботов a, Н. Н. Кулов b
a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
b Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: eldar@muctr.ru
Поступила в редакцию 24.07.2020
После доработки 27.07.2020
Принята к публикации 27.07.2020
Аннотация
Рассмотрена теоретическая возможность определения коэффициентов разделения изотопов кислорода для систем, содержащих гидратированные галоген-ионы и катионы металлов. Получена зависимость коэффициента разделения от температуры для водных систем, содержащих молекулы карбамида. Обнаружено, что вклад катионов и анионов в разделение изотопов кислорода присутствует, но характеризуется малыми значениями.
ВВЕДЕНИЕ
Физико-химические методы разделения изотопов основаны на различии свойств, которые вносят свой вклад в нулевые колебания атомов, молекул в кристаллических решетках и жидких телах. Теоретическая возможность оценки константы равновесия реакции изотопного обмена была сформулирована в 1940-х годах и описана в работах Юри [1] и Бегеляйзена и Майер [2] и с тех пор успешно применяется.
В последние годы, с увеличением доступной вычислительной мощности, различные методы вычислительной химии стали инструментом для теоретического определения коэффициента разделения. Основной интерес в использовании квантово-статистических методов представляет изучение ионной гидратации в растворах для описания данных, полученных экспериментальным путем, а также для возможности математического описания процесса разделения изотопов кислорода в водных растворах электролитов.
Целью данной работы является оценка теоретических значений коэффициентов разделения изотопов кислорода в водно-солевых растворах с использованием методов квантовой химии и статистической термодинамики.
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
Значения энергий и частот колебаний молекул ϲ использованием квантово-статистических методов могут быть получены только для структур, которые соответствуют минимальным энергетическим состояниям молекул. Кроме того, расчет коэффициентов разделения для реакций обмена изотопов требует знания симметрии участвующих в процессе молекул. Таким образом, обычно на первом этапе расчета осуществляется оптимизация геометрии молекул.
Для получения оптимальной геометрии молекул, расчета энергии и колебательных частот используют теорию функционала плотности (DFT). DFT – метод, позволяющий рассчитать силовое поле молекул, который использует теоретический подход, отличный от традиционных методов ab initio, и имеющий преимущества в том, что он при гораздо меньших вычислительных затратах позволяет получить оптимальную геометрию практически любых молекул. По методу DFT молекулярные свойства описываются с помощью функции электронной плотности систем.
Известно, что простая форма приближения локальной плотности, используемая в DFT-методах для оптимизации молекул, имеет довольно ограниченную точность. Этот недостаток можно исправить с помощью более сложных функционалов, описанных в работах [3–6].
Для гидратированных комплексов катионов и анионов был выбран гибридный функционал PBE0 с тройным зета-базисным набором, параметризованный для прецизионных расчетов термохимии молекул и нековалентных взаимодействий.
Для молекулы карбамида использовался гибридный функционал BP86 c дисперсной коррекцией D3, предназначенный для органических молекул.
Из полученных теоретических значений собственных колебаний были рассчитаны приведенные отношения функции распределения для замещения 18O/16O в гидратных комплексах.
Как показали предварительные расчеты, при окружении катиона пятью и шестью молекулами воды результатом оптимизации являются объемные структуры с правильным расположением вокруг него атомов кислорода. Аналогично для гидратированного аниона при оптимизации геометрии были получены правильные геометрические структуры с координационным числом, равным 6.
Для расчета частоты колебаний для гидратированных ионов были выбраны наиболее стабильные структуры (исходя из энергий Гиббса, полученных в результате расчета). Были рассчитаны частоты колебаний для аналогичных гидратированных ионов, где атомы кислорода-16 были замещены на атомы кислорода-18. При расчете сумм по состояниям и их соотношений было обнаружено, что колебания молекул воды относительно катиона и аниона вносят вклад в эти значения.
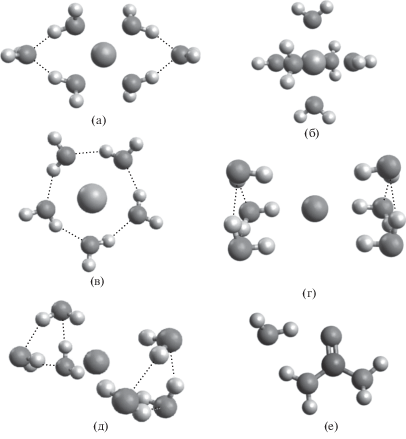
Оптимизированная геометрия катиона калия, окруженного шестью молекулами воды, имеет моноклинную симметрию (рис. 1а). Геометрия молекулы катиона магния, окруженного шестью молекулами воды, представлена на рис. 1б. Атомы кислорода расположены в идеальной октаэдрической симметрии. Оптимизированный гидратированный комплекс натрия имеет пентагональную плоскую молекулярную геометрию (рис. 1в). Полученные оптимизированные геометрии для гидратированных комплексов анионов хлора, брома и молекулы карбамида представлены на рис. 1г–1е. Рассчитать теоретически возможные коэффициенты разделения реакции изотопного обмена можно исходя из представлений о строении веществ, зная колебательные составляющие этих молекул. Поступательные и вращательные суммы по состояниям можно не включать в расчет, так как в жидкости соответствующие виды движений приобретают характер межмолекулярных колебаний с низкими частотами, практически не дающими вклада в коэффициент разделения.
Рис. 1.
(а) – кластер K+·6[Н2О]; (б) – кластер Mg+2 ⋅ 6[Н2О]; (в) – кластер Na+ ⋅ 5[Н2О]; (г) – кластер Cl–·6[Н2О]; (д) – кластер Br– ⋅ 6[Н2О]; (е) – кластер CH4N2O. Пунктирными линиями обозначены водородные связи.
Для реакции химического изотопного обмена
(1)
$m{{{\text{A}}}_{n}}{\text{X}} + n{{{\text{B}}}_{m}}{\text{Y}} \leftrightarrow m{{{\text{B}}}_{n}}{\text{X}} + n{{{\text{A}}}_{m}}{\text{Y}}$уравнение для расчета αcalc с использованием сумм по состояниям будет выглядеть следующим образом [7]:
(2)
${\text{ }}{{\alpha }_{{{\text{calc}}}}} = \frac{{\prod\limits_{i = 1} {{{{\left[ {\left[ {\frac{{{{U}_{{i,{{B}_{n}}X}}}}}{{{{U}_{{i,{{A}_{n}}X}}}}}\frac{{\left( {1 - \exp \left( { - {{U}_{{i,{{A}_{n}}X}}}} \right)} \right)}}{{\left( {1 - \exp \left( { - {{U}_{{i,{{B}_{n}}X}}}} \right)} \right)}}} \right.} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0em} m}}}}\exp \left[ { - {1 \mathord{\left/ {\vphantom {1 {2m\sum\limits_{i = 1} {({{U}_{{i,{{B}_{n}}X}}} - {{U}_{{i,{{A}_{n}}X}}})} }}} \right. \kern-0em} {2m\sum\limits_{i = 1} {({{U}_{{i,{{B}_{n}}X}}} - {{U}_{{i,{{A}_{n}}X}}})} }}} \right]} }}{{\prod\limits_{i = 1} {{{{\left[ {\frac{{U{}_{{i,B_{m}^{{}}Y}}}}{{{{U}_{{i,{{A}_{m}}Y}}}}}\frac{{(1 - \exp ( - {{U}_{{{{A}_{m}}Y}}}))}}{{(1 - \exp ( - {{U}_{{{{B}_{m}}Y}}}))}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}}\exp \left[ { - {1 \mathord{\left/ {\vphantom {1 {2n\sum\limits_{i = 1} {({{U}_{{i,{{B}_{m}}Y}}} - {{U}_{{i,{{A}_{m}}Y}}})} }}} \right. \kern-0em} {2n\sum\limits_{i = 1} {({{U}_{{i,{{B}_{m}}Y}}} - {{U}_{{i,{{A}_{m}}Y}}})} }}} \right]} }}.$Здесь Ui = hcωi/kT – частотная составляющая нормальных колебаний в молекулах веществ уравнения (1). Для упрощения записи числитель и знаменатель уравнения (2) записывается через отношение β-факторов [2]:
При этом будет получен коэффициент разделения для реакции обмена изотопов кислорода между молекулами свободной воды и водой, связанной с катионами
(3)
$\begin{gathered} {\text{K}}{{{\text{a}}}^{ + }}n\left[ {{{{\text{Н}}}_{{\text{2}}}}{{{\text{О}}}^{{16}}}} \right] + n{{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}^{{18}}} \leftrightarrow \\ \leftrightarrow \,\,{\text{K}}{{{\text{a}}}^{ + }}n\left[ {{{{\text{Н}}}_{{\text{2}}}}{{{\text{О}}}^{{18}}}} \right] + n{{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}^{{16}}} \\ \end{gathered} $и анионами
(4)
$\begin{gathered} {\text{A}}{{{\text{n}}}^{ - }}n\left[ {{{{\text{Н}}}_{{\text{2}}}}{{{\text{О}}}^{{{\text{16}}}}}} \right] + n{{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}^{{18}}} \leftrightarrow \\ \leftrightarrow \,\,{\text{A}}{{{\text{n}}}^{{ - ~}}}n\left[ {{{{\text{Н}}}_{{\text{2}}}}{{{\text{О}}}^{{{\text{18}}}}}} \right] + n{{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}^{{16}}}. \\ \end{gathered} $Для системы, содержащей молекулу карбамида, изотопный обмен будет протекать по реакции
(5)
${\text{С}}{{{\text{H}}}_{{\text{4}}}}{{{\text{N}}}_{{\text{2}}}}{{{\text{O}}}^{{{\text{16}}}}} + {{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}^{{{\text{18}}}}} \leftrightarrow {\text{С}}{{{\text{H}}}_{{\text{4}}}}{{{\text{N}}}_{{\text{2}}}}{{{\text{O}}}^{{18}}} + {{{\text{H}}}_{{\text{2}}}}{{{\text{O}}}^{{{\text{16}}}}}.$РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
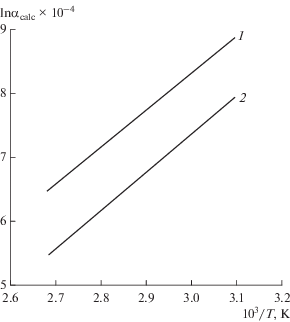
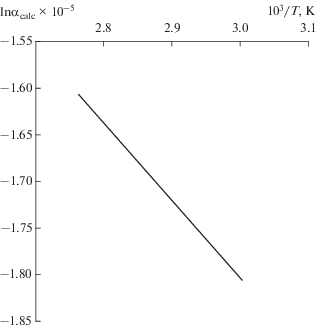
Результаты расчетов коэффициента разделения для реакции обмена изотопов кислорода между отдельными ионами и водой для удобства представлены на графиках (рис. 2, 3).
Рис. 2.
Зависимость коэффициента разделения от обратной температуры для катионов: 1 – K+, 2 – Mg2+, 3 – Na+.
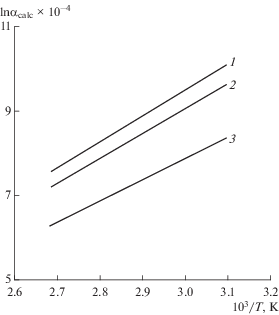
Исходя из полученных результатов, можно сделать вывод о том, что увеличение коэффициента разделения для изотопов кислорода в ряду катионов и анионов может быть связано с увеличением значения энергии гидратации. Зависимость коэффициента разделения от ионного радиуса можно наблюдать только для однотипных ионов. Поэтому можно рассматривать только катионы натрия и калия и анионы хлора и брома. Из графиков (рис. 2 и 3) видно, что с увеличением ионного радиуса (например, для Na+ = 0.98, K+ = 1.33) возрастает и коэффициент разделения. При этом авторы [8] приходят к заключению, что с увеличением порядкового номера разделяющие свойства ионов возрастают, что полностью согласуется с нашими расчетами.
Расчет коэффициента разделения в молекуле карбамида принимает значение αcalc, близкое к 1 (рис. 4), что подтверждается данными эксперимента [9]. При этом известно, что молекула карбамида в воде образует сложные структуры [10], в которых наблюдается высокое значение коэффициентов разделения изотопов водорода [11].
ЗАКЛЮЧЕНИЕ
Конкретный вклад разделяющих агентов в процессе солевой ректификации сложно определить экспериментально, но метод квантовой химии и статистической термодинамики позволяет его оценить с помощью описанной модели.
Рассчитанные коэффициенты разделения для реакций обмена изотопов кислорода между молекулами воды и гидратированными ионами принимают значение выше 1. Это говорит о том, что во всех рассмотренных в настоящей работе реакциях замещения происходит смещение изотопного равновесия в сторону образования форм, содержащих тяжелый изотоп. Наибольшим изотопным эффектом обладает гидратированный анион брома, для катионов наибольшее значение характерно для катиона калия.
При этом для молекулы карбамида подобного эффекта не наблюдается, что не отрицает возможность получения высоких разделительных эффектов для изотопов водорода. Представленные данные согласуются с литературными источниками, что говорит о возможности использования данного метода для изучения процессов ионной гидратации и прогнозирования коэффициентов изотопного разделения для различных солевых агентов.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-13-00475).
ОБОЗНАЧЕНИЯ
| с | скорость света |
| h | постоянная Планка |
| k | постоянная Больцмана |
| T | температура, K |
| Ui | суммы по состояниям для молекул уравнения (1) |
| α | коэффициент разделения изотопов |
| ωi | расчетное значение частоты нормального колебания, см–1 |
ИНДЕКСЫ
Список литературы
Urey H.C. The thermodynamic properties of isotopic substances // J. Chem. Soc. 1947. P. 562.
Bigeleisen J., Mayer M.G. Calculation of equilibrium constants for isotopic exchange reactions // J. Chem. Phys. 1947. V. 15. № 5. P. 261.
Grimme S. et al. Consistent structures and interactions by density functional theory with small atomic orbital basis sets // J. Chem. Phys. 2015. V. 143. № 5. P. 054107.
Weigend F., Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy // Phys. Chem. Chem. Phys. 2005. V. 7. № 18. P. 3297.
Neese F. et al. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A “chain-of-spheres” algorithm for the Hartree–Fock exchange // Chem. Phys. 2009. V. 356. № 1–3. P. 98.
Weigend F. Accurate Coulomb-fitting basis sets for H to Rn // Phys. Chem. Chem. Phys. 2006. V. 8. № 9. P. 1057.
Андреев Б.М., Зельвенский Я.Д., Катальников С.Г. Разделение стабильных изотопов физико-химическими методами. М.: Энергоатомиздат, 1982.
Ципарис Й.Н., Добросердов Л.Л., Коган В.Б. Солевая ректификация. Л.: Химия, 1969.
Kakiuchi M., Matsuo S. Fractionation of hydrogen and oxygen isotopes between hydrated and free water molecules in aqueous urea solution // J. Phys. Chem. 1985. V. 89. № 21. P. 4627.
Boek E.S., Briels W.J. Molecular dynamics simulations of aqueous urea solutions: Study of dimer stability and solution structure, and calculation of the total nitrogen radial distribution function GN (r) // J. Chem. Phys. 1993. V. 98. № 2. P. 1422.
Кулов Н.Н., Полковниченко А.В., Лупачев Е.В., Вошкин А.А., Магомедбеков Э.П. Распределение изотопов водорода между фазами при парожидкостном равновесии водных солевых растворов // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 3.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии