Теоретические основы химической технологии, 2020, T. 54, № 6, стр. 768-774
Размер частиц наполнителя, упаковка и составы наполненных полимерных композитов с разным типом структуры и свойствами
И. Д. Симонов-Емельянов a, К. И. Харламова a, *
a МИРЭА – Российский технологический университет (Институт тонких химических технологий
им. М.В. Ломоносова)
Москва, Россия
* E-mail: kseenka.kh@gmail.com
Поступила в редакцию 27.04.2020
После доработки 18.05.2020
Принята к публикации 18.06.2020
Аннотация
Рассматриваются вопросы влияния размера частиц твердых наполнителей на плотность упаковки и максимальную долю наполнителя (φm) в дисперсно-наполненных полимерных композиционных материалах. Приводится зависимость параметра φm от диаметра твердых частиц наполнителей. Показано, что для крупных частиц (более 50 мкм) φm в дисперсно-наполненных полимерных композиционных материалах может достигать ~0.64 об. д., а для наночастиц (1–100 нм) не более ~0.255 об. д. Для деформирующихся под давлением и газообразных частиц, а также для плотных составов наполнителей значение параметра φm в дисперсно-наполненных полимерных композиционных материалах может достигать ~0.90–0.94 об. д. Установлена связь размеров частиц с их упаковкой и обобщенным параметром дисперсной структуры Θ, что позволяет провести классификацию рассматриваемого типа материалов разным размером частиц по структурному принципу и установить их тип структурной организации (разбавленные, низконаполненные, средненаполненные, высоконаполненные и сверхвысоконаполненные системы), который определяет свойства композитов. Предложен алгоритм расчета содержания наполнителя и составов дисперсно-наполненных полимерных композиционных материалов с разными размерами частиц, природой и деформируемостью частиц для проектирования различных типов структур композитов, технологических и эксплуатационных свойств.
ВВЕДЕНИЕ
При создании дисперсно-наполненных полимерных композиционных материалов (ДНПКМ) с требуемым комплексом свойств широко используются дисперсные наполнители.
В качестве наполнителей для создания ДНПКМ можно применять практически все материалы, имеющиеся на земле, после придания им заданной формы, размера и структуры (металлы, керамики, полимеры, жидкости, газы и т.д.).
Порошкообразные дисперсные наполнители для ДНПКМ характеризуются разной природой, формой, размером, удельной поверхностью и пористостью частиц, а также комплексом физико-химических, механических, электрофизических и других специальных характеристик [1].
Введение дисперсных частиц в полимерные матицы позволяют получать полимерные композиты с разнообразными свойствами.
Полимерный композиционный материал (ПКМ) – это многокомпонентный гетерогенный гетерофазный монолитный материал, состоящий из двух и более компонентов (фаз), с непрерывной в объеме полимерной матрицей, имеющий границу раздела фаз, а также новую структуру и комплекс технологических и эксплуатационных свойств.
Природа исходных компонентов, состав, дисперсная структура и ее параметры определяют технологические и эксплуатационные свойства ДНПКМ.
В работе [2] приведена новая модель дисперсной структуры полимерных композитов, ее описание в терминах обобщенных параметров и показана связь с теорией построения решеток.
Классификация всех ДНПКМ по типам структур [разбавленные (РС), низконаполненные (ННС), средненаполненные (СНС; СНС-1 – до предела текучести, СНС-2 с пределом текучести), высоконаполненные (ВНС) и сверхвысоконаполненные системы (СВНС)] проведена по обобщенному параметру Θ, который учитывает упаковку, форму, размеры, содержание дисперсной фазы и функциональное построение полимерной матрицы (связующего) в ДНПКМ. Обобщенный параметр Θ определяет долю полимерной матрицы (связующего) для организации непрерывной прослойки между дисперсными частицами наполнителя в ДНПКМ.
Структурная организация ДНПКМ характеризуется присущим только ей комплексом технологических и эксплуатационных свойств.
В статье приводятся данные о размерах дисперсных частиц, их параметрах, упаковках, построении ДНПКМ разных типов структур, составов и их свойствах.
ЗАВИСИМОСТЬ ПАРАМЕТРА φm ДЛЯ ДИСПЕРСНЫХ НАПОЛНИТЕЛЕЙ С РАЗНЫМИ РАЗМЕРАМИ ЧАСТИЦ
Гетерогенность композиционных материалов определяется размерами включений и частиц наполнителей, а также размерами границы раздела фаз. По размеру частиц наполнители для ДНПКМ можно разделить на следующие: наночастицы (НЧ) размером 1–100 нм, ультрадисперсные частицы (УДЧ) размером 0.1–1.0 мкм, микрочастицы (МикЧ) размером 1.0–10 мкм, макрочастицы (МакЧ) размером 10–40 мкм и крупные частицы (КрЧ) размером более 50 мкм.
Упаковка дисперсных шарообразных частиц, согласно теории, не зависит от их размера и при кубической упаковке максимальное содержание наполнителя в композите должно составлять 0.64 об. д. Однако структура наполнителя, его поверхности, форма и размер частиц существенно влияют на параметры их упаковки – плотность упаковки (kp).
Уменьшение размера частиц от крупных до наночастиц реально сопровождается снижением плотности упаковки и максимальной доли дисперсного наполнителя в ДНПКМ с 0.64 до 0.05 об. д. Избыточная поверхностная энергия приводит к агломерации частиц малых размеров (менее ~10 мкм) с образованием рыхлых агломератов больших диаметров.
Для реальных наполнителей следует определять экспериментально их плотность упаковки kp и максимальную долю наполнителя φm в ДНПКМ, что необходимо при проектировании составов дисперсно-наполненных систем с заданным типом структуры. Собственно, от максимального содержания дисперсного наполнителя φm, можно рассчитать все возможные составы монолитных ДНПКМ с данным дисперсным наполнителем при условии φн ≤ φm, т.е. содержание наполнителя в материале меняется от φmin до φm.
Так, для крупных, любой формы частиц наполнителя с диаметром более 40–50 мкм параметр φm можно рассчитать по значениям истинной и насыпной плотности (по ГОСТ), так как такие наполнителя практически не слипаются и не образуют агломератов:
При уменьшении размера частиц дисперсной фазы менее ~10 мкм их избыточная энергия поверхности возрастает, и частицы слипаются, образуя новые структуры из агломератов. В этом случае методика определения параметров kp и φm по насыпной плотности некорректна.
Как показано в работе [3], для таких частиц используется методика с построением кривой уплотнения порошкообразных наполнителей разной природы, гранулометрического состава, формы, размера и состояния поверхности дисперсных частиц под давлением.
При создании реальных полимерных композитов для выбранных исходных компонентов – полимерная матрица (связующее) и дисперсный наполнитель, можно использовать методику по определению параметра φm по трем концентрациям (по пористости) или по поглощению жидкого масла или пластификатора наполнителем (ГОСТ) [3].
Ниже приведены усредненные значения параметра φm (об. д.) для твердых наполнителей с разными размерами частиц, которые хорошо согласуются с экспериментальными данными:
– наночастицы размером 1–100 нм φm ≈ 0.05–0.20 об. д.
– ультрадисперсные размером 0.1–1.0 мкм φm ≈ 0.20–0.255 об. д.
– микрочастицы размером 1.0–10 мкм φm ≈ ≈ 0.255–0.45 об. д.
– макрочастицы размером 10–40 мкм φm ≈ ≈ 0.45–0.62 об. д.
– крупные частицы размером более 50 мкм φm ≈ ≈ 0.62–0.64 об. д.
На рис. 1 представлена экспериментальная зависимость усредненных значений параметра φm для порошкообразных наполнителей от размера частиц. Приведены данные по значению параметра φm для крупных, макро- и микрочастиц, а также для ультрадисперсных и наночастиц.
Рис. 1.
Зависимость параметра φm для дисперсных наполнителей от диаметра твердых частиц. Пунктир – кривая, аппроксимированная выражением (1).
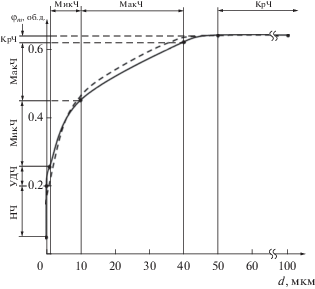
Таким образом, плотность упаковки частиц kp и максимальное содержание наполнителя φm в ДНПКМ зависят от размера частиц, что необходимо учитывать при создании ДНПКМ с заданным типом дисперсной структуры.
Экспериментальная зависимость φm = f(d) хорошо аппроксимируется выражением
При проектировании составов ДНПКМ следует учитывать, что максимальное содержание наполнителя в полимерном двухфазном композите не может превышать значение параметра φm в объемных долях (процентах). При условии, что φf > φm, в композиционном полимерном материале образуются поры, которые существенно снижают физико-механические характеристики, а материал нельзя называть монолитным.
Максимальное содержание наполнителя для наночастиц не может быть больше ~0.255 об. д., а для крупных частиц ~0.64 об. д.
Зависимость, представленная на рис. 1, является границей раздела при построении составов ДНПКМ с максимальной объемной долей наполнителя: под кривой – содержание наполнителя (φf), а над кривой – содержание полимерной матрицы (связующего), которое находят как φpol = 1 – φf.
Таким образом, если в полимер необходимо ввести большое количество твердого жесткого наполнителя, то следует выбирать наполнитель с крупными частицами.
Как показано в работах [1, 2, 4, 5], параметр φm зависит от природы, формы и деформируемости частиц под давлением:
– шарообразные твердые крупные частицы φm ≈ ≈ 0.60–0.64 об. д.
– короткие жесткие волокна (до 15 мм) φm ≈ ≈ 0.15–0.35 об. д.
– газообразные частицы φm ≈ 0.80–0.98 об. д.
– пластичные частицы (деформируются под давлением) φm ≈ 0.80–0.94 об. д.
Для увеличения параметра φm и содержания наполнителей в ДНПКМ проектируют специальные плотные составы, регулируя гранулометрический состав наполнителей. Плотные составы наполнителей, сконструированные по прерывистой гранулометрии, состоят из нескольких узких фракций, как правило, из 2–3 фракций наполнителя (наполнителей) с разными диаметрами частиц. Можно проектировать плотные составы наполнителей с непрерывной гранулометрией, используя специальную методику расчета [1].
Ниже приведены значения параметра φm (об. д.) для плотных составов наполнителей, построенных по принципу прерывистой гранулометрии:
– двухфракционные φm ≈ 0.868 об. д.
– трехфракционные φm ≈ 0.928 об. д.
– четырехфракционные φm ≈ 0.938 об. д.
Использование плотных составов приводит к увеличению содержания наполнителя на ~20–30 об. % по сравнению с наполнителями, состоящими из крупных частиц (φm ≈ 0.62–0.64 об. д.).
Таким образом, размер и форма частиц, гранулометрический состав (кривая распределения частиц по размерам) и деформируемость определяют упаковку дисперсных наполнителей и параметр φm.
Ключевой характеристикой для создания ДНПКМ является параметр φm, который определяет верхнюю границу составов и всю номенклатуру полимерных материалов с данным наполнителем. В этом случае можно проектировать составы ДНПКМ с содержанием наполнителя φf от φmin до φm.
Ниже представлены данные по составам и типам структур ДНПКМ с разными размерами частиц наполнителя и параметром φm.
ДНПКМ с крупными частицами. На рис. 2 приведена зависимость содержания дисперсного наполнителя с крупными частицами от обобщенного параметра Θ с указанием типа структуры ДНПКМ. По приведенной линейной зависимости φf = f(Θ) для крупных частиц с φm ≈ 0.64 об. д. проектируют составы ДНПКМ с разными типами дисперсной структуры (РС, ННС, СНС (СНС-1 и СНС-2), ВНС), в которых φf изменяется в пределах от φmin (РС) до φm ≈ 0.64 об. д. (ВНС).
Рис. 2.
Зависимость содержания наполнителя φf в ДНПКМ с разными типами структур от обобщенного параметра Θ для крупных частиц с параметром φm = = 0.64 об. д.
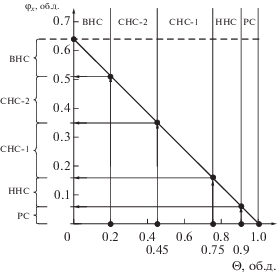
Задавая разное содержание наполнителя и рассчитывая обобщенный параметр Θ по известной формуле [2], можно проектировать разный тип структуры ДНПКМ и регулировать их свойства, или наоборот, при этом в области ВНС содержание наполнителя достигает ~0.50–0.64 об. д.
ДНПКМ с наночастицами. Для наночастиц с диаметром от 1 до 100 нм, которые образуют рыхлые агломераты достаточно сложной структуры, параметр φm, как правило, не превышает ~0.20–0.255 об. д. При расчете обобщенного параметра Θ для нанокомпозитов возникает проблема в определении доли полимера в граничном слое (М). Необходимо знать размеры (толщину) граничного слоя в конкретной системе и учитывать ее при расчетах.
На рис. 3 приведена зависимость φf = f(Θ) для нанокомпозитов. Как видно из представленных данных, для построения дисперсных наносистем с разными типами структур (РС, ННС, СНС (СНС-1 и СНС-2) и ВНС) практически требуется в ~2.5 раза меньше наполнителя по объему (об. д.), чем для крупных частиц.
Рис. 3.
Зависимость содержания нанонаполнителя φf в ДНПКМ с разными типами структур от обобщенного параметра Θ для наночастиц с параметром φm = = 0.255 об. д.
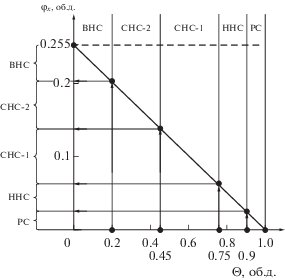
Так, для нанонаполнителей с высокой удельной поверхностью (более 100 м2/г) значение параметра φm, как правило, не превышает ~0.10 об. д. и тогда содержание наполнителей для построения, например, структуры СНС-1 не превышает 0.02–0.03 об. д.
В связи с этим вывод об эффективности малых количеств нанонаполнителей в полимерных нанокомпозитах не является принципиальным, а указывает на общность построения разных типов структур в дисперсных системах.
ДНПКМ с микро- и макрочастицами занимают промежуточное положение по содержанию φн между представленными зависимостями для крупных частиц и наночастиц.
ДНПКМ с деформирующимися частицами наполнителей. Особый интерес вызывает создание ДНПКМ с деформирующимися частицами наполнителей под давлением и плотными составами, у которых параметр φm в технологическом процессе получения и переработки под давлением может существенно меняться, возрастая до предельных значений ~0.90–0.94 об. д.
На рис. 4 представлена зависимость φf = f(Θ) для дисперсных систем с параметром φm → 0.90–0.94 об. д.
Рис. 4.
Зависимость содержания деформирующегося под давлением наполнителя φf в ДНПКМ с разными типами структур от обобщенного параметра Θ (φm = = 0.90 об. д.).
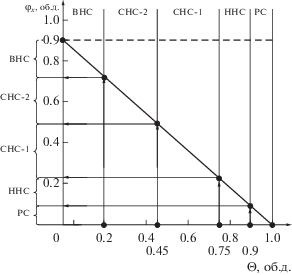
Для таких ДНПКМ при построении структур разных типов (РС, ННС, СНС (СНС-1 и СНС-2) и ВНС) количество наполнителя возрастает в ~1.5 раза по сравнению с крупными частицами. Дисперсные системы с высоким содержанием наполнителей всегда представляют повышенный интерес для потребителей.
Следует учитывать, что монолитные ДНПКМ можно получить при минимальном содержании полимерной матрицы ~0.06 об. д., после чего теряется сплошность материала.
АЛГОРИТМ РАСЧЕТА СОСТАВОВ ДИСПЕРСНЫХ СИСТЕМ С РАЗНЫМ ТИПОМ СТРУКТУР
Алгоритм расчета составов ДНПКМ и нанокомпозитов с разным типом структур для наполнителей различной природы, размеров и формы частиц, включая наночастицы, представлен ниже.
1. Экспериментально по известным методикам для дисперсного наполнителя определяют основные параметры: средний размер частиц (dav) или кривую распределения частиц по размерам, или удельную геометрическую поверхность (Sgeom), насыпную (ρpour) и истинную (ρtrue) плотность, пористость (П) и др.
2. Экспериментально по известным методикам для дисперсного наполнителя с известным средним размером частиц определяют параметр упаковки как φm = ρpour/ρtrue или по кривой уплотнения, или по трем концентрациям (по пористости) [4].
3. Рассчитывают для ДНПКМ значение обобщенного параметра Θ при известном значении параметра φm, задавая разное содержание наполнителя, при условии φf ≤ φm, по формуле
(2)
$\Theta {\text{ }} = {{({{\varphi }_{m}}--{{f}^{3}}{{\varphi }_{{\text{f}}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{m}}--{{f}^{3}}{{\varphi }_{{\text{f}}}})} {{{\varphi }_{{\text{m}}}}}}} \right. \kern-0em} {{{\varphi }_{{\text{m}}}}}},$При толщинах граничного слоя δ от 10 до 500 нм в ДНПКМ и для дисперсных частиц с диаметром более ~10 мкм для расчета обобщенного параметра Θ можно использовать упрощенную формулу
(3)
$\Theta = {{({{\varphi }_{{\text{m}}}}--{{\varphi }_{{\text{f}}}})} \mathord{\left/ {\vphantom {{({{\varphi }_{{\text{m}}}}--{{\varphi }_{{\text{f}}}})} {{{\varphi }_{m}}}}} \right. \kern-0em} {{{\varphi }_{m}}}}.$4. По значениям обобщенного параметра Θ определяют тип дисперсной структуры ДНПКМ согласно классификации: РС, ННС, СНС (СНС-1, СНС-2) и ВНС.
5. Находят содержание наполнителя φf для данного типа структуры ДНПКМ и проектируемого состава из формул (2) или (3) в объемных долях (процентах).
6. Проектируют состав ДНПКМ с заданным типом структуры, обобщенными параметрами и свойствами. По рассчитанному значению содержания наполнителя (φf) определяют объемную долю полимерной матрицы (φpol) как φpol = 1 – φf; при условии монолитности композита – φf + φpol = 1.
7. Для расчета навесок при приготовлении композиций ДНПКМ с известным объемным содержанием наполнителя и полимерной матрицы проводят пересчет объемных единиц в массовые согласно формуле
(4)
$\begin{gathered} {{\varphi }_{{{\text{mass}}{\text{.f}}{\text{.}}}}} = \\ = \,\,{{{{\varphi }_{{{\text{vol}}{\text{.f}}{\text{.}}}}}} \mathord{\left/ {\vphantom {{{{\varphi }_{{{\text{vol}}{\text{.f}}{\text{.}}}}}} {[{{\varphi }_{{{\text{vol}}{\text{.f}}}}}}}} \right. \kern-0em} {[{{\varphi }_{{{\text{vol}}{\text{.f}}}}}}}(1--{{{{\rho }_{{\text{p}}}}_{{{\text{ol}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{\text{p}}}}_{{{\text{ol}}}}} {{{\rho }_{{\text{f}}}})}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}})}} + {{{{\rho }_{{{\text{pol}}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{{\text{pol}}}}}} {{{\rho }_{{\text{f}}}}]}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}}]}},\,{\text{мас}}{\text{.д}}{\text{.}} \\ \end{gathered} $Можно решить и обратную задачу: при известном содержании дисперсного наполнителя в ДНПКМ (в объемных долях), его геометрических параметрах (d) и максимальной упаковке (φm) рассчитывают значение обобщенного параметра Θ и определяют тип дисперсной структуры композиционного материала (РС, ННС, СНС (СНС-1 и СНС-2) и ВНС). При этом содержание наполнителя в объемных долях (процентах) определяют по данным содержания наполнителя в массовых долях (процентах) в ДНПКМ по формуле
(5)
$\begin{gathered} {{\varphi }_{{{\text{vol}}{\text{.f}}{\text{.}}}}} = {{({{{{\rho }_{{{\text{pol}}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{{\text{pol}}}}}} {{{\rho }_{{\text{f}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}}}})} \mathord{\left/ {\vphantom {{({{{{\rho }_{{{\text{pol}}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{{\text{pol}}}}}} {{{\rho }_{{\text{f}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}}}})} {{\text{ }}[({1 \mathord{\left/ {\vphantom {1 {{{\varphi }_{{{\text{mass}}{\text{.f}}{\text{.}}}}}}}} \right. \kern-0em} {{{\varphi }_{{{\text{mass}}{\text{.f}}{\text{.}}}}}}}}}} \right. \kern-0em} {{\text{ }}[({1 \mathord{\left/ {\vphantom {1 {{{\varphi }_{{{\text{mass}}{\text{.f}}{\text{.}}}}}}}} \right. \kern-0em} {{{\varphi }_{{{\text{mass}}{\text{.f}}{\text{.}}}}}}}}}) + \\ + \,\,({{{{\rho }_{{{\text{pol}}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{{\text{pol}}}}}} {{{\rho }_{{\text{f}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}}}})--1],\,\,{\text{об}}{\text{.д}}{\text{.}} \\ \end{gathered} $В табл. 1 приведены значения содержания дисперсного наполнителя с различными размерами (d) и упаковкой частиц (φm) для создания разных типов структур ДНПКМ.
Таблица 1.
Тип структуры и содержание наполнителя в ДНПКМ для частиц разного размера при значениях параметра φm от 0.1 до 0.85 об. д.
| Тип структуры ДНПКМ | Обобщен-ный параметр Θ, об. д. |
Содержание наполнителя (φf, об. д.) для частиц разных размеров и значений параметра φm, об. д. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| НЧ | УДЧ | МикЧ | МакЧ | КрЧ | ||||||||
| 0.1 | 0.25 | 0.35 | 0.40 | 0.50 | 0.60 | 0.64 | 0.85 | |||||
| РС | 0.99–0.90 | 0.001–0.01 | 0.001–0.03 | 0.001–0.04 | 0.001–0.04 | 0.001–0.05 | 0.001–0.06 | 0.001–0.06 | 0.001–0.09 | |||
| ННС | 0.90–0.75 | 0.01–0.03 | 0.03–0.06 | 0.04–0.09 | 0.04–0.10 | 0.05–0.13 | 0.06–0.15 | 0.06–0.16 | 0.09–0.21 | |||
| СНС-1 | 0.75–0.45 | 0.03–0.06 | 0.06–0.14 | 0.09–0.19 | 0.10–0.22 | 0.13–0.28 | 0.15–0.33 | 0.16–0.35 | 0.21–0.47 | |||
| СНС-2 | 0.45–0.20 | 0.06–0.08 | 0.14–0.20 | 0.19–0.28 | 0.22–0.32 | 0.28–0.40 | 0.33–0.48 | 0.35–0.51 | 0.47–0.68 | |||
| ВНС | 0.20–0.00 | 0.08–0.10 | 0.20–0.25 | 0.28–0.35 | 0.32–0.40 | 0.40–0.50 | 0.48–0.60 | 0.51–0.64 | 0.68–0.85 | |||
Тип дисперсной структуры и ее параметры определяют поведение ДНПКМ как при переработке, так и эксплуатации, которые существенно зависят от размера и упаковки дисперсных частиц [2].
ВЛИЯНИЕ ОБОБЩЕННЫХ ПАРМЕТРОВ И ТИПА СТРУКТУРЫ НА СВОЙСТВА ДНПКМ
Влияние типа структуры, обобщенного параметра Θ и содержания дисперсного наполнителя с известными размерами частиц на свойства ДНПКМ можно проследить на примере зависимости относительной вязкости от обобщенного параметра Θ (рис. 5). В качестве примера приведены данные по вязкости для ДНПКМ на основе полиэтилена низкой плотности (ПЭНП) и стеклянных шариков марки ШСО-30 с диаметром частиц ~30 мкм и параметром φm ≈ 0.50 об. д.
Рис. 5.
Зависимость относительной вязкости при 220°С ДНПКМ на основе ПЭНП от объемной доли стеклянных шариков марки ШСО-30 (а) и от обобщенного параметра Θ (б): 1 – экспериментальная зависимость; 2 – расчет вязкости по уравнению Муни.
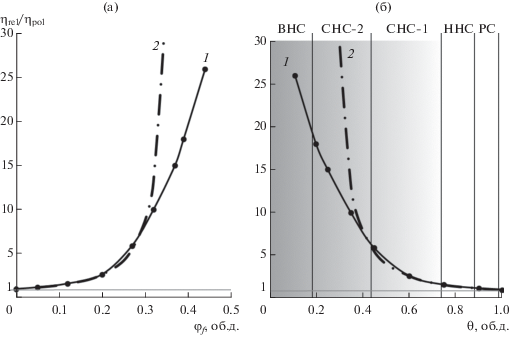
С увеличением содержания твердой дисперсной фазы в полимерной матрице вязкость ДНПКМ возрастает. Зависимость относительной вязкости, представленная в традиционных координатах ηrel = f(φf) (рис. 5а), не учитывает размер, форму, упаковку частиц и не позволяет судить о структуре ДНПКМ, так как содержание наполнителя (φf) не является структурным параметром дисперсной системы.
Зависимость вязкости от обобщенного параметра Θ структуры (рис. 5б) учитывает параметры дисперсной фазы (форму, размер, упаковку частиц), функциональное построение полимерной матрицы и тип дисперсной системы согласно классификации: РС, ННС, СНС (СНС-1 и СНС-2) и ВНС.
Видно, что изменение типа структуры приводит к возрастанию вязкости при переходе от разбавленных систем к низконаполненным, средненаполненным и высоконаполненным системам. В области разбавленных и низконаполненных ДНПКМ вязкость увеличивается всего на ~20–50% от вязкости полимерной матрицы (ПЭНП).
При переходе к средненаполненным системам уже при Θ = 0.6 об. д. (СНС-1) вязкость возрастает в 2.5 раза, а с появлением у систем предела текучести при Θ = 0.45 об. д. (СНС-2) происходит резкий рост вязкости (в ~6 раз), которая возрастает в области высоконаполненных ДНПКМ в ~25 раз, что ухудшает переработку полимерных композитов в изделия.
В качестве примера на рис. 5 приведена расчетная зависимость вязкости по известному уравнению Муни (кривая 2), которая хорошо описывает реологическое поведение дисперсных систем только до Θ = 0.45 об. д., т.е. до появления у ДНПКМ предела текучести (до СНС-2).
ЗАКЛЮЧЕНИЕ
Основным параметром для создания ДНПКМ с заданными типами дисперсной структуры является параметр φm – максимальное содержание наполнителя. В работе представлена зависимость параметра φm от размера частиц наполнителя и показано, что с уменьшением размера частиц происходит снижение максимальной доли наполнителя в ДНПКМ.
По обобщенному параметру Θ проведена классификация ДНПКМ по структурному принципу и рассчитано содержание наполнителей с разными размерами частиц и упаковкой для получения дисперсных структур заданного типа.
Показано, что, например, реологические свойства ДНПКМ определяются типом структуры и значением обобщенных параметров. Так, при переходе от разбавленных и низконаполненных дисперсных систем к средне- и высоконаполненным вязкость резко возрастает, что связано с формированием структур с более плотной упаковкой дисперсных частиц.
Установленные зависимости параметра φm от размера частиц и обобщенного параметра Θ от параметра φm позволяют рассчитывать содержание наполнителя и проектировать составы ДНПКМ с разными типами структур, согласно их классификации по структурному принципу (РС, ННС, СНС (СНС-1 и СНС-2) и ВНС), а также комплексом технологических и эксплуатационных свойств.
ОБОЗНАЧЕНИЯ
| d | диаметр дисперсных частиц |
| f3 | коэффициент, учитывающий отношение толщины граничного слоя (δ) к диаметру (d) дисперсных частиц |
| kp | плотность упаковки |
| S | площадь поверхности |
| δ | толщина граничного слоя |
| η | вязкость |
| П | пористость |
| ρ | плотность |
| φ | доля дисперсной фазы |
ИНДЕКСЫ
Список литературы
Наполнители для полимерных композиционных материалов (справочное пособие) / Под ред. Каца Г.С., Милевски Д.В. М.: Химия, 1981.
Симонов-Емельянов И.Д. Параметры решетки и структуры дисперсно-наполненных полимерных композиционных материалов с регулируемым комплексом свойств // Констр. композ. матер. 2019. № 3. С. 37.
Симонов-Емельянов И.Д., Шембель Н.Л., Прокопов Н.И., Ушакова О.Б., Гервальд А.Ю., Суриков П.В., Марков А.В., Пашкин И.И. Методы технологических свойств наполнителей и полимерных материалов. М.: МИТХТ им. М.В. Ломоносова, 2014.
Анциферов В.Н., Перельман В.Е. Механика процессов прессования порошковых и композиционных материалов. М.: Грааль, 2001.
Прикладная механика ячеистых пластмасс / Под ред. Хильярда Н.К. М.: Мир, 1985.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


