Теоретические основы химической технологии, 2021, T. 55, № 2, стр. 135-142
Исследование кинетики процесса массообмена при ректификации изотопов водорода воды в присутствии карбамида
Н. Н. Кулов a, *, А. В. Полковниченко a, Е. В. Лупачев a, А. В. Кисель b, А. А. Вошкин a, Э. П. Магомедбеков b
a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
b Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия
* E-mail: kulovnn@mail.ru
Поступила в редакцию 23.11.2020
После доработки 27.11.2020
Принята к публикации 04.12.2020
Аннотация
Проведена оценка эффективности массообмена при разделении изотопов водорода путем ректификации воды в присутствии разделяющего агента карбамида. Опыты проведены для систем жидкость–пар и водный солевой раствор–пар в режиме с независимыми потоками. Рассмотрены два режима массообмена: первый, когда рабочая концентрация дейтерия в жидкой фазе ниже, чем равновесная пару (xD < $x_{D}^{*}$), и второй, когда она выше, чем равновесная пару (xD > $x_{D}^{*}$). Обнаружено существенное различие числа теоретических ступеней разделения для этих режимов. При (xD > $x_{D}^{*}$) в присутствии разделяющего агента карбамида число теоретических ступеней разделения оказалось в 3 раза меньше по сравнению с системой вода–пар. Таким образом, в процессе ректификации изотопов водорода воды карбамид препятствует переносу дейтерия из жидкой в паровую фазу, образуя с атомами дейтерия нелетучие комплексы.
ВВЕДЕНИЕ
Наиболее экологически чистым и безопасным методом разделения изотопов водорода и кислорода считается ректификация воды, которая характеризуется небольшими значения коэффициента разделения α, но достаточно высокой производительностью. Среди подходов, направленных на интенсификацию и совершенствование процессов изотопного разделения воды, весьма перспективным представляется использование метода солевой ректификации. Введение в рабочий поток воды разделяющего агента в виде растворимой в воде соли приводит к изменению равновесного состава пара и жидкости, что влияет на величину коэффициента разделения изотопов. В работе [1] нами был экспериментально изучен однократный разделительный эффект между дейтерием и протием при равновесии в системе водный солевой раствор–пар для ряда неорганических и органических солей с целью отыскания рационального разделяющего агента для процесса солевой ректификации воды. Опыты проводили в диапазоне температур от 59 до 94°C динамическим методом в кубе Бушмакина. Было установлено, что присутствие в воде карбамида существенно увеличивает коэффициент разделения D/H в рассматриваемом диапазоне температур, в отличие от остальных изученных 8 неорганических и 4 органических солей. Таким образом, однократные разделительные эффекты указывают на относительно высокий потенциал карбамида как солевого агента для разделения системы D/H при ректификации воды. Цель настоящей работы – изучение массообмена при разделении изотопов водорода методом ректификации воды в присутствии разделяющего агента карбамида.
МАТЕРИАЛЫ И МЕТОДЫ
Схема экспериментальной ректификационной колонны насадочного типа, спроектированной и изготовленной для изучения процесса разделения изотопов водорода и кислорода воды, изложена в работе [2]. Основные конструктивные характеристики установки приведены в табл. 1. Гидравлические характеристики колонны при атмосферном давлении приведены в табл. 2.
Таблица 1.
Конструктивные характеристики ректификационной установки
| Наименование характеристики | Значение | |
|---|---|---|
| Внутренний диаметр колонны, м × 103 | 48 | |
| Высота насадочного слоя H, м | 2 | |
| Тип насадки | Спирально-призматическая | |
| Диаметр насадки, м × 103 | 3 | |
| Поверхность теплообмена дефлегматора, м2 | 0.25 | |
| Объем, м3 × 103 | кубовой емкости | 7 |
| дистиллятной емкости | 3 | |
| емкости солевого раствора | 5 | |
| приемной емкости | 20 | |
| дефлегматора | 0.1 | |
Таблица 2.
Гидравлические характеристики колонны при атмосферном давлении
| G, кг/с × 103 | 0.0572 | 0.1663 | 0.2682 | 0.3933 | 0.4867 | 0.5238 |
| ∆Р, мм рт. ст. | 5.2 | 14.0 | 22.6 | 33.1 | 40.9 | 44.1 |
| ${{\mathcal{W}}_{0}}$, м/с | 0.053 | 0.154 | 0.248 | 0.364 | 0.451 | 0.485 |
Оценку разделительной способности колонны и эффективности массообменного устройства проводили в условиях ректификации чистой воды природного изотопного состава в режиме полной флегмы при атмосферном давлении и величине ${{\mathcal{W}}_{0}}$ = 0.408 м/с. Для этих условий время выхода колонны на стационарный режим по изотопному равновесию для пары изотопов D/H составило 172 ч. Количество теоретических ступеней разделения рассчитано для режима полной флегмы по уравнению Фенске–Андервуда
где xw = 0.00017 ат.д.; xd = 0.0000195 ат.д.; αD/H = = 1.026.
Высота, эквивалентная теоретической ступени разделения, ВЭТС = H/N ≈ 2.4 см. Следует отметить, что экспериментально полученные величины N и значение ВЭТС близки к принятым при расчете в работе [2].
Серию экспериментов по оценке эффективности разделения изотопов водорода при ректификации воды в присутствии карбамида проводили в насадочной ректификационной колонне в режиме с независимыми потоками. Следует отметить, что ректификация изотопных систем характеризуется большим временем выхода на стационарный режим по изотопному равновесию. Режим работы с независимыми потоками позволяет значительно сократить время проведения эксперимента, а также провести оценку массообменного процесса в большом диапазоне движущих сил. Схема материальных потоков в насадочной ректификационной колонне в режиме с независимыми потоками представлена на рис. 1.
Рис. 1.
Схема материальных потоков в насадочной ректификационной колонне в режиме с независимыми потоками.
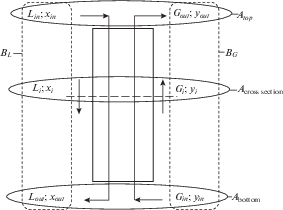
Опыты проведены для систем жидкость–пар и водный солевой раствор–пар в режиме с независимыми потоками. Рассмотрены два режима массообмена: первый, при пониженном содержании дейтерия в поступающем растворе, когда рабочая концентрация дейтерия в жидкой фазе ниже, чем равновесная пару (xD < $x_{D}^{*}$); и второй, при повышенной концентрации дейтерия в поступающем на орошение колонны потоке жидкости, когда рабочая концентрация дейтерия выше, чем равновесная пару (xD > $x_{D}^{*}$). В верхнюю часть колонны (рис. 1) подается поток жидкости Lin состава xin с концентрацией карбамида Curea. Расход жидкости Lin регулируется насосом ProMinent® серии gamma/L. Температура потока Lin соответствует температуре пара Gout в верху колонны. Прошедшая через слой насадки жидкость Lout состава xout поступает на “глухую” тарелку, расположенную ниже слоя насадки, и стекает в приемник жидкой фазы. Входящий поток пара Gin состава yin из куба колонны через “глухую” тарелку поступает в насадочную секцию. Расход пара регулируется нагрузкой на кипятильник. Прошедший через колонну пар Gout состава yout конденсируется в дефлегматоре и в полном объеме отводится в приемник парового конденсата. В ходе эксперимента измеряли расходы и составы выходящих из колонны потоков – парового конденсата (Gout, yout) и стекающей со слоя насадки жидкости (Lout, xout).
Образцы жидкости и парового конденсата после предварительной подготовки анализировали на спектральном жидкостном изотопном анализаторе T-LWA-45-EP, предназначенном для анализа воды на уровне природного содержания изотопов с погрешностью измерения ±0.0001 ат. % (1 млн–1). В экспериментах использовали дистиллированную воду природного изотопного состава, а также воду с повышенным содержанием дейтерия. Для приготовления исходных солевых растворов использовали карбамид категории “ч. д. а.” чистотой не менее 99.9 мас. %.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Изотопный солевой эффект при ректификации изотопов водорода воды обусловлен рядом факторов макроскопического и молекулярного масштаба, таких как различие молекулярных масс испаряющихся и конденсирующихся молекул, энергия образования комплекса с разделяющим агентом и энергия связи молекул воды в гидратной оболочке, что определенным образом влияет на соотношение величины потоков конденсации и испарения. Так, подача солевого раствора, поступающего в колонну при температуре пара в данном сечении, приводит к разности количества конденсируемого и испаряемого вещества, поскольку солевой раствор подается при температуре, отличающейся от температуры кипения потока жидкости. В случае карбамида также следует обратить внимание и на эндотермический эффект смешения потоков, а также частичный гидролиз [3–5]. Таким образом, в этих условиях трудно в точности соблюсти тепловые потоки для системы водный солевой раствор–пар, а организация области смешения в аппарате требует дополнительного исследования с точки зрения создания оптимального теплового режима.
Для систем жидкость–пар и водный солевой раствор–пар ректификационная колонна в режиме с независимыми потоками работала при следующих расходах по жидкости и по пару:
(1)
${{G}_{{in}}} \ne {{G}_{{out}}};\,\,\,\,{{L}_{{in}}} \ne {{L}_{{out}}};~\,\,\,\,{{L}_{i}} = {{G}_{i}}.$Заметим, что величина входящего потока по пару (жидкости) не равна величине выходящего потока (рис. 1, контур B). При этом абсолютную величину потерь тепла по высоте колонны считаем постоянной. Таким образом, соотношение потоков по высоте колонны составило ${{G}_{{in}}} \approx {{L}_{{out}}},$ ${{G}_{{out}}} \approx {{L}_{{in}}},$ ${{G}_{i}} \approx {{L}_{i}}$ (рис. 1, контур A).
Материальный баланс по потокам (рис. 1) имеет вид
(2)
$\begin{gathered} {{L}_{{in}}} + {{G}_{{in}}} = {{L}_{{out}}} + {{G}_{{out}}},\,\,\,\,{{L}_{{in}}} + {{G}_{i}} = {{L}_{i}} + {{G}_{{out}}}, \\ {{L}_{i}} + {{G}_{{in}}} = {{L}_{{out}}} + {{G}_{i}}, \\ \end{gathered} $(3)
$\begin{gathered} {{L}_{{in}}}{{x}_{{in}}} + {{G}_{{in}}}{{y}_{{in}}} = {{L}_{{out}}}{{x}_{{out}}} + {{G}_{{out}}}{{y}_{{out}}}, \\ {{L}_{{in}}}{{x}_{{in}}} + {{G}_{i}}{{y}_{i}} = {{L}_{i}}{{x}_{i}} + {{G}_{{out}}}{{y}_{{out}}}, \\ {{L}_{i}}{{x}_{i}} + {{G}_{{in}}}{{y}_{{in}}} = {{L}_{{out}}}{{x}_{{out}}} + {{G}_{i}}{{y}_{i}}, \\ \end{gathered} $(4)
${{y}_{i}} = {{x}_{i}}\frac{{{{L}_{i}}}}{{{{G}_{i}}}} + {{y}_{{in}}}\frac{{{{G}_{{in}}}}}{{{{G}_{i}}}} - {{x}_{{out}}}\frac{{{{L}_{{out}}}}}{{{{G}_{i}}}}.$Коэффициенты уравнения (4), согласно уравнению (1), имеют следующие соотношения: $\frac{{{{G}_{{in}}}}}{{{{G}_{i}}}} \approx \frac{{{{L}_{{out}}}}}{{{{G}_{i}}}},$ ${{y}_{{in}}} - {{x}_{{out}}} \approx {\text{const}}$ и $\frac{{{{L}_{i}}}}{{{{G}_{i}}}} \approx {\text{const}}.$ Таким образом, уравнениe (4) можно представить в виде зависимости $y = ax + b,$ где коэффициент $b = {{y}_{{in}}}\frac{{{{G}_{{in}}}}}{{{{G}_{i}}}}$ – ${{x}_{{out}}}\frac{{{{L}_{{out}}}}}{{{{G}_{i}}}} = f\left( H \right)$ – линейная функция по высоте колонны. В условиях настоящего эксперимента ввиду небольших величин ${{\alpha }_{{D{\text{/}}H}}}$ примем, что состав жидкой фазы по высоте колонны $x = f\left( H \right)$ меняется линейно. Таким образом, сложение двух линейных функций $b = f\left( H \right)$ и $x = f\left( H \right)$ в уравнении $y = ax + b$ позволяет утверждать, что зависимость $y = f\left( x \right)$ уравнения (4) также линейна.
Эффективность процесса ректификации изотопов водорода D/H воды в присутствии карбамида можно выразить через отношение $\frac{{{{N}^{{pw}}}}}{{{{N}^{{urea}}}}}$ –числа теоретических ступеней разделения в режиме с независимыми потоками для систем жидкость–пар Npw и водный солевой раствор–пар Nurea. На практике, для случая $0.5 \leqslant \frac{{{{{\bar {m}}}_{F}}G}}{L} \leqslant 2.0$ (${{\bar {m}}_{F}}$ – средний наклон равновесной линии), число теоретических ступеней разделения может быть аппроксимировано с погрешностью менее 4% как среднеарифметическое числа единиц переноса по пару Noy и по жидкости Nox [6]:
Таким образом, отношение Npw/Nurea примет вид
(6)
$\frac{{{{N}^{{pw}}}}}{{{{N}^{{urea}}}}} = \frac{{\left( {N_{{ox}}^{{pw}} + N_{{oy}}^{{pw}}} \right)}}{{\left( {N_{{ox}}^{{urea}} + N_{{oy}}^{{urea}}} \right)}}.$Числа единиц переноса по пару Noy и по жидкости Nox представляют собой результат совместного решения уравнений равновесной и рабочей линий процесса, задаваемых начальными и конечными концентрациями:
(7)
$\begin{array}{*{20}{c}} {{{N}_{{oy}}} = \int {\frac{{dy}}{{\left( {y - y{\text{*}}} \right)}}} } \\ {{{N}_{{ox}}} = \int {\frac{{dx}}{{\left( {x{\text{*}} - x} \right)}}} } \end{array}.$Коэффициент разделения ${{\alpha }_{{D{\text{/}}H}}}$ для системы жидкость–пар принимаем равным $\alpha _{{D{\text{/}}H}}^{{PW}} = 1.026$ [1]. Для системы водный солевой раствор–пар, вследствие разбавления потока жидкости по высоте колонны, коэффициент разделения $\alpha _{{D{\text{/}}H}}^{{urea}}$ изменяется как функция от моляльности раствора и для произвольного сечения колонны рассчитывается как
(8)
$\begin{gathered} \alpha _{{\frac{D}{H}}}^{{urea}} = 0.0038C_{i}^{{urea}} + 1.026, \\ C_{i}^{{urea}} = \frac{{C_{{urea}}^{{in}}{{L}_{{in}}}M_{{\left( {{{M}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}\left( {1 - x_{{in}}^{D}} \right) + {{M}_{{{{{\text{D}}}_{{\text{2}}}}{\text{O}}}}}x_{{in}}^{D}} \right)}}^{{{\text{\;среднее}}}}}}{{{{L}_{i}}M_{{\left( {{{M}_{{{{{\text{H}}}_{{\text{2}}}}{\text{O}}}}}\left( {1 - x_{i}^{D}} \right) + {{M}_{{{{{\text{D}}}_{{\text{2}}}}{\text{O}}}}}x_{i}^{D}} \right)}}^{{{\text{\;среднее}}}}}}. \\ \end{gathered} $Результаты экспериментов для систем жидкость–пар и водный солевой раствор–пар в режиме с независимыми потоками для случаев массообмена, когда рабочая концентрация дейтерия в жидкой фазе ниже, чем равновесная пару (xD < $x_{D}^{*}$), и выше, чем равновесная пару (xD > $x_{D}^{*}$) представлены в табл. 3.
Таблица 3.
Результаты экспериментов для систем жидкость–пар и водный солевой раствор–пар в режиме с независимыми потоками для случаев массообмена xD < $x_{D}^{*}$ и xD > $x_{D}^{*}.$ Td = 99.9 ± 0.1°C, Tw = 100.8 ± 0.3°C, ∆P = 9.8 ± 2.3 мм рт. ст.
| xD< $x_{D}^{*}$ (процесс, когда в ходе массообмена происходит преимущественный перенос легколетучего компонента из жидкой фазы в паровую) | |||||||||||||
| τ, мин | Эксперимент (1): жидкость–пар |
Эксперимент (3): водный солевой раствор–пар $C_{{urea}}^{{in}} = 5$ моль/кг |
$\frac{{{{N}^{{pw}}}}}{{{{N}^{{urea}}}}} = \frac{{(N_{{ox}}^{{pw}} + N_{{oy}}^{{pw}})}}{{(N_{{ox}}^{{urea}} + N_{{oy}}^{{urea}})}}$ | ||||||||||
| Lin = 55.5 ± 1 моль воды/ч; Gin = 82.8 ± 1.5 моль воды/ч | Lin= 55.5 ± 1 моль воды/ч; Gin = 93.9 ± 1.5 моль воды/ч | ||||||||||||
| $x_{D}^{{in}} = 0.00014$, ат. д. | $y_{D}^{{in}} = 0.12066$, ат. д. | $x_{D}^{{in}} = 0.00014$, ат. д. | $y_{D}^{{in}} = 0.09976$, ат. д. | ||||||||||
| $x_{D}^{{out}}$, ат. д. | Lout, моль воды/ч | Nox | $y_{D}^{{out}}$, ат. д. | Gout, моль воды/ч | Noy | $x_{D}^{{out}}$, ат. д. | Lout, моль воды/ч | Nox | $y_{D}^{{out}}$, ат. д. | Gout, моль воды/ч | Noy | ||
| 60 | 0.11531 | 82.3 | 14.2 | 0.00797 | 56.2 | 14.2 | 0.08358 | 95.7 | 8.8 | 0.00369 | 53.1 | 10.5 | 1.5 |
| 120 | 0.11184 | 87.9 | 15.2 | 0.00426 | 51.9 | 16.2 | 0.08436 | 97.9 | 14.8 | 0.00111 | 53.3 | 18.1 | 1.0 |
| 180 | 0.11323 | 86.9 | 17.9 | 0.00356 | 52.9 | 19.0 | 0.08243 | 96.5 | 14.6 | 0.00099 | 49.4 | 18.2 | 1.1 |
| 210 | 0.11408 | 85.6 | 18.9 | 0.00361 | 54.4 | 19.8 | 0.08807 | 102.7 | 16.1 | 0.00134 | 52.6 | 18.8 | 1.1 |
| 240 | 0.11579 | 83.6 | 19.9 | 0.00423 | 56.4 | 20.5 | 0.08684 | 102.6 | 16.5 | 0.00112 | 47.6 | 19.5 | 1.1 |
| 270 | 0.11687 | 83.0 | 19.8 | 0.00519 | 57.9 | 20.0 | – | – | – | – | – | – | – |
| 300 | 0.11835 | 80.1 | 20.6 | 0.00634 | 58.0 | 20.4 | – | – | – | – | – | – | – |
| xD > $x_{D}^{*}$ (процесс, когда в ходе массообмена происходит преимущественный перенос тяжелолетучего компонента из жидкой фазы в паровую) | |||||||||||||
| τ, мин | Эксперимент (2): жидкость–пар |
Эксперимент (4): водный солевой раствор–пар $C_{{urea}}^{{in}}$ = 5 моль/кг |
$\frac{{{{N}^{{pw}}}}}{{{{N}^{{urea}}}}} = \frac{{(N_{{ox}}^{{pw}} + N_{{oy}}^{{pw}})}}{{(N_{{ox}}^{{urea}} + N_{{oy}}^{{urea}})}}$ | ||||||||||
| Lin = 55.2 ± 1 моль воды/ч; Gin= 83.3 ± 1.5 моль воды/ч | Lin = 55.3 ± 1 моль воды/ч; Gin = 94.4 ± 1.5 моль воды/ч | ||||||||||||
| $x_{D}^{{in}} = 0.12747$, ат. д. | $y_{D}^{{in}} = 0.00014$, ат. д. | $x_{D}^{{in}} = 0.09836$, ат. д. | $y_{D}^{{in}} = 0.00015$, ат. д. | ||||||||||
| $x_{D}^{{out}}$, ат. д. | Lout, моль воды/ч | Nox | $y_{D}^{{out}}$, ат. д. | Gout, моль воды/ч | Noy | $x_{D}^{{out}}$, ат. д. | Lout, моль воды/ч | Nox | $y_{D}^{{out}}$, ат. д. | Gout, моль воды/ч | Noy | ||
| 60 | 0.00769 | 88.7 | 12.4 | 0.11254 | 52.4 | 11.9 | 0.00967 | 109.8 | 6.4 | 0.07590 | 50.7 | 5.6 | 2.0 |
| 120 | 0.01381 | 93.5 | 13.4 | 0.11983 | 48.5 | 14.4 | 0.01737 | 105.6 | 4.4 | 0.07570 | 41.9 | 4.2 | 3.2 |
| 180 | 0.01401 | 92.2 | 13.2 | 0.11977 | 48.7 | 14.2 | 0.01751 | 105.1 | 4.6 | 0.07776 | 41.1 | 4.6 | 3.0 |
| 210 | 0.01527 | 91.2 | 14.2 | 0.12112 | 48.7 | 15.7 | 0.01659 | 104.9 | 5.1 | 0.07966 | 41.8 | 5.1 | 2.9 |
| 240 | 0.01472 | 91.9 | 14.0 | 0.12071 | 48.6 | 15.2 | 0.01602 | 106.5 | 5.1 | 0.07890 | 42.5 | 5.1 | 2.9 |
| 270 | 0.01416 | 90.4 | 15.4 | 0.12131 | 48.9 | 16.8 | 0.01655 | 107.3 | 5.1 | 0.07955 | 42.1 | 5.1 | 3.2 |
| 300 | 0.01282 | 88.8 | 16.1 | 0.12109 | 51.5 | 17.3 | 0.01697 | 105.0 | 4.8 | 0.07788 | 40.7 | 4.7 | 3.5 |
Из данных табл. 3 видно, что концентрации дейтерия во входящих потоках, обогащенных по тяжелому компоненту, для систем жидкость–пар (эксперименты 1, 2) и водный солевой раствор–пар (эксперименты 3, 4) различны. Однако, для каждой из систем при различном положении рабочей линии относительно равновесной концентрации дейтерия во входящих потоках, обогащенных по тяжелому компоненту, приблизительно равны. Изменение направления массообмена для системы жидкость–пар не вызывает существенного различия в числе теоретических ступеней разделения $\frac{{N_{{{\text{эксперимент\;1}}}}^{{PW}}}}{{N_{{{\text{эксперимент\;2}}}}^{{PW}}}} \approx 1.3.$ Напротив, для системы водный солевой раствор–пар изменение направления массообмена приводит к существенному различию числа теоретических ступеней разделения $\frac{{N_{{{\text{эксперимент\;3}}}}^{{Urea}}}}{{N_{{{\text{эксперимент\;4}}}}^{{Urea}}}} > 3.$ Подобная тенденция согласуется с теоретическим анализом. Согласно приведенным данным по растворам карбамида [7] и распределению дейтерия между паровой и жидкой фазами [1, 8–10], карбамид препятствует переносу дейтерия из жидкой в паровую фазу. Таким образом, присутствие карбамида должно способствовать массообмену для случая xD < $x_{D}^{*}$ и препятствовать массообмену для случая xD > $x_{D}^{*}.$
Для случая, когда в ходе массообмена происходит преимущественный перенос тяжелолетучего компонента из жидкой фазы в паровую, число теоретических ступеней разделения в присутствии карбамида для системы водный солевой раствор–пар в 3 раза меньше по сравнению с системой жидкость–пар $\frac{{N_{{{\text{эксперимент\;2}}}}^{{PW}}}}{{N_{{{\text{эксперимент\;4}}}}^{{Urea}}}} \approx 3.$ Однако для систем жидкость–пар и водный солевой раствор–пар для случая, когда в ходе массообмена происходит преимущественный перенос легколетучего компонента из жидкой фазы в паровую, число теоретических ступеней разделения приблизительно равно $\frac{{N_{{{\text{эксперимент\;1}}}}^{{PW}}}}{{N_{{{\text{эксперимент\;3}}}}^{{Urea}}}} \approx 1.1$ (табл. 3). Таким образом, присутствие карбамида увеличивает коэффициент относительной летучести ${{\alpha }_{{D{\text{/}}H}}}$ и не оказывает существенного влияния на число теоретических ступеней разделения в процессе ректификации для случая xD < $x_{D}^{*}.$ Интенсификация процесса разделения в таком случае будет происходить за счет увеличения относительной летучести между молекулами воды, содержащими и не содержащими дейтерий.
Объемные коэффициенты массопередачи в паровой ${{K}_{{oy}}}a$ и жидкой ${{K}_{{ox}}}a$ фазе, рассчитанные через изменение количества вещества в потоке ∆G (∆L), представлены в табл. 4 и рассчитаны как [6]
(9)
${{K}_{{oy}}}a = \frac{{{{N}_{{oy}}}\Delta G}}{{fH}},\,\,\,\,{{K}_{{ox}}}a = \frac{{{{N}_{{ox}}}\Delta L}}{{fH}}.$Таблица 4.
Объемные коэффициенты массопередачи по паровой ${{K}_{{oy}}}a$ и жидкой ${{K}_{{ox}}}a$ фазе для систем жидкость–пар и водный солевой раствор–пар в режиме с независимыми потоками для случаев массообмена xD < $x_{D}^{*}$ и xD > $x_{D}^{*}$
| xD < xD* (процесс, когда в ходе массообмена происходит преимущественный перенос легколетучего компонента из жидкой фазы в паровую) | ||||
| τ, мин | жидкость–пар | водный солевой раствор–пар | ||
| ${{K}_{{oy}}}a$* | ${{K}_{{ox}}}a$* | ${{K}_{{oy}}}a$* | ${{K}_{{ox}}}a$* | |
| 60 | 18.71 | 18.58 | 13.34 | 9.72 |
| 120 | 21.93 | 20.66 | 23.24 | 16.90 |
| 180 | 25.75 | 24.36 | 23.45 | 16.00 |
| 210 | 26.86 | 25.44 | 24.01 | 20.14 |
| 240 | 27.70 | 26.66 | 25.07 | 20.25 |
| 270 | 26.84 | 26.52 | – | – |
| 300 | 27.07 | 26.93 | – | – |
| xD > xD* (процесс, когда в ходе массообмена происходит преимущественный перенос тяжелолетучего компонента из жидкой фазы в паровую) | ||||
| τ, мин | жидкость–пар | водный солевой раствор–пар | ||
| ${{K}_{{oy}}}a$* | ${{K}_{{ox}}}a$* | ${{K}_{{oy}}}a$* | ${{K}_{{ox}}}a$* | |
| 60 | 9.65 | 10.86 | 2.98 | 3.85 |
| 120 | 11.58 | 10.65 | 1.85 | 2.19 |
| 180 | 11.47 | 10.49 | 2.02 | 2.30 |
| 210 | 12.75 | 11.09 | 2.36 | 2.61 |
| 240 | 12.33 | 10.96 | 2.33 | 2.63 |
| 270 | 13.74 | 12.23 | 2.36 | 2.56 |
| 300 | 14.92 | 13.11 | 2.05 | 2.40 |
Согласно данным табл. 4 присутствие карбамида занижает коэффициенты массопередачи в жидкой фазе по сравнению с чистой водой, а объемные коэффициенты массопередачи в жидкой и паровой фазе выше для случая xD < $x_{D}^{*}$ (процесс, когда в ходе массообмена происходит преимущественный перенос легколетучего компонента из жидкой фазы в паровую).
ЗАКЛЮЧЕНИЕ
В работе проведена оценка эффективности разделения изотопов водорода при ректификации воды в присутствии карбамида. Опыты для систем жидкость–пар и водный солевой раствор–пар в режиме с независимыми потоками проводили для случаев массообмена xD < $x_{D}^{*}$ (процесс, когда в ходе массообмена происходит преимущественный перенос легколетучего компонента из жидкой фазы в паровую) и xD > $x_{D}^{*}$ (процесс, когда в ходе массообмена происходит преимущественный перенос тяжелолетучего компонента из жидкой фазы в паровую). Показано, что изменение направления массообмена для системы водный солевой раствор–пар приводит к существенному различию числа теоретических ступеней разделения $\frac{{N_{{{\text{эксперимент\;3}}}}^{{Urea}}}}{{N_{{{\text{эксперимент\;4}}}}^{{Urea}}}} > 3.$ Таким образом, в процессе ректификации изотопов водорода воды карбамид препятствует переносу дейтерия из жидкой в паровую фазу. Для случая массообмена, когда xD < $x_{D}^{*},$ число теоретических ступеней разделения в присутствии карбамида для системы водный солевой раствор–пар в 3 раза меньше по сравнению с системой жидкость–пар $\frac{{N_{{{\text{эксперимент\;2}}}}^{{PW}}}}{{N_{{{\text{эксперимент\;4}}}}^{{Urea}}}} \approx 3.$ Заметим, что для систем жидкость–пар и водный солевой раствор–пар для случая массообмена, когда xD > $x_{D}^{*},$ число теоретических ступеней разделения приблизительно равно $\frac{{N_{{{\text{эксперимент\;1}}}}^{{PW}}}}{{N_{{{\text{эксперимент\;3}}}}^{{Urea}}}} \approx 1.1$ (табл. 3), а объемные коэффициенты массопередачи в жидкой фазе ${{K}_{{ox}}}a$ в присутствии карбамида ниже по сравнению с чистой водой. Интенсификация процесса разделения в таком случае будет происходить за счет увеличения относительной летучести между молекулами воды, содержащими и не содержащими дейтерий.
Изменение относительной летучести D/H воды в присутствии карбамида происходит в основном за счет различия в энергии образования комплекса с разделяющим агентом и различия энергии связи молекул воды в гидратной оболочке. Появляющаяся при этом скоростная неравномерность потоков пара и жидкости вызывает изменение коэффициентов массопередачи в результате возникающей неэквимолярности массообмена между паром и жидкостью. Таким образом, присутствие карбамида оказывает существенное влияние как на равновесие жидкость–пар, так и на кинетику процесса, что согласуется с данными работы [11].
Настоящая работа является одной из первых попыток в данной области. Несмотря на то, что присутствие карбамида увеличивает коэффициент относительной летучести между дейтерием и протием воды, его использование ограничено. Ограничения связаны с температурным режимом в результате частичного гидролиза при T > 60°С, эндотермическим эффектом смешения, а также возникающей неэквимолярностью между паром и жидкостью. Это требует проведения дополнительных исследований для отыскания оптимального теплового режима и рациональной организации узла рекуперации солевого агента.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-13-00475).
ОБОЗНАЧЕНИЯ
| C | моляльность, моль/(кг воды) |
| f | площадь сечения аппарата, м2 |
| G | поток пара, (моль воды)/ч |
| H | высота насадочной части колонны, м |
| K | степень разделения |
| ${{K}_{{ox}}}a$ | объемный коэффициент массопередачи в жидкой фазе, кмоль/(ч м3 ед. движ. силы) |
| ${{K}_{{oy}}}a$ | объемный коэффициент массопередачи в паровой фазе, кмоль/(ч м3 ед. движ. силы) |
| L | поток жидкости, (моль воды)/ч |
| M | молекулярная масса, г/моль |
| ${{\bar {m}}_{F}}$ | средний наклон равновесной линии |
| N | число теоретических ступеней разделения |
| Nox | число единиц переноса по жидкой фазе |
| Noy | число единиц переноса по паровой фазе |
| P | давление, мм рт. ст. |
| T | температура, °С |
| x | концентрация в жидкой фазе, ат. д. |
| y | концентрация в паровой фазе, ат. д. |
| ВЭТС | высота, эквивалентная теоретической ступени разделения, см |
| α | коэффициент разделения |
| τ | время, ч |
| ${{\mathcal{W}}_{0}}$ | приведенная скорость пара в расчете на полное сечение колонны, м/с |
ИНДЕКСЫ
Список литературы
Kulov N.N., Polkovnichenko A.V., Lupachev E.V., Voshkin A.A., Magomedbekov E.P. Distribution of hydrogen isotopes between phases at vapor–liquid equilibrium in aqueous salt solutions // Theor. Found. Chem. Eng. 2020. V. 54. № 4. P. 132. https://doi.org/10.1134/ S0040579520010108 [Кулов Н.Н., Полковниченко А.В., Лупачев Е.В., Вошкин А.А., Магомедбеков Э.П. Распределение изотопов водорода между фазами при парожидкостном равновесии водных солевых растворов // Теор. осн. хим. технол. 2020. Т. 54. № 4. С. 3. https://doi.org/10.31857/S0040357120010108]
Kulov N.N., Polkovnichenko A.V., Lupachev E.V., Rastunova I.L, Magomedbekov E.P. Fractionation of D/H and 18O/16O water isotopes in a packed distillation column // Theor. Found. Chem. Eng. 2020. V. 54. № 3. P. 389. https://doi.org/10.1134/S0040579520030094 [Кулов Н.Н., Полковниченко А.В., Лупачев Е.В., И.Л. Растунова, Магомедбеков Э.П. Фракционирование изотопов воды D/H и 18О/16О в насадочной ректификационной колонне // Теор. осн. хим. технол. 2020. Т. 54. № 3. С. 267. https://doi.org/10.31857/S0040357120030094]
Rahimpour M.R. A non-ideal rate-based model for industrial urea thermal hydrolyser // Chem. Eng. Process. 2004. V. 43. № 10. P. 1299. https://doi.org/10.1016/j.cep.2003.12.005
Abuzarova K., Korchuganova O. Nanosized iron oxyhydroxide: properties, application, preparation // J. Phys.: Conf. Ser. 2020. V. 1534. Article number 012002. https://doi.org/10.1088/1742-6596/1534/1/012002
Shahebrahimi Y., Fazlali A. Vapor–liquid equilibrium of aqueous urea solution from dynamic vapor sorption measurements at 283.15–343.15 K // J. Chem. Eng. Data. 2020. V. 65. № 7. P. 3528. https://doi.org/10.1021/acs.jced.9b01160
Кафаров В.В. Основы массопередачи. Системы газ–жидкость, пар–жидкость, жидкость–жидкость. М.: Высшая школа, 1979.
Jakli G., Van Hook W.A. Isotope effects in aqueous systems. 12. Thermodynamics of urea-h4/water and urea-d4/water-d2 solutions // J. Phys. Chem. 1981. V. 85. № 23. P. 3480. https://doi.org/10.1021/j150623a025
Kakiuchi M., Matsuo S. Fractionation of hydrogen and oxygen isotopes between hydrated and free water molecules in aqueous urea solution // J. Phys. Chem. 1985. V. 89. № 21. P. 4627. https://doi.org/10.1021/j100267a043
Horita J., Wesolowski D.J. Liquid–vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature // Geochim. Cosmochim. Acta. 1994. V. 58. № 16. P. 3425. https://doi.org/10.1016/0016-7037(94)90096-5
Kakiuchi M. Distribution of isotopic water molecules, H2O, HDO, and D2O, in vapor and liquid phases in pure water and aqueous solution systems // Geochim. Cosmochim. Acta. 2000. V. 64. № 9. P. 1485. https://doi.org/10.1016/S0016-7037(99)00281-1
Lotkhov V.A., Kvashnin S.Y., Kulov N.N. Effect of separating agent in extractive distillation // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 172. https://doi.org/ 10.1134/S0040579520010145 [Лотхов В.А., Квашнин С.Я. Кулов Н.Н. Эффект разделяющего агента в экстрактивной дистилляции // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 45 https://doi.org/10.31857/S0040357120010145]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


