Теоретические основы химической технологии, 2021, T. 55, № 2, стр. 235-241
Определение эффективности насадочных газосепараторов капельных аэрозолей с учетом неравномерности профиля скорости газа
А. Г. Лаптев a, *, Е. А. Лаптева a
a Казанский государственный энергетический университет
Казань, Россия
* E-mail: Tvt_kgeu@mail.ru
Поступила в редакцию 06.07.2020
После доработки 19.10.2020
Принята к публикации 20.11.2020
Аннотация
Рассмотрен процесс турбулентной миграции жидких аэрозольных частиц в хаотичном насадочном слое газосепаратора. Записаны дифференциальные уравнения массопереноса частиц в плоскопараллельном и цилиндрическом каналах, а также в аппарате с хаотичным насадочным слоем. Неравномерность профиля скорости газа на входе в слой и далее в слое насадки учитывается локальным объемным источником массы осаждающихся частиц на поверхность за счет турбулентно-инерционного механизма, а также коэффициентом турбулентной диффузии частиц. Даны выражения для расчета параметров источника массы, связанные с динамической скоростью на поверхности насадочных тел. Представлены результаты численного решения уравнения массопереноса частиц при равномерном и неравномерном профиле скорости газа на входе. Установлено, что неравномерность снижает эффективность сепарации частиц, что необходимо учитывать в расчетах при проектировании аппаратов. Сделаны выводы о наиболее эффективных конструкциях насадок.
ВВЕДЕНИЕ
Эффективность тепломассообменных и сепарационных аппаратов промышленных размеров существенно зависит от однородности распределения фаз в рабочем объеме (в насадке, на тарелке и других контактных устройствах). При равномерных профилях скоростей фаз достигается максимальная эффективность процессов при заданных режимных и конструктивных параметрах работы аппаратов. Известные методы расчета эффективности сепарации капельных аэрозолей основаны на модели идеального вытеснения [1, 2], что справедливо для каналов без внутренних интенсификаторов (шероховатостей, выступов, насадок и т.д.). При применении интенсификаторов эффективность сепарации повышается в несколько раз, однако структура потока отличается от идеального вытеснения, что необходимо учитывать при составлении математической модели процесса разделения. Кроме того, неравномерности профиля скорости газа в контактных устройствах зависят от условий подачи газа в аппарат. На рис. 1 в качестве примера приводятся профили скорости при различных условиях подачи газа в аппарат [3].
Рис. 1.
Схемы растекания узкой струи в рабочей камере аппарата: (а), (в) – с центральным распределением потока; (б) – распределение потока за плоской решеткой в аппарате $Н_{{\text{р}}}^{'}$ = 0.15.
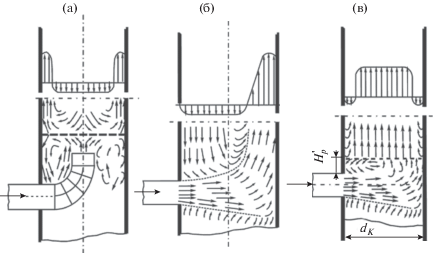
Следовательно, неоднородности распределения фаз связаны с входными неравномерностями, с дефектами конструкции и монтажа контактных устройств, а также с внутренними закономерности движения двухфазных потоков. Особенно неоднородности усиливаются при увеличении размеров аппаратов, что получило название “масштабных эффектов” [4]. Отсюда следует проблема масштабного перехода от лабораторных установок и стендов небольшого размера к аппарату промышленного размера [4–6]. При масштабном переходе эффективность может снижаться в несколько раз, т.е. работа аппарата не будет соответствовать технологическим требованиям на разделение смесей.
Согласно известным исследованиям, распределение газа по сечению и высоте насадочной колонны имеет сложный характер и зависит от многих факторов [4, 7, 8]. Профили скорости газа (без орошения), полученные разными авторами в хаотичном слое (в основном цилиндры, таблетки и шары), представлены в работе [7]. Так, при ${{{{D}_{к}}} \mathord{\left/ {\vphantom {{{{D}_{к}}} {{{d}_{э}}}}} \right. \kern-0em} {{{d}_{э}}}} \approx 16$ ширина области повышенных скоростей составляет от (0.4–1.0) r/R, причем данные различных авторов часто противоречивы: некоторые отмечают повышенную скорость у стенки колонны, а другие – в центре. При увеличении ${{{{D}_{к}}} \mathord{\left/ {\vphantom {{{{D}_{к}}} {{{d}_{э}}}}} \right. \kern-0em} {{{d}_{э}}}}$ от 40 до 100 происходит некоторое уменьшение отношения максимальной и минимальной скоростей газового потока [7]. Показано, что в насадке с кольцами Рашига [8] неравномерности могут находиться от ${{{{W}_{m}}} \mathord{\left/ {\vphantom {{{{W}_{m}}} {{{W}_{0}}}}} \right. \kern-0em} {{{W}_{0}}}} = 0.4$ (в центре аппарата) до ${{{{W}_{m}}} \mathord{\left/ {\vphantom {{{{W}_{m}}} {{{W}_{0}}}}} \right. \kern-0em} {{{W}_{0}}}} = 1.6$ (у стенок аппарата).
Цель настоящей работы – представить приближенную математическую модель разделения капельных аэрозолей в газосепараторе с хаотичной насадкой с учетом неравномерности потока газа в слое, а также рассмотреть технические решения по снижению неоднородного распределения фаз и повышению эффективности сепарации.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СЕПАРАЦИИ
Сепараторы с насадками имеют простую конструкцию и применяются в различных процессах химической технологии, когда в обрабатываемых газах нет твердой фазы из-за отложения на поверхности элементов.
Рассматривается турбулентный режим движения газа с жидкими аэрозольными частицами в слое хаотичной насадки, который, как известно, начинается при ${\text{R}}{{{\text{е}}}_{{\text{э}}}} > 15{\kern 1pt} - {\kern 1pt} 40.$
При теоретическом анализе всех форм движения аэрозольных частиц в турбулентном потоке газа принимаются следующие предположения и допущения [1].
1. Диаметр частиц ${{d}_{{\text{ч}}}}$ мал по сравнению с масштабом несущих их пульсационных молей l: ${{d}_{{\text{ч}}}} \ll l.$ Тогда частица совершает движение, оставаясь в пределах исходного пульсационного моля. Этому условию удовлетворяют следующие частицы: высокодисперсные (${{d}_{{\text{ч}}}} < 0.5{\kern 1pt} - {\kern 1pt} 1\,\,мкм$); тонкодисперсные ($0.5{\kern 1pt} - {\kern 1pt} 1 < {{d}_{{\text{ч}}}}$ < $10{\kern 1pt} - {\kern 1pt} 20\,\,мкм$) и грубодисперсные ($10{\kern 1pt} - {\kern 1pt} 20 < {{d}_{{\text{ч}}}}$ < $100{\kern 1pt} - {\kern 1pt} 200\,\,мкм$).
2. Частицы по форме близки к сферическим. При сильном отклонении от сферической формы вводится коэффициент формы, а в случае полидисперсности частиц аэрозоль рассматривается пофракционно.
3. Частицы при небольших концентрациях на входе в аппарат $\left( {С < 0.2\,\,{{кг} \mathord{\left/ {\vphantom {{кг} {{{м}^{3}}}}} \right. \kern-0em} {{{м}^{3}}}}} \right)$ не стесняют движение друг друга, не коагулируют друг с другом и не оказывают заметного влияния на турбулентные характеристики среды.
Далее в статье применяется теория турбулентной миграции частиц в газах, подробно рассмотренная в монографиях [1, 2, 9].
Частица аэрозолей в стационарном режиме движения газа приобретает поступательную скорость, равную осредненной скорости среды. Зависимость степени увлечения частицы ${{\mu }_{р}}$ турбулентными пульсациями среды от индекса инерционности ${{\omega }_{{\rm E}}}{{\tau }_{р}}{\text{:}}$ при полном увлечении частиц турбулентными пульсациями среды ${{\mu }_{р}} = 1$ и ${{\omega }_{{\rm E}}}{{\tau }_{р}} \ll 1;$ формула для квадрата осредненной степени увлечения частиц имеет вид $\bar {\mu }_{р}^{2} = {{(1 + {{\omega }_{{\rm E}}}{{\tau }_{р}})}^{{ - 1}}}.$
Перемещаясь с газом в канале аэрозольные частицы достигают пристенной области, касаются стенки и осаждаются на ней. Предполагается, что поверхность стенки удерживает частицы, т.е. является поглощающей. При осаждении на стенку канала частиц в виде капель жидкости на стенке будет образовываться пленка, которая под действием силы тяжести стекает в низ канала. Мерой интенсивности осаждения из турбулентного потока газа на стенках является скорость турбулентного осаждения частиц ${{u}_{{\text{t}}}} = {j \mathord{\left/ {\vphantom {j {\bar {С}}}} \right. \kern-0em} {\bar {С}}},$ м/с [1]. Фактически скорость ut является аналогом коэффициента массоотдачи в теории массопередачи и характеризует скорость турбулентно-инерционного переноса частиц к стенке канала. В теоретических исследованиях и расчетах аппаратов используется безразмерный эквивалент скорости осаждения $u_{t}^{ + } = {{{{u}_{t}}} \mathord{\left/ {\vphantom {{{{u}_{t}}} {{{u}_{*}}}}} \right. \kern-0em} {{{u}_{*}}}}$ [1].
Для расчета $u_{{\text{t}}}^{ + }$ наибольшее применение получила формула Е.П. Медникова, обобщающая большое количество экспериментальных исследований различных авторов [1]:
при $\bar {\mu }_{{\text{р}}}^{2}{{\tau }^{ + }} \leqslant 16.6$
(1)
$u_{t}^{ + } = 7.25 \times {{10}^{{ - 4}}}{{\left( {\frac{{{{\tau }^{ + }}}}{{1 + {{\omega }_{\operatorname{E} }}{{\tau }_{{\text{р}}}}}}} \right)}^{2}},$при $\bar {\mu }_{{\text{р}}}^{2}{{\tau }^{ + }} > 16.6$
В приведенных выражениях не учитывается гравитационный и продольно-диффузионный механизмы переноса ввиду их относительной малости.
Для расчета среднего значения динамической скорости на поверхности хаотичной насадки используем формулу, полученную с применением средней объемной скорости диссипации энергии [9]:
(3)
${{u}_{*}} = 1.55{{W}_{г}}{{({\xi \mathord{\left/ {\vphantom {\xi {{{{\operatorname{Re} }}_{{\text{э}}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}_{{\text{э}}}}}})}^{{0.25}}},$ЭФФЕКТИВНОСТЬ РАЗДЕЛЕНИЯ СМЕСИ
Для определения эффективности газосепарации аэрозолей можно использовать численное решение уравнения конвективного массопереноса частиц, которое для вертикального плоскопараллельного канала без насадки запишется в виде [1]
(4)
${{W}_{г}}(y)\frac{{\partial C}}{{\partial z}} = \frac{\partial }{{\partial y}}\left\{ {\left[ {{{D}_{{\text{d}}}}(y)\frac{{\partial C}}{{\partial y}}} \right] - [C{{u}_{t}}(y)],} \right\}.$Для цилиндрического канала
(5)
${{W}_{г}}(r)\frac{{\partial C}}{{\partial z}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left\{ {\left[ {r{{D}_{{\text{d}}}}(y)\frac{{\partial C}}{{\partial y}}} \right] - [C{{u}_{t}}(r)]} \right\}.$Как отмечено в монографии [1], отсутствие в правой части представленных уравнений $[C{{u}_{{\text{t}}}}(y)]$ или $[C{{u}_{{\text{t}}}}(r)]$ приводит к равномерному распределению частиц по поперечному сечению канала, что не согласуется с экспериментальными данными.
Решение уравнений (4) или (5) для вертикальных гладких каналов при $Н \gg {{d}_{{\text{э}}}}$ при равномерном профиле скорости на входе ${{W}_{г}}(y)$ или ${{W}_{г}}(r)$ дает результаты, близкие к модели идеального вытеснения газа [1, 2, 9].
В газосепараторах с контактными хаотичными насадками структура потока отличается от модели идеального вытеснения. Кроме того, численное решение уравнения массопереноса (5), записанного для цилиндрической части газосепаратора с насадками, не представляется возможным, так как задать граничные условия на каждом элементе насадки (элементов может быть несколько тысяч) затруднительно. В таких случаях в уравнение массопереноса в правую часть вводят объемный источник массы частиц, осаждающихся на поверхность насадки. При равномерной подаче газа в аппарат объемный источник записывается для всего слоя насадки [9, 10], а при наличии неравномерностей – по локальному объему. Аналогичный подход применяется при численном исследовании пленочных градирен [11] и абсорберов с насадкой [12].
Тогда уравнение массопереноса частиц представляется в следующим виде:
(6)
${{W}_{г}}(r)\frac{{\partial C}}{{\partial z}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{D}_{{\text{d}}}}(r)\frac{{\partial C}}{{\partial r}}} \right) + {{\bar {u}}_{t}}C(z,r){{a}_{{\text{v}}}}(r),$Коэффициент турбулентной диффузии частиц в ядре потока газа в хаотичной насадке найдем из соотношения [1]
(7)
${{D}_{{\text{d}}}} = \frac{{{{D}_{т}}}}{{1 + {{{{\omega }}}_{{\rm E}}}{{{{\tau }}}_{{\text{р}}}}}},$(8)
${{{{\nu }}}_{т}}(r) \approx 3.87{{{{\nu }}}_{г}}\sqrt {\xi (r){{{\operatorname{Re} }}_{э}}(r).} $К уравнению массопереноса (6) записываются следующие граничные условия:
при $z = 0,$ ${{u}_{{\text{г}}}}(r) = {{u}_{{\text{н}}}}(r)$ (вход газа);
при $z = H,$ ${{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial z}}} \right. \kern-0em} {\partial z}} = 0$ (выход газа);
при $r = R,$ ${{\partial C} \mathord{\left/ {\vphantom {{\partial C} {\partial r}}} \right. \kern-0em} {\partial r}} = 0$ (на стенке аппарата).
Конструктивные и режимные характеристики хаотичной насадки учитываются за счет объемного источника в правой части уравнения (6) и коэффициента турбулентной диффузии частиц (7).
Далее в качестве примера показано влияние профиля скорости газа ${{W}_{г}}(r)$ в поперечном сечении колонны на профили концентрации частиц и эффективность разделения смеси.
Точно описать профиль скорости в слое не представляется возможным, так как это связано с большим разнообразием конструкций хаотичных насадок, режимов работы и физическими свойствами смесей. Если распределение перепада давления по сечению насадки известно, то можно использовать приближенную связь профиля скорости газа и гидравлического сопротивления отдельных областей насадки. Это соотношение имеет следующий вид:
(9)
$\frac{{{{W}_{{гi}}}}}{{{{W}_{{гi + 1}}}}} = \sqrt {\frac{{\Delta {{Р}_{{i + 1}}}}}{{\Delta {{Р}_{i}}}}} ,\,\,\,\,i = 1,2,...,n.$Таким образом, чем больше гидравлическое сопротивление области $i + 1,$ тем меньше там скорость газа. Число областей можно выбирать по заданному относительному изменению перепада давления в соседних зонах, например на 5%.
Представленное выражение следует решать совместно с уравнением расхода газа
где ${{S}_{к}}{{W}_{{\text{о}}}} = {{V}_{г}}$ – объемный расход газа, м3/с.При совместном решении (9), (10) должен выполняться баланс энергии газового потока в насадочном аппарате
Перепад давления записывается по известному выражению
(12)
$\Delta {{Р}_{г}} = \xi \frac{Н}{{{{d}_{{\text{э}}}}}}\frac{{{{\rho }_{г}}W_{г}^{2}}}{2};\,\,\,\,\Delta {{Р}_{i}} = \xi (r)\frac{Н}{{{{d}_{{\text{э}}}}}}\frac{{{{\rho }_{г}}W_{г}^{2}(r)}}{2};$РЕЗУЛЬТАТЫ РАСЧЕТОВ
Расчеты профилей концентраций частиц в хаотичном слое выполнялись на основе применения уравнения массопереноса (6) с экспериментальным неравномерным профилем скорости газа ${{W}_{г}}(r),$ а также коэффициентом турбулентной диффузии частиц ${{D}_{{\text{d}}}}(r)$ (7) и скорости турбулентной миграции частиц ${{\bar {u}}_{t}}$ в каждой локальной в зависимости динамической скорости ${{u}_{*}}$ (3) от скорости газа, которая связана со скоростью газа ${{W}_{г}}(r)$ и с коэффициентом гидравлического сопротивления области $\xi (r).$
Результаты исследования неравномерности профиля газа в слое насадки из различных хаотичных элементов представлены в работах [7, 8], где показано, что неравномерности могут находиться в диапазоне от ${{{{W}_{m}}} \mathord{\left/ {\vphantom {{{{W}_{m}}} {{{W}_{o}}}}} \right. \kern-0em} {{{W}_{o}}}} = 0.4$ (в центре аппарата) до ${{{{W}_{m}}} \mathord{\left/ {\vphantom {{{{W}_{m}}} {{{W}_{o}}}}} \right. \kern-0em} {{{W}_{o}}}} = 1.6$ (у стенок аппарата).
Далее в качестве наиболее характерного примера рассмотрена насадка из колец Рашига, которая широко применялась в аппаратах во второй половине прошлого столетия. Из решения уравнения массопереноса (6) получен профиль концентрации частиц в зависимости ${{W}_{г}}(r)$ и вычислена локальная и осредненная эффективность газосепарации по формулам
(13)
${{\eta }_{i}} = \frac{{{{\eta }_{{i - 1}}} - {{\eta }_{i}}}}{{{{\eta }_{{i - 1}}}}},\,\,\,\,\eta = \frac{{{{C}_{{\text{н}}}} - {{С}_{{\text{к}}}}}}{{{{С}_{{\text{н}}}}}},$(14)
${{С}_{{\text{к}}}} = \frac{{\sum\limits_{i - 1}^n {{{C}_{i}}{{V}_{{{\text{г}}i}}}} }}{{{{V}_{{\text{г}}}}}}.$Результаты расчетов ${{\eta }}$ приведены на рис. 2.
Рис. 2.
Зависимость осредненной эффективности газосепарации капель воды диаметром 5 мкм от неравномерности профиля скорости газа в поперечном сечении слоя насадки из колец Рашига 10 мм. Средняя скорость газа W0 = 6 м/с.
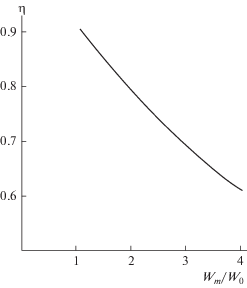
Установлено, что поперечная неравномерность профиля скорости газа может снижать эффективность разделения на 30–35% по сравнению с равномерным профилем скорости, т.е. при ${{{{W}_{m}}} \mathord{\left/ {\vphantom {{{{W}_{m}}} {{{W}_{o}}}}} \right. \kern-0em} {{{W}_{o}}}} = 1.$ Наибольшие неоднородности наблюдаются у насадки из колец Рашига (снижение ${{\eta }}$ на 35%). Наиболее эффективными являются насадки из колец Мебиуса и “Инжехим-2012” (снижение эффективности на 3–5%).
Выполнены расчеты высоты слоя насадки и перепада давления при заданной эффективности разделения $\eta = 0.985$ аэрозолей для частиц dч = 5 мкм – система воздух–вода при нормальных условиях. Численно исследовались металлические хаотичные насадки из колец Мебиуса 40 × 40 мм (аv = 191 м2/м3), "Инжехим-2012” (аv = = 160 м2/м3), кольца Рашига 35 × 35 мм (аv = = 150 м2/м3) и кольца GMP № 1 фирмы Mass Transfer Inc (аv = 220 м2/м3) [8, 13, 14].
Из представленных на рис. 3 результатов следует, что наиболее рациональным является применение насадок из колец Мебиуса и “Инжехим-2012”.
Рис. 3.
Высота насадки и перепад давления: 1 – кольца Мебиуса 40 × 40; 2 – “Инжехим-2012”; 3 – кольца Рашига 40 × 40; 4 – кольца GMR № 1 фирмы Mass Transfer Inc. Скорость газа 5 м/с.
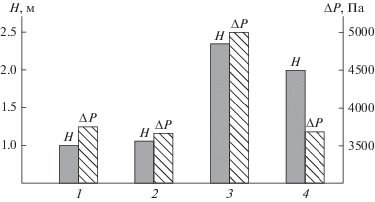
На рис. 4 приведены расчетные зависимости требуемой высоты насадочного слоя при заданной эффективности η = 0.985, а также перепада давления газа для насадки “Инжехим-2012” (16 мм, аv = = 340 м2/м3).
Рис. 4.
Зависимость высоты насадки и перепада давления от скорости газа при эффективности газосепарации η = 0.985 (98.5%) для капель диаметром dч = 5 мкм (система воздух–капли воды при нормальных условиях). Насадка “Инжехим-2012” размером 16 мм (av = = 340 м2/м3).
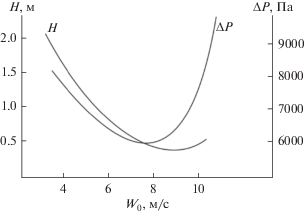
Сложные зависимости кривых на рис. 4 объясняются расчетами ${{u}_{t}} = u_{t}^{ + }{{u}_{*}}$ по формуле (1) или (2) в зависимости от значений $\bar {\mu }_{{\text{р}}}^{2}{{\tau }^{ + }}.$ При $\bar {\mu }_{{\text{р}}}^{2}{{\tau }^{ + }} \leqslant 16.6$ зависимость ${{u}_{t}}$ от скорости газа примерно в четвертой степени. Тогда при заданной эффективности η при увеличении скорости газа требуемая высота насадки снижается, также понижается и перепад давления. При $\bar {\mu }_{{\text{р}}}^{2}{{\tau }^{ + }} \geqslant 16.6$ зависимость ${{u}_{t}}$ от скорости газа примерно в первой степени, и тогда при увеличении скорости газа требуемая высота насадки повышается, что дает также повышение перепада давления.
Из расчетов следует, что в заданных условиях разделения оптимальной скоростью газа является W0 = 6–7 м/с, обеспечивающая наименьшие энергозатраты при небольшой высоте слоя $\left( {Н = 0.55{\kern 1pt} - {\kern 1pt} 0.65\,\,{\text{м}}} \right).$
Таким образом, представленная математическая модель позволяет учесть неоднородности распределения насадки, а также газа с аэрозольными частицами и выбирать наиболее эффективные конструкции контактных устройств. Газосепараторы с насадками “Инжехим” внедрены на предприятиях нефтегазохимического комплекса и удовлетворяют требованиям технического задания [10, 15].
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 18-79-101-36).
ОБОЗНАЧЕНИЯ
| ${{а}_{\nu }}$ | удельная поверхность насадки, м2/м3 |
| C | концентрация частиц, кг/м3 |
| $\bar {С}$ | средняя по поперечному сечению концентрация частиц, кг/м3 |
| ${{С}_{н}},$${{С}_{к}}$ | начальная и конечная концентрации аэрозольных частиц, кг/м3 |
| ${{D}_{к}}$ | диаметр колонны, м |
| ${{D}_{{\text{d}}}}$ | коэффициент турбулентной диффузии частиц, м2/с |
| ${{D}_{{\text{т}}}}$ | коэффициент турбулентной диффузии в потоке, м2/с |
| d | диаметр насадочного элемента слоя, м |
| dч | диаметр частиц (капель), м |
| ${{d}_{э}}$ | эквивалентной диаметр насадки (канала), м |
| $F$ | площадь стенок канала, м2 |
| $G$ | массовый расход газа, кг/с |
| Н | высота слоя насадки, м |
| j | плотность потока частиц к стенке, кг/(м2 с) |
| N | мощность, затрачиваемая на подачу газа в аппарат, Вт |
| n | число областей в поперечном сечении аппарата |
| $\Delta {{Р}_{i}}$ | перепад давления газа в i-й области, Па |
| R | радиус колонны, м |
| Rэ | эквивалентный радиус насадки (канала), м |
| $r$ | радиальная координата, м |
| ${{S}_{{\text{к}}}}$ | площадь поперечного сечения газосепаратора с насадкой, м2 |
| ${{S}_{i}}$ | площадь сечения аппарата i-й области, м2 |
| ut | скорость турбулентного осаждения частиц, м/с |
| $u_{{\text{t}}}^{ + }$ = ut/u* | безразмерная скорость осаждения |
| u* | динамическая скорость, м/с |
| ${{V}_{г}}$ | объемный расход газа, м3/с |
| ${{{v}}_{г}}$ | кинематический коэффициент вязкости газа, м2/с |
| ${{\nu }_{{\text{т}}}}$ | коэффициент турбулентной вязкости, м2/с |
| W0 | средняя скорость газа в аппарате без насадки, м/с |
| Wг | средняя скорость газа в слое, м/с |
| Wm | локальная скорость газа в зоне с насадкой, м/с |
| $z,у$ | вертикальная и поперечная координаты, м |
| ${{\varepsilon }_{{св}}}$ | удельный свободный объем насадки, м3/м3 |
| η | эффективность разделения аэрозолей |
| $\xi $ | коэффициент гидравлического сопротивления насадочного слоя |
| ${{\rho }_{г}}$ | плотность газа, кг/м3 |
| ρч | плотность частицы, кг/м3 |
| ${{\tau }_{р}}$ | время релаксации частиц, с |
| ${{\tau }^{ + }} = {{{{\tau }_{р}}u_{ * }^{2}} \mathord{\left/ {\vphantom {{{{\tau }_{р}}u_{ * }^{2}} {{{\nu }_{г}}}}} \right. \kern-0em} {{{\nu }_{г}}}}$ | безразмерное время релаксации |
| ${{\omega }_{{\rm E}}} = {{{{u}_{*}}} \mathord{\left/ {\vphantom {{{{u}_{*}}} {0.1{{R}_{э}}}}} \right. \kern-0em} {0.1{{R}_{э}}}}$ | частота энергоемких низкочастотных пульсаций среды, с–1 |
| $R{{е}_{э}} = {{{{W}_{г}}{{d}_{э}}} \mathord{\left/ {\vphantom {{{{W}_{г}}{{d}_{э}}} {{{{v}}_{г}}}}} \right. \kern-0em} {{{{v}}_{г}}}}$ | число Рейнольдса для насадки |
ИНДЕКСЫ
Список литературы
Медников Е.П. Турбулентный перенос и осаждение аэрозолей. М.: Наука, 1980.
Сугак Е.В., Войнов Н.А., Николаев Н.А. Очистка газовых выбросов в аппаратах с интенсивными гидродинамическими режимами. Казань: Отечество, 2009.
Справочник по гидравлическим сопротивлениям. М.: Машиностроение, 1992.
Масштабный переход в химической технологии: разработка промышленных аппаратов методом гидродинамического моделирования / Под ред. Розена A.M. М.: Химия, 1980.
Костанян А.Е., Белова В.В. О масштабном переходе в химической технологии // Хим. технол. 2016. № 3. С. 118.
Лаптев А.Г., Фарахов М.И., Лаптева Е.А. Проблемы и решения масштабного перехода в химической технологии // Тр. Академэнерго. 2019. № 4. С. 33.
Пушнов А.С., Балтернас П., Каган А., Загорскис А. Аэродинамика воздухоочистных устройств с зернистым слоем. Вильнюс: Техника, 2010.
Витковская Р.Ф., Пушнов А.С., Шинкунас С. Аэрогидродинамика и тепломассообмен насадочных аппаратов. СПб.: Лань, 2019.
Модели и эффективность процессов межфазного переноса. Часть 1. Гидромеханические процессы / Под ред. Лаптева А.Г.: Казань: Центр инновационных технологий, 2017.
Ageev A.A., Yakhontov D.A., Kadyrov T.F., Farakhov M.M., Lapteva E.A. Mathematical model of dispersed phase gas separation in a combined equipment // Chem. Pet. Eng. 2019. V. 55. № 7–8. P. 611.
Lapteva E.A., Stolyarova E.Yu., Laptev A.G. Numerical Estimation of the Heat and Mass Transfer Efficiency Considering Nonuniformity in Water and Air Distribution // Therm. Eng. 2020. V. 67. № 4. P. 234.
Laptev A.G., Farakhov T.M. Mathematical Model of Mass Transfer in Randomly Packed Columns with Phase Maldistribution // J. Eng. Thermophys. 2019. V. 28. № 3. P. 392.
Насадки массообменных колонн / Под ред. Баранова Д.А. М., 2009.
Каган А.М., Лаптев А.Г., Пушнов А.С., Фарахов М.И. Контактные насадки промышленных тепломассообменных аппаратов. Казань: Отечество, 2013.
Агеев А.Л., Яхонтов Д.А., Кадыров Т.Ф., Фарахов М.М., Фарахов М.И. Расчет и внедрение высокоэффективных сепарационных аппаратов очистки природного газа от дисперсной фазы // Газов. пром-сть. 2020. № 1. С. 30.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


