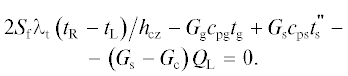Теоретические основы химической технологии, 2021, T. 55, № 4, стр. 442-451

Образование пылевых частиц в технологических многофазных реакторах

В. П. Мешалкин^a, С. В. Панченко^b, М. И. Дли^b, Е. И. Лобанева^c, *

^a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

^b Национальный исследовательский университет “МЭИ” в г. Смоленске
Смоленск, Россия

^c Национальный исследовательский университет “МЭИ”
Москва, Россия

^* E-mail: lobaneva94@mail.ru

Поступила в редакцию 24.01.2021
После доработки 22.03.2021
Принята к публикации 23.03.2021

DOI: 10.31857/S0040357121040102

Полный текст (PDF)

Аннотация

Рассмотрены вопросы образования пылевых частиц в высокотемпературных технологических реакторах. Акцент сделан на процессы, протекающие в электротермических рудовосстановительных печах фосфорного производства, когда пыль служит источником шлама, загрязняющего продукт. Предложена модель формирования пыли на основе гидродинамического взаимодействия пузырьков газа с жидкостью при их выходе на границе раздела фаз, когда разрушение пузырьков приводит к появлению капель, уносимых потоком газа. Рассмотрение положений устойчивости для максимальных возмущений в цилиндрических струях жидкости дает возможность оценить размеры капель, над поверхностью жидкости и получить качественные и количественные оценки для капель, уносимых потоком газа. Аналитические зависимости для пылеобразования в фосфорной печи позволяют связать содержание пыли с режимными параметрами, характеризующими работу печей – температурой в зоне реакции, свойствами расплава, управляющими параметрами – напряжением на электродах и дозировкой кокса. Расчеты, проведенные на основе полученных соотношений, обнаруживают удовлетворительную корреляцию с экспериментальными данными по образованию пыли в фосфорных, мартеновских печах, а также барботажных тепломассообменных установках. Представлена модель теплофизических процессов в электротермическом восстановительном реакторе в приближении сосредоточенно-распределенных параметров, учитывающая взаимодействие зон различного фазового состава, позволяющая проводить анализ режимов работы реактора от основных управляющих параметров – напряжения на электродах и доли кокса-восстановителя. Полученные результаты могут быть использованы при оптимизации режимов работы оборудования в пределах допустимых выбросов пыли.

Ключевые слова: технологический реактор, гетерогенная реакция, гидродинамика струй жидкости, формирования капель, разрыв пузырьков, гидродинамика системы газ–жидкость, гидродинамика каплеобразования, модель формирования пыли

ВВЕДЕНИЕ

Процессы химической электротермии, такие как получение карбида кремния, фосфора и т.д., являющиеся реакциями восстановления и ряд реакций растворения протекают с выделением продуктов в газовой фазе. В электротермических рудовосстановительных реакторах по производству фосфора пыль является загрязнителем продукта – фосфора, в мартеновских печах, в производстве карбида кальция образование пыли нежелательно с точки зрения экологии, в испарительных, барботажных, контактных теплообменных устройствах унос влаги – это потери чистого теплоносителя.

Одной из основных причин образования пыли при работе промышленных гетерогенных реакторов (фосфорных, мартеновских, карбидных и других печей) является унос капель расплава барботирующими газами и их отвердевание наряду с химическими реакциями в газовой фазе с образованием твердых частиц и процессами испарения и конденсации возгонов. Число сторонников гидродинамического подхода [1–3] с гипотетическим взглядом на проблему превышает количество последователей испарительного механизма [4–6] и предлагающих учитывать оба механизма [7–9]. Понятно, что при наличии теории, адекватно описывающей экспериментальные исследования, можно говорить о долевом участии каждой составляющей. Основной аргумент в пользу гидромеханики – это отсутствие пыли над зеркалом расплавленного металла, где нет потоков газа, и, совсем уж очевидно, брызгообразование и каплеунос в барботажных теплообменниках, где нет возгонов.

Печные газы рудовосстановительной фосфорной печи содержат до 200 г/м³ твердых пылевых частиц. Этот нежелательный компонент – источник образования шлама в конденсаторах фосфора и снижает качество продукта. Наиболее вероятным механизмом образования пыли является формирование капель расплава при выходе газа из реакционной зоны печи. В пользу этого механизма говорят результаты анализа химического состава пыли, который характерен для расплава в зоне плавления, когда процесс восстановления еще не протекал. Высокое содержание K₂О (до 20%) в пробах печной пыли можно отнести за счет процессов возгонки и последующей коагуляции на пылевых частицах [6]. Кроме того, режим работы печи, т.е. ее мощность существенным образом влияет на запыленность Z [6]. Эмпирически получена одна из абсурдных зависимостей, где с очевидностью следует зависимость электросопротивления от мощности через температуру, что недопустимо в уравнениях регрессии:

(1)

$Z = {\text{ }}125\varphi q_{{\text{v}}}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}\rho _{{el}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}--62.5,$

где ρ_el – удельное электрическое сопротивление расплава; φ – постоянная, характеризующая геометрическое подобие проводников; q_v – объемная мощность печи.

Химический состав шихты также влияет на запыленность посредством изменения удельного электрического сопротивления и коэффициента поверхностного натяжения расплава, который аддитивно зависит от содержания и свойств отдельных компонент [6].

Механизм образования пыли можно трактовать исходя из того, что пузыри газа в результате своего разрыва образуют мельчайшие капли. Поэтому при увеличении расхода газа резко усиливается пылеобразование.

В экспериментах [1] было установлено, что процесс разрыва пузырей составляет неотъемлемую часть механизма пылеобразования, и образованию пыли всегда предшествовало появление брызг металла. В тех случаях, когда брызг не наблюдалось, отсутствовало и образование дыма.

Согласно современным представлениям, транспортирующий унос жидкости обуславливается “струйным” и “оболочечным” механизмом образования капель при выходе газов из жидкой фазы [10].

По данным [1], основная масса брызг образуется за счет разрыва небольшой части тонкой поверхностной пленки, выступающей над расплавом. В момент ее разрыва мельчайшие брызги устремляются вверх, а окружающая пузырь жидкость стремится заполнить возникшую пустоту, одновременно вызывая на поверхности расплава кольцевую волну. Происходит так называемое схлопывание поверхностного пузырька. Смыкаясь, он создает кумулятивную струю (струю Рэлея) – выбрасывает вверх столбик воды, от подножья которого распространяется волна. Выброс расплава также сопровождается образованием брызг, крупные капельки возвращаются обратно в ванну, мелкие капельки удаляются в газовую фазу.

По [1] 60% всей образующейся пыли представляют собой мелкие капли разорвавшейся при всплывании пузыря газа пленки расплава. На долю паров и оксидов приходится около 27% от массы пыли [1].

ГИДРОДИНАМИЧЕСКИЙ ПОДХОД К ТЕОРИИ ОБРАЗОВАНИЯ ПЫЛИ И РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Рассмотрим образование капель над поверхностью жидкости полагая, что газ несет энергию, сконцентрированную в пузырьках за счет подъемных сил жидкости. Эта энергия трансформируется в энергию поверхностного натяжения капель, образуемых при разрыве пленки жидкости [11].

Баланс энергии в этом случае можно записать как

(2)

$\frac{{{{G}_{{\text{g}}}}}}{{{{\rho }_{{\text{g}}}}}}\Delta \rho gl = \frac{{dn}}{{d\tau }}\pi d_{{\text{k}}}^{2}\sigma ,$

где $\frac{{dn}}{{d\tau }}$ – скорость образования капель; l – характерный размер системы; G_g – массовый расход газа; ρ_g – плотность газа; ρ_l – плотность жидкости; d_к – диаметр капли; σ – коэффициент поверхностного натяжения жидкой фазы; g – ускорение свободного падения; Δρ = ρ_l – ρ_g.

Преобразуем это выражение:

$\frac{{{{G}_{{\text{g}}}}}}{{{{\rho }_{{\text{g}}}}}}\Delta \rho gl = \frac{{dn}}{{d\tau }}\frac{{\pi d_{{\text{k}}}^{3}{{\rho }_{{\text{l}}}}6}}{{6{{d}_{{\text{k}}}}{{\rho }_{{\text{l}}}}}}\sigma = {{G}_{{{\text{lk}}}}}\frac{{6\sigma l}}{{{{d}_{{\text{k}}}}{{\rho }_{{\text{l}}}}l}}.$

Получим

(3)

${{g}_{{{{t}_{0}}}}} = \frac{{{{G}_{{{\text{lk}}}}}}}{{{{G}_{{\text{g}}}}}} \sim \frac{{{{\rho }_{{\text{l}}}}}}{{6{{\rho }_{{\text{g}}}}}}\frac{{{{d}_{{\text{k}}}}}}{l}\frac{{\Delta \rho g{{l}^{2}}}}{\sigma } \sim \frac{{{{\rho }_{{\text{l}}}}}}{{6{{\rho }_{{\text{g}}}}}}\frac{{{{d}_{k}}}}{l}{\text{B}}{{{\text{o}}}_{l}},$

где ${{g}_{{{{t}_{0}}}}}$ – масса капель в единице массы газа над жидкостью; G_lk – масса образованных в единицу времени капель жидкости; ${\text{B}}{{{\text{o}}}_{l}} = \frac{{\Delta \rho g{{l}^{2}}}}{\sigma }$ – критерий Бонда по параметру l.

Оценки по (3) дают значение доли уноса порядка 10, что практически совпадает с экспериментальными значениями ${{g}_{{{{t}_{0}}}}}$ ≈ 4 для системы воздух–вода.

Экспериментальные результаты по уносу жидкой фазы в металлургических системах при продувке расплава газом приведены в табл. 1, где просматривается линейная зависимость уноса у поверхности от отношения плотности жидкости к плотности газа [12]. Эта же пропорция характерна для соотношения (3).

Таблица 1.

Зависимость уноса капель расплава при продувке

(ρ_l /ρ_g) × 10^–3(кг/м³)/(кг/м³)	0.83	1.0	1.25	1.67	2.5	5.0
g_t0	36	37	38	42	50	80

При диспергировании капли распределены по размерам. Наиболее характерной является зависимость, экспериментально найденная в виде распределения Розина–Раммлера. Интегральная функция распределения частиц пыли по размерам для фосфорных печей имеет значения [6], представленные в табл. 2.

Таблица 2.

Функция распределения частиц пыли по размерам на колошнике фосфорной печи

g(d)	5	15	35	57	77	87	92	95	97	98	99	100
d, мкм	0.5	1	3	5	8	12	20	30	50	100	150	200

Доля капель с диаметрами, меньше характерного, может быть выражена интегрированием функции плотности распределения в соответствующих пределах. Кроме того, в этом случае справедливо упрощенное соотношение после разложения в ряд при малых d_t:

(4)

${{g}_{{\text{t}}}} = {{g}_{{{{{\text{t}}}_{{\text{o}}}}}}}\left[ {1 - \exp {{{\left( { - \frac{{{{d}_{{\text{t}}}}}}{{{{d}_{{{\text{dis}}}}}}}} \right)}}^{n}}} \right] \approx {{g}_{{{{{\text{t}}}_{{\text{o}}}}}}}{{\left( {\frac{{{{d}_{{\text{t}}}}}}{{{{d}_{{{\text{dis}}}}}}}} \right)}^{n}},$

где d_t и d_dis – диаметр витания и средний диаметр капель после диспергирования.

Показатель степени n = 2/s, где s – дисперсия логарифмически нормального распределения (s ~ 1).

Диаметр витания определяется из баланса сил сопротивления и веса тел:

(5)

$\Delta \rho g\left( {\frac{{\pi d_{{\text{t}}}^{3}}}{6}} \right) = \left( {\frac{{\pi d_{{\text{t}}}^{2}}}{4}} \right)\xi \frac{{{{\rho }_{{\text{g}}}}\upsilon _{{\text{g}}}^{2}}}{2} \simeq 3\pi {{d}_{{\text{t}}}}{{\rho }_{{\text{g}}}}{{\nu }_{{\text{g}}}}{{\upsilon }_{{\text{g}}}}.$

Откуда для малых скоростей газов:

$\frac{{d_{{\text{t}}}^{2}}}{{{{\delta }^{2}}}} = 18{{\left( {\frac{{{{{{\rho }}}_{{\text{g}}}}\upsilon _{{\text{g}}}^{{\text{2}}}{{\delta }}}}{{{\sigma }}}} \right)}^{{0.5}}}\left( {\frac{\sigma }{{\Delta \rho g{{\delta }^{2}}}}} \right)\left( {\frac{{{{\nu }_{{\text{g}}}}\rho _{{\text{g}}}^{{0.5}}}}{{{{\sigma }^{{0.5}}}{{\delta }^{{0.5}}}}}} \right),$

или

(6)

$\frac{{{{d}_{{\text{t}}}}}}{\delta } = \sqrt {18} {\text{W}}{{{\text{e}}}^{{0.25}}}{\text{B}}{{{\text{o}}}^{{ - 0.5}}}{\text{Lp}}_{{{\delta }}}^{{ - 0.25}}.$

где ${\text{We}} = \frac{{{{{{\rho }}}_{{\text{g}}}}\upsilon _{{\text{g}}}^{{\text{2}}}{{\delta }}}}{{{\sigma }}}$ – критерий Вебера; ${\text{Bo}} = \frac{{\Delta \rho g{{\delta }^{2}}}}{\sigma }$ – критерий Бонда; ${\text{L}}{{{\text{p}}}_{{{\delta }}}} = \frac{{\sigma \delta }}{{\nu _{{\text{g}}}^{2}{{\rho }_{{\text{g}}}}}}$ – эквивалентный критерий Лапласа.

Если считать, что в результате выхода пузырьков на поверхность образуются цилиндрические полые пленки, которые обтекаются ускоренными потоками газа из пузырьков, то случайные возмущения сил трения вызывают поперечные и продольные колебания пленок. Из-за развития этих колебаний осуществляется “струйный” механизм диспергирования. Проблемам распада струй и диспергированию посвящены множество работ [13–17]. Взаимосвязь между средним диаметром при генерации капель и характерным размером системы обратно пропорциональна критерию Вебера. Эту зависимость приближенно можно оценить из соотношения

(7)

$\frac{{{{\rho }_{{\text{g}}}}\upsilon _{{\text{g}}}^{2}}}{2} \sim 4\frac{\sigma }{{{{d}_{{{\text{dis}}}}}}},\,\,\,\,\frac{{{{d}_{{{\text{dis}}}}}}}{\delta } = 8\chi {\text{We}}_{{{\delta }}}^{{ - 1}},$

где δ – характерный размер системы; χ – коэффициент пропорциональности.

Для обтекания жидкой струи газами имеет место соотношение

${{{{d}_{{{\text{dis}}}}}} \mathord{\left/ {\vphantom {{{{d}_{{{\text{dis}}}}}} \delta }} \right. \kern-0em} \delta }\sim We_{{{\delta }}}^{{ - 0.5}}.$

Более обоснованно диаметр капли получают исходя из рассмотрения неустойчивости струи жидкости, испытывающей радиальные возмущения, считая, что, струя распадается на капли, объем каждой равен объему вращения синусоиды волны около оси, проходящей через ее минимум [16]:

${{d}_{{{\text{dis}}}}} = {{\left( {\frac{{9{{\delta }^{2}}}}{4}{{\lambda }_{0}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$

Связь между критерием Вебера и волновым числом k₀ в этом случае:

${\text{W}}{{{\text{e}}}_{{{\delta }}}} = 1.5{{k}_{0}}\delta = \frac{{3\pi \delta }}{{{{\lambda }_{0}}}},$

где ${{\lambda }_{0}} = \frac{{3\pi \delta }}{{{\text{W}}{{{\text{e}}}_{{{\delta }}}}}}$ – длина волны наиболее быстро растущего возмущения.

Тогда

(8)

$\frac{{{{d}_{{{\text{dis}}}}}}}{\delta } = \sqrt[3]{{\frac{{27\pi }}{4}}}{\text{We}}_{{_{l}}}^{{ - 0.33}}.$

Таким образом, в зависимости от режима генерации капель имеет место диапазон показателей степени для скорости газа.

Тогда принимая процесс дробления струй на основе строгих положений устойчивости, получим

(9)

${{g}_{{\text{t}}}} = c\frac{{{{\rho }_{l}}}}{{{{\rho }_{{\text{g}}}}}}{\text{B}}{{{\text{o}}}_{l}}{\text{We}}_{{{\delta }}}^{{0.83}}{\text{Bo}}_{{{\delta }}}^{{ - 1}}{\text{Lp}}_{{{\delta }}}^{{ - 0,5}}.$

Безразмерная форма уравнения позволяет применять его для систем с различными свойствами.

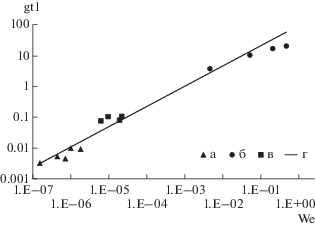
Проверка адекватности модели образования пыли и каплеуноса. На рис. 1 приведено сопоставление экспериментальных данных [18–24, 31, 32] и рассчитанных значений для уноса пыли в фосфорных, мартеновских печах и уноса капель воды в контактных теплообменниках. Коэффициент с определяется подбором. За характерный размер в газожидкостных системах обычно полагают постоянную Лапласа:

(10)

${{l}_{{{\sigma }}}} = \sqrt {\frac{\sigma }{{\Delta \rho g}}} ,$

где l_σ – постоянная Лапласа (капилярная).

Рис. 1.

Зависимость комплекса ${{{\text{g}}}_{{\text{t}}}}1$ от критерия Вебера: (а) – эксперимент [16–19] (фосфорные печи); (б) – эксперимент [22] (контактный теплообменник); (в) – эксперимент [20, 21] (мартеновские печи); (г) – теория.

Для более наглядного графического представления результатов соотношение (9) преобразовано к виду

(11)

${{{\text{g}}}_{{\text{t}}}}\frac{{{{{{\rho }}}_{{\text{g}}}}}}{{{{{{\rho }}}_{{\text{l}}}}}}{\text{Lp}}_{{{\delta }}}^{{0,5}} = {\text{cW}}{{{\text{e}}}^{{0.83}}}.$

Коэффициент с = 100. Обозначим g_t1 = ${{{\text{g}}}_{{\text{t}}}}\frac{{{{{{\rho }}}_{{\text{g}}}}}}{{{{{{\rho }}}_{{\text{l}}}}}}{\text{Lp}}_{{{\delta }}}^{{0.5}},$ тогда ${{{\text{g}}}_{{\text{t}}}}1 = {\text{cW}}{{{\text{e}}}^{{0.83}}}.$

Нижняя серия точек для уноса пыли в мартеновских печах, средняя – для фосфорных, верхняя для барботажных теплообменников.

Таким образом обнаруживается удовлетворительное совпадение данных эксперимента с теоретической кривой в широком диапазоне изменения параметров в обобщенном представлении для разных агрегатов.

АНАЛИЗ ВЛИЯНИЯ РЕЖИМОВ РАБОТЫ ТЕХНОЛОГИЧЕСКОГО РЕАКТОРА НА ОБРАЗОВАНИЕ ПЫЛИ

Рассмотрим задачу на примере фосфорной печи, модель которой, учитывающая полную взаимосвязь всех параметров, характеризующих режимы функционирования, проанализирована в [25].

Описание стационарных состояний фосфорной электротермической рудовосстановительной печи в приближении сосредоточенных параметров для реакционной зоны в соответствии с фазовым составом и механизмом физико-химических превращений базируется на представлении объекта в зональном виде, когда ванна реактора для восстановления фосфора условно подразделяется на следующие зоны: шихтовая, плавления, углеродистая, шлака, ферросплава.

Процессы тепло и массопереноса оказывают существенное влияние на качество продукта (температура газа на выходе из печи не должна быть ниже температуры конденсации фосфора, вынос твердых частиц газом должен быть минимальным для предотвращения образования шлама и т.п.) и на надежность работы реактора (температура свода, наличие слоя гарнисажа и т.п.). Учет энергетического взаимодействия различных зон реактора дает возможность отразить такую особенность, как саморегулирование.

Показатели экономичности, надежности работы элементов печи и показатели качества получаются из описания процессов во взаимосвязи для всех зон.

При описании используется стехиометрия реакции восстановления фосфора:

(12)

${{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}} + 5{\text{C}} \to 5{\text{CO}} + {{{\text{P}}}_{2}}.$

Анализ стационарных состояний электротермического реактора для восстановления фосфора в приближении сосредоточенных параметров базируется на уравнениях сохранения массы и энергии.

Общий баланс массы, покомпонентные балансы массы – для пятиокиси фосфора, для кокса имеют следующий вид:

(13)

${{G}_{{\text{s}}}} - {{G}_{{\text{g}}}} = {{G}_{{\text{l}}}},$

(14)

${{{{G}_{{\text{f}}}}С_{{\text{f}}}^{{{\text{p2o5}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{f}}}}С_{{\text{f}}}^{{{\text{p2o5}}}}} {{{\rho }_{{\text{f}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{f}}}}}} - {{\omega }_{{\text{R}}}} = {{{{G}_{{\text{l}}}}С_{{\text{l}}}^{{{\text{p2o5}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{l}}}}С_{{\text{l}}}^{{{\text{p2o5}}}}} {{{\rho }_{{\text{l}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{l}}}}}},$

(15)

${{G}_{{\text{c}}}} - {{g}_{{\text{c}}}}{{\omega }_{{\text{R}}}} = 0.$

Баланс энергии в печи:

(16)

$\begin{gathered} {{G}_{{\text{s}}}}{{c}_{{{\text{ps}}}}}t_{{\text{s}}}^{'} + {{\xi }_{e}}{{P}_{{{\text{el}}}}} = {{G}_{{\text{l}}}}{{c}_{{{\text{pl}}}}}{{t}_{{\text{R}}}} + {{G}_{{\text{g}}}}{{c}_{{{\text{pg}}}}}t_{{\text{g}}}^{*} + {{\omega }_{{\text{R}}}}{{Q}_{{\text{R}}}} + \\ + \,\,\left( {{{G}_{{\text{s}}}} - {{G}_{{\text{c}}}}} \right){{Q}_{{\text{L}}}}. \\ \end{gathered} $

Баланс энергии на границе фазового перехода:

(17)

Электрическая мощность, потребляемая реактором:

(18)

${{P}_{{{\text{el}}}}} = {{U_{{{\text{el}}}}^{2}} \mathord{\left/ {\vphantom {{U_{{{\text{el}}}}^{2}} {({{\xi }_{{{\text{e1}}}}}{{h}_{{{\text{cz}}}}})}}} \right. \kern-0em} {({{\xi }_{{{\text{e1}}}}}{{h}_{{{\text{cz}}}}})}},$

где ξ_e1 = ρ_el/S_f.

Скорость химической реакции восстановления в макропредставлении имеет вид

(19)

${{\omega }_{{\text{R}}}}~ = {{k}_{0}}{{S}_{{\text{c}}}}{{\left( {1 + {{M}_{{\text{k}}}}} \right)}^{m}}C_{{\text{l}}}^{{{\text{p2o5}}}}{\text{exp}}\left( {{{ - E} \mathord{\left/ {\vphantom {{ - E} {R{{T}_{{\text{R}}}}}}} \right. \kern-0em} {R{{T}_{{\text{R}}}}}}} \right),$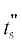

где $C_{{\text{f}}}^{{{\text{p2o5}}}}$ – содержание пятиокиси фосфора в руде; $C_{{\text{l}}}^{{{\text{p2o5}}}}$ – концентрация пятиокиси фосфора в расплаве; G_s, G_l, G_g – расход шихты, шлака, газа; ρ_f – плотность материала шихты; ρ_l – плотность жидкости-расплава; c_ps, c_pl, c_pg – теплоемкость шихты, шлака, газа; t_L, t_R – температура плавления и расплава; ω_R, Q_R – скорость и тепловой эффект реакции восстановления; P_el, ξ_e – мощность печи и ее доля используемая для реакционной зоны; ${{U}_{{{\text{el}}}}}$ – напряжение на электродах; Q_L – теплота плавления; $t_{{\text{s}}}^{{\text{'}}}$ – температура шихты на входе в печь; $t_{{\text{g}}}^{{\text{*}}}$ – температура печных газов в подсводовом пространстве. S_f – площадь поверхности фазового перехода; S_c = M_cz(6(1 – ε_c)/d_c)/ρ_c – площадь поверхности коксовых частиц; E – энергия активации; k₀ – предэкспоненциальный множитель.

– температура шихты на входе в реакционную зону.

Баланс энергии в шихтовой зоне и условия на границе фазового перехода представлены в приближении распределенных параметров в одномерной постановке. Из системы уравнений, которая является существенно нелинейной, при линеаризации арениусовской зависимости можно получить основные соотношения для анализа показателей реактора от управляющих параметров – дозировки кокса и напряжения на электродах.

Расход газа определяется условиями протекания реакции восстановления фосфора:

(20)

$\begin{gathered} {{G}_{{\text{g}}}} = {{\gamma }_{{\text{g}}}}{{k}_{0}}\left[ {{{{{M}_{{{\text{cz}}}}}(1 - {{\varepsilon }_{c}})6} \mathord{\left/ {\vphantom {{{{M}_{{{\text{cz}}}}}(1 - {{\varepsilon }_{c}})6} {({{\rho }_{c}}{{d}_{c}}}}} \right. \kern-0em} {({{\rho }_{c}}{{d}_{c}}}}} \right]C_{1}^{{{{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}}} \times \\ \times \,\,\exp \left[ {{{ - E} \mathord{\left/ {\vphantom {{ - E} {R{{T}_{{\text{R}}}}}}} \right. \kern-0em} {R{{T}_{{\text{R}}}}}}} \right]{{(1 - {{M}_{{\text{K}}}})}^{m}}. \\ \end{gathered} $

Удельный расход электроэнергии:

(21)

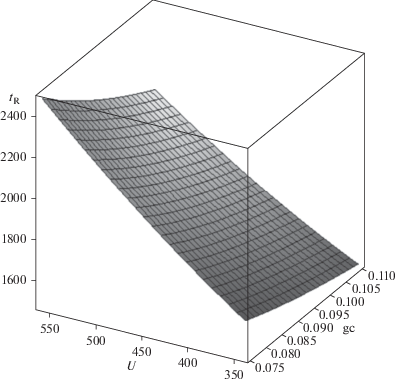
$\begin{gathered} {{b}_{{{\text{el}}}}} = {{{{\zeta }_{{\text{e}}}}{{P}_{{{\text{el}}}}}} \mathord{\left/ {\vphantom {{{{\zeta }_{{\text{e}}}}{{P}_{{{\text{el}}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}} = \left( {{{{{G}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{s}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}}--1} \right){{c}_{{{\text{pl}}}}}{{t}_{{\text{R}}}} + {{g}_{{\text{g}}}}{{Q}_{{\text{R}}}} + \\ + \,{{{{G}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{s}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}}\left( {1{\text{ }}--{{g}_{{\text{c}}}}} \right){{Q}_{{\text{L}}}} + {{c}_{{{\text{pg}}}}}t_{g}^{*} - ({{{{G}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{G}_{{\text{s}}}}} {{{G}_{{\text{g}}}}}}} \right. \kern-0em} {{{G}_{{\text{g}}}}}}){{c}_{{{\text{pg}}}}}t_{g}^{{''}}, \\ \end{gathered} $

где ${{g}_{{\text{i}}}}$ – массовые доли компонентов шихты; ${{G}_{{\text{g}}}} = {{g}_{{\text{g}}}}{{G}_{{\text{s}}}}$ – расход газа, ${{G}_{{\text{f}}}} = {{g}_{{\text{f}}}}{{G}_{{\text{s}}}}$ – расход фосфорита, ${{G}_{{{\text{si}}}}} = {{g}_{{{\text{si}}}}}{{G}_{{\text{s}}}}$ – расход кварцита, ${{G}_{{\text{c}}}} = {{g}_{{\text{c}}}}{{G}_{{\text{s}}}}$ – расход кокса.

Анализ зависимости температуры в реакционной зоне от напряжения на электродах и дозировки кокса (рис. 2) позволяет сделать вывод о концентрации продукта реакции на выходе из реактора, об удельном расходе электроэнергии и других технологических параметрах. Очевидно, что режимом работы реактора можно управлять, воздействуя на дозировку кокса и напряжение на электродах.

Рис. 2.

Зависимость температуры реакционной зоны (К) от напряжения на электродах (В) и дозировки кокса (массовая доля).

Состояние восстановительной зоны определяет режим работы реактора в целом. Там выделяется основное количество тепла, там же происходит образование продуктов реакции при восстановлении исходных веществ.

Высота слоя кокса определяется скоростью его подачи в реактор и скоростью расходования в результате химической реакции. Скорость реакции в свою очередь определяется температурой реакционной зоны, площадью поверхности реакции, а также концентрацией исходного вещества. Скорость расходования кокса определяется температурой в реакционной зоне, зависящей от тепловой мощности, поэтому высота коксовой зоны уменьшается с увеличением мощности печи, определяемой напряжением на электродах (рис. 3). В случае, когда основной вклад в сопротивление реакционной зоны вносит слой кокса, электрическое сопротивление реактора определяется высотой слоя кокса.

Рис. 3.

Зависимость высоты слоя восстановителя (м) от напряжения на электродах (В) и дозировки кокса (массовая доля).

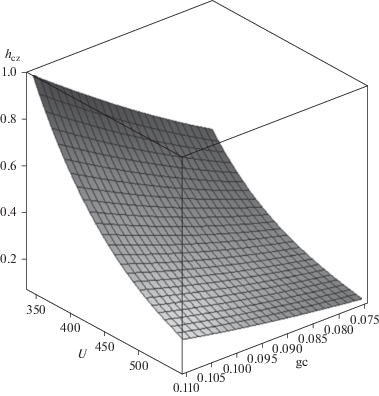
С увеличением дозировки восстановителя толщина слоя h_cz увеличивается, следовательно, увеличивается сопротивление реакционной зоны, что приводит к уменьшению выделяемой мощности и, как следствие, к уменьшению температуры реакционной зоны. Температура газообразных продуктов реакции при этом тоже уменьшается.

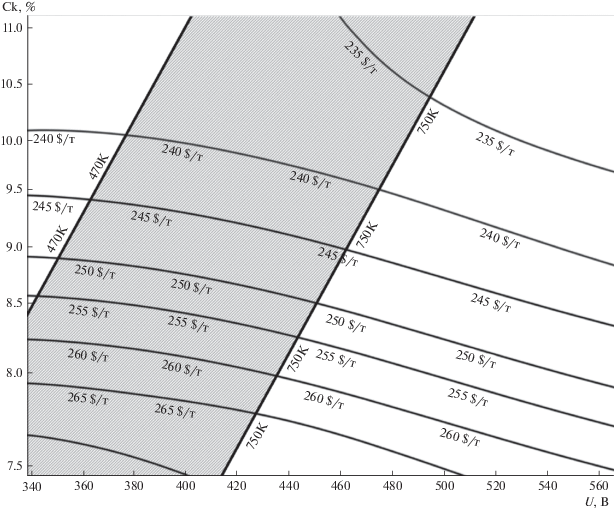
Рассмотренная модель является оценочной. Для более сложных многомерных представлений процессов, в такого типа, агрегатах использовалась двумерная модель, реализованная методом конечных элементов [26–30]. На рис. 4 представлены изолинии затрат в зависимости от управляющих переменных. Из соотношения (20) и (9) можно получить значения запыленности и уровень затрат на очистку от шлама. К сожалению, затраты на очистку от шлама экстремума не имеют и довольствоваться можно лишь предельными значениями подобно тому, как изображены пределы изменения температуры на рис. 4.

Рис. 4.

Зависимость затрат на производство фосфора от напряжения на электродах и дозировки кокса.

Анализ полученных соотношений позволяет практически полностью описать тепловую работу печи. Удельный расход энергии зависит от управляющих параметров – напряжения на электродах и дозировки кокса – посредством влияния на промежуточные технологические показатели, такие как температура в реакционной зоне, высота коксовой зоны, расход газа, расход шихты. При повышении напряжения на электродах удельный расход энергии снижается, такое же воздействие оказывает снижение дозировки кокса.

Таким образом, есть альтернативные воздействия управлений – это повышение напряжения, приводящее к снижению удельного расхода энергии, росту производительности, повышению степени полезного использования сырья и возрастанию нежелательных показателей, таких как температура печных газов, запыленность и повышение дозировки кокса, позволяющее снизить температуру газов под сводом, запыленность, содержание пятиокиси фосфора в шлаке, при этом снижается производительность и возрастает удельный расход электроэнергии в печи. Все зависимости существенно нелинейны. Особое внимание следует обратить на связь напряжения и мощности, которая определяется высотой коксовой зоны и, следовательно, зависит от режима работы печи. Размер коксовой зоны характеризует сопротивление зоны реагирования и потому становится понятным весьма сложный механизм формирования электрического режима печи. Описание работы печи в стационарных условиях позволяет получить аналитически полную взаимосвязь управляющих и технологических параметров. Из результатов анализа основных зависимостей определяются области экономичных, надежных и ресурсосберегающих режимов функционирования печи. На основе комплексного описания процессов переноса в гетерогенных химически реагирующих системах на основе взаимодействия всех фаз разработана теория рудовосстановительных агрегатов, включающая весь спектр явлений, присущих аппаратам данного типа. Анализ зависимостей температуры в реакционной зоне от напряжения на электродах и дозировки кокса позволяет сделать вывод о концентрации фосфора на выходе из печи, о температуре газов в подсводовом пространстве, об удельном расходе электроэнергии и других технологических параметрах.

В принципе оптимальные условия могут быть найдены минимизацией функции удельного расхода с учетом ограничений по всем показателям, учитываемым, например, методом штрафных функций.

Особое внимание следует обратить на связь напряжения и мощности, которая определяется высотой коксовой зоны и, следовательно, зависит от режима работы печи. Размер коксовой зоны характеризует сопротивление зоны реагирования и потому становится понятным весьма сложный механизм формирования электрического режима печи.

ЗАКЛЮЧЕНИЕ

Полученное выражение для образования пыли обобщает зависимость уноса капель от критерия Вебера как режимного параметра для различных типов технологических реакторов. Из зависимости (9) следует, что режим химического реагирования существенным образом сказывается на транспорте жидкой фазы из зоны реакции за счет увеличения скорости газа. Состав жидкой фазы, определяя коэффициент поверхностного натяжения, влияет на долю транспортируемой жидкости [11]. Количество газовой фазы или газосодержание зависит от режима работы реакционной зоны, т.е. выделяемой мощности, температуры, и интенсифицирует процесс образования капель.

Пылевые частицы являются центрами конденсации для возгонов и потому химический состав пыли может меняться по ходу газового тракта.

Кроме того, геометрия слоя коксовых частиц в реакционной зоне формирует условия роста газовых пузырьков и, следовательно, определяет режим уноса капель расплава. Количество газовой фазы или газосодержание зависит от режима работы реакционной зоны, т.е. выделяемой мощности, температуры, и интенсифицирует процесс образования капель.

Используя полученную зависимость, можно прогнозировать образование шлама в конденсаторах фосфорных печей и определять условия работы печи с максимальным качеством продукта.

Из рассмотренного выше ясно, что на появление шлама можно воздействовать режимными мероприятиями, и карты режимов должны включать изолинии зависимости потоков с тем, чтобы учесть снижение качества продукта при интенсивном образовании пыли.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-29-24094 и Министерства науки и высшего образования РФ в рамках государственного задания № FSWF-2020-0019.

ОБОЗНАЧЕНИЯ

$С_{{\text{f}}}^{{{{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}}}$	содержание пятиокиси фосфора в руде, кг/м³
$С_{{\text{l}}}^{{{{{\text{P}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{5}}}}}}$	концентрация пятиокиси фосфора в расплаве, кг/м³
E	энергия активации, Дж/моль
G_c	расход кокса, кг/с
G_f	расход фосфорита, кг/с
G_g	расход газа, кг/с
G_l	расход шлака, кг/с
G_s	расход шихты, кг/с
G_si	расход кварцита, кг/с
G_lk	масса образованных в единицу времени капель жидкости, кг/с
M_cz	масса коксовой зоны, кг
M_k	модуль кислотности
P_el	мощность печи, Вт
Q_L	теплота плавления, кДж/кг
Q_R	тепловой эффект реакции восстановления, кДж/кг
R	газовая постоянная, Дж/(моль К)
T_R	температура расплава, К
S_c	поверхность кокосовых частиц, м²
S_f	поверхность частиц шихты, м²
Z	запыленность, кг/м³
b_el	удельный расход электроэнергии, Вт/кг
c_pg	теплоемкость газа, кДж/(кг К)
c_pl	теплоемкость шлака, кДж/(кг К)
c_ps,	теплоемкость шихты, кДж/(кг К)
$\frac{{dn}}{{d\tau }}$	скорость образования капель, 1/с
d_c	диаметр коксовых частиц, м
d_dis	средний диаметр капель после диспергирования, м
d_t	диаметр витания, м
d_к	диаметр капли, м
g	ускорение свободного падения, м/с²
g_i	массовые доли компонентов шихты
g_t0	масса капель в единице массы газа
g_t	уносимая масса капель в единице массы газа
h_cz	высота слоя восстановителя, м
k₀	предэкспоненциальный множитель, с^–1
${{l}_{{{\sigma }}}}$	постоянная Лапласа (капилярная)
l	характерный размер системы, м
q_v	объемная мощность печи, Вт/м³
s	дисперсия логарифмически нормального распределения
$t_{{\text{g}}}^{*}$	температура печных газов в подсводовом пространстве, K
t_L	температура плавления, K
t_R	температура расплава, K
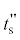	температура шихты на входе в реакционную зону, K
$t_{{\text{s}}}^{'}$	температура шихты на входе в печь, K
${{\gamma }_{{\text{g}}}}$	стехиометрический коэффициент
ν	кинематическая вязкость, м²/с
δ	характерный размер системы, м
ξ_e	доля мощности используемая в реакционной зоне
${{\lambda }_{0}}$	длина волны наиболее быстро растущего возмущения, м
ρ_el	удельное электрическое сопротивление расплава, Ом м
ρ_f	плотность материала шихты
ρ_g	плотность газа, кг/м³
ρ_l	плотность жидкости, кг/м³
σ	коэффициент поверхностного натяжения жидкой фазы, Н/м
φ	постоянная, характеризующая геометрическое подобие проводников
χ	коэффициент пропорциональности
ω_R	скорость реакции восстановления, кг/с
${{U}_{{{\text{el}}}}}$	напряжение на электродах, В
Bo	критерий Бонда
Bo_l	критерий Бонда по параметру l
${\text{L}}{{{\text{p}}}_{{{\delta }}}}$	эквивалентный критерий Лапласа
We	критерий Вебера

ИНДЕКСЫ

0	начальный
L	плавление
R	реакция
c	кокс
cz	коксовая зона
dis	диспергирование
el	электрический
f	фосфор
g	газ
i	номер
k	капля
l	жидкость
p	постоянное давление
g	газ
s	шихта
si	кварцит
t	витание
t₀	начальный момент времени
v	объем
δ	характерный размер
σ	поверхностное натяжение

Список литературы

Guézennec A. G., Huber J. Ch., Patisson F. et al. Dust formation in Electric Arc Furnace: Birth of the particles // Powder Technol. 2005. V. 157. P. 2.
Nedar L. Dust formation in BOF converter // Steel Res. 1996. № 8. P. 320.
Gritzan A., Neuschütz D. Rates and mechanisms of dust generation in oxygen steelmaking // Steel Res. 2001. № 9. P. 324.
Доронин И.Е. Экспериментальное исследование испарения компонентов сталеплавильной пыли // Металлург. 2014. № 10. С. 37.
Zhang X., Guo K., Qi W., Zhang T., Liu C., Gas holdup, bubble behaviour, and mass transfer characteristics in a two-stage internal loop airlift reactor with different screens // Can. J. Chem. Eng. 2017. V. 95. № 6. P. 1202.
Ершов В.А., Пименов С.Д. Электротермия фосфора. СПб.: Химия, 1996.
Meshalkin V.P., Panchenko S.V., Dli M.I., Bobkov V.I., Chernovalova M.V. Mechanism of the Intensification of a Heterogeneous Reduction Reaction with the Liberation of Gas Bubbles // Theor. Found. Chem. Eng. 2020. V.54. № 2. P. 304. [Мешалкин В.П., Панченко С.В., Дли М.И., Панченко Д.С. Механизм интенсификации гетерогенной реакции восстановления с выделением пузырьков газа // Теор. осн. хим. технол. 2020. Т. 54. № 2. С. 192.]
Свяжин А.Г. Механизм образования пыли при производстве стали // Сталь. 1999. № 12. С. 78.
Баптизманский В.И. Физико-химические основы кислородно-конвертерного процесса / Под. ред. Баптизманский В.И., Охотский В.Б. Донецк: Вища школа, 1981.
Кутателадзе С.С., Стырикович М.А. Гидродинамика газожидкостных систем. М.: Энергия, 1967.
Mengxu Zhang, Jianli Li, Qiang Zeng, Qiqiang Mou. et al. An Experimental Study on the Reduction Behavior of Dust Generated from Electric Arc Furnace // Appl. Sci. 2019. V. 9. № 17. P. 3604.
Сурин В.А., Назаров Ю.Н. Массо- и теплообмен, гидрогазодинамика металлургической ванны. М.: Металлургия, 1993.
Meshalkin V.P., Panchenko S.V., Bobkov V.I., Dli M.I. Analysis of the Thermophysical and Chemical-Technological Properties of Mining and Processing Waste Materials // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 157. [Мешалкин В.П., Панченко С.В., Бобков В.И., Дли М.И. Анализ теплофизических и химико-технологических свойств отходов горно-обогатительных комбинатов // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 30.]
Левич В.Г. Физико-химическая гидродинамика. М.: Физматгиз, 1959.
Нигматулин Р.И. Динамика многофазных сред. М.: Наука, 1987.
Дитякин Ю.Ф., Клячко Л.А., Новиков Б.В., Ягодкин В.И. Распыливание жидкостей. М.: Машиностроение, 1977.
Зайцев А.И., Бытев Д.О. Ударные процессы в дисперсно-пленочных системах. М.: Химия, 1994.
Ермаков В.Ф., Харламова И.Н., Вильк Ю.Н. О процессе пылеобразования при электровозгонке фосфора из фосфатно-кремнистых пород бассейна Каратау // Исследования в области электротермии. Л.: Ленниигипрохим, 1972. С. 49.
Белов В.Н., Ермаков В.Ф., Ершов В.А. Характеристика пылеуноса при электротермической переработке фосфоритов // Фосфатное сырье и его термическая подготовка для электровозгонки желтого фосфора. Л.: Ленниигипрохим, 1982. С. 60.
Альперович И.Г. О прогнозе выхода шлама в производстве фосфора (методические аспекты) // Совершенствование процессов и аппаратов производств карбида кальция, фосфора и фосфорных солей. Л.: Ленниигипрохим, 1988. С. 23.
Белов В.Н., Бескин М.Д., Жихова А.Н. и др. Испытания агломерата на промышленной фосфорной печи // Фосфорная промышленность. М.: Ниитэхим, 1978. № 2. С. 42.
Меркер Э.Э. Газодинамическая защита зоны продувки в сталеплавильных агрегатах. М.: Металлургия, 1994.
Марков Б.Л. Продувка мартеновской ванны. М.: Металлургия, 1987.
Таубман Е.И., Горнев В.А., Мельцер В.Л. и др. Контактные теплообменники. М.: Химия, 1987.
Pancnehko S.V., Dli M.I., Borisov V.V., Panchenko D.S. Analysis of thermalphysic processes in near-electrode zone of electrothermal reactor // Non-ferrous Met. 2016. № 2. P. 57.
Utikar R.P., Ranade V.V. Intensifying multiphase reactions and reactors: Strategies and examples // ACS Sustainable Chem. Eng. 2017. V. 5. № 5. P. 3607.
Панченко С.В., Панченко Д.С. Моделирование теплового состояния рудотермической фосфорной печи // Проблемы рудной электротермии. СПб.: СПбТИ, 1996. С. 12.
Бурляева Е.В., Разливинская С.В., Трегубов А.В. Разработка и применение обобщенной функциональной модели одностадийного химического производства // Прикл. инф. 2016. Т. 11. № 1(61). С. 64.
Meshalkin V.P., Panchenko S.V., Dli M.I., Panchenko D.S. Analysis of the Thermophysical Processes and Operating Modes of Electrothermic Reactor Using a Computer Model // Theor. Found. Chem. Eng. 2018. V. 52. № 2. P. 166. [Мешалкин В.П., Панченко С.В., Дли М.И., Панченко Д.С. Анализ теплофизических процессов и режимов работы электротермического реактора с использованием компьютерной модели // Теор. осн. хим. технол. 2018. Т. 52. № 2. С. 141.]
Страхов А.Ф., Страхов О.А. Особенности применения информационных технологий на стадиях жизненного цикла сложных технических систем // Прикл. инф. 2017. Т. 12. № 3(69). С. 80.
Стырикович М.А., Петухов В.И., Колокольцев В.А. Влияние плотности газовой фазы на величину капельного уноса // Теплоэнергетика. 1964. № 11. С. 78.
Розен А.М., Голуб С.И., Давыдов И.Ф. Об уносе влаги на малых расстояниях от зеркала испарения // Теор. осн. хим. технол. 1972. Т. 6. № 3. С. 57.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал