Теоретические основы химической технологии, 2021, T. 55, № 5, стр. 602-611
Сопротивление тангенциальных завихрителей с прямыми стенками каналов
А. С. Фролов a, Н. А. Войнов a, *, А. В. Богаткова a, Д. А. Земцов a, О. П. Жукова a
a Сибирский государственный университет науки и технологий им. акад. М.Ф. Решетнева
Красноярск, Россия
* E-mail: n.a.voynov@mail.ru
Поступила в редакцию 21.12.2020
После доработки 22.03.2021
Принята к публикации 23.03.2021
Аннотация
Представлены результаты экспериментального исследования и численного моделирования распределения скорости газа и давления в тангенциальных завихрителях. Моделирование осуществлялось методом конечных элементов с использованием модели турбулентности k–ε в программе Comsol Multiphysics. Экспериментально определен коэффициент сопротивления тангенциальных устройств при различных конструктивных параметрах завихрителя. После комплексной обработки полученных данных установлено влияние количества каналов, их длины и угла наклона на сопротивление завихрителя. Подтверждено, что с увеличением ширины канала при прочих равных условиях величина коэффициента сопротивления завихрителя возрастает. Рассмотрены потери напора, связанные с такими факторами, как вход–выход в канал газа и его длина. Установлено, что наибольшее влияние на величину коэффициента сопротивления оказывают потери напора, обусловленные силами вязкого трения в канале. Представлена зависимость для оценки величины коэффициента сопротивления тангенциального завихрителя.
ВВЕДЕНИЕ
Вращающиеся газожидкостные потоки используются для осуществления различных технологических процессов в химической и нефтехимической промышленности с целью интенсификации тепло и массопереноса, а также сепарации дисперсных частиц.
Вращающийся слой нашел применение при интенсификации многофазных реакций [1, 2], абсорбции и десорбции [3–6], очистке газовых выбросов [7, 8].
Устройства (завихрители) для придания газу (пару) вращательного движения применяются в сепараторах для очистки газа от капель и дисперсных частиц [9–11], скрубберах [12, 13], в контактных ступенях ректификационных колонн [14, 15], испарителях и выпарных аппаратах [16].
Вихревые потоки получили распространение в газовых турбинах, и камерах сгорания [17], в центробежных контакторах [18] а также системах охлаждения оборотной воды, градирнях [19].
Из всего многообразия завихрителей наибольшее применение нашли устройства тангенциального типа, обеспечивающие интенсивное вращение потока при сравнительно простом конструктивном исполнении. В полной мере это относится к завихрителем с прямыми стенками каналов [20].
Основными характеристиками завихрителя являются его сопротивление и скорость газа в каналах устройства. Исходя из них, осуществляется расчет конструктивных и технологических параметров разрабатываемого оборудования. Сложность расчета гидродинамических параметров завихрителей затрудняет их эффективное использование на практике и требует всесторонних исследований.
Известные зависимости для расчета величины коэффициента сопротивления завихрителей тангенциального типа представлены в табл. 1.
Таблица 1.
Зависимости для расчета коэффициента сопротивления тангенциальных завихрителей
| № | Зависимость | Литературный источник |
|---|---|---|
| 1 | ξ = exp(4.23 – 2.345А) | [21] |
| 2 | ξ = 3.1α0.7(δ/b)1.54(h/Dst)–1.48 | [22] |
| 3 | ξ = 0.5(1 – А) | [23] |
| 4 | ξ = ξin + ξout + ξg + ξtur ${{{{\xi }}}_{{{\text{tur}}}}} = 1.36 \times {{10}^{{ - 2}}}{{{{\alpha }}}^{{0.75}}}{{b}^{{1.3}}}{{n}^{{1.3}}}{{R}_{{{\text{out}}}}}^{{ - 2.5}}$ ξg = 0.2–0.6 |
[24] |
| 5 | ${{\xi }} = 21{\text{R}}{{{\text{e}}}^{{ - 0.28}}}{{\left( {\frac{h}{b}} \right)}^{{ - 0.25}}}$ | [25] |
Согласно представленным в табл. 1 данным, сопротивление тангенциального устройства зависит от фактора крутки, радиуса завихрителя, количества каналов, их ширины и высоты, толщины стенок каналов и угла их наклона. Имеющиеся литературные данные противоречивы. Так, согласно [22], с увеличением ширины канала сопротивление уменьшается, тогда как другие авторы [25] утверждают, что оно увеличивается. Наряду с этим, не достаточно изучено влияние угла наклона стенок канала и их длины на потери напора.
Многообразие факторов, влияющих на сопротивление завихрителя, не позволяет в ходе натурного эксперимента выявить степень воздействия каждого из них в отдельности. В связи с этим были использованы численные методы расчета по трехмерной модели данного устройства, описывающие поведение газа в завихрителе [26, 27].
Целью данной работы является экспериментальное исследование и численное моделирование параметров, влияющих на гидродинамику и сопротивление каналов тангенциальных завихрителей, определение уравнения для инженерных расчетов величины коэффициента сопротивления.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Завихрители продувались воздухом при температуре 25°С. Расход газа измерялся диафрагмами с помощью дифференциального манометра фиксирующего перепад давления и составил до 100 м3/ч.
Общий перепад давления определялся как разность давлений на входе и выходе из завихрителя. Экспериментальная установка была детально описана нами ранее в работе [25].
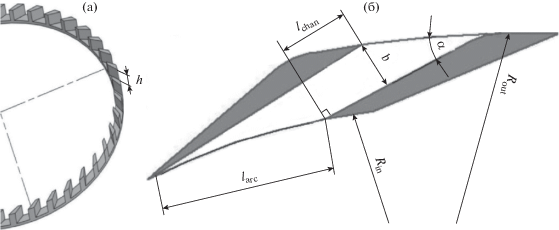
Схема тангенциального завихрителя представлена на рис. 1.
Конструктивные параметры экспериментально исследованных завихрителей приведены в табл. 2.
Таблица 2.
Параметры тангенциальных завихрителей
| № завихрителя | Rout, м | Rin, м | h, м | b, м | n | α, град | Профиль стенки канала |
|---|---|---|---|---|---|---|---|
| 1 | 0.085 | 0.057 | 0.010 | 0.0030 | 40 | 26 | Прямые параллельные |
| 2 | 0.075 | 0.07 | 0.006 | 0.0040 | 40 | 26 | |
| 3 | 0.084 | 0.077 | 0.008 | 0.0030 | 40 | 45 | |
| 4 | 0.087 | 0.078 | 0.008 | 0.0030 | 5, 10, 40 | 26 | |
| 5 | 0.087 | 0.078 | 0.010 | 0.0050 | 25, 40 | 26 | |
| 6 | 0.093 | 0.088 | 0.005 | 0.0015 | 40 | 26 | |
| 7 | 0.065 | 0.055 | 0.005 | 0.0012 | 40 | 26 | |
| 8 | 0.084 | 0.077 | 0.006 | bin = 0.006 b = 0.003 |
40 | 45 | Прямые, сужающиеся на конус |
| 9 | 0.094 | 0.087 | 0.009 | bin = 0.007 b = 0.004 |
40 | 45 |
Завихрители (рис. 1) выполнялись по 3D-модели. Высота каналов варьировалась от 0.005 до 0.01 м, ширина – 0.0012–0.007 м, угол наклона канала составил 26° и 45°. Длина канала завихрителя изменялась от 0.002 до 0.022 м, диаметр ступени Dst = 0.2 м. Для определения экспериментальной величины коэффициента сопротивления завихрителя использовалась зависимость
(1)
$\xi = {{2\Delta Р} \mathord{\left/ {\vphantom {{2\Delta Р} {\rho {{{\bar {u}}}^{2}}}}} \right. \kern-0em} {\rho {{{\bar {u}}}^{2}}}},$Среднерасходная скорость газа рассчитывалась по наименьшему сечению канала завихрителя.
Расчетный коэффициент сопротивления определялся согласно выражению (1) по полученному при численном моделировании расчетному перепаду давлений.
Число Рейнольдса определялось по зависимости
(2)
$\operatorname{Re} = {{(\bar {u}b\rho )} \mathord{\left/ {\vphantom {{(\bar {u}b\rho )} \mu }} \right. \kern-0em} \mu },$Для изучения гидродинамических характеристик завихрителя, расчета полей скоростей и перепадов давлений был применен метод численного моделирования в программе Comsol Multiphysics, которая является интерактивной средой, основанной на дифференциальных уравнениях в частных производных.
Программное обеспечение пакета поддерживает конечно-элементную технологию вместе с адаптивным построением сетки и контролем ошибок в процессе расчета модели.
Первоначально для подготовки завихрителя к гидродинамическому анализу была создана твердотельная модель (рис. 2а) его внутреннего пространства, т.е. его рабочая полость со всеми подробностями геометрии. Полученная таким образом геометрия импортировалась в программное обеспечение Comsol Multiphysics и была подвержена разбиению на элементы расчетной сетки.
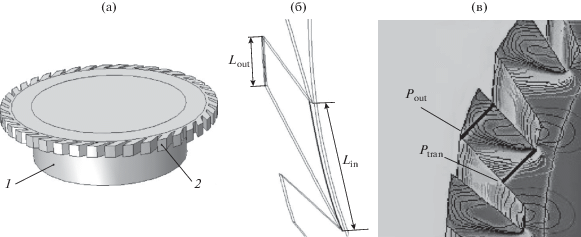
Рис. 2.
Модель завихрителя (а): 1 – газовый патрубок; 2 – канал; линии считывания давления и скорости в работе (б); линии, используемые при обработке эпюр давления (в).
Для повышения точности расчета, улучшения сходимости и оптимизации времени расчета была сгенерирована сетка, состоящая из элементов различной формы. Построенная расчетная сетка имела значительное сгущение элементов в местах наибольшего градиента скорости, что значительно отличает ее от равномерно построенной сетки. Проведенный тест на сеточную сходимость выявил оптимальную расчетную сетку, состоящую из 1200000 элементов различной формы.
В качестве рабочей среды в модели задан воздух с физико-химическими свойствами соответствующими натурным испытаниям. Искомыми величинами являлись давление и скорость газа. Определялось полная скорость up, а также ее составляющие по осям координат ux, uz, uy. Полученное давление P в процессе постобработки результатов численного эксперимента характеризует общие потери завихрителя ΔP.
Расчетное давление и скорость на входе в канал и его выходе при моделировании считывались по линиям Lin и Lout (рис. 2б), а при обработке полученных данных согласно рис. 2в.
Потери перепада давлений, обусловленные входом, ΔРin определялись (рис. 2б) согласно
где Р – общее расчетное давление в камере завихрителя, Па; Рtran –давление на входе в канал в его узком сечении.При моделировании диаметр газового патрубка завихрителя принимался равным 0.12 м, высота канала 0.008–0.04 м, ширина 0.0015–0.006 м, угол наклона канала составил 26° и 45°, количество каналов изменялось от 4 до 40, длина каналов составила 0.002–0.022 м.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
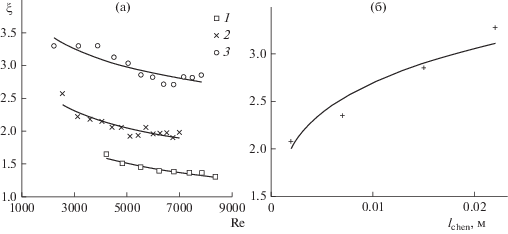
Согласно экспериментальным данным (рис. 3), с увеличением длины канала от 0.002 до 0.022 м коэффициент сопротивления завихрителя увеличивается в 1.9 раза и подчиняется зависимости ξ ~ ~ $l_{{{\text{chan}}}}^{{ - 0.184}}.$
Рис. 3.
Зависимость коэффициента сопротивления завихрителя № 5 (по табл. 2) от числа Рейнольдса (a): экспериментальные точки: 1 – длина канала lchan = 0.002 м; 2 – 0.007; 3 – lchan = 0.022 м; и длины канала lchan (б): экспериментальные точки при Re = 3000.
Как установлено, при доле свободного сечения канала в зоне их размещения равной 0.04–0.2 различие в сопротивлении составило не более 15%. Результаты численного моделирования в этих условиях также показали не существенное изменение перепада давлений.
Результаты численного моделирования выявили зависимость коэффициента сопротивления от геометрического симплекса подобия в виде ξ ~ (h/b)–0.22, что согласуется с данными [25] (табл. 1). Также результаты моделирования, при изменении высоты канала от 0.008 до 0.08 м, показали зависимость коэффициента сопротивления ξ ~ (h)–0.13.
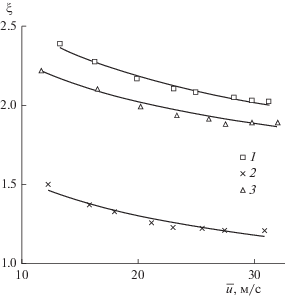
Согласно экспериментальным данным, при одинаковой ширине канала на выходе b = 0.003 м завихритель с сужающимися каналами (рис. 4, точки 1) по сравнению с устройством с каналами постоянного сечения (точки 2) имеет больший коэффициент сопротивления. Вероятно, это обусловлено переменным сечением канала, которое формирует профиль скорости по его длине.
Рис. 4.
Зависимость экспериментальной величины коэффициента сопротивления от скорости газа в каналах завихрителя при b = 0.003 м, α = 45°. Экспериментальные точки: 1 – завихритель № 8; 2 – завихритель № 3; 3 – завихритель № 4, α = 26°.
Согласно результатам численного моделирования (рис. 5) и экспериментального исследования (рис. 4 точки 2 и 3), давление завихрителя с постоянным сечением каналов при уменьшении угла наклона их стенок возрастает.
Рис. 5.
Распределение давления в завихрителе при угле наклона канала α = 45° (а) и 26° (б) при b = 0.003 м, h = 0.008 м, $\bar {u}$ = 14 м/с.

Распределение скоростей газа (при угле наклона 26° и 45°) на входе и выходе из канала представлено на рис. 6. С изменением угла наклона профили скоростей газа на выходе из канала претерпевают несущественное изменение, и потери напора на выходе (табл. 3) сравнимы. Однако распределение скоростей на входе в канал существенно изменяется при разных углах наклона стенок канала. При α = 26° (рис. 6, вход канала) формируется вогнутый профиль скорости, обусловленный увеличением длины стенки и расстояния larc между стенками соседних каналов на входе. Это приводит к росту потерь напора на входе, а также в самом канале (табл. 3) по сравнению с каналами, размещенными под углом 45°. Экспериментально определенная величина коэффициента сопротивления при изменении α с 26° до 45° уменьшилась в 1.5 раза, а при численном моделировании – в 1.9 раз.
Рис. 6.
Изменение полной скорости up по линии считывания на входе канала Lin и на выходе Lout при b = 0.003 м, h = 0.008 м, $\bar {u}$ = 14 м/с: (а) – α = 45°; (б) – α = 26°. Линии 1–3 – место считывания по высоте канала h: 1 – h = 0.004 м; 2 – 0; 3 – h = 0.008 м.
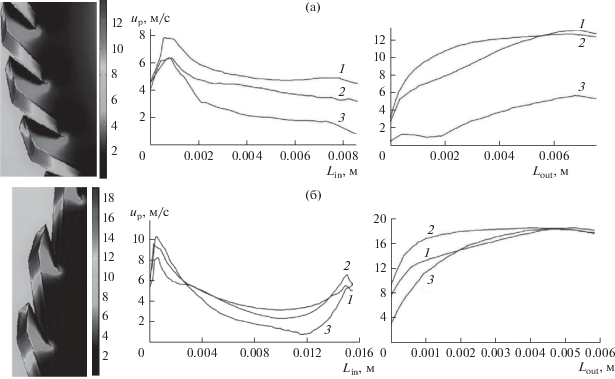
Таблица 3.
Расчетные параметры завихрителей с прямыми стенками каналов
| b, м | 0.003 | 0.006 | 0.003 | 0.006 | 0.0015 | 0.003 |
| h, м | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 | 0.008 |
| α, град | 45 | 26 | 26 | 26 | 26 | 26 |
| ΔРin, Па | 42.52 | 29.69 | 66.55 | 82.32 | 465.80 | 146.38 |
| ΔРchan, Па | 44.50 | 60.25 | 207.50 | 267.00 | 665.00 | 140.00 |
| ΔРout, Па | 19.00 | 1.25 | 18.00 | 53.50 | 35.00 | 16.00 |
| Р, Па | 109.02 | 91.19 | 292.05 | 402.82 | 1165.80 | 302.38 |
| Рtran, Па | 66.50 | 61.50 | 225.50 | 320.50 | 700.00 | 156.00 |
| Re | 2796 | 2658 | 2819 | 5638 | 2919 | 2796 |
| $\bar {u}$, м/с | 14 | 7 | 14 | 14 | 29 | 14 |
| ξ | 0.86 | 3.25 | 2.31 | 3.19 | 2.15 | 2.39 |
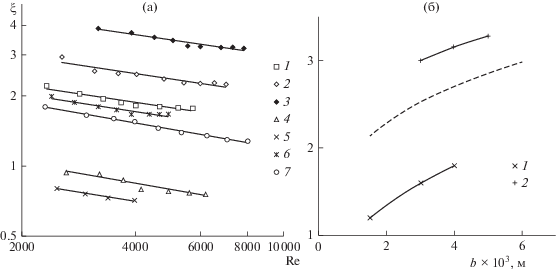
Экспериментальные значения коэффициента сопротивления завихрителей, параметры которых представлены в табл. 2, показаны на рис. 7. Как установлено моделированием (рис. 7б, пунктирная линия) и подтверждено экспериментально (рис. 7а, точки 1–7), с увеличением ширины канала величина коэффициента сопротивления завихрителя возрастает как ξ ~ b0.6, при этом ξ ~ Re0.28.
Рис. 7.
Зависимость коэффициента сопротивления от числа Рейнольдса при lchan = 0.005–0.012 м, α = 26° (а): экспериментальные точки: 1 – завихритель № 4; 2 – завихритель № 5; 3 – завихритель № 5 при lchan = 0.022 м; 4 – завихритель № 6; 5 – завихритель № 7; 6 – завихритель № 1; 7 – завихритель № 2; и от ширины канала (б) при Re = 2200–2700: 1 – длина канала lchan = 0.005 м; 2 – lchan = 0.022 м. Пунктирная линия – данные полученные при моделировании при lchan = 0.012 м.
Расчетные значения давления и коэффициентов сопротивления при моделировании параметров завихрителя с прямыми стенками каналов представлены в табл. 3.
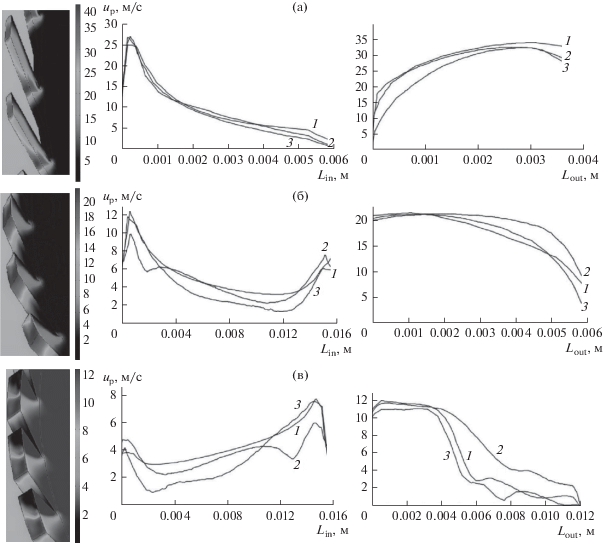
Профили скоростей, полученные при моделировании завихрителей с разной шириной канала, представлены на рис. 8. Сравнение давлений завихрителей при одинаковом числе Re показывает, что c увеличением ширины канала снижается среднерасходная скорость газа и, следовательно, динамическая скорость на стенке, что приводит к увеличению толщины пограничного слоя [28, 29] и росту потерь напора завихрителя.
Рис. 8.
Изменение полной скорости up по линии считывания на входе канала Lin и на выходе Lout при разной ширине канала завихрителя при α = 26°, Re = 2200: (а) – b = 0.0015 м; (б) – 0.003; (в) – b = 0.006 м; линии 1–3 согласно рис. 7.
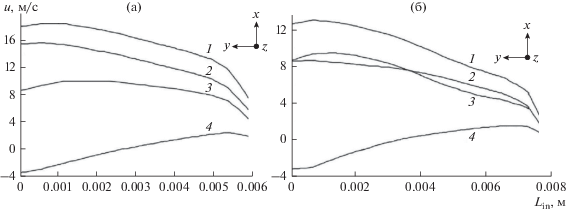
Распределение полной скорости up и ее составляющих по осям координат uz, uу и uх представлены на рис. 9. Скорости uу и uх сопоставимы и имеют большие значения в сравнении со скоростью uz. Кроме того, при угле наклона каналов 26° скорости uу и uх примерно в два раза больше, чем при угле наклона каналов 45°. Таким образом, результатами моделирования подтверждается, что с уменьшением угла наклона стенки канала интенсивность вращения потока возрастает.
Рис. 9.
Эпюры скорости на выходе из канала при разных углах наклона: (а) – α = 26°; (б) – α = 45°; линии скорости 1–4: 1 – uр; 2 – ux; 3 – uy; 4 – uz.
На основании обработки экспериментальных значений коэффициента сопротивления завихрителя, представленных на рис. 7, и результатов моделирования получена эмпирическая зависимость в виде
(4)
$\xi = {{10}^{4}}{{\alpha }^{{--0.71}}}{{\operatorname{Re} }^{{--0.28}}}{{l}_{{{\text{chan}}}}}^{{0.19}}{{b}^{{0.6}}}{{h}^{{--0.13}}}.$Уравнение (4) проверено при α = 26°–45°, b = = 0.0012–0.005 м, lchan = 0.005–0.022 м, h = 0.008–0.08 м.
ЗАКЛЮЧЕНИЕ
Результаты, полученные в ходе численного моделирования, согласуются с данными экспериментальных исследований и позволяют определять не только гидравлическое сопротивление, но и структуру потока (полей скоростей и давлений) в канале. Влияние числа каналов на общий перепад давления тангенциального завихрителя находится в пределах погрешности. Наибольшее влияние на общее сопротивление завихрителя оказывают потери напора в канале и на входе в него, что обусловлено силами вязкого трения и изменяющимися профилями скорости. Общий перепад давления завихрителей с суживающимися каналами и каналами постоянного сечения при одинаковой их ширине на выходе дает большее сопротивление, что обусловлено различием в формировании пограничного слоя по длине канала. Уменьшение угла наклона каналов завихрителя с 45° до 25° приводит к росту перепада давления до 1.5–1.9 раза, вследствие изменения профиля скорости, который оказывает влияние как на потери на входе, так и потери по длине канала.
Численным моделированием установлено и экспериментально подтверждено влияние ширины канала завихрителя на его сопротивление. Величина коэффициента сопротивления возрастает при увеличении ширины канала. Получена эмпирическая зависимость для расчета коэффициента гидравлического сопротивления тангенциального завихрителя, учитывающая его геометрические параметры.
ОБОЗНАЧЕНИЯ
| А = f/F | безразмерный фактор крутки |
| b | ширина канала в самом узком месте, м |
| D | диаметр, м |
| F = πDsh | площадь завихрителя, м2 |
| f = nhb | суммарная площадь каналов, м2 |
| h | высота канала, м |
| L | линия считывания давления, м |
| l | длина, м |
| n | количество каналов |
| Р | расчетное давление, Па |
| ΔР | перепад давлений, Па |
| u | скорость, м/с |
| среднерасходная скорость газа, м/с | |
| α | угол наклона канала, град |
| δ | толщина стенки канала, м |
| μ | коэффициент динамической вязкости, Па с |
| ξ | безразмерный коэффициент сопротивления |
| ρ | плотность газа, кг/м3 |
| Re | число Рейнольдса |
ИНДЕКСЫ
Список литературы
Wang Z., Yang T., Liu Z., Wang S., Gao Y., Wu M. Mass Transfer in a Rotating Packed Bed: A Critical Review // Chem. Eng. Process. 2019. V. 139. P. 78. https://doi.org/10.1016/j.cep.2019.03.020
Chen Y.S., Lin C.C., Liu H.S. Mass Transfer in a Rotating Packed Bed with Various Radii of the Bed // Ind. Eng. Chem. Res. 2005. V. 44. № 20. P. 7868. https://doi.org/10.1021/ie048962s
Sun B., Zou H., Chu G., Shao L., Zeng Z., Chen J. Determination of Mass-Transfer Coefficient of CO2 in NH3 and CO2 Absorption by Materials Balance in a Rotating Packed Bed // Ind. Eng. Chem. Res. 2012. V. 51. № 33. P. 10949. https://doi.org/10.1021/ie202983x
Qian Z., Xu L., Cao H., Guo K. Modeling Study on Absorption of CO2 by Aqueous Solutions of N-Methyldiethanolamine in Rotating Packed Bed // Ind. Eng. Chem. Res. 2009. V. 48. № 20. P. 9261. https://doi.org/10.1021/ie900894a
Chen Q.Y., Chu G.W., Luo Y., Sang L., Zhang L.L., Zou H.K., Chen J.F. Polytetrafluoroethylene Wire Mesh Packing in a Rotating Packed Bed: Mass-Transfer Studies // Ind. Eng. Chem. Res. 2016. V. 55. № 44. P. 11606. https://doi.org/10.1021/acs.iecr.6b02630
Sun B.C., Wang X.M., Chen J.M., Chu G.W., Chen J.F., Shao L. Simultaneous Absorption of CO2 and NH3 into Water in a Rotating Packed Bed // Ind. Eng. Chem. Res. 2009. V. 48. № 24. P. 11175. https://doi.org/10.1021/ie9001316
Qian Z., Li Z.H., Guo K. Industrial Applied and Modeling Research on Selective H2S Removal Using a Rotating Packed // Ind. Eng. Chem. Res. 2012. V. 51. № 23. P. 8108. https://doi.org/10.1021/ie2027266
Guo K., Wen J., Zhao Y., Wang Y., Zhang Z., Li Z., Qian Z. Optimal Packing of a Rotating Packed Bed for H2S Removal // Environ. Sci. Technol. 2014. V. 48. № 12. P. 6844. https://doi.org/10.1021/es404913e
Овчинников А.А. Динамика двухфазных закрученных турбулентных течений в вихревых сепараторах. Казань: Новое знание, 2005.
Гурбанов А.Н. Высокоэффективное сепарационное оборудование для очистки природного газа и газов нефтепереработки // Нефтепромысл. дело. 2017. № 6. С. 46.
Замалиева А.Т., Зиганшин М.Г. Повышение энергетической и экологической эффективности систем газоочистки на ТЭС // Изв. ТПУ. 2019. Т. 330. № 9. С. 143. https://doi.org/10.18799/24131830/2019/9/2263
Войнов Н.А., Жукова О.П., Кожухова Н.Ю., Богаткова А.В. Вихревое контактное устройство для очистки газовых выбросов // Хим. растит. сырья. 2018. № 2. С. 217. https://doi.org/10.14258/jcprm.2018023448
Коньков О.А., Дмитриев А.В., Николаев А.Н. Применение вихревых аппаратов для очистки газовых выбросов при производстве и переработке пластмасс // Экол. пром-сть. Росс. 2010. № 1. С. 8.
Voinov N.A., Zhukova O.P., Voinov A.N., Zemtsov D.A. Efficiency of a vortex contact stage in thermal distillation // Theor. Found. Chem. Eng. 2016. V. 50. № 5. P. 705. https://doi.org/10.1134/S0040579516050390 [Войнов Н.А., Жукова О.П., Войнов А.Н., Земцов Д.А. Эффективность вихревой ступени при термической ректификации // Теорет. основы хим. технол. 2016. Т. 50. № 5. С. 525-531. https://doi.org/ 10.7868/S0040357116050134]
Voinov N.A., Frolov A.S., Bogatkova A.V., Zemtsov D.A., Zhukova O.P. Hydrodynamics and Mass Transfer at the Vortex Stage and during Bubbling // Theor. Found. Chem. Eng. 2019. V. 53. № 6. P. 972. https://doi.org/10.1134/S0040579519060149 [Войнов Н.А., Фролов А.С., Земцов Д.А., Жукова О.П., Богаткова А.В. Гидродинамика и массообмен на вихревой ступени при барботаже // Теор. осн. хим. технол. 2019. Т. 53. № 6. С. 622. https://doi.org/10.1134/S0040357119060149]
Voinov N.A., Zhukova O.P., Konovalov N.M. Hydrodynamics and Heat Transfer during Boiling in a Rotating Gas–Liquid Layer // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 987. https://doi.org/10.1134/S0040579518060143 [Войнов Н.А., Жукова О.П., Коновалов Н.М. Гидродинамика и теплоотдача при кипении во вращающемся газожидкостном слое // Теорет. основы хим. технол. 2018. Т. 52. № 6. С. 689–697. https://doi.org/10.1134/S0040357118060179]
Eldrainy Y.A., Ibrahim M.F.A., Jaafar M.N.M. Investigation of radial swirler effect on flow pattern inside a gas turbine combustor // Mod. Appl. Sci. 2009. V. 3. № 5. P. 21.
Sandilya P., Rao D.P., Sharma A., Biswas G. Gas-Phase Mass Transfer in a Centrifugal Contactor // Ind. Eng. Chem. Res. 2001. V. 40. № 1. P. 384. https://doi.org/10.1021/ie0000818
Дмитриева О.С., Дмитриев А.В., Николаев А.Н. Распределение циркулирующей воды в рабочей зоне вихревой камеры с дисковым распылителем с целью повышения эффективности процесса охлаждения // Chem. Pet. Eng. 2014. V. 50. Р. 169. https://doi.org/10.1007/s10556-014-9874-1
Ishak M.S.A., Jaafar M.N.M., Omar W.Z.W. Experimental Analysis on the Formation of CO-NO-HC in Swirling Flow Combustion Chamber // J. Teknol. 2015. V. 72. № 4. P. 21. https://doi.org/10.11113/jt.v72.3909
Лаптев У.Г. Модели пограничного слоя и расчет тепломассообменных процессов. Казань: Казанск. ун-т, 2007.
Собин В.М., Ершов А.И. Исследование структуры и гидравлического сопротивления турбулентного закрученного потока в коротких трубах // Изв. Акад. наук Б. ССР. Сер. Физ. энерг. наук. 1972. № 3. С. 56.
Идельчик Е.И. Справочник по гидравлическим сопротивлениям. М.: Наука, 1992.
Voinov, N.A., Zhukova, O.P., Nikolaev, N.A. Hydrodynamics of the vortex stage with tangential swirlers // Theor. Found. Chem. Eng. 2010. V. 44. № 2. P. 213. https://doi.org/10.1134/S0040579510020132 [Войнов Н.А., Жукова О.П., Николаев Н.А. Гидродинамика вихревой ступени тангенциальными завихрителями // Теор. осн. хим. технол. 2010. Т. 44. № 2. С. 225].
Voinov N.A., Zemtsov D.A., Zhukova O.P., Bogatkova A.V. Hydraulic Resistance of Tangential Swirlers // Chem. Pet. Eng. 2019. V. 55. P. 51. https://doi.org/10.1007/s10556-019-00584-y
Wu W., Luo Y., Chu G.W., Liu Y., Zou H.K., Chen J.F. Gas Flow in a Multiliquid-Inlet Rotating Packed Bed: Three-Dimensional Numerical Simulation and Internal Optimization // Ind. Eng. Chem. Res. 2018. V. 57. № 6. P. 2031. https://doi.org/10.1021/acs.iecr.7b04901
Candel S., Durox D., Schuller T., Bourgoin J.F., Moeck J.P. Dynamics of Swirling Flames // Annu. Rev. Fluid Mech. 2014. V. 46. P. 147. https://doi.org/10.1146/annurev-fluid-010313-141300
Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974.
Хьюитт Дж., Холл-Тейлор Н. Кольцевые двухфазные течения. М.: Энергия, 1974.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии