Теоретические основы химической технологии, 2021, T. 55, № 6, стр. 670-689
Автоматизированное технологическое проектирование оптимальной системы теплообмена установки брагоректификации
И. И. Емельянов a, Н. Н. Зиятдинов a, *, Т. В. Лаптева a, А. А. Рыжова a, Р. В. Семин a
a Казанский национальный исследовательский технологический университет
Казань, Россия
* E-mail: nnziat@yandex.ru
Поступила в редакцию 08.07.2021
После доработки 12.07.2021
Принята к публикации 12.07.2021
Аннотация
Рассматриваются декомпозиционные NLP/LP/NLP-методы автоматизированного технологического проектирования экономически оптимальных распределенных систем рекуперативного теплообмена технологических потоков на основе задачи о назначениях и принципа закрепления промежуточных переменных, обсуждаются вопросы организации суперструктур системы теплообмена и их декомпозиции, способы снижения вычислительных затрат решаемых задач оптимальной тепловой интеграции. Проводится исследование предлагаемых методов синтеза на примере установки брагоректификации, решается задача синтеза оптимальной многостадийной системы теплообмена и системы теплообмена с разделением технологических потоков.
ВВЕДЕНИЕ
Одним из эффективных подходов к решению задач энергосбережения является тепловая интеграция технологических потоков производственных систем [1, 2]. Под тепловой интеграцией понимается минимизация потребления энергии химико-технологических систем (ХТС) путем организации оптимальной схемы передачи термодинамически осуществимой целевой энергии между технологическими потоками, подвода и отвода тепловой энергии внешними горячими и холодными агентами, создания оптимальных условий эксплуатации теплообменного оборудования. В настоящее время в практике оптимального проектирования стоят вопросы совместной интеграции водноэнергетических систем [3], крупномасштабной теплоинтеграции процессов [4, 5]. Авторы работы [6] разработали модель P-графа, дающую хорошие результаты при синтезе интегрированных систем теплообмена и водоподготовки. В [7] предложен двухэтапный алгоритм решения задачи интегрального синтеза водноэнергетической системы. Для достижения высокой степени рекуперации энергии и утилизации низкопотенциального тепла в технологические процессы в ряде работ предлагается интегрировать газовые и паровые турбины, тепловые насосы и циклы глубокого охлаждения [8–12]. Однако развитие методов синтеза гетерогенных систем требует эффективных методов синтеза гомогенных систем, а эта задача по-прежнему не теряет своей актуальности.
В общем случае задача технологического проектирования оптимальных систем теплообмена (СТО) формализуется в виде задачи дискретно-непрерывного нелинейного программирования, где вектор поисковых переменных включает структурные переменные, определяющие связи между теплообменным оборудованием, и непрерывные переменные, характеризующие размеры и режимы работы аппаратов. На сегодняшний день разработаны многочисленные подходы и методы оптимальной теплоинтеграции, позволяющие проектировать системы теплообмена технологических потоков, оптимальные в некоторой локальной области. Однако, как показывает практический опыт ряда исследователей, глобальное решение задачи может значительно отличаться от найденных экстремальных значений, определенных исходя из соображений термодинамической эффективности или на основе эвристик. Алгоритмические методы синтеза, использующих в качестве начального приближения такие соображения, оказываются ограничены некоторой локальной областью. Причиной этого, в частности, является большая размерность решаемых задач, наличие большого множества экстремумов вследствие многовариантности организации систем теплообмена [13].
Основанный на термодинамическом подходе пинч-метод проектирования позволяет эффективно распределить энергетические ресурсы ХТС от горячих холодным потокам на основе анализа температурно-энтальпийных интервалов композитных кривых [14]. Но, к сожалению, системы оптимальные по термодинамическому критерию могут оказаться неоптимальны по критерию экономического избытка теплообменных аппаратов малых определяющих размеров. На решение этой проблемы направлена одна из последних работ [15], в которой предлагается алгоритм поддержки принятия решений при проектировании систем теплообмена в зависимости от заранее определенных структурных ограничений, таких как максимальное число теплообменников, наибольшее число последовательно установленных теплообменников на каждом потоке, наибольшее число разделений потока и т.д. В работе [16] задача формулируется и решается путем расширения структуры P-графа для комбинаторной оптимизации системы теплообмена, что позволяет учесть компромисс между энергетическими и капитальными затратами на организацию системы теплообмена. Полученные результаты демонстрируют решения, которые не могут быть получены с помощью пинч-методов проектирования. В работе [17] предлагается вариант синтеза основанный на минимизации диссипации для заданной общей тепловой нагрузки в виде минимальной общей площади поверхности теплообмена, коррелирующей со стоимостью системы теплообмена. В [18] рассматривается алгоритм оценки необратимости при синтезе сложных систем теплообмена, в работе [19] проводят исследование необратимости при теплообмене с различной гидродинамической структурой потоков, что дает хорошую теоретическою основу для развития термодинамического подхода.
Несмотря на широкое применение и эффективность термодинамического подхода к проектированию, лучшие результаты позволяют получить методы, формализованные на моделях математического программирования. Их можно условно разделить на методы последовательного и интегрального синтеза. В методах последовательного синтеза применяются способы декомпозиции задачи синтеза СТО на ряд подзадач, что значительно упрощает процесс решения. Среди множества методов последовательного синтеза хорошие результаты дает алгоритм, предложенный в работе [20], включающий последовательность трех локальных подзадач: минимизации потребления внешних утилит, минимизации числа теплообменников и минимизации капитальных затрат на СТО или суммарной площади поверхностей теплообмена. Для решения двух первых подзадач предлагается использовать известные в линейном программировании транспортную модель [21] или модель с промежуточными пунктами [22]. Недостатком последовательного подхода является очевидное отсутствие компромисса между оптимальным количеством энергии, подводимой к системе, числом теплообменников и требованиями к площадям теплообмена вследствие независимого решения оптимизационных задач. Тем не менее последовательный подход часто используется для решения задачи синтеза СТО промышленных масштабов.
Интегральные методы оптимизации рассматривают все упомянутые ранее компромиссы на гипотетически обобщенной, агрегированной строгой модели (суперструктуре), содержащей избыточное число вариантов организации СТО. В качестве эффективных примеров интегральных методов можно привести метод на основе многостадийной суперструктуры, предложенной в [23], модель, разработанную в [24], модель смешанного дискретно-непрерывного нелинейного программирования (MINLP) на основе температурных интервалов [25] и т.д. Интегральные подходы в большинстве случаев превосходят последовательные. Однако избыточность суперструктуры порождает множество локальных минимумов критерия оптимальности, что требует использования хорошего начального приближения и методов глобальной оптимизации. Поскольку интегральный синтез сопряжен с рядом вычислительных сложностей, широкое развитие приобретают безградиентные методы: методы роя частиц [26], дифференциальной эволюции [27], генетические алгоритмы [28] и их комбинации [29, 30]. К сожалению, из-за большой размерности поискового пространства задач промышленных масштабов, алгоритмы стохастической оптимизации не могут гарантировать достижения глобальности решения и требуют больших вычислительных ресурсов. Детерминированные решатели, такие как алгоритм BARON пакета GAMS [31], дают хороший результат, но также требуют больших затрат машинного времени даже для задач малых размерностей [32].
В работе [33] предложен метод синтеза оптимальных одностадийных систем теплообмена основе декомпозиции суперструктуры СТО на суперструктуры элементарных структурных блоков теплообмена каждой совокупности горячего и холодного технологических потоков. Метод позволяет построить итерационную процедуру, в которой направление дальнейшего поиска определяется комбинацией структурно связанных элементарных блоков, определяющих схему оптимального теплообмена каждой совокупности горячего и холодного технологических потоков. В последующих работах авторами рассмотрены задачи синтеза систем многостадийного теплообмена [34, 35] и систем одностадийного теплообмена с делением технологических потоков [13], где предложен алгоритм сведения исходной MINLP-задачи к трехуровневой итерационной последовательности задач NLP/LP/NLP. Для этого рассмотрен новый подход к целевой и структурной декомпозиции исходной задачи на основе закрепления группы поисковых переменных.
Несмотря на успехи в решении проблемы оптимальной теплоинтеграции, лишь в нескольких публикациях исследуются реальные примеры промышленного масштаба [36–39]. Настоящая статья посвящена исследованию предлагаемого нами алгоритмического подхода, основанного на задаче о назначениях и декомпозиционном принципе закрепления переменных на примере установки брагоректификации. Выбор установки брагоректификации как объекта теплоинтеграции неслучаен и, как показано нами в [33], имеет множество технологических потоков, удовлетворяющих термодинамическим условиям для теплоинтеграции.
МЕТОДЫ СИНТЕЗА ОПТИМАЛЬНЫХ СИСТЕМ РЕКУПЕРАТИВНОГО ТЕПЛООБМЕНА НА ОСНОВЕ ЗАДАЧИ О НАЗНАЧЕНИЯХ
Предположим, мы построили математическую модель химико-технологической системы, в которой определены положения теплообменного оборудования, необходимого для создания условий ведения технологического процесса. Отсюда известны составы, расходы, теплоемкости, входные и выходные температуры холодных (нагреваемых) и горячих (охлаждаемых) технологических потоков, тепловые нагрузки теплообменников. Задача синтеза оптимальных СТО состоит в определении оптимальной топологии организации передачи тепловой энергии от потоков, которые требуется нагреть, технологическим потокам, которые необходимо охладить, режимов работы теплообменного оборудования, площадей поверхностей теплопередачи, при которых суммарные приведенные капитальные и эксплуатационные затраты примут минимальное значение. Такая задача относится к классу недетерминированных задач с полиномиальным временем. Эффективность решения задачи синтеза оптимальной СТО во многом определяется синтезированной моделью суперструктуры, определяющей связи между горячими и холодными потоками, способа поиска оптимального решения на суперструктуре, выбранных методов оптимизации и значений начальных приближений по поисковым переменным. Рассмотрим несколько частных вариантов организации суперструктуры системы рекуперативного теплообмена.
Суперструктура систем одностадийного рекуперативного теплообмена потоков. Система одностадийного рекуперативного теплообмена (рис. 1) может быть представлена в виде двух подсистем – подсистемы рекуперативных теплообменников и концевых нагревателей и холодильников. Возможные варианты организации передачи тепловой энергии от горячих (охлаждаемых) потоков системы холодным (нагреваемым) потокам определяются в виде матрицы рекуперативных теплообменников. После прохождения подсистемы рекуперативных теплообменников потоки поступают в подсистему концевых нагревателей и холодильников, в которых с участием внешних энергетических потоков реализуется их донагревание и доохлаждение до требуемых температур и фазовых состояний. Согласно представленной избыточной модели системы теплообмена (суперструктуры) для каждого горячего потока в матрице рекуператоров может быть назначен лишь один холодный поток. При этом установка рекуперативного теплообменника не является обязательным условием вследствие отсутствия в некоторых случаях необходимой движущей силы целенаправленного рекуперативного теплообмена. В таком случае для совокупности этих потоков достижение требуемых выходных условий обеспечивается концевыми нагревателями и холодильниками.
Очевидно, что полученная оптимальная структура системы теплообмена будет характеризоваться высоким значением экономического критерия. Поэтому нами предлагаются варианты ее модификации.
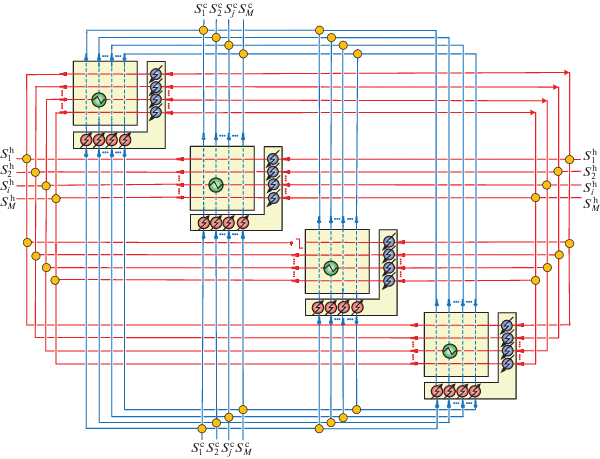
Суперструктура последовательного (многостадийного) теплообмена. Случай организации системы многостадийного теплообмена предполагает, что каждый поток системы может обмениваться тепловой энергией с множеством других потоков последовательно в несколько стадий. Форма представления суперструктуры (рис. 2) определена множественным прохождением каждого горячего и холодного потоков системы рекуперативных теплообменников.
Ввиду того что заранее неизвестны количества теплоты, отбираемой от горячих и передаваемой холодным потокам на каждой стадии, в представленной модели суперструктуры вектор независимых переменных должен быть дополнен коэффициентами, характеризующими для каждого потока распределение тепловых нагрузок по стадиям. Таким образом, суммарная тепловая нагрузка теплообменников на q-й стадии системы теплообмена определяется в виде (1) с ограничениями (2):
(1)
$\begin{gathered} Q_{{{{q}_{i}}}}^{{\text{h}}} = \alpha _{{{{q}_{i}}}}^{{\text{h}}}\Delta H_{i}^{{\text{h}}},\,\,\,\,Q_{{{{q}_{j}}}}^{{\text{c}}} = \alpha _{{{{q}_{j}}}}^{{\text{c}}}\Delta H_{j}^{{\text{c}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{q}_{i}} = 1 \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}, \\ \end{gathered} $(2)
$\begin{gathered} \sum\limits_{{{q}_{i}}} {\alpha _{{{{q}_{i}}}}^{{\text{h}}} - 1 = 0} ,\,\,\,\,\sum\limits_{{{q}_{i}}} {\alpha _{{{{q}_{j}}}}^{{\text{h}}} - 1 = 0} , \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}. \\ \end{gathered} $Поскольку нам заранее не известны оптимальные значения этих коэффициентов, предлагается организовывать итерационный алгоритм с их последовательным уточнением. На k-й итерации алгоритма они определяются в виде
(3)
$\begin{gathered} \alpha _{{{{q}_{i}}}}^{{{\text{h,}}(k)}} = \frac{{Q_{{{{q}_{i}}}}^{{{\text{h,(}}k{\text{)}}}}}}{{\Delta H_{i}^{{\text{h}}}}},\,\,\,\,\alpha _{{{{q}_{j}}}}^{{{\text{c,}}(k)}} = \frac{{Q_{{{{q}_{j}}}}^{{{\text{c,}}(k)}}}}{{\Delta H_{j}^{{\text{c}}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{q}_{i}} = 1 \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}. \\ \end{gathered} $Отметим, что веденные начальные приближения $\alpha _{{{{q}_{i}}}}^{{{\text{h,}}(0)}},\alpha _{{{{q}_{j}}}}^{{{\text{c,}}(0)}}$ могут в некоторых случаях привести к ситуациям, когда на выходе потоков из подсистемы рекуперативных теплообменников для обеспечения передачи заданного количества тепла на стадии необходимо установить концевые холодильники и нагреватели. Однако в процессе оптимизации все промежуточные теплообменники будут ликвидированы, что обусловлено их экономической нецелесообразностью.
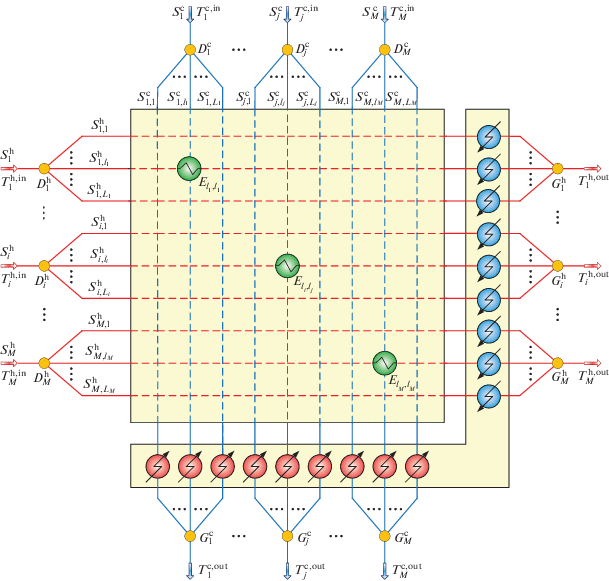
Суперструктура параллельного теплообмена с разделением технологических потоков. Форма представления суперструктуры предполагает деление технологических потоков на входе в подсистему рекуперативного теплообмена и смешение на выходе из нее. Она может быть представлена состоящей из систем одностадийного теплообмена для каждой совокупности технологических потоков, полученных делением входных потоков системы теплообмена (рис. 3). Каждый поток, проходящий через матрицу рекуперативных теплообменников будем в дальнейшем называть элементарным потоком СТО.
Преимущество такого варианта представления состоит в возможности организации параллелизма при расчете оптимальных структур для каждой совокупности горячих и холодных элементарных потоков при известных значениях коэффициентов деления потоков. Однако независимость синтеза отдельных подсистем может нарушить правило эмерджентности проектирования оптимальных систем. В качестве альтернативного варианта организации решения может рассматриваться суперструктура, в которой элементарные технологические потоки проходят через единый блок рекуперативных теплообменников (рис. 4).
Управляющими переменными, характеризующими представленные топологии суперструктур выступают коэффициенты разделения входных потоков. Суммарная тепловая нагрузка теплообменников на l-м элементарном потоке системы теплообмена и массовый расход l-го элементарного потока определяются из выражений (4) и (5) соответственно с учетом ограничений-равенств (6):
(4)
$\begin{gathered} Q_{{{{l}_{i}}}}^{{\text{h}}} = \beta _{{{{l}_{i}}}}^{{\text{h}}}\Delta H_{i}^{{\text{h}}},\,\,\,\,Q_{{{{l}_{j}}}}^{{\text{c}}} = \beta _{{{{l}_{j}}}}^{{\text{c}}}\Delta H_{j}^{{\text{c}}},\,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}, \\ \end{gathered} $(5)
$\begin{gathered} F_{{{{l}_{i}}}}^{{\text{h}}} = \beta _{{{{l}_{i}}}}^{{\text{h}}}F_{i}^{{\text{h}}},\,\,\,\,F_{{{{l}_{j}}}}^{{\text{c}}} = \beta _{{{{l}_{j}}}}^{{\text{c}}}F_{j}^{{\text{c}}},\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}, \\ \end{gathered} $(6)
$\begin{gathered} \sum\limits_{{{l}_{i}}} {\beta _{{{{l}_{i}}}}^{{\text{h}}} - 1 = 0} ,\,\,\,\,\sum\limits_{{{l}_{j}}} {\beta _{{{{l}_{j}}}}^{{\text{c}}} - 1 = 0} , \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}. \\ \end{gathered} $Коэффициенты $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$ на k-й итерации определяются в виде
(7)
$\begin{gathered} \beta _{{{{l}_{i}}}}^{{{\text{h,(}}k{\text{)}}}} = \frac{{F_{{{{l}_{i}}}}^{{{\text{h,(}}k{\text{)}}}}}}{{F_{i}^{{{\text{h,(}}k{\text{)}}}}}},\,\,\,\,\beta _{{{{l}_{j}}}}^{{{\text{c,(}}k{\text{)}}}} = \frac{{F_{{{{l}_{j}}}}^{{{\text{c,}}(k)}}}}{{F_{j}^{{{\text{c,}}(k)}}}},\,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}. \\ \end{gathered} $Поскольку описанные суперструктуры характеризуют пространство всех возможных вариантов организации представленных вариантов СТО, исходная задача MINLP может быть сведена к задаче нелинейного программирования (NLP). Однако прямое решение задачи синтеза оптимальной СТО на представленных суперструктурах сопряжено с рядом вычислительных трудностей. Ввиду избыточности моделей суперструктур критерий оптимальности имеет множество локальных минимумов, что, как отмечалось раннее, требует использования методов глобальной детерминированной или стохастической оптимизации. Учитывая большую размерность поискового пространства, даже решение задач синтеза оптимальных СТО малой размерности может характеризоваться значительными вычислительными затратами. Однако преимуществом представленных суперструктур является возможность их декомпозиции на суперструктуры более низкого иерархического уровня организации при закреплении коэффициентов распределения нагрузок по стадиям $\alpha _{{{{q}_{i}}}}^{{\text{h}}},\alpha _{{{{q}_{j}}}}^{{\text{c}}}$ и разделения потоков $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$. Нами предлагается трехуровневый алгоритм синтеза оптимальных систем теплообмена, включающий NLP-задачу нахождения оптимальных экономических оценок на теплообмен каждой совокупности горячего и холодного технологических потоков на уровне 1, задачу линейного программирования (LP) определения оптимальной топологии СТО на уровне 2 и NLP-задачу определения нового приближения по закрепляемым переменным на уровне 3. На основе рассмотренных суперструктур формализуем основные постановки задач на различных уровнях предлагаемого алгоритма синтеза.
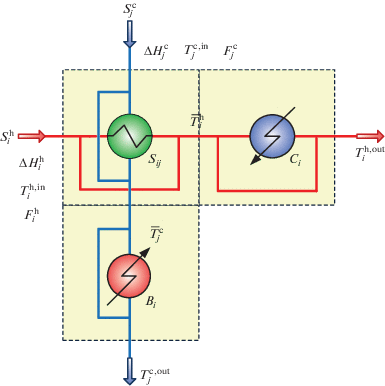
Уровень 1. Задача NLP нахождения оптимальных экономических оценок на теплообмен двух технологических потоков. Для каждой совокупности i-го горячего и j-го холодного потоков выделим элементарную суперструктуру организации теплообмена (рис. 5). Она определена в составе приведенных суперструктур для каждого элементарного потока и агрегирует все возможные варианты передачи тепловой энергии на q-й стадии или в l-м делении исходных потоков СТО. Оптимальную структуру блока в составе приведенной суперструктуры назовем элементарным блоком системы теплообмена (ЭБСТ). Структура ЭБСТ и режимы входящих в его состав теплообменников могут быть определены путем оптимизации представленной суперструктуры. Эта задача формализуется в виде модели NLP и имеет эффективные методы решения. Следовательно, каждой совокупности горячего и холодного технологических потоков может быть назначена оптимальная экономическая оценка на организацию ЭБСТ. В качестве критерия оптимальности ЭБСТ выберем суммарные приведенные капитальные и эксплуатационные затраты.
Для известного k-го приближения по коэффициентам $\alpha _{{{{q}_{i}}}}^{{\text{h}}},\alpha _{{{{q}_{j}}}}^{{\text{c}}}$ или $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$, для заданного значения минимально допустимой разности температур $\Delta {{T}_{{\min }}}$ на концах противоточного теплообменника определим несколько стратегий нахождения экономической оценки на ЭБСТ.
Если эксплуатационные затраты значительно превышают капитальные, то оценка на организацию ЭБСТ может быть найдена на основе расчета предельной нагрузки рекуперативного теплообменника, зависящей от величины$\Delta {{T}_{{\min }}}.$ Максимально допустимая нагрузка на рекуперативный теплообменник в многостадийной СТО определяется из следующих выражений:
(8)
$\begin{gathered} Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he}}}} = \\ = \min \left\{ {Q_{{{{q}_{i}}}}^{{\text{h}}},Q_{{{{q}_{j}}}}^{{\text{c}}},\max \left\{ {\min \{ F_{i}^{{\text{h}}}cp_{i}^{{\text{h}}},F_{j}^{{\text{c}}}cp_{j}^{{\text{c}}}\} \Delta {{t}_{{ij}}},0} \right\}} \right\}, \\ \end{gathered} $(9)
$\begin{gathered} {\text{где}}\,\,\,\,\Delta {{t}_{{ij}}} = \left( {T_{i}^{{{\text{h,in}}}} - \frac{{\Delta H_{i}^{{\text{h}}}\sum\limits_{s = 1}^{{{q}_{i}} - 1} {\alpha _{s}^{{\text{h}}}} }}{{F_{i}^{{\text{h}}}cp_{i}^{{\text{h}}}}}} \right) - \\ - \left( {T_{j}^{{{\text{c,in}}}} + \frac{{\Delta H_{j}^{{\text{c}}}\sum\limits_{s = 1}^{{{q}_{j}} - 1} {\alpha _{s}^{{\text{c}}}} }}{{F_{j}^{{\text{c}}}cp_{j}^{{\text{c}}}}}} \right) - \Delta {{T}_{{\min }}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{q}_{i}} = \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}. \\ \end{gathered} $Предельная нагрузка на рекуперативный теплообменник в суперструктуре с разделениями технологических потоков определяется в следующем виде:
(10)
$\begin{gathered} Q_{{{{l}_{i}},{{l}_{j}}}}^{{{\text{he}}}} = \min \{ Q_{{{{l}_{i}}}}^{{\text{h}}},Q_{{{{l}_{j}}}}^{{\text{c}}},\max \{ \min \{ F_{{{{l}_{i}}}}^{{\text{h}}}cp_{i}^{{\text{h}}},F_{{{{l}_{j}}}}^{{\text{c}}}cp_{j}^{{\text{c}}}\} \times \\ \times \,\,(T_{i}^{{{\text{h,in}}}} - T_{j}^{{{\text{c,in}}}} - \Delta {{T}_{{\min }}}),0\} \} , \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}. \\ \end{gathered} $Очевидно, что найденная нагрузка на рекуперативный теплообменник определяет нагрузки на концевые холодильник и нагреватель. Они определяются по выражениям (11) и (12) для суперструктур систем многостадийного теплообмена и систем теплообмена с разделением потоков соответственно:
(11)
$\begin{gathered} Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{cr}}}} = \alpha _{{{{q}_{i}}}}^{{\text{h}}}\Delta H_{i}^{{\text{h}}} - Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he}}}},\,\,\,\,Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{hr}}}} = \alpha _{{{{q}_{j}}}}^{{\text{c}}}\Delta H_{j}^{{\text{c}}} - Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,{{q}_{i}} = 1 \ldots {{N}_{i}},\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}; \\ \end{gathered} $(12)
$\begin{gathered} Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{cr}}}} = \beta _{{{{l}_{i}}}}^{{\text{h}}}\Delta H_{i}^{{\text{h}}} - Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he}}}},\,\,\,\,Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{hr}}}} = \beta _{{{{l}_{j}}}}^{{\text{c}}}\Delta H_{j}^{{\text{c}}} - Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}. \\ \end{gathered} $Найденные значения тепловых нагрузок рекуперативного теплообменника холодильника и нагревателя позволяют определить суммарные приведенные затраты на организацию ЭБСТ. Они включают капитальные затраты на теплообменное оборудование и эксплуатационные затраты на подвод горячего и холодного внешних агентов. Для их нахождения будем использовать модель теплообменника, основанную на вычислении среднелогарифмической разности температур. Приведем их в общем виде для i-го горячего и j-го холодного потоков. Капитальные затраты определяются в виде
(13)
$\begin{gathered} f_{{ij}}^{{{\text{cap}}}} = \left[ {\tilde {m}_{1}^{{{\text{he}}}} + \tilde {m}_{2}^{{{\text{he}}}}{{{\left( {\frac{{Q_{{ij}}^{{{\text{he}}}}}}{{U_{{ij}}^{{{\text{he}}}}\Delta T_{{LM}}^{{{\text{he}}}}}}} \right)}}^{{{{\gamma }^{{{\text{he}}}}}}}}} \right] + \\ + \,\,\left[ {\tilde {m}_{1}^{{{\text{hr}}}} + \tilde {m}_{2}^{{{\text{hr}}}}{{{\left( {\frac{{Q_{{ij}}^{{{\text{hr}}}}}}{{U_{{ij}}^{{{\text{hr}}}}\Delta T_{{LM}}^{{{\text{hr}}}}}}} \right)}}^{{{{\gamma }^{{{\text{hr}}}}}}}}} \right] + \\ + \,\,\left[ {\tilde {m}_{1}^{{{\text{cr}}}} + \tilde {m}_{2}^{{{\text{cr}}}}{{{\left( {\frac{{Q_{{ij}}^{{{\text{cr}}}}}}{{U_{{ij}}^{{{\text{cr}}}}\Delta T_{{LM}}^{{{\text{cr}}}}}}} \right)}}^{{{{\gamma }^{{{\text{cr}}}}}}}}} \right]. \\ \end{gathered} $Эксплуатационные затраты определяются на основе нагрузок концевых теплообменников:
(14)
$f_{{ij}}^{{{\text{oper}}}} = {{\hat {m}}^{{{\text{hu}}}}}Q_{{ij}}^{{{\text{hr}}}} + {{\hat {m}}^{{{\text{cu}}}}}Q_{{ij}}^{{{\text{cr}}}}.$Суммарные приведенные затраты на организацию ЭБСТ определяются по выражению
(15)
$f_{{ij}}^{{}} = {{\mu }^{{{\text{cap}}}}}f_{{ij}}^{{{\text{cap}}}} + {{\mu }^{{{\text{oper}}}}}f_{{ij}}^{{{\text{oper}}}}.$В качестве альтернативного варианта критерия оптимальности могут быть выбраны удельные затраты на единицу передаваемой энергии:
(16)
$\begin{gathered} f_{{ij}}^{{}} = \frac{1}{{Q_{{ij}}^{{{\text{he}}}}}}\left[ {\tilde {m}_{1}^{{{\text{he}}}} + \tilde {m}_{2}^{{{\text{he}}}}{{{\left( {\frac{{Q_{{ij}}^{{{\text{he}}}}}}{{U_{{ij}}^{{{\text{he}}}}\Delta T_{{LM}}^{{{\text{he}}}}}}} \right)}}^{{{{\gamma }^{{{\text{he}}}}}}}}} \right] + \\ + \,\,\frac{1}{{Q_{{ij}}^{{{\text{hr}}}}}}\left[ {\tilde {m}_{1}^{{{\text{hr}}}} + \tilde {m}_{2}^{{{\text{hr}}}}{{{\left( {\frac{{Q_{{ij}}^{{{\text{hr}}}}}}{{U_{{ij}}^{{{\text{hr}}}}\Delta T_{{LM}}^{{{\text{hr}}}}}}} \right)}}^{{{{\gamma }^{{{\text{hr}}}}}}}} + {{{\hat {m}}}^{{{\text{hu}}}}}Q_{{ij}}^{{{\text{hr}}}}} \right] + \\ + \,\,\frac{1}{{Q_{{ij}}^{{{\text{cr}}}}}}\left[ {\tilde {m}_{1}^{{{\text{cr}}}} + \tilde {m}_{2}^{{{\text{cr}}}}{{{\left( {\frac{{Q_{{ij}}^{{{\text{cr}}}}}}{{U_{{ij}}^{{{\text{cr}}}}\Delta T_{{LM}}^{{{\text{cr}}}}}}} \right)}}^{{{{\gamma }^{{{\text{cr}}}}}}}} + {{{\hat {m}}}^{{{\text{cu}}}}}Q_{{ij}}^{{{\text{cr}}}}} \right]. \\ \end{gathered} $Описанная стратегия нахождения оптимальных экономических оценок на организацию ЭБСТ характеризуется безитерационным характером нахождения экономической оценки и дает хорошее приближение для дальнейших расчетов. Отметим, что оптимальный компромисс между составляющими критерия оптимальности может быть достигнут на уровне 3 рассматриваемого алгоритма. Однако в случаях, когда выбрано достаточно малое значение $\Delta {{T}_{{\min }}}$ и капитальные затраты на организацию ЭБСТ соразмерны затратам эксплуатационным, оценка $f_{{ij}}^{{}}$ может быть улучшена решением задачи NLP, для всех совокупностей $i = 1 \ldots {{M}^{{\text{h}}}},$ $j = 1 \ldots {{M}^{{\text{c}}}}$, принимающей вид (17)–(25):
где(18)
$U_{{ij}}^{{{\text{he}}}} = \frac{1}{{\chi _{i}^{{\text{h}}} + \chi _{j}^{{\text{c}}}}},\,\,\,U_{{ij}}^{{{\text{cr}}}} = \frac{1}{{\chi _{i}^{{\text{h}}} + \chi _{{}}^{{{\text{cu}}}}}},\,\,\,U_{{ij}}^{{{\text{hr}}}} = \frac{1}{{\chi _{j}^{{\text{c}}} + \chi _{{}}^{{{\text{hu}}}}}},$(19)
$\bar {T}_{j}^{{\text{c}}} = T_{j}^{{{\text{c,in}}}} + \frac{{Q_{{ij}}^{{{\text{he}}}}}}{{F_{j}^{{\text{c}}}cp_{j}^{{\text{c}}}}},\,\,\,\,\bar {T}_{i}^{{\text{h}}} = T_{i}^{{{\text{h,in}}}} - \frac{{Q_{{ij}}^{{{\text{he}}}}}}{{F_{i}^{{\text{h}}}cp_{i}^{{\text{h}}}}},$(20)
$\Delta T_{{LM}}^{{\text{p}}} = \left\{ {\begin{array}{*{20}{c}} {\frac{{DT_{1}^{p} - DT_{2}^{p}}}{{\ln \frac{{DT_{1}^{p}}}{{DT_{2}^{p}}}}},\,\,\,\,DT_{1}^{p} \ne DT_{2}^{p},} \\ {DT_{1}^{p},\,\,\,\,DT_{1}^{p} = DT_{2}^{p},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \end{array}} \right.\,\,\,\,\forall p \in \Omega ,$(21)
$DT_{1}^{{{\text{he}}}} = T_{i}^{{{\text{h,in}}}} - \bar {T}_{j}^{{\text{c}}},\,\,\,\,DT_{2}^{{{\text{he}}}} = \bar {T}_{i}^{{\text{h}}} - T_{j}^{{{\text{c,in}}}},$(22)
$DT_{1}^{{{\text{cr}}}} = \bar {T}_{i}^{{\text{h}}} - {{T}^{{{\text{cu,out}}}}},\,\,\,\,DT_{2}^{{{\text{cr}}}} = T_{i}^{{{\text{h,out}}}} - {{T}^{{{\text{cu,in}}}}},$(23)
$DT_{1}^{{{\text{hr}}}} = {{T}^{{{\text{hu,in}}}}} - T_{j}^{{{\text{c,out}}}},\,\,\,\,DT_{2}^{{{\text{hr}}}} = {{T}^{{{\text{hu,out}}}}} - \bar {T}_{j}^{{\text{c}}},$(24)
$DT_{1}^{p} - \Delta {{T}_{{\min }}} \geqslant 0,\,\,\,\,DT_{2}^{p} - \Delta {{T}_{{\min }}} \geqslant 0,\,\,\,\,Q_{{ij}}^{p} \geqslant 0,$Отметим, что приведенная постановка задачи справедлива для любой q-й стадии или любой l-й части разделенного потока. Однако в случае синтеза систем многостадийного теплообмена требуется нахождение температур на входе и выходе каждой стадии. Они определяются в следующем виде:
(26)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,in}}}} = T_{{({{q}_{j}} - 1)}}^{{{\text{c,out}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,in}}}} = T_{{({{q}_{i}} - 1)}}^{{{\text{h,out}}}},\,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{q}_{i}} = 2 \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 2 \ldots {{N}_{j}}, \\ \end{gathered} $(27)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,in}}}} = T_{j}^{{{\text{c,in}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,in}}}} = T_{i}^{{{\text{h,in}}}},\,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1..{{M}^{{\text{c}}}},\,\,\,\,\,{{q}_{i}} = 1,\,\,\,\,{{q}_{j}} = 1, \\ \end{gathered} $(28)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,out}}}} = T_{j}^{{{\text{c,out}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,out}}}} = T_{i}^{{{\text{h,out}}}},\,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{q}_{i}} = {{N}_{i}},\,\,\,\,{{q}_{j}} = {{N}_{j}}, \\ \end{gathered} $(29)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,out}}}} = T_{j}^{{{\text{c,in}}}} + \frac{{\Delta H_{j}^{{\text{c}}}\sum\limits_{s = 1}^{{{q}_{j}}} {\alpha _{s}^{{\text{c}}}} }}{{F_{j}^{{\text{c}}}cp_{j}^{{\text{c}}}}},\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,out}}}} = T_{i}^{{{\text{h,in}}}} - \frac{{\Delta H_{i}^{{\text{h}}}\sum\limits_{s = 1}^{{{q}_{i}}} {\alpha _{s}^{{\text{h}}}} }}{{F_{i}^{{\text{h}}}cp_{i}^{{\text{h}}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,{{q}_{i}} = 1 \ldots ({{N}_{i}} - 1), \\ {{q}_{j}} = 1 \ldots ({{N}_{j}} - 1). \\ \end{gathered} $Результатом решения задачи уровня 1 является матрица экономических оценок на теплообмен каждой совокупности горячего и холодного элементарных потоков, что позволяет в каждой строке и каждом столбце определить такие ЭБСТ, суммарная оценка на интеграцию которых примет минимальное значение. Эта задача может быть решена с использованием задачи линейного программирования о назначениях.
Уровень 2. Задача LP поиска оптимальной топологии организации системы теплообмена по частным экономическим оценкам. Для формализации задачи LP о назначениях введем двоичную переменную $z_{{ij}}^{{}}$, характеризующую включение ЭБСТ в топологию системы теплообмена на k-м приближении по коэффициентам $\alpha _{{{{q}_{i}}}}^{{\text{h}}},\alpha _{{{{q}_{j}}}}^{{\text{c}}}$ или $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$ (в случае суперструктуры многостадийного теплообмена задача принимает вид (15)–(16)):
(30)
$\min \sum\limits_i {\sum\limits_{{{q}_{i}}} {\sum\limits_j {\sum\limits_{{{q}_{j}}} {{{f}_{{{{q}_{i}}{{q}_{j}}}}}} } } } {{z}_{{{{q}_{i}}{{q}_{j}}}}},\,\,\,\,{{z}_{{{{q}_{i}}{{q}_{j}}}}} \in \left\{ {0,1} \right\},$(31)
$\begin{gathered} \sum\limits_i {\sum\limits_{{{q}_{i}}} {{{z}_{{{{q}_{i}}{{q}_{j}}}}}} } = 1,\,\,\,\,\sum\limits_j {\sum\limits_{{{q}_{j}}} {{{z}_{{{{q}_{i}}{{q}_{j}}}}} = 1,} } \,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,{{q}_{i}} = 1 \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}. \\ \end{gathered} $Для суперструктуры системы теплообмена с разделением технологических потоков, представленной на рис. 4, задача формализуется в следующем виде:
(32)
$\min \sum\limits_i {\sum\limits_{{{l}_{i}}} {\sum\limits_j {\sum\limits_{{{l}_{j}}} {{{f}_{{{{l}_{i}}{{l}_{j}}}}}} } } } {{z}_{{{{l}_{i}}{{l}_{j}}}}},\,\,\,\,{{z}_{{{{l}_{i}}{{l}_{j}}}}} \in \left\{ {0,1} \right\},$(33)
$\begin{gathered} \sum\limits_i {\sum\limits_{{{l}_{i}}} {{{z}_{{{{l}_{i}}{{l}_{j}}}}}} } = 1,\,\,\,\,\,\,\sum\limits_j {\sum\limits_{{{l}_{j}}} {{{z}_{{{{l}_{i}}{{l}_{j}}}}} = 1,} } \,\,\,\,i = 1..{{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}. \\ \end{gathered} $Решение задачи о назначениях может быть организовано с использованием технологий параллельных вычислений (как и задачи уровня 1) при использовании суперструктуры, предложенной на рис. 3. Таким образом, задача примет следующий вид:
(32)
$\min \sum\limits_i {\sum\limits_j {{{f}_{{{{l}_{i}}{{l}_{j}}}}}{{z}_{{{{l}_{i}}{{l}_{j}}}}}} } ,\,\,\,\,{{z}_{{{{l}_{i}}{{l}_{j}}}}} \in \left\{ {0,1} \right\},$(33)
$\begin{gathered} \sum\limits_i {{{z}_{{{{l}_{i}}{{l}_{j}}}}}} = 1,\,\,\,\,\,\sum\limits_j {{{z}_{{{{l}_{i}}{{l}_{j}}}}} = 1,} \,\,\,\,i = 1 \ldots {{M}^{{\text{h}}}}, \\ j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}. \\ \end{gathered} $Отметим, что приведенные постановки задач оптимизации справедливы для квадратных матриц экономических оценок. В случае, когда число горячих элементарных потоков не равно числу холодных исходные матрицы предлагается достраивать до квадратного вида путем введения дополнительных фиктивных потоков, что обсуждается в работах [13, 35]. Результатом решения задачи о назначениях является структура СТО, оптимальная для текущих значений коэффициентов $\alpha _{{{{q}_{i}}}}^{{\text{h}}},\alpha _{{{{q}_{j}}}}^{{\text{c}}}$ или $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$. Поэтому на уровне 3 будет определяться новое приближение по этим переменным на найденной структуре СТО.
Уровень 3. Задача NLP поиска новых приближений по закрепляемым коэффициентам. Задача нахождения новых приближений по коэффициентам $\alpha _{{{{q}_{i}}}}^{{\text{h}}},\alpha _{{{{q}_{j}}}}^{{\text{c}}}$ или $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$ формализуется как задача нелинейного математического программирования. Критерий оптимальности включает экономические оценки на множество Z(k) всех ЭБСТ, для которых двоичная переменная z принимает значение 1. Для структуры многостадийного теплообмена формализованная постановка задачи принимает следующий вид:
(34)
$\mathop {\min }\limits_{\alpha _{{{{q}_{i}}}}^{{{\text{h,(}}k{\text{)}}}},\alpha _{{{{q}_{j}}}}^{{{\text{c,(}}k{\text{)}}}},Q_{{_{{{{q}_{i}}{{q}_{j}}}}}}^{{{\text{he,(}}k{\text{)}}}},\forall ({{q}_{i}},{{q}_{j}}) \in {{Z}^{{(k)}}}} {{\Phi }^{{(k)}}},$(35)
$\begin{gathered} {{\Phi }^{{(k)}}} = \sum\limits_{{{q}_{i}}} {\sum\limits_{{{q}_{j}}} {\left[ {\tilde {m}_{1}^{{{\text{he}}}} + \tilde {m}_{2}^{{{\text{he}}}}{{{\left( {\frac{{Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he,}}(k)}}}}{{U_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he}}}}\Delta T_{{LM}}^{{{\text{he,}}(k)}}}}} \right)}}^{{{{\gamma }^{{{\text{he}}}}}}}}} \right]} } + \\ + \,\,\left[ {\tilde {m}_{1}^{{{\text{hr}}}} + \tilde {m}_{2}^{{{\text{hr}}}}{{{\left( {\frac{{Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{hr,}}(k)}}}}{{U_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{hr}}}}\Delta T_{{LM}}^{{{\text{hr,}}(k)}}}}} \right)}}^{{{{\gamma }^{{{\text{hr}}}}}}}} + {{{\hat {m}}}^{{{\text{hu}}}}}Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{hr,}}(k)}}} \right] + \\ + \,\,\left[ {\tilde {m}_{1}^{{{\text{cr}}}} + \tilde {m}_{2}^{{{\text{cr}}}}{{{\left( {\frac{{Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{cr,}}(k)}}}}{{U_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{cr}}}}\Delta T_{{LM}}^{{{\text{cr,}}(k)}}}}} \right)}}^{{{{\gamma }^{{{\text{cr}}}}}}}} + {{{\hat {m}}}^{{{\text{cu}}}}}Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{cr,}}(k)}}} \right], \\ \forall ({{q}_{i}},{{q}_{j}}) \in {{Z}^{{(k)}}}, \\ \end{gathered} $(36)
$\begin{gathered} U_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he}}}} = \frac{1}{{\chi _{{{{q}_{i}}}}^{{\text{h}}} + \chi _{{{{q}_{j}}}}^{{\text{c}}}}},\,\,\,\,U_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{cr}}}} = \frac{1}{{\chi _{{{{q}_{i}}}}^{{\text{h}}} + \chi _{{}}^{{{\text{cu}}}}}}, \\ U_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{hr}}}} = \frac{1}{{\chi _{{{{q}_{j}}}}^{{\text{c}}} + \chi _{{}}^{{{\text{hu}}}}}}, \\ \end{gathered} $(37)
$\begin{gathered} Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{cr,}}(k)}} = \alpha _{{{{q}_{i}}}}^{{{\text{h,}}(k)}}\Delta H_{i}^{{\text{h}}} - Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he,}}(k)}}, \\ Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{hr,}}(k)}} = \alpha _{{{{q}_{j}}}}^{{{\text{c,}}(k)}}\Delta H_{j}^{{\text{c}}} - Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he,}}(k)}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{q}_{i}} = 1 \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}. \\ \end{gathered} $(38)
$\begin{gathered} \sum\limits_{{{q}_{i}}} {\alpha _{{{{q}_{i}}}}^{{{\text{h,}}(k)}} - 1 = 0} ,\,\,\,\,\sum\limits_{{{q}_{i}}} {\alpha _{{{{q}_{j}}}}^{{{\text{h,}}(k)}} - 1 = 0} , \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}. \\ \end{gathered} $(39)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,in,}}(k)}} = T_{{({{q}_{j}} - 1)}}^{{{\text{c,out,}}(k)}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,in,}}(k)}} = T_{{({{q}_{i}} - 1)}}^{{{\text{h,out,}}(k)}}, \\ i = 1..{{M}^{{\text{h}}}},\,\,\,j = 1..{{M}^{{\text{c}}}},\,\,\,{{q}_{i}} = 2..{{N}_{i}},\,\,\,{{q}_{j}} = 2 \ldots {{N}_{j}}, \\ \end{gathered} $(40)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,in,}}(k)}} = T_{j}^{{{\text{c,in}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,in,}}(k)}} = T_{i}^{{{\text{h,in}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{q}_{i}} = 1,\,\,\,\,{{q}_{j}} = 1, \\ \end{gathered} $(41)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,out,}}(k)}} = T_{j}^{{{\text{c,out}}}},\,\,\,\,T_{{{{q}_{i}}}}^{{{\text{h,out,}}(k)}} = T_{i}^{{{\text{h,out}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,\,\,{{q}_{i}} = {{N}_{i}},\,\,\,\,{{q}_{j}} = {{N}_{j}}, \\ \end{gathered} $(42)
$\begin{gathered} T_{{{{q}_{j}}}}^{{{\text{c,out,}}(k)}} = T_{j}^{{{\text{c,in,}}(k)}} + \frac{{\Delta H_{j}^{{\text{c}}}\sum\limits_{s = 1}^{{{q}_{j}}} {\alpha _{s}^{{{\text{c,}}(k)}}} }}{{F_{j}^{{\text{c}}}cp_{j}^{{\text{c}}}}}, \\ T_{{{{q}_{i}}}}^{{{\text{h,out}}}} = T_{i}^{{{\text{h,in}}}} - \frac{{\Delta H_{i}^{{\text{h}}}\sum\limits_{s = 1}^{{{q}_{i}}} {\alpha _{s}^{{{\text{h,}}(k)}}} }}{{F_{i}^{{\text{h}}}cp_{i}^{{\text{h}}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{q}_{i}} = 1 \ldots ({{N}_{i}} - 1),\,\,\,\,{{q}_{j}} = 1 \ldots ({{N}_{j}} - 1), \\ \end{gathered} $(43)
$\begin{gathered} \bar {T}_{{{{q}_{j}}}}^{{{\text{c,}}(k)}} = T_{{{{q}_{j}}}}^{{{\text{c,in,}}(k)}} + \frac{{Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he,}}(k)}}}}{{F_{j}^{{\text{c}}}cp_{j}^{{\text{c}}}}}, \\ \bar {T}_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{h,}}(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,in,}}(k)}} - \frac{{Q_{{{{q}_{i}}{{q}_{j}}}}^{{{\text{he,}}(k)}}}}{{F_{i}^{{\text{h}}}cp_{i}^{{\text{h}}}}}, \\ \end{gathered} $(44)
$\begin{gathered} \Delta T_{{LM}}^{{{\text{p,}}(k)}} = \\ = \left\{ {\begin{array}{*{20}{c}} {\frac{{DT_{1}^{{p{\text{,}}(k)}} - DT_{2}^{{p{\text{,}}(k)}}}}{{\ln \frac{{DT_{1}^{{p{\text{,}}(k)}}}}{{DT_{2}^{{p{\text{,}}(k)}}}}}},\,\,DT_{1}^{{p{\text{,}}(k)}} \ne DT_{2}^{{p{\text{,}}(k)}},} \\ {DT_{1}^{{p{\text{,}}(k)}},\,\,\,DT_{1}^{{p{\text{,}}(k)}} = DT_{2}^{{p{\text{,}}(k)}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \end{array}} \right.\,\forall p \in \Omega , \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,j = 1 \ldots {{M}^{{\text{c}}}},\,\,{{q}_{i}} = 1 \ldots {{N}_{i}},\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}, \\ \end{gathered} $(45)
$DT_{1}^{{{\text{he,}}(k)}} = T_{{{{q}_{i}}}}^{{{\text{h,in,}}(k)}} - \bar {T}_{{{{q}_{j}}}}^{{\text{c}}},\,\,DT_{2}^{{{\text{he}}}} = \bar {T}_{{{{q}_{i}}}}^{{{\text{h,}}(k)}} - T_{{{{q}_{j}}}}^{{{\text{c,in,}}(k)}},$(46)
$\begin{gathered} DT_{1}^{{{\text{cr,}}(k)}} = \bar {T}_{{{{q}_{i}}}}^{{{\text{h,}}(k)}} - {{T}^{{{\text{cu,out}}}}}, \\ DT_{2}^{{{\text{cr}}}} = T_{{{{q}_{i}}}}^{{{\text{h,out,}}(k)}} - {{T}^{{{\text{cu,in}}}}}, \\ \end{gathered} $(47)
$\begin{gathered} DT_{1}^{{{\text{hr,}}(k)}} = {{T}^{{{\text{hu,in}}}}} - T_{{{{q}_{j}}}}^{{{\text{c,out,}}(k)}}, \\ DT_{2}^{{{\text{hr,}}(k)}} = {{T}^{{{\text{hu,out}}}}} - \bar {T}_{{{{q}_{j}}}}^{{{\text{c,}}(k)}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{q}_{i}} = 1 \ldots {{N}_{i}},\,\,\,\,{{q}_{j}} = 1 \ldots {{N}_{j}}, \\ \end{gathered} $(48)
$\begin{gathered} DT_{1}^{{p{\text{,}}(k)}} - \Delta {{T}_{{\min }}} \geqslant 0, \\ DT_{2}^{{p{\text{,}}(k)}} - \Delta {{T}_{{\min }}} \geqslant 0,Q_{{{{q}_{i}}{{q}_{j}}}}^{{p{\text{,}}(k)}} \geqslant 0, \\ \end{gathered} $Для структуры с разделением технологических потоков задача NLP формализуется в следующем виде:
(50)
$\mathop {\min }\limits_{\beta _{{{{l}_{i}}}}^{{{\text{h,(}}k{\text{)}}}},\beta _{{{{l}_{j}}}}^{{{\text{c,(}}k{\text{)}}}},Q_{{_{{{{l}_{i}}{{l}_{j}}}}}}^{{{\text{he,(}}k{\text{)}}}},\forall ({{l}_{i}},{{l}_{j}}) \in {{Z}^{{(k)}}}} {{\Phi }^{{(k)}}},$(51)
$\begin{gathered} {{\Phi }^{{(k)}}} = \sum\limits_{{{l}_{i}}} {\sum\limits_{{{l}_{j}}} {\left[ {\tilde {m}_{1}^{{{\text{he}}}} + \tilde {m}_{2}^{{{\text{he}}}}{{{\left( {\frac{{Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he,}}(k)}}}}{{U_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he}}}}\Delta T_{{LM}}^{{{\text{he,}}(k)}}}}} \right)}}^{{{{\gamma }^{{{\text{he}}}}}}}}} \right]} } + \\ = \left[ {\tilde {m}_{1}^{{{\text{hr}}}} + \tilde {m}_{2}^{{{\text{hr}}}}{{{\left( {\frac{{Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{hr,}}(k)}}}}{{U_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{hr}}}}\Delta T_{{LM}}^{{{\text{hr,}}(k)}}}}} \right)}}^{{{{\gamma }^{{{\text{hr}}}}}}}} + {{{\hat {m}}}^{{{\text{hu}}}}}Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{hr,}}(k)}}} \right] + \\ + \,\,\left[ {\tilde {m}_{1}^{{{\text{cr}}}} + \tilde {m}_{2}^{{{\text{cr}}}}{{{\left( {\frac{{Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{cr,}}(k)}}}}{{U_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{cr}}}}\Delta T_{{LM}}^{{{\text{cr,}}(k)}}}}} \right)}}^{{{{\gamma }^{{{\text{cr}}}}}}}} + {{{\hat {m}}}^{{{\text{cu}}}}}Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{cr,}}(k)}}} \right], \\ \forall ({{l}_{i}},{{l}_{j}}) \in {{Z}^{{(k)}}} \\ \end{gathered} $(52)
$U_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he}}}} = \frac{1}{{\chi _{{{{l}_{i}}}}^{{\text{h}}} + \chi _{{{{l}_{j}}}}^{{\text{c}}}}},\,\,\,U_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{cr}}}} = \frac{1}{{\chi _{{{{l}_{i}}}}^{{\text{h}}} + \chi _{{}}^{{{\text{cu}}}}}},\,\,\,U_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{hr}}}} = \frac{1}{{\chi _{{{{l}_{j}}}}^{{\text{c}}} + \chi _{{}}^{{{\text{hu}}}}}},$(53)
$\begin{gathered} Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{cr,}}(k)}} = \beta _{{{{l}_{i}}}}^{{{\text{h,}}(k)}}\Delta H_{i}^{{\text{h}}} - Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he,}}(k)}}, \\ Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{hr,}}(k)}} = \beta _{{{{l}_{j}}}}^{{{\text{c,}}(k)}}\Delta H_{j}^{{\text{c}}} - Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he,}}(k)}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}. \\ \end{gathered} $(54)
$\begin{gathered} F_{{{{l}_{i}}}}^{{{\text{h,}}(k)}} = \beta _{{{{l}_{i}}}}^{{{\text{h,}}(k)}}F_{i}^{{\text{h}}},\,\,\,\,F_{{{{l}_{j}}}}^{{{\text{c,}}(k)}} = \beta _{{{{l}_{j}}}}^{{{\text{c,}}(k)}}F_{j}^{{\text{c}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}, \\ \end{gathered} $(55)
$\begin{gathered} \sum\limits_{{{l}_{i}}} {\beta _{{{{l}_{i}}}}^{{{\text{h,}}(k)}} - 1 = 0} ,\,\,\,\,\sum\limits_{{{l}_{j}}} {\beta _{{{{l}_{j}}}}^{{{\text{c,}}(k)}} - 1 = 0} , \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ \end{gathered} $(56)
$\begin{gathered} T_{{{{l}_{j}}}}^{{{\text{c,in,}}(k)}} = T_{j}^{{{\text{c,in,}}(k)}},\,\,\,T_{{{{l}_{i}}}}^{{{\text{h,in,}}(k)}} = T_{i}^{{{\text{h,in,}}(k)}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}, \\ \bar {T}_{{{{l}_{j}}}}^{{{\text{c,}}(k)}} = T_{{{{l}_{j}}}}^{{{\text{c,in,}}(k)}} + \frac{{Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he,}}(k)}}}}{{F_{{{{l}_{j}}}}^{{{\text{c,}}(k)}}cp_{j}^{{\text{c}}}}}, \\ \bar {T}_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{h,}}(k)}} = T_{{{{l}_{i}}}}^{{{\text{h,in,}}(k)}} - \frac{{Q_{{{{l}_{i}}{{l}_{j}}}}^{{{\text{he,}}(k)}}}}{{F_{{{{l}_{i}}}}^{{{\text{h,}}(k)}}cp_{i}^{{\text{h}}}}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}, \\ \end{gathered} $(57)
$\begin{gathered} \Delta T_{{LM}}^{{{\text{p,}}(k)}} = \\ = \left\{ {\begin{array}{*{20}{c}} {\frac{{DT_{1}^{{p{\text{,}}(k)}} - DT_{2}^{{p{\text{,}}(k)}}}}{{\ln \frac{{DT_{1}^{{p{\text{,}}(k)}}}}{{DT_{2}^{{p{\text{,}}(k)}}}}}},\,\,DT_{1}^{{p{\text{,}}(k)}} \ne DT_{2}^{{p{\text{,}}(k)}},} \\ {DT_{1}^{{p{\text{,}}(k)}},\,\,DT_{1}^{{p{\text{,}}(k)}} = DT_{2}^{{p{\text{,}}(k)}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \end{array}} \right.\,\,\,\,\forall p \in \Omega , \\ \end{gathered} $(58)
$\begin{gathered} DT_{1}^{{{\text{he,}}(k)}} = T_{{{{l}_{i}}}}^{{{\text{h,in,}}(k)}} - \bar {T}_{{{{l}_{j}}}}^{{{\text{c,}}(k)}}, \\ DT_{2}^{{{\text{he,}}(k)}} = \bar {T}_{{{{l}_{i}}}}^{{{\text{h,}}(k)}} - T_{{{{l}_{j}}}}^{{{\text{c,in,}}(k)}}, \\ \end{gathered} $(59)
$\begin{gathered} DT_{1}^{{{\text{cr,}}(k)}} = \bar {T}_{{{{l}_{i}}}}^{{{\text{h,}}(k)}} - {{T}^{{{\text{cu,out}}}}}, \\ DT_{2}^{{{\text{cr,}}(k)}} = T_{{{{l}_{i}}}}^{{{\text{h,out,}}(k)}} - {{T}^{{{\text{cu,in}}}}}, \\ \end{gathered} $(60)
$\begin{gathered} DT_{1}^{{{\text{hr,}}(k)}} = {{T}^{{{\text{hu,in}}}}} - T_{{{{l}_{j}}}}^{{{\text{c,out,}}(k)}}, \\ DT_{2}^{{{\text{hr,}}(k)}} = {{T}^{{{\text{hu,out}}}}} - \bar {T}_{{{{l}_{j}}}}^{{{\text{c,}}(k)}}, \\ i = 1 \ldots {{M}^{{\text{h}}}},\,\,\,\,j = 1 \ldots {{M}^{{\text{c}}}}, \\ {{l}_{i}} = 1 \ldots {{L}_{i}},\,\,\,\,{{l}_{j}} = 1 \ldots {{L}_{j}}, \\ \end{gathered} $(61)
$\begin{gathered} DT_{1}^{{p{\text{,}}(k)}} - \Delta {{T}_{{\min }}} \geqslant 0, \\ DT_{2}^{{p{\text{,}}(k)}} - \Delta {{T}_{{\min }}} \geqslant 0,\,\,\,Q_{{{{l}_{i}}{{l}_{j}}}}^{{p{\text{,}}(k)}} \geqslant 0, \\ \end{gathered} $В результате оптимизации СТО заданной структуры определяются новые приближения по коэффициентам $\alpha _{{{{q}_{i}}}}^{{\text{h}}},\alpha _{{{{q}_{j}}}}^{{\text{c}}}$ или $\beta _{{{{l}_{i}}}}^{{\text{h}}},\beta _{{{{l}_{j}}}}^{{\text{c}}}$. Они позволят найти новый вариант организации структуры СТО. Итерационная последовательность задач уровней 1–3 продолжается до тех пор, пока выполняется условие $\left| {{{\Phi }^{{(k)}}} - {{\Phi }^{{(k - 1)}}}} \right| \geqslant \xi .$ В противном случае принимается k = k + 1.
СИНТЕЗ ОПТИМАЛЬНОЙ СИСТЕМЫ ТЕПЛООБМЕНА УСТАНОВКИ БРАГОРЕКТИФИКАЦИИ
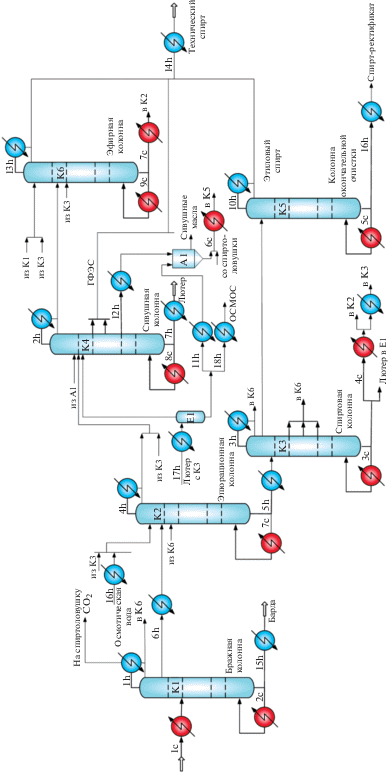
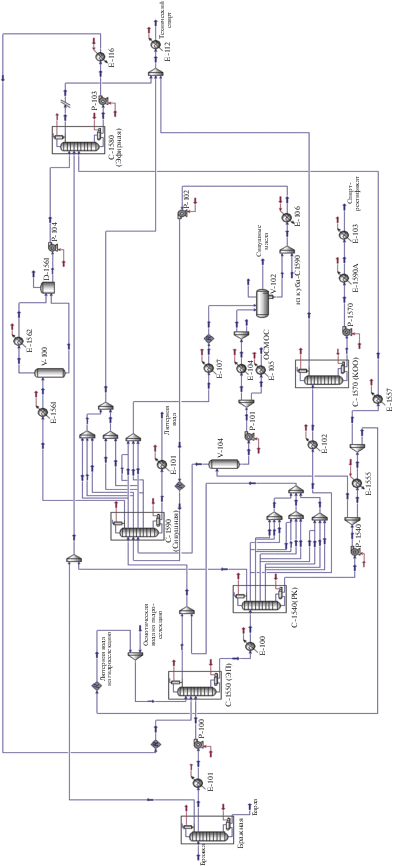
Предлагаемый подход рассмотрим на примере решения задачи оптимальной теплоинтеграции установки брагоректификации. Установка включает шесть ректификационных колонн. Исходным сырьем является спиртовая бражка, конечным продуктом – ректификованный и технический спирт, побочными продуктами – барда, сивушные масла и лютерная вода. Технологическая схема установки представлена на рис. 6. В бражной колонне с секциями дегазации и концентрации производится отгонка спирта с сопутствующими этанолу примесями с получением бражного дистиллята. В эпюрационной колонне проводится удаление головных и промежуточных примесей с применением гидроселекции. В ректификационной колонне происходит концентрирование и очистка этилового спирта от хвостовых, промежуточных и оставшихся головных примесей. Колонна окончательной очистки предназначена для доочистки ректификованного спирта от концевых примесей. В сивушной колонне производится концентрирование промежуточных примесей и выделение их из спирта. В эфирной колонне проводится выделение головных примесей из спирта. В качестве питания подается головная фракция с конденсатора сивушной колонны, конденсат бражной колонны и непастеризованный спирт.
Для оценки энергетического потенциала установки в среде универсальной моделирующей программы (УМП) Aspen HYSYS была построена и рассчитана компьютерная модель установки. На рис. 7 представлена информационная блок-схема модели исследуемой установки. В табл. 1 приведены расчетные параметры ректификационных колонн.
Таблица 1.
Параметры ректификационных колонн
| Наименование аппарата | Давление верха, кгс/см2 | Давление низа, кгс/см2 | Температура верха, °С | Температура низа, °С | Число тарелок |
|---|---|---|---|---|---|
| Бражная колонна К1 | 0.51 | 0.61 | 75 | 87 | 26 |
| Эпюрационная колонна К2 | 5.1 | 5.51 | 132.9 | 148.4 | 50 |
| Спиртовая колонна | 2.29 | 2.45 | 100.5 | 130 | 75 |
| Сивушная колонна К3 | 1.02 | 1.23 | 78.1 | 100.5 | 40 |
| Колонна окончательной очистки К4 | 0.21 | 0.41 | 41.77 | 56.4 | 50 |
| Эфирная колонна К5 | 1.02 | 1.23 | 80 | 98 | 40 |
На основе построенной компьютерной модели был проведен термодинамический анализ системы теплообмена установки. В качестве исходных данных использовалась информация о параметрах технологических потоков (табл. 2), полученных в результате расчета материально-теплового баланса.
Таблица 2.
Исходные данные
| Горячий поток | $T_{i}^{{{\text{h,in}}}},$ К | $T_{i}^{{{\text{h,out}}}},$ К | Fсp МВт/К |
Q, МВт | Холодный поток | $T_{j}^{{{\text{c,in}}}},$ К | $T_{j}^{{{\text{c,out}}}},$ К | Fcp МВт/К |
Q, MВт |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| H1 | 341.4 | 335.8 | 0.399 | 2.23 | C1 | 301.1 | 338.1 | 0.046 | 1.69 |
| H2 | 351 | 350.9 | 10.74 | 1.07 | C2 | 359.1 | 359.2 | 66.23 | 6.62 |
| H3 | 372.8 | 372.7 | 77.52 | 7.75 | C3 | 399.2 | 399.3 | 70.94 | 7.09 |
| H4 | 419.1 | 406 | 0.317 | 4.16 | C4 | 399.3 | 420 | 0.047 | 0.98 |
| Н5 | 421.5 | 407.1 | 0.069 | 0.98 | С5 | 329.5 | 329.6 | 18.953 | 1.89 |
| Н6 | 349.2 | 339.1 | 0.287 | 2.90 | С6 | 303.2 | 365.1 | 0.005 | 0.33 |
| Н7 | 375.9 | 319.7 | 0.0 | 0.33 | С7 | 418.2 | 421.4 | 1.49 | 4.77 |
| Н8 | 374 | 325.7 | 0.006 | 0.29 | С8 | 372.8 | 375.8 | 0.26 | 0.78 |
| Н9 | 329.6 | 293.1 | 0.003 | 0.12 | С9 | 346.4 | 367.7 | 0.034 | 0.74 |
| Н10 | 315.2 | 315.1 | 19.633 | 1.96 | |||||
| Н11 | 399.3 | 303 | 0.010 | 1.02 | |||||
| Н12 | 356.1 | 303.1 | 0.0006 | 0.03 | |||||
| Н13 | 347.3 | 339.6 | 0.118 | 0.91 | |||||
| Н14 | 315.3 | 293.1 | 0.0002 | 0.01 | |||||
| Н15 | 359.1 | 293.1 | 0.037 | 2.41 | |||||
| Н16 | 325.6 | 293.1 | 0.006 | 0.19 | |||||
| Н17 | 375.9 | 293.1 | 0.006 | 0.49 |
Суммарное количество энергии, которое необходимо отобрать от горячих технологических потоков, составило 26.89 МВт. Суммарное количество энергии, которое необходимо передать холодным потокам, оценивается на уровне 24.91 МВт.
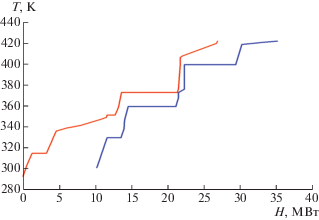
По данным технологических потоков в системе T–H были построены композитные кривые, представленные на рис. 8. Минимально допустимая разность температур $\Delta {{T}_{{\min }}}$была задана равной 5°С. Горячая и холодная композитные кривые определили достаточно большую зону перекрытия, характеризующая предельно возможное количество рекуперированной энергии. Так, предельно возможное количество рекуперируемой энергии составляет 16.66 МВт, количество энергии, отводимое холодными теплоносителями, – 10.18 МВт, количество энергии, подводимое горячими теплоносителями, – 8.26 МВт. Это является хорошей предпосылкой для решения задачи оптимальной теплоинтеграции технологических потоков рассматриваемой установки.
Для этих целей был в пакете прикладных программ Matlab был разработан программный комплекс HeatNET [40]. Выбор пакета Matlab обоснован поддержкой встроенных методов оптимизации для решения описанных задач. Разработанный программный комплекс основан на описанном трехуровневом итерационном алгоритме, включающем расчет оптимальных экономических оценок на теплообмен каждой пары технологических потоков, решение задачи о назначениях для определения оптимальной структуры системы теплообмена и решения задачи поиска новых приближений коэффициентов распределения тепловых нагрузок между стадиями СТО и коэффициентов разделения потоков. Результат синтеза оптимальной СТО представляется через графический интерфейс пользователя в виде HEN-диаграммы, определяющей топологию СТО, тепловые нагрузки входящих в ее состав теплообменников и площади поверхностей теплопередачи. Графический интерфейс пользователя был разработан в межплатформенной среде Unity на языке C#. Для автоматизации процесса оценки энергетического потенциала системы на языке Matlab разработан COM/ActiveX – интерфейс взаимодействия с пакетом Aspen HYSYS.
В табл. 3 приведены результаты синтеза оптимальной многостадийной системы теплообмена, полученные из различных начальных приближений.
Таблица 3.
Результаты экономической оценки синтеза оптимальной многостадийной системы теплообмена
| Наименование показателей | Схема 1 (оптимальная) |
Схема 2 | Схема 3 |
|---|---|---|---|
| Площадь рекуператоров, м2 | 315 | 274.3 | 286.2 |
| Площадь холодильников, м2 | 170.4 | 172.6 | 173.1 |
| Площадь нагревателей, м2 | 63.7 | 69.0 | 72.8 |
| Суммарное количество рекуперируемой энергии, МВт | 16.67 | 16.44 | 16.37 |
| Суммарное количество отводимой энергии, МВт | 10.22 | 10.45 | 10.51 |
| Суммарное количество подводимой энергии, МВт | 8.24 | 8.47 | 8.54 |
| Число рекуператоров | 9 | 10 | 10 |
| Число холодильников | 13 | 14 | 15 |
| Число нагревателей | 4 | 3 | 4 |
| Суммарные приведенные затраты, тыс. у.е./год | 1084.5 | 1111.1 | 1114.9 |
| Время расчета, с | 38 | 32 | 31 |
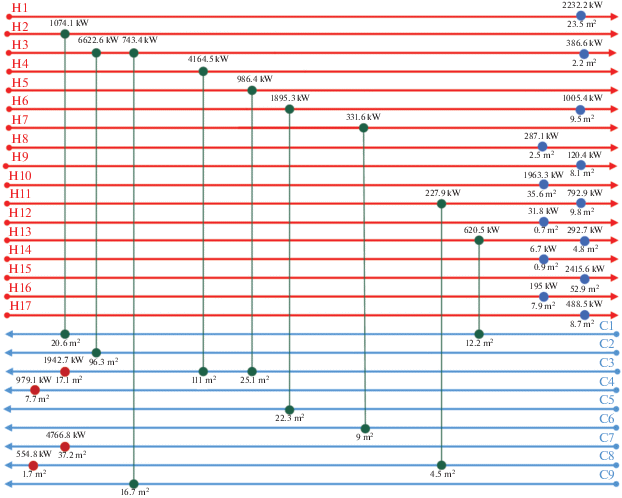
На рис. 9 представлены оптимальная структура многостадийной системы теплообмена (схема 1 в табл. 3) и режимы работы входящих в ее состав теплообменников.
Как видно из полученных результатов, разработанный алгоритм синтеза обеспечивает рекуперацию тепловой энергии в предельно возможном количестве, что объясняется высокими ценами на энергоносители.
В результате решения задачи синтеза оптимальной системы теплообмена с разделением потоков получено несколько альтернативных схем (табл. 4). Схемы 1 и 2 были синтезированы с использованием суперструктуры, представленной на рис. 4, схема 3 синтезирована на основе суперструктуры, показанной на рис. 3.
Таблица 4.
Результаты экономической оценки синтеза оптимальной одностадийной системы теплообмена с разделением потоков
| Наименование показателей | Схема 1 (оптимальная) |
Схема 2 | Схема 3 |
|---|---|---|---|
| Площадь рекуператоров, м2 | 303.4 | 316.4 | 308.2 |
| Площадь холодильников, м2 | 170.4 | 170.3 | 171.1 |
| Площадь нагревателей, м2 | 67 | 63.7 | 64.2 |
| Суммарное количество рекуперируемой энергии, МВт | 16.67 | 16.67 | 16.66 |
| Суммарное количество отводимой энергии, МВт | 10.22 | 10.22 | 10.22 |
| Суммарное количество подводимой энергии, МВт | 8.24 | 8.24 | 8.25 |
| Число рекуператоров | 10 | 9 | 9 |
| Число холодильников | 13 | 13 | 13 |
| Число нагревателей | 3 | 4 | 4 |
| Суммарные приведенные затраты, тыс. у.е./год | 1083.9 | 1084.7 | 1084.2 |
| Время расчета, с | 27 | 18 | 22 |
Лучший по критерию суммарных приведенных затрат вариант организации структуры системы теплообмена с разделением потоков (схема 1 в табл. 4) представлен в виде HEN-диаграммы на рис. 10.
Результаты синтеза показали близкие значения критерия оптимальности при различных вариантах организации суперструктуры. Алгоритм синтеза на основе суперструктуры рис. 3 позволил сократить время за счет понижения размерности задачи уровня 2, однако потребовал больше итераций.
ЗАКЛЮЧЕНИЕ
Как показывают результаты синтеза установки брагоректификации, рассмотренные методы и алгоритмы позволяют находить хорошее решение за приемлемое время. Предложенные варианты организации суперструктур и способ их декомпозиции позволяют понизить размерность исходной задачи синтеза и ликвидировать значительную часть локальных минимумов критерия оптимальности. Однако не теряет актуальности вопрос выбора начальных приближений по закрепляемым переменным, что, в сущности, определяет ограниченное множество структур. Среди достоинств методов отметим возможность детализации моделей теплообменного оборудования, оценки транспортных затрат, использование нетиповых элементов суперструктур, в частности, тепловых насосов, газовых и паровых турбин, печей и циклов глубокого охлаждения, при оптимизации которых может быть аналогичным образов определена экономическая оценка. В число преимуществ описанного подхода отнесем также возможность учета неопределенности в исходной информации при решении задачи синтеза. Декомпозиция суперструктуры на ЭБСТ позволяет корректировать экономические оценки с учетом изменяющихся условий эксплуатации с использованием предложенного нами в работах [41, 42] алгоритма.
Перспективы развития изложенного подхода охватывают вопросы оптимальной организации систем теплообмена с возможностью как последовательного, так и параллельной передачи тепловой энергии от горячих технологических потоков холодным. Анализ возможностей крупномасштабной интеграции систем сопряженных установок [43] дает предпосылки для расширения изложенного подхода для решения задач автоматизированного технологического проектирования систем теплообмена в комплексе установок, работающих на различных энергетических уровнях, в частности, нефтеперерабатывающих заводов.
Работа выполнена при поддержке Министерства науки и высшего образования Российской Федерации (грант № 075-00315-20-01).
ОБОЗНАЧЕНИЯ
| A | площадь поверхности теплообмена, м2 |
| cp | удельная изобарная теплоемкость, (МВт ч)/(кг К) |
| F | массовый расход, кг/ч |
| f | суммарные приведенные капитальные и операционные затраты, у.е./год |
| H | теплосодержание, МВт |
| $\tilde {m}$ | цена единицы расхода горячего или холодного теплоносителей, у.е./кг |
| ${{\hat {m}}_{1}}$ | приведенные ценовые коэффициенты затрат, у.е./год |
| ${{\hat {m}}_{2}}$ | приведенные ценовые коэффициенты затрат, у.е./(год м2) |
| Q | количество теплоты, МВт |
| T | температура потока, К |
| $\bar {T}$ | температура потока на выходе рекуперативного теплообменника, К |
| ΔTmin | минимально допустимая разность температур, К |
| U | коэффициент теплопередачи, (МВт ч)/(м2 К) |
| Z(k) | массив пар горячих и холодных потоков, для которых определен элементарный блок, входящий в схему система теплообмена на k-й итерации |
| γ | корреляционный коэффициент |
| $\mu $ | коэффициенты приведения по фактору времени |
| Φ | сумма приведенных капитальных затрат и операционных затрат СТО, у.е./год |
| $\chi $ | коэффициенты теплоотдачи, (МВт ч)/(м2 К) |
| $\Omega $ | массив аппаратов входящих в состав ЭБСТ |
ИНДЕКСЫ
| с | холодный поток |
| h | горячий поток |
| he | рекуперативный теплообменник |
| cr | холодильник/конденсатор |
| hr | нагреватель/кипятильник |
| cu | холодный внешний агент |
| hu | горячий внешний агент |
| in | входной поток |
| out | выходной поток |
| i | номер горячего потока |
| j | номер холодного потока |
| k | номер итерации |
| l | элементарный поток, полученный разделением исходного потока |
| q | номер стадии теплообмена |
Список литературы
Boldyryev S. Achievements and perspectives of process integration in CIS countries // Resour.-Effic. Technol. 2020. № 2. P. 1.
Klemeš J.J., Kravanja Z. Forty years of heat integration: pinch analysis (PA) and mathematical programming (MP) // Curr. Opin. Chem. Eng. 2013. V. 2. № 4. P. 461.
Ibrić N., Ahmetović E., Kravanja Z., Grossmann I.E. Simultaneous optimisation of large-scale problems of heat-integrated water networks // Energy. 2021. Article number 121354.
Nemet A., Isafiade A.J., Klemeš J.J., Kravanja Z. Two-step MILP/MINLP approach for the synthesis of large-scale HENs // Chem. Eng. Sci. 2019. V. 197. P. 432.
Song R., Wang Y., Panu M., El-Halwagi M.M., Feng X. Improved Targeting Procedure To Determine the Indirect Interplant Heat Integration with Parallel Connection Pattern among Three Plants // Ind. Eng. Chem. Res. 2018. V. 57. № 5. P. 1569.
Chin H.H., Foo D.C.Y., Lam H.L. Simultaneous water and energy integration with isothermal and non-isothermal mixing – a P-graph approach // Resour., Conserv. Recycl. 2019. V. 149. P. 687.
Bogataj M., Bagajewicz M.J. Synthesis of non-isothermal heat integrated water networks in chemical processes // Comput. Chem. Eng. 2008. V. 32. № 12. P. 3130.
Chua K.J., Chou S.K., Yang W.M. Advances in heat pump systems: a review // Appl. Energy. 2010. V. 87. P. 3611.
Jana A.K. Advances in heat pump assisted distillation column: A review // Energy Convers. Manage. 2014. V. 77. P. 287.
Zhao X.G., O’Neill B.K., Roach J.R., Wood R.M. Heat Integration for Batch Processes: Part 2: Heat Exchanger Network Design // Chem. Eng. Res. Des. 1998. V. 76. № 6. P. 700
Klemeš J.J., Varbanov P.S. Heat Integration Including Heat Exchangers, Combined Heat and Power, Heat Pumps, Separation Processes and Process Control // Appl. Therm. Eng. 2012. V. 43. P. 1.
Wang B., Klemeš J.J., Gai L., Varbanov P.S., Liang Y. A Heat and Power Pinch for Process Integration targeting in hybrid energy systems // J. Environ. Manage. 2021. V. 287. Article number 112305.
Ziyatdinov N.N., Emel’yanov I.I., Chen Q., Grossmann I.E. Optimal Heat Exchanger Network Synthesis by Sequential Splitting of Process Streams // Comput. Chem. Eng. 2020. V. 142. Article number 107042.
Alhajri I.H., Gadalla M.A., Elazab H.A. A conceptual efficient design of energy recovery systems using a new energy-area key parameter // Energy Rep. 2021. V. 7. P. 1079.
Orosz Á., How B.S., Friedler F. Multiple-solution heat exchanger network synthesis using P-HENS solver // J. Taiwan Inst. Chem. Eng. 2021 (in press).
Orosz Á., How B.S., Friedler F. Multiple-solution heat exchanger network synthesis for enabling the best industrial implementation // Energy. 2020. V. 208. Article number 118330.
Boykov S.Y., Andresen B., Akhremenkov A.A., Tsirlin A.M. Evaluation of irreversibility and optimal organization of an integrated multi-stream heat exchange system // J. Non-Equilib. Thermodyn. 2020. V. 45. № 2. P. 155.
Цирлин А.М., Ахременков А.А., Бойков С.Ю. Оценка необратимости и оптимальная организация интегрированной системы многопоточного теплообмена // Теор. осн. хим. технол. 2019. Т. 53. № 6. С. 652. [Tsirlin A.M., Akhremenkov A.A., Boikov S.Y. Evaluation of irreversibility and optimal design of an integrated system of multiflow heat exchange // Theor. Found. Chem. Eng. 2019. V. 53. № 6. P. 1001.]
Ахременков А.А., Цирлин А.М., Бойков С.Ю. Необратимость процессов теплообмена в двухпоточных ячейках с различной гидродинамикой потоков // Инж.-физ. ж. 2020. Т. 93. № 1. С. 30. [Akhremenkov A.A., Tsirlin A.M., Boikov S.Y. Irreversibility of heat-transfer processes in double-flow cells of varying flow hydrodynamics // J. Eng. Phys. Thermophys. 2020. V. 93. № 1. P. 28.
Papoulias S.A., Grossmann I.E. A structural optimization approach in process synthesis—II: Heat recovery networks // Comput. Chem. Eng. 1983. V. 7. № 6. P. 707.
Cerda J., Westerberg A.W., Mason D., Linnhoff B. Minimum utility usage in heat exchanger network synthesis: A transportation problem // Chem. Eng. Sci. 1983. V. 38. P. 373.
Chen Y., Grossmann I.E., Miller D.C. Computational strategies for large-scale MILP transshipment models for heat exchanger network synthesis // Comput. Chem. Eng. 2015. V. 82. P. 68.
Yee T.F., Grossmann I.E. Simultaneous optimization models for heat integration–II. Heat exchanger network synthesis // Comput. Chem. Eng. 1990. V. 14. № 10. P. 1165.
Ciric C.R., Floudas C.A. Heat exchanger network synthesis without decomposition // Comput. Chem. Eng. 1991. V.15. № 6. P. 385.
Isafiade A.J., Fraser D.M. Interval-based MINLP superstructure synthesis of heat exchange networks // Chem. Eng. Res. Des. 2008. V. 86. P. 245.
Silva A.P., Ravagnani M.A.S.S., Biscaia E.C.Jr., Caballero J.A. Optimal heat exchanger network synthesis using particle swarm optimization // Optim. Eng. 2009. V. 11. P. 459.
Thuy N.T.P., Pendyala R., Rahmanian N., Marneni N. Heat exchanger network optimization by differential evolution method // Appl. Mech. Mater. 2014. V. 564. P. 292.
Rathjens M., Fieg G. A novel hybrid strategy for cost-optimal heat exchanger network synthesis suited for large-scale problems // Appl. Therm. Eng. 2020. V. 167. Article number 114771.
Pavão L.V., Caballero J.A., Ravagnani M.A.S.S., Costa C.B.B. A pinch-based method for defining pressure manipulation routes in work and heat exchange networks // Renewable Sustainable Energy Rev. 2020. V. 131. Article number 109989.
Aguitoni M.C., Pavão L.V., Ravagnani M.A.S.S. Heat exchanger network synthesis combining simulated annealing and differential evolution // Energy. 2019. V. 181. P. 654.
Ryoo H.S., Sahinidis N.V. A branch-and-reduce approach to global optimization // J. Global Optim. 1996. V. 8. № 2. P.107.
Escobar M., Trierweiler J.O. Optimal heat exchanger network synthesis: A case study comparison // Appl. Therm. Eng. 2013. V. 51. № 1–2. P. 801.
Зиятдинов Н.Н., Островский Г.М., Емельянов И.И. Построение системы теплообмена при реконструкции и синтезе оптимальных систем ректификационных колонн // Теор. осн. хим. технол. 2016. Т. 50. № 2. С. 184. [Ziyatdinov N.N., Ostrovskii G.M., Emel’yanov I.I. Designing a Heat Exchange System upon the Reconstruction and Synthesis of Optimal Systems of Distillation // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 178.]
Зиятдинов Н.Н., Емельянов И.И., Туен Л.К. Метод синтеза оптимальных многостадийных систем теплообмена // Теор. осн. хим. технол. 2018. Т. 52. № 6. С. 614. [Ziyatdinov N.N., Emel’yanov I.I., Tuen L.Q. Method for the Synthesis of Optimum Multistage Heat Exchange Networks // Theor. Found. Chem. Eng. 2018. V. 52. № 6. P. 614.]
Зиятдинов Н.Н., Емельянов И.И., Лаптева Т.В. и др. Метод автоматизированного синтеза оптимальных систем теплообмена на основе принципа закрепления переменных // Теор. осн. хим. технол. 2020. Т. 54. № 2. С. 144. [Ziyatdinov N.N., Emel’ya-nov I.I., Lapteva T.V., Ryzhova A.A., Ignat’ev A.N. Method of Automated Synthesis of Optimal Heat Exchange Network (HEN) Based on the Principle of Fixation of Variables // Theor. Found. Chem. Eng. 2020. V. 54. № 2. P. 258.
Товажнянский Л.Л., Капустенко П.А., Ульев Л.М. и др. Интеграция тепловых процессов на установке первичной переработки нефти АВТ А12/2 при работе в зимнее время // Теор. осн. хим. технол. 2009. Т. 43. № 6. С. 665. [Tovazhnyanskii L.L., Kapusten-ko P.A., Ul’ev L.M., Boldyrev S.A., Arsen’eva O.P., Tarnovskii M.V. Thermal process integration in the AVDU A12/2 crude distillation unit during winter operation // Theor. Found. Chem. Eng. 2009. V. 43. № 6. P. 906.]
Feng X., Pu J., Yang J., Chu K.H. Energy recovery in petrochemical complexes through heat integration retrofit analysis // Appl. Eng. 2011. V. 5. № 88. P. 1965.
Rašković P., Anastasovski A., Markovska Lj., Meško V. Process integration in bioprocess indystry: waste heat recovery in yeast and ethyl alcohol plant // Energy. 2010. V. 2. № 35. P. 704.
Bagajewicz M., Valtinson G., Thanh D.Q.N. Retrofit of Crude Units Preheating Trains: Mathematical Programming versus Pinch Technology // Ind. Eng. Chem. Res. 2013. V. 52. № 42. P. 14913.
Зиятдинов Н.Н., Емельянов И.И., Рыжова А.А. и др. Программный комплекс синтеза оптимальной системы теплообмена с делением технологических потоков “HeatNet”. Свидетельство о государственной регистрации программы для ЭВМ № 2020663657 РФ. 2020.
Лаптева Т.В., Зиятдинов Н.Н., Емельянов И.И. Проектирование химико-технологических систем при учете объединенных мягких ограничений // Теор. осн. хим. технол. 2020. Т. 54. № 1. С. 17. [Lapteva T.V., Ziyatdinov N.N., Emel’yanov I.I. Chemical process design taking into account joint chance constraints // Theor. Found. Chem. Eng. 2020. V. 54. № 1. P. 145.]
Островский Г.М., Лаптева Т.В., Зиятдинов Н.Н., Сильвестрова А.С. Проектирование химико-технологических систем при учете вероятностных ограничений // Теор. осн. хим. технол. 2017. Т. 51. № 6. С. 618. [Ostrovsky G.M., Lapteva T.V., Ziyatdinov N.N., Silvestrova A.S. Design of chemical engineering systems with chance constraints // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 961.]
Ryzhova A., Emelyanov I., Ziyatdinov N., Khalirakhmanov Z. Optimal Heat Integration of Large-Scale Cyber-Physical Oil Refining Systems // Cyber-Physical Systems: Design and Application for Industry 4.0 (Studies in Systems, Decision and Control. V. 342) / Eds. Kravets A.G., Bolshakov A.A., Shcherbakov M. Cham: Springer, 2021. P. 335. https://doi.org/10.1007/978-3-030-66081-9_27
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии