1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 56, № 1, 2022

Теоретические основы химической технологии, 2022, T. 56, № 1, стр. 72-87

Оценка параметров модели процесса сверхкритической флюидной экстракции методом Монте-Карло

А. А. Саламатин a, b, *, **, А. С. Халиуллина b

a Институт механики и машиностроения, Казанский научный центр РАН
Казань, Россия

b Казанский (Приволжский) федеральный университет
Казань, Россия

* E-mail: arthur.salamatin2@gmail.com
** E-mail: salamatin@imm.knc.ru

Поступила в редакцию 08.04.2021
После доработки 10.06.2021
Принята к публикации 12.07.2021

Полный текст (PDF)

Аннотация

Исследуется проблема идентификации моделей процесса сверхкритической флюидной экстракции из высокомасличного растительного сырья по данным серии лабораторных опытов для отдельных фракций молотого материала. На основе метода Монте-Карло для марковских цепей анализируется информативность данных лабораторных опытов. Определяется точность идентификации основных эффективных параметров модели, таких как коэффициент диффузии, концентрация насыщения масла в растворителе и полное содержание целевых соединений в сырье. Последовательно рассмотрены различные параметризации обратной задачи. Так, при известном начальном маслосодержании коэффициент диффузии возможно оценить по индивидуальной кривой выхода масла, отвечающей достаточно грубому помолу. В то же время одновременная оценка всех трех параметров возможна только при совокупном анализе хотя бы двух кривых выхода масла. Они отвечают тонкому и грубому помолу сырья. Эксперимент при тонком измельчении позволяет идентифицировать только полное содержание целевых соединений и концентрацию насыщения и не может быть использован для оценки коэффициента диффузии.

Ключевые слова: сверхкритическая флюидная экстракция, модель сжимающегося ядра, полидисперсный зернистый слой, байесовский метод, выборка из распределения, метод Монте-Карло для марковских цепей

ВВЕДЕНИЕ

Современные промышленные технологии, основанные на применении диоксида углерода (CO2) в сверхкритическом состоянии, предполагают отказ от токсичных органических растворителей [1]. Это ведет к существенному снижению антропогенной нагрузки на окружающую среду. Сверхкритические условия достигаются при увеличении рабочих температуры T и давления P процесса выше критической точки (для CO2 304 K, 7.4 МПа) вещества-растворителя. В таком состоянии существенно повышаются растворяющая и проникающая способность экстрагента [2].

Одной из технологий нового поколения является сверхкритическая флюидная экстракция (СКФЭ) ценных биологически активных веществ (масла) из высокомасличного растительного материала: семена рапса, подсолнечника, тыквы, абрикоса и др. [3–12].

Технология [9, 13–15] реализуется фильтрацией сверхкритического CO2, через загруженный в экстракционную колонку стационарный зернистый слой частиц молотого сырья. Содержащееся в растительных клетках масло растворяется в пропитывающем зерна флюиде, диффундирует к их поверхности и транспортируется экстрагентом к выходному сечению экстрактора по поровым каналам слоя.

Задачей фундаментальных исследований в области СКФЭ в настоящее время является масштабирование технологии на промышленный уровень реализации. Это предполагает развитие и параметрическое наполнение прогностических математических моделей процесса, а также их идентификации. Полная модель СКФЭ должна включать в себя две подмодели: “внешнюю”, макромасштабную, описывающую процессы переноса на уровне аппарата-экстрактора, содержащего зернистый слой, и “внутреннюю”, микромасштабную, в которой представлена кинетика извлечения масла из одиночной частицы слоя. Первая обычно формулируется [16–18] как модель “аппарата идеального вытеснения” [19], в предположении, что раствор движется вдоль колонки в поршневом режиме. Существенным оказывается учет полидисперсности навески сырья [6, 20, 21]. Внутренняя подмодель предполагает схематизацию формы и структуры частиц слоя, конкретизацию процессов растворения и диффузионного переноса внутри частиц. Кинетика экстракции из одиночной частицы определяет поток целевых соединений с единицы поверхности молотого материала. При описании СКФЭ из высокомасличного сырья хорошее согласие с экспериментом [14, 22] обеспечивает модель сжимающегося ядра (SC – shrinking core) [18, 23, 24]. Она позволяет учесть существенно многофазный характер экстракции на микромасштабном уровне. Соответствующее уравнение решается для каждой фракции частиц, формирующих зернистый слой.

Идентификация модели процесса традиционно проводится на данных серии лабораторных опытов (рис. 1). Как правило, эксперимент предполагает предварительное разделение молотого сырья на отдельные фракции посредством набора сит. Однако полного разделения достичь не удается в силу адгезивных свойств молотого сырья [21, 25–27]. Поэтому каждая фракция состоит из частиц двух характерных размеров, a1$ \ll $ a2, а соответствующая плотность $f(a)$ объемного распределения частиц по размерам является бимодальной. В предположении сферической формы радиус пылевых, мелкодисперсных частиц a1 < 100 мкм, и радиус основных, крупнодисперсных частиц a2 ~ ~ 500 мкм. При ситовом разделении пылевые частицы захватываются поверхностью крупных, поэтому объемная доля пыли α(a2) в навеске зависит от удельной поверхности ${3 \mathord{\left/ {\vphantom {3 {{{a}_{2}}}}} \right. \kern-0em} {{{a}_{2}}}}$ крупных частиц в ней.

Рис. 1.

Типичные кривые выхода масла на примере экстракции из косточек абрикоса. Точки – экспериментальные данные. Линии – рассчитанные КВМ. Числа у кривых – номер эксперимента при соответствующем размере $a_{2}^{{(j)}}$, j = 1, … 4. Пучок КВМ для каждого эксперимента – выбранные случайным образом модели из выборки, построенной по изложенному в работе методу.

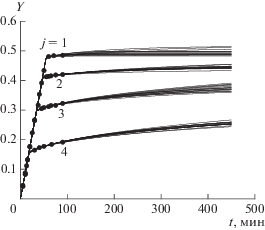
“Бимодальная фракция” с одного сита используется для проведения индивидуального эксперимента в серии при заданных T и P. Результатом эксперимента является кривая выхода масла (КВМ) Y(t). Она показывает накопленную его интегральную добычу к текущему моменту времени t, отнесенную к единице массы зернистого слоя ms. В данной работе анализируется серия из четырех опытов [7], которая предполагает выполнение отдельных экспериментов для разных фракций одного и того же помола и регистрацию соответствующего числа КВМ. Результаты эксперимента (точки) и адаптации модели (сплошные линии) приведены на рис. 1.

Рассматриваемая модель поршневого вытеснения жидкости, дополненная подходом SC на микроуровне, содержит три параметра, характеризующих систему сырье–растворитель и считающихся независимыми от степени измельчения. Эти параметры, эффективный коэффициент диффузии Deff(T, P) масла по транспортным каналам растительного сырья, предельная концентрация ${{\theta }_{*}}$(T, P) насыщения целевых соединений в растворителе и их начальная плотность θ0(T, P) в сырье, наблюдаются косвенно посредством измерения серии КВМ. Одновременно должны быть определены и объемные доли α(j), j = 1–4 пылевых частиц в навеске для каждого эксперимента. В результате оценка набора параметров $\left\{ {{{D}_{{eff}}},{{\theta }_{*}},{{\theta }_{0}},\{ {{\alpha }^{{(j)}}}\} } \right\}$ проводится путем согласования теоретических зависимостей Yj(t) со всеми данными в выполненной серии экспериментов. Зачастую метод наименьших квадратов не отвечает сложности соответствующей обратной задачи. Ее высокая размерность, сильная коррелированность параметров процесса требуют разработки новых методов идентификации характеристик сырья [28, 29].

Обозначенные проблемы удается решить в рамках байесовского подхода к исследованию обратных задач с привлечением методов Монте-Карло для марковских цепей [30–34]. В этом подходе решением является апостериорная плотность вероятности. Она характеризует шанс того, что некоторый набор значений параметров модели $\{ {{D}_{{eff}}},{{\theta }_{*}},{{\theta }_{0}}\} $ действительно отвечает наблюдаемым данным [35]. При этом каждый параметр модели трактуется как случайная величина, а функция правдоподобия оказывается эквивалентной плотности распределения этих величин. Методы Монте-Карло позволяют сгенерировать случайную выборку по распределению для оценивания статистик апостериорного распределения. В результате возможно проанализировать информативность выполненного эксперимента в отношении каждого параметра, оценить их взаимную коррелированность и наиболее правдоподобные значения, а также дисперсию в рамках точности выполненного эксперимента и выбранной модели.

Целью данной работы является развитие и апробация подходов к идентификации параметров сырья Deff, ${{\theta }_{*}}$ и θ0 по данным лабораторных наблюдений при постоянных давлении и температуре с применением методов Монте-Карло, определение наиболее информативного плана эксперимента, подходящего для идентификации отдельных параметров модели. В следующем разделе описывается эксперимент, на примере которого демонстрируется предложенный подход. Затем формулируется прямая модель процесса, приведена постановка обратной задачи и описывается способ ее решения на основе байесовского подхода. В последнем разделе обсуждаются полученные результаты. Так “минимальный” лабораторный опыт, позволяющий идентифицировать все параметры сырья в заданных условиях СКФЭ, должен включать два эксперимента. Один для крупнодисперсной, а другой – для мелкодисперсной фракции просеянного молотого сырья. Показано, что наблюдение дополнительных КВМ не позволяет существенно уточнить оценки.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

В данной работе анализируются данные по СКФЭ из молотых косточек абрикоса [7], полученные независимой группой исследователей. В эксперименте очищенные высушенные семена абрикоса измельчались в кофемолке и разделялись на фракции в вибрационном ситовом аппарате Octagon 200 (Endecotts Ltd., Англия). Было выполнено 4 эксперимента. Далее индексом j = = 1–4 будем обозначать соответствующий эксперимент и зарегистрированную КВМ.

Условия экспериментов отличаются средним размером $a_{2}^{{(j)}}$ крупных частиц, который оценен авторами как (1) $a_{2}^{{(1)}}$ = 106 мкм, (2) $a_{2}^{{(2)}}$ = 315 мкм, (3) $a_{2}^{{(3)}}$ = 460 мкм и (4) $a_{2}^{{(4)}}$ = 750 мкм. При этом данные о диаметрах ситовых отверстий, $a_{ - }^{{(j)}} < a_{2}^{{(j)}} < a_{ + }^{{(j)}}$, ограничивающих отдельную фракцию, не приводятся. Поэтому в дальнейшем примем, что указанные выше размеры $a_{2}^{{(j)}}$ заданы точно.

В каждом эксперименте в аппарат загружалась навеска массой ms = 5 г. Размеры экстракционной колонки цилиндрической формы составляли: высота H = 57 мм и внутренний диаметр 20 мм. Во время эксперимента в аппарате поддерживались температура T = 323 K и давление P = 450 бар. Плотность растворителя CO2 в этих условиях оценивается как ρf = 951 кг · м–3. Массовый расход растворителя составил Qf = 0.05 г · с–1, что отвечает скорости фильтрации $v = 1.67 \times {{10}^{{ - 4}}}$ м · с–1. Как и для эффективных размеров частиц, для этих параметров пренебрежем экспериментальной погрешностью их определения.

По оценкам авторов оригинальной работы [7] пористость упаковки частиц в зернистый слой составляет ε = 0.85. Однако такое ее значение не согласуется с известными оценками для случайных упаковок [36], и ему отвечает нереалистичное значение начальных запасов масла. Поэтому далее вместо приведенного авторами оригинальной работы фиксируется меньшее значение пористости ε = 0.35. Тогда соответствующая средняя плотность неэкстрагированного сырья составляет ${{\rho }_{s}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {(1 - \varepsilon )}}} \right. \kern-0em} {(1 - \varepsilon )}}HS = 430$ кг · м–3, где S – площадь сечения экстракционной колонны.

Исходное содержание масла авторы оценивают равным 48.1% от массы сырья, что отвечает значению θ0 = 0.481ρs = 206.8 кг · м–3. Предельная концентрация насыщения масла в экстрагенте оценена авторами оригинальной работы по начальному линейному участку КВМ как ${{\theta }_{*}}$ = = 14.075 кг · м–3. Далее в зависимости от рассматриваемой параметризации обратной задачи значения величин θ0 и ${{\theta }_{*}}$ либо фиксированы согласно оценкам авторов оригинальной работы, либо подлежат оценке наряду с остальными параметрами в рамках решения обратной задачи.

В ходе эксперимента для каждой КВМ Yj, j = 1, … 4, измеряется текущая добыча масла ${{Y}_{{ji}}} = {{Y}_{j}}(t_{i}^{{(j)}})$ в дискретные моменты времени $t = t_{i}^{{(j)}}$, i = 1, … Nj. Число Nj таких моментов времени и интервал между ними не фиксированы для индивидуальной КВМ. Результаты описанного эксперимента, точки $(t_{i}^{{(j)}};{{Y}_{{ji}}})$, приведены на рис. 1.

ПРЯМАЯ И ОБРАТНАЯ ЗАДАЧИ ИНТЕРПРЕТАЦИИ ДАННЫХ ЭКСПЕРИМЕНТА

Прямая задача: количественное описание процесса. Прямая задача интерпретации результатов экспериментов заключается в вычислении значений наблюдаемых величин (данных) δ по значениям вектора параметров модели μ. Индивидуальный набор значений задает конкретную систему в рамках принятой схематизации процесса. Конкретный набор параметров в векторах δ и μ зависит от постановки обратной задачи и определяется ниже.

Будем различать данные, зарегистрированные в ходе эксперимента, δexp и аналогичные вычисленные значения δcal, отвечающие модели μ процесса. Тогда рассматриваемая далее схематизация СКФЭ устанавливает связь

(1)
${{\delta }_{{cal}}} = g(\mu )$

между μ и δ и конкретизирует оператор g. Здесь используется подход взаимопроникающих и взаимодействующих континуумов для описания процессов массопереноса в многофазной среде, и принимаются следующие допущения. Начальные запасы масла равномерно распределены по всему объему частиц измельченного сырья с плотностью θ0. Растворение масла в CO2 в сверхкритическом состоянии характеризуется предельной концентрацией насыщения (плотностью) ${{\theta }_{*}}$, которая остается достаточно малой по сравнению с плотностью ρf растворителя, $\theta {\text{*}}$/ρf ~ 0.01 $ \ll $ 1. Аналогично для высокомасличного сырья справедливо $\theta {\text{*}}$/θ0 ~ ~ 0.07 $ \ll $ 1. В этих условиях запасенное масло не может быть полностью растворено в проникающем внутрь молотых частиц растворителе. Поэтому СКФЭ из высокомасличного сырья существенно многофазный процесс.

Обозначим время как t. Определим ось 0 < z < H цилиндрической системы координат, совпадающую с осью симметрии экстракционной колонки и направленной в сторону осредненного макроскопического движения фильтрующегося со скоростью v раствора. Координаты z = 0 и z = H отвечают входному и выходному сечению аппарата соответственно. Далее, $0 \leqslant c(z,t) \leqslant 1$ – нормированная на $\theta {\text{*}}$ концентрация масла в растворителе в порах зернистого слоя.

Микромасштабная схематизация определяется внутренней, клеточной структурой растительного сырья. В литературе предлагаются разные модели, учитывающие влияние внутренней структуры на динамику экстракции [6, 17, 20, 23, 37–40]. Сопротивление массопереносу масла принято связывать с клеточными мембранами, ограничивающими клетку с запасенными веществами, и с клеточными стенками, окруженными межклеточным пространством, которые в совокупности играют роль транспортных каналов. По ним масло диффундирует по закону Фика с эффективным коэффициентом диффузии Deff.

Для описания экстракции из высокомасличного сырья часто используется модель сжимающегося ядра [41–44], в которой основное сопротивление связано с транспортными каналами. Согласно модели в сферической частице радиуса a образуются две концентрические зоны, разделенные подвижной границей – узким диффузионным фронтом, как показано на рис. 2. На фронте содержание масла на единицу объема сырья изменяется скачком от θ0 до ${{\theta }_{*}}$.

Рис. 2.

Иллюстрация динамики внутреннего маслосодержащего ядра (1) и его замещения внешней транспортной зоной (2). Прямая стрелка показывает направление убывания R со временем, волнистые стрелки – диффузию масла в радиальном направлении по транспортной зоне. Пунктирные линии – положение фронта R в разные моменты времени.

Внутренняя область (1) – маслосодержащее ядро радиуса R(t). В ядре масло присутствует в двух фазах: в клетках в исходном, нерастворенном виде с плотностью θ0 и в транспортных каналах в растворенном виде в экстрагенте. Обе фазы находятся в термодинамическом равновесии в силу высокой проводимости клеточных мембран, и концентрация раствора в транспортных каналах в ядре равна $\theta {\text{*}}$.

Внешняя область (2) – транспортная зона истощения – содержит только масло, растворенное в CO2. Причем как в клетках, так и в транспортных каналах. Здесь плотность текущих запасов изменяется от $\theta {\text{*}}$ на поверхности маслосодержащего ядра до c${{\theta }_{*}}$ на поверхности частицы [38]. Движущей силой экстракции является перепад концентрации ${{\theta }_{*}}$(1–с) в транспортной зоне. Основной характеристикой частицы радиуса a является ее объемная доля 0 < s(z, t, a) < 1, занятая транспортной зоной. Для сферических частиц s = = 1 – (R/a)3. Во время экстракции радиус ядра уменьшается и происходит его постепенное замещение зоной истощения. Частица считается полностью истощенной, когда внутреннее ядро стягивается в точку R = 0, что отвечает s = 1.

В принятых обозначениях уравнения баланса массы извлекаемых соединений в индивидуальной частице принимают следующий вид [14, 18]:

(2)
$\frac{{{{\theta }_{0}}}}{{{{\theta }_{*}}}}\frac{{\partial s}}{{\partial t}} = \frac{3}{a}q,\,\,\,\,{{\left. s \right|}_{{t = 0}}} = 0,$
(3)
$q = \frac{{2{{D}_{{eff}}}}}{a}\lambda (s)(1 - c),\,\,\,\,\lambda (s) = \frac{{0.5{{{(1 - s)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{1 - {{{(1 - s)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}$

и сводятся к дифференциальному уравнению (2) для скорости увеличения объемной доли s транспортной зоны. Здесь $q{{\theta }_{*}}$ – массовый поток масла с единицы поверхности сырья в единицу времени, 2Deffλ(s)/a – коэффициент массопереноса через транспортную зону от внутреннего ядра к поверхности частицы. Интенсивность экстракции определяется удельной поверхностью частицы 3/a.

Ранее было показано [18], что в зернистых слоях, составленных из полидисперсных частиц, макроскопический эффект конвективной диффузии (дисперсии) несущественен в рамках рассматриваемых моделей. Аналогично оказывается малым сопротивление внешнего диффузионного пограничного слоя в сравнении с сопротивлением транспорту соединений по внутренним каналам сырья [14, 18]. Также учитывая высокую начальную масличность сырья, можно записать уравнение переноса концентрации c в квазистационарном приближении

(4)
$\begin{gathered} v\frac{{\partial c}}{{\partial z}} = 3(1 - \varepsilon )\left( {q(c,{{s}_{1}},{{a}_{1}})\frac{\alpha }{{{{a}_{1}}}} + q(c,{{s}_{2}},{{a}_{2}})\frac{{1 - \alpha }}{{{{a}_{2}}}}} \right), \\ {{\left. c \right|}_{{z = 0}}} = 0. \\ \end{gathered} $

Здесь не учитывается возможная пространственная стратификация частиц [41, 45], и принято гомогенное приближение для распределения частиц двух фракций с размерами a1$ \ll $ a2 в объеме аппарата; α – объемная доля пылевой фракции a1. Для вычисления потоков qk = q(c, sk, ak), k = 1, 2, микромасштабная задача (2)–(3) должна решаться независимо для каждой фракции частиц в навеске при общей омывающей концентрации c(z, t).

Наблюдаемой в эксперименте величиной является кривая выхода масла. Через yj(t) будем обозначать рассчитанную КВМ, отвечающую объемной доле α(j) пылевой фракции и размеру $a_{2}^{{(j)}}$ основной крупнодисперсной фракции при заданных значениях остальных параметров СКФЭ:

${{y}_{j}}(t) = y(\left. t \right|{{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}},{{\alpha }^{{(j)}}},a_{2}^{{(j)}}),\,\,\,\,{{y}_{{ji}}} = {{y}_{j}}(t_{i}^{{(j)}}).$

Согласно определению количество масла y(t), прошедшее через выходное сечение аппарата z = H к текущему моменту времени t и нормированное на массу зернистого слоя ms, вычисляется по следующей формуле:

(5)
$y(t) = \frac{{{{Q}_{f}}{{\theta }_{*}}}}{{{{\rho }_{f}}{{m}_{s}}}}\int\limits_0^t {c(H,\vartheta )d\vartheta {\kern 1pt} } .$

При решении обратной задачи вычисленные значения ${{\delta }_{{cal}}} = \{ {{y}_{{ji}}}\} $ сопоставляются с экспериментальными данными ${{\delta }_{{{\text{exp}}}}} = \{ {{Y}_{{ji}}}\} $.

В типичном эксперименте с высокомасличным сырьем на КВМ можно выделить два основных участка. Это начальный этап линейного роста, t < t–, и завершающий этап нелинейного накопления масла (рис. 1). В данном эксперименте продолжительности t– ≈ {60, 55, 38, 22} мин начального этапа (для j = 1, 2, 3, 4 соответственно) остаются порядка общей продолжительности лабораторного эксперимента 90 мин. За все время СКФЭ только одна кривая (1) достигла своего максимального значения. Иногда дополнительно выделяют промежуточный, переходный этап. Его продолжительность мала по сравнению с остальными этапами и в рамках рассматриваемой модели определяется только размером a1 частиц пылевой фракции [24].

Вначале из аппарата выходит раствор при максимальной концентрации c = 1 и КВМ растет линейно

(6)
$y(t < {{t}_{ - }}) = \frac{{{{Q}_{f}}\theta {\text{*}}}}{{{{\rho }_{f}}{{m}_{s}}}}t.$

Так как величины ms, Qf и ρf известны с высокой точностью, начальный этап эксперимента служит для оценки концентрации насыщения ${{\theta }_{*}}$. Продолжительность линейного участка определяется преимущественно количеством α пылевой фракции в навеске частиц с высокой удельной поверхностью ${3 \mathord{\left/ {\vphantom {3 {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}$.

Начало завершающего этапа отвечает полной выработке мелкодисперсной фракции частиц. Малая удельная поверхность крупнодисперсной фракции a2 не позволяет растворителю насытиться целевыми соединениями за время фильтрации в зернистом слое. На завершающем этапе из аппарата выходит раствор при исчезающе малой концентрации c $ \ll $ 1 при t > t–.

Так как размер a1 частиц мелкодисперсной фракции влияет на форму КВМ только на краткосрочном переходном этапе, в дальнейшем устремим a1 к нулю с сохранением объемной доли α пылевой фракции в зернистом слое. Такое упрощение позволяет сократить число параметров модели без ущерба точности описания наблюдаемых величин Yji.

Обратная задача: байесовский подход. В рамках прямой задачи (2)–(5) конкретизируется оператор (1). В результате решения обратной задачи различные модели μ (при фиксированной параметризации) классифицируются на более и менее правдоподобные на основе известных данных δexp.

Очевидно, в рамках выбранного подхода (2)–(5) возможно рассмотрение различных параметризаций процесса, отвечающих различным наборам параметров μ. Вначале остановимся на анализе отдельных КВМ, полагая μ ≡ μ(j) = {Deff, α(j)}. Значения θ0, ${{\theta }_{*}}$ в этом случае фиксируются на основе оценок авторов оригинальной работы [7], которые приведены в разделе “Экспериментальная часть”. Соответственно ${{\delta }_{{{\text{exp}}}}} \equiv \delta _{{{\text{exp}}}}^{{(j)}} = \{ {{Y}_{j}}(t_{i}^{{(j)}})\} $ включает только одну КВМ Yj. Затем рассматривается информативность отдельных КВМ в отношении всех трех параметров сырья $\mu \equiv \mu _{{full}}^{{(j)}}$ =  $\{ {{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}},{{\alpha }^{{(j)}}}\} $ и обсуждается точность идентификации θ0 и ${{\theta }_{*}}$ одновременно с Deff в условиях полного отсутствия информации о значении α(j) на основе одного эксперимента. В завершение сравниваются два плана эксперимента. Один состоит из двух КВМ, J = {1, 4}, а второй – из всех доступных КВМ, J = {1–4}. Соответствующие параметризации моделей принимают вид $\mu \equiv \mu _{{full}}^{{(1,4)}}$ = $\{ {{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}},{{\alpha }^{{(1)}}},{{\alpha }^{{(4)}}}\} $ и $\mu \equiv \mu _{{full}}^{{(1 - 4)}}$ = = $\{ {{\theta }_{0}},{{\theta }_{{\text{*}}}},{{D}_{{eff}}},{{\alpha }^{{(1)}}},{{\alpha }^{{(2)}}},{{\alpha }^{{(3)}}},{{\alpha }^{{(4)}}}\} $. Соответственно, δexp включает две либо все четыре доступные КВМ.

Решение обратной задачи строится в рамках байесовского подхода в теории вероятности [33, 34, 46]. Вектор μ трактуется как случайный. Решением является апостериорная плотность распределения

(7)
$\Gamma (\mu ) = b\varphi (\mu )L({{{{Y}_{{ji}}}} \mathord{\left/ {\vphantom {{{{Y}_{{ji}}}} \mu }} \right. \kern-0em} \mu }),$
где b – нормировочный множитель (константа), L(Yji|μ) – функция правдоподобия. Априорная плотность распределения φ(μ) характеризует доступную информацию о процессе до проведения эксперимента.

Примем, что φ отвечает равномерному распределению внутри гиперкуба – область в пространстве моделей процесса. Его границы выбираются из эмпирических соображений. Примем весьма общие ограничения. Для объемных долей, исходя из их физического смысла, справедливо $0 < {{\alpha }^{{(j)}}} < 1$. Предельная концентрация масла в CO2 ограничена значениями $12\,\,{\text{кг}}\,{{{\text{м}}}^{{ - 3}}} < \theta {\text{*}} < 15\,\,{\text{кг}}\,{{{\text{м}}}^{{ - 3}}}$ [47, 48]. Для коэффициента диффузии принято 3 × 10–13 м2 с–1 < < Deff < 1 × 10–11 м2 с–1. Очевидно, что значение начального содержания масла должно быть больше нуля и не может превосходить плотности сырья ρs = 430 кг м–3. Однако КВМ при j = 4 предполагает, что θ0 > 80 кг м–3, и сырье не может полностью состоять из чистого масла. Поэтому степень неопределенности полного содержания целевых соединений в сырье до проведения опытов по СКФЭ (априорная информация) достаточно охарактеризовать интервалом $80\,\,{\text{кг }}{{{\text{м}}}^{{ - 3}}} < {{\theta }_{0}} < 400\,\,{\text{кг }}{{{\text{м}}}^{{ - 3}}}$.

Апостериорная плотность вероятности Γ(μ) описывает конечное состояние информации о параметрах модели. Она объединяет априорную информацию о параметрах μ вместе с информацией, полученной из эксперимента. Последняя выражается функцией правдоподобия L(Yji|μ).

При записи функции L примем, что отдельные наблюдения значений индивидуальной КВМ Yj статистически независимы. Ошибка измерения распределена по нормальному закону с нулевым средним значением и дисперсией $\sigma _{j}^{2}$. Общее для всех точек отдельной кривой значение дисперсии оценивалось по стандартному правилу

$\sigma _{j}^{2} = \frac{1}{{{{N}_{j}}}}\sum\limits_{i = 1}^{{{N}_{j}}} {{{{({{y}_{j}}(\left. {t_{i}^{{(j)}}} \right|{{{\hat {\mu }}}_{j}}) - {{Y}_{{ji}}})}}^{2}}} \equiv \frac{1}{{{{N}_{j}}}}{{l}_{j}}(\left. {{{Y}_{{ji}}}} \right|{{\hat {\mu }}_{j}}),$
где Nj – число точек на отдельной КВМ Yj. Оцененные значения приведены в табл. 1. Оптимальная модель ${{\hat {\mu }}_{j}}$ определялась в ходе предварительного сканирования двумерной области $({{\alpha }^{{(j)}}};{{D}_{{eff}}})$. Она минимизирует логарифмическое правдоподобие отдельной КВМ

${{l}_{j}}(\left. {{{Y}_{{ji}}}} \right|{{\mu }_{j}}) = \sum\limits_{i = 1}^{{{N}_{j}}} {{{{\left( {{{y}_{j}}(\left. {t_{i}^{{(j)}}} \right|{{\mu }_{j}}) - {{Y}_{{ji}}}} \right)}}^{2}}} .$
Таблица 1.  

Выборочная дисперсия ${{\sigma }_{j}}$ нормально распределенной ошибки измерения, выборочные моменты распределений $\Gamma _{D}^{{(j)}}({{D}_{{eff}}})$ и оптимальное значение Deff, оцененные по индивидуальной КВМ Yj (θ0 = 206.8 кг м–3 и $\theta {\text{*}}$ = 14.075 кг м–3)

j ${{\sigma }_{j}} \times {{10}^{3}}$ Оптимальное значениеa, м2 с–1 Среднее значение, м2 с–1 Стандартное отклонение, м2 с–1 Коэффициент вариацииb, %
1 2.5 $4.65 \times {{10}^{{ - 12}}}$ $3.26 \times {{10}^{{ - 12}}}$ $1.14 \times {{10}^{{ - 12}}}$ 35
2 1 $2.15 \times {{10}^{{ - 12}}}$ $2.30 \times {{10}^{{ - 12}}}$ $0.59 \times {{10}^{{ - 12}}}$ 26
3 1.3 $2.20 \times {{10}^{{ - 12}}}$ $2.26 \times {{10}^{{ - 12}}}$ $0.39 \times {{10}^{{ - 12}}}$ 17
4 1.2 $2.64 \times {{10}^{{ - 12}}}$ $2.66 \times {{10}^{{ - 12}}}$ $0.30 \times {{10}^{{ - 12}}}$ 11

a Оптимальное значение отвечает максимальному правдоподобию в выборке по распределению. b Отношение стандартного отклонения к среднему значению выборки.

Заметим, что минимизация ${{l}_{j}}(\left. {{{M}_{{ji}}}} \right|{{\mu }_{j}})$ по μj эквивалентна решению обратной задачи по методу наименьших квадратов и в отличие от байесовского подхода характеризует единственную точку пространства моделей.

Функция правдоподобия всего эксперимента определена следующим образом:

(8)
$L(\left. {{{Y}_{{ji}}}} \right|\mu ) = \exp \left( { - \sum\limits_j {\frac{{{{l}_{j}}(\left. {{{Y}_{{ji}}}} \right|{{\mu }_{j}})}}{{\sigma _{j}^{2}}}} } \right).$

Метод Монте-Карло для марковских цепей. Выборка последовательности случайных точек μw, w = 1, …W, по распределению Γ является реализацией марковской цепи с использованием правила Метрополиса–Гастингса. В силу высокой коррелированности параметров модели используется алгоритм [31, 32]. Параллельно генерируется 2N последовательностей (цепочек), где N – число параметров в векторе μ. Очередное поколение w + 1 строится на основе текущего w по следующему правилу. По порядку перебираются все цепочки. Для текущей последовательности k = 1, … 2N случайным образом выбираются еще две цепи с индексами ${{k}_{1}} \ne {{k}_{2}} \ne k$ и строится пробная модель согласно правилу

$\mu _{{wk}}^{'} = {{\mu }_{{wk}}} + \gamma \left( {{{\mu }_{{w{{k}_{1}}}}} - {{\mu }_{{w{{k}_{2}}}}}} \right) + \xi {\kern 1pt} ,$
где ξ – многовариантная нормально распределенная случайная величина с нулевым средним и диагональной ковариационной матрицей. Дисперсия по каждому направлению нормирована на характерное значение параметра и составляет 10–4. Рекомендуемое оптимальное значение параметра γ составляет $2.38{{(2N)}^{{ - 1/2}}}$ [30].

Если пробная модель $\mu _{{wk}}^{'}$ оказывается за пределами гиперкуба, отвечающего априорному распределению φ, то заданием периодических граничных условий она возвращается внутрь области допустимых моделей. Затем пробная модель принимается, ${{\mu }_{{w + 1,k}}} = \mu _{{wk}}^{'}$, с вероятностью

(9)
$p = \min \left( {1;\frac{{\Gamma (\mu _{{wk}}^{'})}}{{\Gamma ({{\mu }_{{w + 1,k}}})}}} \right),\,\,\,\,\frac{{\Gamma (\mu _{{wk}}^{'})}}{{\Gamma ({{\mu }_{{w + 1,k}}})}} = \frac{{L(\mu _{{wk}}^{'})}}{{L({{\mu }_{{w + 1,k}}})}},$

либо отвергается, и ${{\mu }_{{w + 1,k}}} = {{\mu }_{{wk}}}$. Последнее равенство в уравнении (9) учитывает, что в качестве априорной вероятности принято равномерное распределение, φ(μ) = const. В таком подходе не требуется предварительное вычисление нормирующего множителя b в уравнении (7).

Существенным преимуществом рассматриваемого алгоритма является то, что он содержит всего два подстроечных параметра, множитель γ и диагональная ковариационная матрица случайной величины ξ. Причем рекомендуемые в литературе значения полностью удовлетворяют требованиям текущей работы.

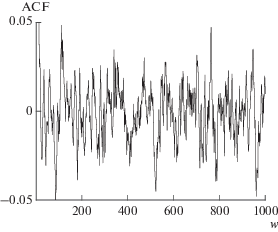
В расчетах строились 91 500 поколений. Из них первые 1500 относились к стадии разогрева (англ. burn-in) и в анализе не учитывались. Таким образом, обеспечивалась стационарность процесса. Из оставшихся 90 000 поколений принимался только каждый девятый элемент для достижения независимости отдельных элементов выборки. В результате из отдельной цепочки сохранялись только 104 элементов. Окончательная выборка формировалась объединением независимых элементов из всех цепей с образованием множества из $2N \times {{10}^{4}}$ элементов. Представление о степени независимости элементов выборки, построенной по такому алгоритму, дают диагональные элементы выборочной автокорреляционной функции (ACF) для одной цепочки. Для коэффициента диффузии результат одного расчета представлен на рис. 3.

Рис. 3.

Типичная выборочная автокорреляционная функция, построенная согласно изложенному алгоритму, на примере диагонального элемента Deff автокорреляционной матрицы многопараметрической модели.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Идентификация Deff по индивидуальным КВМ. На рис. 4 показаны гистограммы плотности маргинальной апостериорной функции распределения

$\Gamma _{D}^{{(j)}}({{D}_{{eff}}}) = \int\limits_0^1 {{{\Gamma }^{{(j)}}}({{D}_{{eff}}},{{\alpha }^{{(j)}}})d{{\alpha }^{{(j)}}}} ,\,\,\,\,j = 1 \ldots 4.$
Рис. 4.

Гистограммы плотности $\Gamma _{D}^{{(j)}}$ апостериорных маргинальных функций распределения для значений эффективного коэффициента диффузии Deff, оцененных по индивидуальным КВМ j = 1 … 4 (числа у кривых). Сплошные линии – параметрическая аппроксимация полученных гистограмм нормальным распределением. КВМ j = 1 неинформативна в отношении Deff.

Гистограммы получаются в результате приближенного интегрирования на основе выборки по распределению. Высота столбца показывает (нормированное) число попаданий элементов выборки в соответствующий интервал. Сумма площадей столбцов нормирована на единицу. Каждый график j (числа 1–4 у кривых) и исходная плотность вероятности $\Gamma ({{D}_{{eff}}},{{\alpha }^{{(j)}}})$ получены в результате адаптации двух параметров, ${{\mu }^{{(j)}}} = \{ {{D}_{{eff}}},{{\alpha }^{{(j)}}}\} $, по индивидуальной КВМ Yj. Значения θ0 = 206.8 кг м–3 и ${{\theta }_{*}}$ = 14.075 кг м–3 фиксированы.

Отдельным столбцом в табл. 1 сведены оптимальные значения Deff, отвечающие модели ${{\mu }^{{(j)}}}$ с максимальным значением правдоподобия (8). Остальные столбцы содержат моменты распределений $\Gamma _{D}^{{(j)}}$. В двухпараметрической постановке обратной задачи первый момент (среднее значение Deff по распределению $\Gamma _{D}^{{(j)}}$) практически не отличается от оптимальной величины, принимает весьма близкие значения для кривых j = 2, 3 и лишь немного отличается от значения, характеризующего кривую j = 4. В то же время именно КВМ, отвечающая наиболее грубому измельчению, дает наиболее точную оценку коэффициента диффузии. Для нее коэффициент вариации является наименьшим и составляет всего 11%. Качественно иная гистограмма наблюдается для кривой j = 1.

Увеличение информативности индивидуального эксперимента в отношении Deff с увеличением $a_{2}^{{(j)}}$ можно объяснить границами применимости принятой схематизации (2)–(5) СКФЭ. Так, модель SC (2)–(3), являясь главным членом разложения более общей микромасштабной схематизации [38], полностью игнорирует сопротивление клеточных мембран. Обобщенная модель [38] характеризуется критерием подобия

$\Pi = \frac{{a_{2}^{2}{{\beta }_{c}}}}{{{{a}_{c}}{{D}_{{eff}}}}},$
где βс – коэффициент массоотдачи клеточных мембран, ac – радиус клетки. Все величины, входящие в комплекс Π, кроме a2, принимаются постоянными для сырья в заданных термодинамических условиях. Процесс СКФЭ тем точнее описывается в рамках подхода SC, чем точнее выполняются условия: (1) высокая начальная масличность сырья, ${{\theta }_{*}} \ll {{\theta }_{0}}$, и (2) малое характерное время ac/βc диффузии масла через клеточную мембрану, Π $ \gg $ 1. Соответственно при более тонком измельчении значение Π падает, и динамика СКФЭ все более зависит от ac/βc. Таким образом, на физическом уровне описания процесса падает точность самой модели (2)–(5), на которой базируется решение обратной задачи.

Расхождение средних (и оптимальных) значений для оценок Deff между тремя КВМ, j = 2–4, может быть также объяснено с привлечением идей теории подобия. Из анализа размерностей следует, что в пределе Π → ∞ независимым критерием подобия для индивидуальной КВМ Y остается отношение двух характерных времен

$\tilde {\Pi } = \frac{{a_{2}^{2}v}}{{H(1 - \varepsilon ){{D}_{{eff}}}}}.$

Именно наиболее правдоподобное значение $\tilde {\Pi }$ определяется в ходе адаптации модели (2)–(5), например, по методу наименьших квадратов. И лишь затем пересчитывается соответствующее значение коэффициента

${{D}_{{eff}}}\left( {\left. {{{a_{2}^{2}} \mathord{\left/ {\vphantom {{a_{2}^{2}} {\tilde {\Pi }}}} \right. \kern-0em} {\tilde {\Pi }}}} \right|H,v,\varepsilon } \right) = \frac{v}{{H(1 - \varepsilon )}}\frac{{a_{2}^{2}}}{{\tilde {\Pi }}}.$

Как правило, величины v, H и ε считаются заданными точно. Однако размер ${{a}_{2}}$ крупных частиц неизвестен в связи с тем, что он является эффективным и характеризует “в среднем” полидисперсный ансамбль просеянных частиц измельченного сырья. Единственным разумным ограничением на выбор ${{a}_{2}}$ видится размер отверстий сит ${{a}_{ - }} < {{a}_{2}} < {{a}_{ + }}$ ограничивающих рассматриваемую фракцию. Следовательно, каждая экспериментальная КВМ может быть охарактеризована спектром значений коэффициента диффузии ${{D}_{{eff}}}\left( {{{a_{2}^{2}} \mathord{\left/ {\vphantom {{a_{2}^{2}} {\tilde {\Pi }}}} \right. \kern-0em} {\tilde {\Pi }}}} \right)$. После фиксации $\tilde {\Pi }$ по методу наименьших квадратов неопределенность в Deff  сохраняет одну степень свободы. Если одновременно анализируется серия КВМ, то эффективные значения $a_{2}^{{(j)}}$ не могут задаваться произвольно, так как обратная задача оценки коэффициента диффузии становится переопределенной. Одновременно получается набор разных значений Deff в количестве, равном числу анализируемых КВМ.

В настоящей работе $a_{2}^{{(j)}}$, j = 1, … 4, зафиксированы согласно рекомендации авторов оригинальной работы [7], что позволяет установить взаимно однозначное соответствие между ${{D}_{{eff}}}$ и $\tilde {\Pi }$ при анализе индивидуальной КВМ. Однако, как следует из рис. 4, такой выбор размеров частиц приводит к несогласованным наиболее правдоподобным значениям Deff между индивидуальными КВМ и не является строго обоснованным.

За счет небольшого изменения фиксированных значений $a_{2}^{{(j)}}$ внутри соответствующего интервала $a_{ - }^{{(j)}} < a_{ + }^{{(j)}}$ гистограммы на рис. 4 могут быть смещены так, что их максимумы будут отвечать единому значению Deff. Следовательно, истинная погрешность в идентификации значения ${{D}_{{eff}}}$ определяется и неточностью задания размера крупных частиц в навеске и должна быть выше, чем найдено в настоящей работе. В этой связи более адекватной видится постановка обратной задачи в рамках байесовского подхода, когда $a_{2}^{{(j)}}$ трактуется как случайная величина и является параметром, подлежащим идентификации аналогично объемной доле α(j) пыли. Аналогичным образом на точность оценок влияет и пористость зернистого слоя. Однако расширение параметризации модели μ усиливает коррелированность параметров, и столь общая постановка здесь не рассматривается.

Как и ожидалось, эксперимент при наиболее тонком измельчении, j = 1, является наименее информативным в отношении эффективного коэффициента диффузии. В течение начального линейного этапа КВМ Y1 зернистый слой истощается в значительной степени. Лишь два последних экспериментальных значения принадлежат завершающему нелинейному этапу. На соответствующей маргинальной плотности распределения $\Gamma _{D}^{{(1)}}$ отсутствует ярко выраженный максимум. Следовательно, любое значение из выбранного интервала имеет примерно одинаковые шансы быть истинным значением оцениваемого параметра Deff.

На основе выполненного анализа можно предположить, что для оценки эффективного коэффициента диффузии при заданных давлении и температуре процесса по единственному эксперименту подойдет навеска сырья наиболее грубого помола, a2 ~ 1 мм. Однако с учетом неопределенности задания a2 для более точной идентификации может потребоваться проведение серии экспериментов.

Идентификация всех параметров по индивидуальной КВМ. Рассмотрим возможность одновременной идентификации всех трех параметров сырья θ0, ${{\theta }_{*}}$ и Deff по индивидуальному эксперименту при известном эффективном среднем размере a2 основной фракции. Доля α(j) также подлежит оцениванию. Параметризация модели представляется вектором $\mu \equiv \mu _{{full}}^{{(j)}} = ~({{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}},{{\alpha }^{{(j)}}})$, j = 1, … 4.

Плотность $\Gamma _{{full,*}}^{{(j)}}({{\theta }_{*}})$ маргинальной функции распределения для концентрации насыщения ${{\theta }_{*}}$ получается интегрированием плотности $\Gamma _{{full}}^{{(j)}}$ совместной функции распределения по остальным переменным

$\begin{gathered} \Gamma _{{full,*}}^{{(j)}}({{\theta }_{*}}) = \\ = \int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {\int\limits_0^1 {\Gamma _{{full}}^{{(j)}}({{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}},{{\alpha }^{{(j)}}})d{{\alpha }^{{(j)}}}} d{{D}_{{eff}}}} d{{\theta }_{0}}} . \\ \end{gathered} $

Соответствующие гистограммы приведены на рис. 5. Выборочные моменты сведены в табл. 2. В то время как отдельные КВМ позволяют с высокой точностью оценить наиболее правдоподобное значение ${{\theta }_{*}}$, они получаются несколько разными. Это различие составляет ~5%, что на порядок выше коэффициента вариации для отдельных КВМ.

Рис. 5.

Гистограммы плотности $\Gamma _{{full,*}}^{{(j)}}({{\theta }_{*}})$ апостериорных маргинальных функций распределения, полученных в результате оценки параметров модели $\mu _{{full}}^{{(j)}}$ на основе индивидуальной КВМ, j = 1, … 4 (числа у кривых). Сплошные линии – параметрическая аппроксимация гистограммы нормальным распределением.

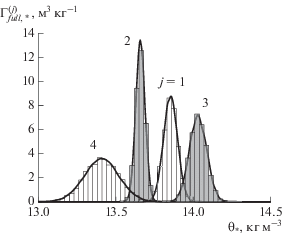
Таблица 2.  

Выборочные моменты распределений $\Gamma _{{full,*}}^{{(j)}}({{\theta }_{*}})$ и $\Gamma _{{full,*}}^{{(J)}}({{\theta }_{*}})$ и оптимальное значение ${{\theta }_{*}}$, оцененные по индивидуальной КВМ Yj или серии КВМ YJ

j/J Оптимальное значениеa, кг м–3 Среднее значение, кг м–3 Стандартное отклонение, кг м–3 Коэффициент вариацииb, %
1 13.85 13.85 0.0454 0.3
2 13.68 13.66 0.03 0.2
3 13.95 14.03 0.055 0.4
4 13.53 13.4 0.11 0.8
1, 4 13.78 13.79 0.042 0.3
1–4 13.75 13.75 0.022 0.16

a Оптимальное значение отвечает максимальному правдоподобию в выборке по распределению. b Отношение стандартного отклонения к среднему значению выборки.

Наблюдаемое расхождение значений в разных строках табл. 2 можно объяснить на основе уравнения (6). Именно наклон начального линейного участка КВМ наиболее информативен в отношении параметра ${{\theta }_{*}}$. Точность его идентификации непосредственно связана с точностью задания массового расхода растворителя Qf, оценки его плотности ρf в рассматриваемых условиях и массы навески ms. Естественно ожидать, что точность контроля значений этих параметров лежит в интервале 5–10%. Однако в отдельных экспериментах [9] расхождение между безразмерными значениями ${{\theta }_{*}}$/ρf для отдельных КВМ доходит до 40%. Объяснение столь сильному расхождению в настоящее время не предложено.

Два других параметра, коэффициент диффузии и полное содержание целевых соединений, преимущественно идентифицируются по завершающему нелинейному участку КВМ. Поэтому они сильно коррелированы. Эту связь в рамках микромасштабной модели SC можно выразить следующим образом. В зависимости от значения Deff фронт выработки R(t) проникает вглубь частицы на разную кажущуюся глубину Δ(Deff). Соответственно, средний объем транспортной зоны в крупных частицах на момент окончания экстракции можно оценить как

$\left\langle {{{V}_{2}}} \right\rangle = {\text{ }}4\pi a_{2}^{2}\Delta ({{D}_{{eff}}}) \equiv \frac{{4\pi }}{3}a_{2}^{3}\left\langle {{{s}_{2}}} \right\rangle ,\,\,\,\,\Delta = \frac{{{{a}_{2}}}}{3}\left\langle {{{s}_{2}}} \right\rangle ,$
где $\left\langle {{{s}_{2}}} \right\rangle $ – средняя объемная доля транспортной зоны в частицах a2 к завершению экстракции. При этом среднее количество масла, извлеченное из этих частиц за тот же период времени,

$\Delta m_{2}^{{{\text{(exp)}}}} = {{\theta }_{0}}\left\langle {{{V}_{2}}} \right\rangle $

измеряется в ходе эксперимента и поэтому является инвариантным по отношению к моделям μ. Таким образом, экспериментальные данные фактически устанавливают связь θ0 Δ(Deff) = const между θ0 и Deff для заданного измельчения сырья.

В данной работе зафиксирована высокая априорная степень неопределенности параметра θ0. Соответственно, неопределенным остается и коэффициент диффузии. Рассмотрим результаты оценки этого параметра на основе соответствующей плотности $\Gamma _{{full,{\text{D}}}}^{{(j)}}({{\theta }_{*}})$ маргинальной функции распределения. Полученные гистограммы приведены на рис. 6. Выборочные моменты сведены в табл. 3.

Рис. 6.

Гистограммы $\Gamma _{{full,D}}^{{(j)}}({{D}_{{eff}}})$ апостериорных маргинальных функций распределения для значений эффективного коэффициента диффузии Deff в результате оценки параметров модели $\mu _{{full}}^{{(j)}}$ на основе индивидуальной КВМ. Линии – непараметрическая аппроксимация гистограммы непрерывной функцией [50]. Сами гистограммы не приведены.

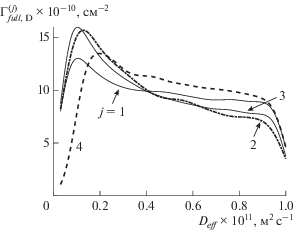
Таблица 3.  

Выборочные моменты распределений $\Gamma _{{full,{\text{D}}}}^{{(j)}}({{D}_{{eff}}})$ и $\Gamma _{{full,{\text{D}}}}^{{(J)}}({{D}_{{eff}}})$ и оптимальное значение Deff, оцененные по индивидуальной КВМ Yj или серии КВМ YJ

j/J Оптимальное значениеa, м2 с–1 Среднее значение,
м2 с–1		 Стандартное отклонение, м2 с–1 Коэффициент вариацииb, %
1 $3.95 \times {{10}^{{ - 12}}}$ $4.74 \times {{10}^{{ - 12}}}$ $2.88 \times {{10}^{{ - 12}}}$ 61
2 $8.3 \times {{10}^{{ - 12}}}$ $4.42 \times {{10}^{{ - 12}}}$ $2.85 \times {{10}^{{ - 12}}}$ 64
3 $6.53 \times {{10}^{{ - 12}}}$ $4.32 \times {{10}^{{ - 12}}}$ $2.81 \times {{10}^{{ - 12}}}$ 65
4 $5.4 \times {{10}^{{ - 12}}}$ $5.12 \times {{10}^{{ - 12}}}$ $2.64 \times {{10}^{{ - 12}}}$ 52
1, 4 $2.51 \times {{10}^{{ - 12}}}$ $2.54 \times {{10}^{{ - 12}}}$ $0.305 \times {{10}^{{ - 12}}}$ 12
1–4 $2.1 \times {{10}^{{ - 12}}}$ $2.02 \times {{10}^{{ - 12}}}$ $0.271 \times {{10}^{{ - 12}}}$ 13

a Оптимальное значение отвечает максимальному правдоподобию в выборке по распределению. b Отношение стандартного отклонения к среднему значению выборки.

Каждая гистограмма характеризуется глобальным максимумом в области значений Deff ~ 10–12 м2 с–1. Однако максимум не является выраженным. Плотность распределения $\Gamma _{{full,D}}^{{(j)}}({{D}_{{eff}}}) \approx {\text{const}}$ принимает близкие значения на всем интервале, фактически оставаясь плотностью равномерного распределения. Этот результат принципиально отличается от предыдущего раздела, где значения ${{\theta }_{*}}$ и θ0 были зафиксированы. Таким образом, ни одна индивидуальная КВМ не является информативной в отношении параметра Deff в условиях, когда неопределенным остается параметр θ0. Эту ситуацию отражают высокие значения коэффициента вариации и дисперсии в табл. 3. С некоторой долей уверенности можно лишь оценить порядок величины коэффициента диффузии.

Так как набор групп извлекаемых соединений существенно определяется используемым растворителем, давлением и температурой, эффективное содержание θ0 также возможно оценить только из эксперимента по СКФЭ. Для этого также предлагается использовать байесовский подход. Гистограмма соответствующей маргинальной плотности распределения

$\begin{gathered} \Gamma _{{full,0}}^{{(j)}}({{\theta }_{0}}) = \\ = \int\limits_0^{ + \infty } {\int\limits_0^{ + \infty } {\int\limits_0^1 {\Gamma _{{full}}^{{(j)}}({{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}},{{\alpha }^{{(j)}}})d{{\alpha }^{{(j)}}}} d{{D}_{{eff}}}} d{{\theta }_{*}}} \\ \end{gathered} $

показана на рис. 7 для всех КВМ. Ее выборочные моменты сведены в табл. 4.

Рис. 7.

Гистограммы $\Gamma _{{full,0}}^{{(j)}}({{\theta }_{0}})$ апостериорных маргинальных функций распределения (j = 1–4 – числа у кривых) для значений полного начального содержания θ0 в результате оценки параметров модели $\mu _{{full}}^{{(j)}}$ на основе индивидуальной КВМ. Сплошные линии – непараметрическая аппроксимация гистограммы непрерывной функцией [50].

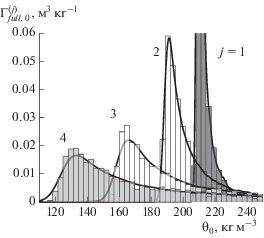
Таблица 4.  

Выборочные моменты распределений $\Gamma _{{full,0}}^{{(j)}}({{\theta }_{0}})$ и $\Gamma _{{full,0}}^{{(J)}}({{\theta }_{0}})$ и оптимальное значение θ0, оцененные по индивидуальной КВМ Yj или серии КВМ YJ

j/J Оптимальное значениеa, кг м–3 Среднее значение, кг м–3 Стандартное отклонение, кг м–3 Коэффициент вариацииb, %
1 212 214 7.19 3.3
2 200.22 203.8 16.12 8
3 170 201 46.8 23
4 126–205 180.88 61.06 34
1, 4 213.22 215 4.5 2
1–4 210 212 3.8 1.8

a Оптимальное значение отвечает максимальному правдоподобию в выборке по распределению. b Отношение стандартного отклонения к среднему значению выборки.

Полученные гистограммы существенно асимметричны, характеризуются сильно выраженным правым хвостом и резко обрываются слева от локального максимума. В то же время положение максимума и нижняя граница носителя функции $\Gamma _{{full,0}}^{{(j)}}({{\theta }_{0}})$ сдвигаются в область больших значений θ0 с уменьшением a2. Это связано с тем, что можно записать оценку

$\Delta {{m}^{{{\text{(exp)}}}}} \leqslant {{\theta }_{0}}(1 - \varepsilon )HS,$
где Δm(exp) – количество масла, извлеченного из зернистого слоя за время эксперимента. Значение Δm(exp) растет с уменьшением a2 и определяет нижнюю границу интервала возможного изменения θ0.

Выраженный правый хвост гистограммы связан с тем, что оценивание θ0 эквивалентно экстраполяции КВМ вплоть до момента полного истощения зернистого слоя. Поведение КВМ достоверно неизвестно на временах, больших по сравнению с продолжительностью эксперимента. Поэтому имеющиеся экспериментальные данные не позволяют полностью исключить возможность того, что истинное значение θ0 окажется выше положения максимума гистограммы. Особенно это выражено для КВМ j = 4, отвечающей наиболее грубому помолу. Для нее Δm(exp) принимает наименьшее значение, а также велико время, необходимое для полного истощения зернистого слоя. Данная проблема выражена в большей степени при исследовании процессов экстракции, где сорбционные механизмы являются определяющими [49].

Здесь важно отметить, что оценивание параметра θ0 по индивидуальной КВМ имеет смысл только для достаточно тонкого измельчения. В остальных случаях оценка по методу наибольшего правдоподобия является неверной.

Формирование выраженного максимума на гистограмме наблюдается с уменьшением характерного размера a2. Самой информативной оказывается КВМ при j = 1, характеризуемая наиболее полным истощением зернистого слоя. Максимум на гистограмме наблюдается в области θ0 = 208–224 кг м–3, что позволяет уточнить оценку исходного содержания масла до уровня 48.4–52.1%. В результате наблюдения КВМ Y1 при малом характерном размере $a_{2}^{{(1)}}$ исчезающе малым становится шанс того, что истинное полное содержание лежит в интервале θ0 < 206 кг м–3.

Таким образом, индивидуальные КВМ в зависимости от среднего размера a2 частиц крупнодисперсной фракции позволяют с высокой точностью оценить наиболее правдоподобные значения отдельных параметров. Так, концентрация насыщения может быть определена по любой КВМ. Однако оценка полного содержания требует выполнения эксперимента при возможно тоньшем измельчении сырья. Но при стремлении a2 к нулю теряется информация о коэффициенте диффузии Deff. Таким образом, минимальный план эксперимента должен включать экстракцию как для тонкого, так и для грубого измельчения сырья чтобы обеспечить высокую точность идентификации всего набора параметров при заданных термодинамических условиях процесса.

Оценивание по совокупности кривых. Сравним информативность эксперимента по СКФЭ для двух фракций, J = {1, 4}, и для всех четырех зарегистрированных КВМ, J = {1, … 4}. В каждом случае определялись все три параметра сырья $\{ {{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}}\} $ и необходимое количество (по числу анализируемых КВМ, 2 или 4 объемных долей пылевой фракции $\{ {{\alpha }^{{(J)}}}\} $. Вторая постановка обратной задачи, J = {1, … 4}, позволяет учесть всю доступную информацию о косвенно измеряемых параметрах $\{ {{\theta }_{0}},{{\theta }_{*}},{{D}_{{eff}}}\} $. Однако, как следует из рис. 8, избыточная по отношению к случаю J = {1, 4} информация оказывается несущественной. Здесь пунктирные линии аппроксимируют гистограммы, изображенные на рис. 5–7, и приведены для удобства визуального сравнения результатов решения обратной задачи в разных постановках.

Рис. 8.

Сравнение гистограмм и их аппроксимаций (сплошные линии) непараметрическим распределением [50] для плотностей маргинальных функций распределения параметров сырья θ0 (а), ${{\theta }_{*}}$ (б) и Deff (в). Гистограммы некоторых распределений не приводятся. Постановка задачи предполагает анализ двух или четырех КВМ, J = {1, 4} и J = {1, … 4} (числа у кривых).

Полученные оптимальное и среднее по распределению значения, а также соответствующее стандартное отклонение сведены в двух последних строчках табл. 2–4. Одновременный учет двух серий экспериментов при малом и большом значении a2 позволил оценить все параметры сырья с достаточно высокой точностью. Так, гистограмма для коэффициента Deff характеризуется ярко выраженным максимум, гистограмма для θ0 стала более симметричной с весьма узким носителем.

Одновременный анализ всех четырех КВМ не дает существенного уточнения оценок параметров. Так, идентифицированное значение ${{\theta }_{*}}$ можно считать точным в сравнении с неоднозначностью остальных величин. Среднее значение θ0 изменилось на 2% при таком же коэффициенте вариации. Наибольшая неопределенность сохраняется для эффективного коэффициента диффузии, для которого коэффициент вариации в обоих случаях составляет ~12%. При этом среднее значение по распределению изменяется на ~20% при увеличении числа рассматриваемых КВМ с 2 до 4. По-прежнему, это может быть связано с выбором среднего размера частиц крупнодисперсной фракции a2 в навеске.

ЗАКЛЮЧЕНИЕ

В работе на основе микромасштабной схематизации сжимающегося ядра и квазистационарного приближения процессов массопереноса на уровне аппарата сформулирована обратная задача идентификации параметров высокомасличного сырья в условиях СКФЭ. В эксперименте косвенно наблюдаются параметры сырья, такие как коэффициент диффузии Deff, предельная концентрация насыщения ${{\theta }_{*}}$ масла в растворителе и начальная плотность целевых соединений θ0 в единице объема сырья. Измеряемой характеристикой процесса является кривая выхода масла. Показано, что отдельные параметры характеризуют разные участки КВМ.

В результате выполненной работы проанализиирована информативность как отдельных КВМ в отношении каждого параметра, так и всей серии. Показано, что в типичных условиях низкой информированности о начальном маслосодержании план эксперимента должен включать экстракцию для двух характерных размеров частиц молотого сырья, для крупной и мелкодисперсной фракций. Первая КВМ фиксирует полное содержание, в то время как вторая – коэффициент диффузии. Одновременная оценка всех трех параметров наряду с (неизвестной) объемной долей пылевых частиц a1 в навеске по индивидуальным КВМ дает ошибочные значения. Одновременный анализ большего числа КВМ не позволяет сущесвенно улучшить полученные оценки параметров. Таким образом, оказывается возможным сократить стоимость лабораторного эксперимента за счет адекватного его планирования.

Дальнейшая работа в данном направлении предполагает учет неопределенности в задании характерного размера частиц основной фракции частиц в навеске. Наиболее разумной априорной оценкой для a2 видится интервал ${{a}_{ - }} < {{a}_{2}} < {{a}_{ + }}$ размеров отверстий сит, между которыми осела соответствующая навеска сырья.

Исследование выполнено в рамках гранта Российского фонда фундаментальных исследований № 19-31-60013. Создание алгоритма построения выборки из распределения и его верификация выполнены при поддержке средств гранта № 18-41-160001 и частично Программы стратегического академического лидерства Казанского (Приволжского) федерального университета.

Авторы выражают благодарность А.А. Заикину, доценту кафедры математической статистики КФУ, за полезные обсуждения в ходе подготовки статьи.

ОБОЗНАЧЕНИЯ

$a$ радиус частиц сырья, м
${{a}_{ \pm }}$ размеры сит, ограничивающих рассматриваемую фракцию молотых частиц, м
c нормированная массовая концентрация масла в сверхкритическом флюиде в поровом пространстве
${{D}_{{eff}}}$ эффективный коэффициент диффузии в молотом сырье, м2 с–1
$f$ плотность объемного распределения частиц по размерам, м–1
g формальный оператор, выражающий связь между параметризацией μ модели и измеряемыми величинами δ
H высота экстракционной колонны аппарата, м
L функция правдоподобия
l функция невязки, равная $\ln L$
ms масса навески, кг
P давление в аппарате, МПа
Qf объемный расход растворителя, м3 с–1
$q$ безразмерная плотность диффузионного потока масла из зерна размера $a$ в поровое пространство
$R$ радиус маслосодержащего ядра в частице, м
s объемная доля частицы, занятая транспортной зоной, равная $1 - {{({R \mathord{\left/ {\vphantom {R a}} \right. \kern-0em} a})}^{3}}$
T температура в аппарате, K
$t$ время, с
${{t}_{ - }}$ продолжительность линейного этапа экстракции, с
$v$ скорость фильтрации флюида, м с–1
$Y$ экспериментальная кривая выхода масла из экстрактора, нормированная на ms
$y$ рассчитанная кривая выхода масла из экстрактора, нормированная на ms
$z$ координата, отсчитываемая от входного сечения вдоль оси экстрактора, м
$\alpha $ объемная доля мелкодисперсной фракции пыли
Γ плотность апостериорной функции распределения оцениваемых параметров
Δ средняя по ансамблю частиц глубина проникновения фронта сжимающегося ядра вглубь крупных частиц за время экстракции, м
$\delta $ набор величин, измеряемых в эксперименте
ε пористость зернистого слоя
${{\theta }_{0}}$ отношение массы начальных запасов масла в частице зернистого слоя к ее объему, кг м–3
${{\theta }_{*}}$ равновесная (при заданных давлении и температуре) концентрация масла в сверхкритическом растворителе, кг м–3
μ набор параметров модели
ρf плотность растворителя в сверхкритических условиях, кг м–3
ρs плотность сырья, кг м–3

Список литературы

  1. Гумеров Ф.М. Сверхкритические флюидные технологии. Экономическая целесообразность. Казань: Академия наук РТ, 2019.

  2. Гумеров Ф.М., Хайрутдинов В.Ф., Зарипов З.И. Дополнительное условие эффективности сверхкритического флюидного экстракционного процесса // Теор. осн. хим. технол. 2021. Т. 55. С. 273.

  3. Касьянов Г.И. Технологические основы СО2-обработки растительного сырья. М.: Россельхозакадемия, 1994.

  4. Meyer F., Stamenic M., Zizovic I., Eggers R. Fixed bed property changes during scCO2 extraction of natural materials – Experiments and modeling // J. Supercrit. Fluids. 2012. V. 72. P. 140.

  5. Fiori L. Grape seed oil supercritical extraction kinetic and solubility data: Critical approach and modeling // J. Supercrit. Fluids. 2007. V. 43. P. 43.

  6. Fiori L. Supercritical extraction of sunflower seed oil: Experimental data and model validation // J. Supercrit. Fluids. 2009. V. 50. P. 218.

  7. Özkal S.G., Yener M.E., Bayındırlı L. Mass transfer modeling of apricot kernel oil extraction with supercritical carbon dioxide // J. Supercrit. Fluids. 2005. V. 35. P. 119.

  8. Özkal S.G., Salgin U., Yener M.E. Supercritical carbon dioxide extraction of hazelnut oil // J. Food Eng. 2005. V. 69. P. 217.

  9. Salgin U., Korkmaz H. A green separation process for recovery of healthy oil from pumpkin seed // J. Supercrit. Fluids. 2011. V. 58. P. 239.

  10. Salgin U., Salgin S. Effect of main process parameters on extraction of pine kernel lipid using supercritical green solvents: Solubility models and lipid profiles // J. Supercrit. Fluids. 2013. V. 73. P. 18.

  11. Salgin S., Salgin U. Supercritical fluid extraction of walnut kernel oil // Eur. J. Lipid Sci. Technol. 2006. V. 108. P. 577.

  12. Romero-Guzmán M.J., Vardaka E., Boom R.M., Nikiforidis C.V. Influence of soaking time on the mechanical properties of rapeseed and their effect on oleosome extraction // Food Bioprod. Process. 2020. V. 121. P. 230.

  13. Егоров А.Г., Мазо А.Б., Максудов Р.Н. Экстракция полидисперсного зернистого слоя молотых семян масличных культур сверхкритическим диоксидом углерода // Теор. осн. хим. технол. 2010. Т. 44. С. 498. [Egorov A.G., Mazo A.B., Maksudov R.N. Extraction from a polydisperse granular layer of milled oilseeds with supercritical carbon dioxide // Theor. Found. Chem. Eng. 2010. V. 44. P. 642.]

  14. Максудов Р.Н., Егоров А.Г., Мазо А.Б., Аляев В.А., Абдуллин И.Ш. Математическая модель экстрагирования семян масличных культур сверхкритическим диоксидом углерода // Сверхкрит. флюиды: теор. практ. 2008. Т. 3. С. 20. [Maksudov R.N., Egorov A.G., Mazo A.B., Aljaev V.A., Abdullin I.S. Mathematical model of oil-bearing crop seeds extraction by supercritical carbon dioxide // Sverkhkrit. Flyuidy: Teor. Prakt. 2008. V. 3. P. 20.]

  15. Касьянов Г.И. Итоги научных исследований обработки растительного и животного сырья диоксидом углерода // Изв. высш. учебн. завед. Пищ. технол. 2007. Т. 298. С. 79.

  16. Rai A., Mohanty B., Bhargava R. Fitting of broken and intact cell model to supercritical fluid extraction (SFE) of sunflower oil // Innovative Food Sci. Emerging Technol. 2016. V. 38. P. 32.

  17. Sovová H. Broken-and-intact cell model for supercritical fluid extraction: Its origin and limits // J. Supercrit. Fluids. 2017. V. 129. P. 3.

  18. Salamatin A.A. Supercritical Fluid Extraction of the Seed Fatty Oil: Sensitivity to the Solute Axial Dispersion // Ind. Eng. Chem. Res. 2020. V. 59. P. 18126.

  19. Кольцов Н.И. Квазиинварианты химических реакций в реакторе идеального вытеснения // Теор. осн. хим. технол. 2020. Т. 54. С. 643. [Koltsov N.I. Quasi-Invariants of Chemical Reactions in the Ideal Displacement Reactor // Theor. Found. Chem. Eng. 2020. V. 54. P. 913.]

  20. Fiori L., Basso D., Costa P. Seed oil supercritical extraction: Particle size distribution of the milled seeds and modeling // J. Supercrit. Fluids. 2008. V. 47. P. 174.

  21. Egorov A.G., Salamatin A.A. Bidisperse Shrinking Core Model for Supercritical Fluid Extraction // Chem. Eng. Technol. 2015. V. 38. P. 1203.

  22. Goto M., Roy B.C., Hirose T. Shrinking-core leaching model for supercritical-fluid extraction // J. Supercrit. Fluids. 1996. V. 9. P. 128.

  23. Егоров А.Г., Саламатин А.А., Максудов Р.Н. Прямые и обратные задачи сверхкритической экстракции из полидисперсного зернистого слоя растительного материала // Теор. осн. хим. технол. 2014. Т. 48. С. 43. [Egorov A.G., Salamatin A.A., Maksudov R.N. Forward and inverse problems of supercritical extraction of oil from polydisperse packed bed of ground plant material // Theor. Found. Chem. Eng. 2014. V. 48. P. 39.]

  24. Саламатин А.А. Теоретическое исследование режимов сверхкритической флюидной экстракции в полидисперсном слое растительного сырья. Дис. … канд. физ.-мат. наук. Казань: Казанский федеральный университет, 2017.

  25. Ахмадиев Ф.Г., Гиззятов Р.Ф. Стохастическое моделирование процесса разделения зернистых материалов по крупности на ситовых классификаторах // Теор. осн. хим. технол. 2020. Т. 54. С. 554. [Akhmadiev F.G., Gizzyatov R.F. Stochastic Simulation of the Process of Size Separation of Granular Materials on Sieve Classifiers // Theor. Found. Chem. Eng. 2020. V. 54. P. 828.]

  26. Халиуллина А.С., Хазиев Р.Ш., Саламатин А.А. Количественное определение дитерпеновых кислот в листьях шалфея лекарственного // Журн. анал. хим. 2017. Т. 72. С. 681. [Khaliullina A.S., Khaziev R.S., Salamatin A.A. Quantitative determination of diterpene acids in garden sage leaves // J. Anal. Chem. 2017. V. 72. P. 810.]

  27. Саламатин А.А., Егоров А.Г., Максудов Р.Н., Аляев В.А. Интерпретация кривых выхода извлекаемых компонентов при сверхкритической флюидной экстракции // Вестн. Казан. технол. унив. 2013. Т. 16. С. 74.

  28. Кольцов Н.И. Метод решения обратной задачи химической кинетики для неизотермического безградиентного реактора по стационарным данным // Теор. осн. хим. технол. 2020. Т. 54. С. 592. [Kol’tsov N.I. A Method for Solving the Inverse Problem of Chemical Kinetics for a Nonisothermal Gradientless Reactor Based on Steady-State Data // Theor. Found. Chem. Eng. 2020. V. 54. P. 863.]

  29. Оразбаев Б.Б., Шангитова Ж.Е., Оразбаева К.Н., Серимбетов Б.А., Шагаева А.Б. Исследование зависимости эффективности работы реактора клауса от значений технологических факторов и оценка качества серы на основе нечеткой информации // Теор. осн. хим. технол. 2020. Т. 54. С. 726. [Orazbayev B.B., Shangitova Zh.Ye., Orazbayeva K.N., Serimbetov B.A., Shagayeva A.B. Studying the Dependence of the Performance Efficiency of a Claus Reactor on Technological Factors with the Quality Evaluation of Sulfur on the Basis of Fuzzy Information // Theor. Found. Chem. Eng. 2020. V. 54. P. 1235.]

  30. Vrugt J.A., Ter Braak C.J.F. DREAM(D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems // Hydrol. Earth Syst. Sci. 2011. V. 15. P. 3701.

  31. Vrugt J.A., Ter Braak C.J.F., Diks C.G.H., Robinson B.A., Hyman J.M., Higdon D. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling // Int. J. Nonlinear Sci. Numer. Simul. 2009. V. 10. P. 273.

  32. Ter Braak C.J.F. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces // Stat. Comput. 2006. V. 16. P. 239.

  33. Mosegaard K. Resolution analysis of general inverse problems through inverse Monte Carlo sampling // Inverse Probl. 1998. V. 14. P. 405.

  34. Cordua K.S., Hansen T.M., Mosegaard K. Monte Carlo full-waveform inversion of crosshole GPR data using multiple-point geostatistical a priori information // Geophysics. 2012. V. 77. P. H19.

  35. Ганин П.Г., Маркова А.В., Мошинский А.И., Рубцова Л.Н., Сорокин В.В. Расчет выхода вещества из пористой системы при переменном коэффициенте диффузии // Теор. осн. хим. технол. 2020. Т. 54. С. 565. [Ganin P.G., Markova A.V., Moshinskii A.I., Rubtsova L.N., Sorokin V.V. Calculating the Extraction of a Substance from a Porous System with a Variable Diffusion Coefficient // Theor. Found. Chem. Eng. 2020. V. 54. P. 838.]

  36. Хейфец Л.И., Неймарк А.В. Многофазные процессы в пористых средах. М.: Химия, 1982.

  37. Salamatin A.A. Numerical scheme for non-linear model of supercritical fluid extraction from polydisperse ground plant material: Single transport system // IOP Conf. Ser.: Mater. Sci. Eng. 2016. V. 158. Article number 012081.

  38. Salamatin A.A. Detection of Microscale Mass-Transport Regimes in Supercritical Fluid Extraction // Chem. Eng. Technol. 2017. V. 40. P. 829.

  39. Sovová H., Kučera J., Jež J. Rate of the vegetable oil extraction with supercritical CO2–II. Extraction of grape oil // Chem. Eng. Sci. 1994. V. 49. P. 415.

  40. Sovová H. Rate of the vegetable oil extraction with supercritical CO2—I. Modelling of extraction curves // Chem. Eng. Sci. 1994. V. 49. P. 409.

  41. Salamatin A.A., Egorov A.G. Optimization of supercritical fluid extraction: Polydisperse packed beds and variable flow rates // J. Supercrit. Fluids. 2015. V. 105. P. 35.

  42. del Valle J.M. Extraction of natural compounds using supercritical CO2: Going from the laboratory to the industrial application // J. Supercrit. Fluids. 2015. V. 96. P. 180.

  43. Eikani M.H., Khandan N., Feyzi E., Ebrahimi I.M. A shrinking core model for Nannochloropsis salina oil extraction using subcritical water // Renewable Energy. 2019. V. 131. P. 660.

  44. Oliveira E.L.G., Silvestre A.J.D., Silva C.M. Review of kinetic models for supercritical fluid extraction // Chem. Eng. Res. Des. 2011. V. 89. P. 1104.

  45. del Valle J.M., Carrasco C.V., Toledo F.R., Núñez G.A. Particle size distribution and stratification of pelletized oilseeds affects cumulative supercritical CO2 extraction plots // J. Supercrit. Fluids. 2019. V. 146. P. 189.

  46. Mosegaard K., Sambridge M. Monte Carlo analysis of inverse problems // Inverse Probl. 2002. V. 18. P. R29.

  47. del Valle J.M., Aguilera J.M. An Improved Equation for Predicting the Solubility of Vegetable Oils in Supercritical CO2 // Ind. Eng. Chem. Res. 1988. V. 27. P. 1551.

  48. del Valle J.M., de la Fuente J.C., Uquiche E. A refined equation for predicting the solubility of vegetable oils in high-pressure CO2 // J. Supercrit. Fluids. 2012. V. 67. V. 60.

  49. Salamatin A.A., Khaliullina A.S., Khaziev R.S. Extraction of aromatic abietane diterpenoids from Salvia officinalis leaves by petroleum ether: Data resolution analysis // Ind. Crops Prod. 2020. V. 143. Article number 111909.

  50. Bowman A.W., Azzalini A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations (Oxford Statistical Science Series. V. 18). Oxford: Clarendon, 1997.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал