Теоретические основы химической технологии, 2022, T. 56, № 1, стр. 3-10
О влиянии следовых течений на процессы тепло- и массообмена в аппаратах с перемешивающими устройствами
В. М. Барабаш a, *, М. А. Белевицкая b, Н. Н. Кулов c, **
a ООО “МИКСИНГ”
Санкт-Петербург, Россия
b ООО “НОРД Приводы”
Санкт-Петербург, Россия
c Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: barabash@mixing.ru
** E-mail: kulovnn@mail.ru
Поступила в редакцию 20.09.2021
После доработки 26.09.2021
Принята к публикации 29.09.2021
- EDN: AVRNDA
- DOI: 10.31857/S0040357122010031
Аннотация
В работе рассматриваются вопросы образования турбулентных следовых течений, возникающих при обтекании неподвижных и движущихся тел в потоках с различной степенью турбулизации. Показано влияние характеристик течения в следовых областях на интенсивность теплообмена от змеевиков, установленных в рабочем объеме аппаратов с перемешивающими устройствами. Рассмотрены вопросы формирования газожидкостных систем и массообмена от газовых пузырьков в жидкость при перемешивании газожидкостных систем с учетом особенностей течения в турбулентных областях следа при движении большого количества пузырьков газа. Выполненный анализ позволил разработать расчетные методики процессов тепло -и массообмена для аппаратов с перемешивающими устройствами, особенности конструкции которых способствуют образованию следовых течений.
ВВЕДЕНИЕ
Турбулентный след или, как его еще называют, спутная струя [1], может образовываться при обтекании как неподвижных, так и движущих тел в потоках сплошной среды, обладающих различной степенью турбулизации. Основной особенностью следовой области является наличие устойчивой границы следа, которая является своего рода экраном, предотвращающим взаимное влияние особенностей течения внутри следа и вне его. Области следа можно непосредственно наблюдать при полете реактивных самолетов (конверсионный след), на поверхности движущейся жидкости при обтекании неподвижной преграды (опоры моста), а также при обтекании неподвижных и движущихся тел, расположенных внутри среды.
Так, например, за подводной лодкой при ее движении под водой образуется турбулентный след, особенности движения в котором обеспечивают возможности ее обнаружения. При поперечном обтекании пучков труб в теплообменной аппаратуре за каждой трубой также образуется турбулентный след, течение в котором непосредственно влияет на интенсивность теплообмена от труб, расположенных в зоне следа. Влияние течения в следовой области отчетливо проявляется и на интенсивности теплообмена при использовании в аппаратах с перемешивающими устройствами змеевиков различных конструкций. В гетерогенных системах наличие турбулентных следовых областей при движении элементов дисперсной фазы (капель, пузырьков и твердых частиц) также может иметь место [2].
Следует отметить, что характеристики течения в следовых областях (интенсивность турбулентности, скорость диссипации энергии и др.) могут существенно отличаться от соответствующих величин для среды, находящейся вне следа. В зависимости от степени турбулизации потока вне следовых областей и условий формирования следа, особенности движения в последнем могут обеспечивать как интенсификацию процессов тепло- и массообмена, так и приводить к снижению их эффективности. В ряде случаев, интенсивность турбулентного движения в области следа оказывается настолько высокой, что может привести к разрушению конструктивных элементов, находящихся в следовой области.
Все эти обстоятельства необходимо учитывать при расчете и проектировании оборудования, особенности конструкции которого, как и особенности технологического процесса, предполагают образование в рабочем объеме следовых течений.
ТЕПЛООБМЕН ОТ ЗМЕЕВИКОВ
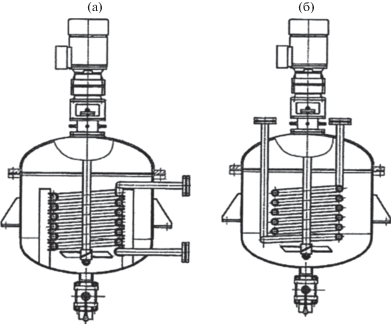
При анализе процессов теплообмена в аппаратах с перемешивающими устройствами необходимо учитывать ситуации, в которых влияние следовых течений может оказаться определяющим. Так, например, при использовании в качестве теплообменного устройства встроенных змеевиков (рис. 1), довольно часто встречаются конструктивные решения, при которых в рабочем объеме аппарата возникает интенсивная меридиональная циркуляция. В этом случае каждый виток змеевика оказывается расположенным в следе витка предыдущего. Особенно характерна такая гидродинамическая структура потоков для крупных аппаратов, в которых змеевики устанавливаются на стойках (рис. 1а), состоящих из вертикальных пластин, имеющих по аналогии с отражательными перегородками высокое гидравлическое сопротивление и трансформирующих тангенциальное движение рабочей среды в движение с интенсивной меридиональной циркуляцией. В аппаратах небольшого объема змеевик часто крепиться к крышке аппарата (рис. 1б) и не имеет достаточно высокого гидравлического сопротивления, способного полностью трансформировать тангенциальное движение рабочей среды в осевое с образованием циркуляционного контура.
Рис. 1.
Аппараты с мешалкой и обогревом с помощью змеевика: а – крепление змеевика на стойках, б – крепление змеевика на крышке аппарата.
Принимая во внимание соотношение для расчета коэффициентов теплоотдачи [3]
(1)
$\alpha = \frac{{0.267{{с}_{р}}\rho ~{{{\left( {\varepsilon _{o}^{{\text{л}}}\nu } \right)}}^{{0.25}}}}}{{{\text{P}}{{{\text{r}}}^{{0.75}}}}},$При креплении змеевика на крышке аппарата (рис. 1б) происходит продольное обтекание трубок змеевика тангенциальным потоком, создаваемым перемешивающим устройством. В этой ситуации в качестве локального значения скорости диссипации энергии $\varepsilon _{o}^{{\text{л}}}$ может быть использовано среднее значение этой величины, определяемое через мощность, потребляемую при перемешивании:
(2)
$\varepsilon _{o}^{{\text{л}}} = \varepsilon _{о}^{{{\text{ср}}}} = \frac{{{{N}_{{\text{м}}}}}}{{\rho {{V}_{a}}}}.$Крепление змеевика на стойках (рис. 1а) приводит, как и в случае установки отражательных перегородок, к значительному росту мощности, затрачиваемой на перемешивание, а, следовательно, и к росту средней скорости диссипации энергии в формуле (2). В соответствии с формулой (1) это должно приводить к росту коэффициентов теплоотдачи от трубок змеевика, что не подтверждается на практике. При креплении змеевика на стойках (рис. 1а) происходит поперечное обтекание трубок змеевика осевым потоком (тангенциальное движение трансформируется в меридиональную циркуляцию).
В этом случае трубки змеевика, оказываются расположенными в следовой области, образующейся при обтекании предыдущего по отношению к потоку витка змеевика. Следует отметить, что образованная при этом граница следа является своего рода экраном, изолирующим область следа от воздействия основного потока, что подтверждается экспериментами с окрашиванием потока при подаче красящего вещества (трассера) на поверхность рабочей среды. В аппарате с отражательными перегородками, где основным движением является меридиональная циркуляция, при подаче трассера на поверхность аппарата происходит практически мгновенное окрашивание по радиусу.
При наличии змеевика, установленного на стойках, образуется, как было отмечено выше, следовая область, граница которой препятствует радиальному перемещению трассера и окрашивание объема происходит в течение более длительного времени при движении трассера по циркуляционному контуру вне следовой области. В этой ситуации интенсивность теплообмена определяется особенностями течения внутри следа, а не вне его. При этом турбулентность внешнего по отношению к следу потока не оказывает на интенсивность теплообмена практически никакого влияния.
Величина диссипации энергии $\varepsilon _{{\text{o}}}^{{\text{л}}}$ для этого варианта компоновки аппарата может быть определена, как отношение мощности, расходуемой на преодоление гидравлического сопротивления последовательности поперечно обтекаемых труб [4] к массе жидкости, заключенной в зоне следового течения.
(3)
$\varepsilon _{{\text{o}}}^{{\text{л}}} = \frac{{{{N}_{{{\text{сл}}}}}}}{{\rho {{V}_{{{\text{сл}}}}}}},$(4)
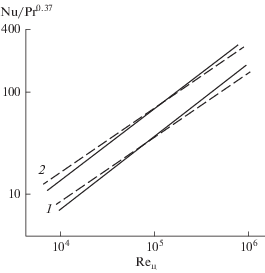
${{N}_{{{\text{сл}}}}} = \zeta \frac{{\rho {{w}^{3}}}}{2}{{F}_{{\text{o}}}}\,\,\,{\text{и}}\,\,\,{{V}_{{{\text{сл}}}}} = {{F}_{{\text{o}}}}L.$На рис. 2 сопоставлены расчетные и опытные значения коэффициентов теплоотдачи от змеевика в аппарате с отражательными перегородками, снабженном пропеллерной (1) и открытой турбинной (2) мешалками:
Рис. 2.
Сравнение расчетных и экспериментальных значений теплоотдачи в аппаратах с отражательными перегородками: сплошные линии – расчет по уравнениям (1), (4); пунктирные – расчет по эмпирическим уравнениям, полученным в работах: 1 – [5], 2 – [6].
МАССООБМЕН В СИСТЕМЕ ЖИДКОСТЬ–ГАЗ
При перемешивании газожидкостных систем влияние характеристик течения в следовых областях становится определяющим не только в процессе формирования двухфазной системы (образование пузырей), но и при массообмене между элементами дисперсной фазы (пузырями) и сплошной средой.
В литературе предложен ряд зависимостей для определения размера пузырей в зависимости от свойств рабочих сред и условий перемешивания. В основу практически всех этих соотношений положен механизм дробления пузырьков в турбулентном потоке, предложенный Кальдербанком [7] по аналогии с моделью Колмогорова для дробления капель [8]. При рассмотрении дробления пузырьков в поле однородной и изотропной турбулентности, в работе [7] была получена зависимость, связывающая максимальный устойчивый размер пузыря с характеристиками рабочей среды и локальной скоростью диссипации энергии.
(5)
${{d}_{п}} \sim {{\left( {\frac{\sigma }{\rho }} \right)}^{{0.6}}}{{\left( {\varepsilon _{о}^{{\text{л}}}} \right)}^{{ - 0.4}}}.$Поскольку в аппаратах с мешалками, несмотря на локальную однородность и изотропность потока [9, 10], в масштабах всего рабочего объема экспериментально наблюдается существенная неоднородность распределения скорости диссипации энергии [11, 12], то в соответствии с формулой (5) должен иметь место широкий спектр размеров пузырей, что, однако, не наблюдается на практике [7]. Для разрешения этого противоречия в настоящей работе предпринята попытка теоретического анализа процесса дробления пузырьков в рабочем объеме аппаратов с перемешивающими устройствами. Остановимся на двух случаях, отличающихся по характеру формирования газожидкостной системы: 1) в рабочей среде отсутствуют добавки, препятствующие коалесценции, 2) рабочая среда содержит ПАВ или электролиты, препятствующие коалесценции.
В основе теоретического анализа процесса дробления пузырьков при наличии коалесценции (вариант 1) были использованы следующие допущения: а) в рабочем объеме аппарата существуют две зоны (основной объем аппарата и радиальная струя, создаваемая лопастями мешалки), в каждой из которых в результате дробления и коалесценции образуется свой, характерный для этой зоны, размер пузырька; б) пузырьки газа участвуют в колебательном движении.
Рассмотрим первоначально область основного объема аппарата, для которого характерно достаточно равномерное распределение газовой фазы [13]. В рамках принятого в настоящей работе механизма, дробление пузырьков в этой зоне обусловлено воздействием на пузырь сплошной среды при условии резонанса между частотой собственных колебаний пузыря и частотой пульсационного движения рабочей среды, вызванного сходом вихревых образований с поверхности обтекаемого колеблющегося тела. Как правило, газосодержание в объеме аппаратов с перемешивающими устройствами составляет 5–20%, что соответствует среднему расстоянию между пузырьками, не превышающему диаметр пузыря. Принимая это во внимание, а также учитывая зигзагообразный характер всплывания пузыря [7] и наличие следовой области, которая образуется за каждым всплывающим пузырьком (рис. 3) [2], можно предположить, что размер пузыря в основном определяется характеристиками течения в зоне следа.
Для оценки величины скорости диссипации энергии в этой области, запишем выражение для мощности, затрачиваемой на обтекание пузырька сферической формы в следующем виде:
(6)
${{N}_{{\text{п}}}} = {{\zeta }_{{\text{п}}}}\frac{{\rho V_{{{\text{вс}}}}^{2}}}{2}{{V}_{{{\text{вс}}}}}\frac{{\pi d_{{\text{п}}}^{2}}}{4}.$Поскольку число Рейнольдса для всплывающих пузырьков рассматриваемых размеров оказывается не менее 103, величина ζп может быть принята постоянной и равной 0.8 [14]. Так как практически вся мощность Nп рассеивается в ближнем следе (область, объем которой приблизительно равен объему пузырька) [15], с учетом выражения для скорости всплывания пузырька [14]
(7)
${{V}_{{{\text{вс}}}}} = \sqrt {\frac{{2\sigma }}{{{{d}_{{{\text{п}}\left( {\rho - {{\rho }_{{\text{г}}}}} \right)}}}}} + \frac{{g{{d}_{{\text{п}}}}}}{2}\left( {1 - \frac{{{{\rho }_{{\text{г}}}}}}{\rho }} \right)} ,$скорость диссипации энергии в зоне отрывного течения может быть определена следующим образом:
(8)
$\varepsilon _{о}^{{\text{л}}}\frac{{{{N}_{{\text{п}}}}}}{{\rho {{V}_{{{\text{сл}}}}}}} = \frac{{0.6}}{{{{d}_{{\text{п}}}}}}~{{\left[ {\frac{{2\sigma }}{{{{d}_{{\text{п}}}}(\rho - {{\rho }_{r}})}} + \frac{{g{{d}_{{\text{п}}}}}}{2}\left( {1 - \frac{{{{\rho }_{r}}}}{\rho }} \right)} \right]}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$Общей особенностью, характерной для достаточно больших газовых пузырьков является их колебательные движения. При этом амплитуда колебаний в ряде случаев оказывается больше, чем размер пузырька. Так, например, у очень больших пузырей амплитуда может быть настолько большой, что при первом же колебании пузыри прорываются, как бы сами себя прокалывая. Пузыри меньшего диаметра колеблются с меньшими амплитудами и при отсутствии дополнительных внешних воздействий сохраняют свою целостность. Оценка минимального размера пузырька, подвергающегося деформации, и результаты измерения диаметра пузырьков в основном объеме аппарата показывают, что при отсутствии в системе ПАВ и электролитов пузырьки находятся в постоянном колебательном движении. Процесс дробления пузырьков рассматривается, как результат действия разности динамических напоров, деформирующих пузырек, которая должна превышать капиллярное давление, препятствующее деформации [16]. Принимая во внимание это условие, а также сведения о максимальном значении скорости диссипации энергии вблизи края лопасти мешалки [12]
(9)
$\left( {\varepsilon _{o}^{{\text{л}}}} \right) \approx \frac{{0.16~{{{\left( {\pi ~n{{d}_{{\text{м}}}}} \right)}}^{3}}}}{{{{h}_{{\text{л}}}}}},$с учетом максимального значения пульсационной скорости фиксированного масштаба V при нормальном законе распределения пульсационных скоростей
оказалось возможным получить соотношение для расчета диаметра пузырьков в объеме аппарата при наличии в рабочей среде ПАВ или электролитов
(11)
${{d}_{{\text{п}}}} \approx 0.706{{\left( {\frac{\delta }{\rho }} \right)}^{{0.6}}}{{\left( {\frac{\rho }{{{{\rho }_{r}}}}} \right)}^{{0.2}}}{{\left( {\varepsilon _{о}^{{\text{л}}}} \right)}^{{ - 0.4}}}.$Определение размера пузырьков в основном объеме газожидкостного слоя по формуле (11) позволяет сделать вывод о том, что при отсутствии в системе ПАВ или электролитов в диапазоне изменения среднего значения скорости диссипации энергии от 0.4 до 3 Вт/кг для системы вода – воздух в аппаратах с мешалками различных типов диаметр пузырьков практически не меняется и может быть принят равным 4.5 мм.
Анализ характеристик газожидкостного потока, выполненный применительно к аппаратам барботажного типа, также свидетельствует об инвариантности размера пузырьков по отношению к конструктивным характеристикам оборудования и интенсивности перемешивания. Данные для системы вода–воздух свидетельствует о том, что при относительно высоких расходах газа, обеспечивающих газосодержание в объеме жидкости более 10%, средний размер пузырьков можно также принимать практически постоянным и равным 4.5 мм.
Информация о размере пузырьков, характере затухания турбулентности вблизи подвижной поверхности пузырька [16], а также величине скорости диссипации энергии в следовой области за всплывающими пузырями согласно формуле (8), позволяют выполнить количественную оценку линейного коэффициента массоотдачи [21]
(12)
$\beta = \frac{{0.54~{{{\left( {\varepsilon _{{о~~}}^{{\text{л}}}\nu } \right)}}^{{0.25}}}~}}{{{\text{S}}{{{\text{c}}}^{{0.5}}}}}.$Принимая во внимание результаты исследований объемных значений газосодержания и удельной поверхности контактирующих фаз в рабочем объеме аппарата [13], можно определить объемные значения коэффициентов массоотдачи [21], которые в полной мере характеризуют интенсивность массобмена при перемешивании газожидкостных систем.
Следует отметить, что линейный коэффициент массотдачи в используемом на практике диапазоне изменения скорости диссипации энергии остается неизменным (рис. 4), а изменение объемного коэффициента массоотдачи (рис. 5) обусловлено исключительно изменением удельной площади поверхности контакта фаз
Рис. 4.
Зависимость коэффициента массоотдачи от интенсивности перемешивания: сплошная линия – расчет, пунктирная – опытные данные для одиночных пузырей [17]; а – опытные данные по десорбции (кислород–вода) [18]; б – опытные данные по десорбации (углекислый газ–вода) [18]; в – опытные данные по окислению сульфата натрия [18].
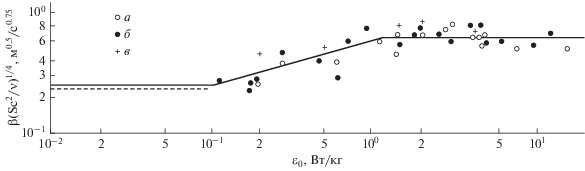
Рис. 5.
Зависимость объемного коэффициента массоотдачи от удельной мощности (N – мощность, потребляемая в отсутствии подачи газа).
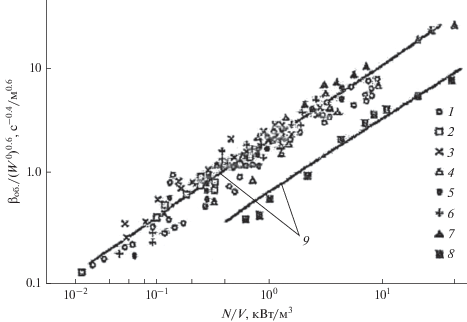
В водно-воздушных системах с коалесценцией величина Fуд зависит только от объемного газосодержания, поскольку диаметр пузырька в этом случае, как было показано выше, не изменяется, оставаясь равным 4.5 мм.
Таблица 1
| Точки | Тип Мешалки | Объем аппарата, м3 | Условия измерений |
|---|---|---|---|
| 1 | Турбинная | 0.02…0.25 | Окисление сульфата натрия |
| 2 | » | 0.2 | » |
| 3 | Закрытая турбинная | 0.2...0.25 | » |
| 4 | Листовая | 0.5 | » |
| 5 | Лопастная | 0.02…0.05 | » |
| 6 | Импеллерная | 0.02…0.05 | » |
| 7 | Трехлопастная | 0.01…0.005 | » |
| 8 | » | 0.01…0.005 | Физическая абсорбция в системе воздух–сульфат натрия |
| Точки 1–7 | Данные [19] | ||
| Точки 8 | Данные [20] | ||
| Линии 9 | Расчет [21] |
ЗАКЛЮЧЕНИЕ
Многочисленные исследования процессов перемешивания в аппаратах различных конструкций [22] показывают, что только изучение реальной гидродинамической обстановки в рабочем объеме и механизма взаимодействия рабочих сред между собой и с отдельными конструктивными элементами, позволяет определить наиболее надежные схемы компоновки аппарата и рекомендовать оптимальные конструкторские решения, обеспечивающие получение требуемого технологического результата.
В представленной работе рассмотрена структура потоков и параметры процессов тепло- и массообмена в зоне следовых турбулентных течений, образующихся в рабочем объеме аппарата при перемешивании как гомогенных, так и гетерогенных систем.
Представлено описание гидродинамики, а также процессов тепло- и массообмена в следовых областях, образованных как за счет конструктивных особенностей аппарата, так и в результате движения элементов дисперсной фазы (пузырьков) при перемешивании газожидкостных систем.
Полученные расчетные зависимости апробированы при проектировании аппаратов с перемешивающими устройствами вместимостью от 1 до 1000 м3 и могут быть рекомендованы для использования при решении широкого круга задач по аналогичной тематике.
ОБОЗНАЧЕНИЯ
| Cp | удельная теплоемкость, Дж/кг · К |
| D | коэффициент молекулярной диффузии, м2/с |
| Da | диаметр аппарата, м |
| dп | диаметр пузырька, м |
| dм | диаметр мешалки, м |
| Fo | площадь поперечного сечения межтрубного пространства, м2 |
| Fуд | удельная поверхность контакта фаз, м–1 |
| g | ускорение свободного падения, м/с2 |
| n | частота вращения мешалки, с–1 |
| hл | высота лопасти мешалки, м |
| L | длина следовой области, м |
| Nм | мощность, потребляемая при перемешивании, Вт |
| Nсл | мощность, расходуемая в следе, Вт |
| Nп | мощность затрачиваемая при обтекании пузырька, Вт |
| Vа | рабочий объем аппарата, м3 |
| Vсл | объем жидкости в следе, м3 |
| Vвс | скорость всплывания пузырька, м/с |
| w | скорость среды, м/с |
| α | коэффициент теплоотдачи, Вт/м2 · К |
| β | линейный коэффициент массоотдачи, м/с |
| βоб | объемный коэффициент массоотдачи, 1/с |
| ε0 | скорость диссипации энергии, Вт/кг |
| ε0, л | локальная скорость диссипации энергии, Вт/кг |
| ζ | коэффициент гидравлического сопротивления последовательности поперечно обтекаемых труб |
| ζп | коэффициент гидравлического сопротивления пузырька |
| λ | теплопроводность, Вт/м · К |
| µ | динамическая вязкость, Па · с |
| ν | кинематическая вязкость, м2/с |
| ρ | плотность, кг/м3 |
| ρг | плотность газа, кг/м3 |
| σ | поверхностное натяжение, Н/м |
| φ | объемное газосодержание |
| Nu = αD/λ | число Нуссельта |
| Pr = µCp/λ | число Прандтля |
| Sc = ν/D | число Шмидта |
Список литературы
Абрамович Г.Н. Теория турбулентных струй. М.: ЭКОЛИТ, 2011. 720 с.
Альбом течения жидкостей и газа сост. и авт. Текста М. Ван-Дайка; Пер. с англ. Л.В. Соколовский под ред. Г.И. Баренблата и В.П. Шидловского. М.: Мир, 1986. 180 с., ил. фото.
Барабаш В.М., Бегачев В.И., Брагинский Л.Н. О расчете теплообмена в аппаратах с механическим перемешиванием // Теор. основы хим. технол. 1982. Т. 16. № 6. С. 784–789.
Идельчик И.В. Справочник по гидравлическим сопротивлениям. Энергоиздат, 1964. 365 с.
Oldshue J.Y., Fluid Mixing. Heat transfer and Scale-up // Chem. Proc. Engng. 1966. V. 47. № 4. P. 1836.
Oldshue J.Y., Gretton A.T. Helical coil heat transfer in mixing vessels. Chem. Eng. Prog. 1954. V. 50. № 12. P. 615–619.
Calderbank P.H., Moo-Young M.B. The continues phase heat and masstransfer properties of dispersions // Trans. Inst. Chem. Engrs. 1958. V. 36. № 5. P. 443–448.
Колмогоров А.Н. О дроблении капель в турбулентном потоке ДАН СССР. 1949. Т. 66. № 5. С. 825–828.
Patterson G.K., Wu H. Distribution of turbulence energy dissipation rates in mixers // 5-the European conference on Mixing, Wurzburg, West Germany, June 10–12, 1985. BHRA. P. 355–364.
Laufhatter H.D. Dissipation of power in stirred vessels // 5-the European conference on Mixing. Wurzburg, West Germany, June 10–12, 1985. BHRA. P. 331–339.
Liepe F., Mockel H.O., Winker H. Untersuchungen aber Homogenisieren and aber Turbulen in Rahrmashinen // Chem. Techn. 1971. B. 23. № 4. S. 231–237.
Mockel H.O. Die Verteilund der orlichn Energy dissipation in einem Ruhrwer // Chem. Techn. 1980. B. 32. № 3. S. 127–129.
Брагинский Л.Н., Горбачева Г.В., Барабаш В.М. О расчете газосодержания в аппаратах с мешалками // Теор. основы хим. технол. 1987. Т. 21. № 5. С. 654–660.
Кутателадзе С.С., Стырикович М.А. Гидродинамика газожидкостных систем. М.: Энергия, 1976. 296 с.
Чжен П. Отрывные течения. Пер. в англ., М.: Мир, 1982. 279 с.
Левич В.Г. Физико-химическая гидродинамика. М.: Физмат-гиз, 1959. 799 с.
Соу С. Гидродинамика многофозных систем. М.: МИР, 1971. 536 с.
Ефимов Б.Л. Исследование гидродинамики и массоотдачи в жидкой фазе при механическом перемешивании газожидкостных систем. Дис. … канд. техн. наук. М.: МИХМ, 1973.
Павлушенко И.С., Брагинский Л.Н., Брылов В.Н. // Журн. прикладной химии. 1961. Т. 34. № 5. С. 805–809.
Литманс Б.А., Кукуреченко И.С., Бойко И.Д. и др. // Теор. основы хим. технол. 1972. Т. 6. № 5. С. 821–826.
Барабаш В.М., Белевицкая М.А. Массобмен от пузырей и капель в аппаратах с мешалками // Теор. основы хим. технол. 1995. Т. 29. № 4. С. 362–372.
Барабаш В.М., Абиев Р.Ш., Кулов Н.Н. Обзор работ по теории и практике перемешивания // Теор. основы хим. технол. 2018. Т. 52. № 4. С. 367–383.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии



