Теоретические основы химической технологии, 2022, T. 56, № 1, стр. 103-110
Математическое моделирование структур газожидкостного течения в кольцевом канале с внутренним вращающимся цилиндром
И. В. Моренко *
Институт механики и машиностроения ФИЦ Казанский научный центр РАН
Казань, Россия
* E-mail: morenko@imm.knc.ru
Поступила в редакцию 08.04.2021
После доработки 26.06.2021
Принята к публикации 03.07.2021
- EDN: HTZJXU
- DOI: 10.31857/S0040357122010092
Аннотация
Выполнено математическое моделирование структур газожидкостного течения в канале между соосными цилиндрами в случае, когда внутренний цилиндр вращается с постоянной скоростью вокруг своей оси, а внешний неподвижен. Математическая модель базируется на фундаментальных законах сохранения массы, количества движения. Для отслеживания подвижной границы раздела жидкость-газ используется метод объема жидкости. Показано существование двух различных структур течения: расслоенный режим течения и режим течения, при котором газовая фаза локализуется вдоль винтовой линии около поверхности внутреннего цилиндра. Приведены зависимости безразмерного крутящего момента от осевого и азимутального чисел Рейнольдса.
ВВЕДЕНИЕ
Большинство современных технологических процессов в химической и нефтехимической отраслях производства в той или иной степени связаны с использованием жидкостей и газов. При внедрении любого технологического процесса, важное значение приобретают вопросы, связанные с изучением закономерностей течения сред в рабочих полостях оборудования.
Один из примеров движения гетерогенной двухфазной системы под действием центробежной силы между соосными цилиндрами имеет место в устройствах экстракции с участием двух несмешивающихся жидкостей на этапе диспергирования в химической, фармацевтической, пищевой, нефтеперерабатывающей промышленности, а также в атомной энергетике. В процессе жидкостной экстракции целевой компонент из одной жидкости переводят в другую несмешивающуюся жидкость, содержащую экстрагент.
Способ разделения путем жидкостной экстракции экономически более выгоден по сравнению с ректификацией и выпариванием, обладает такими преимуществами, как низкая температура проведения процесса, возможность подбора высокоселективных экстрагентов с плотностью, отличающейся от плотности рафината и обеспечивающих глубокое извлечение целевого компонента.
Наложение осевого потока на азимутальное движение жидкости между двумя соосными цилиндрами, вызванное вращением поверхности внутреннего цилиндра с постоянной скоростью вокруг своей оси обеспечивает развитую площадь контакта двух несмешивающихся жидкостей для обеспечения массопереноса с возможностью регулирования времени пребывания среды в рабочем пространстве за счет варьирования скоростей осевого потока и вращения ротора. Правильно подобранные режимы течения позволяют создать контролируемые условия в аппаратах непрерывного действия.
В последние годы растет интерес к изучению многофазных течений. Известно [1], что добавление газовой фазы или дисперсной примеси в поток жидкости сильно осложняет картину течения, приводит к возникновению особенностей, влияющих на режимы течения, гидродинамические характеристики установок, элементов технологического оборудования. Примерами могут служить изучение транспортирования твердых шарообразных частиц в движущейся дисперсионной среде [2], придонного слоя в топке с циркулирующим кипящим слоем [3], гидродинамики и теплообмена кругового цилиндра в ограниченном ламинарном потоке вязкой жидкости с частицами примеси [4], гидродинамики контактных массообменных ступеней при проведении процессов абсорбции, ректификации, аэрации [5].
Поскольку совокупность влияния разнообразных факторов на движение газожидкостных смесей затрудняет получение аналитических оценок, большинство исследований проводится в условиях натурных и лабораторных экспериментов, которые позволяют поставить опыт с управляемыми условиями, изучить влияние одних характеристик при варьировании других. Однако исследование процессов с помощью методов математического моделирования имеет свои преимущества, которые заключаются в проведении многовариантных параметрических расчетах, обработке и анализе больших массивов результатов вычислительных экспериментов.
Целью данной работы является моделирование течения двухфазной среды в кольцевом канале, обусловленного перепадом давления и вращением внутреннего цилиндра, определение режимов течения, анализ влияния осевого и азимутального чисел Рейнольдса на безразмерный крутящий момент.
ПОСТАНОВКА ЗАДАЧИ
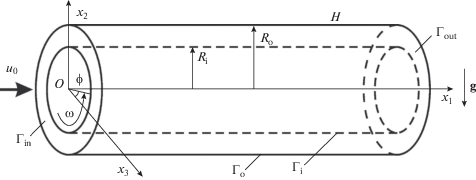
Рассматривается ламинарное двухфазное течение в кольцевом канале, схема которого приведена на рис. 1. Начало прямоугольной декартовой системы координат ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ помещается в торцевой плоскости области таким образом, чтобы ось $O{{x}_{1}}$ совпадала с осью канала. Внутренний цилиндр с радиусом основания ${{R}_{{\text{i}}}}$ вращается с постоянной угловой скоростью $\omega .$ Внешний цилиндр с радиусом ${{R}_{{\text{o}}}}$ неподвижен. Соответственно, обозначим длину $H,$ ширину канала $D = {{R}_{{\text{o}}}} - {{R}_{{\text{i}}}},$ отношение радиусов $\eta = {{{{R}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{i}}}}} {{{R}_{{\text{o}}}}}}} \right. \kern-0em} {{{R}_{{\text{o}}}}}}.$
Для моделирования газожидкостного течения в кольцевом канале используется подход, основанный на эйлеровом континуальном представлении. Для этого через $\gamma $ обозначается объемная доля жидкой фазы. В каждой ячейке расчетной области параметр $\gamma $ определяется следующим образом: $\gamma = 1,$ если в ячейке находится жидкость; $\gamma = 0,$ если в ней газ; в случае, когда через ячейку проходит граница раздела фаз $0 < \gamma < 1.$ Плотность, коэффициент кинематической вязкости рассчитываются по соответствующим значениям параметров жидкости и газа [6]
При выводе дифференциальных уравнений предполагается, что фазовые переходы не происходят. Применяя метод объема жидкости (Volume of Fluid) [7], записывается система уравнений в векторном виде, состоящая из уравнения неразрывности, Навье–Стокса и уравнения для определения положения подвижной границы раздела жидкость-газ:
(2)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \left( {{\mathbf{u}} \cdot \nabla } \right){\mathbf{u}} = - \frac{1}{\rho }\nabla p + \nu {\mathbf{\Delta u}} + {\mathbf{g}} + \frac{1}{\rho }\sigma \kappa \nabla \gamma ,$(3)
$\frac{{\partial \gamma }}{{\partial t}} + \nabla \cdot \left( {\gamma {\mathbf{u}}} \right) + \nabla \cdot \left[ {\left( {1 - \gamma } \right)\gamma {{{\mathbf{u}}}_{{\text{r}}}}} \right] = 0,$здесь ${\mathbf{u}}$ – вектор скорости среды, $t$ – время, $p$ – давление, $\kappa = - \nabla \cdot n$ – кривизна свободной поверхности, $n = {{\nabla \gamma } \mathord{\left/ {\vphantom {{\nabla \gamma } {\left| {\nabla \gamma } \right|}}} \right. \kern-0em} {\left| {\nabla \gamma } \right|}}$ – единичная нормаль к поверхности раздела фаз, $\sigma $ – коэффициент поверхностного натяжения, ${{{\mathbf{u}}}_{{\text{r}}}} = {{{\mathbf{u}}}_{{\text{l}}}} - {{{\mathbf{u}}}_{{\text{g}}}}$ – искусственный член сжатия, ${\mathbf{g}}$ – ускорение свободного падения. Слагаемое $\nabla \cdot \left[ {\left( {1 - \gamma } \right)\gamma {{{\mathbf{u}}}_{{\text{r}}}}} \right]$ в уравнении (3) препятствует размытию границы раздела сред, связанной с численной диффузией, позволяет более точно воспроизводить положение межфазной границы [8], активно только в тех ячейках расчетной области, где выполняется неравенство $\left( {1 - \gamma } \right)\gamma > 0.$
В начальный момент времени $t = 0$ среда покоится ${{u}_{i}} = 0,$ гидростатическое давление среды рассчитывается по формуле: $p = \rho g\left( {{{R}_{{\text{o}}}} - {{x}_{2}}} \right),$ $\gamma = 1.$
На входной границе ${{\Gamma }_{{{\text{in}}}}}$ кольцевого канала задаются компоненты вектора скорости ${{u}_{1}} = {{u}_{0}},$ ${{u}_{2}} = {{u}_{3}} = 0,$ давление $p = {{p}_{0}}.$ На участке границы ${{\Gamma }_{{{\text{in}}}}},$ где осуществляется подача газовой фазы, $\gamma = 0,$ на остальной части $\gamma = 1.$ На поверхности неподвижного внешнего цилиндра задано условие прилипания ${{u}_{i}} = 0,$ $\frac{{\partial p}}{{\partial n}} = 0,$ $\frac{{\partial \gamma }}{{\partial n}} = 0.$ На поверхности вращающегося внутреннего цилиндра ${{u}_{1}} = 0,$ ${{u}_{2}} = {{R}_{{\text{i}}}}\omega \cos \left( \phi \right),$ ${{u}_{3}} = - {{R}_{{\text{i}}}}\omega sin\left( \phi \right),$ $\frac{{\partial p}}{{\partial n}} = 0,$ $\frac{{\partial \gamma }}{{\partial n}} = 0.$ Угол $\phi $ лежит в плоскости $O{{x}_{2}}{{x}_{3}}$ и отсчитывается от оси $O{{x}_{3}}$ против движения часовой стрелки, если смотреть с отрицательного конца $O{{x}_{1}}.$ В выходном сечении канала наложены условия Неймана $\frac{{\partial {{u}_{i}}}}{{\partial n}} = 0,$ $\frac{{\partial p}}{{\partial n}} = 0,$ $\frac{{\partial \gamma }}{{\partial n}} = 0.$
Методы вычислительной аэрогидродинамики стремительно развиваются на протяжении нескольких десятилетий. К настоящему времени среди наиболее распространенных численных методов расчета течений можно выделить: метод конечных разностей, метод спектральных элементов, метод контрольных объемов, метод решеточных уравнений Больцмана, метод сглаженных частиц. Каждый из них обладает своими достоинствами и недостатками.
В данной работе для решения задачи (1)–(3) с начальными и граничными условиями выбран метод контрольных объемов. Он обладает свойством консервативности, что делает данный метод более предпочтительным. Возможность реализации метода для расчетной области со сложной геометрией, дискретизированной как структурированной, так и неструктурированной сеткой с разной формой ячеек используется разработчиками целого ряда современных пакетов программ, ориентированных на решение практических задач аэрогидродинамики.
Для решения системы полученных дифференциальных уравнений привлекаются коды библиотек реализованных на открытой интегрируемой платформе OpenFOAM. Расчетная область покрывается трехмерной сеткой с локальным измельчением к обтекаемым поверхностям. Элементы сетки представляют собой гексаэдры. Дискретные значения скорости и давления рассчитываются в центрах ячеек сетки. Для связывания скорости и давления выбирается алгоритм PIMPLE. При решении системы уравнений для давления использован метод сопряженных градиентов PCG. При решении уравнений для скорости – метод Гаусса–Зейделя. Шаг по времени $\Delta t$ подбирается в процессе вычислений таким образом, чтобы число Куранта ${\text{Co}}$ для всех ячеек расчетной области не превышало 1.0. Число Куранта ячейки ${\text{Co = }}{{\left( {\Delta t\left| u \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\Delta t\left| u \right|} \right)} {\Delta x}}} \right. \kern-0em} {\Delta x}}$ определяется по величине скорости жидкости через ячейку $\left| u \right|,$ размеру ячейки в направлении скорости $\Delta x.$
РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ
Движение жидкости, которое возникает под действием сил вязкого трения между двумя вращающимися соосными цилиндрами известно как течение Куэтта–Тэйлора. Данный класс течений хорошо изучен, накопилась обширная база экспериментальных и теоретических результатов [9–14], которая предоставляет широкие возможности для верификации численных моделей и служит отправной точкой для постановки более общих и сложных задач, таких как исследование газожидкостных структур в кольцевом канале.
Таким образом, в качестве тестовой задачи рассматривается течение вязкой несжимаемой жидкости в цилиндрическом канале, в случае, когда внутренний цилиндр вращается с постоянной скоростью, а внешний – неподвижен. При изучении вязкого течения анализировать результаты удобно в безразмерном виде. Безразмерными параметрами данной задачи будут азимутальное число Рейнольдса ${{\operatorname{Re} }_{\phi }} = \frac{{\omega {{R}_{{\text{i}}}}D}}{{{{\nu }_{{\text{l}}}}}},$ число Тейлора ${\text{Ta}} = {{\operatorname{Re} }_{\phi }}\sqrt {\frac{D}{{{{R}_{{\text{i}}}}}}} ,$ отношение радиусов $\eta = {{{{R}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{i}}}}} {{{R}_{{\text{o}}}}}}} \right. \kern-0em} {{{R}_{{\text{o}}}}}},$ относительная длина канала $\Gamma = {H \mathord{\left/ {\vphantom {H D}} \right. \kern-0em} D}.$
При проектировании технологического оборудования важно знать количество энергии, необходимое для приведения системы в действие на заданных частотах вращения, которое определяется крутящим моментом. Момент сил, действующих со стороны жидкости на выпуклую поверхность внутреннего цилиндра, рассчитывается по формуле
здесь $\tau $ – среднее касательное напряжение на поверхности внутреннего цилиндра. Безразмерный момент сил записывается в виде
Выбор расчетной сетки – это важный этап численного моделирования. Качественная сетка должна быть достаточно мелкой, чтобы получить необходимую точность при решении практических задач и выявить основные особенности течения. Избыточное сгущение сетки приведет к неоправданному увеличению времени счета и потребует больших вычислительных ресурсов. Для проверки сеточной сходимости строится три сетки ${{M}_{1}},$ ${{M}_{2}},$ ${{M}_{3}}$ с разным количеством ячеек $N.$ Сетка ${{M}_{1}}$ имеет 120 разбиений в осевом направлении, 50 – в азимутальном и 18 – в радиальном. Сетки ${{M}_{2}}$ и ${{M}_{3}}$ с количеством разбиений по трем направлениям: 150 × 64 × 20 и 200 × 85 × 26, соответственно. В табл. 1 представлены результаты расчетов для установления степени влияния сеточного разрешения области на безразмерный момент $G$ при ${{\operatorname{Re} }_{\phi }} = 400.$ Видно, что значения параметра $G,$ рассчитанные на сетках ${{M}_{2}}$ и ${{M}_{3}},$ отличаются на 0.05%. Для проведения численного эксперимента выбрана сетка ${{M}_{2}}.$
Таблица 1.
Сеточная сходимость
| $\bar {M}$ | N | G |
|---|---|---|
| M1 | $2.16 \times {{10}^{5}}$ | $5.931 \times {{10}^{5}}$ |
| M2 | $3.84 \times {{10}^{5}}$ | $5.975 \times {{10}^{5}}$ |
| M3 | $8.84 \times {{10}^{5}}$ | $5.978 \times {{10}^{5}}$ |
Тестирование предложенной методики расчета проводится путем сравнения результатов расчета с известными экспериментальными данными других авторов по безразмерному крутящему моменту. На рис. 2 представлены результаты сравнения расчета при значениях относительного радиуса $\eta $ = 0.1, 0.5, 0.9 с данными [15] и [16]. Влияние числа Рейнольдса на безразмерный крутящий момент определяется в работе [15] по следующей формуле
(4)
$\begin{gathered} G = 1.45\frac{{{{\eta }^{{1.5}}}}}{{{{{\left( {1 - \eta } \right)}}^{{{7 \mathord{\left/ {\vphantom {7 4}} \right. \kern-0em} 4}}}}}}{{\operatorname{Re} }^{{1.5}}} \\ {\text{для}}\,\,\,4 \times {{10}^{2}} \leqslant {{\operatorname{Re} }_{\phi }} \leqslant {{10}^{4}}. \\ \end{gathered} $Рис. 2.
Зависимость безразмерного момента $G$ от азимутального числа Рейнольдса ${{\operatorname{Re} }_{\phi }}$ для различных значений относительного радиуса: 1 – $\eta = 0.9,$ 2 – $\eta = 0.5,$ 3 – $\eta = 0.1;$ сплошная линия – расчет (данная работа), пунктирная линия – расчет по формуле (4), точки – данные [18].
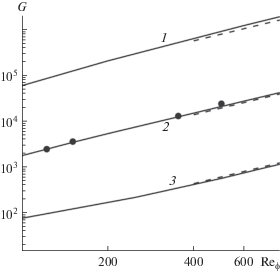
Как видно из рис. 2, согласование расчета с экспериментом вполне удовлетворительное, что свидетельствует об адекватности используемой модели для описания движения жидкости. Видно, что безразмерный момент $G$ монотонно увеличивается с ростом азимутального числа Рейнольдса ${{\operatorname{Re} }_{\phi }}$ и отношения радиусов $\eta .$
Кроме того, предложенная математическая модель была успешно протестирована автором на других зачах механики многофазных сред, таких как, обрушение столба жидкости в резервуаре [17] и схлопывание газовой полости в жидкости [18].
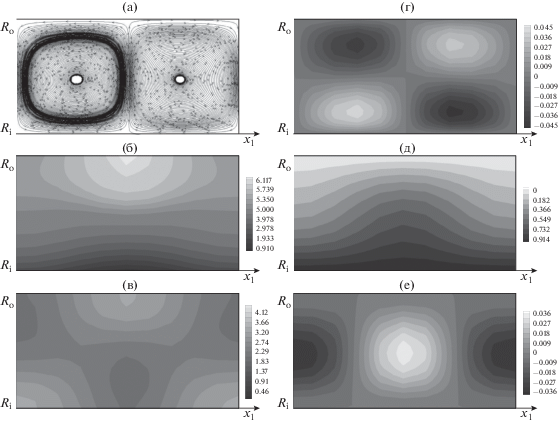
При малых числах Тейлора под действием сил вязкого трения, жидкость увлекается вращением поверхности внутреннего цилиндра. Наблюдается сдвиговое течение Куэтта [19], в котором линии тока представляют собой окружности с центрами на оси канала. Тейлор [20] определил критическое значение ${\text{T}}{{{\text{a}}}_{c}} = 41.3,$ при котором течение Куэтта теряет устойчивость. В пространстве между неподвижным внешним и вращающимся внутренним цилиндрами формируются вихревые ячейки Тейлора. На рис. 3а представлена центральная часть канала длиной $2D,$ на которой изображены два смежных вихря Тейлора, вращающихся в противоположных направлениях. Максимальное давление наблюдается на участке внешнего цилиндра, где соприкасаются между собой соседние вихревые ячейки, а жидкость движется в радиальном направлении от внутреннего цилиндра к внешнему (рис. 3б). Максимальные и минимальные значения поля завихренности регистрируются в местах соприкосновения двух примыкающих вихревых ячеек на поверхностях цилиндров. Максимальное – при растекании жидкости в противоположных направлениях, минимальное – при встречи потоков соседних вихрей (рис. 3в). Характерные распределения компонент скорости в тороидальных вихрях иллюстрируют рис. 3г–3е. Установлено, что линейная скорость вращения вихрей Тейлора составляет порядка 3% от линейной скорости вращения поверхности внутреннего цилиндра ${{R}_{{\text{i}}}}\omega ,$ равной произведению радиуса на угловую скорость вращения. Следует заметить, что режим вихрей Тейлора устойчив к малым возмущениям при условии, что канал достаточно узкий (${{{{R}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{i}}}}} {{{R}_{{\text{o}}}}}}} \right. \kern-0em} {{{R}_{{\text{o}}}}}} \to 1$). При дальнейшем возрастании скорости вращения торы становятся волнистыми. Реализуется режим течения, который называется волнистые вихри. Получение расчетным путем структур потока (рис. 3), соответствующих лабораторным наблюдениям [14], демонстрирует достоверность предложенной модели, методов и алгоритма расчета.
Рис. 3.
Характерное распределение основных параметров течения в осевом сечении канала $\left( {{{x}_{3}} = 0} \right){\text{:}}$ (а) – трейсеры; (б) – поле давления ${p \mathord{\left/ {\vphantom {p {\left( {{{\nu \rho {{R}_{{\text{i}}}}\omega } \mathord{\left/ {\vphantom {{\nu \rho {{R}_{{\text{i}}}}\omega } D}} \right. \kern-0em} D}} \right)}}} \right. \kern-0em} {\left( {{{\nu \rho {{R}_{{\text{i}}}}\omega } \mathord{\left/ {\vphantom {{\nu \rho {{R}_{{\text{i}}}}\omega } D}} \right. \kern-0em} D}} \right)}};$ (в) – поле завихренности, ${{\left| {\nabla \times {\mathbf{u}}} \right|} \mathord{\left/ {\vphantom {{\left| {\nabla \times {\mathbf{u}}} \right|} {\left( {{{\omega {{R}_{i}}} \mathord{\left/ {\vphantom {{\omega {{R}_{i}}} D}} \right. \kern-0em} D}} \right)}}} \right. \kern-0em} {\left( {{{\omega {{R}_{i}}} \mathord{\left/ {\vphantom {{\omega {{R}_{i}}} D}} \right. \kern-0em} D}} \right)}};$ (г) – осевая компонента вектора скорости, ${{{{u}_{1}}} \mathord{\left/ {\vphantom {{{{u}_{1}}} {\left( {{{R}_{{\text{i}}}}\omega } \right)}}} \right. \kern-0em} {\left( {{{R}_{{\text{i}}}}\omega } \right)}};$ (д) – азимутальная компонента, ${{{{u}_{3}}} \mathord{\left/ {\vphantom {{{{u}_{3}}} {\left( {{{R}_{{\text{i}}}}\omega } \right)}}} \right. \kern-0em} {\left( {{{R}_{{\text{i}}}}\omega } \right)}};$ (е) – радиальная компонента, ${{{{u}_{2}}} \mathord{\left/ {\vphantom {{{{u}_{2}}} {\left( {{{R}_{{\text{i}}}}\omega } \right)}}} \right. \kern-0em} {\left( {{{R}_{{\text{i}}}}\omega } \right)}}.$
При более высоких скоростях вращения режимы течения исследованы экспериментально в [9]. Показано, что существует от 20 до 25 различных состояний волнообразного вихревого потока с различными осевыми и азимутальными длинами волн. При этом состояние потока зависит не только от начальных условий, но и от того, как внутренний цилиндр был ускорен до конечной скорости вращения.
Численное моделирование двухфазного потока в каналах между коаксиальными цилиндрическими поверхностями является достаточно сложной задачей в связи с тем, что режим течения зависит от многих факторов, таких как ширина канала, осевое и азимутальное числа Рейнольдса, свойства сред, расходы газа и жидкости, условие ввода фаз в канал, гравитационная сила, сила поверхностного натяжения, шероховатость, смачиваемость поверхности канала, угол наклона канала и других параметров. К настоящему времени на основе обобщения экспериментальных наблюдений составлены карты режимов двухфазного потока только в каналах простых форм: с прямоугольным [21], круглым поперечным сечением [22]. Выделены следующие режимы течений в горизонтальных трубах: пузырьковый, пробковый, расслоенный (стратифицированный), расслоенный волновой, снарядный, дисперсный, кольцевой. Однако следует заметить, что ввиду большого количества определяющих факторов, которые влияют на режим течения, не существует универсальных критериев для создания единой классификации режимов и определения их границ.
При проведении численных расчетов задаются геометрические параметры канала: радиус внешнего цилиндра равен ${{R}_{{\text{o}}}} = 0.1$ м, внутреннего ${{R}_{{\text{i}}}} = 0.09$ м, соответственно, отношение радиусов составляет $\eta = {{{{R}_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{R}_{{\text{i}}}}} {{{R}_{{\text{o}}}}}}} \right. \kern-0em} {{{R}_{{\text{o}}}}}} = 0.9,$ длина канала $H = 30D = 0.3$ м. В работе [23] предложена классификация цилиндрических каналов в зависимости от отношения радиусов $\eta .$ Кольцевой зазор канала считается узким при выполнении условия: $\eta > 0.67,$ средним: $0.33 < \eta < 0.67$ и широким: $\eta < 0.33.$ Соответственно, рассматриваемый канал можно отнести к узким.
В данной работе исследование двухфазного потока в кольцевом канале проведем в случае, когда рабочие среды имеют значительную разницу и плотности, и вязкости. Для этого рассмотрим 73% водный раствор глицерина и воздух. Задаются следующие параметры жидкой фазы: плотность ${{\rho }_{{\text{l}}}} = 1188$ кг/м3, коэффициент кинематической вязкости ${{\nu }_{{\text{l}}}} = 2.19 \times {{10}^{{ - 5}}}$ м2/с, коэффициент поверхностного натяжения $\sigma = 0.0657$ Н/м; параметры газа ${{\rho }_{{\text{g}}}} = 1.2$ кг/м3, ${{\nu }_{{\text{g}}}} = 1.48 \times {{10}^{{ - 5}}}$ м2/с. Объемный расход газа составляет 10%, его подача осуществляется через узкую кольцевую область границы ${{\Gamma }_{{{\text{in}}}}}$ вблизи внутреннего цилиндра.
Угловая скорость вращения внутреннего цилиндра $\omega $ варьируется от 1.22 до 14.6 рад/с, что соответствует азимутальным числам Рейнольдса ${{\operatorname{Re} }_{\phi }}$ от 50 до 600. Осевая компонента скорости ${{u}_{1}}$ на входе в канал изменяется от 0.11 до 1.31 м/c, соответственно, осевое число Рейнольдса ${{\operatorname{Re} }_{z}} = \frac{{uD}}{{{{\nu }_{{\text{l}}}}}}$ изменяется в диапазоне значений $50 \leqslant {{\operatorname{Re} }_{z}} \leqslant 600.$ В ходе численных экспериментов рассчитываются поля скорости, давления, завихренности, положение межфазной границы.
Для оценки относительного влияния сил тяжести и поверхностного натяжения в том или ином канале принято оценивать число Бонда или отношение диаметра канала $D$ и капиллярной постоянной $a = \sqrt {\frac{{2\sigma }}{{\left( {{{\rho }_{{\text{l}}}} - {{\rho }_{{\text{g}}}}} \right)g}}} .$ При заданных параметрах выполняется условие $0.5a < D < 5a,$ согласно классификации [24], рассматриваемый канал относится к гравитационно-капиллярным, которые характеризуются совместным влиянием как капиллярных, так и гравитационных сил. Причем в этом случае гравитационные силы превосходят капиллярные.
В ходе численных расчетов показано, что газожидкостное течение в кольцевом канале имеет сложную пространственную структуру. При малых азимутальных числах Рейнольдса жидкость как более тяжелая фаза имеет тенденцию двигаться по нижней стенке канала, в то время как газовая фаза движется вдоль верхней стенки (рис. 4а). Реализуется расслоенный режим течения. В данном случае действие силы тяжести является определяющим.
Рис. 4.
Визуализация распределения фаз при ${{\operatorname{Re} }_{w}} = 50{\text{:}}$ (а) – ${{\operatorname{Re} }_{\phi }} = 50,$ (б) – ${{\operatorname{Re} }_{\phi }} = 400$ (темно-серый цвет – жидкость, светлый – газ).
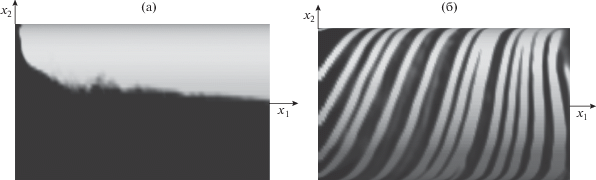
При увеличении угловой скорости вращения поверхности внутреннего цилиндра наблюдается иная картина. Под действием центробежной силы частицы жидкой фазы отбрасываются от оси канала к периферии. Жидкость омывает стенку неподвижного внешнего цилиндра. При этом газовая фаза распределена преимущественно в окрестности выпуклой поверхности внутреннего цилиндра по винтовой линии (рис. 4б).
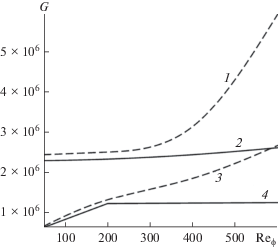
Анализ влияния осевого ${{\operatorname{Re} }_{z}}$ и азимутального ${{\operatorname{Re} }_{\phi }}$ чисел Рейнольдса на безразмерный крутящий момент $G$ показал, что значения $G$ увеличиваются с ростом ${{\operatorname{Re} }_{\phi }}$ и ${{\operatorname{Re} }_{z}}$ (рис. 5). Кроме того, следует отметить, что когда в канале движется двухфазный поток, значение безразмерного крутящего момента выше, чем при течении однофазной жидкости. Так, при малых азимутальных числах Рейнольдса (${{\operatorname{Re} }_{\phi }} = 50$) добавление газовой фазы с объемной концентрацией 10% в поток жидкости приводит к увеличению крутящего момента на 26.8% при ${{\operatorname{Re} }_{z}} = 50$ и на 6.4% при ${{\operatorname{Re} }_{z}} = 600$, однако при больших азимутальных числах Рейнольдса (${{\operatorname{Re} }_{\phi }} = 600$) крутящий момент возрастает в 2 раза. В этом случае значение безразмерного крутящего момента $G$ осциллирует около некоторой средней величины. Осцилляции крутящего момента могут вызывать нежелательные вибрации и шумы, приводить к сокращению срока эксплуатации оборудования.
Рис. 5.
Зависимость безразмерного момента $G$ от азимутального числа Рейнольдса ${{\operatorname{Re} }_{\phi }}{\text{:}}$ сплошная линия – однофазный поток, пунктирная линия – двухфазный поток; 1, 2 – ${{\operatorname{Re} }_{z}} = 600,$ 3, 4 – ${{\operatorname{Re} }_{z}} = 50.$
Причины увеличения напряжения трения на стенке, а значит и крутящего момента, лежат в основе процессов, происходящих в пограничном слое. Многие различные сложные механизмы взаимодействия газа и жидкости задействованы в процессе течения многофазной среды в канале с выпуклой и вогнутой поверхностями. Существующие данные о касательном напряжении стенки газожидкостного потока очень ограничены и зачастую противоречивы, хотя они широко применяются в современных технологиях.
Анализируя имеющиеся данные [25], можно отметить, что на величину напряжения сдвига влияет число Рейнольдса, объемный расход газа, режим течения пограничного слоя. Нагнетание пузырьков в поток жидкости вблизи стенки может способствовать переходу от ламинарного режима погранслоя к турбулентному. Влияет также соотношение размера газовых включений к толщине пограничного слоя, их деформация, удлинение, слияние в крупные структуры.
Известно, газонасыщение турбулентного пограничного слоя пузырьками относительно малых размеров, вдуваемых у стенки, обеспечивает пик объемной доли газа около поверхности, приводит к снижению касательного напряжения на стенке по сравнению со случаем однофазного течения. Однако использование пузырькового слоя для уменьшения крутящего момента ограничивается технологическими режимами.
Многообразие условий, реализующихся в технологическом оборудовании, в особенности в нестационарных режимах его работы, приводит к разным режимам двухфазных потоков и соответственно к разным значениям касательного напряжения на стенке. В работе [26] провели лабораторные эксперименты для оценки изменения напряжения трения для различных режимов течения двухфазного потока. Показано, что напряжение трения уменьшалось в диспергированном и пленочном состояниях по сравнению с однофазным потоком и увеличилось в случае, когда крупные газовые включения находились в растянутом состоянии, а также при вспененном режиме течения.
Особенность движения двухфазного потока в кольцевом канале заключается в чередовании на стенке участков примыкания частиц жидкости и газа, разделенных поверхностью раздела фаз. Возникающие при этом динамические пограничные слои имеют разную толщину, поскольку жидкость и газ имеют разную вязкость. Согласно закону вязкости Ньютона касательные напряжения пропорциональны градиенту скорости по нормали к поверхности. При обновлении пограничного слоя касательные к стенке составляющие скорости резко меняются от нуля до величины порядка скорости основного потока, за счет больших величин производных от скорости по нормали к поверхности тела возникают высокие значения касательных напряжений.
ЗАКЛЮЧЕНИЕ
С помощью методов вычислительной гидродинамики выполнено исследование структур газожидкостного течения в кольцевом канале между вращающимся внутренним цилиндром и стационарным внешним. В рамках предложенного подхода учитывается нестационарность процесса движения среды, вращение поверхности внутреннего цилиндра, трехмерность формируемых структур потока, поверхностное натяжение, действие силы тяжести, а также отслеживается подвижная граница раздела жидкости и газа. Установлено, что в зависимости от скорости вращения поверхности наблюдается два режима течения: раздельный (стратифицированный) и режим, при котором газовая фаза локализуется преимущественно вдоль винтовой линии у поверхности вращающегося цилиндра. Показано, что добавление в поток жидкости газовой фазы оказывает существенное влияние на крутящий момент. В рассматриваемом диапазоне режимных параметров при изменении осевого и азимутального чисел Рейнольдса от 50 до 600 крутящий момент газожидкостного потока увеличивается от 6.4% до 100% по сравнению с аналогичным значением для однофазного потока.
В исследуемом типе технологических аппаратов за счет вращательно-поступательного движения среды можно получить высокоразвитую площадь межфазной поверхности двух несмешивающихся сред в сочетании с компактными габаритами и относительно низкими значениями энергопотребления по сравнению с другими типами оборудования. Увеличение поверхности раздела фаз будет способствовать интенсификации массообменных процессов. Результаты исследования позволяют выполнить подбор благоприятных режимов газожидкостного течения для ряда практических задач, в том числе, для устройств жидкостной экстракции на этапе диспергирования в химической, фармацевтической, пищевой, нефтеперерабатывающей промышленности, определить количество энергии, необходимое для приведения системы в действие на заданных частотах вращения.
ОБОЗНАЧЕНИЯ
| $a$ | капиллярная постоянная, м |
| $D$ | диаметр, м |
| $G$ | безразмерный крутящий момент |
| $g$ | ускорение свободного падения, м/с2 |
| $H$ | длина канала, м |
| $M$ | крутящий момент, Н · м |
| $N$ | количество ячеек расчетной области |
| $n$ | единичная нормаль |
| $p$ | давление, Па |
| $R$ | радиус, м |
| $t$ | время, с |
| ${{u}_{1}},{{u}_{2}},{{u}_{3}}$ | компоненты вектора скорости u, м/с |
| ${{u}_{{\text{r}}}}$ | искусственный член сжатия, м/с |
| ${{x}_{1}}{{x}_{2}}{{x}_{3}}$ | прямоугольная декартова система координат |
| $\Gamma $ | граница расчетной области |
| $\gamma $ | объемная доля жидкой фазы |
| $\eta $ | безразмерный радиус |
| $\rho $ | плотность, кг/м3 |
| $\nu $ | коэффициентом кинематической вязкости, м2/с |
| $\kappa $ | кривизна свободной поверхности |
| $\sigma $ | коэффициент поверхностного натяжения, Н/м |
| $\tau $ | среднее касательное напряжение, Па |
| $\omega $ | угловая скорость вращения, рад/с |
| ${\text{Co}}$ | число Куранта |
| ${{\operatorname{Re} }_{z}}$ | осевое число Рейнольдса |
| ${{\operatorname{Re} }_{\phi }}$ | азимутальное число Рейнольдса |
| $Ta$ | число Тейлора |
ИНДЕКСЫ
Список литературы
Varaksin A.Y. Two-Phase Flows with Solid Particles, Droplets, and Bubbles: Problems and Research Results (Review) // High Temp. 2020. V. 58. № 4. P. 595. [Вараксин А.Ю. Двухфазные потоки с твердыми частицами, каплями и пузырями: проблемы и результаты исследований (обзор) // Теплофизика высоких температур. 2020. Т. 58. № 4. С. 646.]
Ponomarev V.B., Fesun I.P. Mathematical Modeling of the Particle-Deposition Rate Taking into Account Dynamic Relaxation // Theor. Found. Chem. Eng. 2020. V. 54. № 5. P. 906. [Пономарев В.Б., Фесун И.П. Математическое моделирование скорости осаждения частиц с учетом динамической релаксации // Теорет. основы хим. технологии. 2020. Т. 54. № 5. С. 636.]
Kovenskii V.I. Bottom Bed in Circulating Fluidized Bed Combustor // Theor. Found. Chem. Eng. 2019. V. 53. № 5. P. 793. [Ковенский В.И. Придонный слой в топке с циркулирующим кипящим слоем // Теорет. основы хим. технологии. 2019. Т. 53. № 5. С. 572.
Morenko I.V., Fedyaev V.L. Hydrodynamics and Heat Transfer of the Circular Cylinder in the Confined Laminar Viscous Flow with the Particles of the Impurity // Theor. Found. Chem. Eng. 2015. V. 49. № 6. P. 901. [Моренко И.В., Федяев В.Л. Гидродинамика и теплообмен кругового цилиндра в ограниченном ламинарном потоке вязкой жидкости с частицами примеси // Теорет. основы хим. технологии. 2015. Т. 49. № 6. С. 708.]
Voinov N.A., Frolov A.S., Bogatkova A.V., Zemtsov D.A., Zhukova O.P. Hydrodynamics and Mass Transfer at the Vortex Stage and during Bubbling // Theor. Found. Chem. Eng. 2019. V. 53. № 6. P. 972. [Войнов Н.А., Фролов А.С., Богаткова А.В., Земцов Д.А., Жукова О.П. Гидродинамика и массообмен на вихревой ступени при барботаже // Теорет. основы хим. технологии. 2019. Т. 53. № 6. С. 622.]
Kocha M., Lechner C., Reuter F., Köhler K., Mettin R., Lauterborn W. Numerical modeling of laser generated cavitation bubbles with the finite volume and volume of fluid method, using OpenFOAM // Computers and Fluids. 2016. V. 126. P. 71.
Hirt C.W., Nichols B.D. Volume of Fluid (VOF). Methods for the Dynamics of Free Boundaries // J. Comput. Phys. 1981. № 39. P. 201.
Weller H. A new approach to vof-based interface capturing methods for incompressible and compressible flow // OpenCFD Ltd. Report 2008. TR/HGW/04.
Coles D. Transition in circular Couette flow // J. Fluid Mech. 1965. № 21. P. 385.
Donnelly R.J., Simon N.J. An empirical torque relation for supercritical flow between rotating cylinders // J. Fluid Mech. 1960. № 7. P. 401.
Lim T.T., Tan K.S. A note on power-law scaling in a Taylor-Couette flow // Physics of Fluids. 2004. V. 16. № 1. P. 140.
Morenko I.V. Numerical simulation of laminar Taylor–Couette flow // Lobachevskii Journal of Mathematics. 2020. V. 41. № 7. P. 1255.
Andereck C.D., Liu S.S., Swinney H.L. Flow regimes in a circular Couette system with independently rotating cylinders // J. Fluid Mech. 1985. V. 164. P. 155.
Fenstermacher P.R., Swinney H.L., Gollub J.P. Dynamical instabilities and the transition to chaotic Taylor vortex flow // J. Fluid Mech. 1979. V. 94. P. 103.
Wendt F. Turbulente Stromungen zwischen zwei rotierenden konaxialen Zylindern // Ing. Arch. 1933. № 4. P. 577.
Kaneda M., Tagawa T., Noir J., Aurnou J.M. Variations in driving torque in Couette-Taylor flow subject to a vertical magnetic field // J. Physics: Conference Series. 2005. № 14. P. 42.
Моренко И.В. Численное моделирование обрушения столба жидкости в резервуарах разной формы // Вестник Томского государственного университета. Математика и механика. 2019. № 60. С. 119.
Morenko I.V. Numerical simulation of the propagation of pressure waves in water during the collapse of a spherical air cavity // Ocean Engineering. 2020. № 215. 107905.
Couette M.M. Etudes sur le frottement de liquids // Ann. Chim. Phys. 1890. V. 6. Ser. 21. P. 433.
Taylor G.I. Stability of viscous liquid contained between rotating cylinders // Phil. Trans. Roy. Soc. L. 1923. V. A223. P. 289.
Zhao J., Liu G., Li B. Two-phase Flow Patterns in a Square Mini-channel // J. of Thermal Science. 2004. V. 13. №. 2. P. 174.
Yang C.Y., Shieh C.C. Flow pattern of air-water and two-phase R-134a in small circular tubes // Int. J. Multiphase Flow. 2001. № 27. P. 1163.
Biage M., Campos J.C.C. Visualization study and quantitative velocity measurements in turbulent Taylor-Couette flow tagging: a description of the transition to turbulence // J. Braz. Soc. Mech. Sci. Eng. 2003. V. 25. № 4. P. 378.
Chinnov E.A., Kabov O.A. Two-phase flows in pipes and capillary channels // High Temp. 2006. V. 44. № 5. P. 773. [Чиннов Е.А., Кабов О.А. Двухфазные течения в трубах и капиллярных каналах // Теплофизика высоких температур. 2006. Т. 44. № 5. С. 777.]
Лаптева Е.А., Фарахов Т.М. Математические модели и расчет тепломассообменных характеристик аппаратов / Под ред. А.Г. Лаптева. Казань: Отечество, 2013.
Oishi Y., Murai Y., Tasaka Y. Wall shear stress modified by bubbles in a horizontal channel flow of silicone oil in the transition region // International J. Heat and Fluid Flow. 2020. V. 86. 108748.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии