Теоретические основы химической технологии, 2022, T. 56, № 2, стр. 244-251
Математическая модель контактного охлаждения и очистки от дисперсной фазы газов в насадочных скрубберах
Е. А. Лаптева a, *, А. Г. Лаптев a, С. У. Аласгарли a
a Казанский государственный энергетический университет
Казань, Россия
* E-mail: grivka100@mail.ru
Поступила в редакцию 02.12.2021
После доработки 22.12.2021
Принята к публикации 30.12.2021
- EDN: LFDCWR
- DOI: 10.31857/S0040357122020105
Аннотация
Выполнено численное решение научно-технической задачи определения эффективности насадочных скрубберов при конденсационном охлаждении и очистки от дисперсной фазы газов в процессе стационарного пленочного течени яжидкости по регулярным и хаотичным контактным устройствам. Записана система дифференциальных уравнений с частными производными сопряженного переноса теплоты, массы водяного пара и дисперсной фазы в слое насадки. Тепло- и массообмен и перенос дисперсной частиц между газовой и жидкой фазами учитывается с помощью объемных источниковых членов межфазного переноса, осредненных по локальному объему слоя. Даны выражения для определения параметров источников. Представлены результаты численного решения системы уравнений по полям температур и влагосодержанию и сравнение с известными экспериментальными данными. Показана зависимость эффективности очистки газов от тонкодисперсной фазы от скорости газа. Даны сравнительные характеристики насадок, а также научно-технические решения по модернизации скрубберов, внедренные в промышленности.
ВВЕДЕНИЕ
Межфазный тепломассообмен в аппаратах с хаотичными и регулярными контактными устройствами (насадками) при противоточном пленочном режиме широко применяется для проведения процессов абсорбции, ректификации, а также охлаждении или нагреве газов и жидкостей. Причем охлаждение дымовых и технологических газов часто сопровождается очисткой от дисперсной фазы.
Разработка математических моделей таких совмещенных процессов актуальна для энергетики и химической технологиив различных отраслях промышленности [1–4].
Насадочные аппараты межфазного тепломассообмена чаще всего рассчитываются с применением модели идеального вытеснения фаз (метод числа и высоты единиц переноса) или диффузионной модели структуры потока, а также численными методами с использованием различных програмных комплексов [5–8]. Однако, данные модели и программные комплексы невсегда позволяют выполнять расчеты новых типов контактных устройств, не имеющих аналогов, тем более с интенсификаторами процессов.
Газовая фаза на охлаждение и очистку подается в нижнюю часть скруббера под секцию с насадкой. Жидкая фаза (чаще вода) через специальные оросители поступает в верхней части колонны и равномерно распределяется по насадке. Организуется процесс противотока пленки жидкости и газа. Скорость газа для противотока вычисляется исходя из конструктивных особеностей насадки и плотности орошения и при нормальных условиях находятся в приделах 0.5–2.0 м/с, а плотность орошения 10–50 м3/м2 ч, а иногда для специальных конструкций контактных устройств и выше. Режимные и конструктивные параметры скруббера находится при моделировании процессов в зависимости от технических и технологических требований на проектирование или модернизацию колонны.
Целью данной работы является численное решение системы уравнений сопряженного переноса теплоты и массы влаги, а также уравнения турбулентного переноса тонкодисперсных частиц в скруббере с хаотичными и регулярными насадками и сравнительные характеристики контактных устройств.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
При моделировании явлений переноса в двухфазных средах насадочных колонн применяется подход, основанный на составлении макроскопического баланса с осреднением локальных однофазных уравнений сохранения импульса, массы и энергии и условий сопряжения на границе – двужидкостная модель. При таком подходе дифференциальные уравнения записываются для каждой фазы отдельно, но так как макроскопические поля в фазах не являются независящими друг от друга, то в уравнениях применяются локальные по элементарному объему межфазные источниковые члены, учитывающие перенос субстанций между фазами.
Известно, что в нерегулярной (хаотичной) насадке турбулентный режим движения газа начинается при числах Рейнольдса ${{\operatorname{Re} }_{{\text{э}}}}$ более 15–40, а в регулярной с интенсификаторами (просечки, выступы, гофры и т.д.) больше 500, где число Рейнольдса вычисляется по средней действительной скорости газа в насадке и эквивалентному диаметру насадки. Движение стекающей пленки жидкости по поверхности насадочных тел чаще всего происходит при числе Рейнольдса менее 2000, т.е. режим течения ламинарный волновой.
В рассмотренной ниже постановке уравнения сопряженного переноса записываются в цилиндрических координатах для всей колонны с насадкой с фиктивными скоростями фаз, отнесенных ко всему поперечному сечению колонны с применением в правой части объемных локальных источников переноса тепла, массы влаги и тонкодисперсной фазы.
При равномерном распределении фаз объемные источники осредняются по всему объему слоя, а при неравномерном для локальных областей с учетом реальной гидродинамической обстановкой и движущих сил процессов переноса.
Данный подход успешно применяется при моделировании явлений переноса в пленочных градирнях [9], насадочных ректификационных и абсорбционных колоннах [10], газосепараторах аэрозолей [11] и других аппаратах [12, 13].
Для скруббера с регулярными или хаотичными насадками ниже представлена система уравнений сопряженного переноса теплоты и массы, а также дисперсной фазы в цилиндрической системе координат колонны.
Уравнение конвективного теплообмена в жидкой фазе
(1)
${{u}_{{\text{ж}}}}(r){{\rho }_{{\text{ж}}}}{{с}_{{{\text{рж}}}}}\frac{{\partial {{Т}_{{\text{ж}}}}}}{{\partial z}} = \frac{{{{{{\lambda }}}_{{\text{ж}}}}}}{r}\frac{\partial }{{\partial r}}\left[ {r\frac{{\partial {{T}_{{\text{ж}}}}}}{{\partial r}}} \right] + \frac{{qdF}}{{dV}}.$В газовой фазе
(2)
${{W}_{г}}(r){{{{\rho }}}_{{\text{г}}}}\frac{{\partial I}}{{\partial z}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{{{{\lambda }}}_{{тг}}}\frac{{\partial {{T}_{г}}}}{{\partial r}}} \right] - \frac{{qdF}}{{dV}},\,\,\,\,I = f({{T}_{{\text{г}}}},х).$Уравнение переноса влаги в газовой фазе
(3)
${{W}_{г}}(r)\frac{{\partial х}}{{\partial z}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{{D}_{{{\text{тг}}}}}\frac{{\partial х}}{{\partial r}}} \right] + \frac{{{{j}_{х}}dF}}{{{{{{\rho }}}_{{\text{г}}}}dV}}.$Уравнение переноса тонкодисперсной фазы
(4)
${{W}_{г}}(r)\frac{{\partial C}}{{\partial z}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {r{{D}_{{тd}}}\frac{{\partial C}}{{\partial r}}} \right] - \frac{{{{j}_{c}}dF}}{{dV}},$В уравнениях (1)–(4) скорости ${{u}_{ж}}(r),$ ${{W}_{г}}(r)$ – как функции радиальной координаты.
При составлении математической модели приняты следующие допущения:
– основной тепло- и массообмен и сепарация дисперсной фазы (более 90%) происходит в насадочной зоне при пленочном режиме;
– основное сопротивление тепломассообмену сосредоточено в газовой фазе (более 99%);
– движение фаз стационарное и стабилизированное;
– режим движения газа в слое насадки турбулентный;
– срыв и унос капель жидкости с поверхности стекающей пленки незначителен;
– стенки колонны теплоизолированные от окружающей среды.
Профиль скорости жидкой фазы зависит от числа точек орошения и при применении хороших распределителей может быть принят в верхнем сечении слоя ${{u}_{{\text{ж}}}}(r) = {{u}_{{{\text{жн}}}}}$ – равномерным. Однако при стекании жидкости по насадке постепенно происходит перераспределение жидкой фазы к стенке колонны, особенно в хаотичной насадке. Известно, что существенное перераспределение жидкости к стенке происходит при $Н > 4{{D}_{к}}.$ Учитывая, что в скрубберах охлаждения газов значение $Н < 4{{D}_{к}},$ а в случае при $Н > 4{{D}_{к}}$ насадка располагается секциями с перераспределителями фаз. Таким образом, профиль скорости жидкости можно принять равномерным.
Профиль скорости газа существенно зависит от условий входа в аппарат и гидравлического сопротивления насадки по поперечному сечению. Экспериментальные исследования показывают сложную зависимость ${{W}_{{\text{г}}}}(r)$ для различных насадок [14, 15]. В первом приближеннии можно принять ${{W}_{{\text{г}}}}(r) = {{W}_{{{\text{ср}}}}},$ затем уточнить по экспериментальным данным или из численного решения системы уравнений движения газа.
Перенос теплоты при конденсационном охлаждении газа ($х > х{\text{*}}$) происходит за счет соприкосновения фаз (конвективный и молекулярный механизмы переноса), а также за счет конденсации влаги из газов на поверхность стекающей пленки воды (или иной жидкости), что может обеспечивать охлаждение ниже точки росы [16].
Тепловой баланс при коэффициенте испарения близким к единице записывается в виде
(5)
$\begin{gathered} Q = G{{с}_{{рг}}}{\text{(}}{{T}_{{нг}}} - {{T}_{{кг}}}{\text{)}} + \\ + \,\,G{\text{(}}{{I}_{{\text{н}}}}{{х}_{н}} - {{I}_{к}}{{х}_{к}}{\text{)}} - G{\text{(}}{{х}_{{\text{н}}}} - {{х}_{к}}{\text{)}}{{с}_{{рж}}}{{T}_{{жк}}}. \\ \end{gathered} $Также поток теплоты, переданной от газа в жидкую фазу можно представить используя уравнения тепло- и массопередачи при противотоке.
Поток теплоты при охлаждении газа жидкостью при противоточном движении фаз в колонне
При охлаждении газа жидкостью практически все сопротивление теплопередачи сосредоточено в газовой фазе, тогда коэффициент теплопередачи принимается равным коэффициенту теплоотдачи $K = {{{{\alpha }}}_{{\text{г}}}}.$
Применяя аналогию Льюиса в газовой фазе и известные выражения для энтальпии, связанные с температурой газа и влагосодержанием, выражение (6) представляют в форме [17]
Тогда в газовой фазе плотность потока теплоты можно выразить с применением коэффициента массоотдачи, отнесенного к разности влагосодержаний и движущей силы теплообмена в виде разности энтальпий, тогда
Плотность потока массы водяного пара
Локальный поток массы осаждающих частиц на межфазную поверхность пленки
Коэффициент массоотдачи в газовой фазе можно вычислить по выражению [18]
а коэффициент турбулентной диффузии в ядре потока газовой фазы в хаотичных и регулярных насадках с интенсификаторами по формуле [18]
В уравнении (2) принимается ${{\lambda }_{{{\text{тг}}}}} \approx {{\rho }_{{\text{г}}}}{{с}_{{{\text{рг}}}}}{{D}_{{{\text{тг}}}}}.$
Коэффициент турбулентной диффузии частиц в ядре потока газа [19]
(13)
${{D}_{{{\text{т}}d}}} = \frac{{{{D}_{{тг}}}}}{{1 + {{\omega }_{{\text{Е}}}}{{\tau }_{{\text{р}}}}}}.$Многочисленные экспериментальные исследования различных авторов турбулентной миграции аэрозольных частиц, показали, что при турбулентном режиме движения газа скорость осаждения частиц на стенки каналов на несколько порядков выше скорости диффузионного осаждения тех же частиц из ламинарного потока. При чем, при турбулентном режиме эффективность осаждения увеличивается с повышением скорости газа. Это характеризует инерционную природу явления переноса частиц. Такая форма осаждения получила название турбулентно-инерционного механизма осаждения аэрозолей [19, 20].
Турбулентная миграция представляет собой форму поперечного движения частиц в сдвиговом турбулентном потоке. Эта форма, открытая Фортье, Флетчером и независимо от них Медниковым, имеет в механике аэрозолей фундаментальное значение [19].
При теоретическом анализе всех форм движения аэрозольных частиц в турбулентном потоке обычно принимаются следующие предположения и допущения [19].
1. Диаметр частиц небольшой, сравнительно с масштабом несущих их пульсационных вихрей.
2. Обтекания частиц происходит при малых числах Рейнольдса.
3. Частицы имеют форму близкой к сферической. Полидисперсность частиц аэрозоля рассматривается пофракционно.
4. Кроме этого:
а) частицы не стесняют движение друг друга в ходе взаимных перемещений;
б) не соударяются, не коагулируют друг с другом;
в) не оказывают ощутимого влияния на турбулентные характеристики среды.
Значения концентраций частиц при выполнении отмеченных условий, согласно экспериментальным данным Россетки и Пфефера, принимаются <200 г/м3, т.е. примерно ≤0.17 кг/кг (для воздуха при атмосферном давлении).
5. Электростатические и другие силы не гидродинамической природы незначительные.
6. Срыв осажденной дисперсной фазы и капель воды с поверхности пленки жидкости незначительный.
Известен ряд эмпирических и полуэмпирических зависимостей для расчета приведенной (безразмерной) скорости турбулентного осаждения частиц $u_{t}^{ + } = \frac{{{{u}_{t}}}}{{{{u}_{ * }}}},$ связанных с временем релаксации скорости частиц [19]:
(14)
${{\tau }_{{\text{р}}}} = \frac{{{\text{d}}_{{\text{ч}}}^{2}{{{{\rho }}}_{{\text{ч}}}}}}{{18{{{{\rho }}}_{{\text{г}}}}{{\nu }_{{\text{г}}}}}}.$В расчетах используется безразмерное время релаксации:
где ${{u}_{ * }} = \sqrt {{{{{{{\tau }}}_{{{\text{гр}}}}}} \mathord{\left/ {\vphantom {{{{{{\tau }}}_{{{\text{гр}}}}}} {{{\rho }_{{\text{г}}}}}}} \right. \kern-0em} {{{\rho }_{{\text{г}}}}}}} $ – динамическая скорость, м/с; ${{\tau }_{{{\text{гр}}}}}$ – касательное напряжение на границе раздела фаз газа с пленкой жидкости, Па.Для расчета $u_{t}^{ + }$ в математических моделях чаще используются выражения Ужова и Медникова, обобщающие большое количество экспериментальных данных для трубок [19]:
при $\mu _{p}^{2}{{\tau }^{ + }} \leqslant 16.6$
(16)
$u_{t}^{ + } = 7.25 \times {{10}^{{ - 4}}}{{\left( {\frac{{{{{{\tau }}}^{ + }}}}{{1 + {{{{\omega }}}_{{\text{Е}}}}{{{{\tau }}}_{р}}}}} \right)}^{2}},$при $\mu _{p}^{2}{{\tau }^{ + }} > 16.6$
где безразмерный параметр ${{\mu }_{{\text{p}}}} = {1 \mathord{\left/ {\vphantom {1 {{{{(1 + {{\omega }_{{\text{E}}}}{{\tau }_{{\text{p}}}})}}^{{0.5}}}}}} \right. \kern-0em} {{{{(1 + {{\omega }_{{\text{E}}}}{{\tau }_{{\text{p}}}})}}^{{0.5}}}}};$ ${{\omega }_{{\text{Е}}}} = {{{{u}_{ * }}} \mathord{\left/ {\vphantom {{{{u}_{ * }}} {(0.05{{d}_{{\text{э}}}})}}} \right. \kern-0em} {(0.05{{d}_{{\text{э}}}})}}$ – частота энергоемких пульсаций, с–1.Из приведенных выше выражений следует, что размерная скорость турбулентной миграции частиц ${{u}_{t}} = u_{t}^{ + }{{u}_{ * }}$ существенно зависит от значения динамической скорости ${{u}_{ * }}$ или касательного напряжения на поверхности раздела фаз ${{\tau }_{{{\text{ст}}}}} = u_{*}^{2}{{\rho }_{{\text{г}}}}.$
Среднее значение динамической скорости на поверхности хаотичных насадок $({{\operatorname{Re} }_{{\text{э}}}} > 40),$ а также регулярных с интенсификаторами $({{\operatorname{Re} }_{{\text{э}}}} > 500)$ вычисляется по выражению [18] ${{u}_{ * }} = 1.55{{{\text{W}}}_{{\text{г}}}}{{({\xi \mathord{\left/ {\vphantom {\xi {{{{\operatorname{Re} }}_{{\text{э}}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}_{{\text{э}}}}}})}^{{0.25}}}.$
Граничные условия к системе уравнений (1)–(3):
при z = H (вход воды и выход газа):
при z = 0 (выход воды и вход газа):
при r = 0 (на стенке колонны):
На рис. 1, 2 для проверки адекватости математической модели представлены профиль температуры газа и профиль влагосодержания, полученные из численного решения системы уравнений (1)–(3) при равномерном распределении газа и жидкости и экспериментальные данные [16]. При решении использовалась известное выражение, связывающие энтальпию I, влагосодержание х, температуру газа ${{T}_{{\text{г}}}}$ и удельные теплоемкости сухого газа ${{с}_{{{\text{рсух}}}}}$ и теплоемкость пара ${{с}_{{{\text{рп}}}}}{\text{:}}$ $I = ({{с}_{{{\text{рcух}}}}} + {{с}_{{{\text{рп}}}}}х){{Т}_{{\text{г}}}} + {{R}_{{\text{ж}}}}х.$ В результате численного решения (1)–(3) получено удовлетворительное согласование с экспериментом для колец Рашигапри ${{W}_{{\text{г}}}} = 0.4\,\,{\text{до}}\,\,1.9\,\,{\text{м/с}}$ и плотности орошения Uж = 3–55 м3/м2 ч.
Рис. 1.
Зависимость температуры уходящих газов от коэффициента орошения для насадки из керамических колец размерами 35 × 35 × 4 мм при начальной температуре газов Тгн = 250–280°С и воды Тжн = 12°С. Высота насадки – 1000 мм. Сплошная линия – расчет. – эксперимент [13]. 1-1 – область расчетных значений; 2 – расчет осредненный.

Рис. 2.
Зависимость влгагосодержания уходящих газов от коэффициента орошения. Обозначения на рис. 1.

ТЕПЛОВАЯ И СЕПАРАЦИОННАЯ ЭФФЕКТИВНОСТЬ
При известном профиле температуры газа по высоте слоя и ее значения на выходе можно опрелелить тепловую эффективность охлаждения газа.
Тепловую эффективность процесса в газовой фазе запишем в форме
(18)
${{Е}_{{\text{г}}}} = \frac{{{{T}_{{{\text{нг}}}}} - {{T}_{{{\text{кг}}}}}}}{{{{T}_{{{\text{нг}}}}} - {{T}_{{{\text{нж}}}}}}}.$Тепловая эффективность записывается также в виде отношения разности энтальпий
(19)
${{Е}_{{\text{г}}}} = \frac{{{{I}_{{\text{н}}}} - {{I}_{{\text{к}}}}}}{{{{I}_{{\text{н}}}} - I_{{\text{к}}}^{ * }}}.$Значения ${{E}_{г}}$ (18) и (19) записаны исходя из реально достигнутых показателей охлаждения газа, относительно максимально возможных.
Тепловая эффективность нагрева воды
(20)
${{Е}_{{\text{ж}}}} = \frac{{{{T}_{{{\text{кж}}}}} - {{T}_{{{\text{нж}}}}}}}{{{{T}_{{{\text{нг}}}}} - {{T}_{{{\text{нж}}}}}}}.$Эффективности конденсации влаги
(21)
${{Е}_{{\text{г}}}} = \frac{{{{х}_{{\text{н}}}} - {{х}_{{\text{к}}}}}}{{{{х}_{{\text{н}}}} - х_{{\text{к}}}^{ * }}}.$Эффективность сепарации дисперсной фазы
Конечные значения температур ${{Т}_{{{\text{кг}}}}},{\text{ }}{{Т}_{{{\text{кж}}}}},$ влагосодержания ${{х}_{{\text{к}}}}$ и концентрация дисперсной фазы ${{С}_{{\text{к}}}}$ находится из решения системы уравнений (1)–(4).
На рис. 3 представлены результаты расчетов тепловой эффективности ${{Е}_{{\text{г}}}}$ (18) при охлаждении дымовых газов $({{Т}_{{{\text{нг}}}}} = 150^\circ {\text{С}})$ водой $({{Т}_{{{\text{нж}}}}} = 15^\circ {\text{С}})$ в скруббере с хаотичной металлической насадкой “Инжехим 2012” высотой Н = 2.0 мс номинальным размером элементов 45 мм $({{a}_{v}} = 166\,\,{{{{м}^{2}}} \mathord{\left/ {\vphantom {{{{м}^{2}}} {{{м}^{3}}}}} \right. \kern-0em} {{{м}^{3}}}})$ и 60 мм $({{a}_{v}} = 70\,\,{{{{м}^{2}}} \mathord{\left/ {\vphantom {{{{м}^{2}}} {{{м}^{3}}}}} \right. \kern-0em} {{{м}^{3}}}}).$ Насадка 45 мм при скорости газа ${{W}_{{\text{г}}}} = 3\,\,{м \mathord{\left/ {\vphantom {м {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и плотности орошения 25 м3/м2 ч близка к началу подвисания жидкой фазы. Поэтому при таком режиме рекомендуется применение более крупной насадки 60 мм.
Рис. 3.
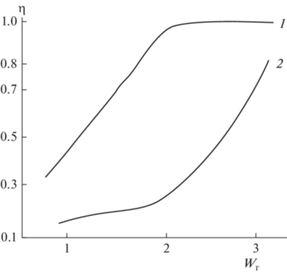
Зависимость тепловой эффективности в газовой фазе от скорости газа в колонне: 1 – насадка “Инжехим 2012” 45 м; 2 – 60 мм. Плотность орошения воды ${{q}_{{\text{ж}}}} = 25\,\,{{{{{\text{м}}}^{{\text{3}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{3}}}}} {{{{\text{м}}}^{2}}{\text{ч}}}}} \right. \kern-0em} {{{{\text{м}}}^{2}}{\text{ч}}}}.$ Высота слоя насадки Н = 2.0 м. Охлаждение дымовых газов

На рис. 4 даны результаты расчетов сепарационной эффективности (22) для частиц ${{d}_{{\text{ч}}}} = 5\,\,мкм$ и плотностью ${{\rho }_{{\text{ч}}}} = 3000\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{м}^{3}}}}} \right. \kern-0em} {{{м}^{3}}}}$ из дымовых газов в слое Н = 2.0 м для насадок 45 и 60 мм. Из расчетов следует значительное повышение эффективности сепарации при ${{W}_{{\text{г}}}} > 2.5\,\,{м \mathord{\left/ {\vphantom {м с}} \right. \kern-0em} с},$ что как было отмечено выше характеризует инерционно-турбулентный механизм переноса частиц.
Рис. 4.
Зависимость эффективности сепарации дисперсной фазы ${{d}_{{\text{ч}}}} = 5\,\,{\text{мкм}}$ от скорости газа. 1 – Насадка “Инжехим 2012” 45 мм; 2 – 60 мм. Плотность орошения ${{q}_{{\text{ж}}}} = 25\,\,{{{{{\text{м}}}^{{\text{3}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{3}}}}} {{{{\text{м}}}^{{\text{2}}}}{\text{ч}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{2}}}}{\text{ч}}}}.$
СРАВНИТЕЛЬНЫЕ ХАРАКТРЕРИСТИКИ КОНТАКТНЫХ УСТРОЙСТВ
На основе применения представленной математической модели выполнены численные исследования и получены сравнительные характеристики различных типов металлических регулярных и нерегулярных насадок [15, 21] при заданной тепловой эффективности ${{Е}_{{\text{г}}}} = 0.8$ и идентичном температурном и гидродинамическом режимах.
1. Кольца Рашига 25 мм: ${{a}_{v}} = 220\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}{\text{;}}$ ${{\varepsilon }_{{{\text{св}}}}} = 0.92.$
2. Кольца Рашига 50 мм: ${{a}_{v}} = 110\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}{\text{;}}$ ${{\varepsilon }_{{{\text{св}}}}} = 0.95.$
3. Кольца Мебиуса – 40 мм: ${{a}_{v}} = 190\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}{\text{;}}$ $\,{{\varepsilon }_{{{\text{св}}}}} = 0.88.$
4. Насадка “Инжехим 2012” – 24 мм: ${{a}_{v}} = 166\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}{\text{;}}$ ${{\varepsilon }_{{{\text{св}}}}} = 0.96.$
5. Насадка “Инжехим 2012” – 45 мм: av = = 100 м2/м3; ${{\varepsilon }_{{{\text{св}}}}} = 0.97.$
6. Сегментно-регулярная рулонная “Инжехим”: ${{a}_{v}} = 380\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}{\text{;}}$ ${{\varepsilon }_{{{\text{св}}}}} = 0.94.$
7. Рулонная гофрированная с шероховатой поверхностью: ${{a}_{v}} = 280\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}}{\text{;}}$ ${{\varepsilon }_{{{\text{св}}}}} = 0.95.$
На гистограмме рис. 5 представлены расчетные данные высоты насадки, которая необходима для достижения тепловой эффективности в газовой фазе ${{Е}_{{\text{г}}}} = 0.8$ при плотности орошения 15 м3/м2 ч и средней скорости газа ${{W}_{{\text{г}}}} = 1.5$ м/c. Также даны значения перепада давления.
Рис. 5.
Требуемая высота насадочного слоя и перепад давления при Eг = 0.8. Хаотичные насадки: 1 – кольца Рашига – 25 мм; 2 – кольца Рашига – 50 мм; 3 – кольца Мебиуса – 40 мм; 4 – “Инжехим 2012” – 24 мм; 5 – “Инжехим 2012” – 45 мм. Регулярные насадки: 6 – сегменто-регулярная; 7 – рулонная гофрированная.
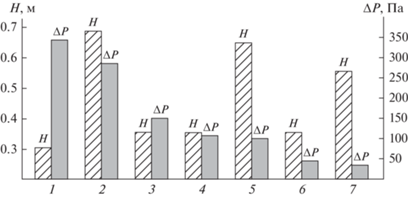
Из полученных результатов следует, что насадки с номерами 3, 4 и 6 обеспечивают заданную эффективность при высоте слоя Н = 0.35–0.4 м и перепаде давления от 50 до 170 Па, т.е. с небольшими габаритами скруббера и энергетическими характеристиками.
Таким образом, в данной работе получена математическая модель сопряженного тепломассообмена в насадочном слое, решение которой численно позволяет прогнозировать эффективность охлаждения и очистки газа и нагрева воды (или иных жидкостей) в зависимости от режимных и конструктивных характеристик пленочногоскруббера.
На основе представленной математической модели расчета охлаждения и очистки газов выполнена разработка технических решений по модернизации трех колонн-скрубберов охлаждения пирогаза водой на установках газоразделения в производстве этилена. Самый большой скруббер имеет диаметр 3.2 м, расход пирогаза G = = 80–120 т/ч и расход охлаждающей воды 200 т/ч в верхней части и до 800 т/ч в нижней. Кроме этого происходит мокрая очистка пирогаза от частиц кокса и смол после печей пиролиза. В результате замены устаревших контактных устройств в верхней части колонны на хаотичную насадку (Н = = 2.0 м), а в нижней части на регулярную гофрированную насадку (Н = 4.0 м) “Инжехим” [21] повышена производительность скруббера и снижена температура пирогаза на выходе до регламентных значений. Следовательно, адекватность математической модели подтверждена данными промышленной эксплуатации скрубберов после их модернизации.
ЗАКЛЮЧЕНИЕ
Решение задач сопряженного тепломассообмена имеет не только теоретическое, но и прикладное значение в теплотехнике, теплоэнергетике и химической технологии. Теоретическое, а точнее численное моделирование сопряженного тепломассообмена связано с решением системы дифференциальных уравнений с частными производными. При взаимодействии стекающей пленки жидкости с газовым потоком в условиях известного распределения межфазной поверхности в пространстве (вертикальные каналы, плоскопараллельные контактные устройства и т.д.) дифференциальные уравнения тепло- и массообменназаписываюются для каждой фазы отдельно с граничными условиями на поверхности раздела четвертого рода. Однако при стекании пленки жидкости по контактным элементам расположенных хаотично задать граничные условия на межфазной поверхности не представляется возможным. В таких случаях используют объемные межфазные источники импульса, энергии и массы, что является упрощенной формой модели многоскоростного континуума. При неравномерном распределении фаз объемные источники записываются для локальных областей, а при условно равномерном для всего рабочего объема аппарата.
Отличительной особенностью математической модели в данной статье является возможность вычислять параметры источников (коэффициенты тепло-и массоотдачи и турбулентной миграции частиц) и средний коэффициент турбулентного обмена, как в локальных областях, так и для всего насадочного слоя с использованием коэффициента гидравлического сопротивления (перепада давления), полученного экспериментально. Это значительно сокращает временные и материальные затраты при моделировании разрабатываемых контактных устройств газ–жидкость.
Исследование выполнено в рамках научного проекта РНФ 18-79-101-36.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ:
| ${{a}_{v}}$ | удельная поверхность насадки, м2/м3 |
| С | концентрация дисперсной фазы, кг/м3 |
| сp | удельная теплоемкость, Дж/(кг·К) |
| D, ${{D}_{т}}$ | коэффициенты молекулярной и турбулентной диффузии, м2/с |
| Dк | диаметр колонны, м |
| dэ | эквивалентный диаметр насадки, м |
| ${{d}_{{\text{ч}}}}$ | диаметр частицы, м |
| F | площадь межфазной поверхности пленки, м2 |
| Н | высота слоя насадки, м |
| ${{j}_{х}}$ | плотность потока массы влаги, кг/м2с |
| ${{j}_{с}}$ | плотность потока массы частиц, кг/м2с |
| I | энтальпия, Дж/кг |
| q | плотность теплового потока, Дж/(м2 · с) |
| r | радиальная координата, м |
| Rж | удельная теплота парообразования жидкости, Дж/кг |
| Sк | площадь свободного сечения колонны, м2 |
| K | коэффициент теплопередачи, Вт/м2 К |
| Т | температура потока, °С |
| ${{u}_{ * }}$ | динамическая скорость, м/с |
| ${{u}_{{\text{ж}}}}$ | скорость жидкости, м/с |
| ${{u}_{t}}$ | скорость турбулентной миграции частиц, м/с |
| V | объем, м3 |
| ${{W}_{г}}$ | скорость газа, м/с |
| x | концентрация влаги в газе, кг/кг |
| z | координата вертикальной оси, м |
| ${{{{\beta }}}_{{\text{г}}}}$ | коэффициент массоотдачи, м/с |
| ${{{{\beta }}}_{х}}$ | коэффициент массоотдачи, отнесенный к разности влагосодержаний, кг/м2с |
| $\Delta P$ | перепад давления, Па |
| $\Delta T$ | средняя движущая сила теплопередачи, °С |
| $\Delta x$ | средняя движущая сила массопередачи влаги, кг/кг |
| $\lambda $ | удельная теплопроводность среды, Вт/(м · К) |
| $\nu ,{{\nu }_{{\text{т}}}}$ | кинематические коэффициенты молекулярной и турбулентной вязкости, м2/с |
| $\xi $ | коэффициент гидравлического сопротивления насадки |
| $\rho $ | плотность фазы, кг/м3 |
| ${{{{\varepsilon }}}_{{{\text{св}}}}}$ | удельный свободный объем насадки, м2/м3 |
| Комплексы: | |
| ${\text{S}}{{{\text{h}}}_{{\text{г}}}} = {{{{{{\beta }}}_{{\text{г}}}}{{d}_{{\text{э}}}}} \mathord{\left/ {\vphantom {{{{{{\beta }}}_{{\text{г}}}}{{d}_{{\text{э}}}}} {{{D}_{{\text{г}}}}}}} \right. \kern-0em} {{{D}_{{\text{г}}}}}}$ | число Шервуда |
| ${{\operatorname{Re} }_{{\text{э}}}} = {{{{W}_{{\text{г}}}}{{d}_{{\text{э}}}}} \mathord{\left/ {\vphantom {{{{W}_{{\text{г}}}}{{d}_{{\text{э}}}}} {{{v}_{{\text{г}}}}}}} \right. \kern-0em} {{{v}_{{\text{г}}}}}}$ | число Рейнольдса |
| ${\text{S}}{{{\text{c}}}_{{\text{г}}}} = {{{{v}_{{\text{г}}}}} \mathord{\left/ {\vphantom {{{{v}_{{\text{г}}}}} {{{D}_{{\text{г}}}}}}} \right. \kern-0em} {{{D}_{{\text{г}}}}}}$ | число Шмидта |
| ${{\omega }_{Е}} = {{{{u}_{ * }}} \mathord{\left/ {\vphantom {{{{u}_{ * }}} {0.05{{d}_{{\text{э}}}}}}} \right. \kern-0em} {0.05{{d}_{{\text{э}}}}}}$ | частота энергоемких пульсаций, с–1 |
| ${{\tau }_{{\text{р}}}} = {{d_{{\text{ч}}}^{2}{{\rho }_{{\text{ч}}}}} \mathord{\left/ {\vphantom {{d_{{\text{ч}}}^{2}{{\rho }_{{\text{ч}}}}} {18{{\rho }_{{\text{ч}}}}{{v}_{{\text{г}}}}}}} \right. \kern-0em} {18{{\rho }_{{\text{ч}}}}{{v}_{{\text{г}}}}}}$ | время релаксации частицы, с |
| Нижние индексы: | |
| “г” | газовая фаза |
| “т” | турбулентность |
| “ж” | жидкая фаза |
| “н, к” | значение параметров на входе и на выходе |
| “гр” | значение параметров на границе раздела |
| “п” | пар |
| “ч” | частица |
| “сух” | сухой газ |
| Верхние индексы: | |
| “*” | равновесное значение |
| “+” | безразмерные параметры |
Список литературы
Bespalov V.V. Simulation of surface-type condensing units for heat recovery from the flue gas with air heating / V.V. Bespalov, L.A. Belyaev, L.S. Kuchman // MATEC Web of Conferences. 2017. № 91. 01003.
Таран Ю.А. Математическое описание фазовых и формально аналогичных им превращений для инженерных расчетов // Теоретические основы химической технологии. 2020. Т. 54. № 3. С. 309–324.
Voinov N.A., Deryagina N.V., Zemtsov D.A., Bogatkova A.V., Zhukova O.P. Intensification of heat removal in diabatic columns // B cбopникe: J. Physics: Conference Series. Krasnoyarsk, RussianFederation, 2020. C. 52080.
Boyadjiev C.H.R.B., Dzhonova D.B., Popova-Krumova P.G., Stefanova K.V., Pavlenko A.N., Zhukov V.E., Slesareva E.Yu. Liquid wall flow in counter-current column apparatuses for absorption processes with random packings // Bulgarian Chemical Communications. 2020. V. 52. P. 74–79.
Ахмадиев Ф.Г., Фарахов М.И., Ахмитшин А.А. Моделирование сопряженного тепломассообмена при пленочной конденсации // Теоретические основы химической технологии. 2020. Т. 54. № 4. С. 463–474.
Пономарев В.Б., Фесун И.П. Математическое моделирование скорости осаждения частиц с учетом динамической релаксации // Теоретические основы химической технологии. 2020. Т. 54. № 5. С. 636–642.
Ageev A.A., Yakhontov D.A., Kadyrov T.F., Farakhov M.M., Lapteva E.A. Mathematical model of dispersed phase gas separation in a combined equipment // Chemical and Petroleum Engineering. 2019. V. 55. № 7–8. P. 611–618.
Shi X. An investigation of the performance of compact heat exchanger for latent heat recovery from exhaust flue gases / Xiaojun Shi, Defu Che, Brian Agnew, Jianmin Gao. // International J. Heat and Mass Transfer. 2011. № 54. P. 606–615.
Lapteva E.A., Stolyarova E.Yu., Laptev A.G. Numerical Estimation of the Heat and Mass Transfer Efficiency Considering Nonuniformity in Water and Air Distribution // Thermal Engineering. 2020. V. 67. № 4. P. 234.
Laptev A.G., Farakhov T.M. Mathematical Model of Mass Transfer in Randomly Packed Columns with Phase Maldistribution // J. Engineering Thermophysics. 2019. V. 28. № 3. P. 392–400.
Лаптев А.Г., Лаптева Е.А. Определение эффективности насадочных газосепараторов капельных аэрозолей с учетом неравномерности профиля скорости газа // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 235–241.
Bespalov V.V. Evaluation of Heat Transfer Coefficients During the Water Vapor Condensation Contained in the Flue Gas / V.V. Bespalov, V.I. Bespalov, D.V. Melnikov // EPJ Web of Conferences. 2016. № 110. 01007.
Jeong K. Analytical modeling of water condensation in condensing heat exchanger / Kwangkook Jeong, Michael Kessen, Harun Bilirgen, Edward Levy // International J. Heat and Mass Transfer. 2010. № 53. P. 2361–2368.
Пушнов А.С., Балтернас П., Каган А., Загорскис А. Аэродинамика воздухоочистных устройств с зернистым слоем. Вильнюс: Техника, 2010. 348 с.
Витковская Р.Ф., Пушнов А.С., Шинкунас С. Аэрогидродинамика и тепломассообмен насадочных аппаратов: Лань-Пресс. 2019. 288 с.
Аронов И.З. Контактный нагрев воды продуктами сгорания природного газа. Л: Недра, 1990. 279 с.
Гладков В.А., Арефьев Ю.И. Вентиляторные градирни / В.А. Гладков, Ю.И. Арефьев, В.С. Пономаренко. М.: Стройиздат, 1976. 216 с.
Лаптев А.Г., Башаров М.М., Лаптева Е.А., Фарахов Т.М. Модели и эффективность процессов межфазного переноса. Ч. 2. Тепломассообменные процессы. Казань: Центр инновационных технологий, 2020. 565 с.
Медников Е.П. Турбулентный перенос и осаждения аэрозолей. М.: Наука, 1980. 176 с.
Сугак Е.В., Войнов Н.А., Николаев Н.А. Очистка газовых выбросов в аппаратах с интенсивными гидродинамическими режимами; Сибирская аэрокосмическая акад., Сибирский гос. технологический ун-т, Казанский гос. технологический ун-т. Казань, (2-е изд.). Издательство: Отечество. 2009. 224 с.
Каган А.М., Лаптев А.Г., Пушнов А.С., Фарахов М.И. Контактные насадки промышленных тепломассообменных аппаратов. Казань, 2013. Издательство: Отечество, 2013. 454 с.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


