Теоретические основы химической технологии, 2022, T. 56, № 3, стр. 379-396
Применение физически обоснованной математической модели массообменного технологического процесса для повышения точности оценивания качества конечного продукта
С. А. Самотылова a, *, А. Ю. Торгашов a
a Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия
* E-mail: samotylova@dvo.ru
Поступила в редакцию 19.08.2021
После доработки 20.12.2021
Принята к публикации 30.12.2021
- EDN: LSPJXF
- DOI: 10.31857/S0040357122020117
Аннотация
Рассматривается задача повышения точности оценивания качества конечного продукта в условиях малого набора обучающего сегмента данных, который расширяется с использованием физически обоснованной модели (first principles model) массообменного технологического процесса производства метил-трет-бутилового эфира (МТБЭ). Показано, что предлагаемый подход превосходит другие методы построения статистических моделей (виртуальных анализаторов) для задачи оценивания качества конечных продуктов, так как позволяет учитывать физически обоснованные зависимости и характеристики технологического процесса, что в итоге приводит к повышению уровня адекватности разрабатываемой модели. Определены условия целесообразности применения физически обоснованной модели массообменного технологического процесса в алгоритме при построении статистических моделей для оценки показателя качества конечного продукта в условиях параметрической неопределенности эффективности массопереноса по Мерфри и параметров бинарного взаимодействия между димерами изобутилена и компонентами из системы производства МТБЭ. В качестве критерия эффективности расширения обучающей выборки предлагается использовать площадь области пересечения распределений выходной переменной между ее значениями в расширенной обучающей и тестовой выборках.
ВВЕДЕНИЕ
Управление технологическими процессами (ТП) с целью повышения качества конечных продуктов является одной из главных задач в промышленности. Постоянный контроль качества выпускаемой продукции играет определяющую роль в управлении, минимизации издержек производства и повышении безопасности. Учитывая тенденцию к использованию систем усовершенствованного управления на основе статистических моделей для оценки показателей качества (виртуальных анализаторов) в реальном времени, совершенствование и разработка новых подходов для их построения в условиях малых обучающих выборок представляют собой актуальную тему исследования [1–5]. Под виртуальными анализаторами (ВА) понимаются различные статистические математические модели (регрессионные, нейронные сети, нейро-нечеткие модели и т.п.), которые используются для оценки определенных физических величин или качества продукции в производственных процессах на основе доступных измерений [6, 7]. Для построения ВА используются выборки исторических данных, содержащие значения целевого показателя качества, так и измеряемых технологических переменных процесса, коррелирующих с ним [8, 9]. ВА создают информационную базу для формирования оптимального управления как отдельными химико-технологическими процессами, так и всем циклом технологического производства.
Используемые для построения ВА методы были существенно улучшены, однако, в большинстве случаев они сосредоточены на подходах, основанных на глубоком обучении [10–12] и регрессии [13]. Следует отметить, что при разработке и внедрении ВА в системы усовершенствованного управления технологическими процессами для оперативного контроля качества конечных продуктов, одной из важнейших проблем, с которой сталкиваются, – это репрезентативность обучающей выборки исторических данных [14–17]. От размера обучающей выборки и ее характеристик будет зависеть точность модели оценки показателей качества конечных продуктов и эффективность применения алгоритмов и методов для ее разработки [18, 19].
Высокая стоимость лабораторных исследований, нелинейность технологического процесса, наличие случайного шума, отсутствие данных технологического режима на всем диапазоне изменения качества продукта приводит к неэффективности применяемых методов при разработке модели (ВА) и снижение ее работоспособности на другом диапазоне функционирования установки. В связи с этим задача построения адекватной модели для оценки качества конечных продуктов в условиях малой выборки данных остается актуальной [18–20].
При построении ВА (или моделей) для оценки показателей качества конечных продуктов в условиях малых выборок широкое распространение получили бутстрэп метод [21] и метод складного ножа [22]. Данные методы позволяют оценить параметры ВА путем формирования новых выборок из исходного набора данных. Используемые методы отличаются друг от друга подходом к формированию выборок. В первом случае формируются бутстрэп выборки путем извлечения элементов из исходного набора данных случайным образом несколько раз. При использовании концепции складного ножа формируются подвыборки складного ножа путем удаления i-ой строки из исходного набора данных.
В [23, 24] рассмотрен подход к работе с малым исходным набором данных на основе генерации виртуальной выборки методом оптимизации роя частиц. Этот метод заполняет “пропуски” между значениями данных выборки за счет добавления новых сгенерированных виртуальных наблюдений. Применение вышеуказанных методов эффективно, если обучающая выборка содержит в себе данные технологического процесса на всем диапазоне изменения качества конечного продукта.
В настоящей работе предлагается алгоритм построения модели (виртуального анализатора) для оценки качества конечного продукта (МТБЭ), отличающийся от известных подходов к построению моделей в условиях малых выборок тем, что основан на расширении обучающей выборки или повышению ее репрезентативности путем добавления данных, полученных с использованием физически обоснованной математической модели технологического процесса.
ОПИСАНИЕ ПРОМЫШЛЕННОГО ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА И ПОСТАНОВКА ЗАДАЧИ
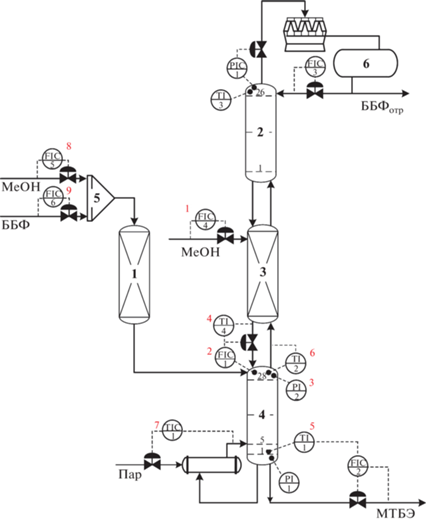
Рассматривается массообменный технологический процесс получения высокооктановой добавки бензинов – метил-трет-бутилового эфира (МТБЭ). Схема процесса производства МТБЭ представлена на рис. 1.
Рис. 1.
Массообменный технологический процесс производства метил‑трет‑бутилового эфира: 1 – реактор предварительного синтеза; 2 – верхняя ректификационная колонна; 3 – реакционно-ректификационный аппарат; 4 – нижняя ректификационная колонна; 5 – смеситель; 6 – емкость; ББФ – бутан-бутиленовая фракция; ББФотр – отработанная бутан-бутиленовая фракция; МеОН – метанол; МТБЭ – метил-трет-бутиловый эфир.
При производстве МТБЭ особое внимание уделяется выбору соотношения изобутилен-метанол. Количество подаваемого метанола определяется в зависимости от расхода бутан-бутиленовой фракции (ББФ) и содержания изобутилена в ней. Определение и поддержание соотношения компонентов осуществляется на основании опыта технолога. При неправильном задании расхода метанола относительно расхода ББФ количество непрореагировавшего метанола на выходе реактора может быть либо больше, либо меньше требуемого значения. В обоих случаях это приводит к перерасходу исходного сырья, недополучению готовой продукции и снижению ее качества. По окончании процесса массовая доля метил-трет-бутилового эфира марки А должна быть не менее 98% в конечном продукте, а массовая доля метанола (МеОН) не должна превышать 1.5%.
Основная химическая реакция (образование МТБЭ) в реакционной зоне протекает в результате взаимодействия изобутилена (IB), содержащегося в ББФ, с метанолом на сульфокатионитном катализаторе:
(1)
${\text{C}}{{{\text{H}}}_{{\text{3}}}}{\text{OH}} + {{\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right)}_{{\text{2}}}}{\text{C}} = {\text{C}}{{{\text{H}}}_{{\text{2}}}} \leftrightarrow {{\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right)}_{{\text{3}}}}{\text{COC}}{{{\text{H}}}_{{\text{3}}}}.$В условиях недостаточного количества метанола изобутилен димеризуется с образованием побочного продукта диизобутена (DIB), который состоит из изомеров 2,4,4-триметилпентена-1 (2,4,4-TMП-1) и 2,4,4-триметилпентена-2 (2,4,4-ТМП-2) [25, 26].
(2)
$\begin{gathered} 2{{\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right)}_{{\text{2}}}}{\text{C}} = {\text{C}}{{{\text{H}}}_{{\text{2}}}} \leftrightarrow \\ \leftrightarrow \,\,{\text{C}}{{{\text{H}}}_{{\text{2}}}}{\text{ = C}}\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right){\text{C}}{{{\text{H}}}_{{\text{2}}}}{{\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right)}_{{\text{3}}}}, \\ \end{gathered} $(3)
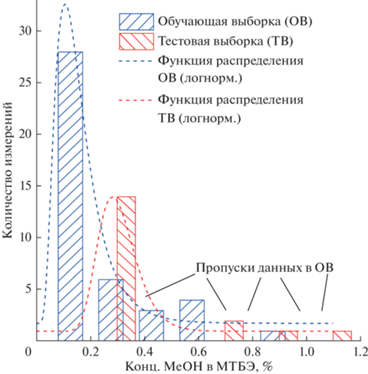
$\begin{gathered} 2{{\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right)}_{{\text{2}}}}{\text{C}} = {\text{C}}{{{\text{H}}}_{{\text{2}}}} \leftrightarrow \\ \leftrightarrow \,\,{\text{C}}{{{\text{H}}}_{3}}{\text{C}}\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right){\text{ = CHC}}{{\left( {{\text{C}}{{{\text{H}}}_{{\text{3}}}}} \right)}_{{\text{3}}}}. \\ \end{gathered} $При построении моделей для оценки качества МТБЭ в обучающей выборке в реальных условиях часто наблюдается полное отсутствие данных технологического режима в области верхней границы диапазона качества продуктов (приближения параметров объекта управления к границам, обозначенным технологическим регламентом) либо частичное отсутствие данных в области всего диапазона технологического режима (рис. 2).
Отсутствие информации по качеству конечных продуктов, соответствующей текущему режиму технологического процесса, вынуждает операторов поддерживать режимы, обеспечивающие большой запас по качеству продуктов. Тем самым повышается расход энергии и увеличивается стоимость конечного продукта. В связи с этим рассматривается задача построения модели для оценки содержания метанола в конечном (нижнем) продукте производства МТБЭ в условиях малой обучающей выборки с отсутствием данных технологического режима во всем диапазоне изменения качества продуктов.
Пусть N обозначает количество наблюдений, а nU и nY обозначают количество входных и выходных переменных, $U \in {{R}^{{N \times {{n}_{U}}}}}$ и $Y \in {{R}^{{N \times {{n}_{Y}}}}}.$ Для обучающего набора данных $U \in {{R}^{{N \times {{n}_{U}}}}},$ $Y \in {{R}^{{N \times 1}}}$ задача состоит в том, чтобы построить некоторую функцию f, связывающую вход и выход. Таким образом модель для оценки показателя качества конечного продукта ($\hat {Y}$) в общем виде имеет вид:
В качестве входных переменных выбираются наиболее коррелируемые с выходом (концентрация метанола в МТБЭ) следующие переменные: u(1) – расход метанола в реактор, м3/ч (FIC4); u(2) – реакционная масса в нижнюю ректификационную колонну, м3/ч (FIC1); u(3) – давление вверху нижней ректификационной колонны, кгс/см2 (PI2); u(4) – температура ректификационной смеси, поступающая в нижнюю ректификационную колонну, °C (TI4); u(5) – температура куба нижней ректификационной колонны, °C (TI1); u(6) – температура углеводородной смеси, отходящей сверху нижней ректификационной колонны, °C (TI2); u(7) – температура на 5-ой тарелке нижней ректификационной колонны, °C (TIC1); u(8) – расход метанола в смеситель, м3/ч (FIC5); u(9) – расход бутан-бутиленовой фракции в смеситель, м3/ч (FIC6); $\hat {\beta }$ – вектор параметров модели.
Общий размер исходной обучающей выборки составляет ${{N}_{{{\text{tr}}{\text{.s}}}}} = 42.$ Для оценки эффективности предлагаемого алгоритма использовалась тестовая (контрольная) выборка размером ${{N}_{{{\text{te}}{\text{.s}}}}} = 18.$
Эффективность построенных моделей оценивается с помощью коэффициента детерминации R2 и абсолютной средней ошибки:
(5)
${{R}^{2}} = 1 - {{\sum\limits_{n = 1}^N {{{{({{Y}_{n}} - {{{\hat {Y}}}_{n}})}}^{2}}} } \mathord{\left/ {\vphantom {{\sum\limits_{n = 1}^N {{{{({{Y}_{n}} - {{{\hat {Y}}}_{n}})}}^{2}}} } {\sum\limits_{n = 1}^N {{{{({{Y}_{n}} - \bar {Y})}}^{2}}} }}} \right. \kern-0em} {\sum\limits_{n = 1}^N {{{{({{Y}_{n}} - \bar {Y})}}^{2}}} }};$ИСПОЛЬЗУЕМЫЕ МЕТОДЫ ПОСТРОЕНИЯ МОДЕЛЕЙ ДЛЯ ОЦЕНКИ ПОКАЗАТЕЛЕЙ КАЧЕСТВА КОНЕЧНЫХ ПРОДУКТОВ
Применение того или иного метода при построении ВА в условиях малой выборки ограничено такими факторами как зашумленностью исходных данных, проблемой выбора структуры модели, наличием сильной корреляции между входами, нелинейностью технологических процессов, переобучением модели и т.д. Оценить оптимальность применения того или иного метода можно по критериям точности полученных моделей [см. (5) и (6)]. Широкое распространение в промышленности получили проекционные методы. Они позволяют выделить латентные (скрытые) переменные, определить эффективную размерность данных, удалить их шумовую составляющую и, как следствие, снизить риск переобучения моделей и тем самым улучшить их качество [27]. В связи с этим для построения моделей оценки целевого показателя качества используется метод проекций на латентные структуры [28–31].
Метод проекций на латентные структуры
Оценка ${{\hat {\beta }}_{{{\text{ПЛС}}}}}$ с помощью метода проекций на латентные структуры (ПЛС) для А главных компонент осуществляется как: ${{\hat {\beta }}_{{{\text{ПЛС}}}}} = W{{{\text{(}}{{P}^{{\text{T}}}}W{\text{)}}}^{{ - {\text{1}}}}}Q,$ где Р – матрица нагрузок U, Q – матрица нагрузок Y, W – матрица весов U, Т – операция транспонирования, $\bar {U},$ $\bar {Y}$ – векторы средних значений матриц U и Y. Расчет ${{\hat {\beta }}_{{{\text{ПЛС}}}}}$ происходит итерационно для каждой главной компоненты.
Шаг 1: для исходной выборки данных входных $U \in {{R}^{{N \times {{n}_{U}}}}}$ и выходной $Y \in {{R}^{{N \times 1}}}$ переменных, переменные U и Y центрируются: ${{U}_{{\text{0}}}} = U - {{1}_{{N \times {{n}_{U}}}}}\bar {U},$ ${{Y}_{0}} = Y - {{1}_{{N \times 1}}}\bar {Y},$ где ${{1}_{{N \times 1}}}$ единичный вектор. На этом шаге также выбирается максимальное значение главных компонент $а = \overline {1,А} $ $\left( {А = {{n}_{U}}} \right).$
Шаг 2: вычисляется вектор взвешенных нагрузок ${{w}_{a}}$ по формуле:
где $c$ – это нормировочный фактор c = = ${{\left( {Y_{{a - 1}}^{{\text{T}}}{{U}_{{a - {\text{1}}}}}U_{{a - 1}}^{{\text{T}}}{{Y}_{{a - {\text{1}}}}}} \right)}^{{ - 0.5}}}.$Шаг 3: определяются cчета ${{t}_{a}}$ как:
Шаг 4: вычисляются “спектральные” и “химические” нагрузки по следующим формулам [см. (9) и (10)]:
(10)
${{q}_{a}} = \frac{{Y_{{a - 1}}^{{\text{T}}}{{t}_{{a - 1}}}}}{{t_{{a - 1}}^{{\text{T}}}{{t}_{{a - 1}}}}}.$Шаг 5: новые остатки U и Y получаются вычитанием вклада главной компоненты: ${{U}_{a}} = {{U}_{{a - 1}}} - {{t}_{a}}p_{a}^{{\text{T}}},$ ${{Y}_{a}} = {{Y}_{{a - 1}}} - {{t}_{a}}q_{a}^{{\text{T}}}.$
Величины ${{U}_{{a - 1}}}$ и ${{Y}_{{a - 1}}}$ заменяются новыми значениями ${{U}_{a}},$ ${{Y}_{a}}$ и увеличиваем номер главной компоненты на единицу и возвращаемся на шаг 2. Итерационный алгоритм повторяется пока номер главной компоненты не достигнет максимальной величины.
Выход статистической модели можно получить как: $\hat {Y} = U{{\hat {\beta }}_{{{\text{ПЛС}}}}}.$
Метод проекций на латентные структуры с использованием функции ядра
Можно получить модель нелинейной регрессии в пространстве исходных входных переменных [32–34]. Для этого сделаем нелинейное преобразование входных переменных $U \in {{R}^{{N \times {{n}_{U}}}}}$ в пространстве признаков F; т.е. отобразим $\Phi {\text{:}}$ $U \in {{R}^{{N \times {{n}_{U}}}}} \to \Phi \left( U \right) \in F.$ Матрица Грама $K$ из компонентов $\Phi $ вычисляется как: $K = \Phi {{\Phi }^{{\text{T}}}} \in {{R}^{{N \times N}}}.$
Используя матрицу $\Phi $ отображенных входных данных и объединив шаги 2 и 3 предыдущего алгоритма, получаем алгоритм для (нелинейной) ядерной модели проекций на скрытые структуры – НПЛС. В общем виде алгоритм можно описать шагами, представленными ниже.
Шаг 1: вычисляется матрица входных данных $\Phi .$
Шаг 2: определяются cчета ${{t}_{a}}$ как:
где $с$ – это нормировочный фактор c = = ${{\left( {Y_{{a - 1}}^{{\text{T}}}{{\Phi }_{{a - {\text{1}}}}}\Phi _{{a - 1}}^{{\text{T}}}{{Y}_{{a - {\text{1}}}}}} \right)}^{{ - 0.5}}}.$Шаг 3: вычисляются “спектральные” и “химические” нагрузки [см. (12) и (13)]:
(12)
${{p}_{a}} = \frac{{{{\Phi }_{{a - 1}}}\Phi _{{a - 1}}^{{\text{T}}}{{t}_{a}}}}{{t_{{a - 1}}^{{\text{T}}}{{t}_{a}}}},$(13)
${{q}_{а}} = \frac{{Y_{{а - 1}}^{{\text{T}}}{{t}_{{а - 1}}}}}{{t_{{а - 1}}^{{\text{T}}}{{t}_{{а - 1}}}}}.$Шаг 4: новые остатки U и Y получаются вычитанием вклада главной компоненты: ${{\Phi }_{а}}\Phi _{а}^{{\text{T}}}$ = = $\left( {{{\Phi }_{{а - 1}}} - {{t}_{а}}p_{а}^{{\text{T}}}} \right)$${{\left( {{{\Phi }_{{а - 1}}} - {{t}_{а}}p_{а}^{{\text{T}}}} \right)}^{{\text{T}}}},$ ${{Y}_{а}} = {{Y}_{{а - 1}}} - {{t}_{а}}q_{а}^{{\text{T}}}.$
Величины ${{\Phi }_{{а - 1}}}\Phi _{{а - 1}}^{{\text{T}}}$ и ${{Y}_{{а - 1}}}$ заменяются новыми значениями ${{\Phi }_{а}}\Phi _{а}^{{\text{T}}},$ ${{Y}_{а}}$ и увеличиваем номер главной компоненты на единицу и возвращаемся на шаг 2. Итерационный алгоритм повторяется пока номер главной компоненты не достигнет максимальной величины.
В таком случае оценка ${{\hat {\beta }}_{{{\text{НПЛС}}}}}$ осуществляется как: ${{\hat {\beta }}_{{{\text{НПЛС}}}}} = Y{{({{T}^{T}}KY)}^{{ - 1}}}{{T}^{T}}Y{\text{,}}$ где K = Φ(U)Φ(U)T = = $\ker \left( {{{u}_{{\tilde {i}}}},{{u}_{{\tilde {j}}}}} \right).$ Функция ядра $\ker \left( {{{u}_{{\tilde {i}}}},\;{{u}_{{\tilde {j}}}}} \right)$ с ее $\left( {\tilde {i},\tilde {j}} \right)$-м элементом определяется формулами:
(14)
$\ker \left( {{{u}_{{\tilde {i}}}},{{u}_{{\tilde {j}}}}} \right) = {{\left( {u_{{\tilde {i}}}^{{\text{T}}}{{u}_{{\tilde {j}}}} + 1} \right)}^{{\text{p}}}},$(15)
$\ker \left( {{{u}_{{\tilde {i}}}},{{u}_{{\tilde {j}}}}} \right) = \exp \left( { - {{{{{\left\| {{{u}_{{\tilde {i}}}} - {{u}_{{\tilde {j}}}}} \right\|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left\| {{{u}_{{\tilde {i}}}} - {{u}_{{\tilde {j}}}}} \right\|}}^{2}}} {2{{{{\sigma }}}^{2}}}}} \right. \kern-0em} {2{{{{\sigma }}}^{2}}}}} \right).$Функция ядра [см. (14), (15)] зависит от выбора параметров p и ${{\sigma ,}}$ соответственно, и влияет на предсказательную способность метода на основе выбранной функции ядра.
Выход модели ВА, полученный методом НПЛС с функцией ядра, можно записать как $\hat {Y} = K{{\hat {\beta }}_{{{\text{НПЛС}}}}}.$ Для тестовой выборки оценка выходного параметра будет осуществляться в соответствии с функцией ядра, полученной на тестовой выборке: ${{\hat {Y}}_{{{\text{te}}{\text{.s}}}}} = {{K}_{{{\text{te}}{\text{.s}}}}}{{\hat {\beta }}_{{{\text{НПЛС}}}}}.$
АЛГОРИТМ РАСШИРЕНИЯ ВЫБОРКИ ИСТОРИЧЕСКИХ ДАННЫХ ПРИ ПОСТРОЕНИИ МОДЕЛЕЙ ДЛЯ ОЦЕНКИ ЦЕЛЕВОГО ПОКАЗАТЕЛЯ КАЧЕСТВА С ИСПОЛЬЗОВАНИЕМ ОПТИМИЗАЦИИ РОЯ ЧАСТИЦ
Метод оптимизации роя частиц (Particle swarm optimization algorithm – PSO) представляет собой алгоритм глобальной оптимизации, использующий имитацию социального поведения роя – группы некоторых объектов, применение которого не требует знания точного градиента оптимизируемой функции [35–37]. В алгоритме рой представляет собой множество частиц, которые на каждой итерации имеют две переменные состояния: ее текущее положение $u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}}$ и текущую скорость ${\text{v}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}},$ где t – счетчик итераций, их позиции на каждой итерации обновляются для достижения решения. На каждой итерации для каждой частицы вычисляется оптимальное значение целевой функции, новое положение частицы ${\text{pbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}},$ которое соответствует лучшему ее значению на итерации в этот момент, и ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$ – лучшие значения, которые получили все частицы на итерации в предыдущий момент. Частицы в рое устремляются к ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}},$ т.е. к лучшим значениям, обнаруженным в рое, с положением ${\text{pbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}.$ Скорость и положение частицы можно рассчитать следующим образом [22, 23]:
(16)
$\begin{gathered} {\text{v}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{{\text{t + 1}}}} = {{{\text{w}}}^{{\text{t}}}}{\text{v}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}} + 2{{{\text{r}}}_{1}}\left( {{\text{pbest}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}} - u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}}} \right) + \\ + \,\,2{{{\text{r}}}_{2}}\left( {{\text{gbest}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}} - u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}}} \right), \\ \end{gathered} $(17)
$\begin{gathered} u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{{\text{t + 1}}}} = u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}} + {\text{v}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{t}}}, \\ {\text{vi}}{{{\text{r}}}_{i}} = 1,2, \ldots ,{{n}_{U}},\,\,\,\,d = 1,2, \ldots ,{{n}_{{\text{p}}}}. \\ \end{gathered} $Новые значения частиц вычисляются после обновления скорости и положения, при необходимости также обновляются ${\text{pbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$ и ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}.$ Процедура выполняется до достижения заданного количества итераций и количества частиц в рое.
Шаги работы алгоритма для расширения обучающей выборки с использованием метода PSO представлены следующим образом:
Шаг 1: строится модель методом проекций на латентные структуры на основе заданной обучающей выборки и тестируется с помощью набора данных тестирования.
Шаг 2: формируется виртуальная выборка следующим образом:
(а) инициализация параметров PSO алгоритма: максимальное количество итераций ${{{\text{t}}}_{{{\text{max}}}}}$ и размер частиц в рое np;
(б) случайным образом генерируются начальные скорости каждой из частиц ${\text{v}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{1}}}$ и устанавливаются соответствующие векторы каждой частицы $u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{\text{1}}}$;
(в) вычисление минимальной среднеквадратичной ошибки качестве функции для нахождения наилучших значений – ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$;
(г) обновление скорости роя частиц ${\text{v}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{{\text{t + 1}}}}$ [см. (16)] и определение нового положения частицы $u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{{\text{t + 1}}}}$ [см. (17)];
(д) при достижении максимального количества итераций ${{{\text{t}}}_{{{\text{max}}}}}$ вывести оптимальные значения параметров ${\text{pbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$ и ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$.
Шаг 3: после достижения заданного на шаге 1 количества итераций ${{{\text{t}}}_{{{\text{max}}}}}$ исходный обучающий набор и полученный на шаге 2 (д) набор виртуальных данных ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$ объединяются в новый обучающий набор данных.
Шаг 4: расчет параметров модели для оценки показателя качества конечного продукта с использованием нового (расширенного) набора обучающих данных (совокупность данных обучающей выборки и данных ${\text{gbes}}{{{\text{t}}}_{{{\text{vi}}{{{\text{r}}}_{i}},d}}}$) и проверка модели на тестовой выборке.
Одной из проблем применения PSO является выбор значений параметров r1, r2, tmax, np. При их некорректных значениях могут наблюдаться значительные колебания $u_{{{\text{vi}}{{{\text{r}}}_{i}},d}}^{{}}$, что снижает эффективность применения метода оптимизации роя частиц.
ПРЕДЛАГАЕМЫЙ ПОДХОД К РЕШЕНИЮ ЗАДАЧИ В УСЛОВИЯХ МАЛОЙ ВЫБОРКИ ИСТОРИЧЕСКИХ ДАННЫХ С ИСПОЛЬЗОВАНИЕМ ФИЗИЧЕСКИ ОБОСНОВАННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Для решения проблемы малой обучающей выборки предлагается алгоритм ее расширения данными физически обоснованной математической модели массообменного технологического процесса, которая содержит уравнения фазового равновесия, материального и энергетического баланса. На основе такой модели можно получить данные технологического режима во всем диапазоне изменения качества продуктов.
В общем виде структуру физически обоснованной математической модели можно представить в виде системы уравнений на каждой j-ой ступени разделения для каждого i-го компонента:
Скорость химической реакции m, протекающей в реакционной зоне реакционно-ректификационной колонны, на j-ой тарелке определяется как:
где $\Delta n$ – изменение количества одного из веществ в реакции, кмоль; s – поверхность соприкосновения фаз, см2; $\Delta t$ – промежуток времени реакции, ч.Исходными данными для проведения расчетов на основе физически обоснованной математической модели являются состав перерабатываемого сырья и технологические параметры процесса, такие как температура, давление и расход подаваемого сырья, а также давление в колонне и расход нижнего продукта.
Зависимость коэффициентов активности компонентов в жидкости ${{\gamma }_{{L,i,j}}}$ от температуры и концентрации, согласно модели UNIQUAC [38, 39], может быть представлена в виде уравнений:
(18)
$\begin{gathered} \ln {{\gamma }_{{L,i,j}}} = \ln \frac{{{{\Phi }_{{i,j}}}}}{{{{x}_{{i,j}}}}} + \frac{z}{2}{{{\tilde {q}}}_{{i,j}}}\ln \frac{{{{\theta }_{{i,j}}}}}{{{{\Phi }_{{i,j}}}}} + {{l}_{{i,j}}} - \frac{{{{\Phi }_{{i,j}}}}}{{{{x}_{{i,j}}}}}\sum\limits_{h = 1}^{nc} {{{x}_{{h,j}}}} {{l}_{{h,j}}} + \\ + \,\,{{{\tilde {q}}}_{{i,j}}}\left( {1 - \ln \sum\limits_h {{{\theta }_{{h,j}}}{{\tau }_{{hi}}}} - \sum\limits_h {\frac{{{{\theta }_{{h,j}}}{{\tau }_{{hi}}}}}{{\sum\limits_k {{{\theta }_{{k,j}}}{{\tau }_{{kh}}}} }}} } \right), \\ \end{gathered} $(19)
${{\theta }_{{i,j}}} = {{{{{\tilde {q}}}_{{i,j}}}{{x}_{{i,j}}}} \mathord{\left/ {\vphantom {{{{{\tilde {q}}}_{{i,j}}}{{x}_{{i,j}}}} {\sum\limits_h {{{{\tilde {q}}}_{{h,j}}}{{x}_{{h,j}}}} }}} \right. \kern-0em} {\sum\limits_h {{{{\tilde {q}}}_{{h,j}}}{{x}_{{h,j}}}} }},\,\,\,{{\Phi }_{{i,j}}} = {{{{{\tilde {r}}}_{{i,j}}}{{x}_{{i,j}}}} \mathord{\left/ {\vphantom {{{{{\tilde {r}}}_{{i,j}}}{{x}_{{i,j}}}} {\sum\limits_h {{{{\tilde {r}}}_{{h,j}}}{{x}_{{h,j}}}} }}} \right. \kern-0em} {\sum\limits_h {{{{\tilde {r}}}_{{h,j}}}{{x}_{{h,j}}}} }},$(20)
$\begin{gathered} {{l}_{{i,j}}} = \frac{z}{2}\left( {{{{\tilde {r}}}_{{i,j}}} - {{{\tilde {q}}}_{{i,j}}}} \right) - \left( {{{{\tilde {r}}}_{{i,j}}} - 1} \right), \\ {{\tau }_{{hi}}} = \exp \left( { - \left[ {{{\left( {{{a}_{{hi}}} - {{a}_{{ii}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{a}_{{hi}}} - {{a}_{{ii}}}} \right)} {\hat {R}T}}} \right. \kern-0em} {\hat {R}T}}} \right]} \right), \\ \end{gathered} $Параметры бинарного взаимодействия взяты из [40] и сведены в табл. 1. Следует отметить, что параметры бинарного взаимодействия димеров изобутилена – 2,4,4-триметилпентена-1 и 2,4,4-триметилпентена-2, практически отсутствуют в литературных источниках. В данной системе н-бутен (NB) выступает в качестве инерта.
Таблица 1.
Параметры бинарного взаимодействия ${{\Lambda }_{{hi}}}$ для расчета коэффициента активности в реакционной системе МТБЭ
| Компонент 1 | Компонент 2 | |||
|---|---|---|---|---|
| МеОН | IB, NB | МТБЭ | DIB | |
| МеОН | 0 | 35.38 | 88.04 | –7.17 |
| IB, NB | –706.34 | 0 | –52.2 | 25.51 |
| МТБЭ | –468.76 | 24.63 | 0 | –17.13 |
| DIB | 706.38 | –19.69 | 45.75 | 0 |
Используемая физически обоснованная математическая модель технологического процесса содержит допущения и с термодинамической точки зрения является приближенной к реальному процессу. В связи с этим необходимо определить условия целесообразности (адекватности) применения такой модели в условиях неопределенности в алгоритме. Для оценки целесообразности применения физически обоснованной математической модели в алгоритме рассчитываются R2, MAE. А также предлагается рассчитывать площадь области пересечения распределений выходной переменной между ее значениями в расширенной обучающей и тестовой выборках: S – критерий эффективности расширения обучающей выборки.
Для расчета площади (S) области пересечения выходной переменной расширенной обучающей (ОВ) и тестовой выборок (ТВ) необходимо определить их функции распределения. Принадлежность данных выборок к каждому распределению проверяется по критерию согласия Колмогорова $K\left( y \right)$ [41], ${{D}_{{{\text{ext}}{\text{.s}}}}}$ = $\mathop {\sup }\limits_y \left| {F_{{{\text{ext}}{\text{.s}}}}^{*}\left( y \right) - {{F}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)} \right|,$ ${{D}_{{{\text{te}}{\text{.s}}}}}$ = = $\mathop {\sup }\limits_y \left| {F_{{{\text{te}}{\text{.s}}}}^{*}\left( y \right) - {{F}_{{{\text{te}}{\text{.s}}}}}\left( y \right)} \right|,$ где $F_{{{\text{ext}}{\text{.s}}}}^{*}\left( y \right),$ $F_{{{\text{te}}{\text{.s}}}}^{*}\left( y \right)$ – эмпирические функции распределения выходной переменной в расширенной ОВ и ТВ; ${{F}_{{{\text{ext}}{\text{.s}}}}}\left( y \right),$ ${{F}_{{{\text{te}}{\text{.s}}}}}\left( y \right)$ – их гипотетические функции распределения. В соответствии с этим критерием, функция распределения случайных величин $\sqrt {{{n}_{1}}} {{D}_{{{\text{ext}}{\text{.s}}}}},$ $\sqrt {{{n}_{2}}} {{D}_{{{\text{te}}{\text{.s}}}}}$ близка к $K\left( y \right).$ Поэтому вероятность того, что любая из случайных величин ${{D}_{{{\text{ext}}{\text{.s}}}}}$ окажется больше, чем 1.36/5.5, а ${{D}_{{{\text{te}}{\text{.s}}}}}$ больше, чем 1.36/3.87, равна 1 – 0.95 = 0.05.
После определения вида плотностей распределения ${{f}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)$ и ${{f}_{{{\text{te}}{\text{.s}}}}}\left( y \right)$ рассчитывается площадь области их пересечения. Для случая, когда ${{f}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)$ пересекается с ${{f}_{{{\text{te}}{\text{.s}}}}}\left( y \right)$ в точке с (при условии, что ${{f}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)$ и ${{f}_{{{\text{te}}{\text{.s}}}}}\left( y \right)$ имеют функции распределения логнормального распределения), S будет рассчитываться как [см. (21)]:
(21)
$S \propto \int\limits_a^с {{{f}_{{{\text{te}}{\text{.s}}}}}\left( y \right)} dy + \int\limits_с^b {{{f}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)} dy,$После преобразования имеем [см. (22)]:
(22)
$\begin{gathered} S \propto \frac{1}{{{{\sigma }_{{{\text{te}}{\text{.s}}}}}\sqrt {2\pi } }}\int\limits_a^c {\exp \left[ {{{ - {{{\left( {\ln y - {{\mu }_{{{\text{te}}{\text{.s}}}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {\ln y - {{\mu }_{{{\text{te}}{\text{.s}}}}}} \right)}}^{2}}} {2\sigma _{{{\text{te}}{\text{.s}}}}^{2}}}} \right. \kern-0em} {2\sigma _{{{\text{te}}{\text{.s}}}}^{2}}}} \right]dy} + \\ + \,\,\frac{1}{{{{\sigma }_{{{\text{ext}}{\text{.s}}}}}\sqrt {2\pi } }}\int\limits_с^b {\exp \left[ {{{ - {{{\left( {\ln y - {{\mu }_{{{\text{ext}}{\text{.s}}}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {\ln y - {{\mu }_{{{\text{ext}}{\text{.s}}}}}} \right)}}^{2}}} {2\sigma _{{{\text{ext}}{\text{.s}}}}^{2}}}} \right. \kern-0em} {2\sigma _{{{\text{ext}}{\text{.s}}}}^{2}}}} \right]dy} , \\ \end{gathered} $Для случая, когда ${{f}_{{{\text{te}}{\text{.s}}}}}\left( y \right)$ содержится в ${{f}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)$ (при условии, что ${{f}_{{{\text{ext}}{\text{.s}}}}}\left( y \right)$ и ${{f}_{{{\text{te}}{\text{.s}}}}}\left( y \right)$ имеют функции распределения логнормального распределения), S будет рассчитываться как [см. (23)]:
или [см. (24)]:
(24)
$S \propto \frac{1}{{{{\sigma }_{{{\text{te}}{\text{.s}}}}}\sqrt {2\pi } }}\int\limits_a^c {\exp \left[ {{{ - {{{\left( {\ln y - {{\mu }_{{{\text{te}}{\text{.s}}}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\left( {\ln y - {{\mu }_{{{\text{te}}{\text{.s}}}}}} \right)}}^{2}}} {2\sigma _{{{\text{te}}{\text{.s}}}}^{2}}}} \right. \kern-0em} {2\sigma _{{{\text{te}}{\text{.s}}}}^{2}}}} \right]dy} .$Если выражение для S не может быть найдено аналитически, то применяется численное интегрирование.
Предлагаемый алгоритм для построения ВА для оценки показателя качества конечного продукта с использованием физически обоснованной математической модели можно представить в виде описанных ниже шагов.
Шаг 1: для данного процесса с независимыми переменными $U \in {{R}^{{N \times {{n}_{U}}}}}$ и зависимой переменной $Y \in {{R}^{{N \times 1}}}$ определить верхнюю и нижнюю границы для зависимых переменных в обучающей и тестовой выборках.
Шаг 2: на основе исходных данных $U \in {{R}^{{N \times {{n}_{U}}}}}$ и $y \in {{R}^{{{{n}_{y}}}}}$ рассчитываются параметры модели $\hat {\beta }$ различными методами, например, методом проекций на латентные структуры.
Шаг 3: на основе физически обоснованной математической модели формируется расширенный набор данных при условии, если $\Delta {{\hat {E}}_{1}} \leqslant \Delta _{{{{{\hat {E}}}_{1}}}}^{{{\text{eff}}{\text{.th}}}},$ $\Delta {{\hat {E}}_{2}} \leqslant \Delta _{{{{{\hat {E}}}_{2}}}}^{{{\text{eff}}{\text{.th}}}}$ и $\Delta {{\hat {\Lambda }}_{{hi}}} \leqslant \Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}}$ (где $\Delta {{\hat {E}}_{1}},$ $\Delta {{\hat {E}}_{2}}$ – отклонения эффективности массопереноса по Мерфри объекта и модели на 6–28 тарелках и на 1–5 тарелках нижней ректификационной колонны: $\Delta {{\hat {E}}_{1}} = \left| {{{E}_{1}} - {{{\hat {E}}}_{1}}} \right|,$ $\Delta {{\hat {E}}_{2}}$ = $\left| {{{E}_{2}} - {{{\hat {E}}}_{2}}} \right|;$ $\Delta {{\hat {\Lambda }}_{{hi}}}$ – отклонения параметров бинарного взаимодействия компонентов объекта и модели: $\Delta {{\hat {\Lambda }}_{{hi}}}$ = $\left| {{{\Lambda }_{{hi}}} - {{{\hat {\Lambda }}}_{{hi}}}} \right|;$ $\Delta _{{{{{\hat {E}}}_{1}}}}^{{{\text{eff}}{\text{.th}}}},$ $\Delta _{{{{{\hat {E}}}_{2}}}}^{{{\text{eff}}{\text{.th}}}}$ и $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}}$ – пороговые значения отклонений, превышение которых при формировании расширенной обучающей выборки приводит к снижению точности построенной статистической модели).
Шаг 4: в исходные данные добавляются новые данные, полученные на Шаге 3, таким образом, получается расширенная обучающая выборка – выборка, содержащая в себе промышленные данные и данные физически обоснованной математической модели технологического процесса.
Шаг 5: нахождение новых параметров модели $\hat {\beta }.$
Шаг 6: адекватность полученного ВА проверяется на основе критериев точности модели [см. (5), (6)].
Шаг 8: конец.
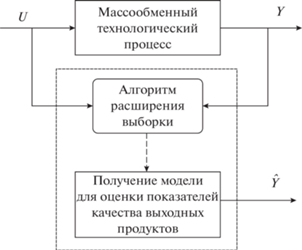
Иллюстрация предложенного подхода изображено на рис. 3.
Рис. 3.
Схема построения модели для оценки показателя качества конечных продуктов на основе расширения исходной малой обучающей выборки.
Преимущество предлагаемого алгоритма по сравнению с известными подходами заключается в возможности учета априорных знаний об исследуемом объекте. Построенные таким образом модели близки, в сущности, к моделям на основе “серого” ящика.
Следует отметить, что использование напрямую в реальном времени (on-line) физически обоснованной математической модели для оценки показателей качества конечного продукта часто на практике оказывается невозможным, так как эффективность массопереноса по Мерфри и параметры бинарного взаимодействия некоторых компонентов в смеси известны лишь приближенно, а состав сырья на каждом периоде управления не измеряется из-за отсутствия поточных анализаторов.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Оценка эффективности массопереноса по Мерфри на основе промышленных данных
Цель калибровки физически содержательной модели заключается в уменьшении ошибки между экспериментальными данными и данными моделирования при варьировании секционными эффективностями массопереноса по Мерфри на 6–28 тарелках и на 1–5 тарелках нижней ректификационной колонны в соответствии со следующими критериями (функциями невязки):
(25)
$\left\{ \begin{gathered} {{J}_{1}} = {{\left( {{{T}_{{{\text{TI}}1}}} - T_{{{\text{TI}}1}}^{'}} \right)}^{2}} + {{\left( {{{T}_{{{\text{TI2}}}}} - T_{{{\text{TI2}}}}^{'}} \right)}^{2}} \hfill \\ {{J}_{2}} = {{\left( {{{x}_{{{\text{МТБЭ}}}}} - x_{{{\text{МТБЭ}}}}^{'}} \right)}^{2}} + {{\left( {{{x}_{{{\text{MeOH}}}}} - x_{{{\text{MeOH}}}}^{'}} \right)}^{2}} + {{\left( {{{x}_{{{\text{DIB}}}}} - x_{{{\text{DIB}}}}^{'}} \right)}^{2}}, \hfill \\ \end{gathered} \right.$Результаты калибровки физически содержательной модели при различной эффективности массопереноса по Мерфри представлена на рис. 4.
Рис. 4.
Результаты определения эффективности массопереноса по Мэрфри при калибровке модели: (а) – зависимость функции невязки температур от ${{\hat {E}}_{1}};$ (б) – зависимость функции невязки температур от ${{\hat {E}}_{2}};$ (в) – зависимость функции невязки концентраций компонентов от ${{\hat {E}}_{1}};$ (г) – зависимость функции невязки концентраций компонентов от ${{\hat {E}}_{2}}.$

Из представленного рис. 4 можно сделать вывод, что минимальное значение функции невязки по содержанию метанола, метил-трет-бутилового эфира и димеров изобутилена в конечном продукте достигается при ${{\hat {E}}_{1}} = 0.5$ и ${{\hat {E}}_{2}} = 0.8.$
Оценка сходимости результатов расчета и экспериментальных данных с промышленной установки производства МТБЭ приведена в табл. 2.
Таблица 2.
Оценка сходимости результатов расчета при ${{\hat {E}}_{1}} = 0.5$ и ${{\hat {E}}_{2}} = 0.8$ с промышленной данными
| Технологический параметр | Экспериментальные данные | Данные моделирования | Относительная ошибка δ, % |
|---|---|---|---|
| TI2, °С | 66.78 | 68.51 | 2.60 |
| TI1, °С | 138.64 | 136.18 | 1.81 |
| MeOH, мас. % | 0.28 | 0.29 | 3.45 |
| MTBE, мас. % | 98.18 | 99.25 | 1.08 |
| DIB, мас. % | 0.008 | 0.0084 | 4.76 |
Относительная ошибка между экспериментальными данными и данными моделирования основных показателей технологического режима по качеству и расходу продуктов разделения не превышает 5%, что подтверждает пригодность физически содержательной модели (табл. 2) для ее дальнейшего применения.
Целесообразность применения алгоритма расширения обучающей выборки
На шаге 3 предлагаемого алгоритма для определения пороговых значений отклонений $\Delta {{\hat {E}}_{1}},$ $\Delta {{\hat {E}}_{2}}$ и $\Delta {{\hat {\Lambda }}_{{hi}}}$ использовалась откалиброванная физически обоснованная математическая модель исследуемого процесса, с допущением о ее соответствии реальному объекту, и установлены границы параметрической неопределенности эффективности массопереноса по Мерфри $\Delta _{{{{{\hat {E}}}_{1}}}}^{{{\text{eff}}{\text{.th}}}} = 0.3$ и $\Delta _{{{{{\hat {E}}}_{2}}}}^{{{\text{eff}}{\text{.th}}}} = 0.1.$ Для определения $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}}$ оценивался % снижения R2 (δR2) для диапазона параметрической неопределенности $\Delta {{\hat {\Lambda }}_{{hi}}} \in \left[ {0.1,0.4} \right]$ относительно базового случая, когда модель полностью соответствует объекту, т.е. относительно $\Delta {{\hat {\Lambda }}_{{hi}}} = 0$ (табл. 3). Если потери δR2 превышали 5%, то для соответствующих параметров бинарного взаимодействия компонентов системы назначалось пороговое значения отклонения $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}}.$
Таблица 3.
Влияние изменения диапазона параметрической неопределенности параметров бинарного взаимодействия на R2, MAE и S
| $\Delta {{\hat {\Lambda }}_{{hi}}}$ | ПЛС | Граница интервала параметрической неопределенности | ||||
|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | ||
| $\Delta {{\hat {\Lambda }}_{{{\text{MTBE,IB}}}}}$ | R2 | 0.5346 | 0.5145 | 0.5104 | 0.5081 | 0.4235 |
| MAE | 0.0886 | 0.0929 | 0.0931 | 0.0930 | 0.1309 | |
| S | 0.5731 | 0.5339 | 0.5276 | 0.5205 | 0.5122 | |
| δR2, % | 3.76 | 4.53 | 4.96 | 20.78 | ||
| $\Delta {{\hat {\Lambda }}_{{{\text{MTBE,MeOH}}}}}$ | R2 | 0.5346 | 0.5135 | 0.5085 | 0.5065 | 0.5048 |
| MAE | 0.0886 | 0.0931 | 0.0935 | 0.0930 | 0.0936 | |
| S | 0.5731 | 0.5372 | 0.5310 | 0.5239 | 0.5157 | |
| δR2, % | 3.95 | 4.88 | 5.26 | 5.57 | ||
| $\Delta {{\hat {\Lambda }}_{{{\text{MTBE,DIB}}}}}$ | R2 | 0.5346 | 0.5310 | 0.5074 | 0.5028 | 0.5017 |
| MAE | 0.0886 | 0.0898 | 0.0929 | 0.0941 | 0.0939 | |
| S | 0.5731 | 0.5319 | 0.5247 | 0.5163 | 0.5060 | |
| δR2, % | 0.67 | 5.09 | 5.95 | 6.15 | ||
| $\Delta {{\hat {\Lambda }}_{{{\text{MeOH,DIB}}}}}$ | R2 | 0.5346 | 0.5073 | 0.5063 | 0.5028 | 0.5016 |
| MAE | 0.0886 | 0.0929 | 0.0939 | 0.0941 | 0.0939 | |
| S | 0.5731 | 0.5383 | 0.5319 | 0.5247 | 0.5163 | |
| δR2, % | 5.11 | 5.29 | 5.95 | 6.17 | ||
В результате определены наиболее чувствительные параметры бинарного взаимодействия компонентов системы: $\Delta {{\hat {\Lambda }}_{{{\text{DIB,MeOH}}}}},$ $\Delta {{\hat {\Lambda }}_{{{\text{MeOH,IB}}}}},$ $\Delta {{\hat {\Lambda }}_{{{\text{MeOH,MTBE}}}}}$ и $\Delta {{\hat {\Lambda }}_{{{\text{DIB,MTBE}}}}}$ с $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0,$ т.е. значения этих параметров необходимо знать точно, чтобы использовать данные физически обоснованной модели для расширения обучающей выборки.
Результаты критериев точности модели для оценки показателей качества конечного продукта и критерий эффективности расширения обучающей выборки при различных отклонениях $\Delta {{\hat {\Lambda }}_{{hi}}}$ представлены в табл. 3.
Из табл. 3 видно, что с увеличением диапазона параметрической неопределенности параметров бинарного взаимодействия точность модели для оценки метанола в МТБЭ снижается (согласно R2 и MAE), также снижаются и значения S. Таким образом установлено, что физически обоснованную математическую модель технологического процесса в алгоритме целесообразно применять при условии, что для ${{\hat {\Lambda }}_{{{\text{MTBE,IB}}}}}$ значение $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0.3;$ для компонентов системы: ${{\hat {\Lambda }}_{{{\text{MTBE,MeOH}}}}},$ ${{\hat {\Lambda }}_{{{\text{MeOH,DIB}}}}}$ пороговые значения совпадают и равны $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0.2;$ для параметров бинарного взаимодействия $\Delta {{\hat {\Lambda }}_{{{\text{MTBE}},{\text{DIB}}}}}$ значение $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0.1.$
Сравнительный анализ методов построения модели для оценки концентрации метанола в конечном продукте в условиях малой обучающей выборки
Проводится сравнение предлагаемого алгоритма расширения обучающей выборки с известными подходами построения моделей для оценки показателей качества конечных продуктов в условиях малых обучающих выборок.
Обучение выполняется с использованием известных (часто применяемых в реальных условиях [6]) методов и их сочетаний: метода проекций на латентные структуры (ПЛС), метода проекций на латентные структуры и метода складного ножа (ПЛС и СН), метода проекций на латентные структуры и бутстрэп метода (ПЛС и БМ) (сформировано 50 бутстрэп выборок, объем каждой выборки составил 80% от исходной), а также нелинейного метода проекций на латентные структуры (НПЛС) с функцией ядра (14) и нейронной сетью (НС) прямого распространения с двумя скрытыми слоями и пятью нейронами в каждом слое, т.е. (5 5). Следует отметить, что количество нейронов в слоях определялось таким образом, чтобы избежать переобучения.
В табл. 4 приведен сравнительный анализ наиболее известных методов на ${{N}_{{{\text{te}}{\text{.s}}}}} = 18$ до и после добавления данных в исходную обучающую выборку.
Таблица 4.
R2 и MAE, полученные на тестовой выборке с использованием статистических методов до и после добавления данных вспомогательной выборки
| Метод | Критерий | Размер вспомогательной выборки | ||||
|---|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | ||
| ПЛС | R2 | 0.3992 | 0.4202 | 0.4296 | 0.4299 | 0.4303 |
| MAE | 0.1389 | 0.1346 | 0.1309 | 0.1306 | 0.1259 | |
| ПЛС и СН | R2 | 0.4574 | 0.4791 | 0.5983 | 0.6023 | 0.6062 |
| MAE | 0.1355 | 0.1287 | 0.1038 | 0.1007 | 0.1002 | |
| ПЛС и БМ | R2 | 0.5333 | 0.6051 | 0.6299 | 0.6397 | 0.6429 |
| MAE | 0.1197 | 0.1035 | 0.0959 | 0.0930 | 0.0920 | |
| НПЛС | R2 | 0.4170 | 0.5236 | 0.5275 | 0.5359 | 0.5425 |
| MAE | 0.1245 | 0.1227 | 0.1120 | 0.1107 | 0.1108 | |
| Нейронная сеть (НС) | R2 | 0.4240 | 0.5569 | 0.5140 | 0.5165 | 0.5324 |
| MAE | 0.1556 | 0.1236 | 0.1405 | 0.1287 | 0.1085 | |
| ПЛС и PSO | R2 | 0.4496 | 0.5250 | 0.5274 | 0.4254 | 0.2852 |
| MAE | 0.1389 | 0.1064 | 0.1126 | 0.1377 | 0.1546 | |
Следует отметить, что значения R2 и MAE, полученные с использованием представленных в табл. 4 методов, имеют определенное сходство. До добавления данных вспомогательной выборки значения R2 не превышают 0.53; т.е. результаты расчетов показывают низкую точность полученных моделей для оценки МеОН в конечном продукте.
В свою очередь учет априорных знаний о массообменном технологическом процессе позволяет увеличить точность моделей для оценки показателей качества конечных продуктов, а также повысить эффективность других методов, что дает особое преимущество предлагаемого подхода в сравнении с известными методами, например с PSO. Значение MAE модели для оценки концентрации метанола в конечном продукте, построенной с использованием ПЛС и бутстрэп метода, снижается на 23% (рис. 5).
Рис. 5.
Значения R2 и MAE модели для оценки содержания концентрации метанола в МТБЭ на тестовой выборке.

Использование метода PSO для расширения обучающей выборки на промышленных данных на первоначальном этапе (когда размер вспомогательной выборки не превышает размер обучающей выборки) позволяет увеличить R2 на ((0.5250 – 0.4496)/0.5250) × 100 ≈ 14%, однако, при повышении размера вспомогательной выборки наблюдается существенное ухудшение критериев точности модели (до 36% от исходного набора данных и до 55% в сравнении с моделью, полученной ПЛС и БМ по критерию R2). Это связано с тем, что нет учета физически-химических особенностей технологического процесса.
Расширение обучающей выборки с использованием физически обоснованной математической модели процесса позволяет учитывать данные (заполнить пропуски в данных) технологического режима на всем диапазоне изменения качества конечного продукта (рис. 6а и рис. 6б).
Рис. 6.
Экспериментальные данные концентрации метанола в конечном продукте после расширения обучающей выборки (а) – значения выходной переменной в расширенной и тестовой выборках частично перекрываются; (б) – значения выходной переменной тестовой выборки содержатся в расширенной обучающей выборке.

Изменение площади области пересечения распределений значений выходной переменной в расширенной обучающей и тестовой выборках представлены в табл. 5.
Таблица 5.
Площадь области пересечения обучающей и тестовой выборок до и после добавления данных вспомогательной выборки
| Площадь области пересечения выборок | Расширение обучающей выборки | ||||
|---|---|---|---|---|---|
| 0 | 10 | 20 | 30 | 40 | |
| S | 0.56 | 0.88 | 0.89 | 0.90 | 0.98 |
Использование физически обоснованной математической модели увеличивает площадь области пересечения значений выходной переменной в расширенной обучающей и тестовой выборках до ((0.98 – 0.56)/0.98) × 100 ≈ 43% (табл. 5).
Результаты функционирования разработанных моделей до и после расширения исходной выборки представлены на рис. 7а и рис. 7б.
Рис. 7.
Оценка метанола в конечном продукте до и после расширения обучающей выборки (а) – до расширения обучающей выборки; (б) – после расширения обучающей выборки.
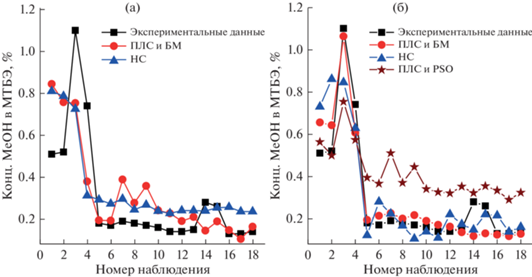
Как показано на рис. 7б расширение исходной обучающей выборки с использованием физически обоснованной математической модели повышает точность оценки показателя качества конечного продукта. После расширения обучающей выборки данными вспомогательной выборки размером 40 (табл. 4) эффективность использования метода проекций на латентные структуры совместно с бутстрэп методом для нахождения параметров ВА увеличилась на ((0.5333 – 0.6429)/0.5333) × 100 ≈ 21% и ((0.1197 – 0.0920)/0.1197) × 100 ≈ 23% по R2 и MAE, соответственно. Использование метода ПЛС совместно с оптимизацией роя частиц для расширения исходной выборки не позволяет улучшить точность ВА, т. к. данные вспомогательной выборки не учитывают физико-химические особенности процесса (рис. 7б).
ЗАКЛЮЧЕНИЕ
Предложен алгоритм расширения обучающей выборки на основе физически обоснованной математической модели ректификационной колонны массообменного технологического процесса, позволяющий повысить точность ВА для оценки показателя качества конечного продукта и эффективность традиционных методов при построении модели (определении параметров ВА). Предлагаемый алгоритм протестирован на промышленном массообменном химико-технологическом процессе производства МТБЭ.
Определены условия применения физически обоснованной математической модели в условиях параметрической неопределенности параметров бинарного взаимодействия компонентов системы. Некоторые из них должны быть известны практически точно, т.е. $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0$ для параметров бинарного взаимодействия: $\Delta {{\hat {\Lambda }}_{{{\text{DIB,MeOH}}}}},$ $\Delta {{\hat {\Lambda }}_{{{\text{MeOH,IB}}}}},$ $\Delta {{\hat {\Lambda }}_{{{\text{MeOH,MTBE}}}}};$ для $\Delta {{\hat {\Lambda }}_{{{\text{MTBE}},{\text{DIB}}}}}$ и ${{\hat {\Lambda }}_{{{\text{MTBE,IB}}}}}$ пороговые значения равны $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0.1$ и $\Delta _{{{{{\hat {\Lambda }}}_{{hi}}}}}^{{{\text{eff}}{\text{.th}}}} = 0.3,$ соответственно.
Применение физически обоснованной математической модели при построении ВА позволяет заполнить пропуски в данных на всем диапазоне изменения качества конечного продукта (значение критерия расширения обучающей выборки S повышается до 43%).
Точность ВА для оценки концентрации метанола в конечном продукте, полученного предложенным подходом, на 55% выше точности ВА, полученным на основе расширения выборки методом оптимизации роя частиц. Использование предлагаемого алгоритма позволяет повысить эффективность существующих методов построения статистических моделей. При разработке ВА методом проекций на латентные структуры совместно с бутстрэп методом точность модели увеличилась на 21 и 23% по критериям R2 и MAE после расширения обучающей выборки данными вспомогательной выборки размером 40. Учет априорных знаний о процессе дает существенное преимущество алгоритма перед другими методами расширения обучающей выборки.
Исследование выполнено при частичной финансовой поддержке РФФИ и Государственного фонда естественных наук Китая в рамках научного проекта № 21-57-53005
ОБОЗНАЧЕНИЯ
| ББФ | бутан-бутиленовая фракция |
| ББФотр | отработанная бутан-бутиленовая фракция |
| МеОН | метанол |
| МТБЭ, MTBE | метил-трет-бутиловый эфир |
| IB | изобутилен |
| DIB | диизобутен |
| 2,4,4-TMП-1 | 2,4,4-триметилпентен-1 |
| 2,4,4-ТМП-2 | 2,4,4-триметилпентен-2 |
| NB | н-бутен |
| N | количество наблюдений |
| ${{n}_{U}}$ | количество входных переменных |
| ${{n}_{Y}}$ | количество выходных переменных |
| U | матрица входных переменных $U \in {{R}^{{N \times {{n}_{U}}}}}$ |
| Y | вектор выходной переменной $Y \in {{R}^{{N \times 1}}}$ |
| $\beta $ | вектор параметров модели для оценки показателя качества конечного продукта $\beta \in {{R}^{{{{n}_{U}} \times 1}}}$ |
| $\hat {\beta }$ | вектор оцененных параметров модели для оценки показателя качества конечного продукта |
| $\hat {Y}$ | значение выходной переменной, полученное на основе модели для оценки показателя качества конечного продукта, мас. % |
| $\bar {Y}$ | среднее значение наблюдаемой выходной переменной, мас. % |
| Р | матрица нагрузок U |
| Q | матрица нагрузок Y |
| W | матрица весов U |
| $\bar {U}$ | вектор средних значений матрицы U |
| a | значение главной компоненты |
| A | максимальное значение главной компоненты |
| w | вектор взвешенных нагрузок |
| c | это нормировочный фактор |
| t | вектор счетов |
| p | “спектральные” нагрузки |
| q | “химические” нагрузки |
| R2 | коэффициент детерминации |
| MAE | абсолютная средняя ошибка |
| K | матрица Грама, $K = \Phi {{\Phi }^{{\text{T}}}} \in {{R}^{{N \times N}}}$ |
| $\Phi $ | матрица отображенных входных данных |
| НПЛС | нелинейная ядерная модель проекций на скрытые структуры |
| $\ker $ | функция ядра |
| p, ${{\sigma }}$ | параметры функции ядра |
| ${\text{v}}$ | скорость движения частицы |
| t | счетчик итераций |
| pbest | новое положение частицы |
| gbest | лучшее значение частицы |
| ${\text{w}}$ | инерционный вес |
| L, V | поток жидкости и пара, соответственно, кмоль/ч |
| x, y | концентрация компонента в жидкой фазе и паровой фазе, соответственно, кмоль/кмоль |
| $y{\text{*}}$ | равновесная концентрация компонента в паровой фазе, кмоль/кмоль |
| F | расход сырья, кмоль/ч |
| $\gamma $ | коэффициент активности компонента в жидкой фазе |
| ${{p}^{0}}$ | парциальное давление компонента, кПа |
| P | общее давление в системе, кПа |
| E | эффективность массопереноса по Мерфри |
| h, H | энтальпия жидкости и пара, соответственно, кДж/кмоль |
| nc | общее количество компонентов в системе |
| nt | общее количество тарелок в ректификационной колонне |
| m | номер реакции |
| r | количество реакций |
| $\nu $ | стехиометрический коэффициент компонента в реакции |
| R | скорость реакции, кмоль/см2 · ч |
| $\varepsilon $ | объем реакционной смеси, м3 |
| $\Delta n$ | изменение количества одного из веществ в реакции, кмоль |
| $\Delta t$ | промежуток времени реакции, ч |
| s | поверхность соприкосновения фаз, см2 |
| $\tilde {r},$$\tilde {q}$ | UNIQUAC параметры объема и площади чистого компонента |
| $\tau $ | приведенный параметр |
| $\hat {R}$ | газовая постоянная, Дж/(моль · K) |
| z | координационное число |
| $\hat {E}$ | эффективность массопереноса по Мерфри |
| ${{\Lambda }_{{hi}}}$ | параметры бинарного взаимодействия |
| J | функция невязки |
| T | значения экспериментальных температур, °С |
| $T_{{}}^{'}$ | значения расчетных температур, °С |
| K(y) | критерий согласия Колмогорова |
| F*(y) | эмпирическая функция распределения выходной переменной |
| F(y) | гипотетическая функция распределения |
| c | точка пересечения |
| f(y) | плотность распределения выходной переменной |
| S | площадь области пересечения плотностей распределения |
ИНДЕКСЫ
Список литературы
Vairo T., Reverberi A.P., Bragatto P.A., Milazzo M.F., Fabiano B. Predictive model and soft sensors application to dynamic process operative control // Chem. Eng. Transaction. 2021. V. 86. P. 535–540.
Jiang Y., Yin Sh., Dong J., Kaynak O. A Review on soft sensors for monitoring, control, and optimization of industrial processes // IEEE Sensors J. 2021. V. 21. № 11. P. 12868–12881.
Shokry A., Vicente P., Escudero G., Pérez-Moya M., Graells M., Espuña A. Data-driven soft-sensors for online monitoring of batch processes with different initial conditions // Comput. & Chem. Eng. 2018. V. 118. P. 159–179.
Lin B., Recke B., Knudsen J.K.H., Jørgensen S.B. A systematic approach for soft sensor development // Comput. & Chem. Eng. 2007. V. 31. I. 5–6. P. 419–425.
Niño-Adan I., Landa-Torres I., Manjarres D., Portillo E., Orbe L. Soft-sensor for class prediction of the percentage of pentanes in butane at a debutanizer column // Sensors. 2021. V. 21. P. 3991.
Kadlec P., Gabrys B., Strandt S. Data-driven soft sensors in the process industry // Comput. Chem. Eng. 2009. V. 33. P. 759–814.
Fortuna L., Graziani S., Rizzo A., Xibilia M.G. Soft sensors for monitoring and control of industrial processes. London, U.K.: Springer-Verlag, 2007.
Graziani S., Xibilia M.G. On the use of correlation analysis in the estimation of finite-time delay in Soft Sensors design // IEEE International Instrumentation and Measurement Technol. Conference. 2021. P. 1–6.
Ge Zh., Huang B. Song Zh. Mixture semisupervised principal component regression model and soft sensor application // AIChE J. 2014. V. 60. I. 2. 533–545.
Sun K., Tian P., Qi H., Ma F., Yang G. An improved normalized mutual information variable selection algorithm for neural network based soft sensors // Sensors. 2019. V. 19. № 24. P. 5368.
Graziani S., Xibilia M.G. Development and analysis of deep learning architectures (Deep learning for soft sensor design). Cham, Switzerland: Springer, ch. 2, 2020.
Sun Q., Ge Zh. A Survey on deep learning for data-driven soft sensors // IEEE Transactions on Ind. Informatics. 2021. V. 17. № 9. P. 5853–5866.
Ge Zh., Song Zh., Kano M. External analysis-based regression model for robust soft sensing of multimode chemical processes // AIChE J. 2014. V. 60. I. 1. P.136–147.
Bakirov R., Gabrys B., Fay D. Multiple adaptive mechanisms for data-driven soft sensors // Comput. & Chem. Eng. 2017. V. 96. P. 42–54.
Zhu J., Ge Z., Song Z., Gao F. Review and big data perspectives on robust data mining approaches for industrial process modeling with outliers and missing data // Annu. Rev. Control. 2018. V. 46. P. 107–133.
Xie R., Jan N.M., Hao K., Chen L., Huang B. Supervised variational autoencoders for soft sensor modeling with missing data // IEEE Transactions on Ind. Informatics. 2019. V. 16. I. 4. P. 2820–2828.
Kaneko H., Funatsu K. Classification of the degradation of soft sensor models and discussion on adaptive models // AIChE J. 2013. V. 59. I. 7. P. 2339–2347.
Hsiao Y.-D., Kang J.-L., Wong D.S.-H. Development of robust and physically interpretable soft sensor for industrial distillation column using transfer learning with small datasets // Processes. 2021. V. 9. P. 667.
Napoli G., Xibilia M.G. Soft Sensor design for a topping process in the case of small datasets // Comput. & Chem. Eng. 2011. V. 35. I. 11. P. 2447–2456.
Chang C.-J., Li D.-C., Huang Y.-H., Chen C.-C. A novel gray forecasting model based on the box plot for small manufacturing data sets // Applied Math. and Comp. 2015. V. 265. P. 400–408.
Andrijić Ž.U., Cvetnić M., Bolf N. Soft sensor models for a fractionation reformate plant using small and bootstrapped data sets // Brazilian J. Chem. Eng. 2018. V. 35. P. 745–756.
Urhan A., Ince N.G., Bondy R., Alakent B. Soft-sensor design for a crude distillation unit using statistical learning methods. In Comp. Aided Chem. Eng. 2018. V. 44. P. 2269–2274.
Chen Z.-S., Zhu B., He Y.-L., Yu L.-A. A PSO based virtual sample generation method for small sample sets: Applications to regression datasets // Eng. applications of artificial intelligence. 2017. V. 59. P. 236–243.
He Y.L., Wang P.J., Zhang M.Q., Zhu Q.X., Xu Y. A novel and effective nonlinear interpolation virtual sample generation method for enhancing energy prediction and analysis on small data problem: A case study of ethylene industry // Energy. 2018. V. 147. P. 418–427.
Di Girolamo M., Lami M., Marchionna M., Pescarollo E., Tagliabue L., Ancillotti F. Liquid-phase etherification/dimerization of isobutene over sulfonic acid resins // Ind. Eng. Chem. Res. 1997. V. 36. P. 4452–4458.
Rehfinger A., Hoffmann U. Kinetics of methyl-tertiary-butyl ether liquid phase synthesis catalyzed by ion exchange resin intrinsic rate expression in liquid phase activities // Chem. Eng. Sci. 1990. V. 45. № 6. P. 1605–1617.
Эсбенсен К. Анализ многомерных данных. Избранные главы. Барнаул: Изд-во Алт. ун-та, 2003.
Wold S. PLS-regression: a Basic Tool of Chemometrics / S. Wold, M. Sjostrom, L. Eriksson // Chemometrics and Intelligent Laboratory System. 2001. V. 58. P. 109–130.
De Jong S. SIMPLS: An Alternative Approach to Partial Least Squares Regression // Chemometrics and Intelligent Laboratory Systems. 1993. V. 18. P. 251–263.
Van Kollenburg G.H., Van Es J., Gerretzen J., Lanters H., Bouman R., Koelewijn W., Davies A.N., Buydens L.M.C., Van Manen H.-J., Jansen J.J. Understanding chemical production processes by using PLS path model parameters as soft sensors // Comput. & Chem. Eng. 2020. V. 139. P. 1–8.
Kaneko H., Arakawa M., Funatsu K. Development of a new soft sensor method using independent component analysis and partial least squares // AIChE J. 2009. V. 55. I. 1. P. 87–98.
Jin H., Chen X., Yang J., Wu L. Adaptive soft sensor modeling framework based on just-in-time learning and kernel partial least squares regression for nonlinear multiphase batch processes // Comput. & Chem. Eng. 2014. V. 71. P. 77–93.
Si Y., Wang Y., Zhou D. Key-performance-indicator-related process monitoring based on improved kernel partial least squares // IEEE Transactions on Industrial Electronics. 2020. V. 68. № 3. P. 2626–2636.
Deng X., Chen Y., Wang P., Cao Y. Soft sensor modeling for unobserved multimode nonlinear processes based on modified kernel partial least squares with latent factor clustering. IEEE Access. 2020. V. 8. P. 35864–35872.
Schwaab M., Biscaia E.C., Monteiro J.L., Pinto J.C. Nonlinear parameter estimation through particle swarm optimization // Chem. Eng. Sci. 2008. V. 63. I. 6. P. 1542–1552.
Ourique C.O., Biscaia E.C., Pinto J.C. The use of particle swarm optimization for dynamical analysis in chemical processes // Comput. & Chem. Eng. 2002. V. 26. Is. 12. P. 1783–1793.
Prata D.M., Schwaab M., Lima E.L., Pinto J.C. Nonlinear dynamic data reconciliation and parameter estimation through particle swarm optimization: Application for an industrial polypropylene reactor // Chem. Eng. Sci. 2009. V. 64. I. 18. P. 3953–3967.
Fredenslund A., Jones R.L., Prausnitz J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures // AIChE J. 1975. V. 21. № 6. P. 1086–1099.
Abrams D.S., Prausnitz J.M. Statistical thermodynamics of liquid mixtures: a new expression for the excess Gibbs energy of partly or completely miscible systems // AIChE J. 1975. V. 21. № 1. P. 116–128.
Sundmacher K., Uhde G., Hoffmann U. Multiple reactions in catalytic distillation processes for the production of the fuel oxygenates MTBE and TAME: Analysis by rigorous model and experimental validation // Chem. Eng. Sci. 1999. V. 54. P. 2839–2847.
Об эмпирическом определении закона распределения / Под ред. Прохорова Ю.В. М.: Наука, 1986.
Samotylova S.A., Torgashov A.Y. Developing a soft sensor for MTBE process based on a small sample // Automation and Remote Control. 2020. V. 81. № 11. P. 2132–2142.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии