Теоретические основы химической технологии, 2022, T. 56, № 4, стр. 496-502
Идеальный многокомпонентный разделительный каскад
О. Е. Александров *
Кафедра технической физики Уральского Федерального Университета
Екатеринбург, Россия
* E-mail: aleks.o.e@mail.ru
Поступила в редакцию 04.06.2021
После доработки 28.01.2022
Принята к публикации 15.02.2022
- EDN: KEBATO
- DOI: 10.31857/S0040357122030010
Аннотация
Предложена схема для расчета противоточного каскада и записаны уравнения сохранения для концентрации и потоков в разделительном каскаде на примере трехкомпонентного разделения. Получены дифференциальные уравнения для несмешивающего (идеального) противоточного каскада.
ВВЕДЕНИЕ
Разделение смесей изотопов, содержащих более двух компонентов, актуальная задача современных технологических процессов [1–3]. Эффективное разделение многокомпонентных смесей требует теоретического осмысления процесса для отыскания оптимальных способов организации.
Важной частью организации процесса разделения является построение разделительного каскада. Это обусловлено сравнительно малым обогащением на единичном разделительном элементе. Для получения желаемой степени обогащения, смесь необходимо подвергнуть разделению многократно. Многократное разделение реализуется соединением нескольких разделительных устройств, такое соединение называют каскадом. Основной задачей конструирования каскада является достижение максимальной эффективности, т.е. получение нужной величины обогащения с помощью минимального числа разделительных элементов.
В настоящее время есть публикации, авторы которых отвергают саму возможность существования идеального каскада для разделения многокомпонентных смесей [4].
Цель статьи – разработка теории идеального (несмешивающего) каскада для разделения многокомпонентных смесей.
ПРОБЛЕМЫ СУЩЕСТВУЮЩЕЙ ТЕОРИИ
Теория разделительных каскадов для многокомпонентных смесей рассматривает, в основном, классическую схему бинарного противоточного каскада с дополнительным отбором [5–8]. Это обусловлено тем, что разделение многокомпонентных смесей ведется с помощью устройств бинарного разделения, например газовых центрифуг, унаследованных от бинарных разделительных каскадов.
Специальные схемы многокомпонентных каскадов, практически, не рассматриваются. Это серьезное упущение, поскольку изучение разделения многокомпонентных смесей в устройствах бинарного разделения показало, что такие устройства не могут обогатить смесь трех и более компонентов до произвольной концентрации. Для получения произвольного обогащения эти устройства приходится снабжать дополнительными отборами, т.е. превращать их из бинарных разделительных устройств – один вход-питание и два выхода-отбора, в многокомпонентные разделительные устройства – один вход-питание и три или более выхода-отбора [5, 6]. Логичным представляется переход к схемам соединения многокомпонентных разделительных устройств и обобщение теории бинарных каскадов. Такой подход всё ещё остаётся мало изученным [9–11].
Таким образом, построение теории противоточного каскада для многокомпонентного разделения и отыскание идеального (несмешивающего) каскада является актуальной задачей. Далее рассматривается разделение смеси трех компонентов, но выводы могут быть обобщены на произвольное число компонентов смеси.
ОСНОВНЫЕ ПОСТУЛАТЫ
Разделительный элемент. Теория бинарного разделения начинается с постулирования существования разделительного элемента [12] с одним входом-питанием и двумя выходами-отборами, способного изменять концентрацию смеси в отборах, относительно концентрации смеси в питании, рис. 1а.
Рис. 1.
Разделительный элемент: (a) – бинарный, (б) – трехкомпонентный, (в) – квазибинарный разделительный элемент. l – поток питания разделительного элемента, θ1l, θ2l и θ3l – потоки отбора, С(0), С(1), С(2) и С(3) – концентрации питания, первого, второго и третьего отбора, соответственно.
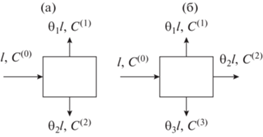
Для бинарного разделительного элемента (см. рис. 1а) вводится коэффициент разделения q:
Для многокомпонентного разделения так же необходимо дать определение разделительного элемента. Разделительный элемент должен допускать построение каскада, способного разделить исходную смесь до любых заданных концентраций любого из компонентов. Это означает, что разделительный элемент должен осуществлять обогащение компонента смеси при любых концентрациях этого компонента в смеси. Известно, что основная современная технология бинарного разделения – центрифуга – для компонента смеси, масса молекулы которого больше минимальной массы молекул смеси и меньше максимальной массы молекул смеси, не может обогащать смесь при произвольной концентрации. Или для этого требуется организация дополнительного отбора [13–21].
Поэтому в качестве элементарного разделительного элемента необходимо постулировать элемент с одним входом-питанием и числом отборов, равным числу компонентов смеси, см. рис. 1б. Без потери общности, можно полагать, что в i-м отборе происходит обогащение по i-му компоненту.
Этот подход был описан в [9, 10], однако правильный выбор схемы разделительного элемента критически важен для возможности построения каскада и имеет смысл повторить основные аргументы. В предыдущих работах была продемонстрирована возможность несмешивающей противоточной циркуляции для каскада указанных элементов, но не были записаны уравнения каскада. В данной работе показано, что можно получить дифференциальные уравнения каскада и аналитическое решение уравнений для противоточной схемы каскада на основе таких элементов.
Компоненты смеси должны полагаться “равноправными”, т.е. для каждого компонента смеси разделительный элемент должен иметь одинаковые характеристики. Нет оснований предполагать, что выделение из смеси молекулы конкретного изотопа требует больших или меньших затрат энергии, чем для молекулы другого изотопа. Тот факт, что самая массовая технология разделения (центрифуга) не обеспечивает этого свойства, не должен останавливать. Имеется, по крайней мере, одна технология – лазерное разделение, где указанное свойство разделительного элемента может быть выполнено.
Лазерные технологии разделения характеризуются сравнительно большими коэффициентами обогащения, но даже лазерное разделение не способно обеспечить полное отделение конкретного сорта частиц от всех остальных частиц смеси. Получение высоких обогащений, в любом случае, требует противоточного каскада. Для анализа каскада удобнее предположить малый коэффициент обогащения. Такой подход позволяет построить дифференциальные уравнения для каскада и получить аналитические решения для концентраций и потоков в каскаде. Для разделительных элементов с большими коэффициентами обогащения, как это показано в теории бинарного разделения, каскад может быть построен в виде ступенчатой аппроксимации идеального противоточного каскада для малых обогащений. Лазерная технология упомянута здесь только как пример, для которого существование разделительного элемента с числом отборов большим двух достаточно очевидно.
Основной характеристикой разделительного элемента является коэффициент разделения q(i). Очевидным образом, его следует ввести как
(1)
${{q}^{{\left( i \right)}}} = \frac{{R_{i}^{{\left( i \right)}}}}{{R_{i}^{{\left( { - i} \right)}}}} = \frac{{C_{i}^{{\left( i \right)}}}}{{(1 - C_{i}^{{\left( i \right)}})}}\frac{{(1 - C_{i}^{{\left( { - i} \right)}})}}{{C_{i}^{{\left( { - i} \right)}}}},$В реальных устройствах коэффициенты обогащения для компонентов смеси могут отличаться, но для базовой теории следует предположить равенство компонентов смеси. Коэффициент обогащения q(i) полагаем одинаковым для всех компонентов смеси.
Равенство величины коэффициента обогащения для всех компонентов смеси есть следствие отсутствия каких-либо термодинамических причин, по которым затраты энергии на выделение из смеси идеальных газов конкретного сорта частиц могли бы отличаться от затрат на выделение из смеси другого сорта частиц [22]. Для бинарной смеси – это очевидно, для многокомпонентной – это можно получить, если рассмотреть квазибинарный случай: произвольный конкретный сорт частиц и все остальные сорта частиц, как вторую компоненту смеси.
Способ, которым введен коэффициент разделения (1), аналогичен классической теории бинарных каскадов [12]: постулируется существование разделительного элемента и коэффициент разделения для этого элемента. Природа физического эффекта, применяемого для разделения, несущественна. Для любого разделительного устройства, изменяющего концентрацию смеси в отборе относительно концентрации смеси в питании, может быть введен коэффициент разделения в форме (1). Этот коэффициент разделения однозначно определяет концентрацию смеси в отборах, при заданной концентрации смеси в потоке питания. Определение универсально и пригодно для любых методов разделения.
Разделительный каскад. В работах [10, 23] была предложена схема соединения разделительных элементов (см. рис. 1б) в схему, которая при равенстве коэффициентов обогащения разделительного элемента, обеспечивает отсутствие смешения в каскаде. Схема для трехкомпонентного разделения изображена на рис. 2а. Эта схема обобщается на произвольное число компонентов смеси. Под ступенью каскада, как и в теории бинарного разделения, понимается соединение нескольких разделительных элементов параллельно, т.е. имеющих общее питание и соответствующие отборы объединены.
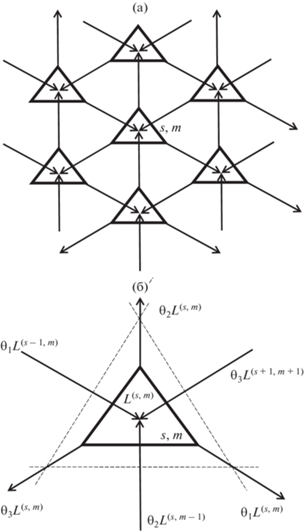
Рис. 2.
Схема несмешивающего трехкомпонентного каскада. (а) – схема соединения ступеней, треугольник обозначает разделительную ступень, стрелки – межступенные потоки; (б) – схема для вывода уравнений сохранения массы в ступени (s, m), пунктирные линии обозначают границу, для которой записываются уравнения сохранения массы
В статье [16] рассмотрен “истинный идеальный каскад”. Однако, фактически, это прямоточный каскад. Схема каскада [16] не предполагает противотока – повторного многократного разделения смеси на ограниченном числе разделительных устройств. В этом смысле, рассматриваемая в данной статье схема каскада принципиально отличается, т.к. обеспечивает противоток смеси и является многокомпонентным аналогом противоточного бинарного каскада.
Основная сложность работы со схемой [10] (см. рис. 2а) – она неудобна для расчета. Схему можно преобразовать к “прямоугольному” представлению (рис. 3). В этом варианте, схема тождественна исходной и допускает простую нумерацию элементов каскада [24]. Элемент (0, 0) будем считать точкой ввода потока питания L в каскад. Предложенное преобразование схемы пригодно для любого количества компонентов смеси.
УРАВНЕНИЯ СОХРАНЕНИЯ ДЛЯ КАСКАДА
Для прямоугольной схемы (см. рис. 3) зможно записать уравнения сохранения массы для разделительного элемента. Предполагаем выполнение условий не смешивания [12]. Детальное рассмотрение условий не смешивания для исходной схемы (см. рис. 2а) приведено в [10].
Входящие в ступень (s, m) потоки считаем объединенными в точке питания и обозначим L(s,m) – поток питания ступени (см. рис. 2б). Выходящие из ступени (s, m) потоки определим через коэффициенты деления потока θi:
Уравнения сохранения для ступени (s, m) могут быть записаны так (см. рис. 3):
(2)
${{\theta }_{2}}{{L}^{{\left( {s,m - 1} \right)}}} = 0.5{\text{ }}({{\theta }_{1}} + {{\theta }_{3}}){{L}^{{(s,m)}}} + {{P}_{2}},$Уравнения (2) должны выполняться “в сумме”, т.е. сумма втекающих потоков на замкнутой границе вокруг ступени должна быть равна сумме вытекающих потоков. В силу симметрии каскада, можно требовать выполнения каждого уравнения (2) в отдельности.
Заменяя s – 1 на s в первом уравнении (2), m – 1 на m – во втором и s + 1 на s, m + 1 на m – в третьем, получим
(3)
${{\theta }_{2}}{{L}^{{\left( {s,m} \right)}}} = 0.5{\text{ }}({{\theta }_{1}} + {{\theta }_{3}}){{L}^{{(s,m + 1)}}} + {{P}_{2}},$Уравнения сохранения массы изотопа для ступени (s, m) можно записать аналогично (см. рис. 2):
(4)
$\begin{gathered} {{\theta }_{2}}{{L}^{{\left( {s,m} \right)}}}{{C}^{{\left( {s,m,2} \right)}}} = 0.5({{\theta }_{1}}{{C}^{{\left( {s,m + 1,1} \right)}}} + \\ + \,\,{{\theta }_{3}}{{C}^{{\left( {s,m + 1,3} \right)}}}){{L}^{{(s,m + 1)}}} + {{P}_{2}}{{C}_{P}}_{2}, \\ \end{gathered} $умножаем уравнение выше на C(s,m,1), получаем
Вычитаем это уравнение из первого уравнения системы (4)
получим:
Перегруппировав члены, уравнение можно записать так
Из определения $C_{i}^{{\left( { - i} \right)}} = {{\sum\limits_{j \ne i} {{{{{\theta }}}^{{\left( j \right)}}}C_{i}^{{\left( j \right)}}} } \mathord{\left/ {\vphantom {{\sum\limits_{j \ne i} {{{{{\theta }}}^{{\left( j \right)}}}C_{i}^{{\left( j \right)}}} } {\sum\limits_{j \ne i} {{{{{\theta }}}^{{\left( j \right)}}}} }}} \right. \kern-0em} {\sum\limits_{j \ne i} {{{{{\theta }}}^{{\left( j \right)}}}} }}$ (см. обозначения для формулы коэффициента разделения (1) ) следует, что
подставляем это выражение в предыдущее уравнение
Выражаем C(s+ 1,m, –1) через коэффициент разделения (1), с учетом ε = q – 1:
В случае малых коэффициентов обогащения, разлагаем выражение в ряд до линейных по ε членов,
Подставляем в уравнение, получаем
Таким образом для малых коэффициентов обогащения уравнение принимает вид:
(5)
$\begin{gathered} {{С}^{{\left( {s + 1,m} \right)}}} - {{С}^{{\left( {s,m} \right)}}} = \varepsilon {{С}^{{\left( {s + 1,m} \right)}}}(1 - {{С}^{{\left( {s + 1,m} \right)}}}) - \\ - \,\,\frac{{\delta \left( {m,s} \right)2{{P}_{1}}\left( {{{С}_{{P1}}} - {{С}^{{\left( {s,m} \right)}}}} \right)}}{{\left( {1 - {{\theta }_{1}}} \right){{L}^{{\left( {s + 1,m} \right)}}}}}\,\,\,\,{\text{для оси}}\,\,OS, \\ {{С}^{{\left( {s,m + 1} \right)}}} - {{С}^{{\left( {s,m} \right)}}} = \varepsilon {{С}^{{\left( {s,m + 1} \right)}}}(1 - {{С}^{{\left( {s,m + 1} \right)}}}) - \\ - \,\,\frac{{\delta \left( {s,m} \right)2{{P}_{2}}\left( {{{С}_{{P2}}} - {{С}^{{\left( {s,m} \right)}}}} \right)}}{{\left( {1 - {{\theta }_{2}}} \right){{L}^{{\left( {s,m + 1} \right)}}}}}\,\,\,\,{\text{для оси}}\,\,OM, \\ \end{gathered} $Для малых изменений концентрации уравнения (5) можно преобразовать к дифференциальным уравнениям, считая s и m непрерывными координатами [12]:
(6)
$\begin{gathered} \frac{{\partial С\left( {s,m} \right)}}{{\partial s}} = \varepsilon С\left( {s,m} \right)\left[ {1 - С\left( {s,m} \right)} \right] - \\ - \,\,\frac{{\delta \left( {m,s} \right)2{{P}_{1}}\left( {{{С}_{{P1}}} - С\left( {s,m} \right)} \right)}}{{\left( {1 - {{\theta }_{1}}} \right)L\left( {s,m} \right)}}\,\,\,\,{\text{для оси}}\,\,OS, \\ \frac{{\partial С\left( {s,m} \right)}}{{\partial m}} = \varepsilon С\left( {s,m} \right)\left[ {1 - С\left( {s,m} \right)} \right] - \\ - \,\,\frac{{\delta \left( {s,m} \right)2{{P}_{1}}\left( {{{С}_{{P1}}} - С\left( {s,m} \right)} \right)}}{{\left( {1 - {{\theta }_{1}}} \right)L\left( {s,m} \right)}}\,\,\,\,{\text{для оси}}\,\,OM. \\ \end{gathered} $Уравнения (6) имеют вид аналогичный уравнению для бинарного каскада. Отличие заключается в том, что каждое уравнение (6) распадается на два уравнения:
(7)
${\text{для}}\,\,m = 0{\kern 1pt} :\frac{{\partial С}}{{\partial s}} = \varepsilon С\left( {1 - С} \right) - \frac{{2{{P}_{1}}\left( {{{С}_{{P1}}} - С} \right)}}{{\left( {1 - {{\theta }_{1}}} \right)L}},$(8)
${\text{для}}\,\,m \ne 0{\kern 1pt} :\frac{{\partial С}}{{\partial s}} = \varepsilon С\left( {1 - С} \right).$Для второго уравнения системы (6) – аналогично. Уравнение (7) подобно уравнению для бинарного каскада [12]. Уравнение (8) является уравнением для безотборного режима бинарного каскада. Точно так же, как в теории бинарного каскада, можно потребовать, чтобы отношение градиента концентрации ∂С/∂s к величине потока L было бы максимальным в каждой точке каскада.
В этом случае, уравнение (7) даст оптимальное распределение потока по оси OS [12]
и уравнение для оптимального градиента концентрации
Уравнение (8) не накладывает никаких ограничений на распределение L(s), поэтому можно для всех m ≠ 0 полагать L(s) = Lopt(s).
Для согласования градиента концентрации по оси OS достаточно, чтобы все ступени каскада при m ≠ 0 имели коэффициент обогащения ε равный половине коэффициента обогащения ступеней при m = 0.
Таким образом, распределение потока в идеальном трехкомпонентном каскаде, по каждой из осей рис. 3, аналогично распределению потока в идеальном бинарном каскаде. Максимальное значение потока L(s) достигает в точке подачи питания и уменьшается до 0 в точке отбора и, следовательно, стремится к нулю на всей границе каскада, кроме точек отборов.
Полученные уравнения и их решения приведены для случая одинаковых и не зависящих от концентрации коэффициентов обогащения для каждого компонента смеси. Случай разных коэффициентов обогащения не изменяет принципиально выводов, все вышеизложенное можно повторить для трех различных коэффициентов обогащения не зависящих от концентрации. Для коэффициентов обогащения зависящих от концентрации, вывод уравнений (6) остается справедливым. Но аналитическое решение уравнений (6) становится невозможным без явной функциональной зависимости коэффициента обогащения от концентрации смеси. Однако, при наличии явной функциональной зависимости коэффициента обогащения от концентрации уравнения можно решить, как минимум, численно.
ЗАКЛЮЧЕНИЕ
Обосновано понятие разделительного элемента для многокомпонентного разделения и необходимость создания и применения разделительных элементов с числом потоков отбора равным числу компонент смеси.
Предложена схема для расчета противоточного каскада.
Получены уравнения для концентрации смеси и величины потоков в разделительном каскаде для трехкомпонентного разделения.
Получены дифференциальные уравнения для несмешивающего (идеального) каскада в случае малых обогащений.
Показано, что распределение потоков в идеальном каскаде для разделения трехкомпонентной смеси очень похоже на случай бинарного идеального каскада.
Предложенная схема каскада и оптимальное распределение потоков может использоваться для оптимизации промышленного разделения многокомпонентных смесей.
ОБОЗНАЧЕНИЯ
| C | концентрации всех компонентов смеси C = (C1, C2, … Ci), безразмерный |
| C(0) | концентрации компонентов в исходной смеси, безразмерный |
| C(i) | концентрации компонентов в отборе i, безразмерный |
| C1, C2, … Cn | концентрация 1, 2… n компонента смеси, безразмерный |
| $C_{i}^{{\left( { - i} \right)}}$ | средняя концентрация i-го компонента во всех отборах разделительного элемента, кроме i-го, безразмерный |
| G(0) | поток питания, кг/c или масса разделяемой смеси, кг |
| G(i) | потоки отбора, кг/c или массы отбора, кг |
| L | поток питания каскада или разделительного элемента, кг/c |
| n | количество компонентов смеси, безразмерный |
| q | коэффициент разделения, безразмерный; |
| q(i) | коэффициент разделения для i-го отбора, безразмерный |
| R | относительная концентрация, безразмерный |
| $R_{i}^{{\left( i \right)}}$ | относительная концентрация i-го компонента в i-м отборе, безразмерный |
| $R_{i}^{{\left( { - i} \right)}}$ | относительная средняя концентрация i-го компонента во всех отборах разделительного элемента, кроме i-го, безразмерный |
| θ(i) | коэффициент деления потока для i-го отбора разделительного элемента или каскада, безразмерный |
| ε | коэффициент обогащения разделительного элемента, безразмерный |
ИНДЕКСЫ
Список литературы
Орлов А.А., Ушаков А.А., Совач В.П., Малюгин Р.В. Математическое моделирование нестационарных разделительных процессов в каскаде газовых центрифуг для разделения изотопов вольфрама // ИФЖ. 2018. Т. 91. № 3. С. 605–614.
Фарахов М.М., Лаптева Е.А. Экспериментальные исследованиябинарной и многокомпонентной ректификации смесей в колонне с новыми насадками // Труды АКАДЕМЭНЕРГО. 2020. № 2(59). С. 43–54.
Белова В.В. Перспективность использования метода рециркуляционнопротивоточной хроматографии для разделения многокомпонентных смесей // Химическая технология. 2020. Т. 21. № 8. С. 373–378.
Смирновa А. Ю., Сулаберидзе Г. А. Универсальный разделительный потенциал для многокомпонентных смесей: причины отсутствия // Журн. Физ. Химии. 2019. Т. 93. № 4. С. 627–631.
De La Garza, Garrett G.A., Murphy J.E. Multicomponent Isotope Separation in Cascades // Chem. Eng. Sci. 1961. V. 15. P. 188–209.
Rutherford W.M. A Generalized Computer Model of the Transient Behavior of Multicomponent Isotope Separation Cascades // Separation Science and Technology. 1981. № 16(10). P. 1321–1337.
Kinoshita M., Naruse Y. Mathematical Simulation Procedure of Multicomponent Separating Cascade. Application to Analysis of Hydrogen Isotope Separation System by Porous Membrane Method // J. Nuclear Science and Technology. 1981. № 18(9). P. 718–726.
Borisevich V., Sulaberidze G., Wood H. The Theory of Isotope Separation in Cascades: Problems and Solutions // Ars Separatoria Acta. 2003. № 2. P. 107–124.
Александров О.Е. Построение трехкомпонентного разделительного каскада // Перспективные материалы, Специальный выпуск. 2011. № 10. С. 61–64.
Гадельшин В.М., Александров О.Е., Шульгин Б.В. Разработка квазиидеального каскада разделительных элементов с тремя отборами // Перспективные материалы, Специальный выпуск. 2013. № 14. С. 65–70.
Палкин В.А. Многопоточные каскады для разделения многокомпонентных изотопных смесей // Атомная энергия. 2015. Т. 119. № 2. С. 101105.
Обогащение урана. / под ред. С.М. Виллани: Энергоатомиздат, 1983. 320 с.
Афанасьев В.Г., Водолазских В.В., Гаврилов П.М., Журин В.А., Калашников А.Л., Колесников А.И., Короткевич В.М. Способ разделения изотопов. Патент на изобретение № 2331463 РФ / Заявл. 25.09.2006. Публ. 20.08.2008.
Палкин В.А., Сбитнев Н.А., Фролов Е.С. Расчет оптимальных параметров каскада для разделения многокомпонентной смеси изотопов – Атомная энергия. 2002. № 92(2). С. 130–133.
Kholpanov L.P., Sulaberidze G.A., Potapov D.V., Chuzhinov V.A. Multicomponent isotope separating cascade with losses // Chemical Engineering and Processing. 1997. № 36. P. 89–193.
Zeng S., Ying Z. A Truly Ideal Cascade: Net Cascade // Separation Science and Technology. 2012. № 47. P. 929–935.
Wankat P.C. Two-Dimensional Cross-Flow Cascades // Separation Science. 1972. № 7(3). P. 233–241.
Wankat P.C. Two-Dimensional Development in Staged Systems // Separation Science. 1972. № 7(4). P. 345–360.
Wankat P.C. Middleton A.R., Hudson B.L. Steady State Continuous, Multicomponent Separations in Regenerated Two-Dimensional Cascades // Industrial & Engineering Chemistry Fundamentals. 1976. № 15(4). P. 309–317.
Oyama Y., Takashima Y., Aoki S. Патент № 42-68490 Japan / Приоритет: 26.10.1967 – Verfahren und Vorrichtung zum Trennen eines Gemisches von Gasen verschiedenen Molekulargewichts – Патент № 1801307 DE / Заявл. 04.10.1968. Публ. 23.04.1970.
Oyama Y., Takashima Y. Патент № 18971 Japan / Приоритет: 29.03.1966 – Gaszentrifuge und Verfahren zum Konzentrieren von Komponenten eines Gasgemisches – Патент № 1619827 DE / Заявл. 17.03.1967. Публ. 23.09.1971.
Александров О.Е., Гадельшин В.М. Многокомпонентный разделительный потенциал. Элементарная кинетическая теория // Инж.-физ. журн., 2013. Т. 86. № 5. С. 1140–1147.
Гадельшин В.М., Шульгин Б.В., Палкин В.А. Способ разделения изотопов – Патент на изобретение № 2500461 РФ / Заявл.11.03.2012. Публ. 10.12.2013. Бюл. № 34.
Маркина М.А., Александров О.Е. Проектирование и расчет схемы идеального разделительного каскада для трехкомпонентной смеси // ФИЗИКА. ТЕХНОЛОГИИ. ИННОВАЦИИ. Сборник материалов VI Международной молодежной научной конференции, посвященной 70летию основания Физико-технологического института УрФУ. Под редакцией В. Ю. Иванова, Д. Р. Байтимирова. Издательство: Уральский федеральный университет. 2019. С. 150–162.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии



