Теоретические основы химической технологии, 2022, T. 56, № 6, стр. 663-669
Движение газовзвеси в разделительной камере прямоточного циклона
Н. А. Марцулевич a, *, О. М. Флисюк a, И. Г. Лихачев a, В. П. Мешалкин a, А. В. Гарабаджиу a, Н. Н. Кулов b
a Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия
b Институт общей и неорганической химии (ИОНХ) им. Н.С. Курнакова РАН
Москва, Россия
* E-mail: tohm1950@mail.ru
Поступила в редакцию 16.06.2022
После доработки 30.06.2022
Принята к публикации 03.07.2022
- EDN: GUPMPH
- DOI: 10.31857/S0040357122060100
Аннотация
С помощью пакета программ FlowVision получены численные решения уравнений движения газовзвеси в разделительной камере прямоточного циклона. Решения позволяют проследить зависимость основных гидродинамических характеристик и профиля концентрации частиц твердой фазы от геометрических параметров разделительной камеры. Показано, что основными факторами, оказывающими негативное влияние на эффективность работы циклона, являются циркуляционные течения газа и турбулентный “след” после завихрителя. Проведенный анализ позволил выработать рекомендации по выбору геометрических параметров камеры, сводящих к минимуму влияние указанных факторов.
ВВЕДЕНИЕ
Проблема очистки крупномасштабных газовых выбросов предприятий химической, нефтехимической и смежных отраслей промышленности, а также теплоэнергетических установок, работающих на угле и мазуте, не теряет своей актуальности. Более того, с каждым годом она становится все острее. В последние годы появились технологии утилизации твердой фазы, которые позволяют из выбрасываемых в атмосферу отходов получать полезные продукты. В силу этих причин число публикаций, посвященных исследованию процесса разделения газовзвесей и разработке эффективных конструкций пылеуловителей, не уменьшается. Немалая доля таких публикаций относится к изучению работы циклонов, обладающих рядом преимуществ по сравнению с другим очистным оборудованием [1–11]. В обзорной работе [5] приводится более трех десятков типовых конструкций циклонов и сепараторов с указанием их достоинств, недостатков и областей их предпочтительного применения. В частности, авторы отмечают сравнительно невысокую эффективность прямоточных циклонов при очистке газов от мелких частиц. При этом делается оговорка о недостаточной изученности циклонов данного типа. С последним утверждением нельзя не согласиться. Действительно, до сих пор не существует надежных методов расчета прямоточных циклонов, позволяющих предсказать степень очистки газа при заданном его расходе и характеристиках дисперсности частиц пыли. Отсутствуют также методы проектирования таких циклонов, включая определение оптимальной геометрии разделительной камеры и лопастей завихрителя. Для создания указанных методов требуется, очевидно, детальное изучение характера движения частиц и газа в циклоне, поскольку именно гидродинамика газовзвеси целиком определяет эффективность его работы. Ранее [12–15] авторами получены аналитические решения уравнений закрученного потока газовзвеси в прямоточном циклоне. При этом использовались достаточно сильные допущения, касающиеся характера движения газа и частиц, что позволяло расценивать указанные решения как качественные.
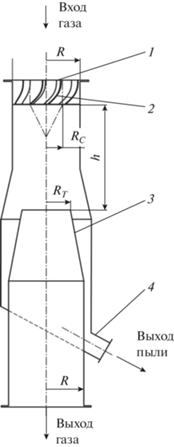
Цель настоящей статьи состоит в анализе картины турбулентного течения запыленного газа в разделительной камере прямоточного циклона на основе результатов численного решения уравнений гидродинамики без использования упрощающих допущений. Анализ проведен на примере прямоточного циклона с конкретной геометрией разделительной камеры [16], представленной на рис. 1. Тем не менее, выводы имеют общий характер и непосредственный практический выход.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Движение газа. Если массовая концентрация частиц в потоке невелика (как это обычно бывает при работе циклонов), то их присутствие слабо влияет на поле скорости газа. Поэтому задачу можно разделить: сначала определить поле скоростей газовой фазы, а затем – характер движения частиц. Введем систему декартовых координат xi (i = 1, 2, 3), направив ось Оx3 вдоль оси циклона. Тогда согласно гипотезе Буссинеска, которая устанавливает линейную связь между тензором Рейнольдсовых напряжений и тензором скоростей деформаций, уравнения, описывающие установившееся движение газа с учетом допущения о его несжимаемости, имеют вид:
(1)
$\begin{gathered} \frac{{\partial {{w}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{w}_{2}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{w}_{3}}}}{{\partial {{x}_{3}}}} = 0, \\ {{\rho }}{{w}_{1}}\frac{{\partial {{w}_{i}}}}{{\partial {{x}_{1}}}} + {{\rho }}{{w}_{2}}\frac{{\partial {{w}_{i}}}}{{\partial {{x}_{2}}}} + {{\rho }}{{w}_{3}}\frac{{\partial {{w}_{i}}}}{{\partial {{x}_{3}}}} = \\ = - \frac{{\partial{ \tilde {p}}}}{{\partial {{x}_{i}}}} + \frac{\partial }{{\partial {{x}_{1}}}}\left[ {\left( {{{\mu }} + {{{{\mu }}}_{t}}} \right)\frac{{\partial {{w}_{i}}}}{{\partial {{x}_{1}}}}} \right] + \\ + \,\,\frac{\partial }{{~\partial {{x}_{2}}}}\left[ {\left( {{{\mu }} + {{{{\mu }}}_{t}}} \right)\frac{{\partial {{w}_{i}}}}{{\partial {{x}_{2}}}}} \right] + \frac{\partial }{{\partial {{x}_{3}}}}\left[ {\left( {{{\mu }} + {{{{\mu }}}_{t}}} \right)\frac{{\partial {{w}_{i}}}}{{\partial {{x}_{3}}}}} \right],~ \\ ~i = 1,~\,\,2,\,\,~3. \\ \end{gathered} $Здесь ${{\mu }}$ и ${{{{\mu }}}_{t}}$ – коэффициенты молекулярной и турбулентной вязкости движущейся среды, Па с. Величина $\tilde {p} = p + \frac{2}{3}k$ учитывает вклад в энергию статического давления кинетической энергии турбулентных пульсаций: $k = \rho \mathop \sum \limits_i \frac{{{{{\left( {w_{i}^{'}} \right)}}^{2}}}}{2}$.
Решение системы уравнений (1) проводилось с помощью пакета программ FlowVision. При этом использовалась стандартная k-ɛ модель турбулентности, в которой коэффициент турбулентной вязкости ${{{{\mu }}}_{t}}$ определяется скоростью диссипации энергии турбулентности ɛ и ее интенсивностью посредством соотношения: ${{{{\mu }}}_{t}} = {{C}_{\mu }}{{\rho }}\frac{{{{k}^{2}}}}{{{\varepsilon }}}$. Указанная модель включает уравнения для величин k и ɛ, которые замыкают систему уравнений (1). Таким образом, в результате решения системы уравнений можно получить не только профили давления и проекций скорости газа во всей области течения, но и распределение энергии турбулентности, скорости ее диссипации и характер затухания на твердых поверхностях. Большие возможности пакета FlowVision обусловили его широкое использование в последнее время для решения разнообразных задач гидродинамики. В частности, в ряде работ с помощью этого инструмента проводилось численное интегрирование уравнений движения закрученного потока газа и содержащихся в нем частиц [17–21].
Выбор расчетной области для уравнений (1) определялся исходя из следующих соображений. Непосредственное измерение скорости газа, а также визуализация потока в прямоточном циклоне убеждают в том, что каждая лопасть завихрителя формирует течение близкое к струйному, так что газ сходит с периферийной части кромки лопасти в виде относительно узкого “жгута”. Этот факт подтверждается и результатами расчетов (рис. 2). Если ограничить расчетную область только разделительной камерой циклона, как это сделано, например, в [22], то задание адекватных граничных условий на входе в нее будет невозможным. Поэтому в качестве одной из границ расчетной области в настоящей работе было взято поперечное сечение трубопровода, расположенное на расстоянии равном его диаметру от завихрителя вверх по потоку. Примерно на таком расстоянии поток “чувствует” предстоящее препятствие, и линии тока начинают искажаться [23]. Предполагалось, что в указанном сечении скорость газа распределена равномерно и направлена вдоль оси трубы. Другим граничным условием было равенство нулю скорости газа на всех твердых поверхностях, включая поверхности лопастей завихрителя (эффект прилипания).
Рис. 2.
Распределение продольной составляющей скорости газа на входе в разделительную камеру циклона.

Рис. 4.
Зависимость энергии турбулентных пульсаций от радиальной координаты на различном расстоянии от входа в камеру 1 – 0.3 м; 2 – 0.45 м; 3 – 0.6 м.

На рис. 3 показаны полученные в результате решения уравнений (1) проекции линий тока на плоскость, проходящую через ось циклона. Число Re, рассчитанное по диаметру трубопровода, составляло значение 110 000. Рисунок дает достаточно полное представление о характере движения газа в разделительной камере с данной геометрией. Область течения делится на две зоны, в которых гидродинамическая картина совершенно различна. В периферийной зоне закрученный поток газа движется строго вдоль стенки камеры с высокими скоростями. Центральную зону занимает турбулентный “след”, в котором генерируются обширные продольные циркуляции газа. Очевидно, что существование “следа” и циркуляционных течений являются факторами, существенно снижающими эффективность циклона. Другим таким фактором, препятствующим выводу частиц пыли из газового потока, служит их турбулентное перемешивание. Поэтому при анализе гидродинамики в разделительной камере представляет интерес профиль турбулентной энергии газа. Рис. 4 иллюстрирует зависимость энергии турбулентных пульсаций от расстояния до оси циклона. Из приведенной зависимости видно, что наибольшая интенсивность турбулентности достигается именно в зоне циркуляционных течений. Следовательно, поток частиц пыли за счет турбулентного перемешивания в этой зоне в направлении к центру камеры (обратное перемешивание) также принимает максимальное значение. Еще одна область повышенной турбулентности расположена вблизи стенки. В этой области за счет больших градиентов средней скорости генерируется дополнительная турбулентность газа [24, 25], которая может быть причиной вторичного вовлечения в поток частиц пыли, уже заторможенных стенкой. Приведенные на рис. 4 зависимости позволяют сделать еще один важный вывод. С увеличением расстояния до входа в разделительную камеру интенсивность турбулентности заметно возрастает. Причиной этого, по-видимому, является резкая неоднородность профиля средней скорости в зоне циркуляций газа. Возникающая здесь турбулентность затем распространяется на остальной объем разделительной камеры.
Совместное движение обеих фаз. Для описания движения фазы частиц в пакете FlowVision используется подход взаимопроникающих континуумов [26], позволяющий сформулировать уравнения движения дисперсной фазы в форме аналогичной уравнениям (1). Отличие состоит в том, что движение газовой фазы обусловлено разностью давлений, а движение фазы частиц – силовым взаимодействием с газом:
(2)
$\begin{gathered} {{v}_{1}}\frac{{\partial mN{{v}_{i}}}}{{\partial {{x}_{1}}}} + {{v}_{2}}\frac{{\partial mN{{v}_{i}}}}{{\partial {{x}_{2}}}} + {{v}_{3}}\frac{{\partial mN{{v}_{i}}}}{{\partial {{x}_{3}}}} = \\ = {{F}_{i}} + \frac{\partial }{{\partial {{x}_{1}}}}\left[ {\left( {{{{{\mu }}}_{t}}} \right)\frac{{\partial {{v}_{i}}}}{{\partial {{x}_{1}}}}} \right] + \frac{\partial }{{~\partial {{x}_{2}}}}\left[ {\left( {{{{{\mu }}}_{t}}} \right)\frac{{\partial {{v}_{i}}}}{{\partial {{x}_{2}}}}} \right] + \\ + \,\,\frac{\partial }{{\partial {{x}_{3}}}}\left[ {\left( {{{{{\mu }}}_{t}}} \right)\frac{{\partial {{v}_{i}}}}{{\partial {{x}_{3}}}}} \right],\,\,\,\,i = 1,\,\,~2,~\,\,3~. \\ \end{gathered} $Равенство динамических коэффициентов турбулентной вязкости сплошной и дисперсной фаз обусловлено небольшим размером частиц пыли, когда они практически полностью увлекаются турбулентными образованиями газового потока [27, 28].
Некоторое отставание частиц от газа учитывается в выражении для силы межфазного взаимодействия, которое для режима стоксового обтекания имеет вид:
где коэффициент сопротивления движению частиц со стороны газа соответствует режиму стоксового обтекания:
(4)
${{C}_{D}} = \frac{{24}}{{{{{\operatorname{Re} }}_{p}}}} = \frac{{24\mu }}{{\rho d\left| {w - v} \right|}}.$Распределение числовой концентрации частиц пыли в разделительной камере циклона подчиняется уравнению конвективной диффузии:
(5)
$\begin{gathered} {{v}_{1}}\frac{{\partial N}}{{\partial {{x}_{1}}}} + {{v}_{2}}\frac{{\partial N}}{{\partial {{x}_{2}}}} + {{v}_{3}}\frac{{\partial N}}{{\partial {{x}_{3}}}} = \\ = \frac{\partial }{{\partial {{x}_{1}}}}\left( {{{D}_{t}}\frac{{\partial N}}{{\partial {{x}_{1}}}}} \right) + \frac{\partial }{{\partial {{x}_{2}}}}\left( {{{D}_{t}}\frac{{\partial N}}{{\partial {{x}_{2}}}}} \right) + \frac{\partial }{{\partial {{x}_{3}}}}\left( {{{D}_{t}}\frac{{\partial N}}{{\partial {{x}_{3}}}}} \right). \\ \end{gathered} $В условиях, когда движение частиц определяется только взаимодействием с газом, коэффициент Dt практически совпадает с кинематическим коэффициентом турбулентной вязкости дисперсной фазы νt = μt/ρ, поскольку механизм переноса импульса и массы один и тот же.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
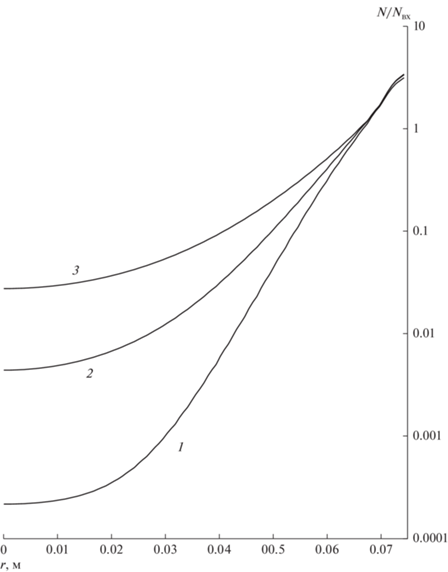
В пакете программ FlowVision уравнения (1)–(5) численно решаются совместно. Решения позволяют получить линии тока дисперсной фазы и распределение концентрации частиц пыли в разделительной камере. На рис. 5 приведены зависимости числовой концентрации частиц в логарифмических координатах от радиальной координаты для трех поперечных сечений, находящихся на различных расстояниях от входа в камеру. Из них видно, что сразу после завихрителя подавляющая доля частиц относится к стенке циклона. Однако затем за счет механизма турбулентного перемешивания начинается отток частиц из пристеночной области в ядро потока. Он достигает максимальных значений в области циркуляционных течений газа, где интенсивность турбулентности наибольшая. По этой причине прямоточный циклон с геометрией разделительной камерой, изображенной на рис. 1, в принципе не может обеспечить высокую степень разделения, особенно для мелких частиц порядка 10 мкм. Более крупные частицы в меньшей степени реагируют на турбулентность газа благодаря большей инерционности. Поэтому эффективность разделения для газовзвесей с такими частицами может быть приемлемой.
Рис. 5.
Распределение относительной числовой концентрации частиц N/Nвх в зависимости от радиальной координаты на различном расстоянии от входа в камеру 1 – 0.3 м; 2 – 0.45 м; 3 – 0.6 м.
Изложенные выше результаты анализа дают возможность сформулировать ряд практических выводов. Предполагаемая некоторыми исследователями невысокая эффективность прямоточных циклонов является мнимой. Она может быть связана только с неудачным проектированием разделительной камеры, включая геометрию завихрителя. Полученные в настоящей работе результаты убедительно показывают, что основными негативными факторами, снижающими эффективность разделения, являются циркуляционные течения и зоны повышенной турбулентности. Поэтому при проектировании прямоточных циклонов необходимо подбирать геометрические параметры камеры таким образом, чтобы гидродинамическая картина в них не содержала ни того, ни другого. Так, авторами [12] предложена конструкция разделительной камеры, устраняющая циркуляционные течения и турбулентный “след” после завихрителя. По-видимому, сокращение длины камеры также будет способствовать увеличению степени очистки газа, поскольку перенос частиц пыли от стенок камеры за счет механизма турбулентного перемешивания начинает существенно сказываться на расстояниях порядка 50-100 мм от входа. Разумеется, более точные рекомендации по выбору оптимальных значений геометрических параметров разделительной камеры прямоточных циклонов могут быть даны после полного изучения их влияния на степень очистки газа от пыли.
ЗАКЛЮЧЕНИЕ
Численное решение уравнений гидродинамики для газовзвесей позволило выявить те физические факторы, которые могут служить причинами снижения эффективности прямоточных циклонов. Указанные решения, кроме того, дают возможность на стадии проектирования провести целенаправленный выбор геометрических параметров разделительной камеры, которые устраняют или сводят к минимуму негативное влияние этих факторов, сохраняя при этом все достоинства прямоточных циклонов.
Исследование выполнено при поддержке гранта РНФ (проект 21-79-30029).
ОБОЗНАЧЕНИЯ
| wi | проекции осредненной скорости газа на соответствующие оси координат, м/с |
| $w_{i}^{'}$ | компоненты пульсационной составляющей скорости газа, м/с |
| vi | проекции осредненной скорости фазы частиц на соответствующие оси координат, м/с |
| p | статическое давление в газе, Па |
| k | кинетическая энергия турбулентных пульсаций в газе, отнесенная к единице объма, Дж/м3 |
| m | масса частицы пыли, кг |
| d | эффективный диаметр частиц пыли, м |
| N | числовая концентрация частиц пыли, м–3 |
| Fi | проекции силы межфазного взаимодействия на оси координат, отнесенные к единице объема, Н/м3 |
| Dt | эффективный коэффициент перемешивания частиц, м2/с |
| ${{\rho }}$ | плотность газа, кг/м3 |
| ${{\mu }}$ и ${{{{\mu }}}_{t}}$ | коэффициенты молекулярной и турбулентной вязкости движущейся среды, Па с |
| ε | скорость диссипации энергии турбулентности, Дж/м3 |
| νt | кинематический коэффициент турбулентной вязкости дисперсной фазы, м2/с |
| Re | число Рейнольдса |
ИНДЕКСЫ
Список литературы
Ужов В.Н. Очистка промышленных газов от пыли / В.Н. Ужов, А.Ю. Вальдберг, Б.И. Мягков, И.К. Решидов. М.: Химия, 1981. 392 с.
Cortes C., Gil A. Modeling the gas and particle flow inside cyclone separators. Progress in energy and combustion science. 2007. V. 33. № 5. P. 409–452. https://doi.org/10.1016/j.pecs.2007.02.001
Li Q., Xu W., Wang J., Jin Y. Performance evaluation of a new cyclone separator – Part I experimental results // Sep. Purif. Technol. 2015. V. 141. P. 53–58. https://doi.org/10.1016/J.SEPPUR.2014.10.030
Xu W., Li Q., Wang J., Jin Y. Performance evaluation of a new cyclone separator – Part II simulation results // Sep. Purif. Technol. 2016. V. 160. P. 112–116. https://doi.org/10.1016/J.SEPPUR.2016.01.012
Мисюля Д.И., Кузьмин В.В., Марков В.А. Сравнительный анализ технических характеристик циклонных пылеуловителей. Труды БГТУ, Химия и технология неорганических веществ. 2012. № 3. С. 154–163.
Кутепов А.М. Разработка и использование высокоэффективных сепараторов для выделения пыли из газа / А.М. Кутепов, А.С. Жихарев // Химическая промышленность. 1998. № 8. С. 36–38.
Ehteram M.A., Tabrizi H.B., Mesbah M., Ahmadi G., Mirsalim M.A. Experimental study on the effect of connecting ducts on demisting cyclone efficiency / Exp. Therm. Fluid Sci. 2012. V. 39. P. 26–36. https://doi.org/10.1016/J.EXPTHERMFLUSCI.2012.01.002
Hreiz R., Gentric C., Midoux N., Lainé R., Fünfschilling D. Hydrodynamics and velocity measurements in gas–liquid swirling flows in cylindrical cyclones // Chem. Eng. Res. Des. 2014. V. 92. P. 2231–2246. https://doi.org/10.1016/J.CHERD.2014.02.029
Elsayed K., Lacor C. The effect of cyclone inlet dimensions on the flow pattern and performance // Appl. Math. Model. 2011. V. 35. P. 1952–1968.
Cortes C., Gil A. Modeling the gas and particle flow inside cyclone separators. Prog. Enegry Combust // Sci. 2007. V. 33. P. 409–452. https://doi.org/10.1016/J.PECS.2007.02.001
Faulkner W., Shaw B. Efficiency and pressure drop of cyclones across a range of inlet velocities // Appl. Eng. Agric. 2006. V. 22. № 1. P. 155–161. https://doi.org/10.13031/2013.20191
Флисюк О.М., Марцулевич Н.А., Топталов В.С. Теоретическо-экспериментальный анализ зависимости эффективности прямоточного циклона от геометрии разделительной камеры // Изв. вузов. Химия и хим. технология. 2021. Т. 64. Вып. 8. С. 98–105. https://doi.org/10.6060/ivkkt.20216408.6419
Топталов В.С., Марцулевич Н.А., Флисюк О.М. Очистка дымовых и технологических газов в прямоточных циклонах. Известия СПбГТИ(ТУ). 2021. № 56(82). С. 44–50. https://doi.org/10.36807/1998-9849-2021-56-82-44-50
Топталов В.С., Марцулевич Н.А. Движение запыленного газа в разделительной камере прямоточного циклона. Материалы ХI научной конференции “Традиции и Инновации”. 1–3 декабря 2020 г. СПб: Изд-во СПбГТИ(ТУ), 2020. 272. С. 161.
Flisiyk O.M., Martculevich N.A., Toptalov V.S. Dusty gas movement in separating chamber of direct-flow cyclone. Vth international conference “Actual scientific & technical issues of chemical safety” ASTICS-2020. Kazan, Russia. P. 336–337.
Прямоточный циклон: пат. 195672, Рос. Федерация. № 2019136768; заявл. 15.11.2019; опубл. 03.02.2020; Бюл. № 4.
Hreiz R., Gentric C., Midoux N. Numerical investigation of swirling flow in cylindrical cyclones // Chem. Eng. Res. Des. 89(2011). 2521–2539. https://doi.org/10.1016/J.CHARD.2011.05.001
Oh J., Choi S., Kim J. Numerical simulation of an internal flow field in a uniflow cyclone separator. Powder Technol. 2015. V. 274. P. 135–145. https://doi.org/10.1016/J.POWTEC.2015.01.015
Gao X., Chen J., Feng J., Peng X. Numerical investigation of the effects of the central channel on the flow field in an oil–gas cyclone separator. Comput. Fluids. 2014. V. 9. P. 45–55. https://doi.org/10.1016/J.IJREFRIG.2013.06.004
Kępa A. The efficiency improvement of a large-diameter cyclone – the CFD calculations // Sep. Purif. Technol. 2013. V. 118. P. 105–111. https://doi.org/10.1016/J.SEPPUR.2013.06.040
Bernardo S., Mori M., Peres A.P., Dionísio R.P. 3-D computational fluid dynamics for gas and gas-particle flows in a cyclone with different inlet section angles. Powder Technol. 162(2006). 190–200. https://doi.org/10.1016/J.POWTEC.2005.11.007
Long Huang, Songsheng Deng, Zhi Chen, Jinfa Guan, Ming Chen. Numerical analysis of a novel gas-liquid pre-separation cyclone / Separation and Purification Technology. 2018. V. 194. P. 470–479. https://doi.org/10.1016/J.SEPPUR.2017.11.066
Альбом течений жидкости и газа: А56 Пер. с англ. / Сост. М. Ван-Дайк. М.: Мир, 1986. 186 с.
Ротта И.К. Турбулентный пограничный слой в несжимаемой жидкости. Л.: Судостроение, 1967. 232 с.
Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974. 712 с.
Нигматулин Р.И. Динамика многофазных сред. Ч. I. М.: Наука. Гл. ред. физ.-мат. лит., 1987. 464 с.
Марцулевич Н.А. Хаотическое движение частиц в турбулентном потоке газа / Теор. основы хим. технологии. 1987. № 3. С. 362–367.
Марцулевич Н.А., Протодьяконов И.О. Хаотическое движение фаз в потоках газовзвесей / Журн. прикл. химии. 1984. Т. 57. № 4. С. 947–950.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии