Теоретические основы химической технологии, 2022, T. 56, № 6, стр. 678-685
Исследование теплопроводности композиционного рудного фосфатного материала с реагирующими включениями карбонатов
В. П. Мешалкин a, В. И. Бобков b, *, М. И. Дли b, В. А. Орехов b, А. В. Гарабаджиу c
a Российский химико-технологический университет имени Д.И. Менделеева, Институт физической химии
и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия
b Национальный исследовательский университет “МЭИ”
г. Смоленск, Россия
c Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия
* E-mail: vovabobkoff@mail.ru
Поступила в редакцию 17.06.2022
После доработки 30.06.2022
Принята к публикации 03.07.2022
- EDN: MNKFIZ
- DOI: 10.31857/S0040357122060112
Аннотация
В представляемой работе предложена комбинированная модель теплопроводности, позволяющая рассчитывать коэффициент теплопроводности слабокарбонатных фосфоросодержащих рудных пород, учитывающая структурные особенности фосфоритов. Для расчета теплопроводности карбонатных фосфоритов предложена структурная модель композиционного материала с реагирующими включениями. Используя комбинацию разработанных моделей и определенные в работе теплофизические свойства основных породообразующих минералов, позволяет рассчитывать коэффициент теплопроводности широкого класса фосфатных руд, включая температурную зону термических превращений в исследуемом материале. Для расчета истинной теплоемкости фосфоритов применена аддитивная модель. Проведено сопоставление результатов расчетов по моделям с натурными экспериментами.
ВВЕДЕНИЕ
Фосфоросодержащие руды и породы имеют сложный и неоднородный полиминеральный состав [1]. Породообразующие минералы при нагревании претерпевают физико-химические превращения, вступают во взаимные реакции, что приводит к изменению состава и структуры материалов [2].
В результате тепловых эффектов реакций и связанных с реакцией структурных изменений, теплофизические характеристики приобретают сложный динамический температурно-временной и температурно-концентрационный характер зависимости [3]. В связи с этим, очевидно, что исследование теплопроводности фосфоритов и фосфатно-кремнистых разностей должны проводиться с учетом происходящих в них термически активируемых процессах [4].
ПРИМЕНЕНИЕ СТРУКТУРНЫХ МОДЕЛЕЙ ТЕПЛОПРОВОДНОСТИ К ФОСФОРИТАМ
Исследования минералогического состава фосфоритов и фосфатно-кремнистых разностей показывают, что основную массу этих пород составляют следующие минералы: фторкарбонатапатит Сa10P5СО24F2 доломит CaMg(CO3)2, кальцит CaCO3, кварц и халцедон SiО2 и минеральные примеси. По структурно-минералогической классификации можно выделить следующие основные типы фосфоритов: неяснозернистые, зернистые, оолитовозернистые, зернисто-псаммитовые. Зерна фосфоритов могут быть представлены чистыми минералами кварца, халцедона, обломками кремнистых пород, карбонатами, гидроокислами железа и фосфатным веществом [5]. Часто наблюдаются смешанные кремнисто-фосфатные и карбонатно-фосфатные зерна. Оолиты округлой формы представлены фосфатом простой и сложной структуры [6]. Иногда встречаются обломки оолитов. Весь этот зернистый материал сцементирован фосфатным, карбонатным или кремнистым цементом, реже встречаются их сочетания [7]. Учитывая, что большинство фосфатных руд представляют собой включения фосфата, карбоната, кремнезема и минеральных примесей в цементирующем материале в различных пропорциях, то появляется возможность расчета коэффициента теплопроводности на основе известных структурных моделей [8]. Основной компонентой, определяющей структуру модели расчета коэффициента теплопроводности фосфоритов, является фосфат, представленный оолитами окатанной формы размером 0.05–0.5 мм. При анализе шлифов фосфоритов основных промышленных типов руд при различном содержании P2O5 можно выделить следующие типы структуры:
• матричная структура с изолированными включениями фосфата;
• переходная структура от матричной к взаимопроникающей;
• взаимопроникающая инвариантная структура;
• матричная структура с изолированными включениями карбонатов и кремнезема;
К первой структуре относятся фосфатизированные кремни и доломиты с небольшим содержанием 5–12% фосфатного вещества, бедные фосфоритные, кремнисто-карбонатные, пелитоморфно-кремнистые, забалансовые и метаморфизованные руды с содержанием P2O5 20%, что соответствует 50% фосфатного вещества [9].
Замечено, что увеличение объемной доли фосфата до 50% не приводит к заметному точечному контактированию оолитов между собой [10]. Фосфатное вещество представлено оолитами или частицами элипсоидальной формы, характеризующиеся концентрически зональным строением. Размеры оолитов от 0.04 до 0.3 мм. Основная масса оолитов простого строения [11]. Оолиты фосфорита заключены в цементирующем материале и не соприкасаются друг с другом (базальный тип цемента). Редко встречаются участки с цементом, выполнения пор между соприкасающимися зернами [12]. Цемент в основном сложен карбонатной массой от мелкозернистой до криптокристаллической структуры. Зерна карбоната изометричной, вытянутой формы с размерами от 0.001 до 0.2 мм.
Теплопроводность таких фосфоритов можно рассчитать по модели трехкомпонентной смеси с замкнутыми включениями:
(1)
$\begin{gathered} {{\lambda }} = {{{{\lambda }}}_{1}}\left( {\frac{{{{m}_{2}}}}{{1 - {{m}_{1}}}}\left[ {1 - \frac{{1 - {{m}_{1}}}}{{{{{\left( {1 - {{{{\nu }}}_{{12}}}} \right)}}^{{ - 1}}} - {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} 3}} \right. \kern-0em} 3}}}} \right]} \right. + \\ \left. { + \,\,\frac{{{{m}_{3}}}}{{1 - {{m}_{1}}}}\left[ {1 - \frac{{1 - {{m}_{1}}}}{{{{{\left( {1 - {{{{\nu }}}_{{13}}}} \right)}}^{{ - 1}}} - {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} 3}} \right. \kern-0em} 3}}}} \right]} \right), \\ \end{gathered} $Дальнейшее увеличение объемной доли оолитов в фосфорите до 60% приводит к точечному контактированию включений с последующим смыканием изолированных объемов, при этом структура в целом приближается к структуре с взаимопроникающими компонентами. Такую систему можно отнести к переходной, которой соответствуют карбонатно-кремнистые и частично высококачественные фосфориты [13].
Структура с взаимопроникающими компонентами является инвариантной по отношению к свойствам компонент и для ориентировочных расчетов можно принять соответствующие данной структуре значения объемной доли фосфата, равные 70% (Р2O5 29%).
В фосфоритах с большей концентрацией фосфата наблюдается появление фосфатцемента и плотное слияние оолитов фосфатного, вещества, Одновременно с этим нарушается непрерывность доминировавшей ранее компоненты (цемента) и происходит переход структуры от взаимопроникающих компонент к изолированным включениям, и смена доминирующей компоненты [14]. К данному типу структуры относятся почти все высококачественные фосфориты с содержанием фосфата 73.8% (Р2О5 > 30%). Структура фосфорита оолитовая. Порода представлена плотно прилегающими друг к другу оолитами зональноконцентрического строения, где чередуются зерна халцедона с фосфатным веществом. Размер оолитов в среднем около 0.2 мм. Цемент породы – аморфный фосфат. Карбонаты наблюдаются в цементе пор и контактовом цементе (в пунктах соприкосновения зерен). В качестве терригенных примесей присутствуют угловатые зерна кварца размером 0.08–0.2 мм. Кварц представлен в основном обломками монокристаллов, реже обломками поликристаллических образований. По трещинкам породы развиты минералы железа. Коэффициент теплопроводности этих фосфоритов можно рассчитать по модели трехкомпонентной смеси, в которой цементом служит фосфатное вещество.
Данные математические модели теплопроводности могут быть применены в любом температурном интервале, где сохраняется неизменной структура самого материала и известны коэффициенты теплопроводности составляющих компонент. К таким материалам можно отнести фосфатизированные кремни, кремнистые, высококачественные и мономинеральные фосфориты.
Однако описать изменения коэффициента теплопроводности от температуры высококарбонатных фосфоритных руд из-за наличия эндотермических реакций диссоциации доломита по приведенным моделям не удается. Это связано с изменением структуры реагирующего материала и соотношения компонент, а следовательно и его, теплопроводности от кинетических параметров реакции декарбонизации
СТРУКТУРНАЯ МОДЕЛЬ ТЕПЛОПРОВОДНОСТИ КОМПОЗИЦИОННОГО МАТЕРИАЛА С РЕАГИРУЮЩИМИ ВКЛЮЧЕНИЯМИ
Включения реагирующей компоненты фосфоритов представляют собой крупно- или среднекристаллические зерна карбоната размером от 0.001 до 0.2 мм, которые в процессе реакции термодеструкции образуют новые вещества: СаМg(СО3)2 = СаО + МgO + CO2, которые в свою очередь вступают в твердофазные реакции с образованием ортосиликатов кальция и магния.
Различными методами [15] было показано, что для разложения отдельных частиц карбонатов применимо топохимическое представление о сокращающейся оболочке.
Как показывают исследования [16] процесс диссоциации карбонатов протекает преимущественно на границе раздела фаз, с появлением в этих местах новой фазы. Развитие процесса может осуществляться как за счет роста старых зародышей, так и путем образования новых. Причем условием возникновения зародышей новой фазы в толще материала является значительное отклонение от состояния равновесия [17].
Модель реагирующего зерна может быть представлена исходным непрореагировавшим материалом (доломитом), заключенным в оболочку продуктов реакции – порошкообразную смесь окислов СаО и МgО или ортосиликатов кальция и магния в кремнисто-карбонатных рудах. Объемное соотношение этих двух фаз будет изменяться в процессе декарбонизации и определяться степенью прокалки фосфорита:
При этом масса реагирующего материала будет представлять собой матричную структуру изолированных включений непрореагировавшего материала в цементе, состоящем из продуктов реакции. Теплопроводность такой системы можно определить по известному соотношению:
(2)
$\frac{{{\lambda }}}{{{{{{\lambda }}}_{{{\text{об}}}}}}} = 1 - \frac{{{{m}_{{\text{с}}}}}}{{{1 \mathord{\left/ {\vphantom {1 {\left( {1 - {{\nu }}} \right) - {{\left( {1 - {{m}_{{\text{с}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {{m}_{{\text{с}}}}} \right)} 3}} \right. \kern-0em} 3}}}} \right. \kern-0em} {\left( {1 - {{\nu }}} \right) - {{\left( {1 - {{m}_{{\text{с}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - {{m}_{{\text{с}}}}} \right)} 3}} \right. \kern-0em} 3}}}}},\,\,\,\,{{\nu }} = \frac{{{{{{\lambda }}}_{{\text{c}}}}}}{{{{{{\lambda }}}_{{{\text{об}}}}}}},$Используя метод расчета многокомпонентной системы путем последовательного сведения к двухкомпонентной можно расcчитать коэффициент теплопроводности композиционного материала с реагирующими включениями.
Таким образом, для описания теплопроводности фосфатного сырья различных месторождений необходимо знать температурную зависимость теплопроводности отдельных компонент, химический или минералогический состав и кинетические параметры гетерогенной реакции диссоциации карбонатов для данного типа фосфорита.
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ТЕПЛОПРОВОДНОСТИ ОСНОВНЫХ ПОРОДООБРАЗУЮЩИХ МИНЕРАЛОВ ФОСФОРИТОВ
Для корректного описания теплопроводности фосфоритов на основе существующих моделей следует предварительно определить теплопроводность входящих в них компонент. Это можно осуществить обработкой экспериментальных значений теплопроводности и плотности методом наименьших квадратов с использованием вида функции для выбранной модели.
В данной работе использован именно такой подход, когда для плотности образцов использовалась зависимость: $\rho = \sum\limits_i {{{m}_{i}}{{\rho }_{i}}} $ где: mi – объемная доля i – того компонента; ${{{{\rho }}}_{i}}$ – плотность i – того компонента.
Для расчета коэффициента теплопроводности фосфоритов необходимо знать объемные доли основных компонент. Для этого необходимо определить удельные плотности минералов, составляющих фосфориты.
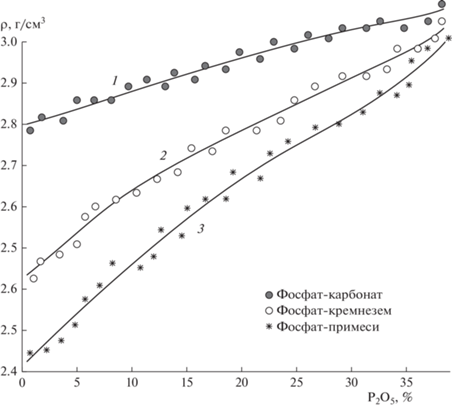
Зависимость плотности образцов от содержания Р2О5 носит явный характер для карбонатных, карбонатно-кремнистых и высококачественных фосфоритов, асимптотически приближаясь к значению плотности, равному 3.1 г/см для субмономинерального фосфорита.
Наименьшую плотность имеют фосфатизированные сланцы. Их плотность лежит в интервале от 2.4 до 2.70 г/см3 при значениях от 0 до 10%. Это объясняется различной порозностью образцов. Отдельно выделяются карбонатные породы (доломиты) и высококарбонатные фосфориты. Их плотность лежит в интервале 2.75–2.85 г/см3 при содержании в них Р2О5 до 15%. Для других видов фосфоритов плотности определились следующим образом:
– карбонатные фосфориты с Р2О5 = 18–25% ρ = 2.75–2.92 г/см3;
– карбонатно-кремнистые высококачественные с Р2О5 = 25–30% ρ = 2.9–3.01 г/cм3;
– высококачественные до субмономинеральных с Р2О5 = 30–35% ρ = 2.96–3.1 г/см3.
Из данной зависимости можно определить плотности минералов или основных компонент, составляющих фосфориты. Так плотность фосфатного вещества оолитов и цемента равна 3 г/см3; плотность карбонатов (доломит кальцит) лежит в интервале 2.8–2.85 г/см3; плотность кремнезема равна 2.5–2.6 г/см3 , что согласуется с литературными данными [18–20].
Следовательно, зная точные значения плотности фосфоритов, можно выделить руды наиболее богатые фосфатным веществом.
На рис. 1 показаны расчетные значения плотности двухкомпонентных систем и результаты натурных экспериментов: 1 – фосфат-карбонат; 2 – фосфат-кремнезем; 3 – фосфат-примеси. Смещение экспериментальных значений плотности по-видимому обусловлено разностью порозности образцов.
Характерная зависимость плотности фосфоритов от содержания фосфата позволяет предположить о существовании аналогичных корреляций и других свойств фосфоритов. В частности, проведенное в данной работе обобщение по теплопроводности методом наименьших квадратов показало, что зависимость от минерального состава весьма существенна [21].
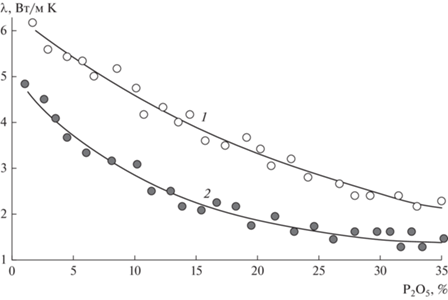
На рис. 2 представлены экспериментальные значения коэффициентов теплопроводности фосфоритов (1) и фосфатизированных сланцев (2), при Т = 373 К, т.е. в просушенном состоянии, в зависимости от процентного содержания Р2О5. Можно отметить, что с увеличением содержания фосфатного вещества в образце, теплопроводность фосфоритов снижается. Наименьшую теплопроводность имеют высококачественные фосфориты. Наибольшие значения (λ ~ 6.5 Вт/м К) имеют фосфатизированные кремни.
Высококарбонатные породы (фосфатизированный доломит) имеют коэффициент теплопроводности в районе 4.0 Вт/м К, а доломит – 4.5 Вт/м К. Для проведения расчетов по структурным моделям предварительно были определены значения коэффициентов теплопроводности отдельных компонент, в качестве которых были приняты, как указано выше, фосфат, карбонаты, кремнезем и примеси, и модель выбиралась согласно описанным выше положениям. Определение теплопроводности составляющих проведено методом наименьших квадратов (нелинейный случай). В качестве определяющей выборки экспериментальных значений теплопроводности фосфоритов выбирались значения, полученные во всем диапазоне минералогического состава фосфоритов.
Таким образом, были получены коэффициенты теплопроводности фосфатного вещества, кремнезема, сырого и прореагировавшего карбоната.
Получить стройную зависимость изменения коэффициента теплопроводности примесей от температуры не удалось, это по-видимому связано со значительным различием состава примесей в отобранных для расчетов фосфоритов и их незначительным объемным содержанием. В таком случае расчет проводился для трех компонент, результаты которых представлены на рис. 3.
Рис. 3.
Зависимость коэффициента теплопроводности от температуры: 1 – фосфатной компоненты; 2 – кремнистой компоненты; 3 – непрореагировавшей карбонатной компоненты; 4 – прореагировавшей карбонатной компоненты
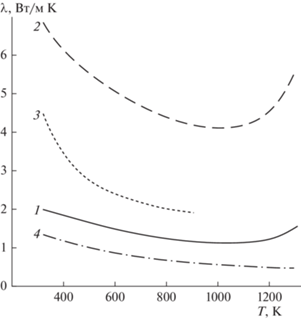
Температурные зависимости теплопроводности компонент достаточно хорошо описываются полиномами второй степени:
для фосфатного вещества λ = 12.6 – 1.75 × 10–2Т + + 0.95 × 10–5Т 2 Вт/м К;
для кремнистой составляющей 2.82 – 0.3 × 10–2Т + + 0.14 × 10–5Т 2 Вт/м·К;
для непрореагировавшей карбонатной компоненты 7.58 – 1.08 × 10–2Т + 0.49 × 10–5Т 2 Вт/м К;
для прореагировавших карбонатов 1.52 – 0.13 × × 10–2Т + 0.48 × 10–6Т 2 Вт/м К;
Так как карбонаты фосфоритов вступают в реакцию декарбонизации, начиная с температуры 850–900 К, то получить экспериментально значения теплопроводности непрореагировавшей компоненты в зоне реакции весьма сложно [22]. Для расчетов теплопроводности фосфоритов в зоне реакции использовались экстраполированные значения коэффициента теплопроводности непрореагировавших карбонатов.
СОПОСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТОВ ТЕПЛОПРОВОДНОСТИ С НАТУРНЫМИ ЭКСПЕРИМЕНТАМИ
Для подтверждения предложенных в данной работе методик расчета теплопроводности карбонатно-фосфатных руд было проведено сопоставление расчетов с экспериментом.
На рис. 4 приведены экспериментальные значения коэффициента теплопроводности высококачественного фосфорита и расчет по структурной модели (1) для трехкомпонентной системы. Для высококачественных фосфоритов погрешность описа-ния теплопроводности не более 6–8%.
Рис. 4.
Сопоставление расчета с натурным экспериментом для теплопроводности высококачественного фосфорита.

Для определения истинного коэффициента теплопроводности в зоне температур реакции декарбонизации карбонатов следует пользоваться формулой (2), значениями коэффициентов теплопроводности сырых и отожженных компонентов и степенью превращения данного фосфорита в определенных условиях. Сравнение на рис. 5 дает погрешность в зоне реакции 5–7%.
Рис. 5.
Сопоставление расчета теплопроводности в зоне реакции высококарбонатного фосфорита с экспериментом.
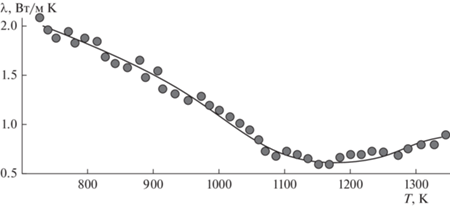
Качественное и количественное совпадение опытных и расчетных значений теплопроводности можно считать вполне удовлетворительным во всем диапазоне изменения температурных параметров.
ЗАКЛЮЧЕНИЕ
В результате представленных исследований, получены следующие основные результаты.
Проведено комплексное исследование температурных зависимостей теплопроводности основных типов литологических разностей фосфатных руд. Научно обосновано, что теплопроводности сырьевых фосфатных материалов существенно различны и определяются структурой и минералогическим составом пород.
В процессе нагрева, в результате физико-химических превращений теплопроводность претерпевает существенные изменения. Диапазон изменения коэффициента теплопроводности 0.5– Вт/м К при температурах от 300 до 1300 К.
Разработана база данных по определению теплоемкостей ряда фосфоритов необходимые для теплотехнических расчетов.
Обобщение экспериментальных данных показывает, что можно выделить основные типы мономинерального сырья с определенным набором технологических свойств, которые могут быть приняты в качестве основных компонент в структурной модели технологических свойств. В качестве таковых были выбраны кремнезем, карбонаты, фосфатное вещество и прочие примеси, теплопроводности которых определены на основе обработки данных и приведены в работе.
На основе анализа применимости структурных моделей теплопроводности композиционных материалов к фосфоритам некоторых месторождений разработана комбинированная структурная модель теплопроводности композиционного материала с реагирующими включениями, позволяющая рассчитать коэффициент теплопроводности всех основных типов фосфоросодержащих руд в широком интервале температур, включая зону эндотермических реакций декарбонизации.
Предложенные в работе методы исследования теплопроводности могут быть распространены на изучение закономерностей широкого класса композиционных реагирующих материалов. Разработанные методы расчета теплопроводности фосфоритов могут быть использованы для оперативной адаптации промышленных установок обжига и руднотермических печей к свойствам обрабатываемых материалов существующих и новых месторождений.
ИСТОЧНИКИ ФИНАНСИРОВАНИЯ
Раздел статьи посвященный разработке структурной модели теплопроводности композиционного материала с реагирующими включениями карбонатов выполнен в части раздела работ на поликапиллярных колонках при финансовой поддержке РНФ в рамках научного проекта № 21-79-30029
Раздел по определению коэффициентов теплопроводности основных породообразующих минералов фосфоритов выполнен при финансовой поддержке РНФ в рамках научного проекта № 22-11-00335
ОБОЗНАЧЕНИЯ
| α | степень реагирования реакции декарбонизации |
| λ | коэффициент теплопроводности, Вт/м К |
| ρ | плотность, кг/м3 |
| Т | температура, К |
| m | объемная доля компонента |
ИНДЕКСЫ
Список литературы
Meshalkin V.P., Dovì V.G., Bobkov V.I., Belyakov A.V., Вutusov O.B., Garabadzhiu A.V., Burukhina T.F., Khodchenko S.M. State of the art and research development prospects of energy and resource-efficient environmentally safe chemical process systems engineering // Mendeleev Communications. 2021. 31(5). P. 593–604.
Егоров А.Ф., Савицкая Т.В., Михайлова П.Г. Современное состояние в областианализа, синтеза и оптимального функционирования многоассортиментных цифровых химических производств: аналитический обзор // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 154–187.
Мешалкин В.П., Дли М.И., Пучков А.Ю., Бобков В.И., Казак А.С. Программное обеспечение эффективных химических технологий переработки отходов апатит-нефелиновых руд // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 496. № 1. С. 48–54.
Леонтьев Л.И., Григорович К.В., Костина М.В. Фундаментальные исследования как основа создания новых материалов и технологий в области металлургии. Часть 1 // Известия высших учебных заведений. Черная металлургия. 2018. Т. 61. № 1. С. 11–22.
Борисов В.В., Курилин С.П., Луферов В.С. Нечеткие реляционные когнитивные темпоральные модели для анализа и прогнозирования состояния сложных технических систем // Прикладная информатика. 2022. Т. 17. № 1(97). С. 27–38.
Bobkov V.I., Fedulov A.S., Dli M.I., Meshalkin V.P., Morgunova E.V. Scientific basis of effective energy resource use and environmentally safe processing of phosphorus-containing manufacturing waste of ore-dressing barrows and processing enterprises // Clean Technologies and Environmental Policy. 2018. T. 20. № 10. C. 2209–2221.
Курилин С.П., Соколов А.М., Прокимнов Н.Н. Компьютерная программа для эксплуатационной диагностики электромеханических систем на основе топологического подхода // Прикладная информатика. 2021. Т. 16. № 4(94). С. 62–73.
Meshalkin V., Bobkov V., Dli M., Dovì V. Optimization of energy and resource efficiency in a multistage drying process of phosphate pellets // Energies. 2019. T. 12. № 17. C. 3376.
Цирлин А.М., Гагарина Л.Г., Балунов А.И. Синтез теплообменных систем, интегрированных с технологическим процессом // Теоретические основы химической технологии. 2021. Т. 55. № 3. С. 347–358.
Мешалкин В.П., Панченко С.В., Бобков В.И., Дли М.И. Анализ теплофизических и химико-технологических свойств отходов горно-обогатительных комбинатов // Теоретические основы химической технологии. 2020. Т. 54. № 1. С. 30–37.
Гуськов А.В., Гагарин П.Г., Гуськов В.Н., Тюрин А.В., Гавричев К.С. Теплоемкость и термодинамические функции твердого раствора LU2O3–2HFO2 // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 500. № 1. С. 84–88.
Гагарин П.Г., Гуськов А.В., Гуськов В.Н., Хорошилов А.В., Гавричев К.С., Иванов В.К. Теплоемкость и термическое расширение М-ортотанталата тербия // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 499. № 1. С. 63–65.
Elgharbi S., Horchani-Naifer K., Férid M. Investigation of the structural and mineralogical changes of Tunisian phosphorite during calcinations // J. Thermal Analysis and Calorimetry. 2015. V. 119. № 1. P. 265–271.
Пучков А.Ю., Лобанева Е.И., Култыгин О.П. Алгоритм прогнозирования параметров системы переработки отходов апатит-нефелиновых руд // Прикладная информатика. 2022. Т. 17. № 1(97). С. 55–68.
Буткарев А.А., Вербыло С.Н., Бессмертный Е.А., Буткарева Е.А. Совершенствование и практическое использование методологии ВНИИМТ для оптимизации теплотехнических схем обжиговых конвейерных машин с рабочими площадями 278, 306 и 552 м2 // Сталь. 2020. № 5. С. 7–13.
Wang S., Guo Y., Zheng F., Chen F., Yang L. Improvement of roasting and metallurgical properties of fluorine-bearing iron concentrate pellets // Powder Technology. 2020. 376. P. 126–135.
Nayak D., Ray N., Dash N., Pati S., De P.S. Induration aspects of low-grade ilmenite pellets: Optimization of oxidation parameters and characterization for direct reduction application // Powder Technology. 2021. 380. P. 408–420.
Кржижановский Р.Е., Штерн З.Ю. Теплофизические свойства неметаллических материалов (окислы). Л.: Энергия, 1973. 335с.
Справочник (кадастр) физических свойств горных пород. Под ред. Мельникова Н.В., Ржевского В.В., Протодьяконова М.М. М.: Недра, 1975. 281 с.
Булах А.Г., Булах К.Г. Физико-химические свойства минералов компонентов гидротермальных растворов. Л.: Недра, 1978.
Тураев Д.Ю., Почиталкина И.А. Теоретические и практические основы селективного извлечения фосфат-ионов из фосфатных руд с высоким содержанием примесей железа рециркуляционным методом // Теоретические основы химической технологии. 2022. Т. 56. № 2. С. 252–264.
Кольцов Н.И. Линейные концентрационные и температурные законы сохранения в открытом безградиентном химическом реакторе // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 210–215.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии