Теоретические основы химической технологии, 2022, T. 56, № 6, стр. 735-747
Сравнение результатов расчета массообмена в распылительных аппаратах для режимов прямо- и противотока фаз
Н. Н. Симаков *
Ярославское высшее военное училище противовоздушной обороны
Ярославль, Россия
* E-mail: nik_simakov@mail.ru
Поступила в редакцию 05.05.2022
После доработки 03.06.2022
Принята к публикации 03.07.2022
- EDN: NFVKWZ
- DOI: 10.31857/S0040357122060161
Аннотация
В статье проведено сравнение результатов расчета гидродинамики двухфазного потока, образующегося при форсуночном распыливании жидкости в газе, с использованием в численной модели двух способов учета раннего кризиса сопротивления капель: 1) зависимости их коэффициента сопротивления Cd(r, z) от координат точек в свободном факеле распыла, 2) его зависимости Cd = 2000/Re2 от числа Рейнольдса, более предпочтительной при расчете распылительных аппаратов. Представлены также результаты расчета межфазного массообмена в распылительных аппаратах в режимах прямо- и противотока фаз с использованием раннее предложенной модели гидродинамики и массообмена фаз в факеле распыла. Получены распределения скоростей фаз и концентрации газовой примеси в потоке, а также интегральные характеристики массообменных аппаратов, которые приводят к выводу об отсутствии существенных преимуществ противоточных аппаратов перед прямоточными.
ВВЕДЕНИЕ. ОСОБЕННОСТИ ВЗАИМОДЕЙСТВИЯ ФАЗ В ФАКЕЛЕ РАСПЫЛА ФОРСУНКИ
В таких отраслях экономики, как: химические технологии, энергетика, транспорт, – используют распыливание жидкости в газе, например, с помощью форсунок. Это делается для увеличения межфазной поверхности и интенсификации тепломассообмена фаз в процессах: сжигания и пиролиза жидких углеводородов, сушки и гранулирования полимеров, мокрой очистки воздуха от пыли и вредных газовых примесей и т.п.
Актуальность данной работы также, как работ [1–3], обусловлена тем, что удовлетворительные методы расчета таких процессов до недавнего времени не были разработаны. Возможной причиной представляется то, что при расчете межфазного взаимодействия в сильнотурбулентном потоке факела распыла не учитывалось обнаруженное в эксперименте возникновение раннего кризиса сопротивления капель [1].
В работах [2] и [3, Sect. 7.2] в качестве основы описания указанных сложных процессов изложена модель гидродинамики факела распыла, сочетающая в себе два известных подхода: метод взаимопроникающих континуумов [4] и теорию турбулентных струй [5].
При моделировании газокапельного потока гидродинамическую силу сопротивления капли обтекающему ее газу обычно вычисляют по формуле
(1)
$F = {{C}_{{{\text{d\;}}}}}S\rho {{V_{{\text{r}}}^{2}} \mathord{\left/ {\vphantom {{V_{{\text{r}}}^{2}} 2}} \right. \kern-0em} 2},$Для ламинарного обтекания шара (капли) газом при малых числах Рейнольдса Re = Vrdρ/μ $ \ll $ 1 справедлива формула Стокса
(2)
${{C}_{{{\text{d\;}}}}} = {{24} \mathord{\left/ {\vphantom {{24} {{\text{Re}}}}} \right. \kern-0em} {{\text{Re}}}},$(3)
${{C}_{{{\text{d\;}}}}} = {{{\text{ }}24} \mathord{\left/ {\vphantom {{{\text{ }}24} {{\text{Re}}}}} \right. \kern-0em} {{\text{Re}}}} + {4 \mathord{\left/ {\vphantom {4 {{\text{R}}{{{\text{e}}}^{{1/3}}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}^{{1/3}}}}},$Согласно экспериментальным данным [1] в сильнотурбулентном потоке при Re порядка 100 величина Cd для капель может уменьшаться в 4–7 раз по сравнению с известными и соответствующими формуле (3) значениями.
Это открытое новое явление было названо ранним кризисом сопротивления по аналогии с известным кризисом сопротивления шара, обтекаемого потоком при Re = Reкр ≈ (2–3) × 105 [9, 10]. Установлено, что с увеличением степени турбулентности потока значение критического числа Рейнольдса Reкр уменьшается [9]. Наименьшими ранее известными были значения Reкр = 400–2200 [11, 12].
В экспериментальной работе [1] самый ранний кризис сопротивления капель в факеле распыла форсунки обнаружен при еще меньших значениях Reкр = 40–120, за что и назван ранним. Ранний кризис сопротивления наблюдался также на одиночном твердом шарике, обтекаемом газовой струей в конфузоре [3, Sect. 5.1].
Несмотря на давнюю известность вышеупомянутых работ [11, 12] о кризисе сопротивления шара в турбулентном газовом потоке и более поздние работы [1–3] о самом раннем кризисе сопротивления, сопровождаемом кризисом тепломассообмена, эти кризисные явления никак не учитываются в относительно свежих работах [13, 14] по близкой к данной статье тематике. Используемые в них аппроксимации коэффициентов сопротивления и тепломассообмена относятся к случаю ламинарного обтекания шара газовым потоком.
Описанная в работах [2] и [3, Sect. 7] модель гидродинамики факела распыла с учетом раннего кризиса сопротивления капель, будучи дополненной уравнениями, учитывающими их массообмен с газовым потоком, позволила рассчитать в согласии с опытными данными двухфазный поток, а также межфазный массообмен в нем.
При расчете факела распыла экспериментальные данные о величине Cd капель аппроксимировались двумя способами в виде функций: 1) Cd(r, z) – от координат точек в факеле распыла и 2) Cd(Re) – от числа Рейнольдса.
Для капель, движущихся по оси факела, в качестве хорошего приближения при 40 < Re < 110 в работе [1] предложена формула
(4)
${{C}_{{\text{d}}}} = {{2000} \mathord{\left/ {\vphantom {{2000} {{\text{R}}{{{\text{e}}}^{2}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}^{2}}}}.$В работах [2] и [3, Sect. 7] приведены результаты расчетов факела распыла с использованием полученных из данных эксперимента [1] формул
(5)
${{C}_{{\text{d}}}}(r,{\text{ }}z) = {{C}_{{\text{d}}}}(0,{\text{ }}z)\left( {0.45\exp \left( {{{--6r} \mathord{\left/ {\vphantom {{--6r} {{{r}_{{\text{m}}}}}}} \right. \kern-0em} {{{r}_{{\text{m}}}}}}\left( z \right)} \right) + 0.55} \right),$(6)
${{C}_{{\text{d}}}}(0,z) = 0.45{\text{ }}{{({z \mathord{\left/ {\vphantom {z {0.1}}} \right. \kern-0em} {0.1}})}^{{--3/4}}}.$Причем на оси факела распыла уменьшение Cd с увеличением расстояния z от форсунки вполне удовлетворительно аппроксимировалось формулой (6).
Граница факела rm(z) = z tg αm в виде поверхности конуса определяется наиболее удаленными от оси траекториями капель, образующими с ней угол αm= 32.5°, равный половине корневого угла факела. На границе при z > 0.1 м скорость газа согласно эксперименту [1] пренебрежимо мала по сравнению со скоростью капель: w $ \ll $ u = = uz/cosαm ≈ Vr. С учетом этого для нескольких поперечных сечений факела (z = 0.1, 0.3, 0.5, 0.7 м) были получены значения Cd(rm(z)), которые оказались, примерно, вдвое (в 1.8 раза) меньше, чем Cd(0, z) в том же сечении на оси факела. В расчетах это уменьшение Cd по радиусу r факела учитывалось вторым множителем в правой части формулы (5).
Поле скоростей газа в аппарате из-за влияния стенок его корпуса может сильно отличаться от поля скоростей в свободном факеле. Это не учитывается в способе определения Cd(r, z) как функции координат, что является его недостатком при расчете факела распыла в аппарате. Заметим, что обычно в расчетах изменение коэффициента сопротивления учитывается в виде функции Cd(Re) от числа Рейнольдса, аналогично уравнениям (2)–(4).
Целями данной работы было, во-первых, устранение указанного недостатка, во-вторых, выполнение нового расчета гидродинамики и межфазного массообмена в распылительном аппарате для сравнения прямо- и противоточного режимов его работы.
АППРОКСИМАЦИЯ КОЭФФИЦИЕНТА СОПРОТИВЛЕНИЯ КАПЕЛЬ ФУНКЦИЕЙ Cd(Re) В РАСЧЕТЕ СВОБОДНОГО ФАКЕЛА РАСПЫЛА
Формула, рекомендуемая для расчета коэффициента сопротивления капель с учетом его раннего кризиса. Для определения зависимости Cd(Re), справедливой не только на оси свободного факела, но и в других частях занимаемого им пространства, необходимо учесть следующие обстоятельства и соображения.
В работе [1] представлены некоторые результаты экспериментального исследования факела распыла воды в воздухе, создаваемого центробежно-струйной форсункой типа ВТИ с диаметром выходного отверстия dh = 2 мм при избыточных давлениях воды PL = 0.3, 0.5, 0.9 МПа.
В этом эксперименте наиболее подробные данные для скоростей фаз были получены в точках на оси факела и в нескольких его поперечных (радиальных) сечениях: z = 0.1, 0.3, 0.5, 0.7 м. У капель измерялась только осевая компонента скорости uz, у газа – модуль вектора w полной скорости и его угол α(r, z) с осью факела. Причем оказалось, что направление вектора w в точке измерения (r, z) примерно совпадало с направлением луча, идущего через нее из центра выходного отверстия форсунки, т.е. с направлением движения капель, увлекающих газ.
С учетом этого обстоятельства в работе [15] для факела в целом (при z > 0.1 м) была подтверждена зависимость Cd(Re) вида (4), представленная на рис. 1, воспроизведенном и аналогичном рисунку 2 из [15].
Рис. 1.
Зависимости Cd(Re): символы – обобщение экспериментальных данных [1] для капель воды в факеле распыла форсунки, сплошная кривая – аппроксимация этих данных по формуле (4), штриховая линия – расчет по формуле (3) Клячко, пунктирная – по формуле (2) Стокса.
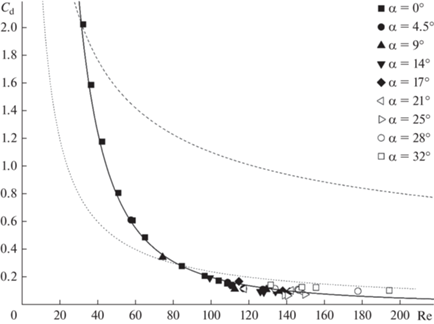
Очевидно, экспериментальные точки, полученные в разных частях факела при PL = 0.5 МПа, расположены вблизи одной общей кривой, соответствующей формуле (4). Это значит, что ранний кризис сопротивления капель в факеле распыла форсунки действительно возникает и обнаружен для всей совокупности капель в объеме факела при z > 0.1 м. При Re > 100 величина Cd уменьшается не менее чем в 5–10 раз по сравнению с зависимостью (3) Клячко.
Заметим, что справедливость формулы (4), полученной в [1] сначала для капель на оси факела распыла при PL = 0.5 МПа, подтвердилась и при других давлениях (0.3 и 0.9 МПа) в форсунке, соответствующих им разных расходах жидкости и разных средних размерах капель.
Таким образом, в расчетах факела распыла в целом можно использовать формулу (4) при разных PL и, возможно, разных dh.
Кроме того, стоит заметить, что в автомодельной зоне факела распыла при z > 300 мм
с приблизительным отклонением ±0.05.Результаты расчета гидродинамики свободного факела распыла с использованием Cd(Re). Формула (4), полученная ранее только для точек на оси факела распыла и подтвержденная в работе [15] для всего занимаемого факелом пространства, совместно с раннее предложенной в работах [2] и [3, Sect. 7.2] моделью гидродинамики факела распыла была использована в новом его расчете, в котором для сравнения с экспериментом были получены пространственные распределения скоростей фаз.
Результаты расчета представлены на рис. 2–3.
Рис. 2.
Изменение безразмерных скоростей капель uz и газа wz на оси факела: символы – эксперимент, кривые – расчет с учетом кризиса сопротивления по формуле (4); uz1 и wz1 – расчет без учета кризиса сопротивления с использованием формулы (3); j = –25 – положение выходного отверстия форсунки.

Рис. 3.
Радиальные профили аксиальной скорости газа в свободном факеле распыла на различных расстояниях z = = (100 + 4j) мм от форсунки, линии – расчет, точки-символы – эксперимент; радиус точки измерения r = 4i, мм.

На рис. 2 приведены в сравнении с экспериментом [1] для PL = 0.5 МПа результаты расчета безразмерных скоростей фаз на оси факела при значениях Cd, рассчитанных по формулам (4) и (3). В первом случае очевидно согласие расчета с экспериментом. Во втором капли тормозятся, а газ разгоняется сильнее, чем по эксперименту. Значения безразмерных скоростей фаз получены делением действительных их значений на начальную скорость истечения струи жидкости из форсунки u0 = kV(2PL/ρ)1/2 = 23.7 м/с, где kV = 0.75 – коэффициент расхода.
На рис. 3 представлены радиальные профили аксиальной скорости газа в факеле распыла на расстояниях z = 100, 150, 300, 500 и 700 мм от форсунки. Точками показаны результаты эксперимента [1], кривыми – результаты расчета.
Очевидно, что приведенные на рис. 2–3 результаты расчета свободного факела распыла форсунки с учетом кризиса сопротивления капель по формуле (4) в целом находятся в хорошем согласии с данными эксперимента для значительной по протяженности области факела: z = 100–700 мм от форсунки.
Заметим, что при расчете двухфазного потока в свободном факеле распыла результаты, полученные при использовании зависимостей: 1) Cd(r, z) по формулам (5)–(6), или 2) Cd(Re) по формуле (4), – практически одинаковы и в одинаковой степени согласуются с экспериментом, по данным которого эти разные зависимости были получены. Другое дело, расчет двухфазного потока, стесненного стенкой распылительного аппарата. В этом случае было бы предпочтительнее проводить расчет, используя зависимость вида Cd(Re), учитывающую возможное изменение полей скоростей фаз из-за влияния стенки аппарата, в частности, путем трения газа о них.
СРАВНЕНИЕ ХАРАКТЕРИСТИК ПРЯМОТОЧНОГО И ПРОТИВОТОЧНОГО РЕЖИМОВ РАБОТЫ МАССООБМЕННОГО РАСПЫЛИТЕЛЬНОГО АППАРАТА
Расчет массообмена фаз в распылительном аппарате. Межфазный массообмен чаще всего сопровождается параллельно и одновременно протекающим теплообменом, что осложняет моделирование и расчет совмещенного процесса.
В процессе мокрой газоочистки воздуха от вредных газовых примесей, например, от оксида серы SO2 межфазный массообмен можно рассчитывать без учета теплообмена, как это сделано в работах [2] и [3, Sect. 7.3]. Этот подход использован также и в данной работе, включая ту же процедуру расчета массообмена, геометрию модели и соответствующие уравнения.
Ниже представлено исследование влияния каждого из двух вышеуказанных способов аппроксимации коэффициента сопротивления капель: 1) Cd(r, z) или 2) Cd(Re), – на результаты расчета профилей скорости газа, концентрации примесей в нем и ряда технологических характеристик прямоточного распылительного аппарата при изменении его конструктивных размеров: радиуса Ra и высоты H.
Все расчеты проведены для цилиндрического распылительного аппарата с вертикальной осью и одной центробежно-струйной форсункой, расположенной соосно в верхней части аппарата, в предположении, что из выходного отверстия форсунки, имеющего диаметр dh= 2 мм, струя жидкости (воды) под избыточным давлением PL = 0.5 МПа вытекала в воздух вертикально вниз.
На рис. 4–7 представлены некоторые результаты расчетов, полученные для прямоточного режима распылительного аппарата радиусом Ra = 140 мм, высотой H = 1100 мм, при малом перепаде давлений газа ΔP = 0.7 Па с использованием для аппроксимации коэффициента Cd сопротивления капель двух вышеуказанных способов: 1) Cd(r, z) по формулам (5)–(6) и 2) Cd(Re) по формуле (4).
Рис. 4.
Сравнение радиальных профилей аксиальной скорости газа wz(i, j) в различных сечениях (z = 100 + 4j, мм) прямоточного распылительного аппарата, темные символы – по формулам (5) и (6), светлые – по формуле (4).

Рис. 5.
Сравнение радиальных профилей концентрации газовой примеси c(i, j) в тех же сечениях распылительного аппарата и при тех же условиях, как на рис. 4.
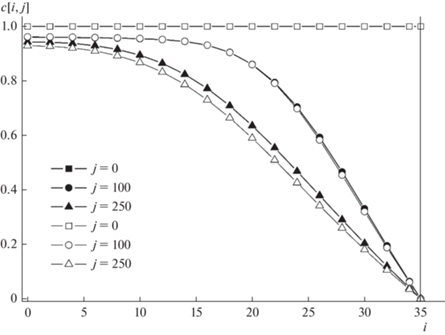
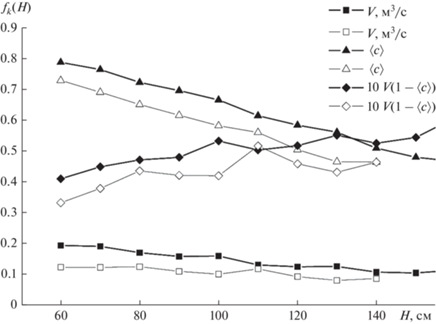
Рис. 6.
Зависимости технологических характеристик V, $\left\langle c \right\rangle $, V(1 – $\left\langle c \right\rangle $) распылительного аппарата от его радиуса Ra при H = 110 см, ΔP = 0.7 Па, темные символы – для Cd(r, z) по формулам (5), (6), светлые – для Cd(Re) по формуле (4).

Заметим, что вертикальная прямая при i = 35 на рис. 4 и 5 обозначает границу расчетной области на внутренней поверхности стенки аппарата.
На рис. 4 очевидно, скорости газа в верхней (для j = 0, z = 100 мм) части аппарата при аппроксимации Cd(r, z) меньше, чем при Cd(Re), но сближаются в его нижней части (при j = 250, z = 1100 мм).
На рис. 5 показаны профили безразмерной относительной концентрации c(i, j) примеси газа, которая равна отношению ее абсолютных концентраций на выходе и входе газа в аппарат. Очевидно, концентрация газовой примеси, одинаковая c(i, j) = 1 во всех точках входного для газа сечения аппарата, к выходу из него уменьшается при Cd(r, z) немного меньше, чем при Cd(Re).
На рис. 6 представлены полученные при тех же двух способах аппроксимации величины Cd результаты расчета для технологических характеристик распылительного аппарата в прямоточном режиме, а, именно: зависимости максимального (при малом противодавлении ΔP) расхода газа V, средней концентрации $\left\langle c \right\rangle $ газовой примеси и убыли ее расхода V (1 – $\left\langle c \right\rangle $) в выходном сечении аппарата от его радиуса Ra.
Объемный расход газа определялся в расчетах как интеграл
по площади нижнего (z = H) сечения аппарата.На рис. 7 показаны изменения тех же, что и на рис. 6, технологических характеристик распылительного аппарата от его высоты H при перепаде давления ΔP = 7 Па, на порядок большем, чем в расчете для рис. 6, но среднем для прямоточного режима.
Различие результатов расчета на рис. 4–7 для двух вышеуказанных способов аппроксимации коэффициента Cd обусловлено тем, что значения Cd(r, z) получены по экспериментальным данным для полей скоростей газа и капель в свободном факеле распыла, а значения Cd(Re) вычисляются при расчете двухфазного потока с учетом поля скоростей газа, измененного влиянием корпуса аппарата, в частности, ограничением пространства движения газа и его трением о внутреннюю поверхность стенки корпуса.
Важным преимуществом формулы (4) явилось то, что для капель на оси свободного факела распыла она оказалась справедливой при разных давлениях жидкости в форсунке PL = 0.3, 0.5, 0.9 МПа, при соответствующих им разных расходах VL жидкости, разных средних размерах d капель. С учетом обобщения и подтверждения в работе [15] справедливости формулы (4) для всего занимаемого факелом пространства она может быть использована для расчета факела распыла при указанных разных условиях и, возможно, при разных диаметрах dh выходного отверстия форсунки, т.е. в более широких пределах, чем это сделано к настоящему времени.
В одном и том же распылительном аппарате в зависимости от величины созданного и поддерживаемого противодавления ΔP (т.е. встречного к движению капель перепада давления газа) могут осуществляться режимы как прямотока фаз, т.е. усредненного по сечению аппарата движения газа в том же направлении, что и жидкость, так и противотока – при усредненном движении газа противоположно жидкости.
Еще одним важным преимуществом зависимости Cd(Re) по формуле (4) перед зависимостью Cd(r, z) по формулам (5), (6) является то, что она может быть с одинаковым основанием использована как для прямоточного, так и для противоточного режимов работы распылительного аппарата
На рис. 8 приведены профили аксиальной и радиальной скорости газа в режиме противотока фаз, когда V < 0.
Рис. 8.
Профили аксиальной wz(i, j) и радиальной wr(i, j) проекций скорости газа в режиме противотока фаз при ΔP = 24.5 Па, Ra = 14 см, H = 110 см.
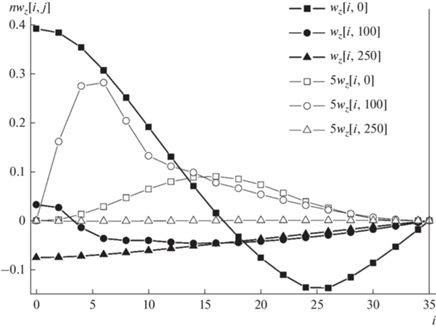
Очевидно, осевая проекция wz[i, j] скорости газа отрицательна по знаку во всем нижнем (j = 250) сечении аппарата. Отрицательные значения wz[i, j] в части сечений j = 0 и j = 100 обусловлены вихревым движением газа в аппарате.
На рис. 9 показаны профили аксиальной скорости капель uz(i, j) и концентрации c(i, j) примеси газа в режиме противотока фаз.
Рис. 9.
Профили аксиальной скорости uz(i, j) капель и концентрации c(i, j) газовой примеси в режиме противотока фаз при ΔP = 28 Па, Ra = 14 см, H = 110 см.
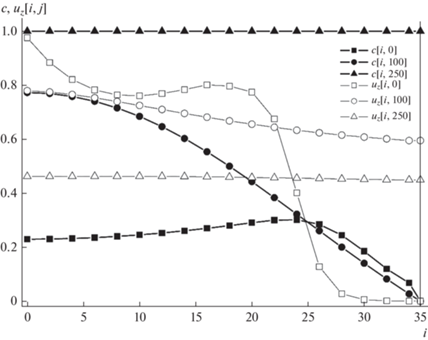
Очевидно, первоначально (при j = 0) неравномерный профиль аксиальной скорости капель выравнивается к выходу из аппарата при достаточной его высоте H. Концентрация газовой примеси в приосевой части аппарата в режиме противотока достигает минимальных значений на выходе газа из аппарата в его верхнем сечении j = 0. Интересно отметить, что эти значения c[i, 0] ≈ 0.23 оказались одинаковыми при разных (использованных в расчетах) перепадах давления ΔP = 21–28 Па газа на аппарате.
Заметим, что концентрация c[i, j] = 0 примеси газа принималась равной нулю на боковой границе (i = n = 35) расчетной области, которой служила внутренняя поверхность корпуса аппарата, смачиваемая жидкостью, поглощающей эту примесь.
Отличия характеристик прямо- и противоточного режимов работы массообменного распылительного аппарата. В работе [16] представлены результаты сравнительного расчета прямо- и противоточного режимов массообменных распылительных аппаратов.
В частности, на рис. 10, воспроизведенном здесь из работы [16] показан график расчетной зависимости V(ΔP) – расхода V газа от перепада его давления ΔP в аппарате радиусом Ra = 140 мм и высотой H = 1100 мм в режимах прямотока (V > 0) и противотока (V < 0).
На графике очевидно, что с ростом противодавления ΔP газа его расход V через аппарат уменьшается, при ΔP ≈ 18 Па расход газа V изменяет знак, вместе с направлением интегрального течения, и затем растет по модулю вместе с ΔP.
Другие результаты работы [16] представлены в данной работе на рис. 11. Это – графики расчетных зависимостей от расхода V газа для средней (по выходному для газа сечению) концентрации $\left\langle c \right\rangle $ газовой примеси, ее количества |V| (1 – $\left\langle c \right\rangle $), извлеченного жидкостью из газа, и величины |V ln$\left\langle c \right\rangle $|.
Рис. 11.
Расчетные зависимости от расхода V газа через аппарат для величин $\left\langle c \right\rangle $, (1 – $\left\langle c \right\rangle $) |V| и |Vln$\left\langle c \right\rangle $|, последняя из которых обратно пропорциональна затратам на проведение массообменного процесса.
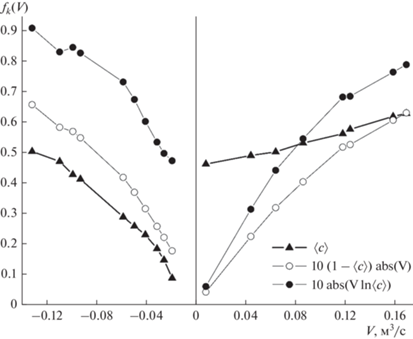
На графике для $\left\langle c \right\rangle $ можно видеть, что в прямоточном режиме (V > 0) минимальная концентрация $\left\langle c \right\rangle $ ≈ 0.46 примеси газа на выходе обеих фаз из аппарата достигается при расходе V ≈ 0.008 м3/с. А в противотоке (V < 0) в верхнем (выходном для газа) сечении минимальная концентрация $\left\langle c \right\rangle $ ≈ 0.088 – в 5 раз меньше при большем расходе |V| ≈ 0.019 м3/с газа. Таким образом, при малом расходе газа степень его очистки в противоточном режиме значительно выше, чем в прямоточном, как и принято считать.
При одинаковом расходе |V| ≈ 0.14 м3/с газа концентрация $\left\langle c \right\rangle $ примеси на выходе газа из аппарата в прямо- и противоточном режимах отличается незначительно – на 15%, т.е. при относительно больших расходах очищаемого воздуха преимущество противотока по степени очистки теряется. Из расчетных зависимостей количества |V| (1 – $\left\langle c \right\rangle $) извлеченной газовой примеси (убыли ее расхода) от расхода |V| газа следует тот же вывод.
Используя полученные расчетные данные, оказалось возможным рассмотреть вопрос об оптимизации и эффективности массообменного процесса в системе (установке) из нескольких распылительных аппаратов.
Для имеющих дело с тепломассообменом в распылительных аппаратах технологов привычно мнение, что противоточные аппараты эффективнее прямоточных. Умозрительно оно обосновано тем, что в противоточном аппарате относительная скорость фаз больше, чем в прямоточном, и вместе с ней больше коэффициенты межфазного тепломассообмена. Истинность этих представлений можно проверить на основании вышеприведенных расчетных результатов, полученных с учетом кризисов сопротивления капель и тепломассообмена фаз из-за сильной турбулентности факела распыла.
Для определенности попробуем рассмотреть массообменный (без теплообмена) процесс мокрой очистки воздуха от вредных газовых примесей, например, от SO2 с использованием распылительных аппаратов [17].
Чтобы обеспечить требования по общему расходу VN очищаемого воздуха и остаточной концентрации cn примеси в нем может оказаться недостаточным использование одного конкретного аппарата с характеристиками V и $\left\langle c \right\rangle $, и тогда может потребоваться их несколько аналогичных.
Необходимое общее количество аппаратов равно произведению их количества N = VN/V на каждой ступени очистки, обеспечивающего общий расход VN, и числа n этих ступеней. Из равенства cn = $\left\langle c \right\rangle $ n следует, что n = ln(cn)/ln $\left\langle c \right\rangle $ Обозначим величину эксплуатационных расходов (в основном – энергозатрат) на один аппарат как ε, а общие затраты на все аппараты очистной установки как E. Тогда
(9)
$E = \varepsilon Nn = {{\varepsilon {{V}_{N}}\ln ({{c}_{n}})} \mathord{\left/ {\vphantom {{\varepsilon {{V}_{N}}\ln ({{c}_{n}})} {(V\ln \left\langle c \right\rangle )}}} \right. \kern-0em} {(V\ln \left\langle c \right\rangle )}}.$Из уравнения (9) очевидно, что общие затраты обратно пропорциональны величине f(V) = V ln $\left\langle c \right\rangle $, характеризующей отдельно взятый аппарат и режим его работы.
На рис. 11 показана расчетная зависимость модуля |f(V)| этой функции от расхода V газа через аппарат. Очевидно, в режиме прямотока при малых значениях |V| < 0.01 достигается минимум функции |f(V)| и, соответственно, максимум затрат E. На порядок меньшие затраты достигаются при значении функции |f(V)| ≈ 0.08 и значениях ее аргумента V ≈ 0.17.
В режиме противотока минимум функции |f(V)| (и максимум затрат) достигается при малых значениях |V| ≈ 0.02, а те же затраты что и в режиме прямотока при |f(V)| ≈ 0.08 будут при расходе V ≈ –0.08, вдвое меньшем, чем в режиме прямотока. Число аппаратов N на каждой ступени очистки при том же общем расходе VN газа в установке будет, соответственно, вдвое большим.
Из формулы (9) следует, что при одинаковых общих расходах VN газа и степени его очистки cn в установках с прямоточным (индекс 1) и противоточным (индекс 2) режимах работы, отношение их общих энергозатрат будет равно
(10)
${{{{E}_{1}}} \mathord{\left/ {\vphantom {{{{E}_{1}}} {{{E}_{2}}}}} \right. \kern-0em} {{{E}_{2}}}} = {{{{\varepsilon }_{1}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{1}}} {{{\varepsilon }_{2}}}}} \right. \kern-0em} {{{\varepsilon }_{2}}}}{{\left| {{{V}_{2}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{V}_{2}}} \right|} {{{V}_{1}}}}} \right. \kern-0em} {{{V}_{1}}}}{{\ln \left\langle {{{c}_{2}}} \right\rangle } \mathord{\left/ {\vphantom {{\ln \left\langle {{{c}_{2}}} \right\rangle } {\ln \left\langle {{{c}_{1}}} \right\rangle }}} \right. \kern-0em} {\ln \left\langle {{{c}_{1}}} \right\rangle }}.$Для рассчитанных вариантов оценка ежесекундных энергозатрат e1 на распыливание жидкости по энергии ее струи выражается произведением давления PL= 5 × 105 Па в форсунке и расхода жидкости
Аналогично, оценка дополнительных энергозатрат на создание противотока газа с помощью дополнительных устройств (вентиляторов) дает Δε = |V| ΔP и ε2 = ε1 + Δε. При максимальном расходе |V2| = 0.13 м3/с и ΔP = 49 Па (см. рис. 10) получим Δε ≃ 0.13 × 49 = 6.4 Вт, что составляет 17% от энергозатрат ε1 на распыление жидкости. При |V2| = 0.08 м3/с и ΔP = 32 Па получим Δε ≃ 0.08 × 32 = = 2.6 Вт или 7% от ε1.
Пользуясь изложенными представлениями, формулами (9)–(10) и данными расчетов (на рис. 10 и 11) можно провести сравнительные оценки затрат на эксплуатацию распылительной установки в прямо- и противоточном режимах.
Подставляя в формулу (10) данные рис. 11, при одинаковом для обоих режимов значении критерия затрат |f(V)| ≈ 0.08, разных |V2| = 0.08, V1 = 0.17, $\left\langle {{{c}_{1}}} \right\rangle $ = 0.62, $\left\langle {{{c}_{2}}} \right\rangle $ = 0.4 получим E1/E2 = 0.84, т.е. эксплуатационные затраты в прямоточном режиме на 16% меньше, чем в противоточном.
При разных максимально возможных расходах |V2| = 0.13 м3/с и V1 = 0.17 м3/с газа и соответствующих им концентрациях $\left\langle {{{c}_{2}}} \right\rangle $ = 0.5, $\left\langle {{{c}_{1}}} \right\rangle $ = 0.62, получим E1/E2 = 0.94. Заметим, что при этом N1/N2 = = |V2|/V1 = 0.76 ≈ 3/4, а n1/n2 = ln $\left\langle {{{c}_{2}}} \right\rangle $/ln $\left\langle {{{c}_{1}}} \right\rangle $ = 1.45 ≈ 3/2, отношение общего числа аппаратов в установке N1n1/(N2n2) ≈ 9/8.
Таким образом, вопреки общепринятому мнению энергетические затраты в прямоточном режиме могу быть на 6–16% меньше, а требуемое число аппаратов, примерно на 10% больше, чем в противоточном.
Кроме того, необходимо учитывать дополнительные капитальные затраты на оборудование каждого противоточного аппарата вентилятором.
Таким образом, приходим к выводу о том, что противоточный режим не имеет конструктивных, эксплуатационных и, как следствие, экономических преимуществ перед прямоточным.
Стоит отметить, что в противоточном режиме отношение энергозатрат при максимальном |V2| = = 0.13 м3/с и минимальном |V2| = 0.019 м3/с расходах газа равно 0.6, т.е. при больших расходах энергозатраты на 40% меньше, чем при малых. Отношение требуемого числа аппаратов в установке N1n1/(N2n2) ≈ 7/13.
ЗАКЛЮЧЕНИЕ
В данной работе исследовано влияние способа аппроксимации коэффициента сопротивления капель в виде функции Cd(r, z) по формулам (5) и (6) или функции Cd(Re) по формуле (4) на результаты расчета профилей скорости газа и концентрации газовой примеси, а также технологических характеристик прямоточного распылительного аппарата с учетом кризисов сопротивления капель и межфазного массообмена.
Отличие результатов расчета факела распыла в аппарате при двух разных способах аппроксимации коэффициента Cd объясняется разным влиянием трения газа о внутреннюю поверхность корпуса аппарата. Для расчета двухфазного потока в аппарате лучше использовать более точную зависимость Cd(Re) вида (4).
Эта рекомендация учтена при выполнении расчетов двухфазного потока в распылительном аппарате в режимах прямо- и противотока фаз. Получены распределения скоростей фаз и концентраций газовой примеси, рассчитаны характеристики аппарата: расход V = f(ΔP) газа через него, а также $\left\langle c \right\rangle $, (1 – $\left\langle c \right\rangle $) |V| и |V ln $\left\langle c \right\rangle $| как функции расхода V газа.
Сравнение этих характеристик для двух режимов работы распылительного аппарата позволило обоснованно сделать вывод о том, что противоточный режим не имеет конструктивных, эксплуатационных и экономических преимуществ перед прямоточным.
ОБОЗНАЧЕНИЯ
| c | концентрация газовой примеси в воздухе |
| Cd | коэффициент гидродинамического сопротивления капли |
| d = d32 | средний объемно-поверхностный диаметр капель, м |
| dh | диаметр выходного отверстия форсунки, мм |
| E | общие энергозатраты на все аппараты очистной установки |
| F | гидродинамическая сила сопротивления капли обтекающему ее газу |
| f(x) | общее обозначение функции аргумента x |
| H | высота аппарата, см |
| i, j | номера точек расчетной сетки по радиусу и по оси потока |
| kV = 0.75 | коэффициент расхода форсунки |
| N | число аппаратов на каждой ступени очистки |
| n | число ступеней очистки в газоочистной установке |
| P | давление, Па |
| Ra | радиус аппарата, см |
| r | радиальная координата точек в факеле распыла, мм |
| S = πd2/4 | площадь миделева сечения сферической капли |
| u | скорость струи или капли жидкости, м/с |
| V | объемный расход газа через аппарат, м3/с |
| Vr = u – w, Vr | вектор и его модуль относительной скорости капли в газе, м/с |
| w | вектор полной скорости газа, w – его модуль, м/с |
| Δx | изменение величины x |
| $\left\langle x \right\rangle $ | среднее значение величины x |
| z | аксиальная координата точек в факеле распыла, мм |
| α | угол между осью факела распыла и вектором скорости капли (газа), ° |
| ε | величина энергозатрат на один аппарат |
| μ | динамический коэффициент вязкости газа, Па с |
| ρ | плотность жидкости, кг/м3 |
| Re = Vdρ/μ и Recr | число Рейнольдса и критическое число Рейнольдса |
ИНДЕКСЫ
| 0 | начальное значение |
| 1 | для прямоточного режима |
| 2 | для противоточного режима |
| k | переменное значение индекса у функций fk(x) |
| L | для жидкости |
| m | максимальное значение |
| n | для общего числа ступеней очистки в газоочистной установке |
| N | для общего числа аппаратов на каждой ступени очистки |
| r | радиальная проекция вектора |
| z | аксиальная проекция вектора |
Список литературы
Simakov N.N. Crisis of Hydrodynamic Drag of Drops in the Two-Phase Turbulent Flow of a Spray Produced by a Mechanical Nozzle at Transition Reynolds Numbers // Tech. Phys. 2004. V. 49. № 2. P. 188. [Симаков Н.Н. Кризис сопротивления капель при переходных числах Рейнольдса в турбулентном двухфазном потоке факела распыла механической форсунки // Журн. техн. физики. 2004. Т. 74. № 2. С. 46.]
Simakov N.N. Calculation of Interphase Mass Transfer in a Spray Flow Produced by a Nozzle with Account of Crisis // Tech. Phys. 2020. V. 65 № 4. P. 534. [Симаков Н.Н. Расчет межфазного массообмена в факеле распыла форсунки с учетом кризиса // Журн. техн. физики. 2020. Т. 90. № 4. С. 560.]
Simakov N.N. Liquid Spray from Nozzles. Cham: Springer Nature Switzerland AG, 2020.
Нигматулин Р.И. Динамика многофазных систем. Ч. 1. М.: Наука, 1987.
Абрамович Г.Н. Теория турбулентных струй. М.: Наука, 1984.
Torobin L.B., Gauvin W.H. // Can. J. Chem. Eng. 1959. V. 37. № 4. P. 129–141.
Шлихтинг Г. Теория пограничного слоя / Пер. с немецкого. М.: Наука, 1974.
Броунштейн Б.И., Фишбейн Г.А. Гидродинамика, массо- и теплообмен в дисперсных системах. Л.: Химия, 1977.
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. IV. Гидродинамика. М.: Наука, 1988.
Torobin L.B., Gauvin W.H. // Can. J. Chem. Eng. 1960. V. 38. № 6. P. 189–200.
Clamen A., Gauvin W.H. Effects of turbulence on the drag coefficients of spheres in a supercritical flow regime // AIChE J., 1969. V. 15. № 2. P. 184–189.
http://www.nature.com/articles/srepl2304 (Duan Z., He B., Duan Y. “Sphere Drag and Heat Transfer”, Scientific Reports 5, Article number: 12304 (2015)).https://doi.org/10.1038/srepl2304
Шиляев М.И. Аэродинамика и тепломассообмен газодисперсных потоков. М.: ФОРУМ: ИНФРА-М, 2019.
Симаков Н.Н. Учет раннего кризиса сопротивления капель в численных моделях двухфазного потока распыленной в газе жидкости // Сб. науч. тр. Междунар. науч.-техн. симпозиума “Повышение энергоресурсоэффективности и экологической безопасности процессов и аппаратов химической и смежных отраслей промышленности”. Т. 1. М.: ФГБОУ ВО “РГУ им. А.Н. Косыгина”, 2021, С. 194–198. https://doi.org/10.37816/eeste-2021-1-194-198
Симаков Н.Н. Сравнительный расчет прямо- и противоточного режимов работы массообменного распылительного аппарата // Сб. науч. тр. Междунар. науч.-техн. симпозиума “Повышение энергоресурсоэффективности и экологической безопасности процессов и аппаратов химической и смежных отраслей промышленности”. Т. 1. М.: ФГБОУ ВО “РГУ им. А.Н. Косыгина”, 2021, С. 153–157. https://doi.org/10.37816/eeste-2021-1-153-157
Страус В. Промышленная очистка газов. М.: Химия, 1981. 616 с.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии