Теоретические основы химической технологии, 2023, T. 57, № 3, стр. 317-324
Об оценках интенсификации конвективного теплообмена
А. А. Коноплев a, *, Б. Л. Рытов a, Ал. Ал. Берлин a, С. В. Романов b
a Федеральное государственное бюджетное учреждение науки Федеральный исследовательский центр
химической физики им. Н.Н. Семенова Российской академии наук
119991 Москва, ул. Косыгина, 4, Россия
b ООО “НПП “Энергосистемы”
105094 Москва, Семеновская наб., 2/1, Россия
* E-mail: alexey.konoplyov@gmail.com
Поступила в редакцию 25.03.2023
После доработки 30.03.2023
Принята к публикации 30.03.2023
- EDN: RPCTSE
- DOI: 10.31857/S0040357123030089
Аннотация
Результаты теплотехнических экспериментов, осуществленных на водо-водяном трубчатом теплообменнике типа “труба в трубе” с теплообменом, интенсифицированным периодическими конфузор-диффузорными сужениями, размещенными по длине канала с шагом, равным удвоенному внутреннему диаметру внутренней трубки, сравниваются с результатами экспериментов с аналогичным гладкотрубным теплообменником, а также с результатами расчетов по критериальным моделям Б.С. Петухова, С.С. Кутателадзе, Нуссельта и М.А. Михеева. Сравнение показало, что соотношение теплоотдачи трубных каналов интенсифицированного и гладкотрубного теплообменников, являясь функцией чисел Рейнольдса и Прандтля, в гораздо большей степени зависит от последнего. И, как следствие, по крайней мере для воды, как среды, в которой число Прандтля зависит от температуры, интенсификация теплообменного процесса определяется не только параметрами профилирования, но и параметрами самого процесса теплообмена. Сравнение также показало, что замещение экспериментальных данных гладкотрубных теплообменников результатами расчетов по критериальным моделям приводит к ухудшению точности оценок, обнаруживая при этом рост расхождений с ростом числа Re.
ВВЕДЕНИЕ
Интенсификация теплообмена позволяет уменьшать массогабаритные характеристики теплообменных устройств, способствуя, тем самым, созданию более совершенного оборудования, что в настоящее время является весьма актуальным, см., напр., [1, 2]. И потому исследованиям в этой области ныне посвящается все большее количество и экспериментальных и теоретических работ.
Для трубчатых теплообменников одним из сравнительно простых и эффективных способов интенсификации является создание теплообменных каналов с изменяющимися величиной и формой проходного сечения, иными словами, профилированных каналов.
К настоящему времени предложено и апробировано уже достаточно большое количество вариантов профилированных каналов, и потому сравнительная оценка их свойств и характеристик имеет весьма важное значение. Однако, на сегодня какого-то общепринятого метода оценки интенсификации конвективного теплообмена, тем не менее, не существует.
Поскольку интенсификация теплообмена приводит к росту теплоотдачи, по сравнению с теплоотдачей гладкотрубных каналов Nu/Nuгл, а также к росту гидродинамического сопротивления ζ/ζгл, весьма распространенной ее оценкой является сопоставление этих изменений (Nu/Nuгл)/(ζ/ζгл), называемое эффективностью интенсификации (теплоотдачи).
Однако то, что касается оценки изменения теплопередачи, являющейся нелинейной функцией теплоотдачи обоих каналов теплообменника, в [3] предложено оценивать эффективность интенсификации теплопередачи как сравнительную характеристику сопоставлением удельных теплообменных поверхностей сравниваемых теплообменников при равных суммарных удельных затратах энергии на прокачку теплоносителей. Такой подход допускает определенную оптимизацию путем изменения некоторых расходных и конструктивных параметров, позволяя, таким образом, находить наиболее приемлемые результаты.
В [4] на основании результатов проведенных экспериментов с трубчатым водо-водяным теплообменником с гладкими трубками сделаны выводы о том, что отличия между экспериментальными результатами и результатами расчетов по рассмотренным там критериальным моделям (модели Б.С. Петухова, С.С. Кутателадзе, Нуссельта и М.А. Михеева) являются следствием не только случайных ошибок эксперимента, но и систематическими ошибками самих критериальных моделей. По крайней мере, в тех случаях, когда число Прандтля Pr зависит от температуры, а аппроксимирующие коэффициенты для критериальной модели находят из разных наборов экспериментальных данных для разных сред и разных условий проведения экспериментов. И в этом смысле различия между экспериментами и расчетами Nuгл/Nuкм(Re,Pr) для каждой из рассмотренных критериальных моделей являются функциями определяющих критериев конвективного теплообмена, т.е., чисел Рейнольдса Re и Прандтля Pr, см. [4].
Поэтому цель настоящей работы является сравнение теплоотдачи трубного канала теплообменника с интенсифицированным теплообменом Nu(Re, Pr) с данными аналогичного гладкотрубного теплообменника Nuгл(Re, Pr), а также и с результатами расчетов по некоторым критериальным моделям конвективного теплообмена.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
В качестве теплообменника с интенсифицированным теплообменом был использован лабораторный трубчатый водо-водяной теплообменник типа “труба в трубе” с профилированной внутренней медной трубкой, практически тех же конструктивных параметров, что и гладкотрубный теплообменник в [4]. А именно, внутренний диаметр трубного канала составлял D = 0.2 м, наружный – Dн = 0.24 м, внутренний диаметр кожуха – Dк = 0.35 м. Длина же теплообменных каналов составляла L = 1.521 м, см. табл. 1, и незначительно отличалась от длины каналов гладкотрубного теплообменника в [4] (Lгл = 1.524 м).
Таблица 1.
Параметры конструктивные теплообменника, режимные эксперимента и расходные для расчетов турбулентного и переходного режимов трубного канала
| № п/п |
Параметры теплообменника1), м |
Экспериментальный режим |
tвх2), °С | ooQ | Эксперимент | Расчет турбулентного режима | Расчет переходного режима | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gт3), мл/с |
Gмт3), мл/с |
Сетка расходов, Gт × Gмт |
Gт3), мл/с |
Gмт3), мл/с |
Сетка расходов, Gт × Gмт |
Gт3), мл/с |
Gмт3), мл/с |
Сетка расходов, Gт × Gмт |
|||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 1.521 0.02 0.024 0.035 |
E1 | 70.01 | 0.0198 | 52 | 108 | 8 × 8 | 104 | 108 | 5 × 5 | 52 | 108 | 5 × 5 |
| 8.62 | 252 | 304 | 252 | 304 | 64 | 304 | |||||||
| 2 | E2 | 4.28 | 0.0105 | 100 | 100 | 245 | 100 | 100 | 100 | ||||
| 70.03 | 304 | 252 | 304 | 252 | 116 | 252 | |||||||
| 3 | E3 | 40.08 | 0.0193 | 64 | 108 | 136 | 108 | 64 | 108 | ||||
| 7.15 | 252 | 304 | 252 | 304 | 100 | 304 | |||||||
| 4 | E4 | 4.27 | 0.0222 | 100 | 100 | 245 | 100 | 100 | 100 | ||||
| 40.04 | 304 | 252 | 304 | 252 | 176 | 252 | |||||||
| 5 | E5 | 79.98 | 0.0235 | 52 | 108 | 104 | 108 | 49 | 108 | ||||
| 9.82 | 252 | 304 | 252 | 304 | 57 | 304 | |||||||
| 6 | E6 | 3.8 | 0.0257 | 100 | 100 | 252 | 100 | 100 | 100 | ||||
| 30 | 304 | 252 | 304 | 252 | 200 | 252 | |||||||
Профилирование внутренней трубки теплообменника осуществлялось конфузор-диффузорными сужениями с шагом S = 2D, число сужений равнялось 36, диаметр минимального проходного сечения составлял – 0.67D, а углы сужения конфузора и раскрытия диффузора составляли по 45°. Изменение теплопередающей поверхности из-за профилирования не учитывались, и, поскольку по длине трубного канала профилирование не являлось сплошным, характеристики течения определялось по течению в недеформированных частях канала.
Эксперименты проводили аналогично тому, как это делалось в [4], с использованием разработанной нами ранее методики. Сущность которой заключается, кратко, в следующем. Зафиксировав две из четырех независимых переменных теплообмена, в данном случае, это входные температуры теплоносителей, в узлах двумерной сетки расходов (сетка из 8 × 8 равноотстоящих узлов) трубного Gт и межтрубного Gмт каналов замерялись экспериментальные параметры (расходы и выходные температуры обоих теплоносителей).
Конструктивные параметры теплообменника, режимные параметры проведения экспериментов, включая значения входных температур теплоносителей трубного и межтрубного каналов и их расходов приведены в табл. 1.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
По данным экспериментов с переменными расходами теплоносителей в обоих каналах теплообменника при постоянных, но разных их входных температурах, были построены зависимости тепловых потоков Q = Q(Gт, Gмт) для каждого из шести обозначенных в табл. 1 режимов проведения эксперимента. Они приведены на рис. 1 в виде контурных графиков.
Рис. 1.
Тепловые потоки Q, кВт, в зависимости от расходов теплоносителей трубного Gт и межтрубного Gмт каналов при различных режимах проведения эксперимента, см. табл. 1; (а) – режим E1; (б) – E2; (в) – E3; (г) – E4; (д) – E5; (е) – E6.
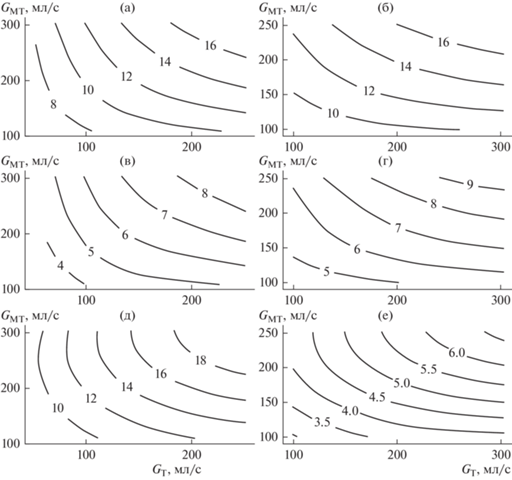
Анализ этих зависимостей позволяет определить значения теплоотдачи и всех искомых теплотехнических параметров для каждого из каналов теплообменника, как трубного, так и межтрубного. Сделать это можно не только в виде их средних значений, но также и в виде распределений по длине теплообменных каналов.
В этом случае теплоотдачу необходимо приблизить какой-либо подходящей функцией, аппроксимирующие коэффициенты для которой могут быть найдены из полученных экспериментальных данных. Распределения же других искомых параметров могут быть построены с помощью распределения теплопередачи, а средние их значения – вычислены осреднением найденных распределений. Несколько подробнее об этом смотри, например, в [4], там же можно найти и ссылки на еще более ранние работы, описывающие эту методику и ее применение.
В настоящей работе мы будем рассматривать только данные, относящиеся к трубному каналу, и использовать приближение теплоотдачи линейной функцией, аналогично тому, как это было сделано в работе [4]. В которой описаны эксперименты с практически аналогичным гладкотрубным теплообменником (длины каналов различаются на 3 мм, или, приблизительно, на 0.2%, и этим отличием, в данном случае, мы сочли возможным пренебречь).
Диапазон изменения экспериментальных расходов позволяет охватить и турбулентный, и переходный режимы течения теплоносителя трубного канала, которые могут быть выделены и рассматриваться раздельно, см. табл. 1. Для проведения последующих расчетов в каждом из выделенных режимов соответствующие диапазоны расходов покрывались расчетной расходной сеткой из 5 × 5 равноотстоящих узлов, см. табл. 1, для значений в узлах которой эти расчеты и производились. Полученные таким образом данные проиллюстрированы приводимыми в таблице 2 результатами для случаев минимальных и максимальных расходов теплоносителей трубного и межтрубного каналов теплообменника.
Таблица 2.
Распределения параметров теплообмена по длине трубного канала1) и их средние значения при минимальных и максимальных расходах теплоносителя при турбулентном режиме течения
| № п/п |
Трубный канал греющий | Трубный канал нагреваемый | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tвх2), °С |
Gвх2), мл/с |
l/L | t, °С | K, кВт/ (м2 К) |
Re × × 10–3 | Pr | α, кВт/ (м2 К) |
Nu | Pr/Prw | tвх2), °С |
Gвх2), мл/с |
l/L | t, °С | K, кВт/ (м2 К) |
Re × 10–3 | Pr | α, кВт/ (м2 К) |
Nu | Pr/Prw | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 70 8.62 |
104 108 |
0 | 50.29 | 1.63 | 11.89 | 3.51 | 8.03 | 247.8 | 0.952 | 4.28 70.03 |
245 100 |
0 | 4.28 | 1.61 | 10.03 | 11.67 | 10.91 | 389.8 | 1.065 |
| 2 | 0.25 | 54.89 | 1.7 | 12.81 | 3.23 | 8.24 | 252 | 0.953 | 0.25 | 6.22 | 1.73 | 10.66 | 10.88 | 12.17 | 431.2 | 1.065 | ||||
| 3 | 0.5 | 59.71 | 1.76 | 13.8 | 2.98 | 8.45 | 256.4 | 0.955 | 0.5 | 8.46 | 1.86 | 11.4 | 10.06 | 13.61 | 477.4 | 1.065 | ||||
| 4 | 0.75 | 64.75 | 1.83 | 14.87 | 2.74 | 8.66 | 261.1 | 0.956 | 0.75 | 11.06 | 1.99 | 12.3 | 9.21 | 15.25 | 528.8 | 1.064 | ||||
| 5 | 1 | 70 | 1.9 | 16 | 2.54 | 8.88 | 266 | 0.958 | 1 | 14.09 | 2.13 | 13.38 | 8.35 | 17.12 | 585.5 | 1.063 | ||||
| 6 | Sr3) | 59.87 | 1.76 | 13.86 | 2.99 | 8.45 | 256.6 | 0.955 | Sr3) | 8.73 | 1.86 | 11.51 | 10.04 | 13.76 | 481.2 | 1.065 | ||||
| 7 | 252 304 |
0 | 52.42 | 3.33 | 29.84 | 3.37 | 17.68 | 543.3 | 0.954 | 305 252 |
0 | 4.28 | 2.9 | 12.48 | 11.67 | 13.97 | 499.2 | 1.105 | ||
| 8 | 0.25 | 56.51 | 3.44 | 31.84 | 3.14 | 18.04 | 550.6 | 0.955 | 0.25 | 7.46 | 3.12 | 13.78 | 10.42 | 16.44 | 579.5 | 1.093 | ||||
| 9 | 0.5 | 60.8 | 3.54 | 34 | 2.92 | 18.41 | 558.1 | 0.956 | 0.5 | 10.94 | 3.35 | 15.26 | 9.25 | 19.1 | 662.6 | 1.082 | ||||
| 10 | 0.75 | 65.3 | 3.65 | 36.31 | 2.72 | 18.8 | 566.1 | 0.957 | 0.75 | 14.73 | 3.57 | 16.94 | 8.19 | 21.9 | 747.1 | 1.073 | ||||
| 11 | 1 | 70 | 3.75 | 38.78 | 2.54 | 19.19 | 574.5 | 0.958 | 1 | 18.84 | 3.79 | 18.83 | 7.23 | 24.82 | 832.2 | 1.065 | ||||
| 12 | Sr3) | 60.95 | 3.54 | 34.11 | 2.93 | 18.42 | 558.4 | 0.956 | Sr3) | 11.16 | 3.35 | 15.4 | 9.32 | 19.21 | 663.7 | 1.086 | ||||
| 13 | 40.08 7.15 |
136 108 |
0 | 32.19 | 1.55 | 11.28 | 5.11 | 8.66 | 278.7 | 0.968 | 4.27 40.04 |
245 100 |
0 | 4.27 | 1.63 | 10.02 | 11.67 | 11.66 | 416.4 | 1.035 |
| 14 | 0.25 | 34.14 | 1.6 | 11.74 | 4.88 | 8.83 | 282.6 | 0.969 | 0.25 | 5.36 | 1.67 | 10.37 | 11.22 | 12.03 | 427.8 | 1.037 | ||||
| 15 | 0.5 | 36.1 | 1.64 | 12.21 | 4.67 | 9 | 286.4 | 0.97 | 0.5 | 6.55 | 1.72 | 10.76 | 10.76 | 12.44 | 440.2 | 1.039 | ||||
| 16 | 0.75 | 38.09 | 1.69 | 12.69 | 4.47 | 9.17 | 290.3 | 0.971 | 0.75 | 7.86 | 1.76 | 11.2 | 10.27 | 12.89 | 453.6 | 1.04 | ||||
| 17 | 1 | 40.08 | 1.73 | 13.18 | 4.28 | 9.34 | 294.1 | 0.972 | 1 | 9.31 | 1.81 | 11.69 | 9.77 | 13.39 | 468.1 | 1.042 | ||||
| 18 | Sr3) | 36.11 | 1.64 | 12.22 | 4.68 | 9 | 286.4 | 0.97 | Sr3) | 6.64 | 1.72 | 10.8 | 10.74 | 12.47 | 441 | 1.039 | ||||
| 19 | 252 304 |
0 | 31.51 | 3.02 | 20.61 | 5.19 | 14.43 | 465.1 | 0.963 | 304 252 |
0 | 4.27 | 2.8 | 12.44 | 11.67 | 14.26 | 509.6 | 1.057 | ||
| 20 | 0.25 | 33.53 | 3.09 | 21.49 | 4.95 | 14.71 | 471.3 | 0.963 | 0.25 | 5.97 | 2.88 | 13.12 | 10.98 | 14.95 | 530.4 | 1.055 | ||||
| 21 | 0.5 | 35.63 | 3.16 | 22.42 | 4.72 | 15 | 477.6 | 0.963 | 0.5 | 7.74 | 2.95 | 13.85 | 10.32 | 15.67 | 551.6 | 1.054 | ||||
| 22 | 0.75 | 37.82 | 3.23 | 23.4 | 4.5 | 15.29 | 484.1 | 0.964 | 0.75 | 9.58 | 3.03 | 14.62 | 9.68 | 16.41 | 573 | 1.052 | ||||
| 23 | 1 | 40.08 | 3.31 | 24.42 | 4.28 | 15.58 | 490.7 | 0.964 | 1 | 11.5 | 3.11 | 15.45 | 9.08 | 17.18 | 594.6 | 1.05 | ||||
| 24 | Sr3) | 35.69 | 3.16 | 22.46 | 4.73 | 15 | 477.7 | 0.963 | Sr3) | 7.79 | 2.96 | 13.88 | 10.34 | 15.69 | 551.7 | 1.054 | ||||
| 25 | 79.98 9.82 |
104 108 |
0 | 56.43 | 1.72 | 13.05 | 3.14 | 8.49 | 259.1 | 0.949 | 3.8 30 |
252 100 |
0 | 3.8 | 1.61 | 10.16 | 11.87 | 11.55 | 413.5 | 1.026 |
| 26 | 0.25 | 61.92 | 1.8 | 14.18 | 2.87 | 8.71 | 263.5 | 0.951 | 0.25 | 4.57 | 1.63 | 10.41 | 11.55 | 11.77 | 420 | 1.028 | ||||
| 27 | 0.5 | 67.68 | 1.87 | 15.4 | 2.62 | 8.94 | 268.3 | 0.953 | 0.5 | 5.4 | 1.66 | 10.69 | 11.2 | 12.01 | 426.9 | 1.029 | ||||
| 28 | 0.75 | 73.7 | 1.94 | 16.72 | 2.41 | 9.17 | 273.6 | 0.956 | 0.75 | 6.32 | 1.69 | 10.99 | 10.85 | 12.26 | 434.4 | 1.031 | ||||
| 29 | 1 | 79.98 | 2.01 | 18.12 | 2.21 | 9.4 | 279.1 | 0.958 | 1 | 7.31 | 1.73 | 11.33 | 10.47 | 12.55 | 442.4 | 1.033 | ||||
| 30 | Sr3) | 67.87 | 1.87 | 15.47 | 2.64 | 8.94 | 268.6 | 0.953 | Sr3) | 5.46 | 1.66 | 10.71 | 11.19 | 12.02 | 427.3 | 1.029 | ||||
| 31 | 252 304 |
0 | 59.39 | 3.44 | 33.08 | 2.99 | 18.86 | 572.8 | 0.953 | 304 252 |
0 | 3.8 | 2.72 | 12.25 | 11.87 | 13.69 | 489.9 | 1.043 | ||
| 32 | 0.25 | 64.18 | 3.54 | 35.51 | 2.77 | 19.24 | 580.3 | 0.954 | 0.25 | 5.02 | 2.77 | 12.73 | 11.36 | 14.08 | 501.4 | 1.043 | ||||
| 33 | 0.5 | 69.21 | 3.65 | 38.12 | 2.57 | 19.64 | 588.5 | 0.956 | 0.5 | 6.27 | 2.81 | 13.24 | 10.86 | 14.48 | 513 | 1.042 | ||||
| 34 | 0.75 | 74.48 | 3.74 | 40.92 | 2.38 | 20.04 | 597.4 | 0.957 | 0.75 | 7.56 | 2.86 | 13.77 | 10.38 | 14.9 | 524.7 | 1.041 | ||||
| 35 | 1 | 79.98 | 3.83 | 43.9 | 2.21 | 20.44 | 606.7 | 0.959 | 1 | 8.9 | 2.91 | 14.33 | 9.91 | 15.32 | 536.6 | 1.041 | ||||
| 36 | Sr3) | 69.39 | 3.64 | 38.26 | 2.58 | 19.64 | 589 | 0.956 | Sr3) | 6.3 | 2.81 | 13.26 | 10.87 | 14.49 | 513.1 | 1.042 | ||||
Результаты, полученные в экспериментах с интенсифицированным теплообменником, сравниваются с результатами экспериментов с гладкотрубным теплообменником при совпадающих значениях определяющих параметров Re–Pr.
Так для турбулентного режима область сравнения составляет 10–3Re = 10.7–36.67 и Pr = 2.39–10.67 при расчетах по средним значениям теплотехнических параметров, и 10-3Re = 10.03–38.78 и Pr = 2.2–11.19 при расчетах по значениям продольных профилей.
Для переходного режима течения значения параметров в областях сравнения составят, соответственно, 10–3Re = 5.02–8.99 и Pr = 2.92–10.39 для расчетов по средним значениям, и 10–3Re = 4.58–9.97, Pr = 2.2–11.19 – для расчетов по значениям продольных профилей.
На рис. 2 в виде контурных графиков показаны теплоотдача интенсифицированного Nu и гладкотрубного Nuгл теплообменников, а так же и их сопоставление (т.е., интенсификация теплоотдачи) Nu/Nuгл в турбулентном режиме в областях их сравнения, обозначенных выше. Те же данные для переходного режима, в соответствующих ему условиях, приведены на рис. 3.
Рис. 2.
Интенсификация теплоотдачи Nu/Nuгл в турбулентном режиме; (a, в, д) – расчеты по средним значениям теплообменных параметров; (б, г, е) – расчеты по значениям продольных профилей теплообменных параметров; (a, б) – Nu; (в, г) – Nuгл; (д, е) – Nu/Nuгл, средние значения равны, соответственно, 3.7 ± 0.39 и 3.95 ± 0.55.
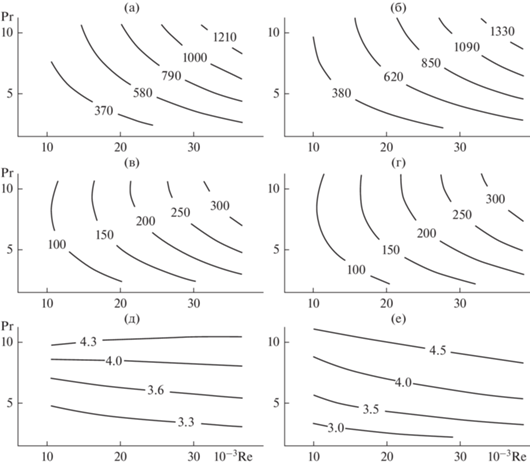
Рис. 3.
Интенсификация теплоотдачи Nu/Nuгл в переходном режиме; (a, в, д) – расчеты по средним значениям теплообменных параметров; (б, г, е) – расчеты по значениям продольных профилей теплообменных параметров; (a, б) – Nu; (в, г) – Nuгл; (д, е) – Nu/Nuгл, средние значения равны, соответственно, 3.72 ± 0.42 и 3.82 ± 0.7.
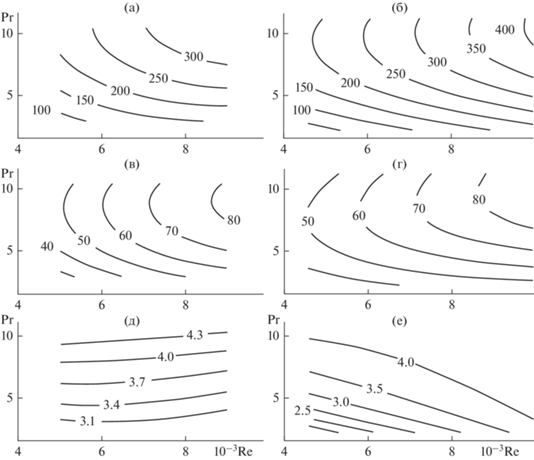
Из этих данных следует, что интенсификация теплоотдачи зависит от параметров процесса теплообмена, т.е., от чисел Re и Pr. По крайней мере для воды, как среды, в которой число Pr зависит от температуры.
Среднеквадратичные отклонения от осредненных в соответствующих областях сравнения Re–Pr значений Nu/Nuгл, как при расчетах по средним значениям, так и при расчетах по продольным профилям, составляют величину, соответственно, порядка 11 и 14% для турбулентного режима, и для переходного, соответственно – 11 и 18%, см. рис. 2–3.
В то же время, некоторое расхождения между средними значениями Nu/Nuгл, оцениваемых по средним значениям параметров теплообмена, и по значениям их продольных профилей, может быть вызвано также некоторым несовпадением их областей сравнения Re–Pr. Хотя в нашем случае оно и невелико, и составляет лишь 11% по числу Re, и 9% по числу Pr.
Определенная из экспериментов теплоотдача трубного канала интенсифицированного теплообменника сравнивалась также с результатами расчетов по критериальным моделям Nu/Nuкм. В качестве критериальных моделей были выбраны те модели, которые использовались ранее в [4] для сравнения с теплоотдачей гладкотрубного теплообменника. Эти модели следующие.
Критериальная модель 1 (КМ1) – модель Б.С. Петухова, см., напр., [5]:
(1)
{\text{Nu}} = \frac{{\zeta \operatorname{Re} \Pr }}{{8 + {{7200} \mathord{\left/ {\vphantom {{7200} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }} + 35.9\sqrt \zeta ({{{\Pr }}^{{2/3}}} - 1)}}.Критериальная модель 2 (КМ2) – модель С.С. Кутателадзе, см., напр., [6]:
(2)
\begin{gathered} {\text{Nu}} = \hfill \\ = \frac{{0.14\operatorname{Re} \Pr \sqrt \zeta }}{{\ln \operatorname{Re} \sqrt \zeta \, + \,2\ln \frac{{1\, + \,5\Pr }}{{1\, + \,0.2\Pr }}\, + \,2.4\Pr f(\Pr )\, - \,6.638}}. \hfill \\ \end{gathered}Критериальная модель 3 (КМ3) – модель Нуссельта–Кроуссольда, см., напр., [6]:
Критериальная модель 4 (КМ4) – модель академика М.А. Михеева, см., напр., [7]:
На рис. 4 в виде контурных графиков показано соотношение (Nu/Nuкм)/(Nu/Nuгл). Фактически, это оценка влияния неточностей критериальных моделей на оценку интенсификации теплообмена, возникающего при использовании критериальных моделей для расчетов теплоотдачи гладкотрубных каналов.
Рис.4.
Соотношение (Nu/Nuкм)/(Nu/Nuгл) для теплоотдачи в турбулентном режиме; (a, в, д, ж) – расчеты по средним значениям теплообменных параметров; (б, г, е, з) – расчеты по значениям продольных профилей теплообменных параметров; (a, б) – Nuкм = NuКМ1, средние значения, соответственно, 1.1 ± 0.06 и 1.1 ± 0.07; (в, г) – Nuкм = NuКМ2, средние значения 1.12 ± 0.07 и 1.13 ± 0.08; (д, е) – Nuкм = NuКМ3, средние значения 1.21 ± 0.08 и 1.23 ± 0.11; (ж, з) – Nuкм = NuКМ4, средние значения 1.26 ± 0.08 и 1.27 ± 0.11.
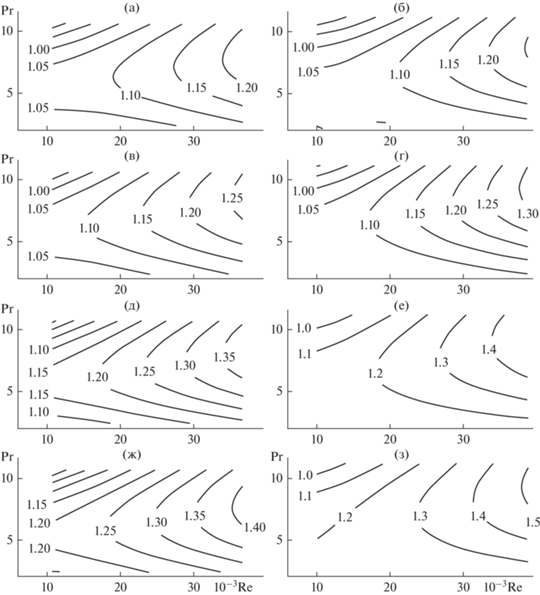
Из этих данных следует, что расхождения между Nu/Nuкм и Nu/Nuгл имеют систематический характер, возрастают с ростом Re, и наименьшую величину имеют в случае использования модели Б.С. Петухова (1).
Пожалуй, учитывая тот факт, что ошибки критериальных моделей теплообмена в 20–25% считаются допустимыми, применение критериальной модели Б.С. Петухова (1) для оценки интенсификации теплоотдачи при не слишком больших значениях 10–3Re ≤ 40, как показывают наши эксперименты, можно считать вполне допустимым. При больших значениях числа Re, или при использовании других критериальных моделей, ошибки будут возрастать.
ЗАКЛЮЧЕНИЕ
По данным из наших экспериментов с трубчатыми водо-водяными теплообменниками следует, что интенсификация теплоотдачи трубного канала его профилированием, является функцией чисел Re и Pr, и, таким образом, зависит от параметров процесса теплообмена. Причем, зависимость от числа Pr значительно сильнее, чем от числа Re. Попытки охарактеризовать процесс (профилирование) некоторым “коэффициентом интенсификации” проводят к ошибкам, величина которых, в нашем случае, при сравнении с не интенсифицированным теплообменником, достигает 11–14%.
Замена значений теплоотдачи гладкотрубного теплообменника, определенной из экспериментов, на результаты расчетов по критериальным моделям приводит к дополнительным ошибкам, не являющимися, при этом, случайными и возрастающими с ростом числа Re. Из рассмотренных моделей наименьшая ошибка имеет место быть при использовании результатов расчетов по модели Б.С. Петухова (1). Осредненная по областям сравнения Re–Pr она составляет 10%. Аналогично, при использовании модели М.А. Михеева (4) – ошибка составляет 26–27%.
Список литературы
Дзюбенко Б.В., Кузма-Кичта Ю.А., Леонтьев А.И. и др. Интенсификация тепло- и массообмена на макро-, микро- и наномасштабах М.: ФГУП “ЦНИИАТОМИНФОРМ”, 2008.
Лаптев А.Г., Николаев Н.А., Башаров М.М. Методы интенсификации и моделирования тепломассообменных процессов. Учебно-справочное пособие. М.: Теплотехник, 2011.
Коноплев А.А., Алексанян Г.Г., Рытов Б.Л., Берлин Ал.Ал. Об эффективности интенсификации теплообмена глубоким профилированием // Теорет. основы хим. технологии. 2012. Т. 46. № 1. С. 24.
Коноплев А.А., Рытов Б.Л., Берлин Ал.Ал., Романов С.В. О некоторых критериальных моделях конвективного теплообмена // Теорет. основы хим. технологии. 2023. Т. 57. №1. С. 81.
Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Е.В. Аметистов, В.А. Григорьев, Б.Т. Емцев и др.; Под общ. Ред. В.А. Григорьева и В.М. Зорина. М.: Энергоиздат, 1982.
Кутателадзе С.С. Теплопередача и гидравлическое сопротивление: Справочное пособие. М.: Энергоатомиздат, 1990.
Михеев М.А.. Средняя теплоотдача при движении жидкости в трубах: Сборник “Теплопередача и тепловое моделирование”. М.: Изд-во АН СССР, 1959.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии


