1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 3, 2023

Теоретические основы химической технологии, 2023, T. 57, № 3, стр. 266-272

Исследование влияния коэффициента теплопроводности фосфатного рудного сырья на эффективность химико-энерготехнологического процесса обжига в динамической плотной многослойной массе

В. П. Мешалкин a, В. А. Орехов b, М. И. Дли b, В. И. Бобков b, *

a Российский химико-технологический университет им. Д.И. Менделеева, Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия

b Национальный исследовательский университет “МЭИ”
г. Смоленск, Россия

* E-mail: vovabobkoff@mail.ru

Поступила в редакцию 13.02.2023
После доработки 23.02.2023
Принята к публикации 01.03.2023

Полный текст (PDF)

Аннотация

В данной работе предлагается физическая и математическая модели химико-энерготехнологического процесса обжига дисперсного рудного фосфатного материала в движущейся плотной многослойной массе на конвейере обжиговой машины с перекрестной подачей газа теплоносителя. На основе построенных моделей, разработана компьютерная модель, на которой проводились вычислительные эксперименты по исследованию влияния теплофизических характеристик рудного сырья, на эффективность обжига. Установлена степень влияния коэффициента теплопроводности рудных фосфатных материалов на энергоэффективность и завершенность термически активируемых эндотермических реакций диссоциации карбонатов. Научно обоснован и подтвержден в вычислительных экспериментах способ активного воздействия на эффективность химико-энерготехнологического процесс обжига, основанный на использовании многослойной полифракционной засыпки рудного дисперсного сырья на колосниковую решетку – конвейер обжиговой машины. Установлено, что изменение температуры газа теплоносителя в плотном слое и на выходе из него, эффективность обжига и неравномерность декарбонизации по высоте плотного слоя термически обрабатываемого рудного сырья, существенно зависят от теплофизических характеристик. По результатам вычислительных экспериментов обнаружено, что применение полифракционной засыпки рудного фосфатного сырья на конвейер обжиговой машины в регламентных условиях обжига приводит к снижению температуры отходящих газов, и увеличивает среднюю по слою степень декарбонизации сырья. Выявлено, что применение полифракционной засыпки, изменяет зависимость температуры газа теплоносителя от координаты высоты слоя.

ВВЕДЕНИЕ

Известно, что теплопроводность зерен дисперсного рудного материала нагреваемого (охлаждаемого) в плотном слое с перекрестной подачей газообразного теплоносителя оказывает влияние на процесс теплообмена [1, 2]. Снижение теплопроводности, при прочих равных условиях, способствует ухудшению тепловосприятия этой многослойной массы [3, 4]. Основываясь на проведенном авторами ранее анализе взаимоопределяющего характера теплообмена и кинетики термической деструкции карбонатов, можно предполагать, что термическое сопротивление зерен рудного материала оказывает двоякое действие на процесс обжига: во-первых, влияет на условия теплообмена в плотной многослойной массе и, во-вторых, изменяет условия протекания гетерогенного превращения в зернах рудного материала [5, 6]. Для количественного анализа зависимости эффективности химико-энерготехнологического процесса обжига в плотной многослойной массе от теплофизических характеристик рудного сырья в настоящем исследовании проведены вычислительные эксперименты с использованием разработанной авторами математической модели [7, 8].

ФИЗИЧЕСКАЯ, МАТЕМАТИЧЕСКАЯ МОДЕЛИ ТЕПЛООБМЕНА В ПЛОТНОЙ МНОГОСЛОЙНОЙ МАССЕ РУДНОГО ФОСФАТНОГО СЫРЬЯ

Для проведения вычислительных экспериментов химико-энерготехнологического процесса обжига была предложена следующая физическая модель. Реальный плотный слой рудного сырья толщиной H заменен системой плоских горизонтальных ячеек в количестве k, имеющих толщину ΔY. В состав ячейки входят пластины толщиной 2X в количестве m, представляющие собой модель зерен реагирующего слоя. Количество пластин в ячейке определяется порозностью ε, моделируемого слоя: $m = \frac{{\Delta Y}}{{2X}}\left( {1 - \varepsilon } \right)$, а толщина пластин 2X задается в соответствии с размером зерен реального слоя рудного сырья на конвейере обжиговой машины [9, 10].

Предполагается, что размеры элементарных ячеек и пластин могут задаваться различными по высоте слоя. При этом обязательным является условие: $H = \sum\limits_{i = 1}^k {\Delta {{Y}_{i}}} $.

Теплообмен между пластинами ячейки и перекрестно подаваемым газом-теплоносителем осуществляется с использованием граничных условий третьего рода [11, 12].

Предполагается также, что в пределах элементарной ячейки температура газа-теплоносителя остается постоянной и изменяется только по высоте плотного слоя, то есть при переходе от предыдущей ячейки к последующей [13]. Перенос тепла в результате теплопроводности слоя считается пренебрежимо малым [14].

Принятая физическая модель слоя, с учетом допущений, позволяет использовать для решения внутренних задач теплообмена и кинетики химико-энерготехнологических процессов декарбонизирующего обжига элементарного рудного зерна математическую модель вида:

(1)
$\left\{ \begin{gathered} \rho {{C}_{p}}\left( {T,{{\alpha }_{W}},{{\alpha }_{1}},{{\alpha }_{2}}} \right)\frac{{\partial T}}{{\partial \tau }} = \hfill \\ = \frac{\partial }{{\partial x}}\left( {\lambda \left( T \right)\frac{{\partial T}}{{\partial x}}} \right) - \left( {C_{1}^{0}Q_{1}^{0}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} + C_{2}^{0}Q_{2}^{0}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }}} \right); \hfill \\ \frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} = {{k}_{{01}}}\exp \left( { - \frac{{{{E}_{1}}}}{{RT}}} \right){{f}_{1}}\left( {{{\alpha }_{1}}} \right); \hfill \\ \frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }} = {{k}_{{02}}}\exp \left( { - \frac{{{{E}_{2}}}}{{RT}}} \right){{f}_{2}}\left( {{{\alpha }_{2}}} \right). \hfill \\ \end{gathered} \right.$

При этом начальные условия принимают вид:

(2)
$T\left( {x,0} \right) = {{T}_{0}};\,\,\,\,{{\alpha }_{1}}\left( {x,0} \right) = 0;\,\,\,\,{{\alpha }_{2}}\left( {x,0} \right) = 0;$

граничные условия принимают вид:

(3)
${{\lambda }}\left( Т \right){{\left( {\frac{{\partial Т}}{{\partial x}}} \right)}_{{x = X}}} = {{K}_{F}}{{\left( {{{T}_{{\text{г}}}} - Т} \right)}_{{x = X}}};\,\,\,\,{{\left( {\frac{{\partial T}}{{\partial x}}} \right)}_{{x = 0}}} = 0.$

Здесь: α – степень превращения, а именно отношение $\alpha = 1 - {{G\left( \tau \right)} \mathord{\left/ {\vphantom {{G\left( \tau \right)} {{{G}_{0}}}}} \right. \kern-0em} {{{G}_{0}}}}$, где G0 – количество карбонатного вещества, вступающего в реакцию, G(τ) – количество не прореагировавшего вещества за время τ, α1 – степень превращения MgCO3, α2 – степень превращения СаСО3. MgCO3 → MgO + + CO2 – $Q_{1}^{0}$ и СаСО3 → CaO + CO2 – $Q_{2}^{0}$, где $Q_{1}^{0}$ = = 1.21 × 105 Дж/моль – тепловой эффект реакции разложения MgCO3, $Q_{2}^{0}$ = 1.78 × 105 Дж/моль – тепловой эффект реакции разложения CaCO3. $C_{1}^{0}$, $C_{2}^{0}$ – начальные концентрации карбонатов магния и кальция соответственно, кг/м3, E1, E2 – энергии активации диссоциации карбонатов, Дж/моль, k01, k02 – предэкспоненциальные множители. Вид функций ${{f}_{1}}\left( {{{{{\alpha }}}_{1}}} \right)$, ${{f}_{2}}\left( {{{{{\alpha }}}_{2}}} \right)$, также считается известным. x – координата по толщине пластины с полутолщиной X, $x \in \left[ { - X;\;X} \right]$, R – универсальная газовая постоянная, T – температура, ${{\lambda }}$ – удельная теплопроводность, $\rho $ – плотность. В настоящей работе предполагается известной зависимость объемной теплоемкости от температуры и степеней превращения, она имеет вид:

(4)
$\begin{gathered} \rho {{C}_{p}}\left( {T,{{\alpha }_{1}},{{\alpha }_{2}}} \right) = \rho {{C}_{p}}{{\left( Т \right)}^{o}} + \\ + \,\,\left[ {\rho {{C}_{p}}{{{\left( Т \right)}}^{c}} - \rho {{C}_{p}}{{{\left( Т \right)}}^{o}}} \right]\left( {1 - {{\alpha }_{\Sigma }}} \right), \\ \end{gathered} $
где ${{{{\alpha }}}_{\Sigma }} = 0.5\left( {{{{{\alpha }}}_{1}} + {{{{\alpha }}}_{2}}} \right)$ – суммарная степень превращения, ${{\rho }}{{C}_{p}}{{\left( Т \right)}^{c}}$, ${{\rho }}{{C}_{p}}{{\left( Т \right)}^{o}}$ – температурные зависимости объемной теплоемкости необожженного $\left( {{{\alpha }_{1}} = {{\alpha }_{2}} = 0} \right)$ и нацело обожженного $\left( {{{\alpha }_{1}} = {{\alpha }_{2}} = 1} \right)$ рудного материала, соответственно. Выбор линейного вида функции (4) основывается на свойстве аддитивности теплоемкости смеси [15].

Условия нагрева плотного слоя рудного фосфатного сырья в обжиговой машине могут быть воспроизведены заданием переменных во времени температур газа-теплоносителя на входе в слой ${{\left( {{{T}_{g}}} \right)}_{{y = 0}}} = {{T}_{{\text{г}}}}\left( \tau \right)$ и скорости газа-теплоносителя на полное сечение аппарата ${{\omega }_{g}} = {{\omega }_{g}}\left( \tau \right)$.

Для расчета распределения температуры газа-теплоносителя по высоте слоя использовалась зависимость

(5)
${{\omega }_{g}}\left( \tau \right){{\rho }_{g}}\left( Т \right){{С}_{{р\,g}}}\left( Т \right)\frac{{d{{T}_{g}}}}{{dy}} = Q,$
где: Q – количество теплоты, воcпринимаемое слоем материала; включает в себя тепловые потоки, расходуемые на нагрев материала и покрытие эндотермических эффектов гетерогенных превращений при диссоциации карбонатов. Это значение определяется из решения внутренней задачи теплообмена пластины, толщиной 2X:

$Q = \int\limits_0^{2X} {\left( {\rho {{С}_{р}}\left( Т \right)\frac{{dT}}{{d\tau }} + Q_{1}^{0}C_{1}^{0}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} + Q_{2}^{0}C_{2}^{0}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }}} \right)} {\kern 1pt} dx.$

В конечных разностях уравнение (5) имеет вид:

(6)
${{\omega }_{g}}\left( \tau \right){{\rho }_{g}}\left( Т \right){{С}_{{р\,g}}}\left( Т \right)\frac{{\left( {{{T}_{{g\;}}}_{i} - {{T}_{{g\;}}}_{{i - 1}}} \right)}}{{\Delta {{Y}_{i}}}} = {{Q}_{i}},$
где ${{Q}_{i}}$ определяется с учетом принятой физической модели

$\begin{gathered} {{Q}_{i}} = \frac{{\Delta {{Y}_{i}}}}{{2X}}\left( {1 - \varepsilon } \right) \times {{90}^{ \circ }} \\ \times \,\,\int\limits_0^{2X} {\left( {\rho {{С}_{р}}\left( Т \right)\frac{{dT}}{{d\tau }} + Q_{1}^{0}C_{1}^{0}\frac{{\partial {{\alpha }_{1}}}}{{\partial \tau }} + Q_{2}^{0}C_{2}^{0}\frac{{\partial {{\alpha }_{2}}}}{{\partial \tau }}} \right)} {\kern 1pt} dx. \\ \end{gathered} $

Выражение (6) используется для определения температур газа-теплоносителя в слое:

${{T}_{{g\;}}}_{i} = {{T}_{{g\;}}}_{{i - 1}} + \frac{{{{Q}_{i}}\Delta {{Y}_{i}}}}{{{{\omega }_{g}}\left( \tau \right){{\rho }_{g}}\left( Т \right){{С}_{{р\,g}}}\left( Т \right)}}.$

Для конвективной теплоотдачи считалась справедливой критериальная зависимость общего вида ${\text{Nu}}\;{\text{ = }}\;a\;{\text{R}}{{{\text{e}}}^{b}}$. Таким образом, температурная зависимость коэффициента теплоотдачи определялась температурной зависимостью теплопроводности ${{{{\lambda }}}_{g}}\left( Т \right)$ и кинематической вязкости ${{{{\eta }}}_{g}}\left( Т \right)$ газа-теплоносителя.

В вычислительных экспериментах использовались следующие зависимости:

$\left\{ \begin{gathered} {\text{Nu}} = 0.108\operatorname{Re} ,\,\,\,\,{\text{при}}\,\,\,\operatorname{Re} < 200 \hfill \\ {\text{Nu}} = 0.61{{\operatorname{Re} }^{{0.67}}},\,\,\,\,{\text{при}}\,\,\,\operatorname{Re} \geqslant 200 \hfill \\ \end{gathered} \right..$

Для проведения вычислительных экспериментов по полученной математической модели, была разработана компьютерная модель, исходными данными для которой являются:

– параметры физической модели: $\Delta {{Y}_{i}} = {{f}_{1}}\left( y \right)$, $2{{X}_{i}} = {{f}_{2}}\left( y \right)$, высота слоя H, порозность слоя, поправочный множитель, учитывающий эффективную поверхность реального плотного слоя рудного сырья [16];

– температурные зависимости теплофизических характеристик сырого и обожженного рудного материала, теплофизические характеристики газа-теплоносителя;

– параметры кинетических уравнений – энергии активации, предэкпоненты, показатели степеней реакций диссоциации карбонатов и процесса сушки, концентрации реагирующих компонентов и влаги [17];

– условия обжига рудных материалов – зависимости расхода и температуры греющих газов от времени [18].

МЕТОДИКА ПРОВЕДЕНИЯ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА

Для анализа нами использовался условный режим обжига, где параметром являлась температурная зависимость коэффициента теплопроводности.

В первом варианте (a) задавалась линейная температурная зависимость следующего вида: λa = 5 – 3.2 × 10–3T, Вт/(м K).

Во втором варианте (b) задавалась температурная зависимость, в которой значение λb составляло 0.7 от первого, во всем диапазоне температур: λb = 0.7(5 – 3.2 × 10–3T), Вт/(м K).

В третьем варианте (с) коэффициент теплопроводности задавался постоянным, не зависящим от температуры, численно равным среднему значению λa в рабочем диапазоне температур 300–1475 К: λc = 2.2, Вт/(м K).

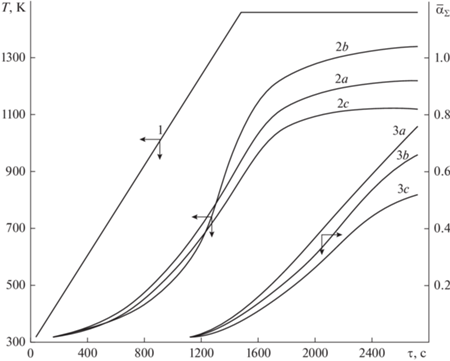
На рис. 1 приведены: температура газа-теплоносителя на входе в плотный слой заданная в вычислительном эксперименте, результаты расчетов температур газа-теплоносителя на выходе из слоя – кривые 2a, 2b, 2c и средних по слою степеней декарбонизации – 3a, 3b, 3c, соответствующие вариантам расчетов.

Рис. 1.

Влияние коэффициента теплопроводности на обжиг рудного фосфатного сырья: 1 – температура газа-теплоносителя на входе в слой, 2 – температура отходящих газов, 3 – средняя по слою степень декарбонизации.

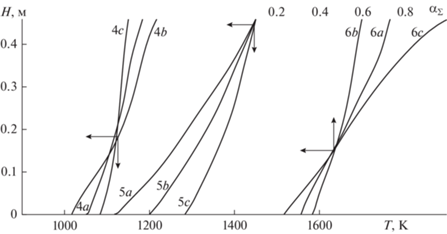
На рис. 2 приведены распределения температур рудного материала – кривые 4a, 4b, 4c, температуры газа-теплоносителя – кривые 5a, 5b, 5c, степени декарбонизации – кривые 6a, 6b, 6c по высоте плотного слоя засыпки соответствующие моменту времени τ = 2200 с от начала процесса обжига.

Рис. 2.

Распределение температур рудного материала, газа-теплоносителя и степень декарбонизации по высоте слоя в сечении времени τ =2200 с от начала процесса обжига: 4 – средняя по объему зерна температура материала, 5 – температура газа теплоносителя, 6 – степень декарбонизации.

Проведенные вычислительные эксперименты свидетельствуют о значительном влиянии коэффициента теплопроводности рудного фосфатного сырья на химико-энерготехнологический процесс обжига в движущейся плотной многослойной массе на конвейере обжиговой машины [19]. В принятых условиях обжига снижение теплопроводности сырья на 30% привело к повышению температуры отходящего газа-теплоносителя на 80 К, что составляет 32% от температурного перепада в слое, и снижению степени превращения на 8%. Характерно, что средняя температура материала в слое изменилась незначительно, на 8–10 К. Использование в расчетах постоянного значения коэффициента теплопроводности λc также изменяет результаты расчета температуры отходящего газа-теплоносителя, которая снизилась на 110 К [20]. Степень декарбонизации обжигаемого фосфатного рудного сырья возросла на 9%. Резко возросла неравномерность прокалки по высоте многослойной массы α = 0.9 в верхних горизонтах и α = 0.25 в нижних.

ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ ПО ИССЛЕДОВАНИЮ ТЕПЛООБМЕНА И ПРОКАЛКИ В МНОГОСЛОЙНОЙ ПОЛИФРАКЦИОННОЙ ЗАСЫПКЕ РУДНОГО ФОСФАТНОГО СЫРЬЯ

В ряде исследований [21–23] отмечается, что снижение фракционных размеров рудного сырья, обжигаемого в плотном слое, благоприятно сказывается на эффективности процесса обжига. Это очевидно связано с интенсификацией теплообмена и снижении тормозящего влияния термического сопротивления крупных фракций на кинетику прокалки.

Вместе с тем, переход на обжиг мелких фракций связан с необходимостью установки дробилок высокой производительности. Дополнительное измельчение рудного сырья приведет к повышению удельных расходов электроэнергии на подготовку сырья и образованию некондиционной мелочи [24].

В данном разделе рассматривается вариант обжига многослойной массы рудного сырья различного фракционного состава. Предполагается, что расположение крупных фракций в верхних горизонтах плотного слоя, то есть в области более высоких температур, будет способствовать повышению средней по высоте слоя степени реагирования реакции термической диссоциации карбонатов.

Для проведения вычислительных экспериментов моделировалась многослойная засыпка плотного слоя рудного материала путем “рассева” полифракционного рудного сырья, на шесть монофракций: 45, 30, 20, 15, 10, 5 мм, составляющих близкие по размеру фракциям рудного фосфатного сырья, поступающего из карьеров на горно-обогатительные комбинаты. Монослои сырья располагались в многослойной массе по мере увеличения размера зерен снизу вверх. Схема многослойной полифракционной засыпки приведена на рис. 4.

Рис. 3.

Влияние коэффициента теплопроводности на обжиг рудного фосфатного сырья в полифракционной засыпке: 1 – температура газа-теплоносителя на входе в слой; 2a и 2b – температуры отходящих газов полифракционной и монофракционной засыпке, 3a и 3b – средние по слою степень декарбонизации для случаев полифракционной и монофракционной засыпок.

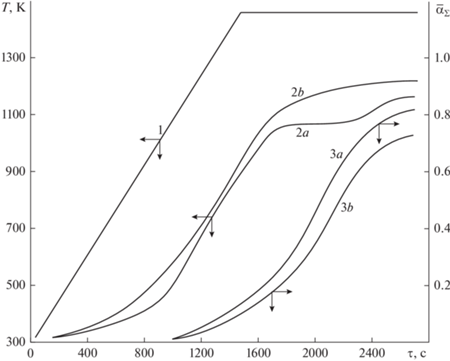
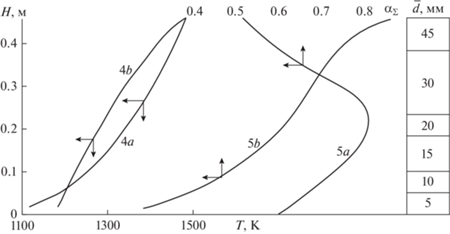
Рис. 4.

Распределение температуры газов и степени превращения по высоте слоя: 4a и 4b – температуры газов в полифракционной и монофракционной засыпке, 5a и 5b – степень декарбонизации в полифракционной и монофракционной засыпке.

Для сравнения проведен расчет в плотном слое полифракционной засыпки с использованием средневзвешенного размера зерен при прочих равных условиях [25]. Результаты расчета представлены на рис. 3 в виде графиков зависимости температур газа теплоносителя на входе в слой – кривая 1, отходящих газов на выходе из слоя, соответствующих двум вариантам расчетов – кривые 2a, 2b и средней по высоте слоя степени декарбонизации – кривые 3a, 3b.

На рис. 4 приведены распределения температур газов – кривые 4a, 4b и степени декарбонизации рудного сырья по высоте слоя – кривые 5a, 5b.

Сопоставление результатов вычислительных экспериментов показывает, что использование полифракционной засыпки в принятых условиях обжига приводит к снижению температуры отходящих газов на 40–70 К, при этом средняя по слою степень декарбонизации к концу обжига в полифракционной засыпке выше на 10%. Характерно, что при использовании полифракционной засыпки, видоизменяется распределение температур газа по высоте слоя. В средние слои реагирующего рудного материала поступает газ с более высоким теплосодержанием. Интересен и тот факт, что в средних горизонтах степень превращения выше на 25–30%, чем в верхних.

ЗАКЛЮЧЕНИЕ

Результаты проведенных вычислительных экспериментов позволяют сделать следующие основные выводы:

– различия в теплофизических характеристиках термически обрабатываемых рудных материалов даже в небольших пределах приводят к значительным изменениям в ходе химико-энерготехнологического процесса обжига – изменению температур газа теплоносителя в плотном слое и на выходе из него, эффективности обжига и неравномерности прокалки по высоте многослойной массы рудного сырья;

– в равной степени искажаются результаты расчетов технологического процесса обжига рудного фосфатного сырья при использовании ошибочных теплофизических характеристик;

– пренебрежение температурной зависимостью коэффициента теплопроводности также приводит к существенным искажениям практически всех результатов расчета.

В вычислительных экспериментах обнаружено, что в равных условиях обжиг рассеянного по фракциям рудного сырья более эффективен, так как способствует снижению температур газа-теплоносителя на колосниковой решетке и повышению степени декарбонизации фосфатного сырья.

Предварительное грохочение рудного сырья и раздельная засыпка монофракций практически исключает возможность образования в слое зон предпочтительного прососа газов и, следовательно, улучшаются условия эксплуатации колосниковой решетки.

Установлено, что монофракционный плотный слой для рудного фосфатного сырья имеет более чем в два раза меньшее аэродинамическое сопротивление, чем полифракционная многослойная засыпка. Следовательно, можно ожидать, что термически активируемый химико-энерготехнологический процесс обжига в полифракционной засыпке на колосниковой решетке обжиговой конвейерной машины будет способствовать снижению расхода электроэнергии на тяго-дутьевые установки.

ИСТОЧНИКИ ФИНАНСИРОВАНИЯ

Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта № 22-11-00335

ОБОЗНАЧЕНИЯ

α степень реагирования реакции декарбонизации
λ коэффициент теплопроводности, Вт/м К
ρ плотность, кг/м3
τ время, с
ε порозность плотного слоя
Т температура, К
x координата
${{C}_{p}}$ удельная теплоемкость, Дж/(кг K)
$C_{i}^{0}$ начальная концентрация карбонатов
$Q$ количество теплоты, Дж
$Q_{i}^{0}$ тепловой эффект декарбонизации, Дж/моль
X полутолщина пластины, м
H высота плотного слоя, м
G количество прореагировавшего вещества, моль
E энергия активации, Дж/моль
$\operatorname{Re} $ критерий Рейнольдса
${\text{Nu}}$ критерий Нуссельта
k0 предэкспоненциальный множитель, с–1

ИНДЕКСЫ

i номер компонента в смеси карбонатов
g для газа

Список литературы

  1. Леонтьев Л.И., Григорович К.В., Костина М.В. Фундаментальные исследования как основа создания новых материалов и технологий в области металлургии. Часть 1 // Известия высших учебных заведений. Черная металлургия. 2018. Т. 61. № 1. С. 11–22.

  2. Bobkov V.I., Fedulov A.S., Dli M.I., Meshalkin V.P., Morgunova E.V. Scientific basis of effective energy resource use and environmentally safe processing of phosphorus-containing manufacturing waste of ore-dressing barrows and processing enterprises // Clean Technologies and Environmental Policy. 2018. T. 20. № 10. C. 2209–2221.

  3. Meshalkin V.P., Dovì V.G., Bobkov V.I., et al. State of the art and research development prospects of energy and resource-efficient environmentally safe chemical process systems engineering // Mendeleev Communications. 2021. V. 31(5). P. 593–604.

  4. Егоров А.Ф., Савицкая Т.В., Михайлова П.Г. Современное состояние в области анализа, синтеза и оптимального функционирования многоассортиментных цифровых химических производств: аналитический обзор // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 154–187.

  5. Bobkov V.A., Dli M.I., Rubin Y.B. Influence of the conditions of internal heat exchange on the process of thermal decomposition of carbonates in iron ore raw materials // CIS Iron and Steel Review. 2022. V. 24. P. 4–8.

  6. Орехов В.А., Бобков В.И. Особенности исследования термической деструкции карбонатов в окомкованных фосфоритах при высокотемпературном обжиге // Тепловые процессы в технике. 2022. Т. 14. № 12. С. 555–562.

  7. Zhu X., Ji Y. A digital twin–driven method for online quality control in process industry // International J. Advanced Manufacturing Technology. 2022. V. 119(5–6). P. 3045–3064

  8. Цирлин А.М., Гагарина Л.Г., Балунов А.И. Синтез теплообменных систем, интегрированных с технологическим процессом // Теоретические основы химической технологии. 2021. Т. 55. № 3. С. 347–358.

  9. Борисов В.В., Курилин С.П., Луферов В.С. Нечеткие реляционные когнитивные темпоральные модели для анализа и прогнозирования состояния сложных технических систем // Прикладная информатика. 2022. Т. 17. № 1(97). С. 27–38.

  10. Курилин С.П., Соколов А.М., Прокимнов Н.Н. Компьютерная программа для эксплуатационной диагностики электромеханических систем на основе топологического подхода // Прикладная информатика. 2021. Т. 16. № 4(94). С. 62–73.

  11. Meshalkin V., Bobkov V., Dli M., Dovì V. Optimization of energy and resource efficiency in a multistage drying process of phosphate pellets // Energies. 2019. T. 12. № 17. C. 3376.

  12. Гуськов А.В., Гагарин П.Г., Гуськов В.Н., Тюрин А.В., Гавричев К.С. Теплоемкость и термодинамические функции твердого раствора LU2O3–2HFO2 // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 500. № 1. С. 84–88.

  13. Гагарин П.Г., Гуськов А.В., Гуськов В.Н., Хорошилов А.В., Гавричев К.С., Иванов В.К. Теплоемкость и термическое расширение М-ортотанталата тербия // Доклады Российской академии наук. Химия, науки о материалах. 2021. Т. 499. № 1. С. 63–65.

  14. Elgharbi S., Horchani-Naifer K., Férid M. Investigation of the structural and mineralogical changes of Tunisian phosphorite during calcinations // J. Thermal Analysis and Calorimetry. 2015. V. 119. № 1. P. 265–271.

  15. Пучков А.Ю., Лобанева Е.И., Култыгин О.П. Алгоритм прогнозирования параметров системы переработки отходов апатит-нефелиновых руд // Прикладная информатика. 2022. Т. 17. № 1(97). С. 55–68.

  16. Tomtas P., Skwiot A., Sobiecka E., Obraniak A, Ławińska K., Olejnik T.P. Bench Tests and CFD Simulations of Liquid–Gas Phase Separation Modeling with Simultaneous Liquid Transport and Mechanical Foam Destruction // Energies 2021. V. 14(6). P. 1740. https://doi.org/10.3390/en14061740

  17. Буткарев А.А., Вербыло С.Н., Бессмертный Е.А., Буткарева Е.А. Совершенствование и практическое использование методологии ВНИИМТ для оптимизации теплотехнических схем обжиговых конвейерных машин с рабочими площадями 278, 306 и 552 м2 // Сталь. 2020. № 5. С. 7–13.

  18. Wang S., Guo Y., Zheng F., Chen F., Yang L. Improvement of roasting and metallurgical properties of fluorine-bearing iron concentrate pellets // Powder Technology. 2020. V. 376. P. 126–135.

  19. Nayak D., Ray N., Dash N., et al. Induration aspects of low-grade ilmenite pellets: Optimization of oxidation parameters and characterization for direct reduction application // Powder Technology. 2021. V. 380. P. 408–420.

  20. Belyakov N.V., Nikolina N.V. Plant protection technologies: From advanced to innovative // J. Physics: Conference Series. 2021. V. 1942(1). P. 012072.

  21. Shekhovtsov V.V., Vlasov V.A., Skripnikova N.K., Semenovykh M.A. Structure Formation of Concrete Systems Modified By Nonstandard Particles // Russian Physics J. 2021. V. 63(9). P. 1590–1595.

  22. Kurilin S., Fedulov Y., Sokolov A. Scientific Substantiation of Topological Diagnostics Methods of Electrical Equipment, 2021 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), 2021. P. 288–293. https://doi.org/10.1109/ICIEAM51226.2021.9446356.

  23. Тураев Д.Ю., Почиталкина И.А. Теоретические и практические основы селективного извлечения фосфат-ионов из фосфатных руд с высоким содержанием примесей железа рециркуляционным методом // Теоретические основы химической технологии. 2022. Т. 56. № 2. С. 252–264.

  24. Ming Yan, Xinnan Song, Jin Tian, Xuebin Lv, Ze Zhang, Xiaoyan Yu, Shuting Zhang. Construction of a New Type of Coal Moisture Control Device Based on the Characteristic of Indirect Drying Process of Coking Coal // Energies 2020. V. 13(16). P. 4162. https://doi.org/10.3390/en13164162

  25. Кольцов Н.И. Линейные концентрационные и температурные законы сохранения в открытом безградиентном химическом реакторе // Теоретические основы химической технологии. 2021. Т. 55. № 2. С. 210–215.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал