Теоретические основы химической технологии, 2023, T. 57, № 4, стр. 467-478
Методы оптимизационной термодинамики в процессах ректификации
А. М. Цирлин a, *, А. И. Балунов a, И. А. Сукин a, А. М. Васильев a
a Ярославский государственный технический университет
Институт программных систем им. А.К. Айламазяна РАН
Ярославль, Россия
* E-mail: tsirlin@sarc.botik.ru
Поступила в редакцию 21.05.2023
После доработки 30.05.2023
Принята к публикации 05.06.2023
- EDN: VKFXLF
- DOI: 10.31857/S0040357123040164
Аннотация
Изложены результаты использования методологии оптимизационной термодинамики для математического описания и оптимизации процессов ректификации. Рассмотрены задачи построения множества реализуемых режимов для колонн, разделяющих бинарную и многокомпонентную смесь, выбор порядка разделения многокомпонентной смеси, целесообразность использования разделяющего агента, выбор температуры и точки ввода питания, оптимизации параллельных и последовательных систем колонн ректификации. Получены расчетные формулы для производства энтропии и коэффициентов теплопередачи в кубе и в дефлегматоре колонны.
ВВЕДЕНИЕ
Задачи о предельных возможностях термодинамических систем, имеющих заданную или предельную интенсивность целевых потоков, применительно к тепловым машинам были рассмотрены еще в середине 19-го века. Но развития это направление не получило до того момента, когда в пятидесятых годах прошлого столетия не стала развиваться атомная энергетика. Для нее капитальные затраты значительно превышают аналогичные затраты тепловых электростанций, а затраты на топливо, наоборот, значительно ниже. Поэтому цикл тепловой машины должен был соответствовать не максимальному КПД, а максимальной мощности. Работа И.И. Новикова [1] была посвящена именно этой задаче. Позднее после появления целого ряда исследований (см. [2–4] и др.) стало ясно, что задачи о предельных показателях термодинамических систем с заданными интенсивностями потоков и задачи о предельных интенсивностях этих потоков представляют собой целый класс проблем, решаемых с применением общей методологии. Возникло направление термодинамики необратимых процессов, которое было названо “Термодинамикой при конечном времени”. Тем самым подчеркивалось, что в отличие от равновесной термодинамики рассматриваются процессы ограниченной продолжительности. Однако в большинстве задач речь идет о стационарных неравновесных процессах и время при этом не фигурирует. Поэтому нам кажется более естественным, следуя Л.И. Розоноэру, называть это направление “Оптимизационной термодинамикой”, подчеркивая, что методами оптимизации исследуются предельные возможности необратимых термодинамических процессов.
Методология оптимизационной термодинамики состоит из нескольких этапов:
– Записывают для исследуемого процесса уравнения термодинамических балансов по энергии, каждому из веществ и по энтропии. Если веществ $n$ то уравнений $n + 2$.
– Решают экстремальную задачу о такой организации процесса, для которой производство энтропии $\sigma $, входящее в условие энтропийного баланса, было минимально при ограничениях на размеры аппарата и интенсивность потоков. При этом используют условия минимальной диссипации [5]. Минимальное производство энтропии $\sigma {\text{*}}$ оказывается функцией интенсивностей потоков и коэффициентов кинетических уравнений.
– Уравнения термодинамических балансов совместно с неравенством $\sigma \geqslant \sigma {\text{*}}$ выделяют в пространстве потоков область реализуемых режимов технологического процесса. При этом режимы с предельными значениями параметров потоков (мощности, КПД, …) как правило лежат на границе этой области.
В данной работе эта методология использована применительно к процессу разделения жидких смесей путем их ректификации, который является одним из самых энергоемких процессов (на разделение нефти затрачивают примерно 6% содержащейся в ней энергии).
Анализу процессов разделения жидких смесей в колоннах ректификации посвящена обширная литература (см. [6–11] и др.). При этом как правило считают заданными не только состав сырья, но и составы продуктовых потоков и находят расчетом от тарелки к тарелке производительность колонны, ее высоту, затраты теплоты и пр. Доля отбора верхнего продукта для заданных составов потоков оказывается фиксированной. В [12, 13] при построении модели использовалось уравнение баланса по энтропии и построена область реализуемых нагрузок с учетом необратимости процессов тепло и массопереноса.
Ниже первоначально рассмотрим математическую модель ректификационной колонны, разделяющей бинарную смесь, и при некоторых упрощающих анализ допущениях найдем связь между затратами теплоты и производительностью. Затем покажем, что КПД колонны с учетом необратимости монотонно зависит от ее обратимого КПД, при этом для принятой формы кинетики тепло- и массопереноса КПД колонны в режиме максимальной производительности не зависит от необратимых факторов и вдвое меньше, чем КПД обратимой колонны. Будем предполагать долю отбора и связанные с ней составы выходных потоков подлежащими выбору. Затем рассмотрим задачи о разделении многокомпонентных смесей в системе колонн ректификации и об оптимизации таких систем.
В первом разделе показано, что связь между производительностью колонны по потоку перерабатываемого сырья и затратами теплоты можно параметризовать функцией, зависящей только от двух параметров, каждый из которых, в свою очередь, зависит от составов разделяемых потоков, кинетических коэффициентов и других факторов. Проведем сравнение колонны ректификации с тепловой машиной и покажем, что ее можно рассматривать как тепловую машину, вырабатывающую работу разделения. Ее возможности в обратимом режиме характеризует термический КПД, аналогичный КПД Карно. Ее мощность при учете необратимых факторов ограничена, а термический КПД экстремально зависит от доли отбора $\varepsilon $ верхнего продукта и достигает максимума, когда эта доля равна концентрации легколетучего компонента в сырье $\varepsilon = {{x}_{{\text{F}}}}$.
Во втором разделе рассмотрена задача разделения многокомпонентных смесей и предложен алгоритм определения порядка разделения.
В третьем разделе параметризованные характеристики колонн использованы для оптимизации систем с параллельной и последовательной структурой и решении задачи об оптимальном порядке выделения из смеси трех компонентов компонента со “средней” температурой кипения.
ГРАНИЦА МНОЖЕСТВА РЕАЛИЗУЕМОСТИ КОЛОННЫ И ЕЕ ПАРАМЕТРИЗАЦИЯ
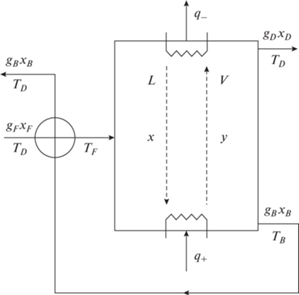
Будем рассматривать традиционную конструкцию колонны с подводом теплоты в куб и отводом из дефлегматора.
Основные допущения. Перечислим основные допущения, использованные при рассмотрении колонны с заданной производительностью:
1. Массообмен эквимолярный.
2. В каждом сечении по высоте колонны давления и температуры потоков пара и жидкости близки друг к другу (от сечения к сечению они изменяются).
3. Колонна близка к насадочной, а потоки пара и флегмы движутся в режиме близком к идеальному вытеснению, так что эффекты диффузии между соседними сечениями пренебрежимо малы.
4. Поступающий в колонну поток сырья подогревается до температуры близкой к температуре флегмы в том сечении колонны, где состав флегмы близок к составу сырья, так что необратимостью смешения этих потоков можно пренебречь. Производство энтропии в теплообменнике подогрева сырья не зависит от режима в колонне и гораздо меньше, чем производство энтропии в колонне.
5. Жидкая фаза в кубе и в дефлегматоре перемешана.
6. Колонна теплоизолирована.
Сделанные допущения снижают необратимость, так что полученное при расчете значение производства энтропии является оценкой снизу для фактического.
Таким образом рассматривается идеализированная модель насадочной колонны, в которой учтены два основных источника необратимости: теплообмен при подаче тепла в куб и при его отборе из дефлегматора и массоперенос между паром и флегмой по высоте колонны. К этой модели близка и тарельчатая колонна при достаточно большом числе тарелок. Отметим, что эффективный коэффициент массопереноса, если его находят по данным действующей колонны, косвенно учитывает внутреннюю диффузию, смешение на тарелках и пр.
Мольные доли низкокипящего компонента в потоке сырья ${{x}_{F}}$ и в потоках, отбираемых из дефлегматора и куба ${{x}_{B}}$ и ${{x}_{D}}$, будем предполагать заданными, как и температуру в дефлегматоре ${{T}_{D}}$, которую выбирают и поддерживают с помощью изменения давления в колонне по условиям использования для охлаждения воды, имеющей температуру окружающего воздуха. Температура в кубе ${{T}_{B}}$ подлежит расчету.
Доля отбора $\varepsilon $ зависит от составов входного и выходных потоков. Действительно, из материального баланса по низкокипящему компоненту получим
СВЯЗЬ МЕЖДУ ЗАТРАТАМИ ТЕПЛОТЫ И ПРОИЗВОДИТЕЛЬНОСТЬЮ КОЛОННЫ
Из уравнений энергетического и энтропийного балансов, предполагая, что смеси близки к идеальным растворам и пренебрегая теплотой смешения, получим:
(2)
${{q}_{ + }} - {{q}_{ - }} + {{g}_{F}}{{h}_{F}} - {{g}_{F}}\varepsilon {{h}_{D}} - {{g}_{F}}(1 - \varepsilon ){{h}_{B}} = 0,$(3)
${{g}_{F}}{{s}_{F}} - {{g}_{F}}\varepsilon {{s}_{D}} - {{g}_{F}}(1 - \varepsilon ){{s}_{B}} + \frac{{{{q}_{ + }}}}{{{{T}_{B}}}} - \frac{{{{q}_{ - }}}}{{{{T}_{D}}}} + \sigma = 0.$Здесь $\sigma > 0$ – производство энтропии в колонне.
Из условий (2), (3) после исключения ${{q}_{ - }}$ следует
(4)
$\begin{gathered} {{q}_{ + }} = {{g}_{F}}\frac{{{{T}_{B}}}}{{{{T}_{B}} - {{T}_{D}}}}\left[ {({{s}_{F}}{{T}_{D}} - {{h}_{F}})} \right. - \varepsilon ({{s}_{D}}{{T}_{D}} - {{h}_{D}}) - \\ - \,\,(1 - \varepsilon )\left. {({{s}_{B}}{{T}_{D}} - {{h}_{B}})} \right] + \sigma \frac{{{{T}_{B}}{{T}_{D}}}}{{{{T}_{B}} - {{T}_{D}}}} = \\ = q_{ + }^{0} + \sigma \frac{{{{T}_{B}}{{T}_{D}}}}{{{{T}_{B}} - {{T}_{D}}}}. \\ \end{gathered} $Первое слагаемое в правой части этого выражения, которое обозначено через $q_{ + }^{0}$, представляет собой затраты теплоты в обратимом процессе, когда коэффициенты тепло- и массообмена (размеры колонны) сколь угодно велики. Оно зависит только от параметров входных и выходных потоков и пропорционально производительности ${{g}_{F}}$, второе – соответствует диссипативным потерям энергии.
Обозначим через ${{C}_{F}},{{C}_{D}},{{C}_{B}}$ теплоемкости потоков сырья, верхнего продукта и кубового остатка. Поток сырья, прежде чем попасть в колонну, обычно проходит через регенеративный теплообменник, в котором контактирует с потоком продукта, выходящим из куба. При этом температура потока сырья на входе в теплообменник близка к ${{T}_{D}}$, в теплообменнике (см. допущение 4) выполнено уравнение теплового баланса
так что поток кубового остатка покидает теплообменник при температуре ${{T}_{D}}$.С учетом того обстоятельства, что разность $(h - {{T}_{D}}s)$ для каждого из потоков равна мольной свободной энергии, т.е. химическому потенциалу $\mu $ смеси при $T = {{T}_{D}}$, связь теплового потока с производительностью примет форму
(5)
$\begin{gathered} q = {{g}_{F}}\frac{{{{T}_{B}}}}{{{{T}_{B}} - {{T}_{D}}}}\left[ {\varepsilon {{\mu }_{D}}({{T}_{D}},{{x}_{D}})} \right. + (1 - \varepsilon ){{\mu }_{B}}({{T}_{D}},{{x}_{B}}) - \\ - \,\,\left. {{{\mu }_{F}}({{T}_{D}},{{x}_{F}})} \right] + \sigma \frac{{{{T}_{B}}{{T}_{D}}}}{{{{T}_{B}} - {{T}_{D}}}}. \\ \end{gathered} $Каждый из химических потенциалов имеет вид
Так как химические потенциалы в каждом сечении колонны соответствуют одним и тем же температуре и давлению, их разность для паровой фазы
Подставив эти равенства в (5), получим:
(7)
$\begin{gathered} q = {{g}_{F}}\frac{{{{T}_{B}}}}{{{{T}_{B}} - {{T}_{D}}}}\left[ {{{A}_{F}} - \varepsilon {{A}_{D}} - (1 - \varepsilon ){{A}_{B}}} \right] + \\ + \,\,\frac{{\sigma {{T}_{D}}{{T}_{B}}}}{{{{T}_{B}} - {{T}_{D}}}} = \frac{{{{p}_{0}}}}{{{{\eta }_{C}}}} + \frac{{\sigma {{T}_{D}}}}{{{{\eta }_{C}}}}. \\ \end{gathered} $Здесь
(8)
$\begin{gathered} {{A}_{i}} = - R{{T}_{D}}\left[ {{{x}_{i}}{\text{ }}\ln {\text{ }}{{x}_{i}} + (1 - {{x}_{i}}){\text{ }}\ln {\text{ }}(1 - {{x}_{i}})} \right], \\ (i = F,D,B), \\ \end{gathered} $– обратимая работа разделения одного моля $i$-го потока на чистые компоненты, а выражение, стоящее в (7) в квадратных скобках, представляет собой обратимую работу разделения Гиббса одного моля потока сырья с концентрацией ${{x}_{F}}$ на потоки с концентрациями ${{x}_{B}}$ и ${{x}_{D}}$ при температуре ${{T}_{D}}$. Обозначим ее как ${{A}_{G}}$. Величина ${{\eta }_{C}} = (1 - {{{{T}_{D}}} \mathord{\left/ {\vphantom {{{{T}_{D}}} {{{T}_{B}}}}} \right. \kern-0em} {{{T}_{B}}}})$ – аналог КПД Карно.
Приравнивая в (7) производство энтропии нулю, получим обратимую оценку ${{q}^{0}} = \frac{{{{g}_{F}}{{A}_{G}}}}{{{{\eta }_{{\text{K}}}}}}$ затрат теплоты в процессе ректификации.
Разрешим уравнение (7) относительно ${{g}_{F}}$. Получим:
(9)
${{g}_{F}} = q\frac{{{{\eta }_{C}}}}{{{{A}_{G}}}} - \sigma (q,{{g}_{F}})\frac{{{{T}_{D}}}}{{{{A}_{G}}}}.$Найдем оценку снизу для второго слагаемого в этом равенстве для чего нужно определить производство энтропии в процессах теплообмена в кубе и в дефлегматоре, а также в процессе массообмена между потоками пара и флегмы.
НЕОБРАТИМЫЕ ПОТЕРИ ЭНЕРГИИ
Необратимость теплообмена в кубе и в дефлегматоре. Дефлегматор и куб представляют собой двухпоточные теплообменники типа смешение-вытеснение. В дефлегматоре в режиме вытеснения находится охлаждающая вода с температурой на входе $T_{ - }^{{{\text{in}}}}$ и теплоемкостью потока ${{W}_{ - }}$ (произведением ее мольного расхода на мольную теплоемкость). В режиме смешения – конденсат с температурой ${{T}_{D}}$. Производство энтропии [14]
(10)
${{\sigma }_{D}} = {{W}_{ - }}\ln \frac{{T_{ - }^{{{\text{in}}}} + {q \mathord{\left/ {\vphantom {q {{{W}_{ - }}}}} \right. \kern-0em} {{{W}_{ - }}}}}}{{T_{ - }^{{{\text{in}}}}}} - \frac{q}{{{{T}_{D}}}} \approx q\left( {\frac{1}{{T_{ - }^{{{\text{in}}}}}} - \frac{1}{{{{T}_{D}}}}} \right).$В кубе в режиме вытеснения поток греющего, обычно насыщенного, пара с температурой конденсации ${{T}_{ + }}$, а в режиме смешения – кубовая жидкость с температурой кипения ${{T}_{B}}$. Производство энтропии
Суммарное производство энтропии за счет теплообмена ${{\sigma }_{q}} = {{\sigma }_{D}} + {{\sigma }_{B}}$.
Необратимость массопереноса по высоте колонны. Для подсчета производства энтропии в процессе массопереноса будем использовать модель, соответствующую насадочной колонне, с противоточным движением потоков пара и флегмы в режиме, близком к вытеснению. Величина потока пара $V = \frac{q}{r}$ при эквимолярном массопереносе не изменяется по высоте колонны и связана с потоком флегмы $L$ равенствами:
для верхней части колонны
для нижней частиВ качестве независимой переменной вместо высоты колонны выберем концентрацию низкокипящего компонента $x$, монотонно зависящую от высоты.
С учетом того, что для бинарной ректификации концентрации высококипящего компонента в жидкостном и паровом потоках равны $1 - x$ и $1 - y$ соответственно, а движущая сила процесса определяется различием текущей концентрации $y(x)$ и равновесной концентрации ${{y}^{0}}(x)$, производство энтропии, связанное с массопереносом, выражается через потоки и химические потенциалы как
(14)
$\begin{gathered} {{\sigma }_{g}} = \int\limits_{{{x}_{B}}}^{{{x}_{D}}} {\frac{1}{{T(x)}}} \{ {{g}_{1}}(y,{{y}^{0}})[{{\mu }_{1}}(T,{{y}^{0}}) - {{\mu }_{1}}(T,y)] + \\ + \,\,{{g}_{2}}(1 - y,1 - {{y}^{0}})[{{\mu }_{2}}(T,1 - y) - {{\mu }_{2}}(T,1 - {{y}^{0}})]\} dx, \\ \end{gathered} $Выражение (14) с учетом вида химических потенциалов (6) и эквимолярности массообмена (${{g}_{1}}(y,{{y}^{0}})\, = \, - {{g}_{2}}(1\, - \,y,1\, - \,{{y}^{0}})\, = \,g$) перепишется в форме
(15)
${{\sigma }_{g}} = R\int\limits_{{{x}_{B}}}^{{{x}_{D}}} g (y,{{y}^{0}})\ln \frac{{{{y}^{0}}(1 - y)}}{{y(1 - {{y}^{0}})}}dx.$Из уравнений материального баланса по низкокипящему компоненту для верха и низа колонны получим
С учетом (12), (13) имеем для верха и низа колонны после замены ${{g}_{D}} = {{g}_{F}}\varepsilon $, ${{g}_{B}} = {{g}_{F}}(1 - \varepsilon )$ рабочие линии:
(18)
${{y}^{D}}\left( {x,\frac{q}{r},{{g}_{F}}} \right) = \left( {1 - \frac{{{{g}_{F}}\varepsilon r}}{q}} \right)x + \frac{{{{x}_{D}}{{g}_{F}}\varepsilon r}}{q},$(19)
${{y}^{B}}\left( {x,\frac{q}{r},{{g}_{F}}} \right) = \left( {1 + \frac{{{{g}_{F}}(1 - \varepsilon )r}}{q}} \right)x - \frac{{{{x}_{B}}{{g}_{F}}(1 - \varepsilon )r}}{q}.$Из этих равенств следует, что ${{y}^{D}}({{x}_{D}}) = {{x}_{D}},~$ $~{{y}^{B}}({{x}_{B}})\, = \,{{x}_{B}},\,\,{{y}^{D}}({{x}_{F}})\, = \,{{y}^{B}}({{x}_{F}})\, = \,{{y}_{F}},\,\,$ а ${{y}_{F}} - {{x}_{F}} = $ $ = \,\,\frac{{{{g}_{D}}r}}{q}({{x}_{D}}\, - \,{{x}_{F}})$.
Подстановка выражений (18), (19) в равенство (15) определяет для заданного закона массопереноса производство энтропии ${{\sigma }_{g}}(q,{{g}_{F}})$. При этом подсчитывают сумму интегралов на интервалах от ${{x}_{B}}$ до ${{x}_{F}}$, когда $y(x) = {{y}^{B}}\left( {x,\frac{q}{r},{{g}_{F}}} \right)$, и от ${{x}_{F}}$ до ${{x}_{D}}$, когда $y(x) = {{y}^{D}}\left( {x,\frac{q}{r},{{g}_{F}}} \right)$, что возможно лишь численно.
Для получения результатов в аналитической форме найдем оценку ${{\sigma }_{g}}$ снизу, приняв закон массопереноса пропорциональным движущей силе
После исключения разности химических потенциалов через поток $g(y,{{y}^{0}})$ равенство (15) примет форму
(21)
${{\sigma }_{g}}(q,{{g}_{F}}) = \frac{2}{k}\int\limits_{{{x}_{B}}}^{{{x}_{D}}} {{{g}^{2}}} (y,{{y}^{0}})dx.$Здесь множитель 2 связан с учетом эквимолярного потока высококипящего компонента из пара в жидкость.
Обозначим среднее значение потока как:
(22)
$\bar {g} = \frac{1}{{{{x}_{D}} - {{x}_{B}}}}\int\limits_{{{x}_{B}}}^{{{x}_{D}}} g (y,{{y}^{0}})dx$и с использованием (21) получим оценку снизу для ${{\sigma }_{g}}$:
Неравенство (23) превращается в равенство в том случае, когда поток массопереноса между паром и флегмой мало изменяется по высоте колонны.
Расход пара по высоте колонны постоянен и для общего количества низкокипящего, перешедшего из жидкости в пар, имеем условие материального баланса
(24)
$\int\limits_{{{x}_{B}}}^{{{x}_{D}}} {g(y,{{y}^{0}})dx} = V[{{y}^{D}}({{x}_{D}}) - {{y}^{B}}({{x}_{B}})] = \frac{q}{r}({{x}_{D}} - {{x}_{B}}),$Правую часть этого неравенства будем использовать для оценки необратимости массопереноса.
Подстановка суммарного производства энтропии в выражение (9) позволяет получить оценку для производительности бинарной ректификации в зависимости от теплового потока:
(26)
$\begin{gathered} {{g}_{F}} = \frac{1}{{{{A}_{G}}}}\left[ {{{\eta }_{c}} - {{T}_{D}}\left( {\frac{1}{{T_{ - }^{{{\text{in}}}}}} - \frac{1}{{{{T}_{D}}}} + \frac{1}{{{{T}_{B}}}} - \frac{1}{{{{T}_{ + }}}}} \right)} \right]q - \\ - \,\,\frac{{2({{x}_{D}} - {{x}_{B}}){{T}_{D}}}}{{{{A}_{G}}k{{r}^{2}}}}{{q}^{2}}. \\ \end{gathered} $Или в параметрической форме
где(28)
$\begin{gathered} b = \frac{1}{{{{A}_{G}}}}\left[ {{{\eta }_{c}} - {{T}_{D}}\left( {\frac{1}{{T_{ - }^{{{\text{in}}}}}} - \frac{1}{{{{T}_{D}}}} + \frac{1}{{{{T}_{B}}}} - \frac{1}{{{{T}_{ + }}}}} \right)} \right], \\ a = \frac{{2({{x}_{D}} - {{x}_{B}}){{T}_{D}}}}{{{{A}_{G}}k{{r}^{2}}}}. \\ \end{gathered} $Эту зависимость будем называть нагрузочной характеристикой колонны.
Здесь ${{\eta }_{c}}$ – аналог КПД Карно, если рассматривать колонну ректификации как машину, преобразующую тепловую энергию в работу разделения. При полном разделении концентрация легколетучего в кубовом продукте ${{x}_{B}}$ равна нулю, в дефлегматоре она равна единице, а доля отбора равна ${{x}_{F}}$. Остановимся на этом режиме подробнее.
СЛУЧАЙ ПОЛНОГО РАЗДЕЛЕНИЯ
Рассмотрим случай, когда разделение полное, т.е. в верхнем отборе содержится только низкокипящий компонент, пока доля отбора не превышает ${{x}_{F}}$. В этом случае
(29)
${{x}_{D}}(\varepsilon ) = 1\,\,{\text{ при }}\,\,~\varepsilon \leqslant {{x}_{F}},\,\,\,\,{{x}_{D}} = \frac{{{{x}_{F}}}}{\varepsilon }~{\text{ при \;}}\varepsilon > {{x}_{F}}.$По условиям материального баланса по легколетучему компоненту
(30)
$\begin{gathered} {{x}_{B}}(\varepsilon ) = \frac{{{{x}_{F}} - \varepsilon }}{{1 - \varepsilon }}{\text{ при }}~\varepsilon \leqslant {{x}_{F}}, \\ {{x}_{B}} = 0~{\text{ при }}~\varepsilon > {{x}_{F}}. \\ \end{gathered} $С учетом того, что ${{x}_{{Di}}} = {{{{x}_{{Fi}}}} \mathord{\left/ {\vphantom {{{{x}_{{Fi}}}} \varepsilon }} \right. \kern-0em} \varepsilon }$, а ${{x}_{{Bi}}} = {{{{x}_{{Fi}}}} \mathord{\left/ {\vphantom {{{{x}_{{Fi}}}} {(1 - \varepsilon )}}} \right. \kern-0em} {(1 - \varepsilon )}}$ выражение для молярной работы разделения смеси при полном разделении примет форму
а величина затрат теплоты на моль разделяемой смесиЭКСТРЕМАЛЬНАЯ ЗАВИСИМОСТЬ ТЕРМИЧЕСКОГО КПД ОТ ДОЛИ ОТБОРА
Присвоим индекс $i = 1$ легколетучему, а $i = 2$ высококипящему компонентам. При любой температуре справедливо неравенство
Давление в колонне зависит от доли отбора и одинаково в кубе и в дефлегматоре, так что
(34)
$\begin{gathered} P = {{P}_{1}}({{T}_{D}}) = \frac{{{{x}_{F}} - \varepsilon }}{{1 - \varepsilon }}{{P}_{1}}({{T}_{B}}) + \\ + \,\,\frac{{1 - {{x}_{F}}}}{{1 - \varepsilon }}{{P}_{2}}({{T}_{B}}),~{\text{ при }}~\varepsilon \leqslant {{x}_{F}}; \\ P = \frac{{{{x}_{F}}}}{\varepsilon }{{P}_{1}}({{T}_{D}}) + \left( {1 - \frac{{{{x}_{F}}}}{\varepsilon }} \right){{P}_{2}}({{T}_{D}}) = {{P}_{2}}({{T}_{B}}),~ \\ {\text{ при }}~\varepsilon > {{x}_{F}}. \\ \end{gathered} $Условие равенства давлений можно переписать в форме ${{F}_{ - }}(\varepsilon ,{{T}_{B}}) = 0$ и ${{F}_{ + }}(\varepsilon ,{{T}_{B}}) = 0$ для $\varepsilon \leqslant {{x}_{F}}$ и $\varepsilon > {{x}_{F}}$ соответственно, что позволяет вычислить производную $\frac{{d{{T}_{B}}}}{{d\varepsilon }}$ как:
(35)
$\frac{{d{{T}_{B}}}}{{d\varepsilon }} = - {{\frac{{dF}}{{d\varepsilon }}} \mathord{\left/ {\vphantom {{\frac{{dF}}{{d\varepsilon }}} {\frac{{dF}}{{d{{T}_{B}}}}}}} \right. \kern-0em} {\frac{{dF}}{{d{{T}_{B}}}}}}.$Для ${{F}_{ - }}(\varepsilon ,{{T}_{B}})$ после дифференцирования получим
(36)
$\begin{gathered} \frac{{d{{F}_{ - }}}}{{d\varepsilon }} = ({{P}_{2}}({{T}_{B}}) - {{P}_{1}}({{T}_{B}}))\frac{{1 - {{x}_{F}}}}{{{{{(1 - \varepsilon )}}^{2}}}} < 0, \\ \frac{{d{{F}_{ - }}}}{{d{{T}_{B}}}} = \frac{{{{x}_{F}} - \varepsilon }}{{1 - \varepsilon }}\frac{{d{{P}_{1}}}}{{d{{T}_{B}}}} + \frac{{1 - {{x}_{F}}}}{{1 - \varepsilon }}\frac{{d{{P}_{2}}}}{{d{{T}_{B}}}} > 0. \\ \end{gathered} $Отношение этих производных отрицательно, так что в соответствии с (35) температура в кубе с ростом доли отбора возрастает.
Аналогично для ${{F}_{ + }}(\varepsilon ,{{T}_{B}})$ после дифференцирования получим
(37)
$\begin{gathered} \frac{{d{{F}_{ + }}}}{{d\varepsilon }} = ({{P}_{2}}({{T}_{B}}) - {{P}_{1}}({{T}_{B}}))\frac{{{{x}_{F}}}}{{{{\varepsilon }^{2}}}} < 0, \\ \frac{{d{{F}_{ + }}}}{{d{{T}_{B}}}} = - \frac{{d{{P}_{2}}}}{{d{{T}_{B}}}} < 0. \\ \end{gathered} $Знаки производных совпадают, а значит в соответствии с (35) температура в кубе с ростом доли отбора падает. Таким образом, в точке $\varepsilon = {{x}_{F}}$ температура в кубе и монотонно зависящий от нее термический КПД максимальны.
Если для расчета давлений пара каждого из компонентов используется уравнение Антуана [11]:
где ${{A}_{i}}$, ${{B}_{i}}$ и ${{C}_{i}}$ – эмпирические коэффициенты, таблицы для которых имеются для большинства веществ, то при $\varepsilon = {{x}_{F}}$ из (34) ${{P}_{2}}(T_{B}^{*}) = {{P}_{1}}({{T}_{D}})$, откуда следует, что максимальное значение температуры в кубе и максимум термического КПД равны(39)
$T_{B}^{*} = \frac{{{{B}_{2}}({{T}_{D}} + {{C}_{1}})}}{{({{A}_{2}} - {{A}_{1}})({{T}_{D}} + {{C}_{1}}) + {{B}_{1}}}} - {{C}_{2}},\,\,\,\eta _{c}^{*} = 1 - \frac{{{{T}_{D}}}}{{T_{B}^{*}}}.$Пример.
Рассмотрим разделение смеси, данные о которой приведены в табл. 1 (см. [11]). Температура в дефлегматоре задана и равна ${{T}_{D}} = 323$ K.
Таблица 1.
Данные о смеси и продуктах разделения для Примера 1
| Компонент | ${{x}_{F}}$ | ${{x}_{D}}$ | ${{x}_{B}}$ | $A$ | $B$ | $C$ |
|---|---|---|---|---|---|---|
| Бензол | 0.4 | 1.00 | 0.00 | 4.01814 | 1203.835 | –53.226 |
| Толуол | 0.6 | 0.00 | 1.00 | 4.07827 | 1343.943 | –53.773 |
По формуле (39) получим
Термический КПД в необратимом процессе, соответствующим максимальной мощности, равен 0.04.
СРАВНЕНИЕ С ТЕПЛОВОЙ МАШИНОЙ
В [15] получена связь между расходом теплоты ${{q}_{ + }}$ от горячего источника и мощностью тепловой машины с источниками бесконечной емкости с законами теплообмена между источниками и рабочим телом вида:
(40)
${{q}_{ + }} = {{k}_{ + }}({{T}_{ + }} - T),\,\,\,\,{{q}_{ - }} = {{k}_{ - }}(T - {{T}_{ - }}),$Эта связь имеет форму:
(41)
$p = \frac{{k({{T}_{ + }} - {{T}_{ - }}){{q}_{ + }} - q_{ + }^{2}}}{{k{{T}_{ + }} - {{q}_{ + }}}},$При разложении зависимости (41) в ряд Тэйлора получим параметризованное представление аналогичное (27)
(42)
$p = c{{q}_{ + }} - dq_{ + }^{2},\,\,\,\,c = {{\eta }_{c}} = 1 - {{{{T}_{ - }}} \mathord{\left/ {\vphantom {{{{T}_{ - }}} {{{T}_{ + }},}}} \right. \kern-0em} {{{T}_{ + }},}}\,\,\,\,d = \frac{1}{{k{{T}_{ + }}}}.$Будем называть параметр $b$ нагрузочной характеристики колонны обратимым КПД, а параметр $a$ – коэффициентом необратимости. Первый из них зависит только от составов разделяемой смеси и отбираемых потоков, второй – так же и от кинетики процесса, а значит от конструктивных особенностей колонны. Обратимый КПД соответствует КПД колонны, имеющей сколь угодно большие коэффициенты тепло и массопереноса. Так как составы потоков обычно заданы, то его величина известна.
СЛЕДСТВИЯ ИЗ ВОЗМОЖНОСТИ ПАРАМЕТРИЗАЦИИ НАГРУЗОЧНОЙ ХАРАКТЕРИСТИКИ
Тот факт, что зависимость максимальной производительности колонны от расхода теплоты может быть параметризована двумя параметрами (они могут быть найдены и по данным эксперимента на действующей колонне), позволяет решать некоторые задачи, используя эти параметры. Ниже приведены решения нескольких таких задач.
ПРЕДЕЛЬНАЯ ПРОИЗВОДИТЕЛЬНОСТЬ
Максимально целесообразные затраты теплоты и предельная производительность определены через характеристические параметры. Из (27) следует, что производительность максимальна при затратах теплоты:
и достигает значенияДальнейшее увеличение потока теплоты нецелесообразно, так как в силу роста диссипации приводит к уменьшению производительности, поэтому ${{q}^{0}}$ является границей рабочего участка нагрузочной характеристики. На рабочем участке расход теплоты монотонно зависит от производительности как:
КПД КОЛОННЫ В РЕЖИМЕ ПРЕДЕЛЬНОЙ ПРОИЗВОДИТЕЛЬНОСТИ
Введем параметр $z = \frac{q}{{{{q}^{0}}}}$ – степень загруженности колонны, изменяющийся от нуля до единицы. Тогда КПД колонны бинарной ректификации (см. (27)) после исключения $a$ через $z$ примет форму:
При максимальной нагрузке, когда $z = 1$, КПД колонны не зависит от необратимых факторов и равен $0.5b$ (половине обратимого КПД). От необратимых факторов зависит само значение предельной производительности и соответствующих ей затрат теплоты. Это обстоятельство соответствует тому известному факту [2], что значение КПД цикла необратимой тепловой машины, соответствующего максимуму ее мощности (КПД Новикова–Курзона–Альборна), не зависит от кинетики теплообмена рабочего тела с источниками, но предельная мощность машины от нее зависит.
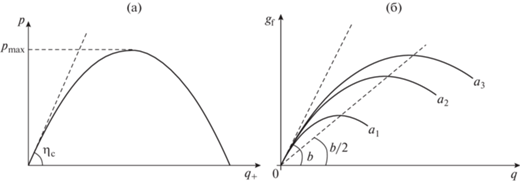
Изменение размеров колонны, соотношения между поверхностями теплообмена в кубе и в дефлегматоре сказывается на величине коэффициентов тепло и массопереноса, влияющих на производительность через параметр необратимости $a$. Семейство зависимостей ${{g}_{F}}(q)$ для различных значений $a$ оказывается при этом таким, что максимумы всех парабол лежат на одной прямой, проведенной из начала координат с наклоном ${b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0em} 2}$ (см. рис. 2б).
Рис. 2.
Области реализуемости тепловой машины (а – зависимость мощности тепловой машины от расхода теплоты) и колонны бинарной ректификации (б – зависимость производительности колонны от расхода теплоты для различных коэффициентов тепло и массопереноса ${{a}_{1}} > {{a}_{2}} > {{a}_{3}}$).
Так как КПД колонны монотонно уменьшается с ростом нагрузки, то он на рабочем участке нагрузочной характеристики удовлетворяет неравенству
(47)
$b \geqslant \eta = \frac{{{{g}_{F}}}}{q} \geqslant {b \mathord{\left/ {\vphantom {b 2}} \right. \kern-0em} 2}.$Таким образом колонна ректификации, как и тепловая машина, имеет выпуклую ограниченную сверху область допустимых режимов, ее КПД с учетом необратимости монотонно зависит от обратимого КПД ${{\eta }_{c}}$, который аналогичен КПД Карно идеальной тепловой машины. КПД колонны в режиме максимальной производительности равен половине ${{\eta }_{c}}$ (рис. 2). Эти особенности позволяют в некоторых задачах использовать в качестве критериев показатели колонны в обратимом режиме. Одной из таких задач является выбор порядка разделения многокомпонентных смесей.
РАСЧЕТ КОЭФФИЦИЕНТА НЕОБРАТИМОСТИ ПО РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ
Если обратимый КПД как правило задан, то коэффициент необратимости найти по формуле (28) гораздо сложнее, так как в выражение (28) входит эффективный коэффициент массопереноса $k$, который как и коэффициенты теплопередачи ${{\beta }_{B}},{{\beta }_{D}}$ зависит от конструкции и размеров колонны. Поэтому коэффициент необратимости для действующей колонны может быть найден по результатам измерений фактического расхода теплоты ${{q}^{{{\text{ex}}}}}$ и фактической производительности по сырью $g_{F}^{{{\text{ex}}}}$. Из (27) следует:
(48)
$a = \frac{{b{{q}^{{{\text{ex}}}}} - g_{F}^{{{\text{ex}}}}}}{{{{{({{q}^{{{\text{ex}}}}})}}^{2}}}}.$Найденное значение $a$ позволяет найти границы рабочего участка, КПД колонны с учетом необратимости и, как показано ниже, флегмовое число. Через условие (28) величина $a$ связывает входящие в его правую часть кинетический коэффициент и при известном и флегмовом числе из этого выражения может быть найден эффективный коэффициент массопереноса.
СВЯЗЬ ФЛЕГМОВОГО ЧИСЛА С НАГРУЗКОЙ КОЛОННЫ И ХАРАКТЕРИСТИЧЕСКИМИ КОЭФФИЦИЕНТАМИ
Флегмовое число $R$, равное отношению потока флегмы, возвращаемого в колонну, к отбору продукта из дефлегматора, является важным управляющим фактором. Выразим его через характеристические коэффициенты. Для этого запишем уравнение материального баланса по потокам, поступающим и выходящим из дефлегматора
Здесь $L$ – поток флегмы, возвращающийся в колонну.
Будем предполагать разделение полным, в этом случае для бинарной смеси $\varepsilon = {{x}_{F}}$. Для многокомпонентной смеси ${{x}_{F}}$ – молярная доля фракции, отделяемой в дефлегматор. С учетом того, что $q = Vr$, а $R = \frac{L}{{{{g}_{F}}{{x}_{F}}}}$, получим:
Откуда:
В режиме максимальной производительности степень загруженности колонны $z = 1$ и
Если флегмовое число измеряют на действующей колонне, то формула (49) может быть использована для расчета коэффициента необратимости.
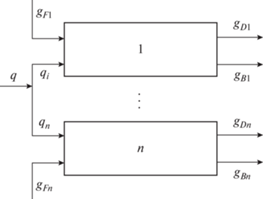
МНОЖЕСТВО РЕАЛИЗУЕМЫХ РЕЖИМОВ КАСКАДА РАЗДЕЛЕНИЯ ТРЕХКОМПОНЕНТНОЙ СМЕСИ
Запишем соотношения, определяющие множество реализуемых режимов каскада, через характеристические параметры колонн при прямом и при обратном порядке разделения с учетом необратимых факторов. Предельная величина теплового потока и предельная производительность колонны обратно пропорциональны $a$. Так как поток сырья, поступающий на первую колонну, больше, чем на вторую, целесообразно сделать первой ту колонну, у которой при выбранном порядке разделения коэффициент необратимости меньше.
Предельная производительность каскада $g_{F}^{*}$ зависит от порядка разделения. Для прямого порядка
(51)
$g_{{Fd}}^{*} = \min \left( {\frac{{b_{{d1}}^{2}}}{{4{{a}_{{d1}}}}};\frac{{b_{{d2}}^{2}}}{{4{{a}_{{d2}}}(1 - {{x}_{0}})}}} \right).$Для обратного порядка
(52)
$g_{{Fi}}^{*} = \min \left( {\frac{{b_{{i1}}^{2}}}{{4{{a}_{{i1}}}}};\frac{{b_{{i2}}^{2}}}{{4{{a}_{{i2}}}(1 - {{x}_{2}})}}} \right).$Производительность каскада ${{g}_{F}}$ связана с затратами теплоты.
Для прямого порядка разделения получим соотношения, определяющие ${{q}_{{d1}}},{{q}_{{d2}}}$ и ${{q}_{d}}$ при заданном расходе смеси:
(53)
$\begin{gathered} {{q}_{{d1}}} = \frac{{{{b}_{{d1}}}}}{{2{{a}_{{d1}}}}} - \sqrt {\frac{{b_{{d1}}^{2}}}{{4a_{{d1}}^{2}}} - \frac{{{{g}_{F}}}}{{{{a}_{{d1}}}}}} , \\ {{q}_{{d2}}} = \frac{{{{b}_{{d2}}}}}{{2{{a}_{{d2}}}}} - \sqrt {\frac{{b_{{d2}}^{2}}}{{4a_{{d2}}^{2}}} - \frac{{{{g}_{F}}(1 - {{x}_{0}})}}{{{{a}_{{d2}}}}}} ,\,\,\,{{q}_{{d1}}} + {{q}_{{d2}}} = {{q}_{d}}. \\ \end{gathered} $Для обратного порядка разделения аналогично:
(54)
$\begin{gathered} {{q}_{{i1}}} = \frac{{{{b}_{{i1}}}}}{{2{{a}_{{i1}}}}} - \sqrt {\frac{{b_{{i1}}^{2}}}{{4a_{{i1}}^{2}}} - \frac{{{{g}_{F}}}}{{{{a}_{{i1}}}}}} , \\ {{q}_{{i2}}} = \frac{{{{b}_{{i2}}}}}{{2{{a}_{{i2}}}}} - \sqrt {\frac{{b_{{i2}}^{2}}}{{4a_{{i2}}^{2}}} - \frac{{{{g}_{F}}(1 - {{x}_{2}})}}{{{{a}_{{i2}}}}}} ,\,\,\,{{q}_{{i1}}} + {{q}_{{i2}}} = {{q}_{i}}. \\ \end{gathered} $Эти затраты ограничены неравенствами, вытекающими из размеров рабочей области каждой колонны:
(55)
${{q}_{{d1}}} \leqslant \frac{{{{b}_{{d1}}}}}{{2{{a}_{{d1}}}}},\,\,\,\,{{q}_{{d2}}} \leqslant \frac{{{{b}_{{d2}}}}}{{2{{a}_{{d2}}}}},$(56)
${{q}_{{i1}}} \leqslant \frac{{{{b}_{{i1}}}}}{{2{{a}_{{i1}}}}},\,\,\,\,{{q}_{{i2}}} \leqslant \frac{{{{b}_{{i2}}}}}{{2{{a}_{{i2}}}}}.$Порядок разделения, для которого при заданном значении производительности затраты теплоты меньше, является оптимальным, что приводит к неравенству,
определяющему выбор прямого порядка разделения с учетом необратимости процессов. Если правая часть этого неравенства больше левой, то оптимальный порядок – обратный.На рабочем участке, производительность каскада монотонно зависит от суммарного расхода теплоты, поэтому решение задачи о минимуме затрат теплоты при заданной производительности совпадает с решением задачи о максимуме производительности при заданных затратах теплоты.
Отметим, что левая и правая части неравенства (57) через условия (53), (54) зависят от расхода ${{g}_{F}}$ разделяемой смеси и может оказаться, что при одной производительности выгоднее использовать прямой, а при другой – обратный порядок разделения.
Предельная производительность по промежуточному продукту равна ${{x}_{1}}g_{F}^{*}$.
ОБЩИЕ СООБРАЖЕНИЯ
Одной из основных задач при разделении многокомпонентных смесей является выбор последовательности разделения смеси на фракции и отдельные компоненты. Критерием такого выбора, естественно, считать минимальные затраты теплоты. Монотонная зависимость затрат теплоты в колоннах при фиксированной производительности от их затрат в обратимом приближении позволяет использовать последние для выбора порядка разделения. Для каскада колонн они равны:
(58)
${{p}^{0}} = \sum\limits_\nu {{{g}_{{F\nu }}}} {{A}_{{G\nu }}}\frac{1}{{{{\eta }_{{c\nu }}}}} = \sum\limits_\nu {{{g}_{{F\nu }}}} {{A}_{{G\nu }}}\frac{{{{T}_{{B\nu }}}}}{{{{T}_{{B\nu }}} - {{T}_{D}}}}.$Температуру ${{T}_{D}}$ будем считать фиксированной за счет изменения давления в колоннах. Суммарная мощность разделения $\sum\limits_\nu {{{g}_{{F\nu }}}} {{A}_{{G\nu }}}$ задана и с точностью до постоянного множителя равна разности энтропии входного и выходных потоков. Второй сомножитель $\frac{{{{T}_{{B\nu }}}}}{{{{T}_{{B\nu }}} - {{T}_{D}}}}$ в каждом слагаемом в (58) монотонно уменьшается с ростом температуры в кубе ${{T}_{{B\nu }}}$. Достижимое значение этой температуры определяется выбором границы разделения. От каскада к каскаду число возможных границ разделения уменьшается и возможности выбора ${{T}_{{B\nu }}}$ сужаются, значит ${{T}_{{B\nu }}} > {{T}_{{B(\nu + 1)}}}$. Чтобы большая доля мощности разделения вырабатывалась с большим термическим КПД, нужно для близких значений температур ${{T}_{{B\nu }}}$ для нескольких границ разделения выбрать ту из них, для которой доля отбора ${{\varepsilon }_{{nu}}}$ ближе к 0.5 (мощность разделения больше).
РАСЧЕТ ТЕМПЕРАТУРЫ В КУБЕ ПРИ РАЗДЕЛЕНИИ СМЕСИ НА ФРАКЦИИ
Рассмотрим колонну, разделяющую смесь $n$ компонентов на два потока, один из которых содержит компоненты от $i = 1$ до $i = j$, а второй от $i = j + 1$ до $n$. При четком разделении и выборе отбора равном концентрации отделяемой фракции в сырьевом потоке, состав верхнего потока зависит от $j$ как
(59)
${{x}_{{iD}}}(j) = \frac{{{{x}_{{iF}}}}}{{\sum\limits_{i = 1}^j {{{x}_{{iF}}}} }},\,\,\,\,{{\varepsilon }_{j}} = \sum\limits_{i = 1}^j {{{x}_{{iF}}}} .$При этом температура в кубе ${{T}_{B}}$ как и монотонно связанный с этой температурой термический КПД имеет локальный максимум, определяемый условием
(60)
$\frac{1}{{1 - {{\varepsilon }_{j}}}}\sum\limits_{i = j + 1}^n {{{x}_{{Fi}}}} {{P}_{i}}({{T}_{{Bj}}}) = \frac{1}{{{{\varepsilon }_{j}}}}\sum\limits_{i = 1}^j {{{x}_{{Fi}}}} {{P}_{i}}({{T}_{D}}).$При этом зависимости давлений каждого компонента от температур имеют форму (38) и ${{P}_{i}}(T) > {{P}_{{i + 1}}}(T),i = 1,...,n$.
В том случае, когда граница разделения подлежит выбору по условию максимума температуры в кубе уравнение (60) нужно решить для $j = 2,...,n - 1$.
Для сокращения записи обозначим левую часть уравнения (60) через $\varphi _{j}^{B}({{T}_{B}})$, а левую как $\varphi _{j}^{D}({{T}_{D}})$. Так как левая часть этого уравнения монотонно возрастает с ростом ${{T}_{B}}$, то условие того что при отборе по $j$-й границе температура в кубе удовлетворяет неравенствам ${{T}_{{B(j - 1)}}} < {{T}_{{Bj}}},{{T}_{{B(j + 1)}}} < {{T}_{{Bj}}}$ запишется как:
(61)
$\frac{{\varphi _{{j - 1}}^{B}({{T}_{{B(j - 1)}}})}}{{\varphi _{j}^{B}({{T}_{{B,j - 1}}})}} > \frac{{\varphi _{{j - 1}}^{D}({{T}_{D}})}}{{\varphi _{j}^{D}({{T}_{D}})}},\,\,\,\,\frac{{\varphi _{j}^{B}({{T}_{{Bj}}})}}{{\varphi _{{j + 1}}^{B}({{T}_{{Bj}}})}} < \frac{{\varphi _{j}^{D}({{T}_{D}})}}{{\varphi _{{j + 1}}^{D}({{T}_{D}})}}.$ГИПОТЕЗА КЛЮЧЕВЫХ КОМПОНЕНТОВ
Расчет температуры в кубе для $j$-й границы разделения можно упростить, предположив, что эта температура определяется только свойствами компонентов, ближайших к границе разделения, ключевых [9]. В этом случае вместо уравнения (60) имеем равенство (см. (39)
(62)
$\begin{gathered} {{P}_{{j + 1}}}({{T}_{{Bj}}}) = {{P}_{j}}({{T}_{D}}) \to {{T}_{{Bj}}} = \\ = \frac{{{{B}_{{j + 1}}}({{T}_{D}} + {{C}_{j}})}}{{({{A}_{{j + 1}}} - {{A}_{j}})({{T}_{D}} + {{C}_{j}}) + {{B}_{j}}}} - {{C}_{{j + 1}}}. \\ \end{gathered} $Алгоритм выбора порядка разделения, таким образом, сводится к тому, что при заданной температуре в дефлегматоре для первого каскада выбирают границу разделения, соответствующую максимальной температуре в кубе колонны. Для нескольких близких температур выбирается та граница, которой соответствует большее значение молярной работы разделения. Аналогичная процедура повторяется для каждой ступени каскада разделения.
Оптимальность полученной схемы нельзя гарантировать, так как выбор границы на предыдущей ступени влияет на возможности выбора на последующих, что в этом алгоритме не учитывается. Но альтернативная процедура динамического программирования, включающая расчет всех вариантов разбиения смеси на трехкомпонентные с выбором границы для каждого варианта, а после этого оптимизации всех возможных вариантов для четырех компонентов, требует громадных вычислительных затрат.
Для найденной структуры системы и заданной производительности каскада нужно выбрать колонны так, чтобы производительность по сырью каждой из них оказалась меньше предельной, и посчитать расходы теплоты с учетом необратимых потерь.
ОПТИМИЗАЦИЯ СИСТЕМЫ КОЛОНН С ПАРАЛЛЕЛЬНОЙ СТРУКТУРОЙ
В том случае, когда поток разделяемой смеси превышает предельную производительность колонны, несколько колонн соединяют параллельно друг другу. В этом случае возникает задача согласования потоков перерабатываемой смеси и потребляемой теплоты.
Параллельной структурой колонн ректификации будем называть структуру, потребляющую ограниченный поток тепловой энергии. На вход каждой колонны поступает поток смеси ${{g}_{{Fi}}}$, состав которого, как и составы потоков, покидающих колонну, известен. Суммарный поток сырья обозначим как ${{g}_{F}}$. Колонны отличаются своими конструктивными характеристиками, температурами потоков, нагревающих смесь компонентов в кубе и охлаждающих ее в дефлегматоре и др. Это обстоятельство приводит к тому, что для каждой $i$-ой колонны характеристические параметры ${{a}_{i}},{{b}_{i}}$, найденные по формулам (28) или подсчитанные по данным эксперимента (см. (48)), различны.
Выразим предельные возможности такой структуры через характеристические параметры колонн.
ОБРАТИМЫЙ КПД И МАКСИМАЛЬНАЯ ПРОИЗВОДИТЕЛЬНОСТЬ
Пусть распределение потоков сырья ${{g}_{{Fi}}}$ между колоннами задано, а ${{\gamma }_{i}}$ – доля этого потока от ${{g}_{F}}$. Тогда обратимый КПД для параллельной структуры равен:
(63)
$b = \frac{{{{g}_{F}}}}{{{{q}_{\Sigma }}}} = \frac{1}{{\sum {({{{{\gamma }_{i}}} \mathord{\left/ {\vphantom {{{{\gamma }_{i}}} {{{b}_{i}}}}} \right. \kern-0em} {{{b}_{i}}}})} }}.$Максимальная производительность системы параллельных колонн и соответствующий ей расход теплоты с учетом необратимости:
ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПОТОКОВ ТЕПЛОТЫ
Рассмотрим задачу о таком распределении потоков теплоты между колоннами, чтобы при заданном суммарном расходе тепла ${{q}_{\Sigma }}$ производительность $n$ параллельных колонн ${{g}_{F}}$ была максимальна. Задача примет форму:
(65)
${{g}_{F}} = \sum\limits_i {({{b}_{i}}{{q}_{i}} - {{a}_{i}}q_{i}^{2})} \to \max ,\,\,\,\,\sum\limits_i {{{q}_{i}}} = {{q}_{\Sigma }} < q{{_{\Sigma }^{{\max }}}^{{}}}.$Так как на рабочем участке нагрузочной характеристики зависимость ${{g}_{{Fi}}}({{q}_{i}})$ монотонна и выпукла, то задача (65) имеет то же самое решение, что и двойственная ей задача о минимальном расходе теплоты при заданной суммарной производительности.
Функция Лагранжа задачи (65) для невырожденного решения имеет вид:
Условия ее стационарности по ${{q}_{i}}$:
После подстановки ${{q}_{i}} = \frac{{{{b}_{i}} - \lambda }}{{2{{a}_{i}}}}$ в (65) и исключения $\lambda $ получим:
(67)
$q_{i}^{*} = \frac{{{{b}_{i}}}}{{2{{a}_{i}}}} - \frac{{\sum\limits_j {\frac{{{{b}_{j}}}}{{2{{a}_{j}}}}} - {{q}_{\Sigma }}}}{{{{a}_{i}}\sum\limits_j {\frac{1}{{{{a}_{j}}}}} }},\,\,\,\,i,j = 1,...,n.$Задача об оптимальном распределении потоков теплоты позволяет решить и важную задачу о построении теплообменной системы, интегрированной с процессом ректификации [17].
ЗАКЛЮЧЕНИЕ
С использованием методов оптимизационной термодинамики показано, что множество реализуемых режимов колонны ректификации в плоскости производительность-затраты теплоты ограничено параболой. Найдены зависимость коэффициентов этой границы (характеристических) от параметров потоков и кинетики тепло- и массопереноса. Получена зависимость флегмового числа от характеристических коэффициентов. Показаны возможности использования параметризованного представления нагрузочной характеристики для решения задач расчета колонн ректификации, таких как задача о максимальной нагрузке, о зависимости КПД колонны от ее нагрузки, об оптимальном распределении потоков в параллельной структуре и о порядке разделения в последовательной структуре. Результаты дают возможность оптимизации сложных систем, разбив их на подсистемы, каждая из которых может быть представлена как параллельная или последовательная структура.
ОБОЗНАЧЕНИЯ
| $g$ | расход, моль/c |
| $h$ | мольная энтальпия, Дж/моль |
| $\bar {k}$ | эффективный коэффициент массопереноса, моль/(с м) |
| $\beta $ | коэффициент теплообмена |
| $l$ | координата, характеризующая положение по высоте колонны, м |
| $P$ | давление, Па |
| $p$ | мощность, Вт |
| ${{q}_{ + }},{{q}_{ - }}$ | потоки теплоты, подводимой в кубе и отводимой в дефлегматоре, Вт |
| $R$ = 8.31 Дж/(моль К) | универсальная газовая постоянная; флегмовое число |
| $s$ | мольная энтропия, Дж/(моль К) |
| ${{T}_{ + }},{{T}_{ - }}$ | температуры греющего пара в кубе и охлаждающей воды в дефлегматоре соответственно К |
| $V$ | расход паровой смеси, моль/c |
| $x$ | мольная концентрация низкокипящего компонента в жидкой фазе, моль/моль; |
| $y$ | мольная концентрация низкокипящего компонента в паровой фазе, моль/моль |
| ${{y}^{0}}$ | равновесная концентрация низкокипящего компонента в паровой фазе, моль/моль; |
| $\alpha $ | коэффициент относительной летучести |
| $r$ | мольная теплота парообразования, Дж/моль |
| $\varepsilon $ | степень отбора |
| $\mu $ | химический потенциал, Дж/моль |
| $\sigma $ | производство энтропии, Вт/К |
ИНДЕКСЫ
Список литературы
Новиков И.И. Эффективный коэффициент полезного действия атомной энергетической установки // Атомная энергия. 1957. № 11. С. 409–412.
Curzon F.L., Ahlborn B. Efficiency of a Carnot engine at maximum power output // Am. J. Phys., 1975. V. 43. № 22. P. 22–24.
Berry R.S., Kasakov V.A., Sieniutycz S., Szwast Z., Tsirlin A.M. Thermodynamic Optimization of Finite Time Processes. Chichester: Wiley, 1999.
Chen L., Wu C., Sun F. Finite time thermodynamic optimization or entropy generation minimization of energy systems // J. Non-Equilib. Thermodyn., 1999. V. 24. P. 327–359.
Tsirlin A.M., Mironova V.A., Amelkin S.A., Kazakov V.A. Finite-time thermodynamics: Conditions of minimal dissipation for thermodynamic process with given rate // Phys. Rev. E., 1998. V. 58. № 1. P. 215–223.
Гельперин Н.И. Основные процессы и аппараты химической технологии. М.: Химия, 1981. 384 с.
Петлюк Ф.Б., Серафимов Л.А. Многокомпонентная ректификация. Теория и расчет. М.: Химия, 1983.
Балунов А.И., Майков В.П. Энтропия и информация в теории ректификации // Известия ВУЗов: Химия и химическая технология, 2003. Т. 46. № 9. С. 54–67.
Плановский А.Н., Николаев П.И. Процессы и аппараты химической и нефтехимической технологии. М.: Химия, 1987. 400 с.
Holland C.D. Fundamentals of Multicomponent Distillation. McGraw-Hill, 1981.
Kister H.Z. Distillation Design. New York: McGraw-Hill, 1992.
Tsirlin A.M., Balunov A.I., Sukin I.A. Estimates of energy consumption and selection of optimal distillation sequence for multicomponent distillation // Theor. Found. Chem. Eng., 2016. V. 50. № 3. P. 258–267.
Tsirlin A.M., Sukin I.A., Balunov A.I., Schwalbe K. The Rule of Temperature Coefficients for Selection of Optimal Separation Sequence for Multicomponent Mixtures in Thermal Systems // J. Non-Equilib. Thermodyn, 2017. V. 42. № 4. P. 359–369.
Tsirlin A.M., Mazikov A.A. Thermodynamic indicators of the perfection of heat exchange systems // J. Eng. Phys. Thermophys., 2023. V. 96. № 3. P. 516–531.
Розоноэр Л.И., Цирлин А.М. Оптимальное управление термодинамическими системами // Автоматика и телемеханика, 1983. № 1. С. 70–79; № 2. С. 88–101; № 3. С. 50–64.
Zaeva M.A., Tsirlin A.M., Sukin I.A. Influence of the Kinetics of Heat and Mass Transfer in a Binary-Rectification Column on the Realizability Range of its Regimes // J. Eng. Phys. Thermophys., 2018. V. 91. P. 515–530.
Зиятдинов Н.Н., Островский Г.М., Емельянов И.И. Построение системы теплообмена при реконструкции и синтезе оптимальных систем ректификационных колонн // Теоретические основы химической технологии. 2016. Т. 50. № 2. С. 184–193.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии