Теоретические основы химической технологии, 2023, T. 57, № 5, стр. 617-626
Сравнительный расчет межфазного тепло- и массообмена в распылительном аппарате для режимов прямо- и противотока фаз с учетом кризисов сопротивления и тепломассоотдачи
Н. Н. Симаков *
Ярославское высшее военное училище противовоздушной обороны
Ярославль, Россия
* E-mail: nik_simakov@mail.ru
Поступила в редакцию 02.07.2023
После доработки 11.07.2023
Принята к публикации 23.07.2023
- EDN: LYZQXK
- DOI: 10.31857/S0040357123050202
Аннотация
В статье представлены новые детали алгоритма и сравнение результатов расчета тепломассообмена воды и воздуха в распылительном аппарате в режимах прямо- и противотока фаз с учетом раннего кризиса сопротивления капель и сопутствующего ему кризиса тепло- и массообмена. Основу использованной математической модели составляют нестационарные дифференциальные уравнения течения сжимаемой среды, дополненные уравнениями тепло- и массопередачи от капель к газу. В разностных аналогах уравнений неразрывности и движения фаз использована известная явная схема Лакса–Вендроффа. Представлены распределения скоростей, температур фаз, плотностей водяного пара в воздухе и насыщенного пара над поверхностью капель в двухфазном потоке, рассчитанные для сравнения режимов прямо- и противотока фаз через цилиндрический аппарат. В расчетах, в частности, установлены зависимости средних температур газа и жидкости по выходному для каждой фазы сечению аппарата от расхода газа через него.
ВВЕДЕНИЕ. ОСОБЕННОСТИ ВЗАИМОДЕЙСТВИЯ ФАЗ В ДВУХФАЗНОМ ПОТОКЕ ФАКЕЛА РАСПЫЛА ФОРСУНКИ
Распыливание жидкости в газе, например, с помощью форсунок часто используется в химических технологиях, энергетике, мероприятиях по экологической защите окружающей среды для интенсификации процессов тепло- и/или массообмена путем увеличения межфазной поверхности, например, при сжигании или пиролизе жидких углеводородов, сушке и гранулировании полимеров, мокрой очистке воздуха от пыли и вредных газовых примесей.
Основой методов расчета таких процессов служат представления о гидродинамике образующегося двухфазного потока, который называют факелом распыла, силовом взаимодействии капель и газа, об элементарных актах тепло- и/или массообмена между газом и отдельной каплей [1, 2].
Методы расчета гидродинамики факела распыла и межфазного тепломассообмена в нем до настоящего времени еще недостаточно разработаны, чем обусловлена актуальность данной работы, продолжающей исследования, описанные в работах [1–3].
Процессы межфазного тепло- и массообмена часто протекают одновременно и параллельно, чем усложняется моделирование и расчет этих совмещенных процессов переноса.
В работах [3, Chapter 7] и [4] было выполнено и описано моделирование и расчет более простого процесса – межфазного массообмена без теплообмена на примере процесса мокрой очистки воздуха от вредных газовых примесей, например, от оксида серы SO2.
В работе [5] выполнены расчеты сложного процесса, включающего испарение и охлаждение капель воды, распыленной в воздухе, с учетом кризисов сопротивления капель и межфазного тепломассообмена.
Целью данной работы было продолжение описанных в работах [4, 5] исследований с устранением некоторых недостатков.
В математическом моделировании двухфазных потоков используются два основных подхода: метод взаимопроникающих континуумов [6] и теория турбулентных струй [7]. В первом каждая из фаз рассматривается как непрерывно распределенная по пространству сплошная среда с переменной плотностью, усредненной по малому объему, а скорости фаз полагают различными. Во втором предполагается, что концентрация дисперсной фазы мала, скорости фаз примерно одинаковы, но при этом учитывается турбулентность газовой фазы.
Одномерная модель гидродинамики факела распыла форсунки [1] – это пример одного из первых применений континуального подхода к расчету двухфазного газокапельного потока. Эта модель впоследствии многократно использовалась в качестве основы для моделирования ряда тепло- и массообменных процессов химической технологии с распыливанием жидкости, в частности, процесса испарения жидкого углеводородного сырья в процессе получения технического углерода [2]. Развитием такого подхода стало создание двумерной модели осесимметричного факела распыла [3, Chapter 7], в которой было учтено несколько его важных особенностей, заключающихся в следующем.
Как было установлено в эксперименте [3, Chapters 2, 3], в факеле распыла течение газа представляет собой турбулентную струю, возникающую из-за взаимодействия фаз у корня факела, которая на достаточном удалении от форсунки развивается автономно от потока капель и отличается структурой и характером турбулентного трения от однофазной газовой струи. В частности, оказалось, что безразмерные профили аксиальной скорости газа более пологие, чем в однофазной струе. А также было установлено заметное различие скоростей фаз в каждой точке потока и наличие перепадов давления газа порядка 1–10 Па по радиусу и оси факела распыла.
Таким образом, оказалось необходимым и целесообразным в двумерной модели факела распыла использовать сочетание континуального подхода [6] с учетом турбулентности струйного газового потока [7].
В эксперименте также была обнаружена очень важная особенность взаимодействия фаз в факеле распыла, которую назвали ранним кризисом сопротивления [3, Chapters 3]. При расчете факела распыла необходимо учитывать и эту особенность, заключающуюся в следующем.
Классически известный кризис сопротивления шара, обтекаемого вязкой средой, заключается в том, что сила и коэффициент сопротивления шара при числе Рейнольдса Re = Recr ≈ (2–3) × 105 уменьшаются примерно в 4–5 раз [8, 9]. Это объясняется переходом ламинарного пограничного слоя у поверхности шара в турбулентный, смещением вниз по течению линии отрыва потока и улучшением обтекания тела с уменьшением его сопротивления [10, 11].
Значение критического числа Рейнольдса Recr определяется степенью турбулентности вязкой среды, обтекающей шар, уменьшаясь с ее увеличением. В работе [12] описаны случаи возникновения кризиса сопротивления шара уже при Recr ≈ 400–2200, и сказано, что при меньших значениях Re возникновение кризиса уже невозможно.
При распыливании жидкости форсункой образуются капли со средним объемно-поверхностным (заутеровским) диаметром d32 порядка 10–4 м. С учетом этих размеров и значительного различия динамических коэффициентов вязкости жидкости капель и обтекающего их газа (для воды и воздуха, примерно, в 60 раз) допустимо пренебречь деформацией капель и внутренним течением жидкости в них, рассматривая их как твердые шарики.
Обычно силу гидродинамического сопротивления обтекаемой газом капли рассчитывают по формуле
(1)
$F~\,\, = \,\,~{{{{C}_{{\text{d}}}}~s~\rho ~{{V}^{2}}} \mathord{\left/ {\vphantom {{{{C}_{{\text{d}}}}~s~\rho ~{{V}^{2}}} 2}} \right. \kern-0em} 2}.$При обтекании шара ламинарным потоком при малых числах Рейнольдса Re = Vdρ/μ $ \ll $ 1 используется зависимость Стокса Cd = 24/Re, а при обтекании в переходном диапазоне 2 < Re < 700 – формула Клячко
(2)
${{C}_{{\text{d}}}}~~ = {{~24} \mathord{\left/ {\vphantom {{~24} {{\text{Re}}}}} \right. \kern-0em} {{\text{Re}}}}~\,\, + \,\,~{4 \mathord{\left/ {\vphantom {4 {{\text{R}}{{{\text{e}}}^{{1/3}}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}^{{1/3}}}}},$В работе [3, Chapters 2–3] показано экспериментально, что в развитом турбулентном потоке факела распыла форсунки при Re = Recr ≈ 100 величина Cd для капель уменьшалась в 4–7 раз по сравнению со значениями, определяемыми формулой (2) Клячко. Это и есть самый ранний кризис сопротивления.
В частности, для движущихся по оси факела капель хорошим приближением при 40 < Re < 110 служит предложенная автором формула
(3)
${{C}_{{\text{d}}}}~\,\, = \,\,~{{2000} \mathord{\left/ {\vphantom {{2000} {{\text{R}}{{{\text{e}}}^{2}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}^{2}}}}.$Последующим анализом экспериментальных данных было показано, что формула (3) верна для всей совокупности капель в объеме факела при z > 0.1 м, а не только для капель на оси факела распыла [5].
При обтекании одиночного твердого шарика газовой струей в конфузоре наблюдался такой же ранний кризис сопротивления [3, Chapter 5].
В качестве одной из возможных причин возникновения раннего кризиса сопротивления рассматривалась гипотеза о влиянии сильной турбулентности газового потока, которую по сравнению со свободной струей еще больше усилил конфузор и сделал достаточной для возникновения раннего кризиса на одиночном твердом шарике [3, Sect. 5.1]. Это предположение подтвердилось численным моделированием обтекания шара как ламинарным, так и сильнотурбулентным потоком газа [3, Sect. 5.3].
Все вышесказанное привело к выводу, что при математическом и численном моделировании факела распыла как двухфазного потока с учетом всех его особенностей для описания движения обеих фаз единым образом целесообразно использовать сочетание метода взаимопроникающих континуумов [6] и теории турбулентных струй [7]. Это и было учтено в двумерной модели гидродинамики свободного факела распыла и двухфазного потока в цилиндрическом аппарате [3, Sect. 7.2].
Чтобы подробнее ознакомиться с рядом важных обстоятельств, относящихся к рассматриваемой проблеме, в том числе с учетом раннего кризиса сопротивления при взаимодействии фаз в факеле распыла, а также описанием основ математической модели, использованной автором в данной работе, читатель может обратиться к его работам [3–5].
УСОВЕРШЕНСТВОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ И АЛЛГОРИТМА РАСЧЕТА ТЕПЛОМАССООБМЕНА ФАЗ В РАСПЫЛИТЕЛЬНОМ АППАРАТЕ
В качестве основы рассматриваемой модели в данной работе (как и в работах [3–5]) для описания и расчета гидродинамики факела распыла использовалась система уравнений (4)–(14) из книги [3, Sect. 7.2].
Коэффициент сопротивления капель Cd(Re) рассчитывался только по вышеприведенной формуле (3), что явилось первым усовершенствованием модели по сравнению с работами [4] и [5], где использовались и другая аппроксимация Cd(r, z) экспериментальных данных.
Для расчета межфазного тепло- и/или массообмена вышеуказанная система уравнений была дополнена другими соответствующими уравнениями (см. в работах [3, Sect. 7.3], [4] и [5]).
Немалую трудность для построения численной модели представляет проблема задания подходящих граничных условий, которые, во-первых, правильно отражали бы сущность моделируемого физического явления, во-вторых, сохраняли устойчивость разностной схемы при том, что в граничных узлах сетки разностная схема имеет другой, нежели во внутренних точках вид.
Некоторые граничные условия для рассчитываемых величин очевидны и понятны. Например, на оси симметрии двухфазного потока (при r = i Δr = 0) радиальные скорости фаз wr = ur = 0. Здесь также могут обращаться в нуль производные по r от некоторых переменных: аксиальных компонент uz и wz скоростей фаз, их температур tg и tl, плотностей воздуха ρ и водяного пара ρv.
Граничные условия можно условно поделить на “жесткие” и “мягкие”. В первом случае значения рассчитываемой величины в граничных узлах сетки могут быть вполне определены: 1) с учетом геометрии расчетной области, например, на оси симметрии факела распыла wr = ur = 0, или 2) с учетом физических свойств моделируемого объекта, например, обращения обеих компонент скорости газа wr и wz в ноль на боковой границе, совпадающей с внутренней поверхностью стенки цилиндрического аппарата, или 3) заданы из экспериментальных данных, например, для компонент скорости капель и газа на части верхней границы расчетной области внутри конуса распыления.
Во втором случае, мягких условий, в граничных узлах разностной сетки расчетные формулы мало отличаются от формул во внутренних точках тем, например, что пространственные производные в направлении перпендикулярном к границе расчетной области аппроксимируются односторонними, а не двухсторонними разностями. Мягкие граничные условия могут быть использованы на верхней и/или нижней границе расчетной области, являющейся для данной фазы выходным сечением аппарата, в частности, для компонент скорости газа wr и wz, его температуры tg и плотности водяного пара ρv на выходной для газа границе: нижней при прямотоке или верхней при противотоке фаз.
Труднее всего задать граничные условия для величин, об изменении которых вблизи и на границе расчетной области мало что известно, и поэтому приходится делать недостаточно обоснованные предположения об их распределении, например, для скоростей фаз u и w, их температур tl и tg на всей верхней границе или на ее части за пределами конуса распыления. Мягкие граничные условия в этих случаях не всегда подходят.
Так, для компонент wz и wr скорости газа на всей верхней границе поначалу задавались мягкие условия в надежде на то, что в процессе расчета реальные значения автоматически установятся как стационарные. Однако, установление их постоянных значений, а также расхода V газа через аппарат достигалось слишком медленно (или совсем не достигалось?). Этим, в частности, можно объяснить не совсем монотонный характер изменения зависимостей расчетных величин от перепада давления ΔP (или связанного с ним расхода газа V), высоты H и радиуса R аппарата в работах [4, 5]. С учетом этого обстоятельства в данной работе значения wz и wr на части верхней границы, находящейся внутри конуса распыления, задавали по данным эксперимента, а на остальной части, используя мягкие условия. Это было второе усовершенствование модели для расчета тепломассообмена фаз в факеле распыла форсунки.
В процессе отладки алгоритма описываемой модели в данной работе проводились расчеты для разных вариантов задания трудноопределимых граничных условий.
Во всех вариантах на части верхней границы расчетной области, находящейся внутри конуса распыления, значения компонент скорости обеих фаз, объемной доли жидкости α задавали по данным экспериментальных измерений в свободном факеле распыла на расстоянии z = 100 мм от форсунки, предполагая, что в верхнем сечении распылительного аппарата они останутся приблизительно такими же. На остальной части верхней границы значения каждой из компонент скорости жидкости, чтобы избежать разрыва, дополнили в виде функции, плавно спадающей по радиусу до нуля (см. рис. ниже), а для скорости газа использовали мягкие условия. На всей верхней границе безразмерную плотность газа ρ = 1, начальную температуру жидкости tl0 и плотность насыщенного пара ρsv вблизи поверхности капель задавали постоянными, полагая, что это является наименьшим произволом при неизвестности действительных распределений этих величин.
Так, в одном из вариантов расчета температуру tl(i, 0) жидкости (и зависящую от нее известным образом величину ρsv) на верхней границе между конусом распыла и стенкой аппарата задавали функцией, плавно спадающей от tl0 до (tl0 + tg0)/2 и более близкой, как казалось, к реальному распределению. Однако, важные результаты расчета при этом более сложном граничном условии практически не отличались от полученных с более простым условием tl(i, 0) = const = tl0 на всей верхней границе при i от 0 до n.
Поэтому в окончательном варианте на верхней границе в режиме прямотока начальные значения температуры газа tg0 и плотности пара ρv0 в воздухе задавали постоянными, близкими к их значениям снаружи, вдали от аппарата. В режиме противотока таким же образом задавали эти величины на нижней, входной для газа, границе, а на верхней, выходной для газа, границе температуру газа tg и плотность пара ρv в воздухе определяли, используя мягкие условия.
На боковой границе, совпадающей с цилиндрической внутренней поверхностью стенки аппарата, для компонент скорости жидкости uz, ur, ее температуры tl и объемной доли α применялись мягкие условия, выражающие, как бы, беспрепятственное проницание жидкости через границу. Для компонент скорости газа использовались “условия прилипания”: wr = wz = 0. С учетом этих условий и того, что по части стенки аппарата, смачиваемой жидкостью, она стекает в виде пленки, в работе [4] на этой части боковой границы применялись условия равенства температур фаз tg = tl и плотностей ρv = ρsv пара в воздухе и насыщенного пара ρsv над поверхностью жидкости при ее температуре tl в данной точке. На верхней, не смачиваемой жидкостью части стенки, для ρv принимались мягкие условия. Заметим, что из тех же соображений в работе [5] для концентрации с газовой примеси, хорошо поглощаемой жидкостью, на смачиваемой части стенки принималось условие c = 0, а на другой части боковой границы – мягкие условия. В данной работе от недостаточно обоснованных условий ρv = ρsv и tg = tl отказались, предпочтя определять ρv и tg из мягких граничных условий. Это было третьим усовершенствованием алгоритма.
На всей нижней границе расчетной области безразмерную плотность газа задавали постоянной ρ = 1 + Δρ, где приращение Δρ связано с задаваемым перепадом давления газа на аппарате. Для остальных расчетных величин в случае прямоточного режима фаз применялись мягкие граничные условия. Как отмечалось выше, в противоточном режиме на нижней границе, входной для газа, начальные значения температуры газа tg0 и плотности пара ρv0 в воздухе задавали постоянными и близкими к их значениям снаружи, вдали от аппарата.
О других особенных деталях граничных условий, при которых были получены приведенные в данной работе результаты будет сказано ниже.
РЕЗУЛЬТАТЫ РАСЧЕТА МЕЖФАЗНОГО ТЕПЛОМАССООБМЕНА В РЕЖИМАХ ПРЯМО- И ПРОТИВОТОКА ФАЗ ЧЕРЕЗ АППАРАТ
На рис. 1–12 представлены результаты новых расчетов межфазного тепло- и массообмена, полученные для режимов прямо- и противотока фаз в цилиндрическом распылительном аппарате с радиусом R = 160 мм и высотой H = 900 мм, вертикальной осью и одной центробежно-струйной форсункой, расположенной соосно в верхней части аппарата. В расчете предполагалось, что из выходного отверстия форсунки, имеющего диаметр dh= 2 мм, струя жидкости (воды) под избыточным давлением Pl = 0.5 МПа вытекала в воздух вертикально вниз. Исходные числовые данные расчета: начальные размеры и скорость капель, температуры фаз, шаг прямоугольной пространственной сетки и т.д. приняты такими же как в работе [4].
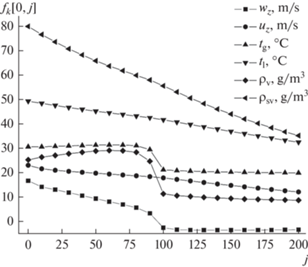
Рис. 1.
Аксиальные профили скорости газа wz и жидкости uz, их температур tg и tl, плотности пара в воздухе ρv и насыщенного пара ρsv вблизи поверхности капель на оси распылительного аппарата, рассчитанные для режима прямотока фаз.
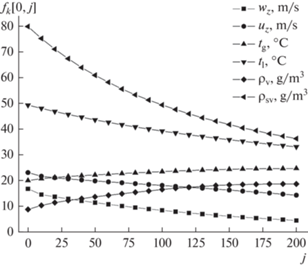
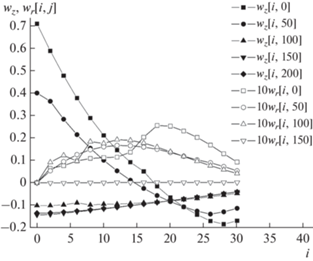
Рис. 3.
Радиальные профили аксиальной и радиальной проекций безразмерной скорости капель на различных расстояниях z = 100 + 4j мм от форсунки для случая прямотока фаз.
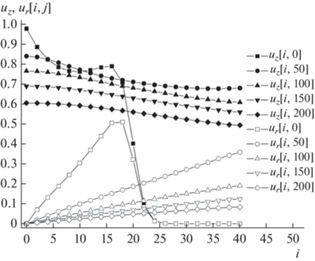
Рис. 4.
Радиальные профили аксиальной и радиальной проекций безразмерной скорости газа на различных расстояниях z = 100 + 4j мм от форсунки для прямотока фаз.
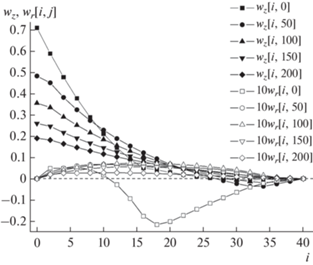
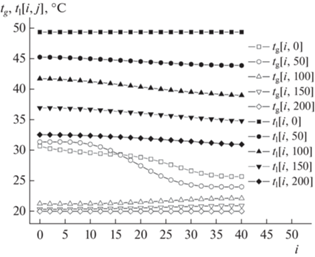
Рис. 6.
Радиальные профили температур газа tg и жидкости tl на разных от форсунки расстояниях z = 100 + + 4j мм для прямотока.
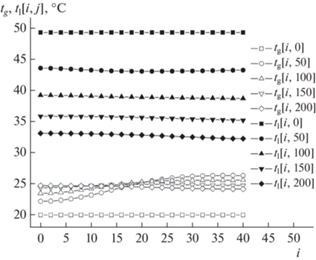
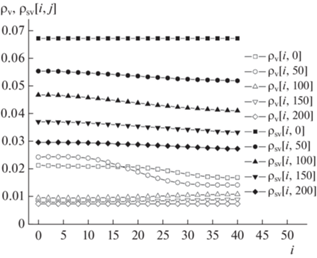
Рис. 8.
Радиальные профили безразмерных плотностей водяного пара в воздухе ρv и насыщенного пара ρsv над поверхностью капель в случае прямотока фаз.
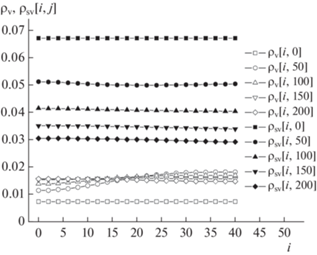
Рис. 11.
Зависимости температур газа и воды на входе (дополнительный индекс in) в аппарат, на выходе (индекс ex) из него и для средних (индекс av) значений по выходному для данной фазы сечению аппарата от расхода газа.
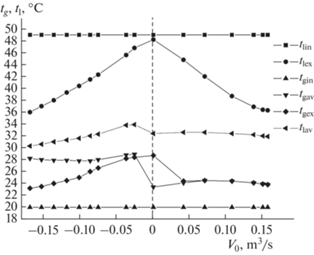
Рис. 12.
Зависимости средних по расходу через выходное сечение аппарата значений температуры воды от модуля расхода газа для прямотока (нижняя кривая) и противотока фаз.
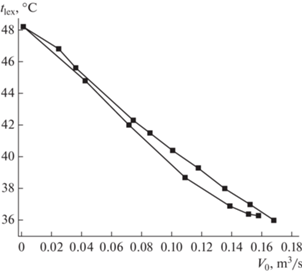
На рис. 1 и 2 показаны с соответствующими обозначениями и индексами аксиальные профили скоростей фаз, температур газа (g) и капель (l), плотности пара (v) в воздухе и насыщенного пара (sv) над поверхностью капель на оси распылительного аппарата, рассчитанные с учетом кризисов сопротивления капель и межфазного тепломассообмена для режимов прямо- и противотока, соответственно.
На рис. 2 очевидно, что в режиме противотока фаз, примерно, на середине высоты аппарата имеется излом в графиках зависимостей аксиальной скорости и температуры газа, а также плотности пара в воздухе. Чего нет на рис. 1 в случае прямотока фаз.
На рис. 3 для случая прямотока фаз представлены на различных расстояниях z = 100 + 4j мм от форсунки радиальные профили аксиальной и радиальной проекций безразмерной скорости капель, полученной делением истинной скорости на uz0 = 23.7 м/с – скорость истечения жидкости из форсунки.
На рис. 3 при j = 0 (на верхней границе) очевиден вышеупомянутый искусственный спад значений скорости за пределами (i > 16) конуса распыла. В случае противотока радиальные профили скоростей капель аналогичны тем, что на рис. 3, отличаются не более чем на 15%, и поэтому здесь не приведены.
На рис. 4 и 5 показаны радиальные профили аксиальной и радиальной проекций безразмерной скорости газа на расстояниях z = 100 + 4j мм от форсунки для режимов прямо- и противотока, соответственно.
На рис. 5 при j ≥ 100 очевидны характерные для противотока фаз отрицательные значения аксиальной скорости газа во всем сечении аппарата, при i = 0–40.
На рис. 6 и 7 показаны радиальные профили температур фаз (по шкале Цельсия) на разных от форсунки расстояниях z = 100 + 4j мм для режимов прямо- и противотока, соответственно.
Очевидно, по мере приближения к выходному сечению профили температуры газа в этих двух режимах изгибаются по-разному, средние температуры в выходном сечении также различны.
На рис. 8 и 9 для режимов прямо- и противотока, соответственно, представлены радиальные профили безразмерных (после деления на плотность воздуха ρ = 1.19 кг/м3) плотностей водяного пара (v) в воздухе и насыщенного пара (sv) над поверхностью капель.
Очевидно, форма профилей плотности водяного пара в воздухе похожа на форму профилей температуры газа на рис. 6 и 7, как и должно быть.
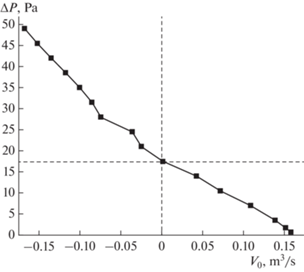
На рис. 10 показан график расчетной зависимости ΔP(V) между расходом V газа и перепадом его давления ΔP в аппарате радиусом R = 200 мм и высотой H = 900 мм в режимах прямотока (V > 0) и противотока (V < 0).
На графике очевидно, что с ростом противодавления ΔP газа его расход V через аппарат уменьшается, при ΔP ≈ 17.5 Па расход газа V изменяет знак, вместе с направлением интегрального течения, и затем растет по модулю вместе с ΔP. Очевидно, для каждого режима в отдельности зависимость ΔP(V) – почти линейная. Иногда ее называют гидравлической характеристикой аппарата.
На рис. 11 представлены зависимости от расхода V0 газа температур tg газа и воды tl на входе (дополнительный индекс in) в аппарат, на выходе (ex) из него и для средних (av) значений по выходному для данной фазы сечению аппарата.
В соответствующем режиму работы аппарата входном сечении (при j равном 0 или nz) для каждой из фаз ее температура задавалась жестко и равномерно. Средние значения температур фаз в выходном сечении (при j равном nzили 0) определялись тремя способами: 1) как среднее арифметическое по радиусу аппарата $\mathop \sum \limits_{i = 0}^n t{{\left( {i,~j} \right)} \mathord{\left/ {\vphantom {{\left( {i,~j} \right)} {\left( {n + 1} \right)}}} \right. \kern-0em} {\left( {n + 1} \right)}}$, 2) среднее значение по площади сечения ${{\iint {t\left( {r,z} \right)ds}} \mathord{\left/ {\vphantom {{\iint {t\left( {r,z} \right)ds}} {\iint {ds}}}} \right. \kern-0em} {\iint {ds}}}$, 3) среднее значение по расходу фазы через сечение аппарата как частное от деления потока тепла фазы на поток ее массы и удельную теплоемкость ${{\iint {t~c~\rho ~v~ds}} \mathord{\left/ {\vphantom {{\iint {t~c~\rho ~v~ds}} {\left( {c\iint {\rho ~v~ds}} \right)}}} \right. \kern-0em} {\left( {c\iint {\rho ~v~ds}} \right)}}$, здесь v – скорость фазы.
Различие значений, полученных для газа первыми двумя, а для жидкости всеми тремя способами, оказалось порядка 0.1°С, поэтому на рис. 11 при каждом расходе V0 приведено только по одному из этих значений: для воды – как tlav, для воздуха – как tgav. Очевидно, что в прямотоке среднее значение температуры газа по третьему способу оказалось tgex ≈ tgav, кроме случая минимального расхода V0 ≈ 0, когда ошибка третьего способа наибольшая, а в противотоке tgex < tgav, что можно объяснить более сложным распределением скорости и температуры газа по выходному (верхнему) сечению.
Заметим, что на рис. 11 среднее значение температуры воды tlav соответствует только капельному потоку жидкости в полости аппарата и не учитывает температуру воды, стекающей в виде пленки по стенке аппарата в общий водосборник охлажденной воды.
Среднее значение температуры воды tlex по ее полному расходу через нижнее сечение аппарата (включая стекающую по стенке пленку) определялось как разность ее начальной температуры tlin = 49.3°С и убыли Δtl, вычисляемой путем деления суммы Ql = Qg + Qv – из отданного газу тепла Qg и тепла Qv, затраченного на испарение капель, – на теплоемкость воды и ее массовый расход через аппарат без учета массы (около 1%) испарившейся воды.
На рис. 12 очевидно, что при одинаковом по модулю расходе газа температура охлажденной воды в прямоточном режиме (нижняя кривая) немного ниже, чем в противоточном (верхняя кривая), например, разница температур tlex в интервале расходов газа |V0| = 0.10–0.14 м3/с составляет, примерно, 1°С.
Указанное обстоятельство приводит к выводу, что противоточный аппарат не имеет преимуществ перед прямоточным вопреки принятым представлениям, умозрительно обоснованным большей величиной относительной скорости фаз и, соответственно, коэффициентов тепломассообмена в противотоке.
СРАВНЕНИЕ ЭФФЕКТИВНОСТИ МЕЖФАЗНОГО ТЕПЛОМАССООБМЕНА В РАСПЫЛИТЕЛЬНОМ АПАРАТЕ В РЕЖИМАХ ПРЯМО- И ПРОТИВОТОКА ФАЗ
Используя полученные расчетные данные, оказалось возможным рассмотреть вопрос об эффективности процесса тепломассообмена в распылительных аппаратах при охлаждении теплой воды воздухом и сделать некоторые оценки.
В качестве меры эффективности процесса (и аппарата) можно принять известное понятие и величину холодильного коэффициента ε [13], обычно используемого для оценки эффективности холодильных машин и определяемого как отношение отбираемой у охлаждаемого тела теплоты Q (называемой холодопроизводительностью), к совершаемой при этом внешней работе A (или затраченной энергии)
В данном случае величина Q равна разности между начальной и конечной теплотой охлаждаемой воды
(5)
$Q = {{c}_{l}}{{\rho }_{l}}{{V}_{l}}({{t}_{{l1}}}--{{t}_{{l2}}}) = 313 \times \Delta {{t}_{{\text{l}}}}\,\,{\text{Вт,}}$Внешняя работа тратится на создание двухфазного потока в аппарате. В прямоточном режиме она равна энергии струи жидкости, истекающей из сопла форсунки
В противоточном режиме к ней нужно добавить работу на создание вентилятором встречной к жидкости воздушной струи
(с учетом данных рис. 10), т.е. энергозатраты выше на 16%.Согласно результатам расчетов, представленным на рис. 11 и 12, при расходе воздуха через аппарат |V0| = 0.14 м3/с в режимах прямо- и противотока вода охлаждается, соответственно, на 12 и 11°С. Из формул (4)–(7) следует, что в прямоточном режиме показатель эффективности ε = 313 × ×12/37.3 = 101, а в противоточном ε = 313 × 11/43.3 = 80, т.е. меньше на 21%.
По данным рис. 10 и 12 в двух случаях: при максимальном для прямотока расходе воздуха |V0| = 0.16 м3/с, а в противотоке при таком же расходе воздуха и перепаде его давления на аппарате ΔP = 47.5 Па, – вода охлаждается практически одинаково на 13°С. Тогда в прямоточном режиме ε = 313 × 13/37.3 = 109, а в противоточном ε = 313 × × 13/43.3 = 90, т.е. на 16% меньше из-за больших энергозатрат.
Таким образом, из результатов расчетов следует, что в режиме противотока эффективность ε охлаждения воды воздухом в распылительном аппарате на 16–21% меньше, чем в режиме прямотока. Этот вывод качественно и количественно согласуется с выводом о массообмене фаз при газоочистке воздуха, полученным в работе [5].
ЗАКЛЮЧЕНИЕ
В данной работе продолжены описанные в работах [3–5] предыдущие исследования с устранением некоторых недостатков в части аппроксимации коэффициента сопротивления капель и задания граничных условий для разностных уравнений при численном моделировании тепломассообмена теплой воды с более холодным воздухом в распылительном аппарате с учетом раннего кризиса сопротивления капель и межфазного тепломассообмена.
Новым в работе является также то, что проведено сравнение результатов расчета характеристик двухфазного потока, полученных для режимов как прямотока, так и противотока фаз в аппарате, включая показатели эффективности этих режимов.
В частности, вопреки существующим представлениям о преимуществах противоточного режима расчетами показано, что из-за больших энергозатрат его эффективность может быть на 16–21% меньше, чем у прямоточного. Это даже без учета дополнительных капитальных затрат на оборудование противоточного аппарата вентилятором.
Таким образом, можно также, как в работе [5], сделать вывод, что противоточный распылительный аппарат для процессов межфазного тепломассообмена не имеет конструктивных, эксплуатационных и, как следствие, экономических преимуществ перед прямоточным.
ОБОЗНАЧЕНИЯ
| ΔA | внешняя работа, Дж |
| Cd | коэффициент гидродинамического сопротивления капли |
| c | удельная теплоемкость, Дж/(кг К) |
| d = d32 | средний объемно-поверхностный диаметр капель, м |
| dh | диаметр выходного отверстия форсунки, мм |
| F | гидродинамическая сила сопротивления капли обтекающему ее газу |
| H | высота аппарата, мм |
| h | шаг расчетной сетки, мм |
| i, j | номера точек расчетной сетки по радиусу и по оси потока |
| n, nz | максимальные значения величин i, j |
| ml | поток массы капель жидкости через поперечное сечение аппарата, кг/с |
| Pl | избыточное давление воды в форсунке, МПа |
| P | давление газа, Па |
| Q | поток тепла от жидкости к газу, Вт |
| R | радиус аппарата, мм |
| r | радиальная координата точек в факеле распыла, м |
| S | площадь сечения аппарата, см2 |
| s = πd2/4 | площадь центрального сечения сферической капли, м2 |
| tg, tl | температуры газа, жидкости по шкале Цельсия, °С |
| u | скорость жидкости, м/с; |
| V = u – w | относительная скорость капли в газе, м/с |
| V | объемный расход газа через аппарат, м3/с |
| Δx | изменение величины x |
| z | аксиальная координата точек в факеле распыла, м |
| w | скорость газа, м/с |
| α | объемная доля жидкости в данной точке факела распыла |
| ε | холодильный коэффициент |
| ρ | плотность, кг/м3 |
| μ | динамический коэффициент вязкости газа, Па с |
| Re = = V d ρ/μ | число Рейнольдса |
ИНДЕКСЫ
| 0 | начальное значение |
| 1, 2 | последовательные значение |
| av | среднее значение |
| cr | для критического числа |
| ex | в выходном для данной фазы сечении аппарата |
| g | для газа |
| in | во входном для данной фазы сечении аппарата |
| L | для жидкости |
| r | для компоненты вектора по радиусу |
| sv | для насыщенного пара |
| v | для пара |
| z | для компоненты вектора по оси потока |
Список литературы
Гельперин Н.И., Басаргин Б.Н., Звездин Ю.Г. О гидродинамике жидко-газовых инжекторов с диспергированием рабочей жидкости // Теорет. основы хим. технологии. 1972. Т. 6. № 3. С. 434.
Звездин Ю.Г., Симаков Н.Н., Пластинин А.П., Басаргин Б.Н. Гидродина-мика и теплообмен при распыливании жидкости в потоке высокотемпера-турного газа // Теорет. основы хим. технологии. 1985. Т. 19. № 3. С. 354.
Simakov N.N. Liquid Spray from Nozzles. Cham: Springer Nature Switzerland AG, 2020.
Simakov N.N. Calculation of the Interphase Heat and Mass Transfer in a Nozzle Spray Cone Taking into Account the Drag Crisis and the Heat and Mass-Transfer Crisis // Theoretical Foundations of Chemical Engineering. 2022. Vol. 56. № 3. P. 339. [Симаков Н.Н. Расчет межфазного тепломассообмена в факеле распыла форсунки с учетом кризиса сопротивления и тепломассообмена // Теорет. основы хим. технологии. 2022. Т. 56. № 3. С. 345.]
Simakov N.N. Comparison of Calculation Results for the Mass Transfer in Spray Apparatus for the Regimes of Cocurrent and Countercurrent of Phases // Theoretical Foundations of Chemical Engineering. 2022. V. 56. № 6. P. 1026. [Симаков Н.Н. Сравнение результатов расчета массообмена в распылительных аппаратах для режимов прямо- и противотока фаз // Теоретические основы химической технологии. 2022. Т. 56. № 6. С. 735.]
Нигматулин Р.И. Динамика многофазных систем. Ч. 1. М.: Наука, 1987.
Абрамович Г.Н. Теория турбулентных струй. М.: Наука,1984.
Шлихтинг Г. Теория пограничного слоя / Пер. с немецкого. М.: Наука, 1974.
Torobin L.B., Gauvin W.H. Fundamental Aspects of Solids–Gas Flow. Part 1: Introductory Concepts and Idealized Motion in Viscous Regime // Can. J. Chem. Eng. 1959. V. 37. № 4. P. 129–141.
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. IV. Гидродинамика. М.: Наука, 1988.
Torobin L.B., Gauvin W.H. Fundamental aspects of solids-gas flow. Part 5: The Effect of Fluid Turbulence on the Particle Drag Coefficient // Can. J. Chem. Eng. 1960. V. 38. № 6. P. 189–200.
Пигарев В.Е., Архипов П.Е. Холодильные машины и установки кондициони-рования воздуха. М.: Маршрут, 2003.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии