Вестник РАН, 2021, T. 91, № 10, стр. 948-955

Позвольте вначале представить свою научную биографию. Я начал научную деятельность ещё студентом МГУ в середине 1950-х годов. Меня привлекла топология, которая тогда бурно развивалась на Западе. Топология была основана гениальным математиком и натурфилософом Анри Пуанкаре в конце XIX в., но длительное время, вплоть до 1970-х годов, не достигала естественных наук. Предшественниками были Л. Эйлер, К.Ф. Гаусс, Г.Ф.Б. Риман, физики Дж.К. Максвелл и У. Кельвин, среди прочих обратившие внимание на отдельные топологические феномены. Хотя в нашей стране и были выдающиеся топологи, начиная с 1920-х, а особенно с 1930-х годов, но к началу 1950-х годов деятельность у нас в этой области ослабла. Мне пришлось начинать заново.

Предмет топологии таков: фигуры любого числа измерений могут деформироваться так, что метрические размеры меняются, но разрывов нет. Какие свойства остаются инвариантными? Это и есть предмет топологии.

I. Cо второй половины 1950-х годов возобновились на много лет прерванные научные контакты, поездки на конгрессы и конференции. Западные учёные, и среди них топологи, начали посещать СССР. В 1961 г. на IV Всесоюзный математический съезд в Ленинграде приехали выдающиеся топологи, среди них Джон Милнор (США), слава которого в математике тогда гремела, а также Ф. Хирцебрух (ФРГ), потом С. Смейл (США). Позднее мне помогли А. Картан (Франция) и М. Атья (Англия). Эти учёные помогли мне достичь мирового уровня. Я работал в этой области 15 лет, но её идеи пронизали мою математическую душу, над чем бы я потом ни работал. Возрождение научных связей происходило под руководством М.А. Лаврентьева и И.Г. Петровского.

Тогда же произошёл распад физико-математического отделения АН СССР на физиков и математиков. Для математиков это не было хорошо, в руководстве отделения присутствовали аморальные явления, которые позднее разрослись. Впрочем, они уже проявлялись в острые для советской науки годы 1929–1933, 1948–1953.

Хотя всю первую половину 1960-х годов меня не выпускали за рубеж на международные конгрессы и конференции по каким-то иррациональным мотивам, к 1966 г. мне удалось полностью стать на ноги в математике, но некоторые потери я понёс. Среди прочих результатов мне удалось решить одну из центральных проблем топологии – я доказал топологическую инвариантность классов Понтрягина (1965). Математические начальники почему-то смягчились, хотя и ненадолго. Меня выбрали членом-корреспондентом АН СССР (1966), присудили Ленинскую премию (1967), большинство крупных математиков и даже математические начальники меня поддержали. Вскоре всё изменилось. У математиков начался аналог варфоломеевой ночи.

В 1970 г. мне присудили медаль Филдса – впервые в истории она была присуждена российскому (советскому) математику, но математические начальники меня не пустили на Международный конгресс математиков в Ницце на процедуру вручения. Это ускорило моё решение порвать с этими людьми, научно я уже был к этому готов и вскоре ушёл в Институт теоретической физики им. Л.Д. Ландау вместе с Я.Г. Синаем, хотя мне препятствовали. Это привело к острым конфликтам.

В конце 1970-х математиков стал фактически возглавлять выдающийся учёный Н.Н. Боголюбов. В начале 1980-х меня выбрали академиком, и Боголюбов просил меня вернуться в математические учреждения для работы по возрождению научной этики. Я этим занимался вместе с ним и затем со следующими директорами “Стекловки”, продолжая работать и в ИТФ им. Л.Д. Ландау. Ряд лет после 1992 г. я работал в США, проводя 4 месяца в году в Москве. Любопытно, что в этот период меня пытались заменить на одного математика, опровергателя всемирной истории, он успел натворить чепухи. Математики безответственны. Кроме А.А. Гончара, ни один не признал ошибок, включая Л.Д. Фаддеева.

II. В конце 1970-х, когда я уже не работал в топологии, её основное направление захлебнулось в своей сложности. Однако появились совсем другие идеи, пришедшие извне и не использующие предыдущий научный багаж топологии, посвящённые маломерным проблемам – в размерностях 3 и 4 (1978–1985). Они привели к значительным результатам. Отметим особо выдающиеся результаты: c помощью крупномасштабного использования компьютеров совместно компьютерщиком и топологом была решена двухсотлетняя проблема 4-х красок (1980-е годы), новым аналитическим методом была доказана столетняя гипотеза Пуанкаре (2004). Квантовая теория поля стала использоваться для построения топологических инвариантов. Это начал мой друг А.С. Шварц в начале 1980-х. Позднее западные люди, развивая эту тему, старались выбросить его из цитирований.

III. К концу 1960-х годов у меня образовались ученики – самый сильный из них В.М. Бухштабер, ныне член-корреспондент РАН, а затем пришла плеяда юных талантов, достигших аспирантуры в начале 1970-х. Позднее пришёл И.А. Тайманов, ныне академик. Это итог моей деятельности в топологии. Часть моих учеников продолжала взаимодействовать со мной в ИТФ им. Л.Д. Ландау.

Пуанкаре основал также качественную теорию динамических систем (наш соотечественник А.М. Ляпунов тоже сыграл важную роль в этом). Эта область достигла классической физики раньше – например, создатель горьковской (нижегородской) школы физиков А.А. Андронов ещё в 1930-х годах вместе с математиком Л.С. Понтрягиным внёс важный вклад в этот раздел математики.

Мы ещё встретим топологию и динамические системы в нашем докладе.

IV. В конце 1960-х пошли разговоры в среде физиков о топологии как о новой области, с которой надо бы познакомиться. Хороший физик И.С. Шапиро из Института теоретической и экспериментальной физики захотел её подучить. Ему порекомендовали учебник двух хороших топологов (фамилии не называю). Их книга написана слишком формально – наверное, это худшее, что они в жизни написали. Шапиро плевался, стал читать Пуанкаре, топологию не выучил – это слишком сырой материал, всё позднее было приведено в ясность и далеко развито, особенно c 1920 по 1970 г.

Мы в Институте Ландау по просьбе физиков организовали курсы для студентов, чтобы они понимали основы топологии, но за пределами института Ландау всё оставалось прежним.

V. Я вместе с Я.Г. Синаем с 1970–71 гг. начал новую жизнь среди физиков-теоретиков молодого тогда замечательного института имени Ландау. Его тогдашний директор И.М. Халатников, ученик Ландау совсем недавно скончался на 102-м году жизни. Там мы работали со звёздами теоретической физики И.М. Халатниковым, В.Ф. Горьковым, И.Е. Дзялошинским, А.А. Абрикосовым, А.И. Ларкиным, А.М. Поляковым, А.В. Покровским, А.В. Анисимовым, А.Б. и А.А. Мигдалами, В.Е. Захаровым, А.Б. Шабатом, В.Н. Грибовым, Г.М. Элиашбергом и их школами – там был ряд молодых талантов. Иногда взаимодействие оказывалось весьма плодотворным. Из моих учеников в ИТФ в разное время успешно поработали О.И. Богоявленский, А.П. Веселов, И.М. Кричевер, П.Г. Гриневич, А.Я. Мальцев, М.В. Павлов. В США моим учеником был Р. Делео. Ещё несколько учеников позднее ушли в другие области.

Для общения необходимо было освоить теоретическую физику – это заняло около 10 лет, из них несколько лет до прихода в мир физиков-теоретиков и несколько лет после. Мы учили некоторые разделы вместе с Синаем, хотя научные цели у нас были разные. Моя работа среди физиков-теоретиков состояла из двух частей. Первая – это помощь физикам в освоении и использовании новых разделов математики, если необходимо – вывести их на правильные контакты в математике, вторая – использование общения с физиками для правильного понимания и постановки новых возникающих в физике математических задач. О второй мы ещё поговорим, а о первой скажу, что мы, в частности, помогли некоторым крупным физикам использовать топологию, изучая особенности в низкотемпературных сверхтекучих системах, способствовали открытию инстантонов в теории полей Янга–Миллса среди прочего.

VI. Я начал работу в институте Ландау с трёхлетнего периода работы о поведении эйнштейновской гравитации на ранней стадии эволюции Вселенной, используя динамические системы. Директор (“Халат”) просил об этом, и мы помогли физикам. Замечательный режим, который они нашли, подтвердился. Но он типичен для сжимающейся Вселенной на ранней стадии, для расширяющейся Вселенной типичны более регулярные режимы. Они не были готовы к этой несимметрии стохастических свойств динамических систем.

VII. Вскоре я перешёл в новую тогда теорию солитонов, красивые открытия которой в 1960-х годах вызвали широкий резонанс в физико-математическом сообществе. Удалось эффективно использовать топологию, динамические системы, риманову и алгебраическую геометрию для математических задач, возникших в теоретической физике.

Последняя область – алгебраическая геометрия – в приложениях сопровождает обычно системы с повышенной точной решаемостью: эту ситуацию называют скрытой симметрией (хотя обычной симметрии может и не быть, как в теории солитонов, есть глубокая связь с квантовой механикой). Это называется “метод обратной задачи рассеяния”, открытый в 1960-х годах. Поначалу алгебраической геометрии не было видно, но при решении нами периодической задачи в середине 1970-х она “вылезла”.

Я много работал в теории нелинейных волн и солитонов, их периодических аналогов и связанных с этим проблем квантовой механики, но сейчас об этом говорить не буду – я упомянул об этом, потому что это вывело меня на задачи квантовой механики. Целый ряд моих самых лучших учеников поработали здесь, сотрудничество с физиком-вычислителем А.А. Авиловым было очень плодотворным.

VIII. Переходим к топологии в теоретической физике. Ещё в древности при связывании верёвок и канатов заметили такой топологический феномен, как узлы. Когда индийские мудрецы предложили Александру Македонскому задачу – распутать узел, он взял и разрубил его мечом.

Сейчас теория узлов – это глубокая наука, но приложений в физике я пока не вижу. Группа талантливых биофизиков из Курчатовского института много лет назад произвела значительный компьютерный эксперимент с узлами, но глубоких закономерностей тогда выявлено не было.

К концу 1960-x годов топология с её своеобразным аппаратом достигла высокого уровня сложности, оказала большое влияние на другие области математики, но даже сейчас лишь небольшая часть этого проявляется в естественных науках, таких, как теоретическая физика. Наиболее полезные топологические характеристики выражаются обычно в величинах типа целых чисел. Начну с такого примера.

Гениальный физик П.А.М Дирак уже будучи пожилым, после войны, поставил такой вопрос: может ли существовать магнитный заряд? Ведь магнитный поток сквозь замкнутую поверхность обычно всегда ноль. Исходя из шрёдингерского квантования он пришёл к выводу, что противоречия с законами квантовой теории нет, если поток целочисленный, разумеется, в квантовых единицах. Ему не верили. Только топология приводит в ясность возникающий здесь набор понятий.

Говоря языком топологии, в магнитном поле пространство функций становится пространством “сечений” векторного расслоения, как, например, векторные или тензорные поля, где значение функции в каждой точке лежит в векторном пространстве, “пришитом” к этой точке, а магнитное поле определяет, как указал Г. Вейль, “связность” (ковариантное дифференцирование) в расслоении – прообраз полей Янга–Миллса позднее. При этом возникают так называемые характеристические классы (Понтрягина, Черна), интегралы от которых по циклам всегда целочисленны. В данном случае мы имеем дело с простейшим классом – первым классом Черна. Пока магнитный монополь не найден.

Альтернативным является фейнмановское квантование, где “действие” системы S является функцией (функционалом) на пространстве путей (полей в многомерном случае). Около 1981 г. я продумывал монополь Дирака с точки зрения фейнмановского квантования (кто-то из крупных физиков тоже это проделал). Важно, что я понял, каков правильный многомерный аналог этого. Оказывается, действие S может быть многозначным функционалом, таким, что exp iS/h однозначно – наподобие угловой функции на плоскости без нуля. Для монополя Дирака действие S определено на бесконечномерном пространстве путей, соединяющих две фиксированные точки в трёхмерном пространстве без нуля. (Немало трудностей принесла школьникам многозначность угла в тригонометрии.) Такие функционалы (лагранжианы) при условии локальности я классифицировал (1981, 1982 гг.). Вскоре эти лагранжианы нашли применение в квантовой теории поля.

Года через два (1983) обнаружилось, что такие добавки к лагранжианам возникали в вычислениях в теории полей Янга–Миллса, но физики тогда не обратили на них внимания и, главное, не увидели их топологических свойств. Мои коллеги – крупные специалисты в квантовой теории поля – и Поляков, который с самого начала приветствовал эту идею, и Фаддеев, который первоначально счёл это чепухой, и другие активно поддерживали мой вклад, когда эта тема взорвалась, так что меня не удалось “выбросить из костюма”, как моего друга Шварца, – но я в этой области больше не работал. В конце 1980-х годов в квантовой теории поля произошёл переход к теории струн – интересной математически, но, как мне кажется, оторванной от физической реальности большим количеством непромеренных порядков.

IX. Перейдем теперь к основной части доклада – топологическим явлениям в “нормальных” металлах. Если металл достаточно чистый, то это кристалл с решёткой периодов порядка одного ангстрема (10^–8 см). Узлы решётки – положительно заряженные ионы. Квантовая механика определяет электронный спектр, начинающийся с какого-то основного состояния и идущий вверх. Электронов должно быть много – ведь система в целом электронейтральна. База спектра – дуальная решётка (координаты в ней имеют размерность импульса).

Размеры элементарной ячейки в дуальной решётке определяются с помощью константы Планка, как и скалярное произведение между геометрической и дуальной решёткой: координаты в геометрической решётке имеют размерность длины SlS и импульса SpS, так что величина Slp/hS безразмерна, это и порождает скалярное произведение. Спектр может иметь бесконечное число ветвей, но любой уровень пересекается лишь с конечным числом.

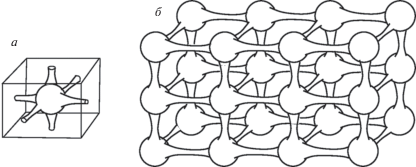
Важно, что дуальная решётка “свёрнута” в силу законов квантовой механики (см. рис. 1 в одномерном случае). Это пространство “квазиимпульсов”. При этом свёрнутая решётка – это, как говорят топологи, компактное многообразие, но несложное – трёхмерный тор T³.

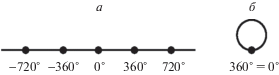
Рис. 1.

Одномерная свёрнутая решётка: a – решётка с шагом 360° – прямая, разбитая на отрезки по 360°; б – свёрнутая решётка – окружность

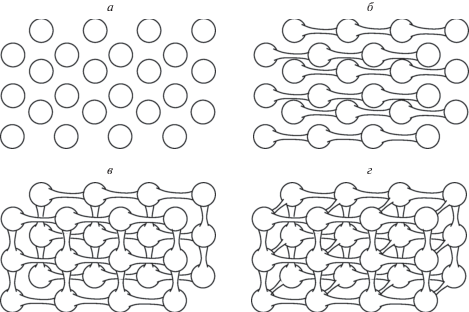
Уместно заметить, что во всех справочниках топологическая сторона этих картинок (Ферми-поверхностей и других) изложена на уровне XIX в., до Пуанкаре. О свёрнутости решётки не говорится, о ручках Ферми-поверхности не говорится, а есть “открытые дыры” там, где в первой зоне Бриллюэна (это – “фундаментальная область” в математике ещё c XIX в. – многогранник) Ферми-поверхность подходит к границе – грани ячейки. Далее мы говорим только о первой зоне Бриллюэна, не оговаривая специально. Сколько таких подходов? На самом деле они разбиваются на пары, которые в свёрнутой решётке отождествлены. Это не указывается на интернет-сайтах и в справочниках (рис. 2).

Рис. 2.

Ферми-поверхность в первой зоне Бриллюэна – а; Ферми-поверхность в несвёрнутой решётке – б

Выходы на границу элементарной ячейки (зоны Бриллюэна) делятся на пары, переходящие друг в друга при базисных сдвигах решётки. Каждая такая пара и есть ручка Ферми-поверхности, кроме тривиальных случаев. Например, для меди и золота имеется по 4 пары – это и есть род, если нет “тривиальных” ручек в несвёрнутом пространстве – в частности, в зоне Бриллюэна. Топологическую информацию в справочниках надо бы улучшить. Ранг определяется как ранг образа фундаментальной группы Ферми-поверхности в решётке Z ³ – он может быть 0, 1, 2, 3. Здесь уже надо немного понимать основы топологии.

Намёк на появление топологии появляется уже в следующем: состояния в дуальной решётке, местоположение которых отличается на вектор дуальной решётки, тождественны – это одно и то же состояние. (Вспомните угол на плоскости без нуля – это свёрнутая прямая с периодами решётки – целыми, кратными 360°.)

Вспомним теперь, что электроны – это Ферми-частицы. Два одинаковых (с учётом спина) электрона не могут сесть в одно состояние. Что происходит при нулевой температуре по Кельвину? Грубо говоря, после занятия нижних по энергии состояний следующим электронам приходится занимать следующие места по энергии и т.д., и электронов много. Где этот процесс кончится, при каких энергиях, в какой области спектра? Ответ таков – при нескольких десятках тысяч градусов. (Впрочем ничего не нагревается.) Конец – это энергия Ферми ε_F. Эта поверхность уровня называется Ферми-поверхностью. Она замкнута в свёрнутой решётке, может быть и несвязной. Мы будем рассматривать каждую компоненту связности по отдельности. Для металлов этот конец заполненного спектра лежит внутри непрерывного спектра, как говорят, в зоне проводимости.

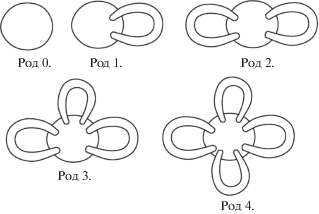
Замкнутые поверхности, их топологические типы классифицировал ещё Пуанкаре. Топологически ориентируемая поверхность – а нам только такие и нужны – определяется числом ручек (рис. 3).

Рис. 3.

Ферми-поверхность как многообразие

Край области, заполненной электронами, – это замкнутая поверхность в трёхмерном торе квазиимпульсов – Ферми-поверхность (в свёрнутой решетке). Какова она? Какой она вообще может быть?

Другой вопрос – как она вложена в трёхмерный тор. Здесь возникает ещё одна топологическая характеристика – ранг. Грубо говоря, ранг – это число базисных сдвигов подрешётки трёхмерной решётки, порождённых путями на Ферми-поверхности. Ранг не может быть больше, чем 3 (рис. 4).

Рис. 4.

Род и ранг: кубическая решётка; a – ранг 0, б – ранг 1, в – ранг 2, г – ранг 3

Математическая модель такова. В трёхмерном (свёрнутом) торе задана вещественная функция ε(р) (уровни энергии) и её поверхность уровня, ε(р) = ε_F, где значение равно энергии Ферми.

При очень низких температурах по Кельвину почти все электроны находятся там, где были при нуле температуры. В сильном магнитном поле квазиимпульсы начнут меняться, но нас интересует только ситуация вдоль поверхности Ферми (надо наложить слабое электрическое поле, чтобы пошёл ток в пространстве). Уравнение имеет вид $\frac{{dp}}{{dt}} = \frac{e}{c}\nabla \varepsilon \times B$. Получается динамическая система. Это и есть нужная нам картина. Сделаем отступление об истории вопроса.

Х. Крупнейшим специалистом по низким температурам и сильным магнитным полям был П.Л. Капица. После трагической катастрофы с Л.Д. Ландау он пригласил из Харькова крупного физика-теоретика И.M. Лифшица. У него была сильная школа, в частности в физике твёрдого тела, ещё в Харькове Лифшиц взаимодействовал с крупным геометром А.В. Погореловым. Я с ними общался с начала 1980-х годов. К нам приходил М.И. Каганов, делал об этом доклады. Видимо, было желание довести эту тему до математиков. У них были ценные наблюдения, но их математических знаний и тренировки не хватало. Я подметил здесь любопытные математические возможности, начал ставить задачи ученикам. Начиная с 1982 г. были выполнены хорошие работы как работы по топологии (В.А. Зорич, С.П. Царёв, И.А. Дынников), но их авторы не знали физики. Как бывает с учениками и особенно с приглашёнными авторами: – сделает что-то ценное и убежит. Приходится приглашать других, развивая тему. Лишь 15 лет спустя вместе с моим учеником А.Я. Мальцевым из ИТФ мы нашли физическую реализацию этих математических исследований.

XI. Перейдём к нашим результатам. Пусть температура очень низкая, скажем, 1 K или ниже, допустим, 10^–2–10^–3 К. Приложим сильное постоянное магнитное поле порядка 1 тесла или больше, например 10–20 тесла (напомним, что один тесла это 10⁴ гаусс, а один гаусс – это по порядку величины магнитное поле Земли). На Ферми-поверхности возникнет движение значений квазиимпульса электронов, $\frac{{dp}}{{dt}} = \frac{e}{c}\nabla \varepsilon \times B$.

Наложим слабое электрическое поле. Тогда в x-пространстве пойдёт ток (внутренность ниже нас не интересует сейчас, хотя она важна, но не для наших целей). Мы будем всё представлять в свёрнутой решётке – легко всё пересчитать в геометрическое пространство, они тождественны, но координаты в них имеют разные размерности. Возникает динамическая система на Ферми-поверхности при данном магнитном поле. Её траектории – это пересечения Ферми-поверхности c плоскостями, ортогональными магнитному полю.

Это картина в дуальном пространстве R³, его ещё надо свернуть. Она весьма нетривиальна, особенно для ранга 3. В ряде случаев электрическое сопротивление оказывается сильно анизотропным в плоскости, ортогональной магнитному полю. Картина ясна для ранга 0 – все траектории замкнуты и гомотопны нулю или упираются в обе стороны в критические точки, то есть замкнуты или конечны в несвёрнутом (как говорят топологи, в накрывающем) пространстве R³, обычно уже в зоне Бриллюэна.

Благородные металлы (золото, платина), а также медь имеют ранг 3 и род 4. Щелочные металлы (литий, натрий, калий, рубидий, цезий) имеют ранг 0. Динамические системы при любом направлении магнитного поля тривиальны в этом случае, сопротивление растёт вместе с полем. Все траектории замкнуты и гомотопически тривиальны, как уже говорилось. Сейчас известны Ферми-поверхности многих металлов. Но в школе Лифшица  были обнаружены и другие, более сложные случаи (М.И. Каганов, А.И. Песчанский, М.Я. Азбель). Это, видимо, и побудило обратиться к математикам, то есть к нам.

XII. Наши результаты таковы. Рассмотрим плоскости, ортогональные к магнитному полю в дуальном пространстве R³. Кроме множества на сфере S² размерности не более 1 имеем такую картину:

Случай 1. Все орбиты компактны в несвёрнутой решётке R³, мы имеем простейший случай, уже обсуждавшийся выше. Согласно правильно переформулированным результатам нашей группы, здесь для множества полной меры в 2-сфере направлений магнитного поля в плоскости все орбиты замкнуты или упираются в обе стороны в седловые критические точки (простейший тип).

Случай 2. Не все орбиты компактны. Имеются открытые орбиты в R³ – полосы; они таковы, что каждая из них заключена в полосу конечной ширины, идущей в определённом направлении в R³. Это – одно направление при данном магнитном поле. Сосуществование сo вторым направлением в этом наборе параллельных плоскостей возможно только на множестве направлений магнитного поля нулевой меры в S².

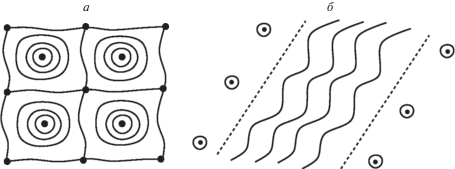
Периодические орбиты в свёрнутой решётке (открытые, в терминологии справочников) и непериодические с определённым средним направлением в несвёрнутом пространстве R³ и полосы вокруг них (см. рис 5 в несвёрнутой решётке) в большинстве непериодичны.

Рис. 5.

Типичные траектории, занимающие множество полной меры:

                                               а – простейший случай, б – полосы

Электрическое сопротивление в случае полосы сильно анизотропно в плоскости ортогональной полю: вдоль одного направления (полосы) оно растёт, а в остальных направлениях этой плоскости выходит на константу. Первые примеры этого были обнаружены в школе Лифшица. Но самое главное состоит в том, что среднее направление полосы в R³ является пересечением плоскости, ортогональной магнитному полю, с целочисленной плоскостью, определяемой тремя целыми числами с точностью до общего множителя. Эта картина устойчива, поэтому можно восстановить целые числа, совершая малые возмущения и следя за изменением направления, где сопротивление (или проводимость) стремится к бесконечности (соответственно к нулю). Это – общий закон.

В случае ранга 1 такие полосы бывают, но они неустойчивы – всё разваливается при почти любом возмущении направления магнитного поля для ранга 1. Для рангов 2 и 3 они устойчивы. Таков общий закон, но что из этого реализуется для конкретного металла – другой вопрос. Чем больше целые числа, тем реже они возникают. Я сейчас планирую развить эту тему, хотя вычислительный эксперимент здесь сложен. Проще всего было бы определить области с полосами физическим экспериментом, но у нас нет такой возможности – мы математики.

Один крупный специалист сказал мне, прикинув мои аргументы: “Похоже, всё так, как ты говоришь, но эксперимент ушёл из этой области. Придётся тебе развивать это как раздел математики значительный период”. Это было в Израиле. В разных странах, особенно в США и России, именно физики более старшего поколения – “поколения великой физики” приветствовали развитие этой темы.

Математическая модель такова. В свёрнутой дуальной решётке (то есть в торе T ³) задана замкнутая поверхность (уровень функции). Пусть её род ≥ 3 и ранг равен 3, то есть максимален. Динамическая система представляет собой сечения поверхности плоскостями, ортогональными магнитному полю. Эти системы определяются направлением магнитного поля. В сфере S², точки которой нумеруют такие системы, присутствуют области, где имеются полосы открытых орбит, устойчивые относительно малых возмущений магнитного поля. Этих областей конечное число для меди и золота – род 4 и ранг 3 (вычисления Р. Делео).

В математической модели имеются весьма экзотические примеры. Например, для кубической решётки с функцией f(p) = cos(p₁) + cos(p₂) + + cos(p₃) (размерности игнорируем) и уровня f(p) = 0 возникает весь букет – бесконечное число областей открытости с разными целыми числами и фракталов, где они скапливаются. Методически этот пример очень любопытен. При немалом возмущении эти режимы разрушаются – либо возникнут новые целые числа, либо все орбиты станут замкнутыми и гомотопными нулю, но, может быть, мы попадём в границы режимов. Фрактальная размерность множества границ режимов не более 1 в сфере S² направлений магнитного поля, то есть на единицу меньше полной размерности, равной 2.

Численный эксперимент (И.А. Дынников и Р. Делео) показывает, что фрактальная размерность особо “хитрых” режимов строго меньше 1, но теорем здесь нет. Примеры фрактальных орбит имеются (первый пример нашёл С.П. Царёв, ещё ряд примеров – И.А. Дынников), но непонятно, какой случай является наиболее общим из возникающих здесь фракталов.

В настоящее время известно или создано много новых материалов с металлическими свойствами. Мы не знаем общего принципа, выделяющего физически реализуемые системы. В последнее время физический эксперимент ушёл из этой области, а численный счёт затруднен. Сейчас мы планируем возобновить активность в этой области.

Существуют и другие задачи – особенно в физике двумерных систем, где возникают математически родственные ситуации, как указал А.Я. Мальцев, но мы их сейчас обсуждать не будем.

XIII. Завершая доклад, я сделаю общее замечание. Физико-математические науки в XX в. подверглись гигантскому, я бы сказал взрывному, развитию. Сейчас ситуация изменилась. Подобно разбеганию галактик во Вселенной, даже в наших теоретических науках разные части их разбегаются друг от друга, перестают друг друга понимать. Мой старший друг и учёный редкостного ума И.М. Гельфанд – выдающийся математик – тратил более половины времени на то, чтобы учиться понимать другие области. Я старался следовать его примеру.

Мы – это Homo sapiens, а не галактики, и должны интеллектуально противостоять разбеганию. Это главная задача теоретиков или хотя бы их лидеров.