Высокомолекулярные соединения (серия А), 2019, T. 61, № 4, стр. 359-365

ВВЕДЕНИЕ

Проводящие полимеры как правило обладают повышенной жесткостью из-за присутствия сопряженных связей. Один из способов улучшения их растворимости, и, как следствие, перерабатываемости, заключается в использовании блок-сополимеров стержень–клубок. Благодаря конформационной асимметрии такие сополимеры образуют разнообразные микродоменные структуры, применяемые в фотовольтаике и смежных областях [1, 2]. В гибких сополимерах микрофазное разделение контролируется соотношением длины химически различающихся блоков и степенью их сегрегации. Замена одного из гибких блоков жестким снижает конформационную энтропию сополимера, облегчая возникновение устойчивых микроструктур. Соотношение между длиной и диаметром стержнеобразного блока становится дополнительным фактором, определяющим вид фазовой диаграммы. Появление в сополимере мезогенного фрагмента делает возможным переход от изотропного к нематическому или смектическому упорядочению стержней в доменах.

К настоящему моменту для диблок-сополимеров стержень–клубок в экспериментах, наряду с обычными морфологиями (мицеллы, цилиндры, биконтинуальные структуры, ламели) наблюдали смектические слои [3–7], стреловидные, z-образные, волнистые и перфорированные ламели [8–24]. Для сополимеров с полужесткими стержнями в рамках самосогласованной теории среднего поля (SCFT) предсказано существование одно- и двуслойных ламелей по типу смектиков A и C, а также разнообразные переходы между ними [22].

Первоначальные теоретические усилия по построению фазовой диаграммы сополимеров стержень–клубок были направлены на сравнение значений свободной энергии для различных морфологий [25, 26]. В предположении о том, что стержни образуют смектик А, было предсказано образование мицелл в форме хоккейной шайбы или гексагонально упакованных цилиндров с ламелярной сердцевиной прямоугольного сечения, состоящей из стержней. Дальнейшие исследования методами мезоскопического молекулярного моделирования [16–18, 23, 24] показали, что энтропийно смектик С часто более выгоден, чем смектик А, поскольку наклон стержней в смектических ламелях статистически более вероятен. Кроме того, в этом случае снижается плотность точек сочленения гибких и жестких блоков на поверхности ламелей и повышается конформационная энтропия гибких блоков.

Впоследствии построение фазовой диаграммы сополимеров стержень–клубок велось главным образом методами SCFT [19–22, 27–31] и молекулярной динамики [16–18, 23, 24, 32]. В работе [18] броуновской молекулярной динамикой с потенциалами Леннард-Джонса систематически исследованы фазовые диаграммы в координатах состав–сегрегация блоков для трех фиксированных значений длины жесткого блока. При этом наблюдались разнообразные нетривиальные морфологии: ламелярная кристаллическая, стреловидная и чередующаяся стреловидная, гексатик B, смектики А и С, ламелярная нематическая, ламелярная, ламелярная гексагонально перфорированная, ламелярная волнистая и цилиндрическая гексагональная.

Первые исследования микрофазного расслоения сополимеров стержень–клубок методом диссипативной динамики частиц (DPD) выполнены в работах AlSunaidi с соавторами [23, 24]. Варьируя температуру и степень сегрегации блоков сополимера R₇C₇ при плотности частиц ρ₀ = 4 авторы наблюдали формирование кристаллической и смектической А фаз. Фазовая диаграмма методом DPD была построена в работе [32] при плотности ρ₀ = 5, длине сополимера N = 10, варьируемом составе сополимера и степени сегрегации его блоков. Были обнаружены кристаллическая ламелярная, ламелярная, гироидная, цилиндрическая и мицеллярная фазы. Следует отметить, что в силу ограниченной длины цепей состав сополимера варьировали с большим шагом (Δf_A = 0.1). Ориентационное упорядочение цепей наблюдали лишь при доле жесткого блока f_A ≥ 0.7, когда жесткий фрагмент содержал 7 и более звеньев. В целом DPD приводит к фазовым диаграммам, близким к тем, что получены броуновской молекулярной динамикой.

До настоящего времени метод DPD мало применялся для исследования фазового поведения сополимеров стержень–клубок. Причина состоит в том, что моделирование проводили при высокой плотности частиц, что не позволяло рассматривать ячейки размерами более 20 × 20 × 20 и сополимеры более чем из N = 10 звеньев. Относительно короткие жесткие блоки в таких молекулах обладали сравнительно невысокой склонностью к ориентационному упорядочению, и его удавалось наблюдать лишь в ламелярной морфологии.

В настоящей работе методом DPD построена более подробная фазовая диаграмма диблок-сополимера стержень–клубок для цепей длиной N = 20 в ячейке размером 32 × 32 × 32 при средней плотности частиц ρ₀ = 3. Благодаря большей длине цепи состав сополимера на фазовой диаграмме варьировали с шагом Δf_A = 0.05, при этом максимальная исследованная степень сегрегации χN_max достигла ≈250 (в работе [32] Δf_A = 0.1, χN_max = 80). Согласно полученной нами диаграмме, ориентационное упорядочение может возникать не только в ламелярной, но и в биконтинуальной морфологии.

МОДЕЛЬ И МЕТОД РАСЧЕТА

Крупномасштабное молекулярное моделирование сополимеров, содержащих жесткие фрагменты, затруднено [33]. Такие системы релаксируют гораздо медленнее, чем гибкие молекулярные цепи той же длины с широким спектром времен релаксации, включающим быстрые моды отдельных звеньев. Среди огрубленных мезоскопических методов одним из наиболее перспективных считается диссипативная динамика частиц. Благодаря большому шагу интегрирования уравнений движения и низким коэффициентам трения частиц с “мягкими” потенциалами, с ее помощью удается наблюдать самоорганизацию макромолекул на относительно больших пространственно-временных масштабах. Методом DPD уже изучали смеси монодисперсных [34, 35] и бидисперсных [36], а также двублочных жестких наностержней [37] с диблок-сополимерами, образующими ламелярную [34, 36, 37] и гексагональную [35–37] микродоменные структуры, а также поведение углеродных нанотрубок в концентрированном растворе диблок-сополимера [38]. “Стандартный” подход, разработанный R.D. Groot и P.B. Warren [39] для гибкоцепных полимеров, недостаточен для моделирования жестких блоков. Для этого в литературе предложен ряд модификаций DPD для введения жесткости. Один из способов связан с корректировкой валентных потенциалов и добавлением угловых потенциалов [40–46], однако он требует уменьшения шага интегрирования в 5–10 раз для сохранения устойчивости численного решения уравнений движения частиц, что замедляет вычисления. Мы используем альтернативный подход, уже показавший ранее свою эффективность, а именно моделирование стержнеобразных фрагментов как жестких тел по алгоритму T.F. Miller с сотрудниками [47] в NVE-ансамбле. Он исключает из рассмотрения взаимодействия частиц внутри жесткого блока, оптимизируя расчет сил.

Другая проблема стандартного метода DPD заключается в том, что нематическое упорядочение наностержней, обусловленное их стерическим отталкиванием, затруднено. Причина этого состоит в “мягкости” межчастичных взаимодействий по сравнению с классическими молекулярными потенциалами, такими как потенциал Леннард-Джонса. Для преодоления указанных трудностей предлагались различные подходы. В работах [40–43] вдвое уменьшали длину связей в жестком блоке, что приводило к повышению плотности и соответствующему усилению стерических взаимодействий. К сожалению, при этом в равной степени возрастает число частиц и, как следствие, вычислительные затраты. В литературе показано, что нематическое упорядочение жестких [23] и полужестких [48] стержней со стандартными потенциалами DPD можно наблюдать лишь при длине жесткого стержня N_R ≥ 7. В данной работе мы провели моделирование как с обычным для DPD значением параметра отталкивания идентичных частиц a_AA = a_BB = = 25, так и при a_AA = a_BB = 50, что облегчает ориентационное упорядочение стержнеобразных частиц. Однако эффект параметра отталкивания оказался относительно слаб, поэтому основные результаты приводятся для стандартного случая.

Более подробное описание метода DPD можно найти, например, в нашей недавней работе [49], посвященной статистической термодинамике гибкоцепных диблок-сополимеров, допированных наностержнями. Для расчетов использовался программный пакет LAMMPS.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Микрофазное разделение в блок-сополимере с изменяемым соотношением длины жесткого A и гибкого B блоков и постоянной суммарной длиной цепи N = 20 моделировали посредством плавного (с шагом 0.1) увеличения параметра отталкивания a_AB частиц разного сорта для исходно разупорядоченного состояния. Эта величина связана с параметром Флори–Хаггинса χ линейным соотношением χ = = (0.306 ± 0.003)(a_AB – a_AA) [39]. Моделирование проводили в ячейке размером 32 × 32 × 32, где за единицу длины принят радиус обрезки взаимодействий между DPD-частицами.

Различные микроструктуры в системе идентифицировали по появлению вторичных пиков на зависимости статического структурного фактора жесткого блока от величины волнового вектора (примеры см. в работе [50]). Ориентационное упорядочение детектировали визуально, а для его количественной оценки рассчитывали величину корреляционной функции S_N(r) в зависимости от расстояния r между связями A–A в стержнях

где угловые скобки означают усреднение по 10⁵ случайно выбранных пар связей А–А, принадлежащих разным стержням c ортами n_i и n_j. В отсутствие дальнего ориентационного порядка S_N → 0 при r → ∞, а в идеальном нематике S_N = 1.

На рис. 1 построена фазовая диаграмма диблок-сополимера AB стержень–клубок в координатах χN – f_A (мольная доля звеньев А в сополимере) для a_AA = a_BB = 25. С точки зрения микрофазного разделения диаграмма морфологически подобна фазовой диаграмме гибкоцепного диблок-сополимера, построенной методом DPD в работе [50]. Степень сегрегации звеньев А и В, отвечающая переходу беспорядок–порядок, зависит от состава сополимера и растет с уменьшением длины жесткого блока.

При  f_A > 0.3 (N_A > 6) в доменах, образованных жесткими блоками, наблюдается ориентационное упорядочение. Соответствующая область диаграммы на рис. 1 расположена справа от сплошной вертикальной линии.

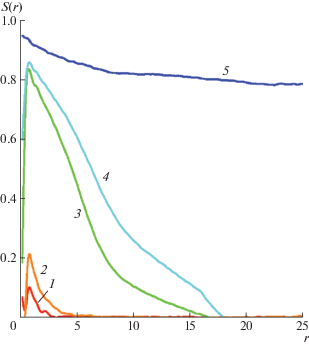
Поведение ориентационной корреляционной функции S_N(r) для сополимера А₈В₁₂ при разной силе сегрегации звеньев блоков А и В показано на рис. 2. В случае слабой несовместимости (a_AB = 25 и 27) упорядочение проявляется лишь на расстояниях менее длины стержня, однако при увеличении a_AB расстояние, на котором S_N отлична от нуля (корреляционная длина ориентационного взаимодействия стержней), заметно возрастает. Для a_AB = 29 и 31 это расстояние сопоставимо с размером доменов, а при формировании ламелярной микроструктуры (a_AB = 33) превышает размер ячейки моделирования, что свидетельствует о возникновении дальнего порядка в расположении жестких блоков.

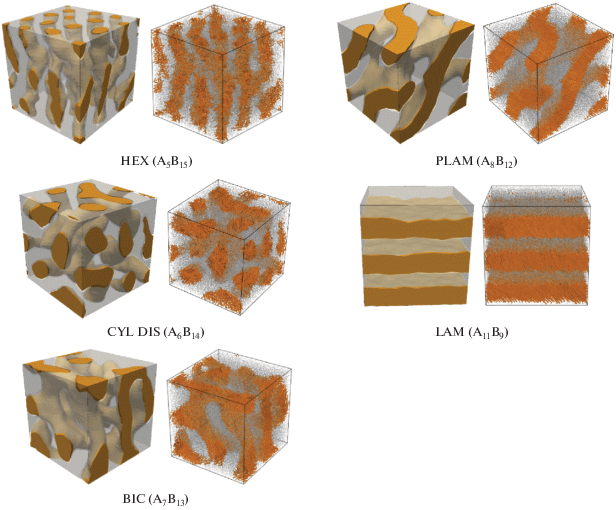
Структура возникающих морфологий представлена на рис. 3. В сополимере A₅B₁₅ с коротким жестким блоком формируютcя гексагонально упорядоченные цилиндры (HEX). Удлинение жесткого блока приводит к разупорядочению цилиндров (CYL DIS) для сополимера A₆B₁₄ и биконтинуальной морфологии (BIC) – для A₇B₁₃. В сополимере A₈B₁₂ образуются ламели (LAM), которые устойчивы и в сополимерах с более длинным жестким блоком А. Обнаружена также регулярная биконтинуальная структура, сходная с перфорированными ламелями (PLAM). Пока неясно, является ли данная структура кинетически стабильной.

Переход от изотропного к упорядоченному распределению жестких блоков наблюдается только в микрофазно-расслоенном состоянии сополимера. В отличие от результатов работы [32] это состояние необязательно отвечает ламелярной морфологии. При этом возникает исключительно смектик C, в котором уменьшение плотности цепей на единицу межфазной поверхности, повышающее конформационную энтропию гибких блоков, достигается наклоном стержней в ламелях. Как следует из рис. 3, направление директора смектической фазы изменяется от одной ламели к другой.

В дальнейшем представляет интерес построить фазовую диаграмму в координатах χN – f_A при N_A = 7 или 8, варьируя длину гибкого блока и полную длину цепи сополимера, поскольку жесткие блоки такой длины всегда ориентационно упорядочены.

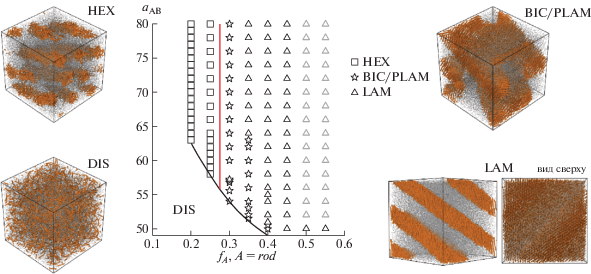
На рис. 4 приведены фазовая диаграмма и мгновенные снимки упорядоченных состояний, аналогичные представленным на рис. 1 и 3, но отвечающие более сильному отталкиванию идентичных звеньев: a_AA = a_BB = 50. Видно, что, с одной стороны, увеличение стерического отталкивания DPD-частиц облегчает ориентационное упорядочение стержней, которое возникает уже при N_A = 6. С другой стороны, существенно повышаются вязкость системы и время ее релаксации. При N_A = 8 не наблюдается заметных перестроек морфологии на временах порядка 10⁷ шагов интегрирования, а при N_A ≥ 10 релаксация дефектов микродоменной структуры за разумное время оказывается невозможной. При N_A > 8 жесткие блоки образуют структуру, по степени упорядоченности близкую к кристаллу.

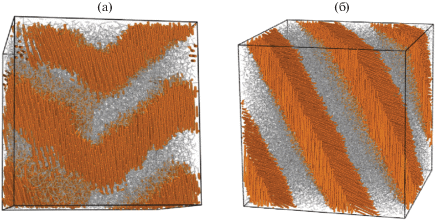
В отдельных численных экспериментах, проведенных в ячейках меньшего размера (20 × 20 × 20), возникали экзотические структуры, встречающиеся в эксперименте: зигзагообразные ламели при N_A = 10, а также неупорядоченные фрагменты двуслойных ламелей при N_A = 11. Они показаны на рис. 5. Повторное моделирование в ячейках размером 32 × 32 × 32 продемонстрировало, что эти морфологии метастабильны и не воспроизводятся, уступая место плоским однослойным ламелям.

Таким образом, при моделировании сополимеров стержень–клубок методом DPD в дальнейшем представляется более обоснованным использовать стандартное значение параметра отталкивания a_AA = a_BB = 25, а проверку устойчивости возникающих морфологий проводить в ячейках большего размера.

Уточненная фазовая диаграмма диблок-сополимера стержень–клубок может быть использована для интерпретации лабораторных экспериментов и сопоставления с теоретическими расчетами.

А.В. Березкин признателен за возможность использования оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 16-13-10280).