Высокомолекулярные соединения (серия А), 2019, T. 61, № 6, стр. 553-558
ПОЛИМЕРНЫЕ СЕТКИ, ОБРАЗОВАННЫЕ МОЛЕКУЛЯРНЫМИ ЩЕТКАМИ: СКЕЙЛИНГОВАЯ ТЕОРИЯ
Е. Б. Жулина a, С. С. Шейко a, b, О. В. Борисов a, c, *
a Институт высокомолекулярных соединений Российской академии наук
199004 Санкт-Петербург, Большой пр., 31, Россия
b Department of Chemistry University of North Caroline at Chapel Hill
27599 Chapel, Hill, USA
c Institut des Sciences Analytiques et de Physico-Chimie pour l’Environnement et les Matériaux,
UMR 5254 CNRS UPPA
64053 Pau, France
* E-mail: oleg.borisov@univ-pau.fr
Поступила в редакцию 24.05.2019
После доработки 20.06.2019
Принята к публикации 03.07.2019
Аннотация
Методом скейлинга развита теория набухания сеток, образованных сшитыми гребнеобразно-разветвленными макрмолекулами (“молекулярными щетками”), в хорошем растворителе. Показано, что равновесный коэффициент набухания таких сеток сложным образом зависит от набора характерных молекулярно-архитектурных параметров: густоты пришивки, длины и числа боковых цепей, исходящих из одной точки ветвления на основной цепи. В частности, предсказано, что замена линейных субцепей сетки на молекулярные щетки той же молекулярной массы приводит в большинстве случаев к уменьшению степени набухания сетки. При фиксированной длине основных цепей молекулярных щеток, формирующих сетку, коэффициент набухания немонотонным образом зависит от длины боковых цепей, проходя через максимум при достижении развязками основной цепи предельной вытяжки.
Эта работа посвящена памяти выдающегося российского ученого Александра Борисовича Зезина с благодарностью
за многие годы замечательного научного сотрудничества
и незабываемого личного общения
Достижения современной химии высокомолекулярных соединений позволяют синтезировать макромолекулы возрастающе сложной и хорошо контролируемой разветвленной архитектуры. Примеры регулярно разветвленных макромолекул включают звездообразные и гребнеобразные макромолекулы, молекулярные щетки, дендронизованные полимеры (дендримеры, дендриграфты) и другие. Ковалентная сшивка разветвленных макромолекул или их прививка к твердой подложке дает возможность создавать новые функциональные или конструкционные материалы, а также полимер-модифицированные поверхности с принципиально новыми свойствами. Важно, что свойствами таких материалов, прежде всего механическими и интерактивными, можно управлять на стадии химического синтеза путем направленного изменения архитектурных параметров (топологии) образующих их индивидуальных макромолекул.
Гребнеобразно-разветвленные полимеры и молекулярные щетки состоят из длинной основной цепи, к которой на регулярных интервалах ковалентно присоединены боковые цепи [1–6]. Мы будем называть молекулярными щетками гребнеобразно-разветвленные макромолекулы, у которых боковые цепи привиты к основной цепи настолько густо, что их характерный размер превышает расстояние между соседними точками прививки. В настоящее время разработан ряд синтетических подходов – “grafting to”, “grafting from” и “grafting through”, которые позволяют синтезировать гребнеобразные (со)полимеры и молекулярные щетки с хорошо контролируемыми архитектурными параметрами, такими как густота прививки и молекулярные массы основной и боковых цепей [6]. Вместе с тем, были синтезированы иерархически разветвленные макромолекулы, в которых индивидуальные боковые цепи обладают дендритной или гребнеобразно разветвленной архитектурой [7, 8].
В работах С.С. Шейко с соавторами [9] убедительно продемонстрировано, что ковалентная сшивка молекулярных щеток концевыми группами основных цепей позволяет получать необычные, “мягкие” эластомерные сетки. Упругие характеристики таких эластомеров в широких пределах деформации могут быть “настроены” путем правильного выбора длины основной и боковых цепей щеток, а также густоты их прививки.
Существенно меньше внимания в литературе уделено изучению набухания сеток, образованных сшитыми молекулярными щетками, в низкомолекулярных растворителях. В частности, систематические связи между равновесной степенью набухания сеток и архитектурными параметрами составляющих ее молекулярных щеток не были изучены. Теоретическому решению этой задачи на основе скейлингового подхода и посвящена настоящая работа.
МОДЕЛЬ СЕТКИ ИЗ МОЛЕКУЛЯРНЫХ ЩЕТОК
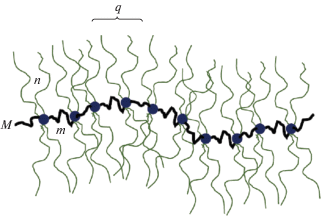
Рассмотрим трехмерную сетку, состоящую из молекулярных щеток, соединенных в узлах сетки концевыми звеньями основных цепей. В рамках используемой в данной работе скейлинговой модели, пренебрегающей численными коэффициентами, число субцепей – молекулярных щеток, исходящих из одного узла сетки, остается произвольным. Основная цепь каждой молекулярной щетки состоит из M ≫ 1 мономерных звеньев. Из каждой точки ветвления, расположенной на основной цепи, исходит q ≥ 1 боковых цепей. Число мономерных звеньев в участке основной цепи между соседними точками ветвления составляет m ≥ 1. Число мономерных звеньев в каждой боковой цепи равно n (рис. 1). Как основная, так и боковые цепи предполагаются в равной мере термодинамически гибкими, длина статистического сегмента приблизительно совпадает с размером одного мономерного звена, который в дальнейшем принимается за единицу длины. Число точек ветвления в каждой молекулярной щетке, входящей в состав сетки, велико, M/m ≫ 1. Полное число мономерных звеньев в молекулярной щетке
где последнее равенство справедливо при qn ≫ m. Мы изучали набухание сетки, образуемой сшитыми молекулярными щетками, помещенной в бесконечный резервуар низкомолекулярного растворителя, который является в равной мере хорошим (атермическим) для всех мономерных звеньев как основных, так и боковых цепей щеток.РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Основной характеристикой, представляющей интерес и измеряемой экспериментально, является равновесный коэффициент набухания сетки в хорошем растворителе. Коэффициент набухания α может быть определен (в условиях изотропного набухания) как отношение размеров макроскопического образца сетки, свободно набухшего в хорошем растворителе, к его размерам в сухом состоянии:
(2)
$\alpha = \frac{{{{H}_{{swollen}}}}}{{{{H}_{{dry}}}}} = {{\left( {\frac{{{{c}_{{dry}}}}}{c}} \right)}^{{1/3}}}$Здесь cdry ~ 1, c – объемные доли полимера в сетке в сухом и набухшем состоянии соответственно. Следуя теории де Жена [10], применим к рассмотрению набухшей сетки c*-теорему. Согласно c*-теореме, средняя концентрация (объемная доля) мономерных звеньев в набухшем геле равна средней концентрации c* мономерных звеньев в индивидуальной субцепи, набухшей в хорошем растворителе. В результате, из уравнения (2):
где концентрация c* может быть выражена как и R – размер индивидуальной молекулярной щетки (субцепи сетки) в хорошем растворителе. Из уравнений (3) и (4) следует, чтоИндивидуальная молекулярная щетка в хорошем растворителе может быть представлена как гибкая самонепересекающая червеобразная цепь, толщина D которой совпадает (с точностью до численного коэффициента порядка единицы) с персистентной длиной и определяется размером вытянутых боковых цепей [11–13]. Как было предположено в работе [11] и подтверждено результатами численного моделирования [12, 13], эффект наведенной персистентной длины, которая может существенно превышать толщину молекулярной щетки, проявляется только в случае столь большой длины боковых цепей, которая не достижима в эксперименте. Вытяжка боковых цепей, так же как и соединяющих соседние точки ветвления участков основной цепи – спейсеров, является следствием отталкивательных взаимодействий между боковыми цепями щетки. Эффективная контурная длина эквивалентной червеобразной цепи равна L ≃ (M/m)h, где h – характерное межконцевое расстояние для индивидуального спейсера. Следовательно, размер индивидуальной молекулярной щетки в хорошем растворителе определяется соотношением
(6)
$R \simeq {{L}^{\nu }}{{D}^{{1 - \nu }}} \simeq {{\left( {\frac{M}{m}} \right)}^{\nu }}{{h}^{\nu }}{{D}^{{1 - \nu }}}$Здесь показатель ν ≈ 3/5 в хорошем растворителе. Полагая, что qn ≫ m можно представить коэффициент набухания сетки в виде
(7)
$\alpha \simeq {{M}^{{(3\nu - 1)/3}}}{{h}^{\nu }}{{D}^{{1 - \nu }}}{{(qn)}^{{ - 1/3}}}{{m}^{{(1 - 3\nu )/3}}}$Используя результаты работы [14], мы различаем три качественно отличных режима внутримолекулярной организации индивидуальных молекулярных щеток – субцепей сетки, реализующихся в зависимости от соотношения между архитектурными параметрами (n, m, q). Каждый из этих режимов характеризуется специфическими степенными зависимостями локальных конформационных свойств молекулярной щетки D и h от набора архитектурных параметров (n, m, q).
Режим Sa – “ожерелье из звезд”
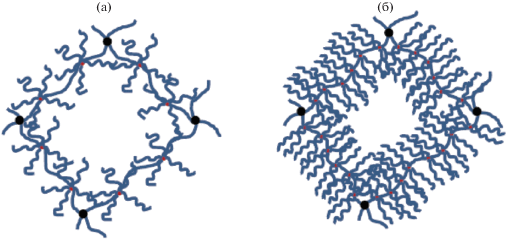
При соотношении параметров nq(ν – 1)/ν ≤ m ≤ n молекулярная щетка может быть представлена в виде ожерелья из густо нанизанных на основную цепь (находящихся в плотном контакте) звездообразно разветвленных макромолекул (рис. 2а). Каждая такая звезда образована q боковыми цепями (лучами), исходящими из одной точки ветвления, расположенной на основной цепи. В этом режиме поперечный размер (толщина) молекулярной щетки и характерное расстояние между соседними точками ветвления совпадают с размером звезды из q ≫ 1 лучей, каждый длины n, полученным ранее в работах [15, 16]:
Рис. 2.
Схема сетки из сшитых молекулярных щеток в режиме ${{S}_{a}}$ локальной сферической симметрии (а) и в режимах ${{C}_{a}},{{C}_{b}}$ локальной цилиндрической симметрии субцепей сетки (молекулярных щеток) (б).
Используя уравнение (7), получаем выражение для коэффициента набухания геля в режиме Sa:
(9)
$\begin{gathered} \alpha \simeq {{N}^{{(3\nu - 1)/3}}}{{q}^{{(1 - 3\nu )/2}}} \simeq \\ \simeq {{M}^{{(3\nu - 1)/3}}}{{\left( {\frac{n}{m}} \right)}^{{(3\nu - 1)/3}}}{{q}^{{(3\nu - 1)/6}}} \\ \end{gathered} $Подставляя ν = 3/5 в уравнение (9), имеем
(10)
$\alpha \simeq {{N}^{{4/15}}}{{q}^{{ - 2/5}}} \simeq {{M}^{{4/15}}}{{\left( {\frac{n}{m}} \right)}^{{4/15}}}{{q}^{{ - 2/15}}}$Как следует из уравнения (10), при постоянной длине основной цепи коэффициент набухания α возрастает как функция соотношения n/m, но убывает с ростом q.
Режим Ca – локальная цилиндрическая симметрия щетки при не полностью растянутых спейсерах
Молекулярные щетки с более короткими спейсерами, nν/(ν + 2)q ≤ m ≤ nq(ν – 1)/ν, характеризуются локальной цилиндрической симметрией в распределении мономерных звеньев боковых цепей вокруг основной цепи (рис. 2б). Только в непосредственной близости от точек ветвления при q ≫ 1 сохраняется сферически-симметричная структура, характерная для отдельной звездообразной макромолекулы. Размер (межконцевое расстояние) растянутых спейсеров h не достигает их контурной длины (~m). В этом режиме, как показано в работе [12]:
(11)
$h \simeq {{m}^{\nu }}{{q}^{{1 - \nu }}}{{\left( {\frac{{qn}}{m}} \right)}^{{\nu (1 - \nu )/2}}}$(13)
$\begin{gathered} \alpha \simeq {{N}^{{(3\nu - 1)/3}}}{{\left( {\frac{{qn}}{m}} \right)}^{{\nu (1 - 3\nu )/2}}} \\ \simeq {{M}^{{(3\nu - 1)/3}}}{{\left( {\frac{{qn}}{m}} \right)}^{{(3\nu - 1)(2 - 3\nu )/6}}}, \\ \end{gathered} $(14)
$\alpha \simeq {{N}^{{4/15}}}{{\left( {\frac{{qn}}{m}} \right)}^{{ - 6/25}}} \simeq {{M}^{{4/15}}}{{\left( {\frac{{qn}}{m}} \right)}^{{2/75}}}$Таким образом, в режиме Ca коэффициент набухания α зависит от универсальной комбинации параметров $qn{\text{/}}m$: убывает как функция $qn{\text{/}}m$ при фиксированной полной молекулярной массе субцепи сетки ~N, но возрастает при фиксированной длине ее основной цепи M.
Режим ${{C}_{b}}$ – локальная цилиндрическая симметрия щетки при полностью растянутых спейсерах
В случае, когда $m \leqslant {{n}^{{\nu /(\nu + 2)}}}q$, спейсеры достигают предельного растяжения:
При этом поперечный размер щетки определяется соотношением [14]
(16)
$D \simeq {{n}^{\nu }}{{\left( {\frac{{q{{n}^{\nu }}}}{m}} \right)}^{{(1 - \nu )/(1 + \nu )}}},$(17)
$\begin{gathered} \alpha \simeq {{N}^{{(3\nu - 1)/3}}}{{n}^{{\nu (1 - 3\nu )/(1 + \nu )}}}{{\left( {\frac{q}{m}} \right)}^{{(1 - 3\nu )/(1 + \nu )}}} \simeq \\ \, \simeq {{M}^{{(3\nu - 1)/3}}}{{n}^{{(2\nu - 1)(1 - 3\nu )/3(1 + \nu )}}}{{\left( {\frac{q}{m}} \right)}^{{(1 - 3\nu )(2 - \nu )/3(1 + \nu )}}}, \\ \end{gathered} $(18)
$\alpha \simeq {{N}^{{4/15}}}{{n}^{{ - 3/10}}}{{\left( {\frac{q}{m}} \right)}^{{ - 1/2}}} \simeq {{M}^{{4/15}}}{{n}^{{ - 1/30}}}{{\left( {\frac{q}{m}} \right)}^{{ - 7/30}}}$Из уравнения (18) видно, что в режиме полной вытяжки спейсеров ${{C}_{b}}$ коэффициент набухания α – убывающая функция как длины боковых цепей n, так и средней плотности их прививки q/m.
Как следует из уравнений (9), (13) и (17), коэффициент набухания сетки, образованной молекулярными щетками, является возрастающей функцией молекулярной массы индивидуальной щетки ~N или молекулярной массы ее основной цепи ~М, так же как это имеет место для обычных полимерных гелей с линейными субцепями. Однако зависимость коэффициента набухания от набора архитектурных параметров $(n,m,q)$, характеризующих степень разветвленности молекулярной щетки, оказывается более сложной и может изменяться от режима к режиму.
Если молекулярные щетки, образующие сетку, обладают цилиндрической симметрией (режимы ${{C}_{a}},{{C}_{b}}$), что имеет место при $m \leqslant n{{q}^{{(\nu - 1)/\nu }}}$, то коэффициент набухания является убывающей функцией как усредненной вдоль основной цепи плотности прививки $q{\text{/}}m$, так и длины боковых цепей $n$ при условии, что полная молекулярная масса каждой субцепи ~N сохраняется постоянной, т.е. линейные субцепи заменяются разветвленными с той же молекулярной массой (и, как следствие, более короткой основной цепью). Однако, если число мономерных звеньев в основной цепи $M$ сохраняется постоянным, то коэффициент набухания возрастает как функция $q{\text{/}}m$ и $n$ в режиме ${{C}_{a}}$ и убывает в режиме ${{C}_{b}}$.
Примечательно, что в режиме ${{C}_{a}}$, характеризующимся умеренным растяжением спейсеров, коэффициент набухания геля является функцией универсальной комбинации $qn{\text{/}}m$ архитектурных параметров, т.е. отношения числа мономенрных звеньев в боковых цепях и числа звеньев в основной цепи, но не зависит от способа распределения мономерных звеньев между боковыми цепями.
Иные закономерности предсказаны для сеток, в которых индивидуальные субцепи находятся в конформации “ожерелья из звезд” (режим Sa). При постоянной молекулярной массе субцепей N = const коэффициент набухания не зависит от $n$ и $m$, но убывает как функция q. Напротив, если длина основной цепи остается постоянной М = = const, то коэффициент набухания возрастает как функция соотношения n/m, и убывает как функция q.
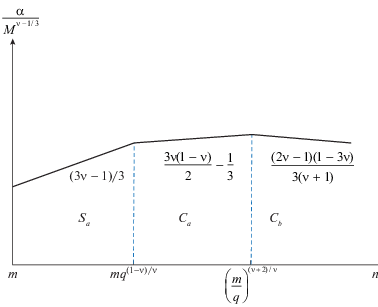
На рис. 3 схематически представлена зависимость коэффициента набухания сетки от длины боковых цепей $n$ при постоянных $M,\;m,\;q$. Видно, что степень набухания геля заметно возрастает как функция n в режиме “ожерелья из звезд” (Sa), продолжает возрастать с меньшей крутизной в режиме ${{C}_{a}}$ и проходит через слабый максимум на границе режимов ${{C}_{a}}$ и ${{C}_{b}}$. Предсказываемое теорией убывание коэффициента набухания как функции n в режиме ${{C}_{b}}$ является очень слабым (показатель степени –1/30) в рассматриваемых условиях хорошего растворителя. Для молекулярных щеток с q = 1 режим Sa отсутствует, но общая форма зависимости коэффициента набухания от n сохраняется.
Рис. 3.
Зависимость коэффициента набухания сетки из молекулярных щеток от числа $n$ мономерных звеньев в боковой цепи при $q \geqslant 1$.
Необходимо отметить, что настоящая модель не учитывает эффектов зацеплений, которые могут повлиять на набухание геля. Сравнение с экспериментальными данными работы [17] показывает, что ряд закономерностей, предсказываемых данной теорией, находится в согласии с экспериментальными результатами. В частности, повышение степени набухания геля при увеличении длины $n$ боковых цепей в режиме ${{C}_{a}}$ и его убывание с ростом длины спейсеров $m$. Однако эксперимент демонстрирует более сильную зависимость коэффициента набухания от длины основной цепи $M$, чем предсказываемая теорией зависимость $\alpha \sim {{M}^{{\nu - 1/3}}}$, что может указывать на роль зацеплений, возникающих при сшивании молекулярных щеток в сетку. Известно, что $c{\kern 1pt} *$-теорема применима к однородно-сшитым в растворах макромолекулам, что было подтверждено в многочисленных экспериментах.
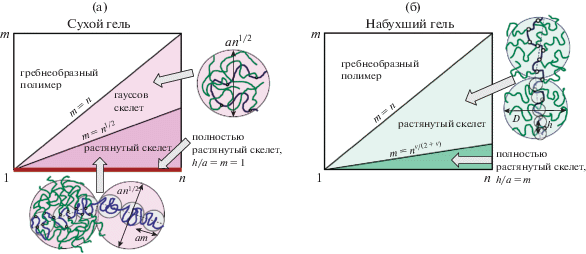
Как следует из модели, представленной в настоящей работе, набухание геля может привести к изменению не только крупномасштабных конформационных характеристик молекулярных щеток–субцепей сетки, но и к локальным конформационным перестройкам. В набухшем состоянии область значений архитектурных параметров $(n,m,q)$, отвечающая полностью вытянутому состоянию спейсеров, расширяется по сравнению с соответствующей областью в условиях отсутствия растворителя. Таким образом, если даже в сухом состоянии спейсеры молекулярной щетки сохраняют локальную гибкость, то при набухании геля в хорошем растворителе они могут достигнуть предельной вытяжки, как это показано на рис. 4.
Рис. 4.
Диаграммы состояния сетки из молекулярных щеток в сухом (без растворителя) (а) и в набухшем состоянии для частного случая q = 1 (б).
Работа выполнена при поддержке Министерства науки и образования Российской Федерации (код проекта 14.W03.31.0022).
Список литературы
Sheiko S.S., Sumerlin B.S., Matyjaszewski K. // Prog. Polym. Sci. 2008. V. 33. P. 759.
Verduzco R., Li X., Pesek S.L., Stein G.E. // Chem. Soc. Rev. 2015. V. 44. P. 2405.
Müllner M., Müller A.H.E. // Polymer. 2016. V. 98. P. 389.
Rzayev J. // ACS Macro Lett. 2012. V. 1. P. 1146.
Liang H., Sheiko S.S., Dobrynin A.V. // Macromolecules. 2018. V. 51. P. 638.
Yuan J., Müller A.H.E., Matyjaszewski K., Sheiko S. // Polymer Science: a Comprehensive Reference / Eds. by K. Matyjaszewski, M. Möller. Amsterdam: Elsevier, 2012.
Rosen B.M., Wilson C.J., Wilson D.A., Peterca M., Imam M.R., Perec V. // Chem. Rev. 2009. V. 109. P. 6275.
Costanzo S., Scherz L.F., Schweizer T., Kröger M., Floudas G., Schlüter A.D., Vlassopoulos D. // Macromolecules. 2016. V. 49. P. 7054.
Daniel W.F.M., Burdynska J., Vatankhah-Varnoosfaderani M., Matyjaszewski K., Paturej J., Rubinstein M., Dobrynin A.V., Sheiko S.S. // Nat. Mater. 2016. V. 15. P. 183.
de Gennes P.-G. Scaling Concepts in Polymer Physics. Ithaca; London: Cornell University Press, 1976.
Бирштейн T.M., Борисов O.В., Жулина Е.Б., Хохлов A.Р., Юрасова T.A. // Высокомолек. соед. А. 1987. Т. 29. С. 293.
Feuz L., Leermakers F.A.M., Textor M., Borisov O.V. // Macromolecules. 2005. V. 38. P. 8891.
Theodorakis P.E., Hsu H.-P., Paul W., Binder K. // J. Chem. Phys. 2011. V. 135. P. 164903.
Zhulina E.B., Sheiko S.S., Borisov O.V. // Macromolecules. 2019. V. 52. P. 1671.
Daoud M., Cotton J.-P. // J. Phys. (France). 1982. V. 43. P. 531.
Birshtein T.M., Zhulina E.B. // Polymer. 1984. V. 25. P. 1453.
Jacobs M., Liang H., Dashtimoghadam E., Morgan B.J., Sheiko S.S., Dobrynin A.V. // Macromolecules. 2019. V. 52. № 14. P. 5095.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)