Высокомолекулярные соединения (серия А), 2020, T. 62, № 1, стр. 3-17
Структура плоской щетки из привитых полиэлектролитных звезд
В. М. Прокачева a, А. А. Полоцкий b, *, Т. М. Бирштейн b
a Department of Physical and Macromolecular Chemistry, Faculty of Science, Charles University in Prague
128 00 Praha 2,
Hlavova 8, Czech Republic
b Институт высокомолекулярных соединений Российской академии наук
199004 Санкт-Петербург, Большой пр., 31, Россия
* E-mail: alexey.polotsky@gmail.com
Поступила в редакцию 17.06.2019
После доработки 18.07.2019
Принята к публикации 23.08.2019
Аннотация
Развита аналитическая теория для плоских щеток из привитых полиэлектролитных звезд, основанная на ступенчатой аппроксимации профиля плотности щетки. Особое внимание уделено эффекту формирования слоистой структуры с разделением звезд на две популяции и влиянию на него степени заряженности лучей и концентрации соли. Показано, что росту числа звезд с предельно растянутым лучом, за который звезда прививается к поверхности, способствует увеличение плотности прививки, числа лучей или степени ионизации лучей. В последнем случае средняя плотность щетки уменьшается, а в первых двух – возрастает. Показано, что теория, основанная на трехступенчатой аппроксимации профиля плотности, хорошо описывает результаты моделирования методом самосогласованного поля, наилучшее соответствие наблюдается при высокой степени ионизации, большом числе лучей и высокой плотности прививки.
ВВЕДЕНИЕ
Полимерные щетки – монослои, образованные макромолекулами, плотно привитыми к непроницаемой поверхности – уже несколько десятилетий привлекают неослабевающее внимание исследователей. Сильное перекрывание привитых макромолекул и их иммобильность обусловливают значительное по сравнению с их невозмущенным размером растяжение цепей в направлении, перпендикулярном поверхности прививки. Среди уникальных свойств полимерных щеток важное практическое значение имеют барьерные (защита от неспецифической сорбции белков и биологического зарастания поверхностей, стабилизация коллоидных дисперсий) и трибологические свойства (уменьшение силы трения между поверхностями, покрытыми полимерными щетками) [1–5].
Модификация поверхности привитыми полимерами открывает возможности создания “умных” поверхностей, способных реагировать на внешние стимулы (облучение светом, варьирование температуры, состава растворителя и т.д.) изменениями конформаций макромолекул, образующих щетку [6–8]. Благодаря плотной прививке и сильному перекрыванию цепей эти изменения оказываются “согласованными”, что обусловливает хорошо выраженный ответ щетки на внешний стимул. В качестве таких “умных” поверхностей могут выступать смешанные щетки, образованные макромолекулами различной химической природы [9]. В данном случае изменения внешних условий могут повлиять на гидрофильность или гидрофобность поверхности.
Другим классическим примером “умных” или “стимулочувствительных” щеток являются полиэлектролитные щетки, состояние которых можно контролировать изменением ионной силы раствора (концентрацией соли в растворе) или pH – в случае, если щетка образована цепями ионизуемого (pH-чувствительного) полиэлектролита.
Говоря об “умных” и “стимулочувствительных” щетках, стоит отметить и то, что щетка может быть “матрицей” для переключателя на основе внедренной в нее одиночной цепи, отличающейся от образующих щетку цепей по химической природе или/и степени полимеризации. В работах [10–12] рассматривался случай, когда внедренная в щетку цепь могла адсорбироваться на поверхности прививки (а цепи, формирующие щетку, были к ней инертны). Тогда щетка-“матрица” служила своеобразным барьером, расположенным вблизи притягивающей поверхности, что делает адсорбционный переход не плавным, как при обычной адсорбции на плоскости, а резким (при этом, естественно, энергия притяжения звеньев к поверхности, отвечающая адсорбционному переходу, увеличивается по сравнению с таковой в отсутствие барьера).
Большой интерес представляют щетки, у которых к поверхности привиты не линейные, а разветвленные макромолекулы. На возможность использовать макромолекулы сложной разветвленной архитектуры в качестве материала для создания полимерных щеток обратили внимание сравнительно недавно. Теоретически щетки из привитых регулярно разветвленных макромолекул исследуются, начиная с середины 1990-х гг. [13–15]. Развитие методов синтеза регулярно разветвленных макромолекул (в частности, дендронов) и разработка способов их прививки на поверхность дали возможность создавать такие щетки в лаборатории [16]. Кроме того, были получены “дендронизованные полимеры” – аналоги графт-сополимеров, у которых боковые цепи представляют собой регулярно разветвленные дендроны [17, 18].
Привлекательность дендронных щеток заключается в том, что прививая одну макромолекулу (один дендрон) за его корневой спейсер, мы связываем с поверхностью большое количество полимерного материала посредством одной-единственной точки. В то же время толщина щетки лимитируется предельной высотой дендрона. Это дает возможность создавать более тонкие и плотные слои по сравнению со щетками из линейных цепей.
Простейший подход к построению аналитической теории дендронных щеток – использование среднеполевого подхода типа Флори – аналога модели Александера–де Жена [19, 20] для обычной щетки из линейных макромолекул. Он позволяет получить степенные зависимости для основных характеристик щетки – толщины щетки, плотности полимера в щетке, равновесной свободной энергии – от параметров системы (для нейтральной щетки из дендронов с гибкими спейсерами это плотность прививки, длина спейсеров, число генераций, функциональность точек ветвления). Теория такого типа впервые была предложена в работе D. Boris и M. Rubinstein [21] для дендримеров (фактически – сферических дендронных щеток), а обобщена для плоской, сферической и цилиндрической геометрий в работе M. Kröger с соавторами [22]. Существенным моментом при разработке теорий подобного рода было предположение о механизме растяжения спейсеров дендронов. В работе [23] было отмечено, что существуют две предельных возможности растяжения дендронов. В первом случае растягивается только один “максимальный путь” в дендроне, соединяющий его точку прививки к поверхности с одним из свободных концов. В другом предельном случае одинаково растянуты все спейсеры дендронов.
Первая аналитическая теория дендронных щеток, учитывающая неоднородность профиля плотности и неодинаковость растяжения дендронов в щетке была предложена G.T. Picket в 2001 году для плоской щетки [24]. Она основывалась на предположении о том, что мономерные звенья дендронов находятся в поле квадратичного (параболического) самосогласованного потенциала, как и в случае щетки из линейных макромолекул. В этот потенциал входит так называемый топологический коэффициент, зависящий от числа генераций, функциональности точек ветвления и длины спейсеров в дендроне.
Как показал дальнейший анализ, теория, основанная на квадратичном потенциале и бесконечной гауссовой растяжимости спейсеров дендронов, оказывается справедливой лишь в области малых плотностей прививки. Исследования дендронных щеток с помощью численного метода самосогласованного поля Схойтенса–Флира [23] и методов компьютерного моделирования [25, 26] на моделях с конечной растяжимостью полимерных цепей (спейсеров дендронов) позволили установить, что щетки из привитых дендронов имеют нетривиальную внутреннюю структуру. При высокой плотности прививки в щетке происходит разделение дендронов на несколько групп (или “популяций”), различающихся по степени растяжения [23, 26, 27]. Это отчетливо проявляется даже у простейшего представителя класса дендронных щеток – щеток из дендронов первой генерации, или щеток из звезд, привитых за один луч [25, 28]. Для них при высокой плотности прививки в щетке сосуществуют две популяции звезд, а щетка становится двуслойной. Часть звезд имеет сильно, фактически предельно, растянутый луч, за который они привиты к поверхности. Свободные лучи таких звезд направлены от поверхности прививки в сторону растворителя и формируют внешний слой. Остальные звезды растянуты слабо и заполняют внутренний приповерхностный слой щетки. Ниже приведено схематическое изображение щетки из привитых звезд с двухпопуляционной (двуслойной) структурой.
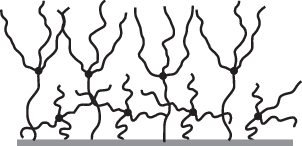
Двухпопуляционная структура щеток из звезд была детально исследована в работах [28–31]. Было установлено, что основной причиной возникновения двухпопуляционной структуры является конечная растяжимость лучей звезд; в предположении о гауссовой (т.е. бесконечной) растяжимости лучей получить двухпопуляционную структуру невозможно.
До недавнего времени исследования дендронных щеток касались в основном незаряженных систем. В то же время несомненный интерес представляют полимерные щетки из разветвленных полиэлектролитов, их исследования начались относительно недавно. В работе О.В. Борисова и Е.Б. Жулиной [32] была развита аналитическая теория дендронных щеток из сильного полиэлектролита. Щетки из дендронов произвольной генерации были рассмотрены в рамках метода скейлинга и модели щетки с однородным профилем плотности. Более детальная теория самосогласованного поля предложена в этой же работе для щеток из дендронов первой генерации, или щеток из полиэлектролитных звезд, привитых к поверхности за один луч. При построении теории предполагалась гауссова упругость лучей звезд, т.е. их бесконечная растяжимость. Как уже указывалось, такой подход не позволяет описать ситуацию с разделением звезд на две популяции, а щетки – на два слоя. Следует отметить, что в полиэлектролитных щетках цепи растянуты более сильно, чем в нейтральных щетках (благодаря осмотическому давлению противоионов в “осмотическом” режиме или перенормировке второго вириального коэффициента в “солевом” режиме), поэтому разделение дендронов на популяции в полиэлектролитной щетке будет еще более выраженным.
Настоящая работа посвящена теоретическому исследованию щеток, образованных привитыми полиэлектролитными звездами (заряженными дендронами первой генерации) с фиксированной степенью ионизации (случай сильного полиэлектролита), в рамках метода самосогласованного поля Схойтенса–Флира и построению “минимальной” теории типа Флори, описывающей конформационные свойства таких щеток. Особое внимание будет уделено формированию “слоистой” двухпопуляционной структуры.
МОДЕЛЬ И МЕТОДЫ ИССЛЕДОВАНИЯ
Исследуемая система
Рассмотрим плоскую щетку из привитых звезд, каждая из которых содержит p лучей из n мономерных звеньев. Размер мономерного звена a примем за единицу длины. Звезды привиты к непроницаемой плоской поверхности с плотностью σ (число звезд на единицу поверхности прививки). Щетка погружена в растворитель, термодинамическое качество которого по отношению к полимеру характеризуется параметром Флори χ. В настоящей работе мы ограничимся рассмотрением случая атермического растворителя, соответствующего χ = 0. Лучи звезд представляют собой линейные цепи полиэлектролитов с фиксированной степенью ионизации лучей α (сильный полиэлектролит). В растворе также присутствуют ионы одновалентной соли, объемная доля которой равна 2Φs.
Аналитическая теория
Согласно картине двухпопуляционной структуры щетки из звезд, звезды в щетке делятся на две группы, или “популяции”. Вблизи поверхности прививки преобладают звезды со слабо растянутыми лучами. Звезды, принадлежащие ко второй популяции, характеризуются сильно растянутым лучом, за который звезда привита к поверхности (“стеблем”), а их свободные лучи направлены к периферии щетки.
Простейшая среднеполевая теория типа Флори для двуслойной щетки из звезд была предложена H. Merlitz с соавторами [29]. Она сочетала в себе элементы модели Александера–де Жена и учет разделения звезд на две популяции (рис. 1а). При этом считалось, что плотность полимера в щетке постоянна, т.е. концентрация полимера в двух слоях была одинаковой (рис. 1б). Другая особенность модели – неучет упругого вклада в свободную энергию от слабо растянутых звезд. Он предполагался пренебрежимо малым по сравнению с аналогичным вкладом от сильно растянутых звезд и с вкладом от объемных взаимодействий (полимер–полимер и полимер–растворитель). Для сильно растянутых звезд учитывалась их конечная растяжимость. Впоследствии авторы работы [29] применили аналогичный аналитический подход для описания и щеток из дендронов второй генерации [33].
Рис. 1.
Два типа звезд в “двухслойной” щетке (а), одноступенчатая (б) и двухступенчатая (в) аппроксимация профиля объемной доли полимера в “двухслойной” щетке из звезд.
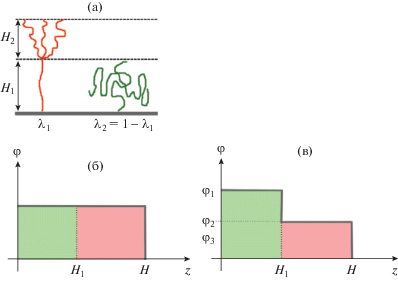
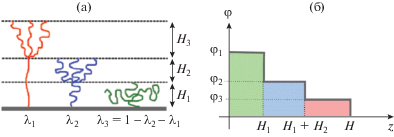
Рис. 2.
Три типа звезд в щетке (а) и трехступенчатая (б) аппроксимация профиля объемной доли полимера в щетке из звезд.
В нашей работе [31] мы использовали подход, развитый в работе [29], внеся в него единственное изменение, а именно, сняв условие постоянства плотности полимера внутри щетки: профиль плотности имел двухступенчатый вид (рис. 1в). Такое различие плотности не означает, что на границе между слоями имеется скачок плотности, оно учитывает различие средней плотности полимера в слоях.
Недостатком модели, построенной в работе [31], был неучет растяжения звезд, относящихся к слабо растянутой популяции. Согласно данным расчетов методом самосогласованного поля [28] и моделирования методами ланжевеновой [25] и броуновской [26] динамики, распределение точек ветвления звезд из условно слабо растянутой популяции оказывается довольно широким (см. также рис. 3 в настоящей работе), так что далеко не все звезды в ней растянуты слабо. Не учитывая растяжения звезд из “приповерхностной” популяции при построении теории, мы тем самым повышаем выгодность нахождения звезд в ней и искусственно уменьшаем долю сильно растянутых звезд. В полиэлектролитных щетках электростатические взаимодействия дополнительно растягивают макромолекулы, образующие щетку, и это требует более аккуратного учета растяжения звезд.
Рис. 3.
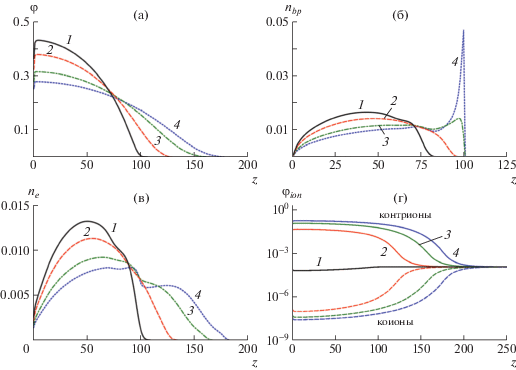
Профиль плотности полимера (а), распределения точек ветвления (б) и концевых групп (в), профили плотности контр- и коионов соли (г) для щетки из полиэлектролитных звезд, привитых с плотностью прививки σ = 0.1, и числом лучей p = 3. Степень ионизации лучей звезд α = 0 (1), 0.1 (2), 0.3 (3) и 0.5 (4). Объемная доля соли в растворе Φs = 10–4. Цветные рисунки можно посмотреть в электронной версии.
Один из способов учесть упругий вклад от слабо растянутых звезд заключается в том, чтобы разделить такие звезды на две группы, выделив у них в отдельный “класс” умеренно растянутые звезды. Таким образом, все звезды в щетке окажутся искусственно разбиты на три группы, а сама щетка – на три части толщиной H1, H2 и H3 (рис. 2a). Будем предполагать, что в пределах каждой из групп звезды растянуты одинаково. Так, для сильно растянутых звезд их точки ветвления расположены на одинаковом расстоянии от поверхности прививки (рис. 2a), равном H1 + H2, а концы свободных лучей – на расстоянии H = H1 + + H2 + H3. Пусть доля таких звезд равна λ1.
Вторая группа звезд – умеренно растянутые звезды. Предположим, что звезды из этой группы растянуты так, что их свободные концы удалены от поверхности прививки на то же расстояние, что и точки ветвления сильно растянутых звезд, H1 + H2, а точки ветвления находятся на расстоянии H1 от поверхности прививки. Обозначим долю таких умеренно растянутых звезд от общего числа звезд λ2.
Наконец, оставшиеся звезды, доля которых составит λ3 = 1 – λ1 – λ2, будем считать по-прежнему очень слабо (незначительно) растянутыми и целиком располагающимися в приповерхностном слое толщиной H1, их вклад в конформационную свободную энергию учитываться не будет.
В соответствии с этим представлением щетка разделяется на три слоя (рис. 2б). В первом слое, примыкающем к поверхности прививки, располагаются очень слабо растянутые звезды, “стебли” умеренно растянутых звезд и часть “стеблей” сильно растянутых звезд. Во втором слое находятся свободные лучи умеренно растянутых звезд и части “стеблей” сильно растянутых звезд. Подчеркнем еще раз, что первый и второй слои – это две части приповерхностного слоя, в которой расположены звезды из популяции со слабо растянутыми лучами [25, 26, 28].
В рамках предложенной модели профиль плотности полимера в щетке имеет трехступенчатый вид: в первом слое толщиной H1 плотность равна φ1, во втором слое толщиной H2 – φ2 < φ1, а во внешнем слое толщиной H3 = H – H1 – H2 она равна φ3 < φ2 < φ1.
С учетом сделанных предположений плотность полимера в слоях дается выражениями
(1)
$\begin{gathered} {{\varphi }_{1}} = \frac{{{{\lambda }_{1}}\left[ {{{H}_{1}}{\text{/}}\left( {{{H}_{1}} + {{H}_{2}}} \right)} \right] + {{\lambda }_{2}} + p{{\lambda }_{3}}}}{{{{H}_{1}}}}~n\sigma = \\ = \sigma \left[ {\frac{{{{\lambda }_{1}}}}{{{{\zeta }_{1}} + {{\zeta }_{2}}}} + \frac{{{{\lambda }_{2}}}}{{{{\zeta }_{1}}}} + \frac{{p{{\lambda }_{3}}}}{{{{\zeta }_{1}}}}} \right] \\ \end{gathered} $(2)
$\begin{gathered} {{\varphi }_{2}} = \frac{{{{\lambda }_{1}}\left[ {{{H}_{2}}{\text{/}}\left( {{{H}_{1}} + {{H}_{2}}} \right)} \right] + \left( {p - 1} \right){{\lambda }_{2}}}}{{{{H}_{2}}}}~n\sigma = \\ = \sigma \left[ {\frac{{{{\lambda }_{1}}}}{{{{\zeta }_{1}} + {{\zeta }_{2}}}} + \frac{{\left( {p - 1} \right){{\lambda }_{2}}}}{{{{\zeta }_{2}}}}} \right] \\ \end{gathered} $(3)
${{\varphi }_{3}} = \frac{{(p - 1){{\lambda }_{1}}}}{{{{H}_{3}}}}~n\sigma = \sigma ~\frac{{(p - 1){{\lambda }_{1}}}}{{{{\zeta }_{3}}}},$Свободная энергия щетки содержит следующие вклады:
Здесь Fconf – конформационная свободная энергия, Fint – вклад от взаимодействия полимер-растворитель, Fsol – вклад, связанный с трансляционной энтропией молекул растворителя, Fion описывает вклад, обусловленный трансляционной энтропией присутствующих в системе подвижных ионов.
Вклад в конформационную свободную энергию Fconf дают только звезды первой и второй групп (сильно и умеренно растянутые). Его легко вычислить, если принять, что “стебель” звезды из i-й группы (i = 1 или 2) растянут под действием силы fi. Тогда каждый из q = p – 1 свободных лучей, которые растянуты равномерно и одинаково, находится под действием силы fi/q, поскольку в точке ветвления должен быть соблюден баланс сил, действующих со стороны “стебля” и свободных лучей. Сила fi таким образом выступает в роли параметра, который удобно использовать для вычисления упругой свободной энергии растянутых звезд. Это означает временный переход в термодинамический ансамбль заданной силы, или силовой ансамбль.
Рассмотрим свободносочлененную цепь на простой кубической решетке, растягиваемую приложенной силой fi, направленной вдоль оси Oz. Статистический вес одного мономерного звена, находящегося в поле силы fi, вычисляется так:
(5)
${{w}_{i}} = {{\lambda }_{z}}{{e}^{{{{f}_{i}}}}} + {{\lambda }_{z}}{{e}^{{ - {{f}_{i}}}}} + {{\lambda }_{{xy}}}{{e}^{0}} = \frac{2}{3} + \frac{1}{3}\cosh {{f}_{i}},$(6)
${{G}_{{stem,~i}}} = - \log {{Z}_{{stem,~i}}} = - n\log \left( {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{i}}} \right)$Среднее расстояние между концами цепи получается дифференцированием свободной энергии Гиббса по силе, которая является параметром, сопряженным расстоянию, поэтому
(7)
${{H}_{1}} = - \frac{{\partial {{G}_{{stem,~2}}}}}{{\partial {{f}_{2}}}} = n~\frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}}$Аналогичным образом получаем свободную энергию Гиббса одного свободного луча звезды, который, как уже было отмечено, находится под действием растягивающей силы fi/q:
(8)
${{G}_{{arm,~i}}} = - n\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{i}}{\text{/}}q} \right)} \right]$Свободная энергия Гиббса одной сильно (i = 1) или умеренно (i = 2) растянутой звезды имеет вид
(9)
$\begin{gathered} {{G}_{i}} = - n\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{i}}} \right] - \\ \, - nq\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{i}}{\text{/}}q} \right)} \right] \\ \end{gathered} $Для перехода от свободной энергии Гиббса G к свободной энергии Гельмгольца F используем преобразование Лежандра: F = G + Hf, где H – среднее расстояние между концами цепи, растягиваемой силой f, связанное со свободной энергией Гиббса: H = –∂G/∂f. В результате конформационная свободная энергия Гельмгольца, учитывающая вклад от звезд двух типов (сильно и умеренно растянутых) имеет вид
(10)
$\begin{gathered} \frac{{{{F}_{{conf}}}}}{n} = {{\lambda }_{1}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{1}}} \right]} \right. - \\ \left. {\, - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{1}}{\text{/}}q} \right)} \right] + \left( {{{\zeta }_{1}} + {{\zeta }_{2}} + {{\zeta }_{3}}} \right){{f}_{1}}} \right\} + \\ \, + {{\lambda }_{2}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{2}}} \right]} \right. - \\ \left. {\, - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh \left( {{{f}_{2}}{\text{/}}q} \right)} \right] + \left( {{{\zeta }_{1}} + {{\zeta }_{2}}} \right){{f}_{2}}} \right\}, \\ \end{gathered} $При этом мы должны также учитывать, что сила f1 растягивает стебель сильно растянутой звезды на расстояние (в приведенных величинах)
что дает условие, связывающее силы f1 и f2:(15)
$\frac{{\sinh {{f}_{1}}}}{{2 + \cosh {{f}_{1}}}} = \frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}} + \frac{{\sinh ({{f}_{2}}{\text{/}}q)}}{{2 + \cosh ({{f}_{2}}{\text{/}}q)}}$Из уравнения (15) можно получить явное выражение зависимости для силы f1 как функции f2:
Здесь
(17)
$A = A({{f}_{2}}) = \frac{{\sinh {{f}_{2}}}}{{2 + \cosh {{f}_{2}}}} + \frac{{\sinh ({{f}_{2}}{\text{/}}q)}}{{2 + \cosh ({{f}_{2}}{\text{/}}q)}}$Свободная энергия взаимодействий полимер-полимер и полимер-растворитель, приходящаяся на одну привитую звезду выражается как
(18)
${{F}_{{int}}} = \mathop \sum \limits_{i = 1}^3 {{n}_{i}}~\chi ~\left( {1 - {{\varphi }_{i}}} \right),$Референтная система: раствор полиэлектролита в равновесии с солевым раствором
Для исследования свойств щеток из привитых полиэлектролитных звезд необходимо учесть соответствующий вклад в свободную энергию щетки, связанный с иммобильными (связанными с полимером) и мобильными (контрионы и ионы диссоциировавшей соли) зарядами. Будем предполагать, что для щетки выполняется условие локальной электронейтральности: внутри щетки удерживаются противоионы, необходимые для нейтрализации зарядов, иммобилизованных на лучах звезд щетки, поэтому щетка в целом остается электронейтральной. Тогда основной вклад в свободную энергию будут вносить осмотическое давление удерживаемых противоионов и энтропия мобильных противоионов. Вне щетки система также будет предполагаться локально электронейтральной.
Для аккуратного вычисления вклада в свободную энергию, связанного с иммобильными и подвижными зарядами, удобно рассмотреть референтную систему, представляющую собой раствор бесконечно длинной цепи ПЭ с фиксированной степенью заряда α, находящуюся в равновесии с раствором одновалентной соли (например, NaCl) [34].
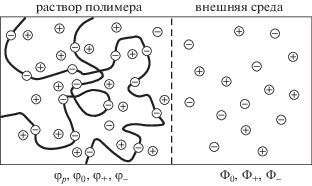
Цепочка располагается в ячейке с полунепроницаемой перегородкой, сквозь которую могут проходить растворитель и подвижные ионы, а полимерная цепи проходить не может. Считаем, что полимерный раствор однородный, объемная доля полимера в этой части ячейки постоянна и равна φp. В растворе также содержатся молекулы растворителя (воды), занимающие долю объема, равную φ0, и положительно и отрицательно заряженные ионы с объемной долей φ+ и φ– соответственно. В рамках решеточной модели будем полагать, что мономерное звено, молекула растворителя, положительно или отрицательно заряженные ионы занимают одну ячейку решетки. Соответственно, должно выполняться условие несжимаемости
Объемные доли положительно и отрицательно заряженных ионов (катионов и анионов) в растворе связаны условием электронейтральности
Во внешней среде полимер отсутствует, там находятся только молекулы растворителя и подвижные ионы, объемная доля которых равна Φ+ и Φ–. Для внешней среды должны выполняться условия электронейтральности
и несжимаемости (Φ0 – объемная доля растворителя во внешней среде). Обозначим Φs = Φ+ = Φ–, тогда Φ0 = 1 – 2Φs.Свободная энергия полимерного раствора представляет собой свободную энергию смешения
(24)
${{F}_{{mix}}} = V{{f}_{{mix}}} = V~~\left[ {f\left( {{{\varphi }_{p}}} \right) - \mathop \sum \limits_i {{\varphi }_{i}}\mu _{i}^{{out}}} \right]$Здесь V – объем системы, занятый полимером, f – плотность свободной энергии в щетке, fmix – плотность свободной энергии смешения в щетке. $\mu _{i}^{{out}}$ – химический потенциал i-го компонента (молекул растворителя и ионов, т.е. i = 0, +, –) во внешней среде, а φi – объемная доля этих компонентов в щетке. Вычитание вкладов в выражении (24) требуется для учета изменения свободной энергии компонентов при их смешении с полимером (при переходе из внешнего раствора в часть, содержащую полимер).
Выражение для плотности свободной энергии в части, занятой полимером, содержит только энтропийные вклады низкомолекулярных компонентов (мы считаем, что дополнительного притяжения или отталкивания между ними не существует, что соответствует нулевому значению параметра Флори χij = 0):
(25)
$f = {{\varphi }_{0}}\log {{\varphi }_{0}} + {{\varphi }_{ + }}\log {{\varphi }_{ + }} + {{\varphi }_{ - }}\log {{\varphi }_{ - }}$Химический потенциал низкомолекулярных компонентов во внешней среде равен $\mu _{i}^{{out}}$ = logΦi (i = 0, +, –). Таким образом, свободная энергия смешения на единицу объема (плотность свободной энергии смешения) есть
(26)
$\begin{gathered} {{f}_{{mix}}} = f - {{{\Phi }}_{0}}\log {{{\Phi }}_{0}} - {{{\Phi }}_{ + }}\log {{{\Phi }}_{ + }} - {{{\Phi }}_{ - }}\log {{{\Phi }}_{ - }} = \\ = {{\varphi }_{0}}\log \frac{{{{\varphi }_{0}}}}{{{{{\Phi }}_{0}}}} + {{\varphi }_{ + }}\log \frac{{{{\varphi }_{ + }}}}{{{{{\Phi }}_{ + }}}} + {{\varphi }_{ - }}\log \frac{{{{\varphi }_{ - }}}}{{{{{\Phi }}_{ - }}}} = \\ = [1 - 2{{\varphi }_{ - }} - (1 + \alpha ){{\varphi }_{p}}]\log \frac{{1 - 2{{\varphi }_{ - }} - (1 + \alpha ){{\varphi }_{p}}}}{{1 - 2{{{\Phi }}_{s}}}} + \\ \, + ({{\varphi }_{ - }} + \alpha {{\varphi }_{p}})\log \frac{{{{\varphi }_{ - }} + \alpha {{\varphi }_{p}}}}{{{{{\Phi }}_{s}}}} + {{\varphi }_{ - }}\log \frac{{{{\varphi }_{ - }}}}{{{{{\Phi }}_{s}}}} \\ \end{gathered} $Это выражение следует минимизировать по φ–: dfmix/dφ– = 0, что приводит к соотношению
(27)
$\frac{{{{\varphi }_{ - }} + \alpha {{\varphi }_{p}}}}{{{{{\Phi }}_{s}}}}~~\frac{{{{\varphi }_{ - }}}}{{{{{\Phi }}_{s}}}} = {{\left[ {\frac{{1 - 2{{\varphi }_{ - }} - (1 + \alpha ){{\varphi }_{p}}}}{{1 - 2{{{\Phi }}_{s}}}}} \right]}^{2}}$Данное условие аналогично условию мембранного равновесия Доннана, оно учитывает собственный объем ионов и представляет собой квадратное уравнение относительно φ–, которое удобно решать, сделав замену φ– = y – αφp/2. Тогда φ+ = y + αφp/2, y = (φ+ + φ–)/2, φ0 = 1 – φp – 2y, и уравнение (27) принимает вид
(28)
$\left[ {{{y}^{2}} - {{{\left( {\frac{{\alpha {{\varphi }_{p}}}}{2}} \right)}}^{2}}} \right]{{(1 - 2{{{\Phi }}_{s}})}^{2}} = {{(1 - {{\varphi }_{p}} - 2y)}^{2}}{\Phi }_{s}^{2}$(29)
$\begin{gathered} (1 - 4{{{\Phi }}_{s}}){{y}^{2}} + 4{\Phi }_{s}^{2}(1 - {{\varphi }_{p}})y - {{(1 - {{\varphi }_{p}})}^{2}}{\Phi }_{s}^{2} - \\ - {{\left( {\frac{{\alpha {{\varphi }_{p}}}}{2}} \right)}^{2}}{{(1 - 2{{{\Phi }}_{s}})}^{2}} = 0 \\ \end{gathered} $Заметим, что зависимость от степени ионизации α содержится только в последнем слагаемом левой части уравнения. Его решение дается соотношением
(30)
$y = y\left( {{{\varphi }_{p}}} \right) = \frac{{\left( {1 - 2{{{\Phi }}_{s}}} \right)\sqrt {{\Phi }_{s}^{2}{{{\left( {1 - {{\varphi }_{p}}} \right)}}^{2}} + {{{\left( {\frac{{\alpha {{\varphi }_{p}}}}{2}} \right)}}^{2}}\left( {1 - 4{{{\Phi }}_{s}}} \right)} - 2{\Phi }_{s}^{2}\left( {1 - {{\varphi }_{p}}} \right)}}{{1 - 4{{{\Phi }}_{s}}}}$Выражение для равновесной плотности свободной энергии получим, учитывая, что
(31)
$\begin{gathered} {{\varphi }_{ - }} = y - \frac{{\alpha {{\varphi }_{p}}}}{2},\quad {{\varphi }_{ + }} = y + \frac{{\alpha {{\varphi }_{p}}}}{2}, \\ {{\varphi }_{0}} = 1 - {{\varphi }_{p}} - 2y \\ \end{gathered} $(32)
$\begin{gathered} {{f}_{{mix}}}\left( {{{\varphi }_{p}}} \right) = \left( {1 - {{\varphi }_{p}} - 2y} \right)\log \frac{{1 - {{\varphi }_{p}} - 2y}}{{1 - 2{{{\Phi }}_{s}}}} + \\ \, + \left( {y - \frac{{\alpha {{\varphi }_{p}}}}{2}} \right)\log \frac{{y - \alpha {{\varphi }_{p}}{\text{/}}2}}{{{{{\Phi }}_{s}}}} + \\ \, + \left( {y + \frac{{\alpha {{\varphi }_{p}}}}{2}} \right)\log \frac{{y + \alpha {{\varphi }_{p}}{\text{/}}2}}{{{{{\Phi }}_{s}}}} = \\ = \left( {1 - {{\varphi }_{p}}} \right)\log \frac{{1 - {{\varphi }_{p}} - 2y}}{{1 - 2{{{\Phi }}_{s}}}} + \frac{{\alpha {{\varphi }_{p}}}}{2}\log \frac{{y + \alpha {{\varphi }_{p}}{\text{/}}2}}{{y - \alpha {{\varphi }_{p}}{\text{/}}2}} \\ \end{gathered} $Это выражение включает в себя вклады трансляционной энтропии мобильных ионов и молекул растворителя (то есть, вклады Fion и Fsol в выражении (4) для свободной энергии щетки).
Свободная энергия щетки из полиэлектролитных звезд с фиксированным зарядом
Таким образом, свободная энергия щетки из ПЭ звезд дается выражением
(33)
$\begin{gathered} \frac{F}{n} = {{\lambda }_{1}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{1}}} \right]} \right. - \\ \,\left. { - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh ({{f}_{1}}{\text{/}}q)} \right] + ({{\zeta }_{1}} + {{\zeta }_{2}} + {{\zeta }_{3}}){{f}_{1}}} \right\} + \\ \, + {{\lambda }_{2}}\left\{ { - \log \left[ {\frac{2}{3} + \frac{1}{3}\cosh {{f}_{2}}} \right]} \right. - \\ \left. {\, - q\log \left[ {\frac{2}{3} + \frac{1}{3}\cosh ({{f}_{2}}{\text{/}}q)} \right] + ({{\zeta }_{1}} + {{\zeta }_{2}}){{f}_{2}}} \right\} + \\ \, + \sum\limits_{i = 1}^3 {\frac{{{{\zeta }_{i}}}}{\sigma } \cdot \left[ {(1 - {{\varphi }_{i}})\log \frac{{1 - {{\varphi }_{i}} - 2y({{\varphi }_{i}})}}{{1 - 2{{\Phi }_{s}}}} + } \right.} \\ \left. { + \frac{{\alpha {{\varphi }_{i}}}}{2}\log \frac{{y({{\varphi }_{i}}) + \alpha {{\varphi }_{i}}{\text{/}}2}}{{y({{\varphi }_{i}}) - \alpha {{\varphi }_{i}}{\text{/}}2}} + \chi \cdot (1 - {{\varphi }_{i}})} \right], \\ \end{gathered} $Свободная энергия щетки F оказывается функцией четырех переменных: f1, λ1, f2 и λ2, при этом переменные f1 и f2 связаны условием (15). Минимизация свободной энергии проводилась численно, с помощью введения множителя Лагранжа, связанного с условием (15).
Численный метод самосогласованного поля Схойтенса–Флира
В настоящей работе использовался численный метод самосогласованного поля Схойтенса–Флира, широко применяемый для моделирования привитых полимерных слоев – полимерных щеток. Метод Схойтенса–Флира и его модификации для исследования полимерных щеток разного типа был неоднократно описан в литературе, поэтому в настоящей работе мы позволим себе опустить подробное описание этого метода, которое можно найти, например, в монографии [35]. Особенности реализации метода самосогласованного поля для щеток из привитых звезд описаны в работе [28].
Для решения задачи о плоской щетке используют так называемый одноградиентный вариант метода Схойтенса–Флира, основанный на предположении, что щетка латерально однородна, и x- и y-компоненты градиента объемной доли полимера, параллельные плоскости прививки цепей, равны нулю, не равна нулю только z-компонента градиента плотности, перпендикулярная плоскости. Это означает, что плотность полимера является только функцией z: φ = φ(z). Электростатические взаимодействия в системе учитываются в рамках уравнения Пуассона–Больцмана [36].
В настоящей работе вычисления проводились с использованием программы SFBox, разработанной в Университете г. Вагенинген (Нидерланды), которая позволяет получить распределения плотности полимера в целом и отдельных сегментов, включая точки ветвления и концевые группы, а также интегральные термодинамические характеристики, например свободную энергию. Важно, что при этом не нужно делать никаких предположений о характере конформаций звезд в щетке, вводя соответствующие модельные упрощения, к чему приходится прибегать при построении аналитической теории.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Результаты численного моделирования методом самосогласованного поля
В расчетах методом самосогласованного поля, результаты которых представлены в настоящей работе, исследовали щетки из звезд, содержащих лучи из n = 100 звеньев, погруженные в атермический растворитель, которому соответствует нулевое значение параметра Флори χ = 0. Рассмотрим щетку из трехлучевых звезд (p = 3) с постоянной плотностью прививки (σ = 0.1), помещенную в раствор с низкой концентрацией соли (Φs = 10–4). На рис. 3а показана эволюция профиля концентрации полимера в щетке φ(z) при варьировании степени ионизации привитых звезд, где z – расстояние от поверхности прививки. Плотность полимера в щетке монотонно спадает от поверхности прививки к периферии. По мере роста степени ионизации увеличивается толщина щетки (расстояние от плоскости прививки z, при котором плотность обращается в нуль), уменьшаются максимальное значение плотности у поверхности прививки и средняя плотность полимера в щетке. Таким образом, можно сделать вывод об общем увеличении растяжения звезд в щетке в направлении, перпендикулярном плоскости прививки, при росте степени ионизации лучей.
Более детальный анализ структуры щетки позволяет получить распределения точек ветвления звезд (nbp) и концевых групп свободных лучей (ne). Для сравнения этих распределений для щеток при разной плотности прививки их удобно нормировать на единицу и представлять в виде
(34)
${{n}_{{bp}}}(z) = \frac{{{{\varphi }_{{bp}}}(z)}}{\sigma },\quad {{n}_{e}}(z) = \frac{{{{\varphi }_{e}}(z)}}{{\left( {p - 1} \right)\sigma }},$На рис. 3б показана эволюция распределения точки ветвления с увеличением плотности заряда на лучах полиэлектролитных звезд. В нейтральной звезде распределение фактически унимодально – имеется один выраженный максимум и небольшое плечо справа. Увеличение степени ионизации лучей α приводит к уширению распределения, что соответствует общей вытяжке цепей и росту толщины щетки, и превращению правого плеча в полноценный максимум, высота и острота которого растут с увеличением α. Положение максимума ограничено справа значением z = n = 100, что отвечает полному растяжению “стебля”. При этом протяженная приповерхностная часть распределения никуда не исчезает, в ней не образуются “мертвые зоны”.
Очень похожие изменения происходят и с распределением концов (рис. 3в): в отсутствие зарядов на лучах имеется один максимум и небольшое “плечо”, которое с повышением степени ионизации становится более выраженным и превращается в максимум, а ширина распределения в целом с ростом α увеличивается.
Такой вид распределений концов и точек ветвления соответствует, как было установлено в работе [23] и доказано в работе [28], разделению звезд в щетке на две популяции: имеется часть звезд с сильно, предельно растянутым стеблем, чему соответствует острый максимум справа на распределении точек ветвления nbp(z) на рис. 3б, и свободными лучами звезд, направленными в растворитель, что отвечает периферийной части распределения ne(z) на рис. 3в. В то же время в щетке имеется и другая популяция звезд, которые растянуты относительно слабо — им отвечают протяженные части профилей распределения точек ветвления и концов, которые начинаются у поверхности прививки. Число звезд с сильно растянутым стеблем растет при повышении степени ионизации, что связано с увеличением количества удерживаемых в щетке противоионов (рис. 5г) и ростом осмотического давления, которое растягивает щетку.
Рис. 4.
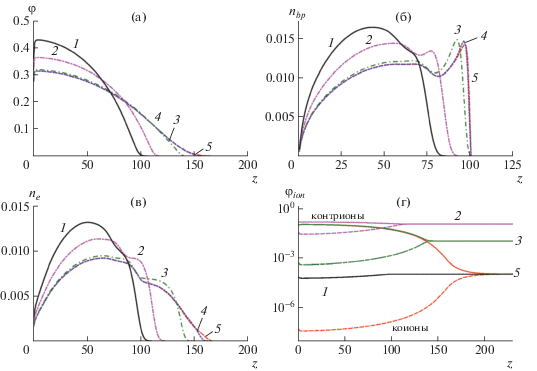
Профиль плотности полимера (а), распределения точек ветвления (б) и концевых групп (в), профили плотности контр- и коионов соли (г) для полиэлектролитной щетки из звезд с числом лучей p = 3. Степень ионизации лучей α = 0 (1) и 0.3 (2–5); плотность прививки σ = 0.1; концентрация соли Φs = 10–1 (2), 10–2 (3), 10–3 (4) и 10–4 (1, 5).
Влияние концентрации соли на структуру щетки из звезд
Влияние концентрации соли на структуру полиэлектролитной щетки из звезд иллюстрирует рис. 4, где представлены результаты для щетки из трехлучевых звезд p = 3 с фиксированной степенью ионизации лучей α = 0.3.
Из профиля плотности полимера (рис. 4a) следует, что с увеличением концентрации соли щетка становится плотнее и ее высота уменьшается. Это связано с тем, что происходит экранировка заряда лучей звезд: число контр- и коионов соли снаружи и внутри щетки растет (рис. 4г). На рис. 4б и 4в также видны бимодальные распределения точек ветвления и концевых групп соответственно, что свидетельствует о разделении звезд на две популяции, особенно при малых концентрациях соли.
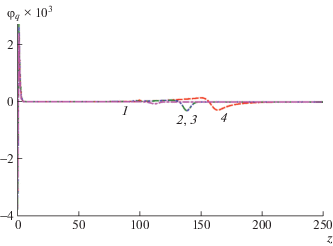
Чтобы проверить выполнение условия локальной электронейтральности в щетке, было рассчитано распределение плотности заряда в системе: φq(z) = αφ(z) + φ–(z) – φ+(z). Как следует из рис. 5, плотность локального заряда в щетке равна нулю, и лишь незначительные, но скомпенсированные отклонения от нуля наблюдаются на границах щетки: возле поверхности прививки звезд и на периферии.
Выше мы описали двухпопуляционную структуру щетки из звезд с использованием различных распределений полимера в системе: профиля плотности полимера, а также распределений точек ветвления и концов. Для характеристики структуры щетки удобно использовать и ее интегральные характеристики, такие как средняя плотность полимера в щетке и доля сильно вытянутых звезд, которые позволяют установить общие закономерности поведения щеток при изменении тех или иных внешних параметров.
Поскольку на существование двухпопуляционной структуры щетки указывают как распределение точек ветвления, так и распределение концов, можно предложить два способа определения доли сильно вытянутых звезд в щетке λ1 (рис. 1а и 2а). Используя нормированные распределения, λ1 можно вычислить следующим образом:
где j = bp или e (точки ветвления или концы), а нижний предел суммирования z = zmin, j соответствует правому минимуму на кривой nj(z). Величина λ, рассчитанная из распределения точек ветвления (j = bp), есть доля звеньев с сильно растянутым “стеблем”, а λ1, найденная из распределения концов (j = e), имеет смысл доли звезд, образующих внешнюю “щетку”, с лучами, направленными в сторону периферии. В работе [28] было показано, что для нейтральных щеток оба способа дают одинаковое значение λ1. Это свидетельствует о том, что лучи, направленные в сторону периферии щетки, принадлежат звездам с сильно растянутым “стеблем”, что подтверждает предложенную картину двух популяций звезд в щетке. В случае щетки из полиэлектролитных звезд определение λ1 двумя способами также дает одинаковые значения.Еще одна интегральная характеристика, средняя плотность полимера в щетке φ, может быть получена из профиля плотности полимера φ(z):
(36)
$\varphi = \frac{{\sum\limits_z^{} {\varphi (z)\varphi (z)} }}{{\sum\limits_z^{} {\varphi (z)} }}$Результаты вычисления этих характеристик по данным моделирования методом самосогласованного поля и сравнение с результатами, получаемыми с помощью численного решения уравнений аналитической теории, развитой в предыдущих разделах, будут представлены ниже.
Влияние степени ионизации на структуру щетки из звезд
На рис. 6 и 7 представлены зависимости объемной доли полимера и доли сильно вытянутых звезд λ1 от плотности прививки звезд для щеток из трех- и пятилучевых звезд, полученные при низкой (Φs = 10–4) и высокой (Φs = 0.1) концентрации соли. Отметим, во-первых, что диапазон изменения плотности прививки здесь ограничен сверху значением, меньшим единицы. Это максимально возможное значение плотности прививки, при котором плотность полимера в щетке максимальна, а сама щетка не содержит молекул растворителя. В данном случае в объеме щетки, приходящемся на одну звезду (V = H/σ), находится сама звезда и удерживаемые ей противоионы, с целью выполнения условия электронейтральности, т.е. V = (1 + α)pn. Приравнивая выражения для объема, получаем зависимость высоты не содержащей растворителя щетки от плотности прививки: H = N(1 + α)σ, где N = np – полное число мономерных звеньев в звезде. Максимально возможное значение высоты щетки равно удвоенной длине луча: Hmax = 2n, поэтому максимально допустимая плотность прививки полиэлектролитных звезд со степенью ионизации α к поверхности щетки равна
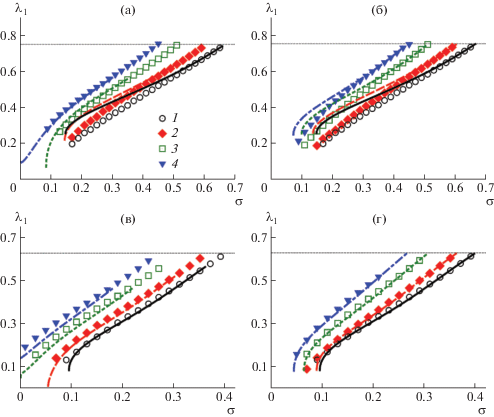
Рис. 6.
Зависимости средней объемной доли полимера φ от плотности прививки σ в щетках из звезд с р = 3 (а, б) и 5 (в, г). Степень ионизации лучей звезд α = 0 (1), 0.1 (2), 0.3 (3) и 0.5 (4); Φs = 10–4 (а, в) и 10–1 (б, г). Точки – результаты численного моделирования, кривые – результаты теории.
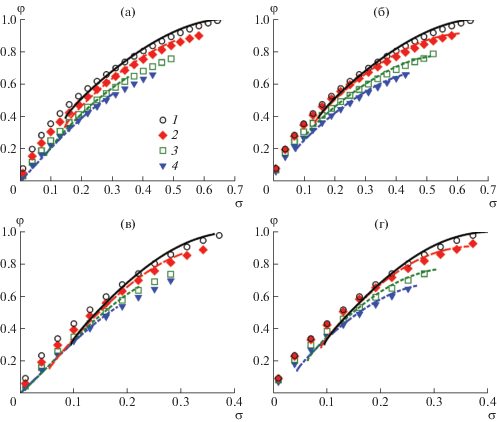
Рис. 7.
Зависимости доли сильно вытянутых звезд λ1 с р = 3 (а, б) и 5 (в, г) от плотности прививки σ. Степень ионизации лучей звезд α = 0 (1), 0.1 (2), 0.3 (3) и 0.5 (4); Φs = 10–4 (а, в) и 10–1 (б, г); λmax = 0.75 (а, б) и 0.624 (в, г). Точки – результаты численного моделирования, кривые – результаты теории. Горизонтальная линия показывает максимально возможное значение доли сильно растянутых звезд.
Приведенное выражение можно переписать в более общем виде для щетки из регулярно разветвленных дендронов произвольной генерации из одинаковых спейсеров $~{{\sigma }_{{max}}} = \mathcal{N}{\text{/}}[N(1 + \alpha )]$, где $\mathcal{N}$ – число мономерных звеньев в максимальном пути, соединяющем точку прививки дендрона к поверхности с любой из его концевых групп (для звезды $\mathcal{N} = 2n$), а N – полное число звеньев в дендроне (для звезды N = np). Величина максимально допустимой плотности прививки уменьшается с ростом α, поскольку при этом увеличивается число контрионов, которые должны удерживаться в щетке, для чего требуется дополнительный объем.
Максимальной плотности прививки отвечает средняя объемная доля полимера, равная φmax = = 1/(1 + α), и доля звезд с предельно растянутым стеблем λ1(σmax) = p/[2(p – 1)] [30], не зависящая от степени ионизации α.
При повышении плотности прививки средняя плотность полимера и доля сильно растянутых звезд в щетке растут – вследствие уплотнения щетки звезды вынуждены располагаться на ее периферии. К аналогичным эффектам приводит и увеличение числа лучей в привитых звездах. Доля сильно растянутых звезд также растет и с повышением степени ионизации, хотя средняя плотность полимера уменьшается. Это связано с увеличением числа удерживаемых в щетке противоионов и, как следствие, ростом осмотического давления, которое приводит к растяжению всех звезд, что также способствует переходу звезд в верхнюю популяцию. Повышение концентрации соли в растворе вызывает экранировку заряда и уменьшение растяжения и набухания звезд в щетке и, как следствие, уменьшение λ1. Отметим, что результаты аналитической теории количественно хорошо согласуются со значениями средней плотности полимера, полученными из данных численных расчетов методом самосогласованного поля. Такое согласие тем лучше, чем сильнее растянуты звезды в щетке (т.е. чем выше плотность прививки, число лучей звезд, степень ионизации и чем ниже концентрация соли).
О необходимости учета растяжения звезд из слабо растянутой популяции
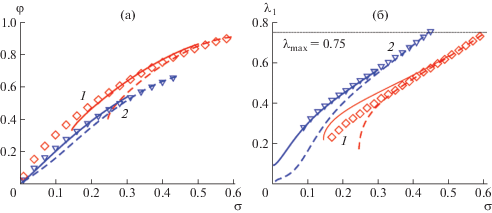
В настоящей работе была развита теория, описывающая двухпопуляционную структуру щеток из привитых полиэлектролитных звезд. Она основана на трехступенчатой аппроксимации профиля плотности и разделении звезд, образующих щетку, на три группы с целью учета упругой свободной энергии звезд, принадлежащих к слабо растянутой популяции (рис. 2). В более ранних теориях, основанных на одно- (рис. 1a, [29]) и двухступенчатой (рис. 1б, [31]) аппроксимации профиля плотности и разделения звезд на две группы, соответствующей разделению на две популяции, растяжением слабо растянутых звезд пренебрегали. Понятно, что теорию для щеток из полиэлектролитных звезд можно строить, основываясь на этой, более простой модели. Такие расчеты были проведены и в рамках настоящего исследования. Зависимости, приведенные на рис. 8, показывают, что модель с двухступенчатой аппроксимацией профиля и неучетом упругого вклада слабо растянутых звезд оказывается недостаточной для адекватного описания щеток из полиэлектролитных звезд. В первую очередь это касается случая низкой концентрации соли и высокой степени ионизации, когда электростатические эффекты проявляются сильнее. Очевидно, что модель с трехступенчатой аппроксимацией профиля плотности вполне ожидаемо дает более точную оценку для средней объемной доли полимера в щетке. Кроме того, она приводит к более высокому значению доли сильно растянутых звезд, поскольку частичный учет упругой энергии слабо растянутых звезд уменьшает выгодность этой популяции по сравнению с “двухступенчатой” моделью.
Рис. 8.
Зависимости средней объемной доли полимера φ (а) и доли сильно вытянутых звезд λ1 (б) из трех лучей от плотности прививки σ при степени ионизации лучей звезд α = 0.1 (1) и 0.5 (2) в щетке, погруженной в раствор с низкой концентрацией соли Φs = 10–4. Точки – результаты численного моделирования, кривые – результаты теории, для моделей с двух- (штриховые линии) и трехступенчатой (сплошные линии) аппроксимацией профиля плотности.
ЗАКЛЮЧЕНИЕ
Настоящая работа посвящена теоретическому исследованию плоской щетки из привитых полиэлектролитных звезд с фиксированной степенью ионизации мономерных звеньев лучей, погруженной в раствор соли. Известно, что характерной особенностью щеток из звезд является формирование в них слоистой структуры с разделением звезд на две популяции, поэтому такому эффекту и влиянию на него степени заряженности лучей и концентрации соли в системе было уделено особое внимание. Систему исследовали в рамках двух подходов: с одной стороны, было проведено моделирование с помощью численного метода самосогласованного поля Схойтенса–Флира, который позволяет получить детальную информацию о структуре щетки в виде распределений плотности полимера, точек ветвления, концевых групп, мобильных катионов и анионов. С другой стороны, была развита простая аналитическая теория типа Флори с трехступенчатой аппроксимацией профиля плотности полимера в щетке и выделением трех групп звезд в щетке – сильно, умеренно и слабо растянутых. Электростатические эффекты были учтены в теории в рамках приближения локальной электронейтральности, корректность такого приближения была подтверждена результатами моделирования методом самосогласованного поля. Для вычисления вклада в свободную энергию, связанную с энтропией мобильных ионов, была рассмотрена референтная система – одиночная бесконечно длинная цепь полиэлектролита, находящаяся в растворе в равновесии с внешней средой. При построении теории также явно учитывался конечный объем ионов.
Было показано, что росту числа звезд с предельно растянутым лучом, за который звезда прививается к поверхности способствует увеличение плотности прививки, числа лучей или степени ионизации лучей. В последнем случае средняя плотность щетки уменьшается, а в первых двух – увеличивается. Показано, что теория хорошо описывает результаты моделирования методом самосогласованного поля, наилучшее соответствие наблюдается при высокой степени ионизации, при большом числе лучей и при высокой плотности прививки – как раз в той области параметров численные вычисления методом самосогласованного поля становятся более трудоемкими. Развитый подход может быть обобщен на случай щетки, образованной ионизуемыми (pH-чувствительными) звездами и на другой тип решеточной или континуальной модели для образующих щетку макромолекул.
Авторы благодарят профессора Ф.А.М. Леермакерса (Университет Вагенингена, Нидерланды) за возможность использования программы “SFBox” для проведения численных расчетов методом самосогласованного поля.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 17-03-01115-а).
Список литературы
Napper D.H. // Polymeric Stabilization of Colloidal Dispersions. London: Acad. Press, 1985.
Gon S., Kumar K.N., Nüsslein K., Santore M.M. // Macromolecules. 2012. V. 45. № 20. P. 8373.
Higaki Y., Okazaki R., Takahara A.// ACS Macro Lett. 2012. V. 1. № 9. P. 1124.
Wen Y., Guo X., Kalasin S., Santore M.M. // Langmuir. 2014. V. 30. № 8. P. 2019.
Bates C.M., Chang A.B., Momčilović N., Jones S.C., Grubbs R.H. // Macromolecules. 2015. V. 48. № 14. P. 4967.
Azzaroni O. // J. Polym. Sci., Polym. Chem. 2012. V. 50. № 16. P. 3225.
Akkilic N., de Vos W.M. // Switchable and Responsive Surfaces and Materials for Biomedical Applications, Oxford: Woodhead Publ., 2015. P. 119.
Cheesman B.T., Neilson A.J.G., Willott J.D., Webber G.B., Edmondson S., Wanless E.J. // Langmuir. V. 29. № 20. P. 6131.
Motornov M., Sheparovych R., Katz E., Minko S. // ACS Nano. 2008. V. 2. № 1. P. 41.
Skvortsov A.M., Gorbunov A.A., Leermakers F.A.M., Fleer G.J. // Macromolecules. 1999. V. 32. № 6. P. 2004.
Klushin L.I., Skvortsov A.M., Polotsky A.A., Qi S., Schmid F. // Phys. Rev. Lett. 2014. V. 113. № 6. P. 068303.
Qi S., Klushin L.I., Skvortsov A.M., Polotsky A.A., Schmid F. // Macromolecules. 2015. V. 48. № 11. P. 3775.
Zhulina E.B., Vilgis T.A. // Macromolecules. 1995. V. 28. № 4. P. 1008.
Carignano M.A., Szleifer I. // Macromolecules. 1994. V. 27. № 3. P. 702.
Irvine D.J., Mayes A.M., Griffith-Cima L. // Macromolecules. 1996. V. 29. № 18. P. 6037.
Gillich T., Benetti E.M., Rakhmatullina E., Konradi R., Li W., Zhang A., Schlüter A.D., Textor M. // J. Am. Chem. Soc. 2011. V. 133. № 28. P. 10940.
Schlüter A.D. // Functional Molecular Nanostructures. Berlin; Heidelberg: Springer, 2005. P. 151.
Schlüter A.D., Halperin A., Kröger M., Vlassopoulos D., Wegner G., Zhang B. // ACS Macro Lett. 2014. V. 3. № 10. P. 991.
Alexander S. // J. phys. (Paris). 1977. V. 38. № 8. P. 983.
De Gennes P.-G. // Macromolecules. 1980. V. 13. № 5. P. 1069.
Boris D., Rubinstein M. // Macromolecules. 1996. V. 29. № 22. P. 7251.
Kröger M., Peleg O., Halperin A. // Macromolecules. 2010. V. 43. № 14. P. 6213.
Polotsky A.A., Gillich T., Borisov O.V., Leermakers F.A.M., Textor M., Birshtein T.M. // Macromolecules. 2010. V. 43. № 22. P. 9555.
Picket G.T. // Macromolecules. 2001. V. 34. № 25. P. 8784.
Merlitz H., Wu C.-X., Sommer J.-U. // Macromolecules. 2011. V. 44. № 17. P. 7043.
Gergidis L.N., Kalogirou A., Vlahos C. // Langmuir. 2012. V. 28. № 49. P. 17176.
Borisov O.V., Polotsky A.A., Rud O.V., Zhulina E.B., Leermakers F.A.M., Birshtein T.M. // Soft Matter. 2014. V. 10. № 13. P. 2093.
Polotsky A.A., Leermakers F.A.M., Zhulina E.B., Birshtein T.M. // Macromolecules. 2012. V. 45. № 17. P. 7260.
Merlitz H., Wu C.-X., Sommer J.-U. // Macromolecules. 2013. V. 46. № 3. P. 1248.
Zhulina E.B., Amoskov V.M., Polotsky A.A., Birshtein T.M. // Polymer. 2014. V. 55. № 20. P. 5160.
Polotsky A.A., Misorin A.K., Zhulina E.B., Birshtein T.M. // Macromol. Symp. 2015. V. 348. № 1. P. 33.
Borisov O.V., Zhulina E.B. // Macromolecules. 2015. V. 48. № 5. P. 1499.
Cui W., Su C.-F., Merlitz H., Wu C.-X., Sommer J.-U. // Macromolecules. 2014. V. 47. № 11. P. 3645.
Amoskov V.M., Birshtein T.M., Mercurieva A.A. // Macromol. Theory Simul. 2006. V. 15. № 1. P. 46.
Fleer G.J., Cohen Stuart M.A., Scheutjens J.M.H.M., Cosgrove T., Vincent B. // Polymers at Interfaces. London: Chapman and Hall, 1993.
Israels R., Leermakers F.A.M., Fleer G.J., Zhulina E.B. // Macromolecules. 1994. V. 27. № 12. P. 3249.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)