Высокомолекулярные соединения (серия А), 2020, T. 62, № 3, стр. 220-226
ОСОБЕННОСТИ ТРАНСПОРТА ЭЛЕКТРОНОВ В ПОЛИЭТИЛЕНТЕРЕФТАЛАТЕ
А. П. Тютнев a, *, В. С. Саенко a, А. Д. Жадов a, Е. А. Крук a
a Национальный исследовательский университет “Высшая школа экономики”
101000 Москва, Мясницкая ул., 20, Россия
* E-mail: aptyutnev@yandex.ru
Поступила в редакцию 12.06.2019
После доработки 27.09.2019
Принята к публикации 09.12.2019
Аннотация
Проведено экспериментальное изучение транспорта электронов путем измерения импульсной радиационной электропроводности полиэтилентерефталата при объемном облучении образцов полимера импульсами быстрых электронов в режиме малого сигнала. Численное моделирование эксперимента выполнено с использованием модели многократного захвата с экспоненциальным распределением ловушек по энергии. Показано, что пролет электронов в условиях эксперимента отсутствует, вопреки сложившейся в литературе трактовке этого явления. В действительности дисперсионный транспорт электронов в ПЭТФ происходит в присутствии мономолекулярного захвата на глубокие ловушки биографического происхождения.
Полиэтилентерефталат до настоящего времени широко применяется в качестве материала экранно-вакуумной теплоизоляции низкоорбитальных космических аппаратов. Такие материалы должны обладать пониженной способностью к накоплению объемных зарядов, которые создают сильные электрические поля, что приводит к возникновению электростатических разрядов и, в конечном счете, к отказам в работе бортовой электроники космических аппаратов.
Основной параметр, контролирующий величину электрического поля в объеме полимера при его облучении электронами, – электрическая проводимость этого полимера. Электрическая проводимость в данном случае является суммой двух слагаемых: темновой электропроводности и радиационной электропроводности. Так как ПЭТФ – хороший диэлектрик, основным параметром для релаксации заряда служит его радиационная электропроводность. Настоящая работа посвящена исследованию радиационной электропроводности ПЭТФ. Общие свойства радиационной электропроводности технических полимеров, таких как ПС, ПЭВД, ПТФЭ, минералнаполненные пенополимеры рассмотрены в нашей монографии [1]. Радиационная электропроводность ПЭТФ изучалась в целом ряде работ [2–7]. Было показано, что радиационная электропроводность в этом полимере обладает целым рядом особенностей, выделяющих его среди других.
Радиационная электропроводность, как известно, используется в качестве основного метода изучения транспорта основных носителей заряда в полимерах. Радиационная электропроводность ПЭТФ во многих отношениях подобна электропроводности в указанных выше технически важных полимерах [1]. Но ряд особенностей выделяют этот полимер среди других. Подвижными носителями заряда в ПЭТФ являются электроны, а не дырки, как в упомянутых выше полимерах. Спад тока после окончания импульса облучения следует степенному закону $j(t) \propto {{t}^{{ - 1.5}}}$ (обычно показатель степени не превышает единицы). Кроме того, при непрерывном облучении с постоянной мощностью дозы легко реализуется ситуация, при которой радиационная электропроводность просто постоянна на протяжении всего времени облучения, достигающего нескольких сотен секунд [8]. Для объяснения двух последних особенностей в цитируемой работе предложена полуколичественная теория, основанная на эффекте пролета электронами пленки полимера в приложенном электрическом поле. Предполагая, что дисперсионный параметр $\alpha $ для электронов равен 0.5, авторам цитируемой работы удалось объяснить обе упомянутые выше особенности его радиационной электропроводности.
Однако все не так однозначно. В нашей недавней работе [9] показано, что несмотря на то, что отмеченные особенности радиационной электропроводности ПЭТФ действительно имеют место, в количественном отношении предложенное в работе [8] описание противоречиво. Нами предложен альтернативный подход к рассматриваемой проблеме, опирающийся на концепцию мономолекулярного захвата электронов в дисперсионном режиме транспорта. Однако этот подход не получил еще детального экспериментального подтверждения.
Задача настоящей работы состоит в проведении дополнительных экспериментальных и теоретических исследований, подтверждающих нашу точку зрения.
ОБЩИЕ ПОЛОЖЕНИЯ
Для описания радиационной электропроводности полимеров применена концепция многократного захвата, основанная на квазизонном механизме подвижности радиационно-генерированных носителей заряда [1]. Тот факт, что в ряде полимеров реализуется прыжковый транспорт, не должен приводить к недоразумению, поскольку концепция транспортного уровня позволяет разрешить эту проблему [10, 11].
Основные уравнения этой модели имеют следующий вид и не зависят от конкретного типа рассматриваемой задачи [1]:
(1)
$\partial \rho {\text{/}}\partial t = ({{N}_{0}}{\text{/}}{{\tau }_{0}})\left[ {M(E) - \rho } \right]{\text{/}}{{M}_{0}} - \rho {{\nu }_{0}}\exp \left( { - \frac{E}{{kT}}} \right)$Здесь $N$ − полная концентрация электронов, ${{N}_{0}}$ − их концентрация в проводящем состоянии с подвижностью ${{\mu }_{0}}$ и временем жизни ${{\tau }_{0}}$. Плотность распределения захваченных электронов описывается функцией $\rho (E)$, $M(E)$ − плотность распределения ловушек по энергии $E \geqslant 0$ (их полная концентрация ${{M}_{0}}$). Частотный фактор равен ${{\nu }_{0}}$. И, наконец, $T$ – температура, $k$ – постоянная Больцмана. В соответствии с основными положениями модели многократного захвата параметры ${{\tau }_{0}}$ и ${{\nu }_{0}}$ считаются постоянными величинами, не зависящими от энергии ловушек E.
Рассматривается экспоненциальное распределение ловушек по энергии
где ${{E}_{0}}$ – параметр распределения. Важный в теории дисперсионный параметр $\alpha $ = $kT{\text{/}}{{E}_{0}}$.Традиционно используется одномерное приближение (координата $x$ отсчитывается от облучаемого электрода и направлена вглубь полимерного слоя нормально к его поверхности). Малосигнальный режим облучения позволяет не учитывать объемную рекомбинацию носителей заряда, считать электрическое поле в образце постоянным и однородным. Таким образом, система уравнений (1), (2) линеаризуется. В умеренно сильных электрических полях (≥106 В/м) можно пренебречь вкладом в регистрируемый ток диффузионной компоненты тока проводимости. Таким образом, в общем случае величины $N$ и ${{N}_{0}}$ зависят от координаты и времени, а $\rho $ дополнительно зависит и от энергии ловушек.
Плотность тока $j(t)$, измеряемого во внешней цепи, равна ($e$ – элементарный электрический заряд и L – толщина полимерного слоя)
В настоящей работе рассматриваются две наиболее распространенные постановки радиационного эксперимента. В первой скорость генерации носителей заряда ${{g}_{0}}$ однородна и постоянна, так что и концентрация электронов оказывается не зависящей от координаты. Уравнение непрерывности используется в следующем виде:
Здесь ${{k}_{{rec}}}$ – коэффициент объемной рекомбинации квазисвободных электронов с неподвижными дырками (условие квазинейтральности требует равенства полных концентраций электронов и дырок). Выражение (4) упрощается и принимает вид $j(t) = {{N}_{0}}(t){{\mu }_{0}}{{F}_{0}}e$.
Вторая постановка задачи предполагает выход электронов на тянущий электрод (времяпролетный эксперимент) и соответственно уравнение непрерывности видоизменяется:
(6)
$\partial N(x,t){\text{/}}\partial t + {{\mu }_{0}}{{F}_{0}}\partial {{N}_{0}}(x,t){\text{/}}\partial x = {{g}_{0}}$В этом уравнении пренебрегается рекомбинационными потерями электронов (малосигнальный режим облучения).
В литературе разработаны приближенные аналитические формулы для случая импульсного малосигнального облучения с постоянной мощностью дозы (${{g}_{0}} = {\text{const}}$) [1]. К сожалению, еще только предстоит разработать программу численного счета переходного тока при одновременном учете времяпролетных и рекомбинационных эффектов. В настоящей работе для оценки эффектов рекомбинации использована модель Роуза–Фаулера–Вайсберга с уравнением непрерывности в виде выражения (5). При анализе эффектов пролета и мономолекулярного захвата мы применили аналитические формулы, предложенные в работе [12]. К сожалению, в них вкралась неточность, поэтому ниже они приведены в исправленном виде:
(7)
$j(t) = \left\{ \begin{gathered} e{{g}_{0}}Lp(t),\quad t < {{t}_{p}} \hfill \\ e{{g}_{0}}L[p(t) - p(t - {{t}_{p}})],\quad t \geqslant {{t}_{p}} \hfill \\ \end{gathered} \right.$В присутствии мономолекулярного захвата с постоянной времени ${{\tau }_{c}}$ формулы (7) по-прежнему справедливы, но вид $\tau $-функции изменяется: ${{\tau }_{\Sigma }}(t) = \tau (t){{\tau }_{c}}{\text{/}}\left[ {\tau (t) + {{\tau }_{c}}} \right]$(см. работу [12]). Теперь ток во время облучения при $l(t) \gg 1.0$ (т.е. в умеренно сильном электрическом поле) $j(t) \to {{g}_{0}}{{\mu }_{0}}{{\tau }_{c}}e{{F}_{0}}$, но в предельно сильных полях ${{F}_{0}} \to \infty $ $j(t)$ → 0.5${{g}_{0}}Le$ (и снова реализуется режим полного сбора генерируемых электронов). Обращаем внимание на то, что при всех временах наблюдения плотность регистрируемого тока пропорциональна скорости объемной генерации (прямое следствие малосигнального режима облучения). Для проведения оценочных расчетов использованы значения модельных параметров радиационной электропроводности ПЭТФ, предложенные нами в работе [9]: μ0 = 10–5 м2/ (В с), τ0 = 2 × 10–11 с, ${{\tau }_{c}}$ = 5.4 × 10–10 с, ν0 = 3 × 107 с–1, ${{k}_{{rec}}}$ = 5.8 × 10–14 м3/с и α = 0.5. Далее радиационно-химический выход свободных электронов в поле 4 × 107 В/м принят равным 0.7 на 100 эВ поглощенной энергии, что при плотности полимера 1.4 г/см3 соответствует скорости объемной генерации электронов ${{g}_{0}} = $ 1.2 × 1024 м–3с–1 для мощности дозы ${{R}_{0}} = $ 1.9 × 104 Гр/с.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для проведения экспериментальных исследований использована электронно-лучевая установка ЭЛА-50/5, позволяющая облучать образцы полимеров ускоренными электронами с энергией 50 кэВ как в импульсном, так и непрерывном режиме [1]. Основная информация относительно нарастания и спада кривых переходного тока получена при работе с прямоугольными импульсами электронов длительностью 20 мкс и 1 мс. Мгновенную компоненту радиационного тока измеряли с использованием короткого (3 мкс по основанию) треугольного импульса.
Если в первом случае применялась компьютерная регистрация кривых переходного тока, то в последнем случае использовали считывание данных с экрана осциллографа с полосой пропускания в 20 МГц. Методика проведения экспериментов и обработки полученных данных подробно рассмотрена нами ранее (см. работы [1, 9]).
Переходный ток в образце полимера под напряжением измеряли в токовом режиме, когда постоянная времени измерения RC была много меньше характерного времени наблюдения. Использовали импульсы электронов с энергией 50 кэВ, при которой обеспечивается достаточно однородное облучение пленок полимеров толщиной до 25 мкм. Дозиметрию пучка осуществляли с помощью цилиндра Фарадея. Диаметр коллиматора непосредственно на входе в измерительную ячейку составлял 20 мм.
Испытания проводили на дисковых образцах пленок ПЭТФ (производитель Открытое акционерное общество “Владимирский химический завод”, пленка полиэтилентерефталатная ПЭТ-Э ГОСТ 24234-80) диаметром 38 мм, вырезанных из промышленных пленок полимера толщиной до 20 мкм Электроды диаметром 32 мм наносили термическим напылением алюминия в вакууме. Толщина слоя алюминия не превышала 50 нм.
При планировании контрольных экспериментов предстояло оценить роль каждого из трех факторов, обусловливающих нестандартное поведение радиационной электропроводности ПЭТФ. Это выход электронов на электроды уже на этапе облучения, их захват на немногочисленные глубокие ловушки биографического происхождения в режиме дисперсионного транспорта, и наконец, бимолекулярная рекомбинация, искажающая ход кривых на этапе спада, даже если она не оказывает заметного влияния на вид кривых, регистрируемых в процессе облучения.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Наиболее однозначные данные получены при работе с импульсами электронов длительностью 20 мкс. Именно в этом режиме облучения достигается оптимум временного разрешения при минимуме рекомбинационных потерь. В типичном эксперименте (электрическое поле 4 × 107 В/м) мощность дозы составляет 3.8 × 104 Гр/с (доза 0.76 Гр), что соответствует скорости генерации электронов ${{g}_{0}} = $ 2.4 × 1024 м–3/с. Расчеты с использованием модели Роуза–Фаулера–Вайсберга показывают, что влияние рекомбинации отсутствует при временах наблюдения, не превышающих 10 мс даже при ${{g}_{0}} = $ 1025 м–3/с, перекрывая весь диапазон использованных мощностей дозы (рис. 1). В случае импульсов длительностью 1 мс необходимо снизить скорость объемной генерации до 1023 м–3/с. Но даже при ${{g}_{0}} = $ 1024 м–3/с кривая нарастания тока все еще не искажается, хотя кривая спада тока претерпевает существенные изменения. Таким образом, в указанном временном диапазоне надежно реализуется малосигнальный режим облучения, когда можно пренебречь влиянием рекомбинации, но в то же время провести эксперименты с необходимым временным разрешением. Мгновенная компонента радиационной электропроводности в исследованном полимере в расчете на единицу мощности дозы ${{K}_{p}}$ оказалась близкой к 10–15 Ом–1м–1Гр–1с. Она, как известно, пропорциональна мощности дозы и практически не зависит ни от поля, ни от температуры. В рамках модели многократного захвата используется ее аналог ${{\hat {\gamma }}_{p}} = {{g}_{0}}{{\mu }_{0}}{{\tau }_{0}}e$, который может значительно отличаться от оригинала.
Рис. 1.
Кривые переходного тока, рассчитанные по модели Роуза–Фаулера–Вайсберга с параметрами диэлектрика, приведенными в тексте. Все кривые нормированы на значение ${{\hat {\gamma }}_{p}}$ (см. текст). ${{g}_{0}} = $ 1026 (1) , 1025 (2), 1024 (3), 1023 (4) и 1022 м–3с–1 (5). Захват на глубокие ловушки не учитывается (${{\tau }_{c}} = $ 5.4 с).
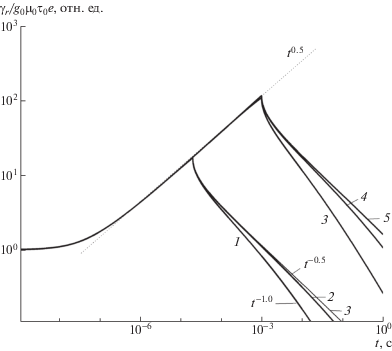
На рис. 2 представлены кривые переходного для нескольких значений электрического поля. Видно, что форма кривых практически не изменяется, а наблюдается лишь возрастание значений приведенной радиационной электропроводности к единице мощности дозы ${{K}_{r}}$ в конце импульса радиации ${{K}_{{rm}}} = {{\gamma }_{{rm}}}{\text{/}}{{R}_{0}}$ за счет увеличения радиационно-химического выхода свободных зарядов по теории Онзагера [1]. Если бы спад тока по закону $j \propto {{t}^{{ - 1.5}}}$ был обусловлен эффектом пролета, то следовало бы ожидать заметного смещения кривой спада в сторону больших времен с понижением электрического поля, чего на самом деле не происходит. Штриховая кривая отражает рост задержанной компоненты по закону $j \propto {{t}^{{0.35}}}$, полученной вычитанием мгновенной компоненты от измеренной кривой 1 на этапе возгорания радиационной электропроводности. При этом ход задержанной компоненты воспроизводит ее ход в сильном поле, как у кривой 3, в которой последняя уже доминирует.
Рис. 2.
Экспериментальные кривые переходного тока, измеренные при длительности импульсов излучения 20 мкс в режиме малого сигнала при значениях электрического поля 107 (1), 4 × 107 (2) и 8 × 107 В/м (3). ${{K}_{{rm}}}$ × 1014 = 0.8 (1), 2.4 (2) и 5.6 Ом–1м–1Гр–1с (3). Пунктирная кривая характеризует рост во времени задержанной компоненты. Пояснения в тексте.
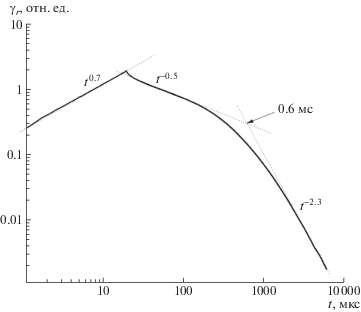
Отметим также то обстоятельство, что в эксперименте видно только “послепролетную” ветвь кривой, в то время как допролетная просто отсутствует. Это кажется странным, и для прояснения данного вопроса был поставлен специальный эксперимент в тех же условиях, используя для этой цели ПК, молекулярно допированный 30 мас. % дифенилгидразон p-диэтиламинобензальдегида (МДП), дырочный транспорт в котором подробно изучался [13]. Его результаты приведены на рис. 3. Примечательно, что подвижность дырок в МДП несколько выше, чем электронов в ПЭТФ, но его времяпролетная кривая имеет четко обозначенные допролетную $j \propto {{t}^{{ - 0.5}}}$ и послепролетную $j \propto {{t}^{{ - 2.3}}}$ветви даже в предельно сильном поле (108 В/м) в пленке полимера толщиной всего 9 мкм. Обращаем внимание также на довольно большую величину времени пролета 0.6 мс.
Рис. 3.
Кривая переходного тока, измеренная в образце МДП. Электрическое поле 108 В/м, длительность импульса 20 мкс, толщина пленки 9 мкм. ${{K}_{{rm}}}$ = 1.1 × 10–13 Ом–1м–1Гр–1с. Стрелкой обозначено время пролета.
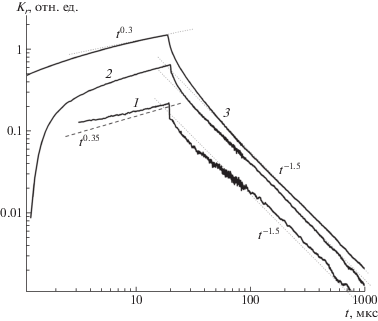
Увеличение длительности импульсов до 1 мс привело к выходу кривых переходного тока на квазистационарное значение (рис. 4). Сшивка двух кривых при $t = $ 20 мкс происходит достаточно гладко, и общая касательная в этой точке описывается выражением $j \propto {{t}^{{0.3}}}$, а в дальнейшем показатель степени $\beta = d\lg j{\text{/}}d\lg t$ только снижается, достигая значения 0.03 к 1 мс. В рамках концепции выноса носителей заряда на электроды [8] подобное поведение формы кривых переходного тока следовало бы связать с полным сбором генерированных зарядов. Данное предположение не соответствует действительности. Даже в поле 8 × 107 В/м плотность тока при 1 мс (1.6 × × 10–3 А/м2) более чем в 15 раз меньше ожидаемого значения при полном сборе генерированного заряда (44 × 10–3 А/м2). Об этом же свидетельствуют теоретические оценки (рис. 5). Плотность тока электронов при их полном сборе (10–2 А/м2) почти в 35 раз больше (2.87 × 10–4 А/м2) расчетного значения для кривой 4 при 1 мс.
Рис. 4.
Кривые переходного тока в образце ПЭТФ, измеренные для импульсов излучения длительностью 20 мкс (1) и 1 мс (2) в электрическом поле 8 × 107 В/м при мощности дозы 3.8 × 103 (1) и 190 Гр/с (2). $RC = $ 0.2 (1) и 2 мкс (2). Стрелкой указано время сшивки двух кривых (20 мкс). ${{K}_{{rm}}}$ в конце импульса равно 7 × 10–14 (1) и 1.2 × 10–13 Ом–1м–1Гр–1с (2) соответственно.
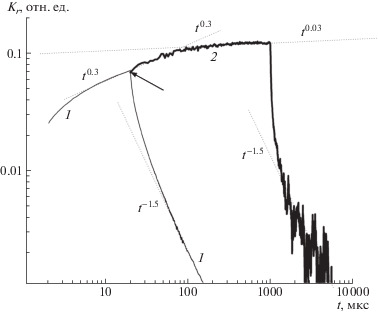
Рис. 5.
Кривые переходного тока, рассчитанные c использованием уравнений (7) для параметров диэлектрика, приведенных в тексте. ${{g}_{0}} = $ 1022 м-3/с. Длительность импульсов 20 мкс (1, 3) и 1 мс (2, 4). ${{\tau }_{c}} = $ 5.4 с (1, 2) и 5.4 × 10–10 с (3, 4). Электрическое поле 4 × 107 В/м.
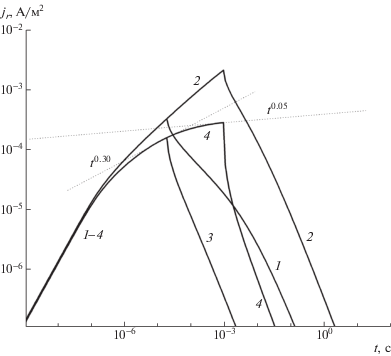
Более правдоподобным выглядит предложенное в работе [9] объяснение, связывающее подобное поведение с захватом на глубокие ловушки, не требующее наличия сильного электрического поля. Численные расчеты полностью подтверждают корректность подобного подхода (рис. 5). Видно, что учет захвата электронов на глубокие ловушки приводит к ограничению роста задержанной компоненты с увеличением длительности импульсного облучения. Более того, при t = = 20 мкс наклон $\beta $ имеет требуемое значение 0.3, как и на рис. 4.
ЗАКЛЮЧЕНИЕ
Таким образом, можно заключить, что транспорт электронов в ПЭТФ происходит в дисперсионном режиме, но в присутствии глубоких ловушек, выходом электронов из которых можно пренебречь. Это обстоятельство объясняет нестандартное поведение его радиационной электропроводности при импульсном и непрерывном облучении в режиме малого сигнала. Для описания такого явления можно использовать аналитические результаты работы [12].
Авторы выражают благодарность Р.Ш. Ихсанову за ряд ценных замечаний.
Исследование осуществлено в рамках Программы фундаментальных исследований Национального исследовательского университета “Высшая школа экономики”.
Список литературы
Тютнев А.П., Саенко В.С., Пожидаев Е.Д., Костюков Н.С. Диэлектрические свойства полимеров в полях ионизирующих излучений. М.: Наука, 2005. С. 453.
Filho R.G., Gross B. // J. Appl. Phys. 1989. V. 66. P. 5478.
Faria R.M., Gross B. // J. Appl. Phys. 1987. V. 62. № 4. P. 1420.
Gross B., Gerhard-Multhaupt R., Labonte K., Berraisoul A. // Colloid Polym. Sci. 1984. V. 262. P. 93.
Frederickson A.R., Woolf S. // IEEE Trans. Nucl. Sci. 1982. V. 29. № 6. P.2004.
Hughes R.C. // J. Appl. Phys. 1980. V. 51. № 11. P. 5933.
Martin E.H., Hirsh J. // J. Appl. Phys. 1972. V. 43. № 1. P. 1001.
Kurtz S.R., Hughes R.C. // J. Appl. Phys. 1983. V. 54. № 1. P. 229.
Tyutnev A.P., Saenko V.S., Ikhsanov R.Sh., Krouk E.A. // J. Appl. Phys. 2019. V. 126. P. 095501.
Nikitenko V.R., Strikhanov M.N. // J. Appl. Phys. 2014. V. 115. 073704.
Baranovskii S.D. // Phys. Status Solidi A. 2018. V. 215. 1700676.
Nикитенко В.Р., Тютнев А.П., Саенко В.С., Пожидаев Е.Д. // Хим. физика. 2004. Т. 23. № 3. С. 92.
Borsenberger P.M., Weiss D.S. Organic Photoreceptors for Xerography. New York: Marcel Dekker, 1998.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)


