Высокомолекулярные соединения (серия А), 2021, T. 63, № 2, стр. 145-160
ВЯЗКОУПРУГОСТЬ РАСТЯНУТОЙ ПОЛУГИБКОЙ ПОЛИМЕРНОЙ ЦЕПИ С ФИКСИРОВАННЫМИ КОНЦАМИ
И. П. Бородин a, *, Н. К. Балабаев b
a Костромской государственный университет
156005 Кострома, ул. Дзержинского, 17, Россия
b Институт математических проблем биологии Российской академии наук –
филиал Института прикладной математики им. М.В. Келдыша Российской академии наук
142290 Пущино, Московская область, ул. проф. Виткевича, 1, Россия
* E-mail: bip2004@mail.ru
Поступила в редакцию 02.07.2020
После доработки 22.09.2020
Принята к публикации 27.10.2020
Аннотация
Методом молекулярной динамики и аналитически исследованы закономерности затухания временных корреляционных функций флуктуаций тензора микроскопических напряжений, характеризующих вязкоупругие свойства, для статически растянутых цепей из упругих звеньев с жесткостью на изгиб. Рассмотрены цепи с персистентной длиной меньше контурной и степенью растяжения почти до разрыва. В области больших растяжений, где возникают искажения локальной структуры цепи, затухание корреляционных функций описывается модифицированной моделью Рауза, состоящей из субцепей с анизотропными жесткостями, зависящими от равновесного растяжения цепи. Это позволяет определить времена релаксации и модули сильно растянутых цепей, что необходимо при изучении прочности полимерных сеток. Сформулировано аналитическое соотношение для корреляционных функций, учитывающее вклад поперечных изгибных флуктуаций, согласующееся при малых растяжениях с результатами компьютерного моделирования. Изменение корреляционных функций с растяжением длинных полугибких цепей качественно сходно с таковым для гибких цепей, но существенно отличается количественно.
ВВЕДЕНИЕ
Исследование вязкоупругих свойств растянутых полимерных цепей важно с точки зрения характеристики прочности полимерных материалов. Так, показано [1–3], что скорость распространения микротрещин в полимерных сетках определяется временами релаксации и модулями сильно растянутых цепей и фрагментов сетки, близких к вершине трещины.
В связи с изучением вязкоупругости сильно растянутых цепей предложены различные подходы, учитывающие конечную растяжимость цепей. Например, рассматривалась модель цепи из блобов, находящейся под действием растягивающей силы [4–6]. Проведено компьютерное моделирование и разработана теоретическая модель для описания динамики свободносочлененной цепи из жестких звеньев во внешнем дипольном поле, т.е. цепи, растянутой за концы [7]. В работе [8] динамика растянутой цепи анализировалась с учетом массы сегментов, упругая энергия которых задавалась потенциалом FENE, учитывающим конечную растяжимость. Показано, что в области предельных растяжений учет массы сегментов цепи может дать существенный вклад в вязкоупругие свойства полимеров.
В работах [9, 10] представлена модифицированная модель Рауза, в которой флуктуации субцепей, образующих растянутую цепь, являются гауссовыми, а коэффициенты упругости субцепей различны в направлениях вдоль оси растяжения цепи и перпендикулярно к ней и зависят от степени равновесного растяжения цепи. С использованием этой модели были вычислены частотные зависимости модулей сдвига растянутых полимерных цепей и сеток [11], которые находятся в качественном согласии с экспериментальными данными [12].
В настоящей работе рассматриваются цепи, обладающие жесткостью на изгиб. Такие полугибкие цепи, их растворы и сетки обладают равновесными и неравновесными механическими свойствами, существенно отличающимися от свойств гибких цепей и их ансамблей (см., например, работы [13, 14]). Интерес к полугибким полимерам обусловлен, в частности, их важной ролью в биологии.
В релаксационном спектре нерастянутой цепи с жесткостью на изгиб появляются времена релаксации, дисперсионная зависимость которых в отличие от раузовских времен имеет вид ${{\tau }_{k}}\sim {{k}^{{ - 4}}}$ [15]. Такая зависимость характерна для малых изгибных колебаний упругого стержня около вытянутой конфигурации и приводит для нерастянутых цепей к релаксационному модулю сдвига G(t) ~ ${{t}^{{ - 3/4}}}$ [13, 16, 17]. Модуль изгиба полугибкой цепи обратно пропорционален температуре, и равновесная зависимость сила–растяжения для нее существенно отличается от таковой для свободносочлененной цепи [13, 18].
В неравновесных процессах существенную роль играют временные корреляционные функции (ВКФ), через которые выражаются коэффициенты переноса и другие величины, характеризующие свойства неравновесных систем [19]. Основной вклад в вязкоупругость связан с ВКФ флуктуаций микроскопического тензора напряжений, определяющих вязкость системы, релаксационные модули, модуль потерь и неравновесную часть модуля накопления.
К примеру, модуль потерь статически одноосно растянутой полимерной сетки, на которую наложена малоамплитудная деформация, осциллирующая с частотой ω, определяется соотношением [20]
Здесь λ – кратность статического растяжения сетки, $E(t,\lambda )$ – релаксационный модуль сетки
(1)
${{K}_{{\alpha \beta \mu \nu }}}(t,\lambda ) = {{\langle {{J}_{{\alpha \beta }}}(t){{J}_{{\mu \nu }}}(0)\rangle }_{\lambda }} - {{\langle {{J}_{{\alpha \beta }}}(t)\rangle }_{\lambda }}{{\langle {{J}_{{\mu \nu }}}(0)\rangle }_{\lambda }},$В работе [20] зависимость модуля потерь статически растянутой сетки гибких цепей от λ изучалась вплоть до растяжений, близких к разрыву, в области частот, где $E{\kern 1pt} '{\kern 1pt} '\sim {{\omega }^{{1/2}}}$ (гауссова область [21]). При умеренных и больших λ величина $Е{\kern 1pt} '{\kern 1pt} '$ растет, что объясняется конечной растяжимостью цепей. При еще больших растяжениях деформация цепей определяется повышением их внутренней энергии в связи с удлинением ориентированных сегментов. Вследствие этого происходит падение $Е{\kern 1pt} '{\kern 1pt} '$ с увеличением λ, что ведет к появлению максимума на кривых $Е{\kern 1pt} '{\kern 1pt} '\, - \,{\kern 1pt} \lambda $, положение и высота которого определяются структурой сетки.
Поведение модуля потерь сетки при растяжении обусловлено закономерностями затухания ВКФ флуктуаций микроскопического тензора напряжений отдельных статически растянутых гибких цепей, изучавшихся в работах [22, 23] методом молекулярной динамики и аналитически. При моделировании в них была принята простая модель цепи из свободносочлененных упругих звеньев, способных растягиваться и сжиматься по гармоническому закону относительно некоторой средней длины [24]. Такие звенья иногда называют “френкелевскими пружинами” [25]. Эта модель позволяет описывать возникающие при растяжениях, близких к разрывным, искажения локальной структуры, определяемой длиной связей, валентными и двухгранными углами, потенциалами внутреннего вращения и т.п. Оказалось, что результаты моделирования затухания ВКФ флуктуаций микроскопического тензора напряжений гибкой цепи хорошо описываются модифицированной моделью Рауза вплоть до предельных растяжений, близких к разрывному.
Здесь мы рассмотрим закономерности затухания ВКФ флуктуаций микроскопического тензора напряжений статически растянутой цепи из упругих звеньев с жесткостью на изгиб. При вычислении ВКФ отдельной цепи усреднение в выражении (1) будет производиться по распределению, равновесному при данном относительном растяжении цепи $u = {{\langle {{h}_{z}}\rangle }_{{eq}}}{\text{/}}N{{l}_{0}}$, где hz – проекция вектора между концами цепи на ось ее растяжения, N – число звеньев в цепи, l0 – равновесная длина недеформированного звена. В отличие от модели цепи из жестких звеньев в модели из упругих звеньев относительное растяжение цепи u может превышать единицу.
Затухание ВКФ флуктуаций тензора микроскопических напряжений статически растянутой цепи с жесткостью на изгиб исследовано методом молекулярной столкновительной динамики [26]. Помимо этого рассмотрены теоретические модели для описания затухания ВКФ при малых и больших растяжениях полугибкой цепи, которые сопоставляются с результатами моделирования.
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Рассмотрим модель дискретной персистентной цепи из $N$ растяжимых звеньев, эффективная потенциальная энергия которой может быть представлена в следующей форме [27]:
Здесь первое слагаемое – энергия изгиба: ${{{\mathbf{t}}}_{i}}$ – единичный вектор вдоль направления i-го звена, A – жесткость на изгиб; второе слагаемое – сумма энергий деформаций звеньев: ${{\varepsilon }_{i}} = \frac{{{{l}_{i}} - {{l}_{0}}}}{{{{l}_{0}}}}$, li – флуктуирующая длина i-го звена, K – коэффициент продольной жесткости звеньев; вид третьего слагаемого (Wd) зависит от того, рассматривается ли цепь с фиксированными концами или цепь, к концам которой приложена постоянная сила. При моделировании цепи с фиксированными концами концевые частицы (1 и N + 1) связаны гармоническими пружинами нулевой длины с неподвижными точками ${\mathbf{r}}_{1}^{0}$ и ${\mathbf{r}}_{{N + 1}}^{0}$, расположенными на оси $Z$ на расстоянии d. В этом случае [22]
Таким образом, расстояние между неподвижными точками $d = {\text{|}}{\mathbf{r}}_{1}^{0} - {\mathbf{r}}_{{N + 1}}^{0}{\text{|}}$ характеризует растяжение цепи.
Введем безразмерные переменные в выражение для энергии цепи W. Так как персистентная длина цепи ${{l}_{p}} = A{\text{/}}{{k}_{{\text{B}}}}T$ [28], то $A{\text{/}}{{l}_{0}} = {{k}_{{\text{B}}}}Tp$, где kB – постоянная Больцмана, отношение $p = {{l}_{p}}{\text{/}}{{l}_{0}}$ – локальная мера жесткости на изгиб, не зависящая от длины цепи. Безразмерный коэффициент продольной жесткости звеньев будет ${{K}_{e}} = Kl_{0}^{2}{\text{/}}{{k}_{{\text{B}}}}T$. Выражение для энергии цепи W принимает вид
(2)
$W = \frac{1}{2}{{k}_{{\text{B}}}}T\left( {p\sum\limits_{i = 1}^{N - 1} {{{{({{{\mathbf{t}}}_{{i + 1}}} - {{{\mathbf{t}}}_{i}})}}^{2}}} + {{K}_{e}}\sum\limits_{i = 1}^N {\varepsilon _{i}^{2}} } \right) + {{W}_{d}}$Движение частиц описывается уравнениями Ньютона, которые включают взаимодействие частиц с виртуальной средой (столкновительным термостатом) [26]:
Термостат, в котором находится цепь, представляется равновесным идеальным газом, виртуальные частицы которого имеют массу m0, а их скорости подчиняются распределению Максвелла при заданной температуре T. Точечные столкновения частиц цепи с виртуальными частицами термостата генерируются с помощью случайного пуассоновского процесса со средней частотой столкновений ν.
Коэффициент трения частицы цепи в столкновительной среде определяется из рассмотрения парных столкновений с частицами термостата и дается соотношением [26]
Параметры термостата m0, ν связаны с вязкостью среды, причем ВКФ, получаемые при моделировании, не должны зависеть от этих параметров после перенормировки единицы времени [22]. В качестве основных единиц при моделировании были взяты единицы длины [L], массы [M] и энергии [E]. Для единицы времени справедливо соотношение ${{t}_{0}} \equiv [t] = [L]{{([M]{\text{/}}[E])}^{{0.5}}}$. Моделирование проводили при следующих значениях параметров: длина звена ${{l}_{0}} = 1$, массы виртуальной частицы термостата и частиц цепи ${{m}_{0}} = m = 1$, температура $T = 1{\text{/}}{{k}_{{\text{B}}}}$, частота столкновений ν = 10. Согласно выражению (3), для коэффициента трения получаем значение $\varsigma = 10$.
Константа K, определяющая жесткость связи, может принимать значения от 100 до 1000 [29]. В данной работе полагали, что K = 100. Отметим, что изменение упругой постоянной Kd не влияет сколько-нибудь заметно на результаты моделирования, что продемонстрировано в работе [22], где Kd изменялась в 5 раз. В указанной работе считали, что ${{K}_{d}} = K$. В принятой системе единиц ${{K}_{e}}$ = K = Kd.
Рассматривались цепи с персистентной длиной, меньшей их контурной длины: ${{l}_{p}} < N{{l}_{0}} = L$. Например, для типичных параметров молекулы ДНК ${{l}_{p}}\sim 50$ нм, $L \lesssim 1$ м [13]. Параметр p принимал значения 0; 5; 10; 20 для цепей с числом звеньев $N = 25,\;50,\;100$.
Программное обеспечение осуществляло параллельные вычисления траекторий ансамбля независимых полимерных цепей (102–103 цепей) с независимыми начальными условиями (координатами и скоростями частиц) на временном интервале 107 шагов. Полученные результаты включали усреднение как по траектории каждой из цепей, так и по всему ансамблю цепей.
При вычислении ВКФ микроскопического тензора напряжений рассматривали времена, на которых в пространстве импульсов устанавливается равновесие. Это означает, что мы пренебрегали кинетической частью микроскопического тензора напряжений. Соответственно выражение для него имеет вид [30]
где ${{r}_{{i\alpha }}}$ – проекция радиус-вектора i-й частицы цепи на ось α декартовой системы координат, ${{F}_{{i\beta }}}$ – проекция на ось β силы, действующей на i-ю частицу.Результаты представлены на рисунках в виде нормированных ВКФ
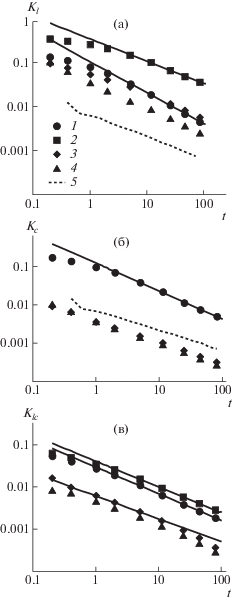
На рис. 1 показано в логарифмических координатах затухание продольной Kl, поперечной Kc и перекрестной ВКФ ${{K}_{{lc}}}$ при различных значениях относительного растяжения цепи $u = d{\text{/}}N{{l}_{0}}$, p = 0, 10 и $N = 100.$ Можно отметить, что при малых растяжениях ВКФ для свободносочлененной цепи (p = 0) из упругих звеньев примерно на порядок меньше, чем ВКФ при p = 10. В области $u \geqslant 1$ ВКФ при разных p становятся одного порядка, стремясь к совпадению с увеличением u. При растяжении цепи углы между соседними звеньями уменьшаются, и при больших растяжениях вклад изгибной энергии в выражении (2) становится малым. Отметим также, что продольная ${{K}_{l}}$ и перекрестная ${{K}_{{lc}}}$ ВКФ вначале увеличиваются с растяжением, а затем по достижении максимума при больших растяжениях уменьшаются. Поперечная ВКФ ${{K}_{c}}$ монотонно убывает.
Рис. 1.
Затухание временных корреляционных функций Kl (а) , Kc (б) и Klc (в) флуктуаций тензора микроскопических напряжений растянутой цепи при степени растяжения u = 0.1 (1, 5), 0.8 (2), 1.1 (3, 4) и $N = 100$ (компьютерное моделирование). p = 10 (1–3) и 0 (4, 5). Сплошные линии – степенная аппроксимация.
Представление о характере зависимости ВКФ от растяжения дают изохроны, т.е. зависимости ВКФ от u в определенный момент времени. На рис. 2 они представлены для цепей длиной 25 и 100 при значениях параметра p = 0, 10, 20 в момент t = 40. Кривые на рис. 2а соответствуют персистентной длине ${{l}_{p}} = 0.1L,\;0.4L,\;0.8L,$ а на рис. 2в – ${{l}_{p}} = 0,\;0.1L,\;0.2L.$ Для изохрон ВКФ Kl и Klc характерно наличие максимума, который увеличивается с уменьшением гибкости цепи. Для ${{K}_{l}}$ он находится вблизи u = 1 (примерно около u = 0.9) независимо от значения p. Для ${{K}_{{lc}}}$ при $p \ne 0$ максимум смещен к более низким растяжениям (u ≈ 0.7) по сравнению с максимумом при p = 0, положение которого такое же, как и для ${{K}_{l}}$. Положение максимумов не зависит от выбранного момента времени.
Рис. 2.
Зависимости ВКФ Kl (а) , Kc (б), Klc (в) и K4 (г) от степени растяжения цепи $u$ в момент времени t = 40 (изохроны) по результатам компьютерного моделирования при p/N = 0 (1), 0.1 (2), 0.2 (3), 0.4 (4) и 0.8 (5).
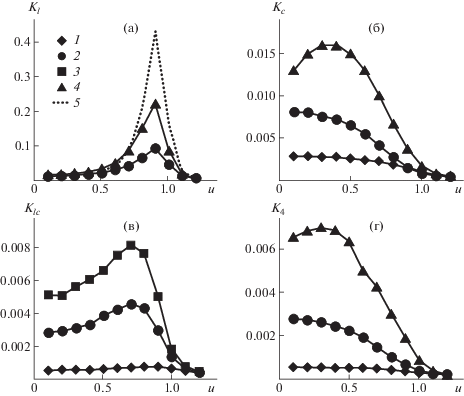
Кривые на рис. 2б и 2г соответствуют персистентной длине ${{l}_{p}} = 0$, 0.1L, 0.4L. При условии, что ${{l}_{p}} \ll L$ ВКФ ${{K}_{c}}$ и K4 монотонно убывают с растяжением. С уменьшением гибкости цепи при ${{l}_{p}} \lesssim L$ появляется максимум, смещенный к более низким растяжениям (находящийся между u = 0.3 и 0.4). В области $u \geqslant 1$ все ВКФ стремятся к ВКФ с p = 0.
СРАВНЕНИЕ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ И АНАЛИТИЧЕСКОЙ ТЕОРИИ ПРИ БОЛЬШИХ РАСТЯЖЕНИЯХ
Результаты моделирования показывают, что в области $u \geqslant 1$ закономерности затухания ВКФ цепей из упругих звеньев с жесткостью на изгиб становятся близкими к закономерностям затухания цепи из свободносочлененных упругих звеньев.
Согласно работам [22, 23], затухание ВКФ флуктуаций тензора микроскопических напряжений растянутых свободносочлененных цепей из упругих звеньев хорошо описывается моделью связанных броуновских осцилляторов (моделью субцепей). В растянутой цепи бусины флуктуируют около своих равновесных положений, и через эти флуктуации выражаются флуктуации компонентов тензора микроскопических напряжений. Коэффициенты упругости пружин, соединяющих бусины, зависят от расстояний между равновесными положениями бусин. Если цепь ориентирована вдоль оси растяжения, то из цилиндрической симметрии растяжения следует существование двух коэффициентов упругости: продольного, соответствующего флуктуациям вдоль оси растяжения, и поперечного, отвечающего флуктуациям, перпендикулярным к данной оси. Флуктуации полагаются малыми, так что их распределение является гауссовым.
Зависимость коэффициентов от растяжения цепи вычисляется из равновесной зависимости u от ${{f}_{0}} = {{F}_{0}}{{l}_{0}}{\text{/}}{{k}_{{\text{B}}}}T$.
Для ВКФ цепей с закрепленными концами такая модель дает [23]
(5)
$\begin{gathered} {{K}_{{zzzz}}} = 2\sum\limits_{k = 1}^N {[{{{\left( {{{C}_{\lambda }}{\text{/}}{{C}_{l}}} \right)}}^{2}}\exp \left( { - 2t{\text{/}}{{\tau }_{{kl}}}} \right) + } \\ \, + 2{{\left( {{{C}_{a}}{\text{/}}{{C}_{c}}} \right)}^{2}}\exp \left( { - 2t{\text{/}}{{\tau }_{{kc}}}} \right)] \\ \end{gathered} $(6)
$\begin{gathered} {{K}_{{z\alpha z\alpha }}} = \frac{{{{C}_{l}}}}{{{{C}_{c}}}}\sum\limits_{k = 1}^N {\exp \left[ { - \left( {\frac{1}{{{{\tau }_{{kl}}}}} + \frac{1}{{{{\tau }_{{kc}}}}}} \right)t} \right],} \\ {{K}_{{z\alpha z\alpha }}} = {{K}_{{\alpha z\alpha z}}},\quad \alpha = x,y \\ \end{gathered} $(7)
$\begin{gathered} {{K}_{{xxxx}}} = {{K}_{{yyyy}}} = 2\sum\limits_{k = 1}^N {\exp \left( { - 2t{\text{/}}{{\tau }_{{kc}}}} \right),} \\ {{K}_{{xyxy}}} = {{K}_{{yxyx}}} = {{K}_{{xxxx}}}{\text{/}}2 \\ \end{gathered} $(8)
${{K}_{{\alpha \alpha \beta \beta }}} = {{K}_{{\beta \beta \alpha \alpha }}} = \frac{{{{C}_{a}}}}{{{{C}_{c}}}}{{K}_{{xxxx}}},\quad \alpha = x,y,\quad \beta = z.$Остальные ВКФ равны нулю. В формулах (5)–(8) ${{C}_{l}}$, Cc – продольный и поперечный коэффициенты упругости субцепей, ${{\tau }_{{kl}}} = {{\tau }_{k}}{{C}_{G}}{\text{/}}{{C}_{l}}$, τkc = ${{\tau }_{k}}{{C}_{G}}{\text{/}}{{C}_{c}}$. Коэффициенты ${{C}_{l}},{{C}_{c}},{{C}_{\lambda }},{{C}_{a}}$ определяются выражениями
(9)
$\begin{gathered} {{C}_{c}} = \frac{{{{C}_{G}}}}{3}\frac{{{{f}_{0}}}}{u},\quad {{C}_{l}} = \frac{{{{C}_{G}}}}{3}\frac{{d{\kern 1pt} {{f}_{0}}}}{{du}}, \\ {{C}_{\lambda }} = {{C}_{l}}\left( {1 - \frac{u}{2}\frac{{{{d}^{2}}u{\text{/}}df_{0}^{2}}}{{{{{(du{\text{/}}d{{f}_{0}})}}^{2}}}}} \right), \\ {{C}_{a}} = \frac{1}{2}{{C}_{c}}\left( {\frac{u}{{{{f}_{0}}}}\frac{{d{{f}_{0}}}}{{du}} - 1} \right),\quad {{C}_{G}} = \frac{{3{{k}_{{\text{B}}}}T}}{{zl_{0}^{2}}} \\ \end{gathered} $Здесь ${{\tau }_{k}}$ – раузовское время релаксации k-й моды нерастянутой цепи, z – число звеньев в субцепи, CG – коэффициент упругости гауссовой субцепи.
В модифицированной модели Рауза, из которой следуют соотношения (5)–(8), сохраняется интерпретация бусин как элементов, огрубленно характеризующих положения субцепей, состоящих из многих атомов. Иначе говоря, приведенные соотношения описывают полулокальные движения цепи, для которых $1 \ll k \ll N$, поэтому суммирование в них должно быть до $n = N{\text{/}}z$ [10]. Однако на сравнительно больших временах, на которых наблюдается степенной спад c показателем $n \geqslant 1{\text{/}}2$, вклад членов с k > n мал, и чтобы не увеличивать число параметров, положим, что число субцепей равно числу сегментов, т.е. z = 1.
Заметим, что в работе [25], в которой методом Монте-Карло моделировалась релаксация сдвиговых напряжений френкелевских цепей в области линейной вязкоупругости, было показано, что затухания релаксационных модулей на медленной стадии совпадают с таковыми из модели Рауза. Отсюда сделан вывод, что размеры сегмента френкелевской цепи и субцепи Рауза одинаковы.
Учитывая выражение для раузовского времени релаксации, можно написать $\frac{2}{{{{\tau }_{k}}}}$ = $\frac{{24}}{\varsigma }\frac{{{{k}_{{\text{B}}}}T}}{{l_{0}^{2}}}{\text{si}}{{{\text{n}}}^{2}}\frac{{k\pi }}{{2(N + 1)}}$, где при компьютерном моделировании было принято, что kBT = 1, l0 = 1 и коэффициент трения, согласно соотношению (3), ς = 10. При сравнении формул (5)–(8) с результатами компьютерного моделирования для вычисления коэффициентов (9) использовалась равновесная зависимость u от f0 для персистентной цепи из упругих звеньев (см. Приложение), поскольку в области $u \geqslant 1$ результаты для обеих моделей сближаются с увеличением u.
Сравнение, проведенное для цепей с N = 25, 50, 100 при $p = 5,\;10,\;20$, для каждого $N$ демонстрирует хорошее согласие результатов компьютерного моделирования с теорией. Для примера на рис. 3 приведены зависимости ВКФ от времени, согласно соотношениям (5)–(9), при u = 1.1 для цепи с $N = 100$ и $p = 0,10$. Сплошные линии построены по формулам (5)–(9) на основе зависимости $u$ от f0 для персистентной цепи, штриховые линии – на основе зависимости $u$ от f0 для свободносочлененной цепи из упругих звеньев. Там, где отсутствуют штриховые линии, различие между двумя моделями пренебрежимо мало.
Рис. 3.
Зависимости ВКФ Kl (а), Kc (б), Klc (в), K4 (г) и K5 (д) от времени при относительном растяжении $u = 1.1$ для цепи длиной $N = 100$ и p = 10. Точки – компьютерные данные, линии – расчет по формулам (5)–(8), в которых коэффициенты, определяемые соотношениями (9), вычислялись из зависимости $u$ от f0 для персистентной цепи (сплошные линии) и из зависимости $u$ от f0 для свободносочлененной цепи (p = 0) (штриховые линии).
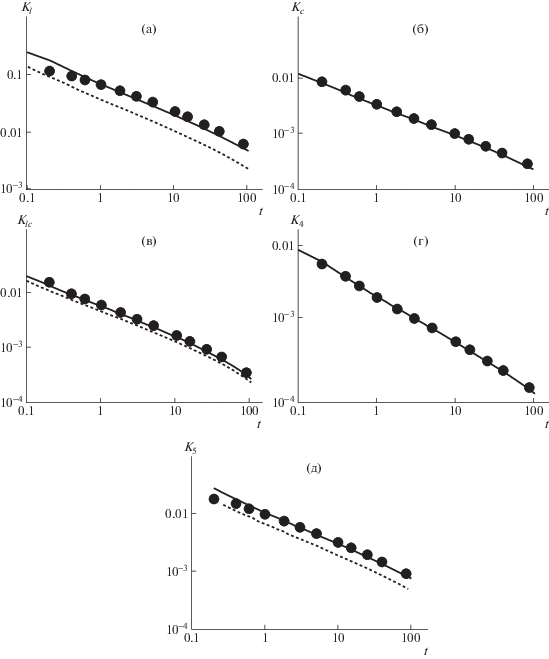
Таким образом, для сильно растянутых цепей наблюдается хорошее согласие ВКФ, полученных с помощью модифицированной модели Рауза с z = 1, и результатами компьютерного моделирования на основе френкелевской модели цепи.
При изображении теоретических зависимостей использовали безразмерное время t = $2t{\kern 1pt} '{\text{/}}{{\tau }_{{N + 1}}}$, где ${{\tau }_{{N + 1}}} = \frac{{\varsigma l_{0}^{2}}}{{12{{k}_{{\text{B}}}}T}}$ – минимальное время релаксации модели Рауза. Другими словами, при вычислениях в безразмерном времени $t = t{\kern 1pt} '{\text{/}}{{t}_{0}}$ характерная единица времени t0 равна ${{\tau }_{{N + 1}}}{\text{/}}2$.
Таким образом, описание вязкоупругих свойств сильно растянутых персистентных цепей при изучении прочности полимерных сеток можно вести на основе модели бусин, связанных нелинейными пружинами, согласно соотношениям (5)–(9). Деформационная зависимость пружин определяется равновесной зависимостью $u$ от f0 для свободносочлененной цепи из упругих звеньев.
ВКЛАД ИЗГИБНЫХ КОЛЕБАНИЙ В ВКФ ФЛУКТУАЦИЙ МИКРОСКОПИЧЕСКОГО ТЕНЗОРА НАПРЯЖЕНИЙ ЦЕПИ
Согласно изложенному выше, для сильно растянутых цепей при u ≤ 1 изгибная энергия не оказывает заметного влияния на затухание ВКФ. Из результатов компьютерного моделирования для цепей с lp < L в области u < 1 следует, что затухание ВКФ может быть аппроксимировано степенной функцией K ~ t–α, исключая интервал малых времен (рис. 1).
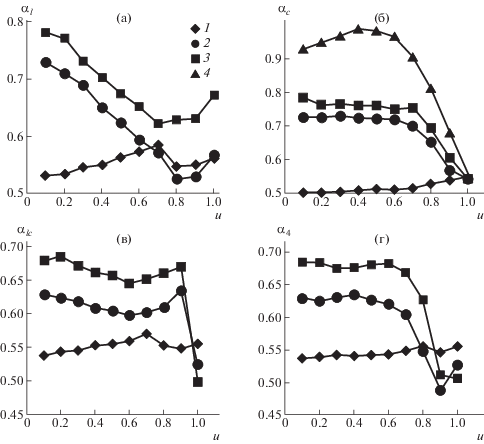
Как показано в работе [21], на частотной зависимости модуля имеется две области степенного поведения. Область с показателем 3/4, связанная с жесткостью на изгиб, и гауссова область с показателем 1/2. При изменении степени растяжения вклад этих двух режимов может изменяться, приводя к изменению параметра α между значениями 1/2 и 3/4. Зависимость показателя α от u в данном компьютерном моделировании показана на рис. 4. При малых растяжениях α близко к 0.75 для ${{K}_{l}}$ при условии $1 \ll p \ll N$ $({{l}_{0}} \ll {{l}_{p}} \ll L)$. Для Kc значение α, близкое к 0.75 при том же условии, имеет место примерно до $u = 0.6$, а для ${{K}_{{lc}}}$ и ${{K}_{4}}$ значения ${{\alpha }_{{lc}}}$, ${{\alpha }_{4}}$ ниже 0.65, но больше значений при p = 0. При заданной персистентной длине показатель α растет с уменьшением длины цепи (с увеличением параметра $p{\text{/}}N = {{l}_{p}}{\text{/}}L$).
Рис. 4.
Зависимости показателя степенной аппроксимации αl (а), αc (б), αlc (в) и α4 (г) затухания ВКФ от $u$ при p = 0, 10 и N = 25, 50, 100. p/N = 0 (1), 0.1 (2), 0.2 (3) и 0.4 (4).
Как отмечалось во Введении, изгибные колебания в нерастянутой персистентной полимерной цепи приводят к степенной зависимости релаксационного модуля сдвига от времени вида G(t) ~ t–3/4 [13]. Следовательно, можно ожидать существенного влияния таких колебаний, на затухание ВКФ слабо растянутых цепей.
Учтем вклад изгибных колебаний в ВКФ флуктуаций тензора микроскопических напряжений цепи. Дисперсионная зависимость τk ~ k–4 соответствует движениям, меньшим по масштабу, чем длина статистического сегмента [15, 31]. Рассмотрим длинную свободносочлененную цепь из n = L/b эффективных сегментов, средний квадрат расстояния между концами которой определяется соотношением 〈h2〉 = Lb, где длина эффективного сегмента b = 2lp [28]. Для этой цепи, аналогично формуле (4), можно записать в переменных bi = Ri+ 1 – Ri выражение для микроскопического тензора напряжений
(10)
${{J}_{{\alpha \beta }}} = \sum\limits_{i = 1}^n {{{b}_{{i\alpha }}}{{F}_{{i\beta }}} = \sum\limits_{i = 1}^n {b{{F}_{i}}{{n}_{{i\alpha }}}{{n}_{{i\beta }}},} } $Отсюда следует, что
(11)
$\Delta {{b}_{{iz}}} \cong {{l}_{0}}\sum\limits_k^{} {(\Delta {{\varepsilon }_{{ik}}} + {{\varepsilon }_{{ik, \bot }}}),} $С учетом этого соотношения подстановка выражения для Fi в (10) дает для цепи из n сегментов формулу
(13)
${{J}_{{\alpha \beta }}} \cong {{l}_{0}}B\sum\limits_i^{} {{{n}_{{i\alpha }}}{{n}_{{i\beta }}}\sum\limits_k^{} {{{\varepsilon }_{{ik, \bot }}}} } $В соотношении (13) {ni} представляют собой крупномасштабные переменные, характеризующие конфигурацию всей цепи. Переменные εik,⊥ – мелкомасштабные, связанные с k-м звеном i-го сегмента цепи. Следовательно, при усреднении (13) можно пренебречь корреляцией крупномасштабных и мелкомасштабных переменных, так что 〈Jαβ〉eq = 0. На основании выражений (1) и (13) затем записываем
(14)
$\begin{gathered} {{K}_{{\alpha \beta \mu \nu }}}(t) = l_{0}^{2}B(t)B(0)\sum\limits_{i,j}^{} {{{{\langle {{n}_{{i\alpha }}}{{n}_{{i\beta }}}{{n}_{{j\mu }}}{{n}_{{j\nu }}}\rangle }}_{{eq}}}} \\ \times \sum\limits_{k,n}^{} {{{{\langle {{\varepsilon }_{{ik, \bot }}}{{\varepsilon }_{{jn, \bot }}}\rangle }}_{{eq}}}} \\ \end{gathered} $Пренебрегая в соотношении (14) корреляцией переменных εik,⊥, принадлежащих разным сегментам цепи, так что 〈εik,⊥εjn,⊥〉eq = δij〈εik,⊥εin,⊥〉eq, получаем
(15)
$\begin{gathered} {{K}_{{\alpha \beta \mu \nu }}}(t) = l_{0}^{2}B(t)B(0){{\langle {{n}_{\alpha }}{{n}_{\beta }}{{n}_{\mu }}{{n}_{\nu }}\rangle }_{{eq}}} \\ \times \sum\limits_i^{} {\sum\limits_{k,n}^{} {{{{\langle {{\varepsilon }_{{ik, \bot }}}{{\varepsilon }_{{in, \bot }}}\rangle }}_{{eq}}}} } \\ \end{gathered} $Поскольку Δhz = $\sum\nolimits_i^{} \Delta $biz, согласно выражению (12), соотношение (15) приобретает вид
(16)
${{K}_{{\alpha \beta \mu \nu }}}(t) = B(t)B(0){{\langle {{n}_{\alpha }}{{n}_{\beta }}{{n}_{\mu }}{{n}_{\nu }}\rangle }_{{eq}}}{{\langle {{(\Delta {{h}_{z}})}^{2}}\rangle }_{{eq}}}$Рассмотрим цепь, равновесно растянутую вдоль оси Z постоянной силой F0 = F0k, приложенной к концам цепи. Наложим на эту систему малоамплитудную осциллирующую с частотой ω силу $\delta \,{\mathbf{F}}(t)$ и найдем реакцию цепи на нее Δ〈hz〉 = = 〈hz〉 – 〈hz〉eq. Здесь 〈hz〉 – среднее по неравновесному ансамблю для проекции вектора между концами цепи на ось Z; 〈hz〉eq – среднее по равновесному ансамблю при постоянной силе F0. Вычисление Δ〈hz〉 = 〈hz〉 – 〈hz〉eq позволяет определить эффективный продольный модуль B.
Для нахождения реакции цепи на малое возмущение δF(t) = δF(t)k можно воспользоваться теорией линейного отклика [19], согласно которой с учетом цилиндрической симметрии растяжения цепи
(17)
$\Delta \langle {{h}_{z}}(t)\rangle = \beta \left[ {\delta F(t){{K}_{{zz}}}(0) - \int\limits_{ - \infty }^t {{{K}_{{zz}}}(t - t{\kern 1pt} ')\delta \dot {F}(t{\kern 1pt} ')dt{\kern 1pt} '} } \right]$Здесь β = 1/kBT; Kzz(t) = 〈Δhz(t)Δhz(0)〉eq – ВКФ флуктуаций Δhz = hz – 〈hz〉e. Так как в равновесном состоянии цепь статически растянута, усреднение при вычислении Kzz(t) ведется по распределению, равновесном при заданном значении F0, т.е. отклик Δ〈hz〉 представляет собой нелинейную функцию силы F0, но является линейным по скоростям ее изменения (см. работу [32]).
Определим приведенную податливость цепочки при приложенном периодическом возмущении δF(t) = δF(0)exp(iωt) соотношением
Из выражения (17) следует, что
(18)
$\begin{gathered} J{\text{*}}(\omega ,{{F}_{0}}) = \\ = \frac{\beta }{{N{{l}_{0}}}}\left[ {{{K}_{{zz}}}(0,{{F}_{0}}) - i\omega \int\limits_0^\infty {{{K}_{{zz}}}(t,{{F}_{0}})\exp ( - i\omega t)dt} } \right] \\ \end{gathered} $Из соотношения (18) для действительной части комплексной податливости имеем соотношение
Отсюда для статической податливости находим формулу J(0, F0) = $\frac{{{{{\langle {{{(\Delta {{h}_{z}})}}^{2}}\rangle }}_{{eq}}}}}{{N{{k}_{{\text{B}}}}T{{l}_{0}}}}$. С учетом данной формулы и выражения B(0, F0) = 1/J(0, F0) соотношение (16) преобразуется к виду
(19)
${{K}_{{\alpha \beta \mu \nu }}}(t,{{F}_{0}}) = N{{k}_{{\text{B}}}}T{{l}_{0}}B(t,{{F}_{0}}){{\langle {{n}_{\alpha }}{{n}_{\beta }}{{n}_{\mu }}{{n}_{\nu }}\rangle }_{{eq}}}$Выражение (19) не учитывает флуктуации деформации звеньев цепи. Зависимость ВКФ от растяжения цепи в нем обусловлена деформационной зависимостью эффективного продольного модуля B(t, f0(u)) и зависимостью от растяжения среднего 〈nαnβnμnν〉eq, определяемого конфигурацией равновесно растянутой свободносочлененной цепи из эффективных сегментов.
ВЫЧИСЛЕНИЕ ЭФФЕКТИВНОГО ПРОДОЛЬНОГО МОДУЛЯ РАСТЯНУТОЙ ЦЕПИ
Для нахождения явного выражения для $B(t,{{f}_{0}}(u))$ нужно вычислить, согласно формуле (18), ВКФ ${{K}_{{zz}}}(t,{{F}_{0}})$. С этой целью сформулируем уравнение Ланжевена для поперечных флуктуаций цепи в равновесном состоянии при данном значении приложенной к ее концам силы ${{{\mathbf{F}}}_{0}} = {{F}_{o}}{\mathbf{k}}$. Для i-й частицы цепочки из N + 1 броуновских частиц записываем уравнение
(20)
$\langle F_{{i\alpha }}^{S}(t){\kern 1pt} {\kern 1pt} F_{{j\beta }}^{S}(t{\kern 1pt} ')\rangle = 2{{k}_{{\text{B}}}}T\varsigma {\kern 1pt} {\kern 1pt} {{\delta }_{{ij}}}{{\delta }_{{\alpha \beta }}}\delta (t - t{\kern 1pt} ').$Вычитая из (i + 1)-го уравнения i-е и переходя к переменным li = ri+ 1 – ri, получаем
(21)
$\begin{gathered} \varsigma {\mathbf{\dot {l}}} + \sum\limits_{k = 1}^{N - 1} {{{g}_{{ik}}}\frac{{\partial W}}{{\partial {{{\mathbf{l}}}_{k}}}}} = {{{\mathbf{f}}}_{{iS}}}, \\ {{g}_{{ik}}} = 2{{\delta }_{{ik}}} - {{\delta }_{{i,k - 1}}} - {{\delta }_{{i,k = 1}}},\quad {{{\mathbf{f}}}_{{iS}}} = {\mathbf{F}}_{{i + 1}}^{S} - {\mathbf{F}}_{i}^{S} \\ \end{gathered} $Для цепи, к концам которой приложена постоянная сила, энергию Wd в выражении (2) представим в виде
Затем выражение (2) переписываем как
(22)
$\begin{gathered} W = \frac{1}{2}{{k}_{{\text{B}}}}T\left( {p\sum\limits_{i = 1}^{N - 1} {{{{({{{\mathbf{t}}}_{{i + 1}}} - {{{\mathbf{t}}}_{i}})}}^{2}} + {{K}_{e}}\sum\limits_{i = 1}^N {\varepsilon _{i}^{2}} } } \right) \\ \, - {{k}_{{\text{B}}}}T{{f}_{0}}\sum\limits_{i = 1}^N {(1 + {{\varepsilon }_{i}}){{t}_{{iz}}}} \\ \end{gathered} $Для малых поперечных флуктуаций относительно вытянутой конфигурации цепи, когда 〈tiα〉eq = 0 (α = x, y) и tiz ≈ 1 – $\frac{1}{2}t_{{i \bot }}^{2}$, где t⊥ = tixi + tiyj, (22) можно записать в виде
(23)
$\begin{gathered} W \cong \frac{1}{2}{{k}_{{\text{B}}}}T\left( {p\sum\limits_{i = 1}^{N - 1} {{{{({{{\mathbf{t}}}_{{i + 1, \bot }}} - {{{\mathbf{t}}}_{{i \bot }}})}}^{2}} + {{f}_{0}}\sum\limits_{i = 1}^N {t_{{i \bot }}^{2}} } } \right) \\ \, + {{k}_{{\text{B}}}}T\sum\limits_{i = 1}^N {\left( {\frac{1}{2}{{K}_{e}}\varepsilon _{i}^{2} - {{f}_{0}}{{\varepsilon }_{i}}} \right) - N{{k}_{{\text{B}}}}T{{f}_{0}}} \\ \end{gathered} $Усреднение деформации звеньев по распределению, пропорциональному exp(–W/kBT), дает 〈ε〉eq = f0/Ke Учитывая это и вводя в выражение (23) замену εi = 〈εi〉eq + Δεi, получаем
(24)
$\begin{gathered} W \cong \frac{1}{2}{{k}_{{\text{B}}}}T\left( {p\sum\limits_{i = 1}^{N - 1} {{{{({{{\mathbf{t}}}_{{i + 1, \bot }}} - {{{\mathbf{t}}}_{{i \bot }}})}}^{2}} + {{f}_{0}}\sum\limits_{i = 1}^N {t_{{i \bot }}^{2}} } } \right) \\ \, + \frac{{{{k}_{{\text{B}}}}T}}{2}{{K}_{e}}\sum\limits_{i = 1}^N {{{{(\Delta {{\varepsilon }_{i}})}}^{2}} - N{{k}_{{\text{B}}}}T{{f}_{0}}\left( {1 + \frac{{{{f}_{0}}}}{{2{{K}_{e}}}}} \right)} \\ \end{gathered} $В приближении εi ≈ 〈εi〉eq имеем li⊥ ≈ l0(1 + 〈εi〉eq) ti⊥, так что ${{{\mathbf{\dot {l}}}}_{{i \bot }}}$ ≈ l0${{{\mathbf{\dot {t}}}}_{{i \bot }}}$. В данном приближении, ограничиваясь для малых изгибных колебаний членами линейными по ti⊥, уравнение (21), согласно (24), преобразуем к виду
(25)
$\begin{gathered} \varsigma {{{{\mathbf{\dot {t}}}}}_{{{\mathbf{i}} \bot }}} + \frac{{{{k}_{{\text{B}}}}T}}{{l_{0}^{2}}}\sum\limits_{j = 1}^N {{{g}_{{ij}}}[p(2{{{\mathbf{t}}}_{{j \bot }}} - {{{\mathbf{t}}}_{{j - 1, \bot }}} - {{{\mathbf{t}}}_{{j + 1, \bot }}}) + } \\ + \,{{K}_{e}}{{\langle \varepsilon \rangle }_{{eq}}}{{{\mathbf{t}}}_{{j \bot }}}] = \frac{{{{{\mathbf{f}}}_{{{\mathbf{i}} \bot }}}}}{{{{l}_{0}}}},\quad {{{\mathbf{f}}}_{{iS}}} = {{f}_{{iz}}}{\mathbf{k}} + {{{\mathbf{f}}}_{{i \bot }}} \\ \end{gathered} $Если учитывать флуктуации деформации звеньев εi = 〈εi〉eq + Δεi, то в уравнении (25) будет фигурировать член Keεjtj⊥, и к соотношению (25) добавится выражение для Δεi, содержащее tj⊥. Таким образом, в данном приближении не учитывается связь поперечных флуктуаций и флуктуаций деформации звеньев.
Далее ограничимся анализом случая l0 ≪ lp ≪ L (1 ≪ p ≪ N). Строгие краевые условия для цепей с жесткостью на изгиб имеют более сложный вид по сравнению с таковыми для гибких цепей [33, 34]. Однако для анализа динамики длинных полугибких цепей при условии lp ≪ L (p ≪ N) возможно применение нормальных мод такого же вида, как для анализа динамики гибких цепей (см., например, работы [15, 35]).
В нормальных координатах ${{{\mathbf{q}}}_{k}} = \sum\nolimits_{i = 1}^N {{{Q}_{{ki}}}{{{\mathbf{t}}}_{{i \bot }}}} $ соотношение для Δhz ≅ l0$\sum\nolimits_{i = 1}^N {{{\varepsilon }_{{i \bot }}}} $ и уравнения (24), (25) приобретают вид
(26)
$\Delta {{h}_{z}} = - \frac{1}{2}{{l}_{0}}\sum\limits_{k = 1}^N {(q_{k}^{2} - {{{\langle q_{k}^{2}\rangle }}_{{eq}}}),} $(27)
$\begin{gathered} W \cong \frac{{{{k}_{{\text{B}}}}T}}{2}\sum\limits_{k = 1}^N {\left[ {(p{{\lambda }_{k}} + {{f}_{0}})q_{k}^{2} + {{K}_{e}}\sum\limits_{i = 1}^N {{{{(\Delta {{\varepsilon }_{i}})}}^{2}}} } \right]} \\ \, - N{{k}_{{\text{B}}}}T{{f}_{0}}\left( {1 + \frac{{{{f}_{0}}}}{{2{{K}_{e}}}}} \right), \\ \end{gathered} $(28)
${{{\mathbf{\dot {q}}}}_{k}} + \frac{1}{{{{\tau }_{k}}}}{{{\mathbf{q}}}_{k}} = \frac{1}{{\varsigma {{l}_{0}}}}{{{\mathbf{S}}}_{{k \bot }}},$(29)
$\langle {{S}_{{k\alpha }}}(t) \cdot {{S}_{{n\beta }}}(t{\kern 1pt} ')\rangle = 2\varsigma kT{{\lambda }_{k}}{{\delta }_{{kn}}}{{\delta }_{{\alpha \beta }}}\delta (t - t{\kern 1pt} ')$Из соотношений (26)–(29) для ВКФ флуктуаций Δhz получаем
(30)
${{K}_{{zz}}}(t) = l_{0}^{2}\sum\limits_{k = 1}^N {\frac{1}{{{{{(p{{\lambda }_{k}} + {{f}_{0}})}}^{2}}}}\exp \left( { - 2t{\text{/}}{{\tau }_{k}}} \right)} $Подстановка выражения (30) в формулу (18) дает
(31)
$J{\kern 1pt} {\text{*}}(\omega ,{{f}_{0}}) = \frac{{{{l}_{0}}}}{{N{{k}_{{\text{B}}}}T}}\sum {\frac{1}{{{{{\left( {p{{\lambda }_{k}} + {{f}_{0}}} \right)}}^{2}}\left( {1 + i\omega {{\tau }_{k}}{\text{/}}2} \right)}}} $Отсюда
и с помощью обратного косинус-преобразования Фурье можно найти эффективный продольный модуль(33)
$B(t,{{f}_{0}}) = \frac{2}{\pi }\int\limits_0^\infty {\frac{{B{\kern 1pt} ''(\omega ,{{f}_{0}})}}{\omega }} \cos \omega tdt$В непрерывном пределе в соотношении (31) λk ≈ (kπ/N)2 и время релаксации τk ≈ τ0N4/(kπ)2(p(kπ)2 + + N2f0), где τ0 = ς$l_{0}^{2}$/kBT в системе единиц, принятой при компьютерном моделировании, с учетом значения $\varsigma = 10$, согласно формуле (3). Для цепи из N = 100 звеньев и параметра p = 10 (1 ≪ p ≪ ≪ N) во всем временном интервале измерений вплоть до растяжений u = 1 выполняется условие t ≪ τ1 = $\frac{{{{\tau }_{0}}{{N}^{4}}}}{{{{\pi }^{2}}(p{{\pi }^{2}} + {{N}^{2}}{{f}_{0}})}}$. На основании этого сумму в выражении (31) можно преобразовать в интеграл
(34)
$J{\text{*}}(\omega ,{{f}_{0}}) \cong \frac{{{{l}_{0}}}}{{N{{k}_{{\text{B}}}}T}}\int\limits_0^\infty {\frac{{dk}}{{{{{\left( {p{{{\left( {\frac{{k\pi }}{N}} \right)}}^{2}} + {{f}_{0}}} \right)}}^{2}}\left( {1 + \frac{{i\omega {{\tau }_{0}}{\text{/}}2}}{{{{{(k\pi {\text{/}}N)}}^{2}}(p{{{(k\pi {\text{/}}N)}}^{2}} + {{f}_{0}})}}} \right)}}} $При f0 = 0 отсюда, согласно выражениям (32) и (33), следует известный результат для нерастянутой цепи [16, 17], который можно представить в виде
(Γ(x) – гамма-функция).РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Вклад изгибных колебаний в ВКФ флуктуаций тензора микроскопических напряжений определяется соотношением (19). Оно получено в приближении, когда не учитываются флуктуации деформации звеньев и их связь с изгибными флуктуациями. Эффективный продольный модуль $B(t,{{f}_{0}})$ в выражении (19) определяется формулами (32)–(34). Сопоставим их с результатами компьютерного моделирования.
Пусть потенциальная энергия свободносочлененной цепи из эффективных сегментов, к концам которой приложена сила ${{{\mathbf{F}}}_{0}} = {{F}_{0}}{\mathbf{k}}$, определяется выражением ${{W}_{F}} = - \sum\nolimits_{i = 1}^n {{{b}_{{iz}}}{{F}_{0}}} $. Переходя к безразмерной силе f0(u), а также учитывая, что p = ${{l}_{p}}{\text{/}}{{l}_{0}}$, и принимая для длинных цепей b = 2lp, преобразуем выражение для ${{W}_{F}}$ к виду WF = = $ - 2{{k}_{{\text{B}}}}Tp\sum\nolimits_{i = 1}^n {{{n}_{{iz}}}{{f}_{0}}(u)} $, в котором f0(u) представляет собой равновесную зависимость силы от растяжения для дискретной персистентной цепи с эффективной энергией (2) (Приложение). Затем найдем зависимость от растяжения среднего 〈nαnβnμnν〉eq с помощью распределения, пропорционального $\exp \left( { - W{\text{/}}{{k}_{{\text{B}}}}T} \right)$.
На рис. 5 приведены данные компьютерного моделирования и результаты, вытекающие из формул (19), (32), (34), для цепи длиной N = 100 и p = 10 при относительном растяжении u = 0.1. Для вычисления $B(t,{{f}_{0}})$ вместо (33), мы воспользовались аппроксимацией Ninomiya–Ferry [36]:
(36)
$B(t) = B{\kern 1pt} '(\omega ) - 0.40B{\kern 1pt} ''(0.40\omega ) + 0.014B{\kern 1pt} ''(10\omega ){{{\text{|}}}_{{\omega = 1/t}}},$Рис. 5.
Сравнение формулы (19) с компьютерными результатами при $N = 100$, p = 10, $u = 0.1$. Сплошная линия – расчет на основе соотношений (32), (34) и (36), штриховая линия – расчет по формулам (19), (35); точки – компьютерные данные для ${{K}_{1}} \equiv {{K}_{l}} = {{K}_{c}}$ (а) и ${{K}_{2}} \equiv {{K}_{{lc}}} = {{K}_{4}}$ (1) и ${{K}_{5}}$ (2) (б).
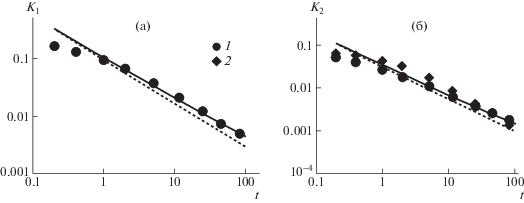
При u = 0.1 распределение сегментов цепи по углам близко к изотропному, поэтому, согласно формуле (19), ${{K}_{1}} \equiv {{K}_{l}} = {{K}_{c}};$ ${{K}_{2}} \equiv {{K}_{{lc}}} = {{K}_{4}} = {{K}_{5}}$. Однако при компьютерном моделировании кривая для K5 несколько отличается от кривой для K2. В связи с этим на рис. 5б зависимости ${{K}_{2}} \equiv {{K}_{{lc}}}$ = = K4 показаны кружками, а зависимость для K5 ромбами. Штриховые линии – зависимости для нерастянутой цепи на основе выражения для продольного модуля (35).
Чтобы представить ситуацию во всей области растяжений, рассмотрим изохроны. Они приведены на рис. 6 для цепей длиной N = 100 при p = 0 (кривая 3) и p = 10 (кривая 1 и 2, более короткие и более длинные времена соответственно). Штриховые линии получены из соотношений (5)–(9), сплошные – из формул (19), (32), (34) с аппроксимацией (36).
Рис. 6.
Зависимости ВКФ Kl (а), Kc (б), Klc (в), K4 (г) и K5 (д) от относительного растяжения цепи $u$ при фиксированных временах $t$ (изохроны). t = 10 и 80 (а), 5 и 60 (б), 20 и 80 (в, г) и 20 (д). Точки – компьютерные результаты для малых (1, 3) и больших времен (2) при p = 10 (1, 2) и 0 (3). Сплошные линии – формула (19) на основе соотношений (32), (34) и (36), штриховые линии – формулы (5)–(9).
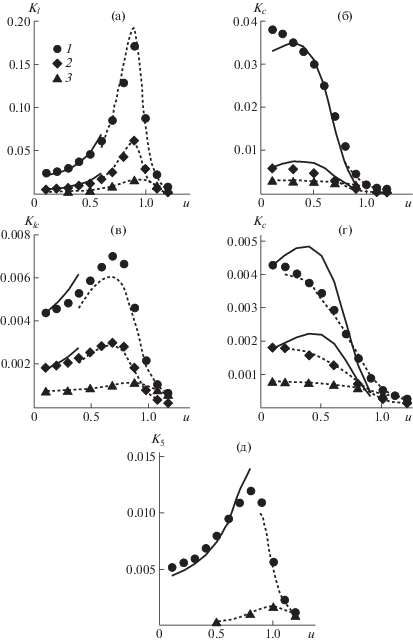
Как уже отмечалось, качественно закономерности изменения зависимостей ВКФ при растяжении при p = 0 и p = 10 сходны. ВКФ Kl, Klc, K5 проходят через максимум при больших растяжениях тогда, как Kc и K4 при растяжении монотонно убывают. В области u > 1 результаты для p = 0 и p = 10 сближаются.
Аналитическая модель, учитывающая вклад изгибных флуктуаций, представленная уравнениями (19), (32), (34) с аппроксимацией (36), дает более быстрое возрастание ВКФ Kl, Klc, K5 с растяжением цепи при u < 1 по сравнению с компьютерными результатами и не приводит к появлению максимума (рис. 6а, 6в, 6д, сплошная линия). В случае Kl рост обусловлен увеличением продольного эффективного модуля $B(t,{{f}_{0}})$ с растяжением, а также повышением среднего ${{\langle n_{z}^{4}\rangle }_{{eq}}}$, стремящегося к единице, при u, стремящемся к единице.
Штриховые линии на рис. 6a, 6в, 6д построены с помощью уравнений (5), (6), (8) и (9), т.е. модифицированная модель Рауза описывает результаты компьютерного моделирования при больших растяжениях. При этом положения максимумов для Kl при p = 0 и $p = 10$ практически совпадают, тогда как для Klc и K5 при $p = 10$ они смещены к более низким растяжениям, чем при p = 0. Как видно, положение максимумов на изохронах не зависит от выбора момента времени.
В приближении модифицированной модели Рауза характер зависимостей ВКФ ${{K}_{l}},\;{{K}_{{lc}}},\;{{K}_{5}}$ от растяжения цепи определяется уменьшением времен релаксации с растяжением и зависимостями от $u$ предэкспоненциальных множителей в соотношениях (5), (6), (8), которые проходят через максимум вблизи u = 1. На рис. 7 приведены зависимости от u для ${{({{C}_{\lambda }}{\text{/}}{{C}_{l}})}^{2}}$, ${{({{C}_{a}}{\text{/}}{{C}_{c}})}^{2}}$, $({{C}_{l}}{\text{/}}{{C}_{c}})$ и ${{C}_{a}}{\text{/}}{{C}_{c}}$. Спад данных коэффициентов с увеличением растяжения обусловлен тем, что вблизи u = 1 в зависимости $u({{f}_{0}})$ определяющую роль играет деформация звеньев, моделирующая искажения локальной структуры цепи при сильных растяжениях [20].
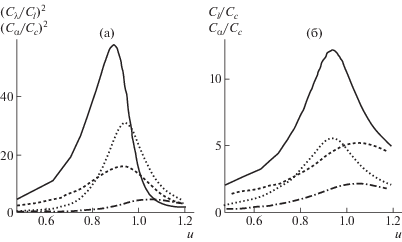
Рис. 7.
Предэкспоненциальные множители ВКФ, входящие в соотношения (5), (6), (8), в зависимости от относительного растяжения цепи. а: ${{({{C}_{\lambda }}{\text{/}}{{C}_{l}})}^{2}}$ при p = 10 (сплошная линия) и 0 (штриховая линия), ${{({{C}_{a}}{\text{/}}{{C}_{c}})}^{2}}$ при p = 10 (пунктир) и 0 (штрихпунктирная линия); б: ${{C}_{l}}{\text{/}}{{C}_{c}}$ при p = 10 (сплошная линия) и 0 (штриховая линия), ${{C}_{a}}{\text{/}}{{C}_{c}}$ при p = 10 (пунктир) и 0 (штрихпунктирная линия). Длина цепи $N = 100$.
Поперечные ВКФ ${{K}_{c}},\;{{K}_{4}}$ при ${{l}_{0}} \ll {{l}_{p}} \ll L$, согласно компьютерному эксперименту, монотонно убывают с растяжением (рис. 6б, 6д). Однако модель для учета вклада изгибных колебаний (19), (32), (34) с аппроксимацией (36) дает для Kc зависимости, проходящие через максимум (рис. 6б, сплошные линии). Такой характер зависимости Kc от растяжения обусловлен увеличением продольного эффективного модуля $B(t,{{f}_{0}})$ с растяжением. При этом средние 〈$n_{z}^{2}n_{x}^{2}$〉eq = 〈$n_{z}^{2}n_{y}^{2}$〉eq вначале несколько возрастают в области растяжений примерно до u = 0.6, а в дальнейшем убывают до нуля. Сочетание двух указанных факторов дает максимум при степенях растяжений в области 0.3–0.4.
На рис. 6г вместе с результатами компьютерного моделирования представлены теоретические зависимости K4 от u согласно формулам (7), (9). При $u = 0.3$ зависимости K4 от времени совпадают с результатами компьютерного моделирования в интервале $t$ от 10 до 100 (см. рис. 8, где кружки соответствуют $u = 0.3$). С ростом растяжения цепи этот временной интервал расширяется и при больших растяжениях охватывает всю исследованную область времен (рис. 8, треугольники для $u = 1.1$).
Рис. 8.
Зависимости ВКФ ${{K}_{4}}$ от времени при растяжении u = 0.3 (1) и 1.1 (2). Точки – результаты компьютерного моделирования; сплошные линии построены на основе соотношений (7). Длина цепи $N = 100$, p = 10.
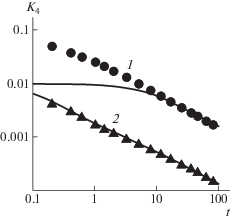
Модель для учета вклада изгибных колебаний дает для K4 максимум, аналогичный максимуму для Kc (рис. 6г).
Согласно данным компьютерного моделирования, максимумы на зависимостях ${{K}_{c}}$ и K4 от $u$ наблюдаются лишь при ${{l}_{p}} \lesssim L$. При больших растяжениях $u \geqslant 0.9$ компьютерные результаты для ${{K}_{c}}$ описываются соотношением (7). В области $u \geqslant 1$ результаты для ${{K}_{c}}$ и K4 при $p = 0$ и $p = 10$ стремятся друг к другу.
Таким образом, изохроны для ВКФ при ${{l}_{0}} \ll {{l}_{p}} \ll L$ для гибких и полугибких цепей качественно сходны. Такие ВКФ как ${{K}_{{zzzz}}},{{K}_{{zxzx}}},{{K}_{{zzxx}}}$, где $Z$– ось растяжения цепи, проходят через максимум при больших растяжениях. Величина максимума растет с увеличением персистентной длины и при ${{l}_{p}} > > {{l}_{0}}$ становится значительно больше величины максимума для свободносочлененной цепи.
Изохроны для ВКФ вида ${{K}_{{xxxx}}},{{K}_{{xyxy}}}$ демонстрируют монотонное убывание с увеличением $u$ в случае ${{l}_{0}} \ll {{l}_{p}} \ll L$. Однако при ${{l}_{0}} \ll {{l}_{p}} \lesssim L$ на зависимостях этих ВКФ от $u$ также появляется максимум, который располагается вдали от u = 1 в отличие от максимумов ВКФ ${{K}_{{zzzz}}},{{K}_{{zxzx}}},{{K}_{{zzxx}}}$. Модель, учитывающая изгибные флуктуации полимерной цепи, дает для ВКФ ${{K}_{{xxxx}}},{{K}_{{xyxy}}}$ максимумы вдали от u = 1 в той же области растяжений (и ~ 0.3–0.4), что и в компьютерном моделировании (см. рис. 2a, 2б и 6б, 6г). Но в модели с изгибными флуктуациями максимумы появляются уже при ${{l}_{0}} \ll {{l}_{p}} \ll L$, тогда как согласно результатам компьютерного моделирования, они в данной области отсутствуют и возникают, когда персистентная длина становится соизмеримой с контурной длиной цепи. Можно отметить, что предложенная модель учета изгибных движений цепи пренебрегает флуктуациями деформации звеньев цепи и их связью с изгибными флуктуациями. Это может быть одной из возможных причин расхождений аналитических результатов и компьютерного моделирования. В рассмотренном приближении модель учета изгибных флуктуаций справедлива для длинных слабо растянутых цепей, удовлетворяющих условию ${{l}_{0}} \ll {{l}_{p}} \ll L$. Модифицированная модель Рауза справедлива и в случае ${{l}_{0}} \ll {{l}_{p}} \lesssim L$ для сильно растянутых цепей.
В области $u \geqslant 1$ результаты для гибких и полугибких цепей сближаются.
ЗАКЛЮЧЕНИЕ
Характер зависимости ВКФ растянутой цепи от степени растяжения определяет вид деформационной зависимости релаксационных модулей цепей и систем, образованных ими. В настоящей работе рассматривается высокочастотная область, в которой имеет место скейлинговая зависимость модуля потерь $E{\kern 1pt} '{\kern 1pt} '\sim {{\omega }^{n}}$ с показателем $n \geqslant 0.5$. Для статически растянутой сетки гибких цепей в переходной зоне частот (гауссова область) модуль потерь проходит через максимум при больших деформациях [20]. Положение и высота максимума определяются такими структурными параметрами сетки, как степень ее однородности, густота, податливость локальной структуры сильно растянутых цепей. Можно полагать, что модуль потерь $E{\kern 1pt} '{\kern 1pt} '$ статически растянутой сетки полугибких цепей в высокочастотной области тоже будет проходить через максимум при больших деформациях, положение которого помимо перечисленных параметров сетки будет также зависеть от параметра p – локальной меры жесткости цепей на изгиб. Сравнение теоретических зависимостей $E{\kern 1pt} '{\kern 1pt} '\; - \lambda $, где $\lambda $ – степень растяжения сетки, в указанной области частот с экспериментальными данными может позволить определить структурные параметры сетки. В высокочастотной области, где $n \geqslant 0.5$, зависимость $E{\kern 1pt} '{\kern 1pt} '\; - \lambda $ обладает слабой чувствительностью к взаимодействиям цепей, приводящим к топологическим ограничениям. Следовательно, данная зависимость позволит проводить изучение наиболее растянутых (несущих нагрузку) цепей в деформированных сетках без учета топологических ограничений.
Как отмечалось, при $u \geqslant 1$ закономерности затухания ВКФ для цепей с $p \gg 1$ близки к закономерностям затухания ВКФ для гибких цепей с p = 0, т.е. для сильно растянутых цепей жесткость на изгиб не играет существенной роли. Зависимости ВКФ от времени и степени растяжения в этой области u можно описать с помощью выражений (5)–(9) для модифицированной модели Рауза, в которой коэффициенты упругости субцепей вычисляются с помощью равновесной зависимости u от f0 для персистентной цепи из растяжимых звеньев. Иными словами, при изучении прочности полимерных сеток с помощью этой модели можно вычислить времена релаксации и модули сильно растянутых цепей сетки, которые согласно работам [1–3] определяют скорость распространения микротрещин в ней.
Для слабо растянутых персистентных цепей определяющую роль играют изгибные колебания, и закономерности затухания ВКФ существенно отличаются от таковых при p = 0. Получено выражение для ВКФ (соотношение (19)), учитывающее такие колебания. Оно было проанализировано при условии ${{l}_{0}} \ll {{l}_{p}} \ll L$ и при игнорировании флуктуаций деформации звеньев и их связи с изгибными флуктуациями цепи. Анализ привел к соотношениям (32), (34), которые вместе с выражением (19) хорошо согласуются с результатами компьютерного моделирования для длинных слабо растянутых цепей при условии ${{l}_{0}} \ll {{l}_{p}} \ll L$.
Однако с увеличением степени растяжения соотношения (32), (34) дают для ВКФ ${{K}_{{zzzz}}},{{K}_{{zxzx}}},{{K}_{{zzxx}}}$, где $Z$ – ось растяжения, возрастание с растяжением более быстрое, чем в компьютерном эксперименте, а для ВКФ типа ${{K}_{{xxxx}}},{{K}_{{xyxy}}}$ дают вначале некоторое увеличение вместо монотонного убывания, наблюдаемого при молекулярном динамическом моделировании в случае ${{l}_{0}} \ll {{l}_{p}} \ll L$. В то же время подобное увеличение ${{K}_{{xxxx}}},{{K}_{{xyxy}}}$ с растяжением имеет место в компьютерном моделировании, когда ${{l}_{0}} \ll {{l}_{p}} \lesssim L$, в той же области степеней растяжения, что и в аналитической модели с изгибными флуктуациями.
Одной из возможных причин обнаруженных расхождений может быть пренебрежение флуктуациями деформации звеньев и их связью с поперечными изгибными флуктуациями цепи.
Вычислительные ресурсы были предоставлены Межведомственным суперкомпьютерным центром РАН.
Список литературы
Persson B.N.J., Albohr O., Heinrich G., Ueba H. // J. Phys. Condens. Matter. 2005. V. 17. № 44. R1071.
Herst T., Heinrich G. // Polymer Science A. 2008. V. 50. № 5. P. 583.
Klüppel M. // J. Phys., Condens. Matter. 2009. V. 21. № 3. 035104.
Pincus P. // Macromolecules. 1997. V. 10. № 1. P. 210.
De Gennes P.G. // Scaling Laws in Polymer Physics. Ithaca: Cornell Univ. Press, 1979.
Marciano Y., Brochard-Wyart F. // Macromolecules. 1995. V. 28. № 4. P. 985.
Даринский А.А., Готлиб Ю.Я., Люлин А.В., Неелов И.М. // Высокомолек. соед. А 1994. Т. 36. № 7. С. 1148.
Febbo M., Milchev A., Rostiashvili V., Dimitrov D., Vilgis T.A. // J. Chem. Phys. 2008. V. 129. № 15. 154908.
Бородин И.П., Хазанович Т.Н. // Высокомолек. соед. А. 1973. Т. 15. № 9. С. 2121.
Borodin I.P., Khazanovich T.N. // Polymer. 1986. V. 27. № 7. P. 1044.
Toshchevikov V.P., Heinrich G., Gotlib Yu.Ya. // Macromol. Theory Simul. 2010. V. 19. № 4. P. 195.
Munch. E., Pelletier J.M., Sixou B., Vigier G. // Polymer. 2006. V. 47. № 10. P. 3477.
Broedersz C.P., Mackintosh F.C. // Revs Modern Phys. 2014. V. 86. № 3. P. 995.
Lamura A., Winkler R.G. // Polymers. 2019. V. 11. № 4. P.737.
Готлиб Ю.Я., Даринский А.А., Светлов Ю.Е. Физическая кинетика макромолекул. Л.: Химия, 1986.
Gittes F., Mackintosh F.C. // Phys. Rev. E. 1998. V. 58. № 2. R1241(R).
Pasquali M., Shankar V., Morse D.C. // Phys. Rev. E. 2001. V. 64. № 2. 020802(R).
Marko J.F., Siggia E.D. // Macromolecules. 1995. V. 28. № 26. P. 8759.
Зубарев Д.Н. Неравновесная статистическая термодинамика. М.: Наука, 1971.
Borodin I.P., Borodina T.I., Khazanovich T.N. // Macromol. Theory Simul. 2012. V. 21. № 7. P. 438.
Saphiannikova M., Toshchevikov V., Gazuz I., Petry F., Westermann S., Heinrich G. // Macromolecules. 2014. V. 47. № 14. P. 4813.
Balabaev N.K., Borodin I.P., Khazanovich T.N. // Polymer Science A. 2008. V. 50. № 12. P. 2132.
Balabaev N.K., Borodin I.P., Borodina T.I., Kha-zanovich T.N. // Polymer Science A. 2011. V. 53. № 11. P. 1085.
Hoffman G.G. // J. Phys. Chem. B. 1999. V. 103. № 34. P. 7167.
Lin. Y.-H., Das A.K. // J. Chem. Phys. 2007. V. 126. № 7. P. 074902.
Lemak A.S., Balabaev N.K. // J. Comput. Chem. 1996. V. 17. № 15. P. 1685.
Kierfeld J., Niamploy O., Sa-Yakanit V., Lipowsky R. // Eur. Phys. J. E. 2004. V. 14. № 1. P. 17.
Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука, 1989.
Hugel T., Rief M., Seitz M., Gaub H.E., Netz R.R. // Phys. Rev. Lett. 2005. V. 94. № 4. P. 048301.
Дой М., Эдвардс С. Динамическая теория полимеров / Пер. с англ. под ред. С. И. Кучанова, В.В. Кислова. М.: Мир, 1998
Rubinstein M., Colby R.H. Polymer Physics. Oxford: Oxford Univ. Press, 2003.
Бородин И.П., Хазанович Т.Н. // Теорет. и мат. Физика. 1974. Т. 21. № 1. С. 130.
Готлиб Ю.Я., Светлов Ю.Е. // Высокомолек. соед. А. 1979. Т. 21. № 7. С. 1531.
Bixon M., Zwanzig R. // J. Chem. Phys. 1978. V. 68. № 4. P. 1896.
Steinhauser M.O. // Mech. Time – Depend Mater. 2008. V. 12. № 4. P. 291.
Ferry J.D. Viscoelastic Properties of Polymers. New York: Wiley, 1980.
Balabaev N.K., Borodin I.P., Khazanovich T.N. // Polymer Science A. 2010. V. 52. № 6. P. 655.
Storm C., Nelson P.C. // Phys. Rev. E 2003. V. 67. № 5. P. 051906.
Odijk T. // Macromolecules. 1995. V. 28. № 20. P. 7016.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)


