Высокомолекулярные соединения (серия А), 2021, T. 63, № 2, стр. 136-144
ОСОБЕННОСТИ ПОВЕДЕНИЯ СТРУИ ПОЛИМЕРНОГО РАСТВОРА ПРИ ЭЛЕКТРОСПИННИНГЕ
a Институт нефтехимического синтеза им. А.В. Топчиева Российской академии наук
119991 Москва, Ленинский пр. 29, Россия
b Институт физической химии и электрохимии им. А.Н. Фрумкина Российской академии наук
119071 Москва, Ленинский пр. 31, Россия
* E-mail: subbotin@ips.ac.ru
Поступила в редакцию 24.09.2020
После доработки 26.10.2020
Принята к публикации 02.11.2020
Аннотация
Методом численного анализа уравнения баланса сил и реологического уравнения модели конечно растяжимых цепей исследована динамика заряженной струи при электроспиннинге полимерного раствора, а также ориентация макромолекул в струе. В относительно слабых электрических полях струя всегда остается прямолинейной, тогда как в сильных полях прямолинейный участок струи имеет конечную длину, после чего движение струи становится неустойчивым. Такое поведение обусловлено конкуренцией между инерционными и вязкоупругими силами, причем вязкоупругость доминирует в сильных полях. Установлено, что полимерные цепи в струе сильно вытягиваются вдоль потока.
ВВЕДЕНИЕ
Известно, что в сильных электрических полях мениски растворов полимеров испускают тонкие струйки, из которых после испарения растворителя формируется волокно [1–3]. Это явление широко используют для получения разнообразных волокнистых материалов, которые нашли применение в медицине, катализе, при создании фильтров и в других областях [3, 4]. Эксперименты показывают, что течение струи под действием электрического поля характеризуется большой скоростью растяжения, которая превышает обратное время релаксации макромолекул, и может сопровождаться фазовым переходом с образованием в ней нитевидных структур [5–7]. Также происходит ориентация макромолекул вдоль оси струи. Ориентация наблюдается и в образующихся на коллекторе нановолокнах [8–10]. Это согласуется с общей картиной поведения растворов полимеров при механическом растяжении, включающем фазовое расслоение и образование волокна [11–15]. Одним из механизмов расслоения растворов при растяжении является изменение баланса между притяжением и отталкиванием макромолекул в результате их ориентации потоком [16–18]. Такой же механизм должен работать и при электроспиннинге.
При типичных условиях проведения процесса электроспиннинга раствор медленно вытекает из сопла электрода и принимает форму конусообразного мениска, вершина которого испускает тонкую струю (рис. 1). Согласно теории Тейлора, стабилизация конусообразного мениска обеспечивается действием нормальной электростатической силы и капиллярной силы [19]. Однако статический конус с углом при вершине 98.6°, который был найден Тейлором, не может испустить струю. Эксперименты показывают, что существует достаточно широкий разброс значений угла [20], и вопрос о предсказании формы мениска пока остается открытым.
Рис. 1.
Схема, иллюстрирующая процесс истечения струи из конусообразного мениска (область I) при электроспиннинге. Радиус переходной области II равен b. В области III происходит струйное течение. Цветные рисунки можно посмотреть в электронной версии.
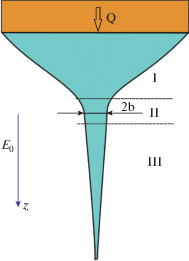
Важную роль в поведении струи играет переходная область между конусом и струей. В данной области происходит изменение механизма течения зарядов вдоль струи, а также меняется баланс действующих сил [1, 21–23]. Кроме того, эта область характеризуется максимальной скоростью деформации раствора [24–26].
Полный электрический ток в системе конус–струя включает в себя ток ионов в объеме Ib, который приводит к заряжению свободной поверхности жидкости, ток поверхностных ионов Is, вызываемый действием поля, и поверхностный конвективный ток Ic, обусловленный потоком жидкости: $I = {{I}_{b}} + {{I}_{s}} + {{I}_{c}}$. Внутри мениска преобладает объемный ток, тогда как в струе он в основном определяется поверхностным током проводимости или конвективным током. В области перехода ${{I}_{b}} \simeq {{I}_{c}}$ или ${{I}_{b}} \simeq {{I}_{s}}$.
Следуя аргументам Тейлора, плотность свободного электрического заряда σf на поверхности струи в зоне перехода находится из баланса капиллярной и нормальной электростатической сил: ${{\sigma }_{f}} \sim {{\left( {\gamma {{\varepsilon }_{0}}{\text{/}}b} \right)}^{{1/2}}}$, где $\gamma $ – поверхностное натяжение, b – радиус переходной области (${{\varepsilon }_{0}}$ – проницаемость вакуума) [1, 2]. Такой заряд создает локальное поле напряженности $E \sim {{\sigma }_{f}}{\text{/}}{{\varepsilon }_{0}}$. Наряду с этим полем на жидкость действует поле ${{E}_{0}}$, создаваемое электродами. Если электрическое поле внутри переходной зоны в основном определяется поверхностными зарядами, а ток в струе обусловлен конвекцией, то радиус переходной зоны равен $b = {{b}_{1}} \sim {{\left( {Q{{\varepsilon }_{0}}{\text{/}}K} \right)}^{{1/3}}}$. При этом электрический ток изменяется как $I \simeq 2{{I}_{b}} \sim {{\left( {\gamma KQ} \right)}^{{1/2}}}$ [21]. Здесь Q – объемный расход жидкости, K – коэффициент электропроводности. Когда электрическое поле в переходной зоне становится порядка внешнего поля, $E \simeq {{E}_{0}}$, возникает другой режим, в котором радиус переходной зоны и электрический ток задаются выражениями b = b2 ~ ~ ${{\left( {\frac{Q}{{K{{E}_{0}}}}} \right)}^{{2/7}}}{{(\gamma {{\varepsilon }_{0}})}^{{1/7}}}$ и $I \sim {{(\gamma {{\varepsilon }_{0}})}^{{2/7}}}{{(K{{E}_{0}})}^{{3/7}}}{{Q}^{{4/7}}}$ соответственно [27]. При заданном поле ${{E}_{0}}$ и большом расходе радиус переходной зоны равен b2, а при малых расходах – b1. Дальнейшее уменьшение расхода жидкости приводит к уменьшению конвективного тока, так что при очень маленьком расходе жидкости радиус переходной зоны определяется условием ${{I}_{b}} \simeq {{I}_{s}}$ и равен b = b3 ~ ~ ${{(\mu {\text{/}}K)}^{{2/3}}}{{(\gamma {{\varepsilon }_{0}})}^{{1/3}}}$ [28, 29]. Здесь $\mu $ – подвижность поверхностных зарядов. Ток изменяется как I ~ ~ $e\gamma \mu $, где e – единичный заряд [28].
В большинстве режимов электроспиннинга электрический ток в основном состоит из объемного тока Ib и конвективного тока Ic, тогда как поверхностный ток проводимости Is относительно невелик. Динамика струи в данном случае определяется балансом тангенциальной электрической силы, с одной стороны, и капиллярной, вязкоупругой и инерционной силами, с другой. Вклад нормальной электрической силы становится несущественным. Это следует из того обстоятельства, что поверхностная плотность заряда струи понижается с уменьшением радиуса струи a как ${{\sigma }_{f}} \sim aI{\text{/}}Q$ [19]. Таким образом, нормальная электрическая сила, действующая на единицу площади свободной поверхности, Fn ~ ~ $\sigma _{f}^{2}{\text{/}}{{\varepsilon }_{0}} \propto {{a}^{2}}$, также уменьшается. В то же время давление Лапласа γ/a внутри струи увеличивается и больше не может компенсироваться нормальным электрическим давлением: оно компенсируется за счет действия касательной электрической силы. Чтобы обеспечить плавное изменение баланса сил в переходной зоне, нормальная и тангенциальная составляющие электрической силы, отнесенные к единице площади поверхности, и давление Лапласа должны быть величинами одного порядка. Для устойчивого истечения струи вязкоупругие и инерционные силы не должны превышать капиллярные силы в переходной зоне.
Форма струи была исследована как теоретически [27, 29–34], так и с помощью различных экспериментальных методов [26, 35, 36]. Анализ уравнения баланса сил показал, что при доминировании тангенциальной электрической силы и капиллярной силы радиус струи уменьшается с расстоянием z как $a(z) \propto {{z}^{{ - 1}}}$. Аналогичное поведение получается из баланса тангенциальной электрической и вязкой сил [27]. При переходе от вязких сил к вязкоупругим, предсказано другое поведение, $a(z) \propto {{z}^{{ - 1/2}}}$ [35]. Наконец, баланс электрических и инерционных сил дает $a(z) \propto {{z}^{{ - 1/4}}}$ [30].
Важной проблемой является определение условий устойчивости струи при электроспиннинге. Данному вопросу посвящено большое число работ [37–44]. Основные теоретические результаты получены с использованием метода линейного анализа устойчивости. При этом струя моделируется длинным заряженным цилиндром. Были рассмотрены случаи как аксиально-симметричных [41, 42], так и изгибных возмущений цилиндрической струи [43, 44].
В настоящей работе на основе численного анализа уравнения баланса электрической, капиллярной, вязкоупругой и инерционной сил и определяющего уравнения модели FENE-P (конечно растяжимой нелинейной упругости) [45], описывающей реологическое поведение раствора полимерных цепей, исследована динамика заряженной струи и ориентация макромолекул в струе. Используемый подход позволяет изучить роль конечной растяжимости в динамике струи при сильном растяжении цепей.
УРАВНЕНИЯ ДИНАМИКИ СТРУИ
Рассмотрим аксиально-симметричную струю полимерного раствора, испускаемую коническим мениском в направлении оси $z$ (рис. 1). Предполагается, что электроды создают электрическое поле напряженности ${{E}_{0}}$ в направлении z. Поскольку радиус струи a(z) медленно меняется с расстоянием, $\left| {\frac{{da}}{{dz}}} \right| \ll 1$, ее поведение можно описать в приближении тонкого тела [31–34]. В стационарном режиме скорость потока в струе и скорость растяжения струи представляются следующим образом:
(1)
${{v}_{z}} = \frac{Q}{{\pi {{a}^{2}}(z)}},\quad \dot {\varepsilon } = \frac{{d{{v}_{z}}}}{{dz}} \simeq - \frac{{2Q}}{{\pi {{a}^{3}}}}\frac{{da}}{{dz}}$Здесь Q – объемный расход жидкости. Далее будем использовать следующие физические параметры: раствор полимера характеризуется плотностью ρ и поверхностным натяжением $\gamma $. Электропроводность ионов в растворе равна K.
Модель FENE-P широко применяется при исследовании динамики растяжения полуразбавленных растворов полимеров [46, 47]. Она также позволяет учитывать конечную растяжимость полимерных клубков. Будем полагать, что полимерные цепи имеют полную длину $L$ и длину сегмента as, так что полное число сегментов в цепи равно $N = L{\text{/}}{{a}_{s}} \gg 1$. Зависимость силы растяжения цепи f от расстояния между ее концами ${\mathbf{R}}$ описывается нелинейным законом ${\mathbf{f}}({\mathbf{R}}) = \frac{{3{{k}_{{\text{B}}}}T}}{{{{{\langle {{{\mathbf{R}}}^{2}}\rangle }}_{0}}}}\frac{{\mathbf{R}}}{{1 - {{{\mathbf{R}}}^{2}}{\text{/}}{{L}^{2}}}}$, где ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $T$ – температура и ${{\langle {{{\mathbf{R}}}^{2}}\rangle }_{0}} \simeq {{a}_{s}}L = a_{s}^{2}N$. Раствор характеризуется модулем упругости $G$ и временем релаксации τ, а вязкость находится из скейлинговой формулы $\eta \simeq G\tau $. В случае полуразбавленных растворов без зацеплений $\tau \propto {{N}^{2}}$ (время Рауза) и $G = n{{k}_{{\text{B}}}}T$, где $n$ – концентрация цепей.
Реологическое уравнение FENE-P модели формулируется в терминах тензора ${\mathbf{A}} = \left\langle {{\mathbf{RR}}} \right\rangle $, где угловые скобки обозначают усреднение по конформациям всех цепей. Тензор напряжений определяется формулой
(2)
${\mathbf{\Sigma }} = G\frac{{{\mathbf{A}}{\text{/}}R_{0}^{2} - {\mathbf{I}}}}{{1 - {\text{tr}}{\mathbf{A}}{\text{/}}{{L}^{2}}}},$(3)
$\begin{gathered} \tau \left[ {\frac{{\partial {\mathbf{A}}}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{A}} - {{{\left( {\nabla {\mathbf{v}}} \right)}}^{T}} \cdot {\mathbf{A}} - {\mathbf{A}} \cdot \nabla {\mathbf{v}}} \right] + \\ \, + \frac{{{\mathbf{A}} - R_{0}^{2}{\mathbf{I}}}}{{1 - {\text{tr}}{\mathbf{A}}{\text{/}}{{L}^{2}}}} = 0, \\ \end{gathered} $Продольное электрическое поле ${{E}_{z}}$, действующее на струю, включает в себя внешнее поле E0 и поле зарядов конусообразного мениска ${{E}_{c}}$, ${{E}_{z}}$ = = E0 + Ec. Вклад от мениска на масштабах больше радиуса переходной зоны $b$ (как правило b < < 100 мкм) можно представить в виде [19–21]
(4)
${{E}_{c}}(z) \simeq \kappa \sqrt {\frac{\gamma }{{{{\varepsilon }_{0}}\left( {b + z} \right)}}} \equiv \frac{{E{\kern 1pt} *}}{{\sqrt {1 + z{\text{/}}b} }}$Здесь численный коэффициент $\kappa $ зависит от угла при вершине конуса, а z = 0 соответствует точке перехода между конусом и струей: Ec(0) = E* = = $\kappa \sqrt {\frac{\gamma }{{{{\varepsilon }_{0}}b}}} $. Очевидно, что формула (4) перестает быть справедливой на масштабах, превышающих размер мениска. В этой области поле в основном определяется электродами. Формула для суммарного поля Ez дает правильное поведение вблизи переходной зоны и на бесконечности и будет использована для оценки поля вдоль всей струи.
Электрический ток, проходящий через струю, определяется выражением
(5)
$I \simeq {{I}_{c}} + {{I}_{b}} \simeq 2\pi a{{\sigma }_{f}}{{v}_{z}} + \pi {{a}^{2}}K{{E}_{z}},$(6)
${{a}^{2}}\frac{d}{{dz}}\left( {\gamma C - {{F}_{n}}} \right) + \frac{d}{{dz}}[{{a}^{2}}(\rho v_{z}^{2} + {{\Sigma }_{{rr}}} - {{\Sigma }_{{zz}}})] = 2a{{F}_{z}}$Будем предполагать, что величина тока известна, следовательно, поверхностную плотность заряда σf можно выразить через ток используя формулу (5). Исключая напряжения из уравнения (6) по формуле (2) и учитывая, что $\gamma \frac{{dC}}{{dz}} \simeq - \frac{\gamma }{{{{a}^{2}}}}\frac{{da}}{{dz}}$, имеем
(8)
$\begin{gathered} \frac{{da}}{{dz}}\left( {\gamma + \frac{{2\rho {{Q}^{2}}}}{{{{\pi }^{2}}{{a}^{3}}}}} \right) + G\frac{d}{{dz}}\left[ {\frac{{{{a}^{2}}\left( {{{A}_{{zz}}} - {{A}_{{rr}}}} \right){\text{/}}R_{0}^{2}}}{{1 - \left( {{{A}_{{zz}}} + 2{{A}_{{rr}}}} \right){\text{/}}{{L}^{2}}}}} \right] = \\ \, = - \frac{{{{E}_{z}}{{a}^{2}}}}{Q}(I - \pi {{a}^{2}}K{{E}_{z}}) \\ \end{gathered} $Здесь компоненты конформационного тензора удовлетворяют уравнению (3). Выражения (8) и (3) запишем в безразмерном виде с помощью подстановки
(9)
$a = b{\kern 1pt} {\text{*}}\bar {a},\quad z = \ell \bar {z},\quad {\mathbf{A}} = {\mathbf{\bar {A}}}R_{0}^{2},$(10)
$\frac{{d{{{\bar {A}}}_{{zz}}}}}{{d\bar {z}}} + \frac{{4{{{\bar {A}}}_{{zz}}}}}{{\bar {a}}}\frac{{d\bar {a}}}{{d\bar {z}}} + \frac{{{{{\bar {a}}}^{2}}\left( {{{{\bar {A}}}_{{zz}}} - 1} \right)}}{{1 - \delta \left( {{{{\bar {A}}}_{{zz}}} + 2{{{\bar {A}}}_{{rr}}}} \right)}} = 0$(11)
$\frac{{d{{{\bar {A}}}_{{rr}}}}}{{d\bar {z}}} - \frac{{2{{{\bar {A}}}_{{rr}}}}}{{\bar {a}}}\frac{{d\bar {a}}}{{d\bar {z}}} + \frac{{{{{\bar {a}}}^{2}}\left( {{{{\bar {A}}}_{{rr}}} - 1} \right)}}{{1 - \delta \left( {{{{\bar {A}}}_{{zz}}} + 2{{{\bar {A}}}_{{rr}}}} \right)}} = 0$(12)
$\begin{gathered} \frac{{d\bar {a}}}{{d\bar {z}}}\left[ {1 + \frac{\omega }{{{{{\bar {a}}}^{3}}}} - \frac{{2\bar {a}({{{\bar {A}}}_{{zz}}} + 2{{{\bar {A}}}_{{rr}}})}}{{1 - \delta ({{{\bar {A}}}_{{zz}}} + 2{{{\bar {A}}}_{{rr}}})}} - } \right. \\ \, - \left. {\frac{{4\delta \bar {a}{{{({{{\bar {A}}}_{{zz}}} - {{{\bar {A}}}_{{rr}}})}}^{2}}}}{{{{{(1 - \delta ({{{\bar {A}}}_{{zz}}} + 2{{{\bar {A}}}_{{rr}}}))}}^{2}}}}} \right] = \frac{{{{{\bar {a}}}^{4}}({{{\bar {A}}}_{{zz}}} - {{{\bar {A}}}_{{rr}}})\left( {1 - 3\delta } \right)}}{{{{{(1 - \delta ({{{\bar {A}}}_{{zz}}} + 2{{{\bar {A}}}_{{rr}}}))}}^{3}}}} - \\ \, - \chi {{{\bar {a}}}^{2}}\psi (\bar {z})\left( {1 - \frac{{{{{\bar {a}}}^{2}}b{\kern 1pt} {{*}^{2}}\psi (\bar {z})}}{{2{{b}^{2}}\psi (0)}}} \right) \\ \end{gathered} $В приведенных уравнениях обозначения следующие:
(13)
$\begin{gathered} \delta = \frac{{R_{0}^{2}}}{{{{L}^{2}}}} = \frac{1}{{3N}},\quad \chi = \frac{{\eta I{{E}_{0}}}}{{\pi {{\gamma }^{2}}}}, \\ \omega = \frac{{2\rho {{Q}^{2}}}}{{{{\pi }^{2}}\gamma b{\kern 1pt} {{*}^{3}}}} = \frac{{2\rho {{Q}^{2}}{{G}^{3}}}}{{{{\pi }^{2}}{{\gamma }^{4}}}}, \\ \psi (\bar {z}) = 1 + \frac{{E{\kern 1pt} *}}{{{{E}_{0}}}}\frac{1}{{\sqrt {1 + \ell \bar {z}{\text{/}}b} }} \\ \end{gathered} $Численное решение системы уравнений (10)–(12) будет проведено для цепей с числом сегментов $N = 600$ и $N = 2000$ и с отношением $E{\kern 1pt} {\text{*/}}{{E}_{0}}$ = 2. Для цепей с $N = 600$ сегментами используем такие значения параметров: χ = 2, $\omega = 0.0095$, $b{\text{/}}b{\kern 1pt} * = 1{\text{/}}\sqrt {20} $, $\ell {\text{/}}b = 0.2$. Для цепей с числом сегментов $N = 2000$ – χ = 3, ω = 0.003, $b{\text{/}}b{\kern 1pt} * = 1{\text{/}}\sqrt {40} $, $\ell {\text{/}}b = 0.1$. Указанные величины получены из реальных значений параметров электроспиннинга [1]. При выборе значений параметров мы также исходили из того, что решения уравнений (10)–(12) описывают бесконечно длинную прямолинейную струю.
Далее напряженность внешнего поля увеличивается в $\nu $ раз, ${{E}_{0}} \to \nu {{E}_{0}}$. При расчетах полагали $\nu = 2$. После увеличения поля радиус переходной зоны $b$ и поле в переходной зоне $E{\kern 1pt} *$ изменяются так: $b \to \beta b$, $E{\kern 1pt} * \to E{\kern 1pt} *{\text{/}}\sqrt \beta $. Коэффициент $\beta $ находится из равенства объемного и конвективного тока в точке перехода: $\pi {{\beta }^{2}}{{b}^{2}}K(\nu {{E}_{0}} + E{\kern 1pt} {\text{*/}}\sqrt \beta ) = \frac{{2Q\sigma _{f}^{*}}}{{\beta b}}$, где $\sigma _{f}^{*} \simeq {{\varepsilon }_{0}}E{\kern 1pt} *{\text{/}}\sqrt \beta $. Используя последнее равенство для $\nu = 1$ и произвольного $\nu $, можно получить уравнение на $\beta $:
Таким образом, значения параметров в формулах (10)–(12), которые зависят от внешнего поля, изменяются следующим образом: $\chi \to \chi \nu {\text{/}}{{\beta }^{{3/2}}}$, E*/E0 → $(E{\kern 1pt} {\text{*/}}{{E}_{0}}){\text{/}}(\nu {{\beta }^{{1/2}}})$, $\bar {a}(0) \to \bar {a}(0)\beta $, $\ell {\text{/}}b$ → → $(\ell {\text{/}}b){\text{/}}\beta $. В точке z = 0 конформация полимерных цепей предполагается гауссовой, ${{\bar {A}}_{{zz}}}(0) = {{\bar {A}}_{{rr}}}(0)$ = 1, а радиус струи равен $\bar {a}(0) = b{\text{/}}b{\kern 1pt} *$. Для приведенных значений параметров сила инерции и вязкоупругая сила в переходной зоне сопоставимы с капиллярной силой. Дифференциальные уравнения (10)–(12) с начальными условиями решались с использованием метода Рунге–Кутты.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Соотношения (10)–(12) позволяют также найти ориентацию цепей в зависимости от координаты $\bar {z}$, характеризуемой параметром порядка s = = $\sqrt {({{A}_{{zz}}} - R_{0}^{2})} {\text{/}}L = \sqrt {\delta ({{{\bar {A}}}_{{zz}}} - 1)} $, который меняется в пределах $0 \leqslant s \leqslant 1$. Для сильно вытянутых цепей $s \simeq {{R}_{z}}{\text{/}}L$, где Rz – размер цепи вдоль оси струи [16–18].
Расчеты показывают возможность существования двух режимов поведения струи, переход между которыми происходит при изменении величины внешнего электрического поля в ν раз (ν = 2). В слабых полях струя остается прямолинейной и бесконечно длинной (режим I). Графики функций $\bar {a}(\bar {z})$, $s(\bar {z})$, ${{\bar {A}}_{{rr}}}(\bar {z})$ для $N = 600$ и $N = 2000$ показаны на рис. 2а и рис. 3а соответственно. Радиус струи монотонно уменьшается, а параметр порядка $s(\bar {z})$ сначала возрастает вдоль оси струи и после достижения максимального значения начинает убывать. Компонента ${{\bar {A}}_{{rr}}}(\bar {z})$ тензора конформаций также ведет себя немонотонно: сначала уменьшается, а затем растет к равновесному значению, соответствующему состоянию клубка. Такое поведение свидетельствует о протекании процессов релаксации цепей после их растяжения и продольного сжатия. Интересно отметить, что релаксация поперечного размера макромолекул начинается раньше, чем продольного.
Рис. 2.
Зависимость радиуса струи $\bar {a}$ (1), параметра порядка s (2) и компоненты ${{\bar {A}}_{{rr}}}$ (3) тензора конформаций от координаты $\bar {z}$ вдоль оси струи для N = 600. ω = 0.0095. а – режим I, б – режим II.
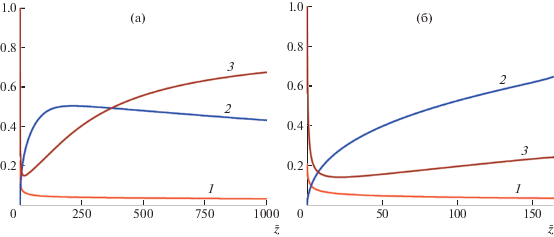
Рис. 3.
Зависимость радиуса струи $\bar {a}$ (1), параметра порядка s (2) и компоненты ${{\bar {A}}_{{rr}}}$ (3) тензора конформаций от координаты $\bar {z}$ вдоль оси струи для $N = 2000$. ω = 0.003. а – режим I, б – режим II.
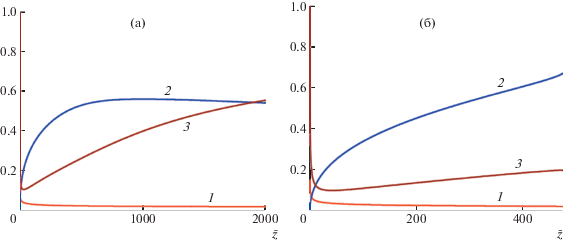
После увеличения напряженности поля в 2 раза поведение струи качественно изменяется: струя остается прямолинейной только на конечном отрезке (режим II). На конце отрезка ее поведение становится сингулярным, $\frac{{d\bar {a}}}{{d\bar {z}}} \to - \infty $. Поведение функций $\bar {a}(\bar {z})$, $s(\bar {z})$, ${{\bar {A}}_{{rr}}}(\bar {z})$ в данном случае показано на рис. 2б и рис. 3б. Параметр порядка монотонно увеличивается вдоль оси струи и достигает максимального значения на конце прямолинейного участка. Радиус струи уменьшается. Функция ${{\bar {A}}_{{rr}}}(\bar {z})$ сначала убывает, а затем растет. Появление сингулярности связано с конечной растяжимостью цепей и математически это происходит за счет обращения в ноль суммы в скобках в левой части уравнения (12). Движение струи после прохождения точки сингулярности должно быть неустойчивым: наиболее вероятный сценарий – изгибание струи. Очевидно, что приближение тонкого тела перестает здесь работать.
Для более детального анализа динамики струи была рассмотрена зависимость числа Вейссенберга ${\text{Wi}} = \dot {\varepsilon }\tau = \frac{2}{{{{{\bar {a}}}^{3}}}}\left| {\frac{{d\bar {a}}}{{d\bar {z}}}} \right|$ от координаты $\bar {z}$ (рис. 4), величины $\bar {A}_{{zz}}^{{1/4}}$ от $1{\text{/}}\bar {a}$ (рис. 5), и скорости потока ${{\bar {v}}_{z}}(\bar {z}) = \frac{{{{v}_{z}}\tau }}{\ell } = \frac{1}{{{{{\bar {a}}}^{2}}}}$ от ${{\bar {z}}^{{1/2}}}$ (рис. 6). Расчеты показывают, что число Вайссенберга в переходной зоне велико, ${\text{Wi}} \gg {\text{1}}$, что согласуется с экспериментом [3–5]. Затем оно начинает уменьшаться по мере удаления от переходной зоны (рис. 4а, б). Падение значений Wi всегда происходит в режиме I, когда электрическое поле слабое (рис. 4, кривые 1). Однако после увеличения напряженности внешнего поля в 2 раза (режим II) картина качественно другая и уменьшение числа Вайссенберга сменяется его быстрым ростом (рис. 4, кривые 2). Это связано с приближением к точке сингулярности. При этом число Вайссенберга всегда больше единицы, Wi > 1.
Рис. 4.
Зависимость числа Вейссенберга Wi от координаты $\bar {z}$. а: N = 600, ω = 0.0095; б: N = 2000, ω = 0.003. Кривая 1 соответствует бесконечно длинной прямолинейной струе, кривая 2 – струе с ограниченным прямолинейным участком.
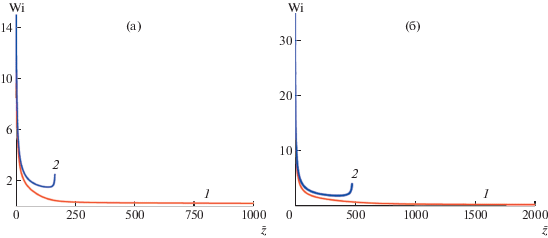
Рис. 5.
Зависимость величины $\bar {A}_{{zz}}^{{1/4}}$ от $1{\text{/}}\bar {a}$. а: N = 600, ω = 0.0095; б: $N = 2000$, ω = 0.003. Кривая 1 соответствует бесконечно длинной прямолинейной струе, кривая 2 – струе с ограниченным прямолинейным участком.
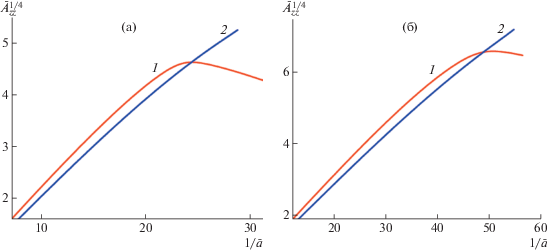
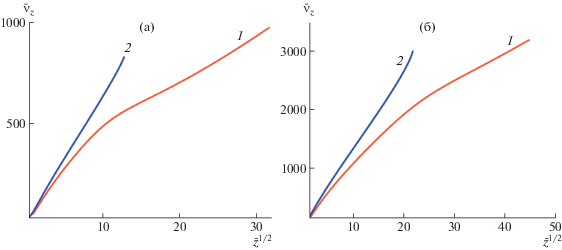
Рис. 6.
Скорость струи в зависимости от $\sqrt {\bar {z}} $. а: N = 600, ω = 0.0095; б: $N = 2000$, ω = 0.003. Кривая 1 соответствует бесконечно длинной прямолинейной струе, кривая 2 – струе с ограниченным прямолинейным участком.
При больших числах Вайссенберга (Wi > 1) раствор должен деформироваться упруго. Для проверки этого факта рассмотрели зависимость величины $\bar {A}_{{zz}}^{{1/4}}$ от $1{\text{/}}\bar {a}$, которая при упругом деформировании (область высокоэластичности) должна быть линейной. Действительно, если внутри переходной зоны взять маленький участок струи длины $\Delta {{\bar {z}}_{0}}$ и объема $\pi \bar {a}_{0}^{2}\Delta {{\bar {z}}_{0}}$, то в силу сохранения объема его длина после перемещения на некоторое расстояние составляет $\Delta \bar {z} = \frac{{\bar {a}_{0}^{2}}}{{{{{\bar {a}}}^{2}}}}\Delta {{\bar {z}}_{0}}$, где $\bar {a}$ – текущий радиус. Таким образом, продольный размер полимерных цепей увеличивается в $\bar {a}_{0}^{2}{\text{/}}{{\bar {a}}^{2}}$ раз [24]. Поскольку ${{\bar {A}}_{{zz}}}$ пропорциональна квадрату продольного размера цепи, должна быть справедлива оценка ${{\bar {A}}_{{zz}}} \simeq \bar {a}_{0}^{4}{\text{/}}{{\bar {a}}^{4}}$. На рис. 5 видно, что функция $\bar {A}_{{zz}}^{{1/4}}$ зависит от $1{\text{/}}\bar {a}$ практически линейно, как в режиме I до момента достижения цепями максимальной длины (кривые 1), так и в режиме II (кривые 2). Таким образом, параметр порядка изменяется по закону $s \simeq \bar {a}_{0}^{2}\sqrt \delta {\text{/}}{{\bar {a}}^{2}}$.
При упругой деформации раствора, когда цепи еще не слишком сильно растянуты, вязкоупругие силы меняются практически так же, как и силы инерции, но с противоположным знаком. Это следует из левой части уравнения (12), где второе и третье слагаемые в скобках показывают одинаковую зависимость от радиуса струи $ \sim {\kern 1pt} 1{\text{/}}{{\bar {a}}^{3}}$. Очевидно, что четвертое слагаемое, которое также обусловлено вязкоупругостью, должно быть относительно малым. Такое поведение влияет и на скорость потока в струе. Зависимость безразмерной скорости от расстояния показана на рис. 6. Видно, что в режиме II (кривые 2) скорость практически линейно зависит от координаты, а в режиме I (кривые 1) можно выделить две области, в которых скорость меняется практически линейно с координатой, однако наклон линий разный. Это связано с тем обстоятельством, что в близкой к переходной зоне области инерция частично компенсируется вязкоупругостью, тогда как в дальней зоне вклад вязкоупругих сил относительно мал. Таким образом, скорость и радиус струи изменяются примерно так: ${{\bar {v}}_{z}}(\bar {z}) \propto {{\bar {z}}^{{1/2}}}$ и $\bar {a}(\bar {z}) \propto {{\bar {z}}^{{ - 1/4}}}$, что согласуется с зависимостями скорости от осевой координаты, полученными экспериментально [35].
ЗАКЛЮЧЕНИЕ
Исследование изменений конформаций полимерных цепей в струе методом численного анализа уравнения баланса сил и реологического уравнения модели конечно растяжимых цепей (FENE-P) позволило установить связь между ориентацией цепей и динамикой струи, а также проанализировать роль нелинейной вязкоупругости, связанной с конечной длиной макромолекул, и ее корреляцию с капиллярными силами и силами инерции. Показано, что полимерные цепи в струе могут сильно вытягиваться вдоль оси растяжения. Обнаружен новый тип неустойчивости струи, который отличается от неустойчивости Рэлея, а также от осесимметричной и неосесимметричной неустойчивостей, возникающих из-за отталкивания между зарядами на поверхности струи [1, 2, 41–44]. При фиксированном объемном расходе жидкости такая неустойчивость появляется при увеличении напряженности внешнего поля, когда число Вайссенберга Wi > 1 и раствор находится в области высокоэластичности. В данном режиме полимерные цепи монотонно растягиваются до некоторого максимального значения, после чего их дальнейшее растяжение становится невозможным, а струя больше не может оставаться прямолинейной. При этом число Вайссенберга изменяется немонотонно: сначала уменьшается, а затем начинает расти. Такое поведение согласуется с экспериментально полученной в работе [36] зависимостью скорости растяжения от аксиальной координаты. Ориентационный параметр порядка, определяемый как отношение продольного размера цепочки к ее контурной длине, монотонно увеличивается вдоль оси струи как $s \simeq \bar {a}_{0}^{2}\sqrt \delta {\text{/}}{{\bar {a}}^{2}} \propto {{\left( {z{\text{/}}N} \right)}^{{1/2}}}$ и достигает максимального значения на конце прямолинейного участка струи. Дальнейшее движение струи становится неустойчивым, и она начинает изгибаться: при этом происходит релаксация полимерных цепей.
В относительно слабых электрических полях роль инерции является определяющей, и струя всегда остается прямолинейной. В таком режиме ориентационный параметр порядка меняется вдоль струи немонотонно: сначала он повышается до некоторого максимального значения (число Вейсенберга уменьшается до Wi ~ 1), а затем понижается. Уменьшение параметра порядка обусловлено релаксацией полимерных цепей и характеризуется временем Рауза. Таким образом, динамика роста и релаксации параметра порядка замедляется с увеличением ММ полимера.
Переход от прямолинейной струи к струе, в которой возникает изгибная неустойчивость (whipping) с увеличением напряженности внешнего электрического поля, экспериментально исследовали, например, при электроспиннинге 2%-ных водных растворов ПЭО [48, 49] и концентрированных растворов полистирола в диметилформамиде [50]. На основе полученных результатов можно предположить, что причина изгибной неустойчивости прямолинейной струи в сильных полях может быть связана не только с отталкиванием между зарядами на ее поверхности [1, 43], но и с ее высокоэластичностью и ориентацией макромолекул вдоль оси струи.
Работа выполнена при финансовой поддержке Российского научного фонда (проект 20-19-00194).
Список литературы
Reneker D.H., Yarin A.L., Zussman E., Xu H. // Adv. Appl. Mech. 2007. V. 41. P. 43.
Lauricella M., Succi S., Zussman E., Pisignano D., Yarin A.L. // Rev. Mod. Phys. 2020. V. 92. № 3. P. 035004.
Xue J., Wu T., Dai Y., Xia Y. // Chem. Rev. 2019. V. 119. № 8. P. 5298.
Energy Harvesting Properties of Electrospun Nanofibers / Ed. By J. Feng, T. Lin. Bristol: IOP Publ., 2020.
Wang C., Hashimoto T. // Macromolecules. 2018. V. 51. № 12. P. 4502.
Wang Y., Wang C. // Macromol. Mater. Eng. 2019. V. 304. № 9. P. 1900281.
Wang C., Hashimoto T., Wang Y., Lai H.-Y., Kuo C.-H. // Macromolecules. 2020. V. 53. № 18. P. 7876.
Kakade M.V., Givens S., Gardner K., Lee K.H., Chase D.B., Rabolt J.F. // J. Am. Chem. Soc. 2007. V. 129. № 10. P. 2777.
Richard-Lacroix M., Pellerin C. // Macromolecules. 2015. V. 48. № 13. P. 4511.
Wang Z., Sun B., Lu X., Wang C., Su Z. // Macromolecules. 2019. V. 52. № 24. P. 9639.
Bazilevskii A.V., Voronkov S.I., Entov V.M., Rozhkov A.N. // Sov. Phys. Dokl. 1981. V. 26. № 4. P. 333.
Sattler R., Gier S., Eggers J., Wagner C. // Phys. Fluids. 2012. V. 24. № 2. P. 023101.
Semakov A.V., Kulichikhin V.G., Tereshin A.K., Antonov S.V., Malkin A.Ya. // J. Polym. Sci., Phys Ed. 2015. V. 53. № 8. P. 559.
Malkin A.Ya., Semakov A.V., Skvortsov I.Yu., Zatonskikh P., Kulichikhin V.G., Subbotin A.V., Semenov A.N. // Macromolecules. 2017. V. 50. № 20. P. 8231.
Kulichikhin V.G., Skvortsov I.Yu., Subbotin A.V., Kotomin S.V., Malkin A.Ya. // Polymers. 2018. V. 10. № 8. P. 856.
Subbotin A.V., Semenov A.N. // J. Polym. Sci., Phys Ed. 2016. V. 54. № 11. P. 1066.
Semenov A.N., Subbotin A.V. // J. Polym. Sci., Polym Phys. 2017. V. 55. № 7. P. 623.
Subbotin A.V., Semenov A.N. // Polymer Science C. 2018. V. 60. № 1. P.106.
Fernández de la Mora J. // Annu. Rev. Fluid Mech. 2007. V. 39. P. 217.
Fernández de la Mora J. // J. Fluid Mech. 1992. V. 243. P. 561.
Fernández de la Mora J., Loscertales I.G. // J. Fluid Mech. 1994. V. 260. P. 155.
Higuera F.J. // J. Fluid Mech. 2003. V. 484. P. 303.
Gañán-Calvo A.M. // J. Fluid Mech. 2004. V. 507. P. 203.
Han T., Yarin A.L., Reneker D.H. // Polymer. 2008. V. 49. № 6. P. 1651.
Yu J.H., Fridrikh S.V., Rutledge G.C. // Polymer. 2006. V. 47. № 13. P. 4789.
Wang Y., Hashimoto T., Li C.-C., Li Y.-C., Wang C. // J. Polym. Sci., Polym. Phys. 2018. V. 56. № 4. P. 319.
Reznik S.N., Zussman E. // Phys. Rev. E. 2010. V. 81. № 2. P. 026313.
Subbotin A.V., Semenov A.N. // Proc. Roy Soc. London. A. 2015. V. 471. № 2182. P. 20150290.
Subbotin A.V., Semenov A.N. // JETP Lett. 2015. V. 102. № 12. P. 815.
Kirichenko N., Petryanov-Sokolov I.V., Suprun N.N., Shutov A.A. // Sov. Phys. Dokl. 1986. V. 31. № 6. P. 611.
Hohman M.M., Shin M., Rutledge G., Brenner M.P. // Phys. Fluids. 2001. V. 13. № 8. P. 2221.
Feng J.J. // Phys. Fluids. 2002. V. 14. № 11. P. 3912.
Carroll C.P., Joo Y.L. // Phys. Fluids. 2006. V. 18. № 5. P. 053102.
Subbotin A., Kulichikhin V.G. // Polymer Science A. 2014. V. 56. № 2. P. 211.
Helgeson M.E., Grammatikos K.N., Deitzel J.M., Wagner N.J. // Polymer. 2008. V. 49. № 12. P. 2924.
Greenfeld I., Fezzaa K., Rafailovich M.H., Zussman E. // Macromolecules. 2012. V. 45. № 8. P. 3616.
Reneker D.H., Yarin A.L. // Polymer. 2008. V. 49. № 10. P. 2387.
Zhakin A.I. // Phys.Usp. 2013. V. 56. № 2. P. 141.
Wang C., Cheng Y.-W., Hsu C.-H., Chien H.-C., Tsou S.-Y.J. // Polym. Res. 2011. V. 18. № 1. P. 111.
Shenoy S.L., Bates W.D., Frisch H.L., Wnek G.E. // Polymer. 2005. V. 46. № 10. P. 3372.
Carroll C.P., Joo Y.L. // J. Non-Newtonian Fluid Mech. 2008. V. 153. № 2–3. P. 130.
Deshawar D., Chokshi P. // Polymer. 2017. V. 131. P. 34.
Reneker D.H., Yarin A.L., Fong H., Koombhongse S. // J. Appl. Phys. 2000. V. 87. № 9. P. 4531.
Shariatpanahi S.P., Bonn D., Ejtehadi M.R., Zad A.I. // J. Polym. Sci., Polym. Phys. 2016. V. 54. № 11. P. 1036.
Larson R.G., Desai P.S. // Annu. Rev. Fluid Mech. 2015. V. 47. P. 47.
Bazilevskii A.V., Rozhkov A.N. // Dynamics of Capillary Breakup of Elastic Jets, Fluid Dynamics. 2014. V. 49. № 6. P. 827.
Szabo P., McKinley G.H., Clasen C. // J. Non-Newtonian Fluid Mech. 2012. V. 169–170. № 2. P. 26.
Shin Y.M., Hohman M.M., Brenner M.P., Rutledge G.C. // Appl. Phys. Lett. 2001. V. 78. № 8. P. 1149.
Shin Y.M., Hohman M.M., Brenner M.P., Rutledge G.C. // Polymer. 2001. V. 42. № 25. P. 9955.
Xin Y., Reneker D.H. // Polymer. 2012. V. 53. № 19. P. 4254.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)


