Высокомолекулярные соединения (серия А), 2021, T. 63, № 3, стр. 221-233
2D МОДЕЛЬ НАНОЛЕНТЫ ГРАФЕНА В ПОЛИМЕРНОЙ МАТРИЦЕ
a Федеральный исследовательский центр химической физики им. Н.Н. Семенова Российской академии наук
119991 Москва, ул. Косыгина, 4, Россия
b Российский экономический университет им. Г.В. Плеханова
117997 Москва, пер. Стремянный, 36, Россия
* E-mail: asavin00@gmail.com
Поступила в редакцию 14.09.2020
После доработки 15.10.2020
Принята к публикации 02.11.2020
Аннотация
Предложена двухмерная модель наноленты графена в полимерной матрице (в кристалле макромолекул полиэтилена), позволяющая рассмотреть образцы полимера большого размера с включенными однослойными и многослойными нанолентами. С использованием модели показано, что нанолентам энергетически более выгодно находиться внутри полимерной матрицы, чем на ее поверхности, а многослойным нанолентам внутри выгодно разделиться на отдельные слои. Проведено моделирование сжатия нанолент, находящихся внутри и на поверхности матрицы. Показано, что независимо от числа слоев наноленты ее продольное сжатие вместе с матрицей может происходить по двум сценариям: однородное сжатие всей системы нанолента + матрица или неоднородное сжатие, при котором у наноленты происходит локализованный изгиб. Первый сценарий реализуется при слабом сжатии, второй – при сильном.
ВВЕДЕНИЕ
Атомы углерода способны создавать многочисленные структуры, среди которых в последнее время большое внимание исследователей привлекает моноатомный кристаллический слой – графен [1–7]. Данный наноматериал демонстрирует высокую электро- и теплопроводность, рекордные жесткость и прочность на разрыв, колоссальную удельную поверхность и другие свойства, обеспечивающие большое разнообразие его потенциальных применений. Замечательные свойства графена позволяют использовать его в качестве нанонаполнителя в полимерных композитах для улучшения их характеристик. Добавление графена в полимерные матрицы заметно модифицирует их механические, тепловые и электрические свойства [8–11].
Молекулярно-динамическое моделирование графен-полимерных композитов проводилось в работах [12–15]. При моделировании использовались полноатомные модели, которые в силу их сложности позволяют рассмотреть только образцы малого размера. Применение двухмерной модели нанолент графена в полимерной матрице позволяет промоделировать образцы полимера (нанокомпозита) большого размера, содержащие многослойные наноленты. В качестве полимерной матрицы будет рассмотрена система параллельных зигзагообразных цепочек макромолекул полиэтилена.
ЦЕПНАЯ МОДЕЛЬ НАНОЛЕНТЫ В ПОЛИМЕРНОЙ МАТРИЦЕ
Графеновая нанолента представляет собой полосу постоянной ширины, вырезанную из плоского листа графена. Для упруго изотропного графена продольная и изгибная жесткости наноленты слабо зависят от ее ориентации. Для определенности рассмотрим наноленту, края которой имеют структуру зигзаг (рис. 1). Модель цепи, описывающая продольные и изгибные движения наноленты, подробно представлена в работах [16, 17].
Рис. 1.
Построение 2D цепной модели наноленты графена в полимерной матрице. Серым цветом показана нанолента графена, лежащая в плоскости xy вдоль оси x, черным цветом − лежащие над ней макромолекулы ПЭ (макромолекулы направлены вдоль оси y). Проекции наноленты и макромолекул на плоскость xz дают двухмерную модель этой системы. Цветные рисунки можно посмотреть в электронной версии.
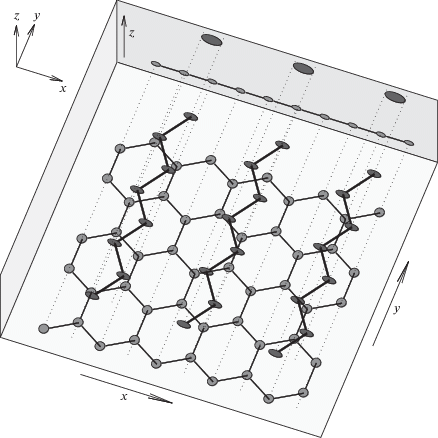
Пусть нанолента лежит в плоскости xy вдоль оси x. В цепной модели наноленты предполагается синхронное движение всех атомов, расположенных на одной поперечной линии (линии, параллельной оси y). В этом случае линию атомов можно считать одним узлом молекулярной цепи, расположенной в плоскости xz (рис. 1).
Однослойная нанолента графена в 2D модели задается как молекулярная цепочка из N1 звеньев, имеющая гамильтониан
(1)
$\begin{gathered} {{H}_{1}} = \sum\limits_{n = 1}^{{{N}_{1}}} \frac{1}{2}{{M}_{1}}({{{{\mathbf{\dot {u}}}}}_{n}},{{{{\mathbf{\dot {u}}}}}_{n}}) + \sum\limits_{n = 1}^{{{N}_{1}} - 1} V({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{{n + 1}}}) + \\ \, + \sum\limits_{n = 2}^{{{N}_{1}} - 1} U({{{\mathbf{u}}}_{{n - 1}}},{{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{{n + 1}}}) + \sum\limits_{n = 1}^{{{N}_{1}} - 6} \sum\limits_{k = n + 6}^{{{N}_{1}}} {{W}_{1}}({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{k}}), \\ \end{gathered} $Потенциал
(2)
$\begin{gathered} V({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{{n + 1}}}) = \frac{1}{2}K{{({{r}_{n}} - a)}^{2}}, \\ {{r}_{n}} = {\text{|}}{{{\mathbf{v}}}_{n}}{\text{|}},\quad {{{\mathbf{v}}}_{n}} = {{{\mathbf{u}}}_{{n + 1}}} - {{{\mathbf{u}}}_{n}}, \\ \end{gathered} $Потенциал
(3)
$\begin{gathered} U({{{\mathbf{u}}}_{{n - 1}}},{{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{{n + 1}}}) = {{\varepsilon }_{c}}[\cos ({{\theta }_{n}}) + 1], \\ \cos ({{\theta }_{n}}) = - ({{{\mathbf{v}}}_{{n - 1}}},{{{\mathbf{v}}}_{n}}){\text{/}}{{r}_{{n - 1}}}{{r}_{n}}, \\ \end{gathered} $Потенциал ${{W}_{1}}({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{k}}) = {{W}_{1}}({{r}_{{n,k}}})$, ${{r}_{{n,k}}} = {\text{|}}{{{\mathbf{u}}}_{n}} - {{{\mathbf{u}}}_{k}}{\text{|}}$, отражает слабые невалентные взаимодействия узлов цепи n и k. Энергию взаимодействия узлов можно найти численно как сумму невалентных взаимодействий атома углерода из одной поперечной линии наноленты со всеми атомами другой поперечной линии, усредненную по поперечным смещениям первого атома.
Энергия невалентного взаимодействия атомов углерода нанолент выражается через потенциал Леннард-Джонса
(4)
${{W}_{0}}(r) = {{\varepsilon }_{0}}{{({{r}_{0}}{\text{/}}r)}^{6}}[({{r}_{0}}{\text{/}}r{{)}^{6}} - 2]$(5)
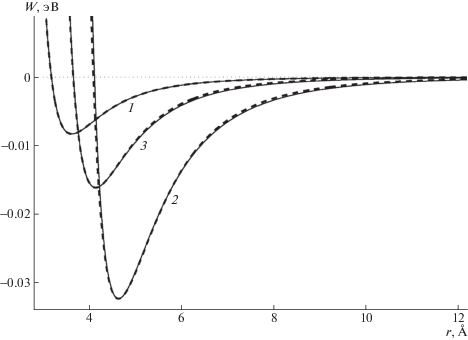
${{W}_{{n,m}}}(r) = {{\varepsilon }_{1}}[m{{({{r}_{1}}{\text{/}}r)}^{n}} - n{{({{r}_{1}}{\text{/}}r)}^{m}}]{\text{/}}(n - m)$Рис. 2.
Вид потенциалов невалентных взаимодействий ${{W}_{i}}(r)$ при i = 1 (1), 2 (2) и 3 (3). Сплошные линии – зависимости, найденные численно, штриховые – их аппроксимации потенциалом Леннард-Джонса (5).
Рассмотрим наноленту, находящуюся в полимерной матрице – в кристалле макромолекул полиэтилена (CH2)∞. Будем считать, что зигзагообразные цепочки ПЭ двигаются как твердое тело и всегда лежат поперек наноленты параллельно ее поверхности (рис. 1). Тогда каждую макромолекулу ПЭ можно заменить эффективным объединенным атомом, находящимся в плоскости xz.
Гамильтониан (1) описывает энергию наноленты, приходящуюся на ее продольную полосу ширины ${{h}_{0}} = 1.5{{r}_{c}} = 2.127$ Å. Макромолекула ПЭ имеет форму плоского зигзага с шагом ${{r}_{p}} = 1.53$ Å (длина валентной связи CH2–CH2) и углом α = 110°. Продольный шаг зигзага ${{a}_{y}} = {{r}_{p}}\sin (\alpha {\text{/}}2)$, ширина зигзага ${{a}_{x}} = {{r}_{p}}\cos (\alpha {\text{/}}2)$. Мы будем рассматривать только смещения зигзага как твердого тела. В этом случае на продольное расстояние h0 приходится масса атомов зигзага ${{M}_{2}} = 14{{m}_{p}}{{h}_{0}}{\text{/}}{{a}_{y}}$ = = 23.76mp.
В плоскости xz каждой макромолекуле ПЭ соответствует частица массы M2. Чтобы определить взаимодействие между такими частицами, найдем зависимость энергии взаимодействия двух параллельных транс-зигзагов от расстояния между ними. При вычислении энергии взаимодействия воспользуемся приближением объединенных атомов, когда группы атомов CH2 соответствуют частицам, взаимодействия которых задаются потенциалом Леннард-Джонса (4) с энергией взаимодействия ${{\varepsilon }_{0}} = 0.004052$ эВ и равновесным расстоянием ${{r}_{0}} = 4.5$ Å [19]. При вычислении энергия взаимодействия усреднялась по сдвигам зигзагов вдоль их продольных осей и по поворотам вокруг них.
Расчеты показали, что усредненная энергия взаимодействия транс-зигзагов ${{W}_{2}}(r)$ с хорошей точностью описывается потенциалом Леннард-Джонса (5) с показателями $n = 11$, $m = 5.5$. При нормировке энергии на длину цепи ${{h}_{0}}$ энергия взаимодействия ${{\varepsilon }_{1}} = 0.0325$ эВ, равновесное расстояние ${{r}_{1}} = 4.62$ Å (рис. 2).
Полимерная матрица, окружающая наноленту, моделируется двухмерной решеткой частиц массы ${{M}_{2}}$ с гамильтонианом
(6)
${{H}_{2}} = \sum\limits_{n = {{N}_{1}} + 1}^N \frac{1}{2}{{M}_{2}}({{{\mathbf{\dot {u}}}}_{n}},{{{\mathbf{\dot {u}}}}_{n}}) + \sum\limits_{n = {{N}_{1}} + 1}^{N - 1} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = n + 1}^N {{W}_{2}}({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{k}}),$Взаимодействие наноленты (узлов цепи) с полимерной матрицей описывается суммой
(7)
${{H}_{3}} = \sum\limits_{n = 1}^{{{N}_{1}}} \sum\limits_{k = {{N}_{1}} + 1}^N {{W}_{3}}({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{k}}).$Вычисления показали, что потенциал взаимодействия узлов цепи с частицами полимерной матрицы ${{W}_{3}}({{{\mathbf{u}}}_{n}},{{{\mathbf{u}}}_{k}}) = {{W}_{3}}({{r}_{{nk}}})$ тоже с высокой точностью аппроксимируется потенциалом Леннард-Джонса (5) с показателями n = 11, m = 5.5, энергией ${{\varepsilon }_{1}} = 0.0162$ эВ и равновесным расстоянием ${{r}_{1}} = 4.125$ Å (рис. 2).
Схематически 2D модель системы нанолента + полимерная подложка представлена на рис. 3. Здесь цепочка маленьких серых частиц соответствует наноленте графена, а крупные черные частицы – макромолекулам ПЭ. Гамильтониан системы имеет вид
Рис. 3.
Основные состояния наноленты длины $L = 12.65$ нм (число звеньев ${{N}_{1}} = 104$), находящейся на $i$-м слое кристалла ПЭ из ${{N}_{p}} = 82 \times 60$ молекул (размер $37.16 \times 23.27$ нм2), i = 1 (a), 2 (б), 3 (в), 4 (г) и 6 (д) (энергия основного состояния системы ${{E}_{i}} = - 557.53, - {\kern 1pt} 561.49, - {\kern 1pt} 561.88$, –561.95 и –561.98 эВ). Показан только фрагмент кристалла вблизи наноленты.

Данная модель легко может быть обобщена на случай многослойной наноленты. Гамильтониан системы, K-слойная нанолента + полимерная матрица, будет иметь вид
(9)
$\begin{gathered} \, + \sum\limits_{n = 2}^{{{N}_{k}} - 1} U({{{\mathbf{u}}}_{{{{n}_{k}} - 1}}},{{{\mathbf{u}}}_{{{{n}_{k}}}}},{{{\mathbf{u}}}_{{{{n}_{k}} + 1}}})\left. { + \sum\limits_{n = 1}^{{{N}_{k}} - 6} \sum\limits_{l = n + 6}^{{{N}_{k}}} {{W}_{1}}({{{\mathbf{u}}}_{{{{n}_{k}}}}},{{{\mathbf{u}}}_{{{{l}_{k}}}}})} \right] + \\ \, + \sum\limits_{k = 1}^{K - 1} \sum\limits_{l = k + 1}^K \sum\limits_{n = 1}^{{{N}_{k}}} \sum\limits_{m = 1}^{{{N}_{l}}} {{W}_{1}}({{{\mathbf{u}}}_{{{{n}_{k}}}}},{{{\mathbf{u}}}_{{{{m}_{l}}}}}) + \sum\limits_{n = {{N}_{c}} + 1}^N \frac{1}{2}{{M}_{2}}({{{{\mathbf{\dot {u}}}}}_{n}},{{{{\mathbf{\dot {u}}}}}_{n}}) + \\ \end{gathered} $Здесь Nk – число узлов в k-й цепи (наноленте), номер звена ${{n}_{k}} = {{N}_{1}} + ... + {{N}_{{k - 1}}} + n$, число узлов в K нанолентах ${{N}_{c}} = {{N}_{1}} + ... + {{N}_{K}}$, Np – число молекул полимерной матрицы, общее число узлов системы $N = {{N}_{c}} + {{N}_{p}}$.
Для нахождения стационарного состояния многослойной наноленты в полимерной матрице нужно численно решить задачу на минимум энергии взаимодействия
(10)
$\begin{gathered} E \to \min : \{ {{{\mathbf{u}}}_{n}}\} _{{n = 1}}^{N}, \hfill \\ \end{gathered} $СТАЦИОНАРНЫЕ СОСТОЯНИЯ УГЛЕРОДНЫХ НАНОЛЕНТ В КРИСТАЛЛИЧЕСКОМ ПЭ
Найдем основные состояния углеродных нанолент в кристалле ПЭ. Вначале проанализируем зависимость энергии основного состояния наноленты от расстояния ее расположения до поверхности кристалла. Для этого рассмотрим однослойную наноленту длины $L = ({{N}_{1}} - 1)a = 12.65$ нм (цепочку из N1 = 104 звеньев) и поместим ее на поверхность прямоугольника из ${{N}_{p}} = 82 \times 60 - 28$ = = 4892 узлов (размер 2D кристалла ПЭ 37.16 × × 23.27 нм2).
Из численного решения задачи на минимум энергии (10) следует, что наноленте энергетически более выгодно располагаться внутри кристалла ПЭ, чем на его поверхности. На рис. 3 представлены основные состояния наноленты при ее расположении на разных слоях молекул ПЭ вблизи поверхности кристалла. Пусть ${{E}_{i}}$ – энергия основного состояния системы нанолента $ \in $ кристалл ПЭ при расположении наноленты в $i$-м слое молекул от поверхности кристалла ($i = 1,2,...$). Определим нормированную на длину L разницу энергий $\Delta {{E}_{i}} = ({{E}_{i}} - {{E}_{1}}){\text{/}}{{N}_{1}}$. Моделирование показало, что $\Delta {{E}_{i}}$ монотонно уменьшается с ростом номера слоя i. Так, $\Delta {{E}_{i}} = - 0.0381, - {\kern 1pt} 0.0418$, –0.0425, –0.0427 эВ для i = 2, 3, 4, 6. При $i > 4$ энергетический выигрыш от погружения наноленты в кристалл практически не меняется (нанолента перестает чувствовать поверхность кристалла при ее помещении в четвертый слой молекул).
Чтобы оценить возможность расслоения многослойных нанолент в полимерной матрице, поместим две наноленты длины $L = 12.65$ нм (число звеньев ${{N}_{1}} = {{N}_{2}} = 104$) в центр кристалла из ${{N}_{p}} = 82 \times 60 - 56$ = 4864 молекул (размер 2D кристалла ПЭ $37.16 \times 23.27$ нм2) (рис. 4). Рассмотрим, как зависит энергия основного состояния системы ${{E}_{i}}$ от числа слоев молекул кристалла между нанолентами $i = 0,1,2,...$ (значение i = 0 соответствует двухслойной наноленте внутри кристалла). Определим удельную разницу энергий ΔEi = = $({{E}_{i}} - {{E}_{0}}){\text{/}}{{N}_{1}}$. Решение задачи на минимум энергии (10) показало, что энергия системы две наноленты $ \in $ кристалл ПЭ монотонно уменьшается с увеличением числа слоев молекул ПЭ между нанолентами. Так, $\Delta {{E}_{i}} = - 0.0354, - {\kern 1pt} 0.0417, - {\kern 1pt} 0.0429$, – 0.0431 эВ для i = 1, 2, 4, 14. При $i > 4$ разница энергий практически не меняется при увеличении числа слоев (наноленты перестают взаимодействовать друг с другом, если между ними находятся более четырех слоев молекул полимерного кристалла).
Рис. 4.
Основные состояния двух нанолент длины $L = 12.65$ нм (число звеньев ${{N}_{1}} = {{N}_{2}} = 104$), находящихся в центре кристалла ПЭ из ${{N}_{p}} = 82 \times 60$ молекул (размер $37.16 \times 23.27$ нм2) при наличии между ними $i$ слоев молекул: i = 0 (a), 1 (б), 2 (в) и 4 (г) (энергия основного состояния системы ${{E}_{i}} = - 565.67, - {\kern 1pt} 569.35$, –570.01 и –570.14 эВ). Показан только центральный фрагмент кристалла.

Проведенное моделирование позволяет заключить, что вблизи температуры плавления полимерного кристалла должна происходить абсорбция кристаллом углеродных нанолент. Наноленты с поверхности кристалла будут перемещаться внутрь, а внутри кристалла многослойные наноленты будут расслаиваться на однослойные.
ПРОДОЛЬНОЕ СЖАТИЕ НАНОЛЕНТ В ПОЛИМЕРНОЙ МАТРИЦЕ
Рассмотрим наноленту длины $L = ({{N}_{1}} - 1)a$, лежащую вдоль оси x, сверху и снизу которой находится прямоугольный фрагмент кристалла ПЭ такой же длины из 30 слоев молекул (ширина слоя H = 11.4 нм) (рис. 5). Найдем вначале основное состояние такой системы (прямоугольный фрагмент кристалла, вдоль центра которого расположена многослойная нанолента) $\{ (x_{n}^{0},z_{n}^{0})\} _{{n = 1}}^{N}$ как решение задачи (10). При $L = 24.4$ нм (N1 = 200) покрывающая наноленту полимерная матрица будет состоять из ${{N}_{p}} = 55 \times 60$, при $L = 36.7$ нм (${{N}_{1}} = 300$) – из ${{N}_{p}} = 82 \times 60$, при $L = 49.0$ нм (${{N}_{1}} = 400$) – из ${{N}_{p}} = 109 \times 60$ молекул.
Рис. 5.
Сжатое состояние однослойной (a) и двухслойной (б) наноленты в полимерной матрице при относительном сжатии $d = 0.03$. Длина наноленты $L = 36.7$ нм (число звеньев ${{N}_{1}} = {{N}_{2}} = 300$). Число молекул полимерной матрицы ${{N}_{p}} = 82 \times 60$.

Затем продольно сожмем эту систему вдоль оси x, положив для всех атомов системы новые координаты ${{x}_{n}} = (1 - d)x_{n}^{0}$. Далее зафиксируем положение атомов из левого и правого края системы, а также вертикальные смещения атомов из нижнего и верхнего края системы. Снова решим задачу на минимум энергии системы (10) с этими граничными условиями. Тем самым мы получим стационарное состояние продольно сжатой наноленты в полимерной матрице при относительном сжатии $d \geqslant 0$.
Моделирование показало, что сжатие наноленты вместе с полимерной матрицей может происходить по двум сценариям: продольное однородное сжатие, при котором все атомы системы равномерно смещаются вдоль оси сжатия, или неоднородное сжатие, при котором в центре наноленты происходит ее зигзагообразный локализованный изгиб, а полимерная матрица подстраивается под этот изгиб (рис. 5).
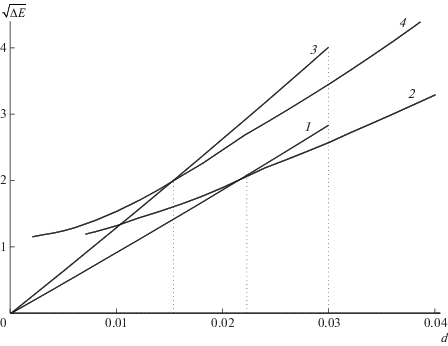
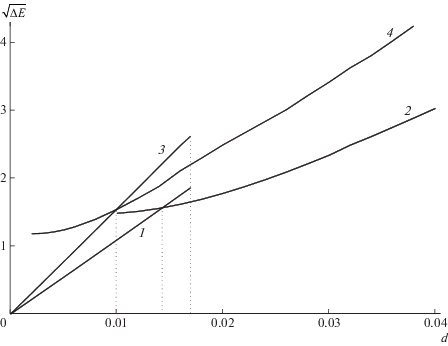
Зависимости изменения энергии системы $\Delta E = E(d) - E(0)$ от относительного сжатия d для однослойных нанолент разной длины представлены на рис. 6. Как видно, при однородном продольном сжатии выполняется закон Гука (энергия системы растет пропорционально квадрату коэффициента сжатия ΔЕ ~ d2) и не выполняется при неоднородном сжатии. Моделирование показало, что однородное продольно сжатое состояние наноленты с полимерной матрицей устойчиво только при сжатии $d < {{d}_{0}} = 0.030$ (пороговое значение сжатия d0 не зависит от длины наноленты). При более сильном сжатии устойчивым будет только неоднородное состояние с локализованным изгибом наноленты. Неоднородное сжатие энергетически более выгодно при $d > {{d}_{1}}$. Критическое значение сжатия d1 зависит от длины наноленты, но всегда ${{d}_{1}} < {{d}_{0}}$. Для длины L = 24.4 нм (число звеньев цепи ${{N}_{1}} = 200$) ${{d}_{1}} = 0.0233$, для L = 36.7 нм (${{N}_{1}} = 300$) ${{d}_{1}} = 0.0188$, для L = 49.0 нм (${{N}_{1}} = 400$) ${{d}_{1}} = 0.0154$. Чем длиннее нанолента, тем при меньшем относительном сжатии неоднородный сценарий ее сжатия с локализованным изгибом становится энергетически более выгодным (d1 → 0 при N1 → ∞).
Рис. 6.
Зависимость изменения энергии однослойной наноленты в полимерной матрице $\Delta E = E(d) - E(0)$ от относительного сжатия системы d. Кривые 1 и 2 дают зависимость при однородном и неоднородном сжатии для наноленты длины $L = 24.4$ нм (N1 = 200), кривые 3 и 4 – для $L = 49.0$ нм (N1 = 400). Здесь и на рис. 7, 9, 10 размерность энергии приведена в эВ.
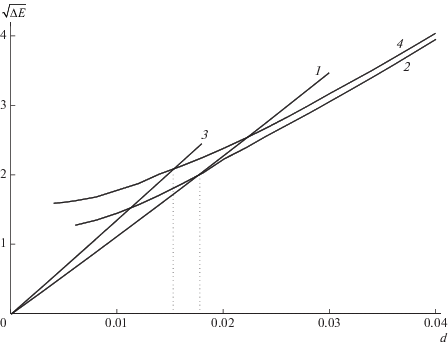
На рис. 7 представлены зависимости изменения энергии системы $\Delta E$ от относительного сжатия d для многослойных нанолент. Здесь тоже закон Гука выполняется только при однородном сжатии. Однородно сжатое состояние системы будет устойчивым при $d < {{d}_{0}}$. Пороговое значение сжатия d0 зависит от числа слоев наноленты K: ${{d}_{0}} = 0.030$ при K = 1 и ${{d}_{0}} = 0.018$ при K = 2, 3. При длине $L = 36.7$ нм (${{N}_{1}} = 300$) состояние с неоднородным сжатием системы энергетически более выгодно при $d > {{d}_{1}}$. Критическое значение сжатия d1 тоже зависит от числа слоев наноленты: ${{d}_{1}} = 0.0188$ при K = 1, ${{d}_{1}} = 0.0153$ при K = 2 и ${{d}_{1}} = 0.0124$ при K = 3. Таким образом, в полимерной матрице увеличение числа слоев наноленты приводит к понижению устойчивости однородного продольно сжатого состояния (критическое значение сжатия d1 снижается при росте К).
Рис. 7.
Зависимость изменения энергии наноленты в полимерной матрице $\Delta E$ от относительного сжатия системы d. Кривые 1 и 2 дают зависимость при однородном и неоднородном сжатии однослойной, кривые 3 и 4 – двухслойной наноленты. Длина наноленты $L = 36.7$ нм (${{N}_{1}} = {{N}_{2}} = 300$).
Отметим, что если нанолента полностью находится в полимерной матрице (ее концы не выходят на поверхность полимерной матрицы), то сжатие матрицы практически не приводит к сжатию наноленты. Для иллюстрации поместим наноленту длины L = 24.4 нм (число звеньев цепи ${{N}_{1}} = 200$) в центр прямоугольной полимерной матрицы, состоящей из ${{N}_{p}} = 82 \times 61 - 54$ молекул (размер матрицы $36.7 \times 23.6$ нм2). Моделирование показывает, что при $d \leqslant 0.1$ продольное сжатие матрицы практически не приводит к сжатию наноленты. Так, при относительном сжатии матрицы d = 0.1 относительное сжатие наноленты ${{d}_{c}} = 0.003$, т.е. здесь всегда ${{d}_{c}} \ll d$.
ПРОДОЛЬНОЕ СЖАТИЕ НАНОЛЕНТ НА ПОВЕРХНОСТИ КРИСТАЛЛА ПЭ
Рассмотрим лежащий вдоль оси $x$ прямоугольный фрагмент кристалла ПЭ, состоящий из 61 слоя молекул (ширина слоя $H = 23.6$ нм). Поместим на нижнюю и верхнюю поверхности кристалла наноленты такой же длины, как сам фрагмент (рис. 8). Найдем вначале основное состояние такой системы (прямоугольный фрагмент кристалла, покрытый сверху и снизу нанолентами) $\{ (x_{n}^{0},z_{n}^{0})\} _{{n = 1}}^{N}$ как решение задачи (10). При длине покрывающих кристалл нанолент $L = 24.4$ нм (число узлов в цепи ${{N}_{1}} = 200$) кристалл будет состоять из ${{N}_{p}} = 55 \times 61$, при $L = 36.7$ нм (${{N}_{1}} = 300$) – из ${{N}_{p}} = 82 \times 61$, а при $L = 49.0$ нм (${{N}_{1}} = 400$) – из ${{N}_{p}} = 109 \times 61$ молекул.
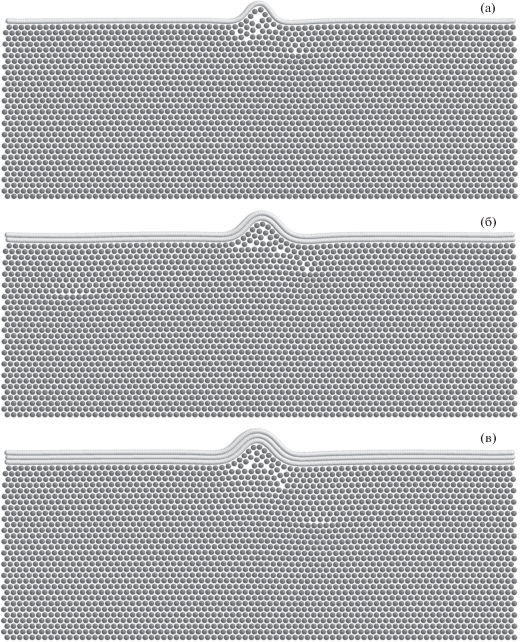
Рис. 8.
Сжатое состояние однослойной (a), двухслойной (б) и трехслойной (в) наноленты, лежащей на поверхности кристалла ПЭ при относительном сжатии системы $d = 0.03$. Длина наноленты $L = 36.7$ нм (число звеньев ${{N}_{1}} = {{N}_{2}} = {{N}_{3}} = 300$). Число молекул полимерной матрицы ${{N}_{p}} = 82 \times 61$. Показана только верхняя половина молекулярной системы.
Сожмем эту систему вдоль оси x, положив для всех атомов системы новые координаты xn = $(1 - d)x_{n}^{0}$. Далее зафиксируем положение атомов из левого и правого края системы. Снова решим задачу на минимум энергии системы (10) с указанными граничными условиями. Мы получим стационарное состояние продольно сжатой системы с безразмерным относительным сжатием $d \geqslant 0$.
Моделирование показало, что сжатие нанолент вместе с полимерной подложкой тоже может происходить по двум сценариям: 1) продольное однородное сжатие нанолент и подложки, все атомы системы равномерно смещаются вдоль оси сжатия; 2) неоднородное сжатие нанолент, при котором в их центрах образуются локальные колоколообразные изгибы, направленные в противоположную сторону от подложки, а область под изгибом частично заполняется молекулами подложки (рис. 8). Первый сценарий реализуется при слабом сжатии, второй – при сильном.
Зависимости изменения энергии системы ΔE от ее относительного сжатия d для однослойных нанолент разной длины представлены на рис. 9. Как видно, закон Гука выполняется только при однородном сжатии. Моделирование показало, что однородное сжатие приводит к устойчивому состоянию наноленты на полимерной подложке только при $d < {{d}_{0}} = 0.017$ (величина порогового значения сжатия d0 не зависит от длины наноленты). При более сильном сжатии (при $d > {{d}_{0}}$) устойчивыми будут только неоднородно сжатые состояния с локальными выпуклыми изгибами нанолент.
Рис. 9.
Зависимость изменения энергии $\Delta E$ однослойных нанолент, лежащих на верхней и нижней поверхностях кристалла ПЭ, от относительного сжатия системы d. Кривые 1 и 2 дают зависимость при однородном и неоднородном сжатии для наноленты длины $L = 24.4$ нм (${{N}_{1}} = 200$), кривые 3 и 4 – для $L = 49.0$ нм (${{N}_{1}} = 400$).
Неоднородное сжатие энергетически более выгодно при $d > {{d}_{1}}$. Критическое значение сжатия d1 зависит от длины наноленты, но всегда ${{d}_{1}}$ < d0. Для длины $L = 24.4$ нм (число звеньев цепи ${{N}_{1}} = 200$) ${{d}_{1}} = 0.0143$, для $L = 36.7$ нм (N1 = 300) ${{d}_{1}}$ = 0.0136, для $L = 49.0$ нм (${{N}_{1}} = 400$) ${{d}_{1}} = 0.010$. Чем длиннее система, тем при меньшем ее относительном сжатии неоднородный сценарий сжатия с локальным изгибом нанолент становится более энергетически выгодным (d1 → 0 при N1 → ∞).
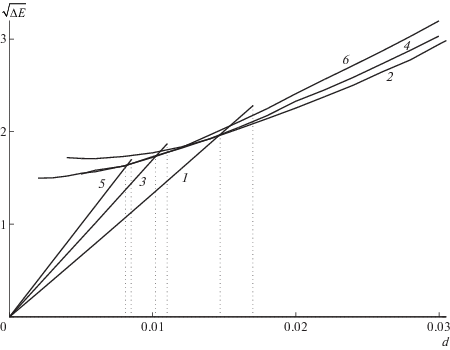
Зависимости изменения энергии системы $\Delta E$ от относительного сжатия $d$ для многослойных нанолент представлены на рис. 10. Здесь тоже закон Гука выполняется только при однородном сжатии. Однородное равномерно сжатое состояние системы будет устойчивым при $d < {{d}_{0}}$. Пороговое значение однородного сжатия ${{d}_{0}} = 0.017$ для однослойных нанолент, ${{d}_{0}} = 0.011$ для двухслойных и ${{d}_{0}} = 0.0085$ для трехслойных нанолент. Таким образом, при расположении нанолент на поверхностях кристалла ПЭ увеличение числа слоев нанолент приводит к понижению устойчивости продольного однородно сжатого состояния и способствует образованию локализованных выпуклых изгибов нанолент (d0 уменьшается с ростом К).
Рис. 10.
Зависимость изменения энергии $\Delta E$ многослойных нанолент, лежащих на верхней и нижней поверхностях кристалла ПЭ, от относительного сжатия системы d. Кривые 1 и 2 дают зависимость при однородном и неоднородном сжатии однослойной, кривые 3 и 4 – двухслойной, кривые 5 и 6 – трехслойной наноленты. Длина наноленты $L = 36.7$ нм (${{N}_{1}} = {{N}_{2}} = {{N}_{3}}$ = 300).
Отметим, что ранее рассматривалось неоднородное сжатие однослойной наноленты, расположенной на плоской недеформированной (“жесткой”) подложке [20]. При сжатии нанолента на такой подложке может образовывать выпуклый изгиб (bubble) или складку – структуры, которые могут двигаться по наноленте, сохраняя свою форму. В рассмотренном нами случае поверхность кристалла ПЭ образует “мягкую” подложку, в области изгиба подложка меняет свою структуру, часть ее молекул частично заполняет пространство под нанолентой.
ЗАКЛЮЧЕНИЕ
Предложенная двухмерная модель нанолент графена в полимерной матрице позволяет промоделировать образцы полимера большого размера с включенными однослойными и многослойными нанолентами графена. С использованием этой модели показано, что нанолентам энергетически более выгодно находиться внутри полимерной матрицы (кристалла макромолекул полиэтилена), чем на его поверхности, а внутри матрицы многослойным нанолентам выгодно разделиться на отдельные слои. Результаты моделирования позволяют заключить, что вблизи температуры плавления наноленты с поверхности матрицы будут перемещаться внутрь, а внутри многослойные наноленты будут расслаиваться на однослойные.
Проведено моделирование сжатия нанолент графена, находящихся внутри полимерной матрицы. Независимо от числа слоев наноленты ее продольное сжатие вместе с матрицей происходит либо посредством однородного сжатия всей системы нанолента + полимерная матрица, либо путем неоднородного сжатия, при котором в центре наноленты возникает локальный зигзагообразный изгиб с подстройкой под него полимерной матрицы. Однородное сжатие ленты энергетически более выгодно при слабом сжатии матрицы, а неоднородное – при сильном. Сжатие наноленты, находящейся на поверхности матрицы, происходит по двум аналогичным сценариям независимо от числа слоев наноленты. В одном случае наблюдается однородное сжатие всей системы нанолента + подложка, а во втором – неоднородное сжатие, при котором у нанолент образуются локализованные колоколообразные изгибы, направленные в противоположную сторону от подложки, а области под изгибами частично заполняются молекулами подложки. Первый сценарий реализуется при слабом сжатии матрицы, второй – при сильном.
Вычислительные ресурсы предоставлены межведомственным суперкомпьютерным центром РАН.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 18-29-19135).
Список литературы
Novoselov K.S., Geim A.K., Morozov S.V., Jiang D., Zhang Y., Dubonos S.V., Grigorieva I.V., Firsov A.A. // Science. 2004. V. 306. P. 666.
Geim A.K., Novoselov K.S. // Nat. Mater. 2007. V. 6. P. 183.
Soldano C., Mahmood A., Dujardin E. // Carbon. 2010. V. 48. P. 2127.
Baimova J.A., Liu B., Dmitriev S.V., Zhou K. // Phys. Status Solidi R. 2014. V. 8. P. 336.
Baimova J.A., Liu B., Dmitriev S.V., Srikanth N., Zhou K. // Phys. Chem. Chem. Phys. 2014. V. 16. P. 19505.
Baimova J.A., Korznikova E.A., Dmitriev S.V., Liu B., Zhou K. // Rev. Adv. Mater. Sci. 2014. V. 39. P. 69.
Orlov A.V., Ovid’ko I.A. // Rev. Adv. Mater. Sci. 2015. V. 40. P. 249.
Stankovich S., Dikin D.A., Dommett G.H., Kohlhaas K.M., Zimney E.J., Stach E.A., Piner R.D., Nguyen S.T., Ruoff R.S. // Nature. 2006. V. 442. P. 282.
Kim H., Abdala A.A., Macosko C.W. // Macromolecules. 2010. V. 43. P. 6515.
Das B., Prasad K.E., Ramamurty U., Rao C.N.R. // Nanotechnology. 2009. V. 20. P. 125705.
Itapu B.M., Jayatissa A.H. // Chem. Sci. Int. J. 2018. V. 23. № 3. P. 1.
Rissanou A.N., Harmandaris V. // Soft Matter. 2014. V. 10. P. 2876.
Atif R., Inam F. // Graphene. 2016. V. 5. P. 96.
Güryel S., Walker M., Geerlings P., De Proft F., Wilson M.R. // Phys. Chem. Chem. Phys. 2017. V. 19. P. 12959.
Rissanou A.N., Baĉová P., Power A.J., Harmandaris V. // Materials Today: Proceedings. 2018. V. 5. P. 27472.
Savin A.V., Korznikova E.A., Dmitriev S.V. // Phys. Rev. B. 2015. V. 92. P. 035412.
Савин А.В., Корзникова Е.А., Дмитриев С.В. // Физика твердого тела. 2015. Т. 57. С. 2278.
Zacharia R., Ulbricht H., Hertel T. // Phys. Rev. B. 2004. V. 69. P. 155406.
Paul W., Yoon D.Y., Smith G.D. // J. Chem. Phys. 1995. V. 103. № 4. P. 22.
Savin A.V., Korznikova E.A., Dmitriev S.V. // Phys. Rev. B. 2019. V. 99. P. 235411.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)


