1. На главную
  2. Электронные версии
  3. Высокомолекулярные соединения (серия А)
  4. T. 63, № 5, 2021

Высокомолекулярные соединения (серия А), 2021, T. 63, № 5, стр. 344-353

РОЛЬ МЕЖМОЛЕКУЛЯРНЫХ ЗАЦЕПЛЕНИЙ В ПРОЦЕССАХ ОБРАЗОВАНИЯ НАНОРАЗМЕРНЫХ ПОР ПРИ ДЕФОРМИРОВАНИИ ПОЛИЭТИЛЕНА: АТОМИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

М. А. Логунов a, b, *, Н. Д. Орехов a, b

a Московский физико-технический институт (Национальный исследовательский университет)
141701 Московская обл., Долгопрудный, Институтский пер., 9, Россия

b Объединенный институт высокомолекулярных соединений Российской академии наук
125412 Москва, ул. Ижорская, 13, Россия

* E-mail: mikhail.logunov@phystech.edu

Поступила в редакцию 01.02.2021
После доработки 26.03.2021
Принята к публикации 09.04.2021

Полный текст (PDF)

Аннотация

Взаимосвязь между локальной топологией молекулярных зацеплений на наноразмерных масштабах и механическими свойствами на макроскопическом уровне – один из открытых вопросов науки о полимерах. В данной работе в рамках метода молекулярной динамики смоделирован процесс порообразования в аморфном полиэтилене в ходе одноосного растяжения. Рассмотрено, каким образом изменение концентрации межмолекулярных зацеплений влияет на динамику образования наноразмерных пор. Полученные результаты статистического анализа размеров пор свидетельствуют о том, что межмолекулярные зацепления замедляют процессы их роста и агрегации в объеме полимера.

ВВЕДЕНИЕ

В силу своих механических свойств и устойчивости к циклическим нагрузкам полимеры и композиты на их основе получили широкое распространение в качестве конструкционных материалов. Высокие прочностные характеристики обусловливают интерес к изучению деградации и растрескивания полимеров. Возникновение необратимых изменений в структуре полимерных материалов в результате внешних нагрузок – это комплексный процесс, охватывающий не только явления, происходящие на макроскопическом и микроскопическом уровнях, но и наноразмерные эффекты, связанные с локальными изменениями в конфигурации отдельных полимерных цепей [1]. Возможности экспериментальных методов при исследовании зарождения пор в полимерных материалах, как правило, ограничены пространственным разрешением в единицы микрометров [2, 3]. Поэтому молекулярная динамика выступает одним из наиболее эффективных инструментов для изучения наноразмерных конформационных перестроек и ранних стадий порообразования [4], а также предсказания свойств углеводородов [5, 6]. Открытым остается вопрос о том, как именно происходит нуклеация наноразмерных пор в ходе деформации полимера, и есть ли взаимосвязь между вероятностью инициирования данного процесса в конкретной области материала и локальной пространственной конфигурацией отдельных полимерных цепочек. В более общем смысле, эта задача сводится к попытке предсказать наиболее вероятные области возникновения необратимых изменений в объеме аморфного полимера (образование пор, возникновение кристаллических зародышей), исходя из особенностей пространственного распределения отдельных полимерных цепочек.

В настоящее время существует несколько гипотез о том, какие области аморфного полимера более предрасположены к зарождению наноразмерных пор. Так, в работе [7] высказывались предположения о том, что нанопоры, в первую очередь, образуются в зонах с наибольшей концентрацией концевых участков молекул. Хотя динамическое поведение концевых участков действительно отличается от поведения центральных участков молекулы полимера [8], гипотеза об их участии в инициировании пор позднее была поставлена под сомнение [9]. Было показано, что локальные флуктуации объемного модуля упругости и возникновение неафинных смещений могут дать информацию о вероятном образовании нанополости в конкретной области материала при дальнейшей деформации. Однако предпосылки, приводящие к негомогенному характеру пространственного распределения объемного модуля упругости, авторы работы [9] не рассматривали.

В качестве альтернативной концепции в ряде теоретических исследований выдвигались идеи о взаимосвязи между процессом образования пор и распутыванием межцепочечных зацеплений [10].

Возможность численной проверки этой гипотезы появилась с развитием методов суперкомпьютерного молекулярного моделирования и созданием алгоритмов построения и анализа примитивного пути [11] – методики, позволяющей рассчитать количественные характеристики межмолекулярных зацеплений. В последнее десятилетие опубликовано значительное число работ, посвященных изучению изменений топологии межмолекулярных зацеплений в ходе деформирования линейных полимеров [12–15] и в процессе фазовых переходов [16]. Влияние локальной концентрации межцепочечных зацеплений на положение областей, в которых происходит зарождение кристаллитов во время охлаждения расплава линейного полимера, продемонстрировано в работе [17]. Также в недавней публикации [18] было показано, что смещение межцепочечных зацеплений в аморфном полимере в процессе деформирования может носить неафинный характер, приводящий к их кластеризации. В результате подобного негомогенного распределения зацеплений в материале возникают как зоны с более высокой, так и с более низкой локальной концентрацией зацеплений. Кроме того, варьирование концентрации межмолекулярных зацеплений может быть обусловлено особенностями самой процедурой полимеризации [19], в частности скоростью протекания этого процесса.

В настоящей работе в рамках метода классической молекулярной динамики предпринята попытка продемонстрировать влияние локальной концентрации зацеплений в аморфном полиэтилене на динамику образования наноразмерных пор в ходе одноосного растяжения.

ОПИСАНИЕ МОДЕЛИ И МЕТОДИКА МОДЕЛИРОВАНИЯ

Потенциал межчастичного взаимодействия

Все молекулярно-динамические расчеты осуществляли с использованием программного пакета “LAMMPS” [20] и потенциала “Dreiding” [21]. Для ускорения расчетов молекулу ПЭ представили в упрощенной геометрии: в качестве атомарных единиц полимерной цепи выступали группы CH2 и CH3 (так называемая “модель объединенного атома”):

(1)
$U = {{U}_{{bond}}} + {{U}_{{angle}}} + {{U}_{{dihedral}}} + {{U}_{{nonbond}}}$
(2)
${{U}_{{bond}}}(r) = \frac{1}{2}{{k}_{r}}{{(r - {{r}_{0}})}^{2}}$
(3)
${{U}_{{angle}}}({{\theta }}) = \frac{1}{2}{{k}_{{{\theta }}}}{{(\cos {{\theta }} - \cos {{{{\theta }}}_{0}})}^{2}}$
(4)
${{U}_{{nonbond}}}(r) = 4u\left( {{{{\left( {\frac{a}{r}} \right)}}^{{12}}} - \left( {{{{\frac{a}{r}}}^{6}}} \right)} \right)$
(5)
${{U}_{{dihedral}}}({{\varphi }}) = {{k}_{{{\varphi }}}}(1 + \cos m{{\varphi }})$

Параметры межчастичного взаимодействия аналогичны параметрам ПЭ из предыдущих работ [22, 23], в которых рассматривали полимерный композит с добавлением углеродных нанотрубок. При моделировании использовали периодические граничные условия по трем осям Ox, Oy, Oz.

Анализ зацеплений между молекулами и процедура расчета объема пор

Для анализа изменений в системе межмолекулярных зацеплений в ходе деформирования (в первую очередь, актов распутывания) применяли метод примитивного пути [11] в рамках молекулярной динамики, предложенный в работе [24]. Он включал в себя три стадии: фиксирование концевых мономеров; плавное уменьшение равновесной длины ковалентных связей между мономерами (в формуле (2) параметр r0) при сохранении межмолекулярных взаимодействий; минимизация энергии путем постепенного охлаждения системы до 0 K.

В отсутствие тепловых флуктуаций ковалентные связи между мономерами пытаются сократить свою длину, и тем самым привести молекулярные цепочки в максимально натянутое состояние. При этом наличие межмолекулярных взаимодействий гарантирует, что отдельные цепи не пройдут сквозь друг друга, и топология зацеплений сохранится. Полученная сетка так называемого примитивного пути состоит из прямых сегментов, выходящих из точек зацеплений. Для каждого пути можно ввести значения полной длины всего контура Lpp, а также среднюю длину прямого сегмента примитивного пути:

${{a}_{{pp}}} = \frac{{R_{{ee}}^{2}}}{{{{L}_{{pp}}}}},$
где Ree – расстояние между зафиксированными концами молекулы.

В свою очередь, среднее расстояние между соседними мономерами выражается следующим образом:

${{b}_{{pp}}} = \frac{{{{L}_{{pp}}}}}{N}.$

Здесь N – общее число мономеров в молекуле, а среднее число мономеров на прямом участке примитивного пути вычисляется как

${{N}_{e}} = \frac{{{{a}_{{pp}}}}}{{{{b}_{{pp}}}}} = N\frac{{R_{{ee}}^{2}}}{{L_{{pp}}^{2}}}$

Параметр Ne использовали в качестве основной численной характеристики концентрации межцепочечных зацеплений. Чем выше Ne, тем более запутанной является система, и наоборот. В случае полного отсутствия зацеплений Ne = N.

Для расчета размеров и количества пор использовали пакеты “OVITO” и “PSDsolv” [25–27]. В программе OVITO рассчитали общий объем пор. Для определения объема поры каждый мономер представляли в виде сфер радиуса ra = 2 Å, после чего строили поверхность, ограниченную этими сферами, и рассчитывали объем, который она охватывала. Радиус отдельного мономера CH2 составлял ra = 2 Å, а минимальный диаметр поры принимали равным 4 Å.

Генерация расчетной ячейки и параметры расчетов молекулярной динамики

Исследовали два типа расчетных ячеек, различающихся концентрацией межмолекулярных зацеплений. В одном случае, рассматривали конфигурацию со значением Ne, близким к равновесному для аморфного ПЭ при заданной температуре (далее “перепутанная” ячейка), во втором – с искусственно увеличенным Ne, т.е. с пониженной концентрацией зацеплений между молекулами (далее “распутанная” ячейка). Для каждого типа независимо сгенерировали по три расчетные ячейки, каждая из которых содержала 560 молекул ПЭ со средней длиной цепочек по 550 мономеров. Рассмотренная длина цепочек лежит в стандартном для молекулярной динамики диапазоне значений. Например, авторы работы [17] изучали системы с полимерами длиной 100, 200 и 500 звеньев, а в статье [28] проводили моделирование полимеров длиной 1000 звеньев.

Ограничения по длине цепочек обычно продиктованы техническими трудностями, возникающими в процессе релаксации расчетной ячейки: чем выше длина молекул, тем больше времени требуется на релаксацию. В настоящей работе для оптимизации этого процесса генерацию начальной конфигурации молекул в расчетной ячейке c перепутанным ПЭ осуществляли с помощью метода псевдорадикальной полимеризации [29]. Для генерации распутанной ячейки в качестве начальной конфигурации взяли ячейку, заполненную монокристаллом ПЭ, количество зацеплений между молекулами которого было близко к нулю. Для обоих типов ячеек использовали единую процедуру релаксации и выхода на заданные значения P и T [30]: в течение 14 нс ячейку охлаждали с 500 до 270 К со скоростью 16.4 × 109 К/с, после чего в течение еще 80 нс ячейку удерживали при 270 К и давлении P = 1 атм. Шаг интегрирования уравнений движения атомов был равен 2 фс. Выведение системы к нужным параметрам проводили при помощи термостата Нозе–Хувера. По окончании релаксации размер ячеек составлял 20.3 × 20.3 × 20.3 нм3, что соответствует плотности 0.857 г/см3. Для недеформированных ячеек среднее значение Ne в перепутанной системе 122, в распутанной – 315.

Определение температуры стеклования

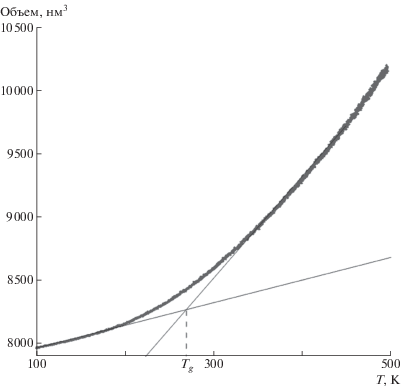
Для верификации используемой модели молекулярной динамики, а также для идентификации температурного диапазона, в котором осуществляли моделирование процесса деформирования, определяли температуру стеклования полимера, рассчитав зависимости атомного объема от температуры во время охлаждения ячейки с 500 до 100 К (рис. 1). Полученное значение Tg ~ 270 K хорошо согласуется как с данными других молекулярно-динамических исследований [28, 31–34], так и с экспериментальными значениями для ПЭ, которые лежат в диапазоне 240–300 К [35–37].

Рис. 1.

Зависимость атомного объема от температуры.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Анализ зарождения пор в ходе одноосного растяжения

Молекулярно-динамическое моделирование одноосного растяжения было проведено при 270 К вдоль оси Оx. Длина ячейки изменялась как x(t) = x0 + ${{\nu }_{x}}t$ со скоростью 5 × 106 с–1 и условием неподвижности боковых стенок νy, νz = 0. Здесь и далее ε – это относительное удлинение расчетной ячейки, которое выражается как ε = $\frac{{x(t) - x(0)}}{{x(0)}}$ × × 100%. На начальных этапах растяжения (ε < 4%) зависимости напряжения от деформации (рис. 2a) для обоих рассмотренных типов ячеек демонстрируют практически идентичное поведение. Небольшие различия наблюдаются в значении пикового напряжения: для перепутанного ПЭ оно достигается при ε = 5.6% растяжения и составляет 58.7 МПа, для распутанного ПЭ – при ε = 5.5% и равно 58.4 МПа (рис. 2б).

Рис. 2.

Зависимости напряжения от деформации (а, б) и суммарного относительного объема пор от величины растяжения (в, г) для перепутанного (1) и распутанного (2) ПЭ.

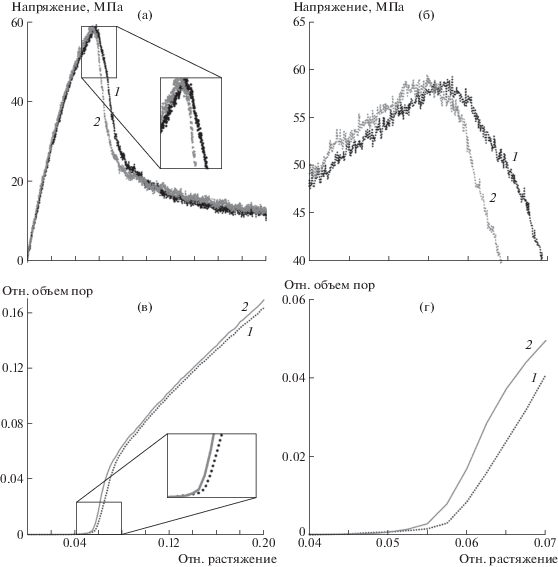
Однако радикальные различия кривых напряжение–деформация прослеживаются в диапазоне ε = 6–8%. Этот интервал характеризуется резким снижением напряжения в результате быстрого роста суммарного объема полостей в системе. Динамика суммарного объема пор показана на рис. 2в, где представлено отношение общего объема пор к объему всей расчетной ячейки. Для обеих систем положение пика текучести совпадает с моментом начала активного образования пор (ε = = 5.5% для распутанного ПЭ и ε = 5.6% для перепутанного ПЭ).

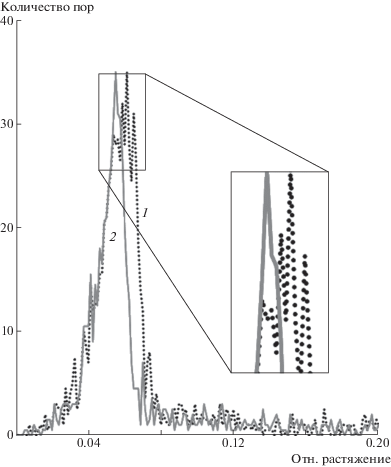
При этом полости малых объемов обнаруживаются в системе и в области ε = 2–5%, т.е. задолго до достижения предела текучести (рис. 3а). Такие полости случайным образом формируются в результате флуктуации свободного объема. При ε < 5.0–5.5% они остаются нестабильными и схлопываются, не достигая критического размера. Проводя аналогии с классической теорией нуклеации, здесь и далее будем называть докритическими те поры, которые схлопываются спустя какое-то время после формирования. Формирование докритических пор не приводит к падению напряжения на диаграмме (рис. 2а), а их общий объем составляет не более доли процента от полного объема расчетной ячейки. Вместе с тем общая численность этих нестабильных пор растет в процессе растяжения до момента ε = 5.0–5.5% (рис. 4), когда в системе формируется одна или несколько крупных полостей (см. рис. 3). Момент их формирования хорошо виден на графиках суммарного объема (рис. 2г), а вызванное этим падение напряжения способствует схлопыванию менее крупных пор в окружающем объеме вещества (рис. 3).

Рис. 3.

Поры в расчетной ячейке с растяжением 5.0 (а), 6.25 (б), 7.5 (в) и 10.0% (г): а – в ячейке присутствуют только поры докритического размера, б – первые стабильные поры закритического размера, в – агрегирование закритических пор.

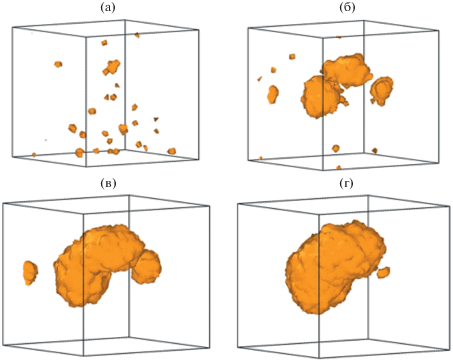
Рис. 4.

Зависимость количества пор от величины относительного растяжения расчетной ячейки для перепутанного (1) и распутанного (2) ПЭ.

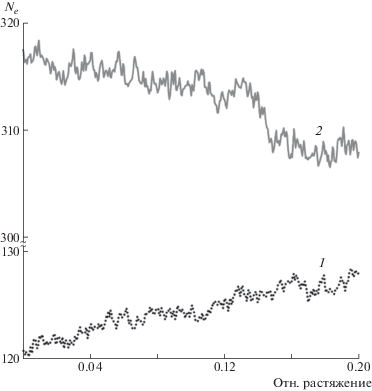
На рис. 5 представлена зависимость Ne от величины растяжения в перепутанной и распутанной системах. Полученные значения Ne для перепутанного аморфного ПЭ отлично согласуются с данными других молекулярно-динамических работ: Ne = 60 [38] и Ne = 110 [39]. Концентрация зацеплений в аморфном полимере напрямую связана с таким макропараметром, как модуль упругости на плато. Эта величина плато рассчитывается по формуле $G_{N}^{0} = \frac{{{{\rho }}RT}}{{{{N}_{e}}{{m}_{{}}}}}$, где m – масса звена полимерной молекулы. В настоящей работе для перепутанного ПЭ с Ne = 122 величина $G_{N}^{0}$ составляет 1.6 МПа для 270 К. Это согласуется с экспериментальным значениями, полученными в работе [40] для Ne = 86, c $G_{N}^{0}$ = 1 МПа. Значение Ne для распутанной системы на старте более чем в 2 раза выше, чем для перепутанной. Как видно на графике рис. 5, во всем диапазоне ε = 0–20% величина Ne для перепутанной системы остается существенно ниже, чем для распутанной. Рост параметра Ne отражает процесс распутывания полимерных макромолекул, в то время как его нисходящая динамика наоборот свидетельствует о релаксации Ne в сторону равновесного значения и перепутывании сети полимерных макромолекул.

Рис. 5.

Динамика параметра Ne в ходе растяжения для перепутанного (1) и распутанного (2) ПЭ.

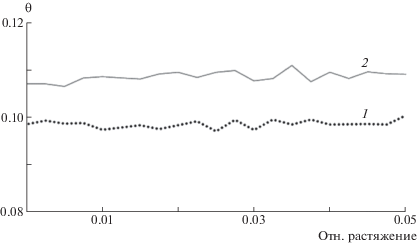
Чтобы убедиться, что в процессе релаксации в ячейках не началось образование кристаллитов, был рассчитан ориентационный фактор Германса: ${{\theta }} = \frac{{(3{{{\cos }}^{2}}{{\alpha }} - 1)}}{2}$, где α – угол между направлениями соседних макромолекул. Для параллельной взаимной ориентации молекул он равен 1.0, для перпендикулярной –0.5, а для случайно ориентированных молекул близок к нулю. На рис. 6 приведена динамика ориентационного фактора для распутанного и перепутанного полиэтилена, показывающая, что до момента начала образования крупных пор оба типа расчетных ячеек содержат разупорядоченный ПЭ.

Рис. 6.

Зависимость ориентационного фактора Германса θ от величины растяжения для перепутанного (1) и распутанного (2) ПЭ.

Анализ зарождения пор в деформированном образце при постоянном объеме

Одна из основных проблем молекулярно-динамического подхода в задачах моделирования динамических процессов в высокомолекулярных системах связана с крайне малой (по сравнению с релаксационными временами) длительностью подобных расчетов. Временные масштабы молекулярно-динамических расчетов, как правило, ограничены несколькими сотнями наносекунд, что не позволяет рассматривать значения скорости деформирования меньшие, чем ν = 104–5 с–1. Это создает трудности для прямого сопоставления расчетных кривых напряжение–деформация с экспериментальными, поскольку их форма и численные характеристики существенным образом зависят от скорости растяжения [32]. В то же время, молекулярная динамика является прекрасным инструментом для анализа процессов, сопутствующих распаду метастабильных состояний вещества в статических условиях при V = = const. В качестве такого метастабильного состояния можно рассмотреть и расчетную ячейку с ПЭ, представленную в данной работе, растянутую до ε = 4.0–4.5%. При этих значениях она уже почти достигла точки предела текучести в расчетах с ν = 5 × 106 с–1 (рис. 2а), но активный рост объема пор еще не успел начаться и спровоцировать падение напряжения. Если остановить процесс растяжения на этих значениях ε и позволить ячейке продолжить релаксировать в условиях постоянного объема и постоянной полной энергии (V = const и E = const), то можно дождаться момента образования пор (т.е. распада метастабильного состояния) на доступных молекулярно-динамических временах в несколько сотен наносекунд. При этом на динамику системы не оказывает вмешательство внешнее напряжение, и образование пор будет происходить уже в квазистационарном режиме.

Для сравнения характеристик процесса образования пор в растянутых ячейках перепутанного и распутанного ПЭ в условиях V = const был выбран момент времени – ε = 4.5%. Соответствующие конфигурации расчетных ячеек были взяты непосредственно из вычислений процесса одноосного растяжения, описанного в предыдущей секции.

Молекулярно-динамические расчеты с такими системами проводились без термостата при условии E = const в течение 100 нс. Моделирование осуществлялось без участия термостата, чтобы исключить возможность его влияния на флуктуацию энергии отдельных молекул в рассматриваемых системах. На рис. 7 показан пример значений объема наибольшей поры в двух ячейках перепутанного и распутанного ПЭ в ходе таких расчетов. За время расчета t = 100 нс во всех ячейках распутанного ПЭ прослеживалось формирование поры закритического объема с ее последующим резким ростом и падением напряжения в системе (рис. 7а). В расчетных ячейках с перепутанным ПЭ на рассматриваемых временах подобное поведение, напротив, не наблюдалось. Такой результат свидетельствует о том, что системы с большим значением Ne (меньшее число межмолекулярных зацеплений) оказываются менее устойчивы, чем системы с большим значением Ne при одинаковых величинах растяжения: в то время как для распутанных ячеек среднее время жизни метастабильного состояния при ε = 4.5% составило 22 нс, для перепутанных ячеек оно заведомо превышает 100 нс – полное время расчета.

Рис. 7.

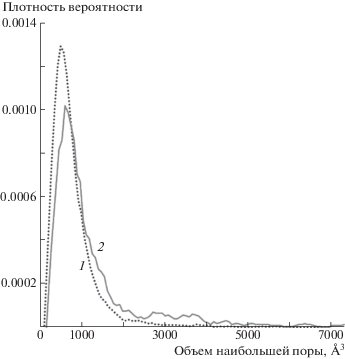
Зависимости объема наибольшей поры от времени для перепутанного (1) и распутанного (2) ПЭ: общая картина (а) и увеличенная начальная область, соответствующая формированию пор докритического объема (б).

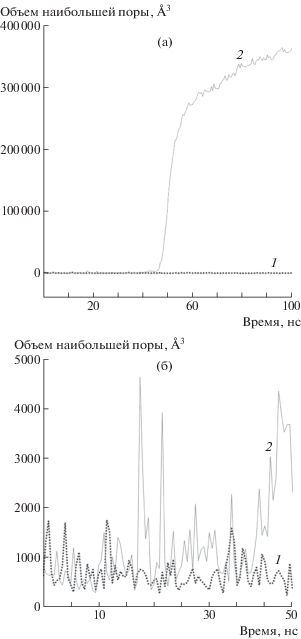
Аналогично ситуации одноосного растяжения, рассмотренной в предыдущей секции, до момента падения напряжения в обеих системах видны образование и гибель пор малых объемов. На рис. 7б представлен увеличенный участок, отвечающий формированию докритических пор. В предположении их сферической формы объемы 2000–4000 Å3 соответствуют диаметрам 8–10 Å. На рис. 8 приведено усредненное распределение вероятности образования докритических пор фиксированного объема в обоих типах расчетных ячеек. Распределение показывает, что при одинаковых значениях величины растяжения (ε = 4.5%) и практически идентичных значениях напряжения, частоты образования больших по размеру пор в распутанном ПЭ выше, чем в случае перепутанного. На качественном уровне этот результат объясняет наблюдаемые на рис. 2 расхождения между зависимостями для двух типов рассмотренных систем в диапазоне ε = 6–8%: наличие межмолекулярных зацеплений затрудняет рост объема докритических пор (о чем также свидетельствует сдвиг максимума распределения на рис. 8 в область меньших объемов), и система с более низким значением Ne должна характеризоваться меньшей вероятностью зарождения пор закритического объема.

Рис. 8.

Распределение вероятности образования пор фиксированного объема для перепутанного (1) и распутанного (2) ПЭ.

ЗАКЛЮЧЕНИЕ

С помощью метода молекулярной динамики исследован процесс образования пор в аморфном полиэтилене в процессе одноосного растяжения. Путем сравнения систем с более высоким и более низким значением Ne было показано, что изменение концентрации межмолекулярных зацеплений существенным образом влияет на динамику образования наноразмерных пор и сдвигает диапазон растяжений, при котором материал остается устойчивым. Результаты статистического анализа размеров пор свидетельствуют о том, что межмолекулярные зацепления замедляют процессы их роста и агрегации в объеме полимера.

Список литературы

  1. Pawlak A., Galeski A., Rozanski A. // Prog. Polym. Sci. 2014. V. 39. № 5. P. 921.

  2. Morgeneyer T.F., Proudhon H., Cloetens P., Ludwig W., Roirand Q., Laiarinandrasana L., Maire E. // Polymer. 2014. V. 55. № 25. P. 6439.

  3. Pawlak A. // Polymer. 2007. V. 48. № 5. P. 1397.

  4. Karatrantos A., Clarke N., Kröger M. // Polym. Rev. 2016. V. 56. № 3. P. 385.

  5. Kondratyuk N.D., Pisarev V.V., Ewen J.P. // J. Chem. Phys. 2020. V. 153. № 15. P. 154502.

  6. Kondratyuk N., Lenev D., Pisarev V. // J. Chem. Phys. 2020. V. 152. № 19. P. 191104.

  7. Sixou B. // Mol. Simul. 2007. V. 33. № 12. P. 965.

  8. Ostrovskaya I.K., Fatkullin N.F. // Polymer Science A. 2020. V. 62. № 2. P. 132.

  9. Makke A., Perez M., Rottler J., Lame O., Barrat J.-L. // Macromol. Theory Simul. 2011. V. 20. № 9. P. 826.

  10. Dettenmaier M., Kausch H.H. // Colloid Polym. Sci. 1981. V. 259. № 9. P. 937.

  11. Everaers R., Sukumaran S.K., Grest G.S., Svaneborg C., Sivasubramanian A., Kremer K. // Science. 2004. V. 303. № 5659. P. 823.

  12. Karatrantos A., Composto R.J., Winey K.I., Kröger M., Clarke N. // Polymers. 2019. V. 11. № 5. P. 876.

  13. Sliozberg Y.R., Yeh I.C., Kröger M., Masser K.A., Lenhart J.L., Andzelm J.W. // Macromolecules. 2018. V. 51. № 23. P. 9635.

  14. Ge T., Tzoumanekas C., Anogiannakis S.D., Hoy R.S., Robbins M.O. // Macromolecules. 2017. V. 50. № 1. P. 459.

  15. Gavrilov A.A. // Polymer Science A. 2018. V. 60. № 1. P. 110.

  16. Luo C., Kröger M., Sommer J.U. // Polymer. 2017. V. 109. P. 71.

  17. Luo C., Sommer J.U. // Phys. Rev. Lett. 2014. V. 112. № 19. P. 195702.

  18. Hsu H.P., Kremer K. // Macromolecules. 2019. V. 52. № 17. P. 6756.

  19. Petrov A., Rudyak V., Kos P., Chertovich A. // Macromolecules. 2020. V. 53. № 16. P. 6796.

  20. Plimpton S. // J. Comp. Phys. 1995. V. 117. № 1. P. 1.

  21. Mayo S.L., Olafson B.D., Goddard W.A. // J. Phys. Chem. 1990. V. 94. № 26. P. 8897.

  22. Orekhov N.D., Stegailov V.V. // Polymer Science A. 2016. V. 58. № 3. P. 476.

  23. Logunov M.A., Orekhov N.D. // J. Phys.: Conf. Ser. 2018. V. 946. № 1. P. 2044.

  24. Sukumaran S.K., Grest G.S., Kremer K., Everaers R. // J. Polym. Sci., Polym. Phys. 2005. V. 43. № 8. P. 917.

  25. Stukowski A. // Modell. Simul. Mater. Sci. Eng. 2009. V. 18. № 1. P. 015012.

  26. Bhattacharya S., Gubbins K.E. // Langmuir. 2006. V. 22. № 18. P. 7726.

  27. Kappel F., Kuntsevich A. // Comp. Optim. Appl. 2000. V. 15. № 2. P. 193.

  28. Hossain D., Tschopp M.A., Ward D.K., Bouvard J.L., Wang P., Horstemeyer M.F. // Polymer. 2010. V. 51. № 25. P. 6071.

  29. Perez M., Lame O., Leonforte F., Barrat J.L. // J. Chem. Phys. 2008. V. 128. № 23. P. 234904.

  30. Vorselaars B., Lyulin A.V., Michels M.A.J. // Macromolecules. 2007. V. 40. № 16. P. 6001.

  31. Capaldi F.M., Boyce M.C., Rutledge G.C. // Polymer. 2004. V. 45. № 4. P. 1391.

  32. Bowman A.L., Mun S., Nouranian S., Huddleston B.D. // Polymer. 2019. V. 170. P. 85.

  33. Gee R.H., Boyd R.H. // Comp. Theoretical Polym. Sci. 1998. V. 8. № 1–2. P. 93.

  34. Polymer Handbook / Eds by J. Brandrup, E.H. Immergut, E.A. Grulke. New York: Wiley, 1999. V. 89

  35. Davis G.T., Eby R.K. // J. Appl. Phys. 1973. V. 44. № 10. P. 4274.

  36. White R.P., Lipson J.E.G. // Macromolecules. 2016. V. 49. № 11. P. 3987.

  37. Foteinopoulou K., Karayiannis N.C., Mayrantzas V.G. // Macromolecules. 2006. V. 39. № 12. P. 4207.

  38. Toepperwein G.N., Karayiannis N.Ch., Riggleman R.A., Kröger M., Pablo de J.J. // Macromolecules. 2011. V. 44. № 4. P. 1034.

  39. Cassagnau P., Montfort J., Marin G., Monge P. // Rheologica Acta. 1993. V. 32. № 2. P. 156.

  40. Psarski M., Piorkowska E., Galeski A. // Macromolecules. 2000. V. 33. № 3. P. 916.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Высокомолекулярные соединения (серия А)

Архивы выпусков Информация о журнале Отправить рукопись в журнал