Высокомолекулярные соединения (серия А), 2022, T. 64, № 2, стр. 142-160
ФАКТОР НЕИДЕАЛЬНОСТИ В ТЕРМОДИНАМИЧЕСКОМ АНАЛИЗЕ РЕАЛЬНЫХ РАСТВОРОВ ПОЛИМЕРОВ
a Учреждение образования “Военная академия Республики Беларусь”
220000 Минск, пр. Независимости, 220, Беларусь
b Северный (Арктический) федеральный университет им. М.В. Ломоносова
163002 Архангельск, наб. Северной Двины, 17, Россия
* E-mail: nikma@tut.by
Поступила в редакцию 27.02.2021
После доработки 22.09.2021
Принята к публикации 01.12.2021
- EDN: JKCOTS
- DOI: 10.31857/S2308112022020031
Аннотация
В уравнения информационной энтропии Реньи и Цаллиса, описывающие самоорганизованные структуры высокомолекулярных соединений в растворе, введен обобщенный фактор неидеальности систем g. Эта относительная термодинамическая характеристика связывает идеальную и реальную модели систем, в которых можно выделить два противоположных по знаку и действию процесса: порядок (–) ↔ хаос (+); притяжение (–) ↔ отталкивание (+); сжатие (–) ↔ расширение (+) и т.д. Значение g =1 – βord + αnord, где βord и αnord – статистически усредненные характеристики противоположно протекающих процессов, изменяется в интервале 0 ≤ $g$ ≤ 2 и зависит от того, какой из конкурентных процессов превалирует. При αnord = 0 фактор $g~$ → 0, при βord = 0 фактор $g$ → 2, при $g$ = 1 поведение элементов системы идеально. Получены новые выражения для энтропии с параметром ${{g}_{{th~}}}{\text{\;}} \equiv g$ для квазиравновесных структур в формализме Реньи $S_{{{{g}_{{th}}}}}^{{M - Rn}} = \frac{R}{{{{g}_{{th}}}}}{\text{ln}}\left( {\mathop \sum \limits_{i = 1}^{N(\varepsilon )} p_{i}^{{{{g}_{{th}}} - 1}}} \right)$ и для неравновесных открытых систем в формализме Цаллиса $S_{{{{g}_{{th}}}}}^{{M - Ts}}\left( p \right) = \frac{{R(1 - \mathop \sum \nolimits_i^{N(\varepsilon )} p_{i}^{{1 - {{g}_{{th}}}}})}}{{{{g}_{{th}}}}}$. Установлена связь обобщенного фактора неидеальности со скейлинговыми индексами ${{a}_{\eta }},{{b}_{D}},~{{с}_{S}}$. Рассчитаны термодинамические функции растворов разветвленных природных и синтетических высокомолекулярных соединений (диоксанлигнины, полистиролы, полиглицерины, пиридинсодержащие полифениленовые дендримеры) по экспериментальным данным, полученным гидродинамическими методами. Результаты обсуждаются с позиций как классической квазиравновесной, так и современной неравновесной термодинамики.
ВВЕДЕНИЕ
В данной обзорно-аналитической работе затрагиваются вопросы термодинамики полимерных растворов на основе представлений о фрактальных структурах, образующихся в квазиравновесных и существенно неравновесных условиях в процессе самоорганизации линейных и разветвленных синтетических и природных полимеров.
Для изучения реальных процессов, протекающих в квазиравновесных (локально равновесных) и существенно неравновесных условиях разработан статистический термодинамический формализм на основе энтропии и свободной энергии Больцмана–Гиббса (B–G) для стохастической динамики, основанной на уравнениях [1, 2] и уравнениях Фоккера–Планка (F–P) [3, 4]. Этот формализм вводит несколько ключевых величин: производство энтропии ds/dt, скорость рассеивания свободной энергии dF/dt, избыток и потребление тепла и т.д. [10, 30]. Статистическая термодинамика малых систем (например, полимер–растворитель) построена на классическом определении термодинамических функций энтропии и свободной энергии и рассматривается как неэкстенсивная [5]. Развитие классического определения энтропии Больцмана–Гиббса обеспечивает основу для изучения систем с дальнодействующими взаимодействиями, мультифрактальными структурами, долговременной памятью или системы, в которых нельзя пренебречь взаимодействием их макроскопических частей [6]. В настоящее время активно развивается термодинамический формализм параллельно для неэкстенсивной энтропии и свободной энергии, например, введены энтропия Цаллиса [7, 10], энтропия Реньи [9] с их модифицированными формами [8, 53] и другие [98–101].
Традиционное изучение термодинамики разбавленных, полуразбавленных, концентрированных растворов и расплавов индивидуальных полимеров их смесей многогранно [11–13, 17, 18, 46, 56, 73, 76, 86]. Tермодинамике растворов полимеров посвящено огромное число теоретических работ: в рамках решеточных моделей (Флори–Хаггинса, Флори–Кригбаума) [11, 12] и n-симплексных решеточных моделей SAW (self-avoiding walk) [14], Санчеса–Лакомба (SL EoS) и коэффициента активности объема [UNIFAC-FV] при прогнозировании фазового поведения растворов полимеров [14] и внерешеточных − модели силового поля, модели с параметрами растворимости Гильдебранда, перколяционной модели, теории графов, теории ветвящихся процессов, теории скейлинга, теории фракталов и других [11, 15–20].
Например, для распространенной в физике полимеров модели SAW с непересекающимися полимерными цепями в аналитическом обзоре [14], d посвященном расчетам критических показателей Флори ${{{v}}_{c}}$ и γ коллапсирующих глобул в атермических растворах c латеральными взаимодействиями цепей линейных и разветвленных полимеров на n-симплексных решетках, доказывается, что в двумерном случае при блуждании элемента цепи по решетке путь пробега самый короткий. При масштабировании в случае большей размерности d > 2 он неограниченно растет, и выясняется, что по модели SAW для размерности d > 4, где критические показатели принимают среднеполевые значения, точное аналитическое решение невозможно. Разумной альтернативой оказалось построение графов, таких как фракталы с размерностью df, для которых найдено точное решение [14, 72]. Для случая линейных и разветвленных полимеров с взаимным притяжением цепей на фракталах может наблюдаться коллапс перехода спираль–глобула [17]. При высоких температурах, когда полимер находится в набухшей фазе в полукомпактном состоянии, ${{{v}}_{c}}$ > 1/df (обнаружено на 5- и 7-симплексных решетках [72]), а при низких температурах, когда полимер находится в сколлапсированной фазе, ${{{v}}_{C}}$ = 1/df (на 4- и 6-симплексных решетках [72]), т.е. коллапсирующая глобула может существовать на некоторых n-симплексных решетках с нечетным n, но структура такой глобулы не совсем такая, как в случае четного n. Следовательно, для линейных и разветвленных структур полимеров на детерминированных конечных разветвленных фракталах можно точно определить критические свойства в реальном пространстве [14, 17, 72]. Получены аналитические выражения не только при растворении полимера, но и при его адсорбции на родственной по природе поверхности подложки [19], и при наличии в полимерной структуре малых (затравочных) концентраций фрактальных наноструктур [16].
Таким образом, подчеркивается теоретическая и практическая значимость роли фракталов и их размерности df, например, при создании новых структурированных нанокомпозиционных материалов [15, 16, 74].
Важным направлением в термодинамическом анализе систем с участием полимеров остается реальная оценка энтропийных вкладов в свободную энергию исследуемых систем [12, 74, 76]. Простейшей в теоретическом отношении выступает теория скейлинга, уходящая в 1970-е годы (P.G. de Gennes) [12] и успешно используемая для интерпретации критических явлений. Последние часто связаны с резким изменением физических величин в процессе самоорганизации системы в точке перехода порядок–беспорядок. В связи с этим в данной работе акцент сделан на реальной оценке энтропийных вкладов в свободную энергию, опирающейся на теорию скейлинга. Как уже отмечено, по численным значениям df возможно вычисление энтропии и других термодинамических функций с помощью любых подходов. Теория скейлинга хорошо зарекомендовала себя для разбавленных и полуразбавленных растворов, в которых макромолекулы находятся в конформации непротекаемого или протекаемого клубка либо глобулы. При этом особенности топологической структуры полимеров оцениваются как по стандартным характеристикам (среднеквадратическое расстояние между концами цепи макромолекулы 〈R2〉, персистентная длина/сегмент Куна b, радиус инерции Rg, коэффициент набухания макромолекулы α), так и по скейлинговым индексам типа Марка–Куна–Хаувинка–Сакурады ${{a}_{\eta }},{{b}_{D}},~{{с}_{S}}$.
Как будет показано ниже, знание величин фрактальной размерности полимерных структур можно использовать и для расчетов энтропийных вкладов в свободную энергию исследуемых систем. В обзорной статье [74], посвященной изучению энтропийных эффектов в полимерных нанокомпозитах, отмечается практическая важность учета такой информации “…при объединении экспериментальных результатов и идей, возникающих на основе теорий и моделирования, наступает понимание, как энтропийные эффекты превращаются в эффективные межчастичные взаимодействия, которые можно использовать для создания наноструктур полимерных нанокомпозитов”. В исследованиях последних лет по термодинамике растворов полимеров акцентируется внимание на связи энтропии с фрактальными характеристиками высокомолекулярных соединений [74–77]. Поэтому обратимся к энтропийно-мультифрактальному подходу как одному из направлений в изучении сложных самоорганизованных структур, включая высокомолекулярные синтетические соединения и биополимеры [26, 28, 31, 37, 38, 77].
В настоящей работе предпринята попытка ввести обобщенный фактор неидеальности систем $g~$ ≡ GNF (The generalized non-ideality factor of systems) [40, 41] в уравнения информационной энтропии [36, 37], описывающие самоорганизованные структуры квази- и существенно неравновесных систем, т.е. фрактальные структуры, в приложении к термодинамическим и топологическим свойствам высокомолекулярных соединений [50–53, 59–62]. Использование GNF в энтропийно-фрактальном анализе сложных систем позволит расширить практические и теоретические возможности этого математического аппарата [21–37] при изучении термодинамики реальных растворов полимеров.
Цель настоящего исследования – адаптация модифицированных уравнений информационной и термодинамической энтропий Реньи (для квазиравновесных) и Цаллиса (для существенно неравновесных) систем с фактором неидеальности [8, 53] для термодинамического анализа реальных растворов полимеров, включая анализ процессов самоорганизации при синтезе высокомолекулярных соединений, биосинтезе природных полимеров и компьютерном моделировании макромолекулярных систем.
ЭНТРОПИЙНО-МУЛЬТИФРАКТАЛЬНЫЙ ПОДХОД К СТРУКТУРНОМУ И ТЕРМОДИНАМИЧЕСКОМУ АНАЛИЗУ САМООРГАНИЗОВАННЫХ СИСТЕМ
Энтропийно-фрактальный подход − универсальный инструмент анализа сложных открытых систем разной природы [21, 24, 25, 27, 38]. В открытых термодинамических системах, обменивающихся энергией и негэнтропией с внешней средой, протекают процессы спонтанного формирования сложных, как правило, фрактальных, структур [29, 31].
Связь между энтропией и информацией была установлена в основополагающей работе L. Szilard [22]. В дальнейшем в работах [23, 30, 37, 77] сформулирован негэнтропийный принцип информации, обобщающий второе начало термодинамики, согласно которому как энтропия, так и информация должны рассматриваться и трактоваться совместно [23, 27, 31].
Применение информационного подхода к статистической механике [23, 26, 28, 31] позволило по-новому обосновать равновесное распределение Гиббса [37] и построить неравновесную термодинамику систем [27, 28] на принципе условного максимума информационной энтропии Гиббса–Шеннона [28, 37].
В случае различных вероятностей pi состояний системы вводится ансамбль микроканонических i-х подсистем, для которых все Wi состояний имеют равные вероятности pi с энтропией Больцмана:
Усреднение энтропий по состояниям системы приводит к информационной энтропии Гиббса–Шеннона
(2)
${{S}^{{{\text{G - Sh}}}}} = \langle S_{i}^{{({\text{В}})}}\rangle p = - \sum\limits_i^W {{{p}_{i}}\ln {{p}_{i}},} $Каноническое распределение Гиббса представляют через плотность распределения как pi = = $\frac{{{{e}^{{ - \beta {{H}_{i}}}}}}}{Z},$ где β = 1/kT, kB − константа Больцмана, T − термодинамическая температура, H = {Hi} − гамильтониан, $Z = \Sigma i{{e}^{{ - \beta {{H}_{i}}}}}$ – статистическая сумма [15, 19, 21, 27].
Большинство систем, находящихся в термодинамическом равновесии, подчиняются статистике Больцмана–Гиббса c ее тремя ключевыми положениями:
− определение функционала энтропии S = = −Σikpiln pi (при условии Σipi = 1 и ΣpiHi = U для канонического ансамбля), U − внутренняя энергия;
− форма равновесного распределения pi = $\frac{{{{e}^{{ - \beta {{H}_{i}}}}}}}{Z}$;
– связь статистической суммы Z с термодинамическими потенциалами G или F, например, F = − (1/β)lnZ и U = −(∂/∂β)lnZ [25, 37, 46].
Однако многие неравновесные системы и системы с “медленной динамикой” обнаруживают асимптотически степенные статистические распределения [23, 29, 32, 33, 36, 76]. В неравновесной термодинамике при описании существенно неравновесных систем, например космических, биологических и т.д., связанных с процессами самоорганизации структур, предложены альтернативные формы информационной энтропии [33, 36, 77]. При изучении сложных систем и процессов (фрактальных и самоорганизующихся структур, явления турбулентности и т.д.) [81] в отличие от экспоненциального распределения Гиббса эффективнее “работают” степенные распределения. Например, энтропия Хаврды–Чарвата–Цаллиса [36, 76]:
(3)
$Ts(p) = \frac{{1 - \sum\limits_i^n {p_{i}^{{q'}}} }}{{1 - q'}} = \frac{{1 - \sum\limits_i^n {p_{i}^{q}} }}{{q - 1}},$Особенностью статистической термодинамики А. Реньи является то, что в соответствии со вторым началом термодинамики соблюдается условие максимума энтропии. Важно также, что при переходе от статистической термодинамики Гиббса наблюдается фазовый переход упорядочения в системе при максимально возможном значении порядка η = −q, т.е. когда эволюция системы идет в направлении спонтанной самоорганизации, сопровождающейся ростом термодинамической энтропии. При этом распределение Реньи [37] в случае степенного гамильтониана становится степенным, а энтропия Rn(p), как и в термодинамике Гиббса, обладает свойством аддитивности, т.е. экстенсивна: S(W1W2) = S(W1) + + S(W2), тогда как энтропия Ts(p) − неэкстенсивна: S(W1W2) ≠ S(W1) + S(W2). Последнее интерпретировано [22, 33, 34, 38, 47, 77] как необходимое условие при изучении различных неэкстенсивных систем, (например, космических) и построении новой термодинамики и новой статистической теории для описания системы с долговременной памятью и системы, каждый элемент которой взаимодействует не только с ближайшими соседями, но и со всей системой в целом или ее частями [33]. Такие взаимодействия наблюдаются в синтетических и природных полимерах, например, компонентах древесины [49, 50], а также в отдельно выделенных компонентах экспериментально и технологически созданных самоорганизованных структур.
Отметим, что энтропия Реньи Rn(p) ≥ 0, возрастая при q = 1, переходит в энтропию SG-Sh(p) в результате предельного перехода $\mathop {\lim }\limits_{q \to 1} Rn = {{S}^{G}}$ и в энтропию SB при любых q для равновероятных распределений p. Параметр порядка Реньи η = = 1− q превращается в нуль, и распределение Реньи [16, 27]
Для наглядности на рис. 1 показаны теоретические зависимости термодинамических энтропий Rn и Ts в Дж/моль K от p и q ≡ q' (для q и q' числовые значения заданы одинаково), отражающие характерные особенности сравниваемых моделей. На рисунках наглядно видны принципиальные закономерности:
Рис. 1.
Зависимости Rn (1) и Ts (2) от p. q = 0.01 (а, в) и 2 (б, г) при n = 100 (а, б) и 10 (в, г). Цветные рисунки можно посмотреть в электронной версии.
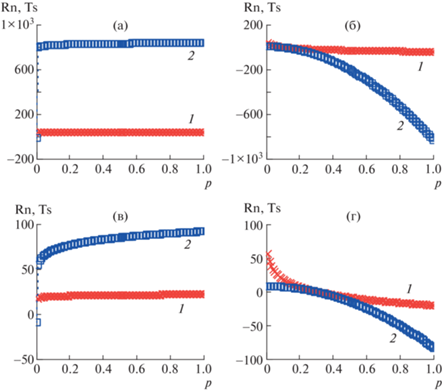
– при изменении q в интервале от 0 до 1 (q ≠ 1) в модели Реньи для всех значений q энтропия по абсолютной величине возрастает медленно, достигая максимального значения вблизи q = 1, в то время как абсолютные величины энтропии в модели Цаллиса растут значительно быстрее, т.е. по степенному закону;
– при изменении q в интервале от 1 до 2 (q ≠ 1) в обеих моделях для текущих значений q энтропия по абсолютной величине, напротив, уменьшается;
− при q = 1 (особый случай) функционалы энтропий в обеих моделях терпят разрыв (причина тому – форма выражения параметров $\frac{1}{{1 - q}}~\,{\text{и}}\,~\frac{{q'\,}}{{q{\kern 1pt} '\, - 1}}$), обусловленный переходом от упорядочения элементов системы к разупорядочению;
− при различных значениях n (далее в модифицированных уравнениях $n~ \equiv N\left( \varepsilon \right)$) расчетные величины энтропий существенно различаются (на что следует особо обращать внимание − см. ниже).
Для перехода от информационной энтропии к термодинамической, т.е. для придания ей физического смысла, в уравнения (2), (3) и (4) необходимо ввести множитель в виде константы Больцмана kB (для одной молекулы) или универсальной газовой постоянной R (для одного моля).
Связи фрактальных размерностей с энтропиями (Л. Больцмана, Дж. Гиббса, К. Шеннона, А. Реньи, К. Цаллиса и других) устанавливаются при рассмотрении предела
где в качестве энтропии S($q)$ может выступать S(R) (Renyi), S(Ts) (Tsallis) и т.д. Например, при скейлинговом показателе τ(q), характеризующим масштабное подобие мультифрактала с обобщенной фрактальной размерностью Реньи ${{d}_{f}}\left( q \right)$ [25, 80] выражение (4) преобразуется в предел(4a)
${{d}_{f}}(q) \approx \frac{1}{{q - 1}}{{\lim }_{{\varepsilon \to 0}}}\ln \left( {\sum\limits_{i = 1}^{N(\varepsilon )} {p_{{i(\varepsilon )}}^{q}} } \right){\text{/}}\ln (1{\text{/}}\varepsilon ),$(4б)
$S(\varepsilon ) \approx \ln {{\varepsilon }^{{ - {{d}_{f}}}}}\quad {\text{или}}\quad {{\varepsilon }^{{ - {{d}_{f}}}}} \approx {{e}^{{S(\varepsilon )}}}$Добавим к сказанному, что величина q при q = 0, q = 1 и q = 2 в уравнениях (3) и (4) совпадает соответственно с размерностью Хаусдорфа dH = d0, информационной d1 и корреляционной d2 размерностями мультифрактального множества, причем dH характеризует плотность объекта, а также то, как он заполняет пространство вложения.
ФАКТОР НЕИДЕАЛЬНОСТИ СИСТЕМ КАК ТЕРМОДИНАМИЧЕСКАЯ ХАРАКТЕРИСТИКА В МОДИФИЦИРОВАННЫХ УРАВНЕНИЯХ РЕНЬИ И ЦАЛЛИСА
В энтропийно-фрактальный математический аппарат логично вписывается предложенный автором [40, 41] важный критерий реальных систем − обобщенный фактор неидеальности систем (GNF ≡ ≡ ($g$)) как относительная термодинамическая характеристика, связывающий идеальную и реальную модели систем, в которых можно выделить два конкурентных (противоположных по знаку и действию) процесса: порядок (−) ↔ хаос (+); притяжение (−) ↔ отталкивание (+); сжатие (−) ↔ ↔ расширение (+); кластеризация (−) ↔ распад (+) и т.д. Численное значение$~g$ изменяется в интервале 0 ≤ $g \leqslant $ 2, и его значение зависит от того, какой из конкурентных процессов превалирует; при g = 1 поведение элементов реальной системы будет таким же, как и для соответствующей ей идеальной системы.
GNF вводится в классические уравнения, пригодные для изучения идеальных систем, процессов и т.д., например в уравнения закона Генри Росм., эксп= $g$Росм; Рауля ΔP = $gP_{1}^{0}$N2, ΔТзам= $g$Km, ΔТкип= $g$Em; Вант-Гоффа Pосм= $g$cRT); Гиббса Γs = −(с/$g$RT)(∂σ/∂lnс)T, p (σ − поверхностное натяжение раствора) и другие уравнения (математические модели) с целью использования их для описания реальных систем [8, 41, 40 ]. При этом фактор может выступать в форме константы, либо уравнения любой сложности, но с обязательным условием, чтобы кроме единицы оно включало разные по знаку, математически и физически обоснованные усредненные характеристики противоположно протекающих процессов − βord ≡ ≡ $\left\langle {1{\text{/}}n\sum\nolimits_i^n {{{\beta }_{i}}} } \right\rangle $ − долю упорядоченных элементов и αnord ≡ $\left\langle {1{\text{/}}n\sum\nolimits_i^n {{{\alpha }_{i}}} } \right\rangle $ − долю разупорядоченных элементов системы. В общем случае g может быть определен через βord и αnord
или через статистические вероятности независимых случайных величин А и В $p_{i}^{'}(B,A)$ = = $\langle - p_{i}^{'}(B)\, + \,p_{i}^{'}~(A)\rangle $ противоположных по знаку и действию событий(5а)
$g = 1 - {{\beta }_{{ord}}} + {{\alpha }_{{nord}}} = 1 + \langle - p_{i}^{'}\left( B \right) + p_{i}^{'}\left( A \right)\rangle ,$В отсутствие диссоциации элементов системы, т.е. при αnord = 0 $g$ → 0, а в отсутствие ассоциации элементов системы, т.е. при βord = 0 g → 2. При сравнении экспериментальной и теоретической (полученной по классическому уравнению) зависимостей по заданным значениям переменных GNF четко фиксирует любые отклонения в исследуемой системе от идеальности.
Физический смысл g как количественной относительной характеристики Ф* − реальной и Ф − идеальной систем ($g = $ Ф*/Ф) виден, например, из рассмотрения уравнений состояния идеального газа
и реального газа где Φ и Φ* − функции состояния, P и P* − давление, n и n* – количество молей идеального и реального газа; V, R, T – объем, универсальная газовая постоянная, абсолютная температура. Обобщенный фактор неидеальности изобарно-изотермического процесса $g$ = P*V/PV = n*/n представляет собой отношение работ реального и идеального газа или количества молей в реальной и идеальной системах. Таким образом, он является относительной энергетической или мольной мерой рассматриваемой системы. Количество молей в системе может изменяться в результате протекания реальных процессов межчастичного взаимодействия (ассоциация, кластеризация), когда мерой является суммарное количество упорядоченных и свободных элементов системы, и межчастичного отталкивания (диссоциация, распад), когда мерой является суммарное количество распавшихся и не подвергнувшихся распаду элементов системы [40, 41].При вириальном разложении фактора неидеальности по степеням молярной концентрации cm (числа частиц) в ряд Камерлинг–Оннеса, вытекающем из уравнения состояния [30, 31], вновь приходим к выражению (5)
Знак (−) указывает на межчастичное притяжение, а (+) − на отталкивание. Чередование знаков в четных и нечетных членах вириального разложения доказано многочисленными экспериментами и компьютерными расчетами, начиная со второго коэффициента [23, 44]. В зависимости от условий (температура, концентрация, природа растворителя), в которой находится система, возможна полная компенсация (точки Кюри, Бойля, θ-условия) или превалирование состояния, связанного с четными или нечетными членами, например, сжатие и набухание отдельных макромолекул или кластеров [48, 49].
Строго математически фактор g может быть определен в виде отношения логарифмов количества состояний объекта в реальном (М*) и идеальном (М0) случае [8, 53]:
где М − мера, R − размер, $d$f − размерность. В качестве М* и М0 может быть выбрано число Nd элементов в структуре фрактального реального (например, кластера) или математического (например, салфетка Серпинского) объекта и число ND элементов в структуре объекта в идеальном состоянии, обладающих свойством многомасштабности и самоподобия. С изменением R* выполняется степенная зависимостьЗдесь df и D − фрактальная и евклидова (в пространстве Минковского − топологическая) размерности. Фрактальная хаусдорфова размерность определяется как
Формулы (6) и (6а) устанавливают связь между размерностями df, D и фактором $g.$
Из представленных выражений следует, что реальный фрактальный объект можно характеризовать мерой множества ${{N}_{{{{d}_{f}}}}}$-элементов, покрывающих (заполняющих) этот объект, а идеальный объект − мерой множества ND-элементов.
Вычисляя $g,$ например, через выражение (6), можно получить три результата:
Для энтропийно-мультифрактального анализа можно ввести энергетический (термодинамический, химический) фактор неидеальности ${{g}_{{th}}}$ через свободную энергию, например, как отношение изобарно-изотермических потенциалов Δ$G_{i}^{*}$/ΔGi реального и идеального состояний. Здесь Δ$G_{i}^{*}$ = = $\mu _{i}^{0}$(p, T) –μi(p, Т, Ni) − изменение изобарного потенциала перехода i-го компонента из стандартного (начального) состояния в реальный раствор RTlnаi, = −Δ$G_{i}^{*}$, а RTlnNi, = −ΔGi – изменение изобарного потенциала при переходе i-го компонента из стандартного состояния в идеальный раствор [40, 41], т.е.
(7)
${{g}_{{th}}} = \frac{{{\text{ln}}{{a}_{i}}}}{{{\text{ln}}{{N}_{i}}~}}~ = 1 + \left\langle {\frac{{{\text{ln}}{{\gamma }_{i}}}}{{{\text{ln}}{{N}_{i}}}}} \right\rangle ~,$Соотношения (7) устанавливают функциональную связь между GNF, активностью и коэффициентом активности, при этом коэффициент активности может принимать значения как меньше единицы (упорядочение, ассоциация, кластеризация), так и больше единицы (диссоциация). Сравнив (7) с основным выражением для GNF (5), сделаем допущение, что выражения математических ожиданий $\left\langle {\frac{{{\text{ln}}{{\gamma }_{i}}}}{{{\text{ln}}{{N}_{i}}}}} \right\rangle $ и 〈$ - {{p}_{i}}\left( \beta \right) + {{p}_{i}}\left( \alpha \right)$〉 как относительные величины должны быть связаны с отношением функционалов для энтропии реальной и идеальной систем Sreal/Sid:
где знак (+) соответствует росту реальной энтропии, а знак (−) − ее убыли. Согласно уравнению (5а), термодинамический фактор равенСледовательно,
Из рассмотренных энтропий идеальному состоянию через {ln${{p}_{i}}$} соответствует термодинамическая энтропия Больцмана Sid ≡ S(B) = $ - {{k}_{{\text{B}}}}\mathop \sum \limits_{i = 1}^N {\text{ln}}{{p}_{i}}$, а через плотность вероятности {$~{{p}_{i}}{\text{ln}}{{p}_{i}}$} − Sid ≡ ≡ S(B-G) $ = - {{k}_{{\text{B}}}}\mathop \sum \limits_{i = 1}^N {{p}_{i}}{\text{ln}}{{p}_{i}}~$ либо информационная энтропия S(G-Sh). Все другие модельные представления энтропий (S(R), S(Ts) и т.д.) будем считать относящимися к реальному состоянию системы.
Исходя из уравнений (7) и (7a) и модельных представлений энтропии Реньи Rn (4) и Цаллиса Ts (3), путем замены в (4) параметра η = 1 − q и в (3) η' = q − 1 на новый параметр ${{g}_{{th}}}$ = 1 + ${{g}_{S}}$ и $g_{{th}}^{'}$ = 1 + ${{g}_{S}}$ получим новые выражения для энтропии. По сравнению с выражениями Реньи и Цаллиса, формально выбираемый от −∞ до +∞ дробный или целочисленный параметр q заменен в них на изменяющийся от 0 до 1 энтропийный фактор неидеальности систем ${{g}_{S}}$ и лежащий в интервале от 0 до 2 термодинамический фактор $~{{g}_{{th}}}$ с физическим смыслом, вытекающим из определений GNF. При этом из выражений (4а) и (5), (7) следует
где qτ ≡ q − текущий дробный или целочисленный параметр преобразования (увеличения) меры, изменяющийся от 0 до qN(ε), а qN(ε) − минимальное число квадратов или кубов с масштабом ε для покрытия всех элементов структуры. Для эвклидовой структуры с размерностью D (отсутствие ограничений на qτ и qN(ε)) при ε → 0 получаем в пределе $~{{g}_{S}} = 1$. При таких условиях формализм Реньи и Цаллиса полностью сохраняется и может быть использован с факторами неидеальности для изучения любых реальных систем, включая полимерные структуры, подчиняющимся экспоненциальным (в трактовке Реньи − квазиравновесные условия) и степенным (в трактовке Цаллиса − существенно неравновесные условия) закономерностям. Заметим, что для обсуждаемых в работе систем полимер–растворитель в реальных условиях идеальное термодинамическое равновесие (полностью изолированная система) в классическом понимании практически недостижимо, но достижимо локальное термодинамическое равновесие [30].В формализме Реньи
(8)
$S_{{{{g}_{S}}}}^{{M - {\text{Rn}}}}\left( p \right) = \frac{R}{{1 - {{g}_{S}}}}{\text{ln}}\mathop \sum \limits_i^{N(\varepsilon )} p_{i}^{{{{g}_{S}}}};$(8а)
$S_{{{{g}_{{th}}}}}^{{{\text{M}} - {\text{Rn}}}} = \frac{R}{{{{g}_{{th}}}}}{\text{ln}}\left( {\mathop \sum \limits_{i = 1}^{N(\varepsilon )} p_{i}^{{{{g}_{{th}}} - 1}}} \right)~$В формализме Цаллиса
(9)
$S_{{{{g}_{S}}}}^{{M - {\text{Ts}}}}\left( p \right) = \frac{{R\left( {1 - \sum\limits_i^{N(\varepsilon )} {p_{i}^{{{{g}_{S}}}}} } \right)}}{{{{g}_{S}} - 1}}$(9а)
$S_{{{{g}_{{th}}}}}^{{M - {\text{Ts}}}}\left( p \right) = \frac{{R\left( {1 - \sum\limits_i^{N(\varepsilon )} {p_{i}^{{1 - {{g}_{{th}}}}}} } \right)}}{{{{g}_{{th}}}}}$Как отмечено ранее [8, 37, 53], энтропия Цаллиса (3), следовательно, и $S_{{{{g}_{S}}}}^{{M - {\text{Ts}}}}$ переходит в энтропию Реньи (4) при |1 – q| $ \ll $ 1 и в энтропию $S_{{{{g}_{S}}}}^{{M - {\text{Rn}}}}{\text{\;}}$ при |1 – gs| $ \ll $ 1.
В выражениях рассматриваемых энтропий $N\left( \varepsilon \right)$ − полное число элементов заданного ε-разбиения (покрытия), т.е. df-мерных кубиков со стороной Δ и объемом ε = ${{\Delta }^{{{{d}_{f}}}}}$, необходимое для покрытия гиперкуба (фрактальной макромолекулы) с номером i = 1, 2, …, N(ε)); факторы ${{g}_{S}}$ и gth − моменты меры ε-покрытия; ${{p}_{i}}$=$~{{N}_{i}}{\text{/}}N(\varepsilon )$ − вероятность, что точка структуры будет принадлежать i-му элементу покрытия объема ε, ${{N}_{i}}~$ – число элементов системы, приходящихся на i-элемент ε-разбиения. Вероятность рi(ε) ≡ wi(ε), характеризующая относительную заселенность ячейки i, есть доля рi(ε) ≡ wi(ε) = ni(ε)/$\mathop \sum \limits_i^{N(\varepsilon )} {{n}_{i}}$, где ni(ε) − число элементов размера Δ в части пространства, занятой фрактальным объектом. При этом рi(ε) ≡ {p1, …, pN(ε)} распределение вероятностей, удовлетворяющее условию вероятностной нормировки $\mathop \sum \limits_i^{{\text{N}}(\varepsilon )} p_{i}^{q}$ = 1, является обязательным базисом уравнений (3), (4) и (8), (9) [77–79]. Поскольку величины энтропии S(R), S(Ts), S(M-R), S(M-Ts) пропорциональны ${{\varepsilon }^{{ - {{d}_{f}}}}}$ и задают информацию о положении элемента фрактального объекта в некоторой ячейке, обобщенную размерность ${{d}_{f}}\left( q \right)$ [25, 27, 28, 37, 77–79] называют информационной размерностью. Это означает, что при стремлении размера ячейки к нулю информация возрастает. В уравнениях (8), (8а) и (9), (9а) g может принимать любые значения от 0 до 1 или от 1 до 2 при условии g ≠ 1, однако смысл S(M-Rn) и S(M-Ts) при этом меняется. Значения $g~$ < 1 дают энтропию S(M-Rn) или S(M-Ts), которая в большей степени и более равномерно взвешивает все возможные события независимо от их вероятностей. Значения $g$ > 1 дают энтропию, которая преимущественно определена через более высокие вероятности событий. Проведенные нами расчеты энтропии для различных систем полимер–растворитель показали, что эта особенность больше касается энтропии, рассчитываемой по модели S(M-Ts). К аналогичному выводу приходят многие исследователи, выбравшие уравнение энтропии Цаллиса [10, 78, 98, 99] для расчета энтропии с параметром q. Выбор величин n ≡ N при расчете энтропии для однородных вероятностей по предлагаемым уравнениям, как будет показано ниже, связан с размерами масштабирования фрактального объекта (макромолекулярного кластера).
ОСОБЕННОСТИ МОДИФИЦИРОВАННЫХ УРАВНЕНИЙ РЕНЬИ И ЦАЛЛИСА
Новые модели энтропии (8а), (9а) с термодинамическим ${{g}_{{th}}}$ и энтропийным ${{g}_{S}}$ факторами неидеальности систем (рис. 2) в отличие от моделей 3–4 логически непротиворечиво предсказывают изменение энтропии как функции вероятности $p$ состояния системы, а именно: с упорядочением (0 < gth < 1) энтропия уменьшается, а с ростом беспорядка (1 < gth ≤ 2) увеличивается. Это выполнимо при условии (7а): ${{g}_{{th}}} = 1 + {{g}_{s}}$, которое легко проверяется соотношениями (6), (6а): ${{g}_{{th}}} = d$f${\text{\;/}}D$. При df < D происходит упорядочение (например, для лигнина − сжатие макромолекулярного клубка в растворе), при df > D − его разупорядочение (набухание).
Рис. 2.
Зависимость энтропии SM-Rn ≡ M-Rn (а, в) и SM-Ts ≡ M-Ts (б, г) от вероятности p при ${{g}_{{th}}} = 0.5,~\;{{g}_{{th}}}$ = 2.0 и энтропии SRn ≡ Rn (а, в) и STs ≡ Ts (б, г) при q = 0.5, q = 2.0 и n ≡ N(ε) = 100.

На рис. 2 показаны теоретические зависимости термодинамических энтропий Rn,Ts и их модификаций RM, TM в Дж/моль K от p (для q в Rn,Ts и g в RM, TM числовые значения заданы одинаково, $N\left( \varepsilon \right) = 100$), отражающие характерные особенности сравниваемых моделей.
Заметим, что при 0 < gth < 1 энтропийный фактор ${{g}_{S}}$ может быть со знаком (−), а при 1 < gth ≤ 2 – со знаком (+). Термодинамический фактор 0 < < gth ≤ 2 всегда положителен.
Предлагаемые полуэмпирические модели энтропии SM−Rn и SM−Ts (8), (8а) и (9), (9a) с новым параметром GNF ${{g}_{{th}}}$ или ${{g}_{S}}$ сохраняют принципиальные особенности оригиналов SRn, STs (3) и (4) с их достоинствами и недостатками. Новые модели могут быть полезными при расчетах в энтропийно-фрактальном анализе сложных систем с учетом того, что в термодинамике экстенсивных систем “работает” SМ-Rn, а неэкстенсивных − SМ-Ts. При обработке экспериментальных данных необходимо обращать внимание на то, что абсолютные величины расчетных значений энтропии зависят от выбора модельных значений N(ε). Для придания физического смысла энтропии требуется вводить в выражения SМ-Rn и SM-Ts размерную константу Больцмана kB либо универсальную газовую постоянную R, как принято в статистической термодинамике [37, 46, 78]. Для макромолекул в растворе или расплаве фрактальность макромолекулярного кластера определяется комбинаторикой мономерных звеньев в пространстве, следовательно, энтропией. Определенная выше вероятность рi − это статистическая (физическая) вероятность, которая в уравнениях (8а) и (9а) соответствует мольной доле wi полимера в системе, изменяющейся в диапазоне от 0 до 1. В макромолекуле под N(ε) ≡ N следует понимать число характерных точек (узлов) или сегментов (например, сегментов Куна). Рассматривая огрубленную конформацию полимерных цепей [12, 79] с N эффективными сегментами Куна длиной b в сфере с радиусом инерции ${{R}_{g}} \approx ~~\left( {\frac{N}{6}b} \right){{{\text{\;}}}^{{1/2}}}$, например, в виде частиц или бусинок, придем к заключению, что средняя концентрация сегментов в этом объеме c ≈ 3.5b−3N−1/2 с ростом степени полимеризации стремится к нулю. О таких объектах говорят как о фракталах [25–28, 78]. Представляя слабо- и гиперразветвленные макромолекулы в виде случайных графов (см. ниже), придем к такому же выводу, но через фрактальную размерность.
Таким образом, при исследовании растворов полимеров с использованием для расчета энтропии SM-Rn (8), (8а) и SM-Ts (9), (9а), по величинам фрактальных размерностей df, факторов ${{g}_{{th}}}$ или ${{g}_{s}}$, N, а также по изменению мольной доли фрактального полимерного объекта ω в исследуемой системе можно оценить изменение энтропийного вклада TΔS в свободную энергию системы. Фактически для расчетов по уравнениям (8а), (9а) достаточно двух параметров ${{g}_{{th}}}$ и N.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Большой интерес в области полимерного материаловедения, медицины, биологии, электроники и т.д. вызывают работы, связанные с исследованиями разветвленных полимеров [84–97]. Обладая такими уникальными свойствами, как высокая растворимость и термодинамическая совместимость, высокая сорбционная способность в совокупности со способностью транспортировки веществ в средах, в которых сорбат нерастворим, гиперразветвленные полимеры используются в качестве наноконтейнеров с гостевыми молекулами (хромофорами, катализаторами, фототропами, фармпрепаратами, наночастицами и т.д.). Все эти свойства оказались востребованными для широкого практического применения и поиска новых систем с участием различных классов синтетических и природных разветвленных полимеров с последующим интенсивным изучением их молекулярных, гидродинамических, фрактальных и других свойств современными физико-химическими методами [59–63, 93–97].
В связи с этим для оценки термодинамических характеристик некоторых полимеров в реальных растворах обратимся к результатам исследований гидродинамических свойств растворов и топологической структуры типичных синтетических гиперразветвленных полимеров [59–63], природных полимеров (лигнинов с хаотически разветвленной структурой) [50–54], ограничившись работами [50, 51] и [60–62], в которых проведены расчеты фрактальных размерностей макромолекул. На основе экспериментальных данных рассчитаем энтропии по моделям SM-Rn и SM-Ts и свободные энергии Гиббса: ΔG = ΔH−TΔS для сравниваемых систем полимер−растворитель. При этом учтем условие выполнения принципа гидродинамической эквивалентности в явлениях поступательного и вращательного трения макромолекул (имитационная модель случайных блужданий без самопересечений), описываемых скейлинговыми соотношениями Марка–Куна–Хаувинка–Сакурады [58] для характеристических величин вязкости $\left[ \eta \right]$, диффузии $\left[ D \right]$ и седиментации $\left[ S \right]$:
Вместо [η] и $\left[ D \right]$ можно использовать гидродинамические радиусы как характеристики вращательного и поступательного трения макромолекул:
(10а)
${{R}_{{{{h}_{\eta }}}}} = {{K}_{{{{R}_{\eta }}}}}{{M}^{{{{a}_{\eta }}}}}\quad {\text{и}}\quad ~{{R}_{{{{h}_{D}}}}} = {{K}_{{{{R}_{D}}}}}{{M}^{{{{b}_{D}}}}}.$В случае захвата макромолекулой растворителя радиус эквивалентной твердой сферы ${{R}_{{{{h}_{{}}}}}}$ = = (3[η]$~\left( {\frac{M}{{{{N}_{A}}}} + {{m}_{s}}} \right)$/10NAπ)1/3, где NA – число Авогадро, ${{m}_{s}}$ – масса растворителя. При самодиффузии $~{{R}_{{{{h}_{D}}}}} = \frac{{kT}}{{6\pi \eta D}}$ [48, 62, 63].
Из (10) и (10а) вытекает важное проверочное соотношение, выраженное через скейлинговые индексы a, c, b и позволяющее сделать достоверные выводы о преимущественной конформации макромолекул в растворе:
Здесь критический показатель Флори νF зависит от размерности пространства D: при D < 4 νF = = 3/(d + 2); при D = 2 νF = 0.749; D = 3 νF = 0.592; D > 4 νF = 1/2, топологическая размерность dt = 1 [21, 35, 36].
Оценку самоподобной фрактальной размерности df можно получить вязкостным, седиментационным и диффузионным методами [38, 39, 52–54]. В трехмерном пространстве вязкостный aη, диффузионный ${{b}_{D}}$ и седиментационный cS показатели скейлинга связаны с термодинамическим фактором неидеальности ${{g}_{{th}}}$ выражениями
Или
(10в)
$~{{g}_{{th}}} = 1{\text{/}}\left( {1 + {{a}_{\eta }}} \right) = 1{\text{/}}3{{b}_{D}} = 1{\text{/}}3\left( {1 - ~{{с}_{S}}} \right).~$При вычислении фрактальных размерностей полимеров по микрофотографиям кластеров или их фрагментов (планиметрический метод), образованных в растворе и помещенных для анализа на решетку [57, 65, 66], фактор неидеальности определяется непосредственно по уравнению (6а): ${{g}_{{th}}} = {{d}_{f}}{\text{/}}D$ при D = 2.
В наших исследованиях выбор объектов исследования [51–54, 60–62] обусловлен тем, что для них изучено гидродинамическое поведение макромолекул в растворе.
Выполнение принципа масштабной инвариантности, а также скейлингового вида зависимости плотности частиц в кластере ρf от его характерных размеров (гидродинамического радиуса ${{R}_{h}}$, радиуса инерции ${{R}_{{\text{g}}}}$) и величины df на рассматриваемом топологическом уровне структурной организации [50–52] в сочетании с теорией фракталов и данными компьютерного моделирования [51, 52] позволили на современном уровне классифицировать лигнины разного ботанического вида не только по фрактальной размерности, но и по известным конформациям (линейные, гибко- и жесткоцепные, хаотически разветвленные, сшитые) [50–52]. Некоторые экспериментальные данные проверены математическими моделями роста фрактальных кластеров в двух принципиально различных режимах − кинетическом и диффузионном (гидродинамическом). Как для природных, так и для синтетических полимеров в кинетическом режиме движение кластера рассматривается как результат прилипания к нему мономеров, а в диффузионном − как диффузия в буферной среде [57]. Иными словами, в зависимости от числовой плотности мономеров, не входящих в состав кластеров, в единице объема среды возможны два механизма роста кластеров с фрактальной структурой. В первом случае кластер растет в результате присоединения к нему мономеров, двигающихся прямолинейно (кинетический режим), во втором кластер и мономеры объединяются в ходе диффузионного движения (гидродинамический режим). Механизмы роста молекулярных цепей в процессах синтеза полимеров в кинетическом и диффузионном режимах теоретически обоснованы в классических трудах, например [45, 46] и подтверждены компьютерным моделированием, например, “синтезом” кластеризованных систем в этих режимах [31, 51, 52, 57, 60].
Для хаотически разветвленных лигнинов с позиций критических фрактальных параметров близкой моделью полимеризации монолигнолов в массе с единичной математической вероятностью считается двух- и трехмерная кинетическая модель необратимого роста фрактальных кластеров Виттера–Сандера DLA P–CL (диффузионно-лимитированная агрегация частица−кластер) при броунском движения частиц [51]. Однако описание реальных кластеров оказалось возможным в рамках модели диффузионно-контролируемой агрегации кластер–кластер (DLA CL–СL), для которой статистической обработкой по числу мономеров в кластере N0 установлена скейлинговая зависимость N0 ∼ $R_{g}^{{{{d}_{f}}}}$, где ${{R}_{g}}$ − радиус инерции кластера [51, 52, 60].
Как для природных, так и для синтетических полимеров при формировании изотропных фрактальных агрегатов в гомогенной среде по механизму кластер-кластерной агрегации число однородных мономеров N0 с массой m0 в составе фрактала с массой Mf традиционно определяют по асимптотическим зависимостям [24, 25, 28], а для фрактального кластера со случайным расположением частиц свойство самоподобия рассматривается статистически [57]:
(11)
$\begin{gathered} {{N}_{0}} = {{({{R}_{g}}{\text{/}}{{r}_{0}})}^{{{{d}_{f}}}}};\quad {{M}_{f}} = {{m}_{0}}{{N}_{0}} = {{m}_{0}}{{({{R}_{g}}{\text{/}}{{r}_{0}})}^{{{{d}_{f}}}}}; \\ {{d}_{f}} = \ln {{N}_{0}}{\text{/}}\ln ({{R}_{g}}{\text{/}}{{r}_{0}}) \\ \end{gathered} $Фрактальные гиперразветвленные структуры, образованные мономерами с двумя и более функциональными группами, очевидно, следует рассматривать как анизотропные. Количественное описание анизотропных фракталов должно проводиться по всем компонентам тензора инерции ${{\langle R_{{g,anis}}^{2}\rangle }^{{1/2}}}$. Главные радиусы вращения можно найти по диагональным элементам тензора, отношение которых и определит степень анизотропии фрактала [71]. Отметим, что оценки анизотропии кластеров практически в любых средах дают близкие погрешности в пределах ≅2% [47], которыми можно пренебречь.
Сравним молекулярные, гидродинамические и фрактальные характеристики природных и синтетических разветвленных полимеров, изученных [50, 51, 60–62] сочетанием методов фотонной корреляционной спектроскопии, поступательной диффузии, скоростной седиментации в аналитической ультрацентрифуге и капиллярной вискозиметрии в различных растворителях. В табл. 1–3 выборочно приведены растворные характеристики разветвленных полимеров с разной топологией, степенью ветвления и функциональности, измеренные в узком температурном диапазоне от 25 до 30°С:
Таблица 1.
Гидродинамические характеристики FDLpin, SDLpiс, в диоксане *
| Лигнин | Mw × 10–3 | [η], см3/г | χ | D × 107, см2/с | A0 × 103, Дж моль–1/3 K–1 | Rh, нм | Rg, нм | Rθ, нм |
|---|---|---|---|---|---|---|---|---|
| FDLpin | 25 | 7.03 | 1.30 | 5.6 | 2.75 | 2.94 | 2.31 | 2.24 |
| SDLpic | 22 | 6.87 | 0.48 | 5.2 | 2.05 | 3.50 | 2.76 | 2.70 |
Таблица 2.
Величины факторов df,${{g}_{{th}}}$, ${{g}_{s}}~$ для FDLpin, SDLpic лигнинов, диапазоны изменения энтропий ΔS при N ≡ N(ε) = 100 в моделях M-Rn и M-Ts в диапазоне статистической вероятности p ≡ w (мольной доли полимера в системе полимер–растворитель ) от 0 до 1 и расчетные значения энтальпии ΔH и свободной энергии ΔGm с вероятностью pi ≈ 0.05 и ΔG с pi ≈ 1 при 298 К (курсив)
Таблица 3.
Сравнительная характеристика расчетных значений df, ${{g}_{{th}}},$ SM-Rn (Дж/моль K), SM-Ts (Дж/моль K) при N = 100 для разветвленных полимеров в моделях M-Rn и M-Ts в диапазоне статистической вероятности p ≡ w* от 0 до 1 и расчетных значений энтальпии ΔH, энтальпийного фактора T$\Delta {{S}_{m}}$ и TΔS и свободной энергии ΔGm с вероятностью pi ≈ 0.05 и ΔG с pi ≈ 1 при 298 К
| 10Kd-8arm | 19Kd-LPs | 20Kd-HBPs | HBPGs* | PPhD | |||||
|---|---|---|---|---|---|---|---|---|---|
| [η] = 1.42 × 10–4$M_{w}^{{0.68}}$ χ = 0.5 |
[η] = 9.9 × 10–5$M_{w}^{{0.73}}$ χ = 0.54 |
[η]=6.45 × 10–4Mw0.39 χ = 0.24 |
[η] = 5.9$M_{w}^{{ \cong 0}}$ χ = 1–1.5 × 10−5 |
[η] ≅ 9.0 $M_{w}^{{0.01}}$ χ = 0.049 |
|||||
| df | ${{g}_{{th}}}$ | df | ${{g}_{{th}}}$ | df | ${{g}_{{th}}}$ | df | ${{g}_{{th}}}$ | df | ${{g}_{{th}}}$ |
| 1.786 | 0.595 | 1.734 | 0.578 | 2.158 | 0.719 | 2.97 | 0.999 | 2.97 | 0.999 |
| SM-Rn | SM-Ts | SM-Rn | SM-Ts | SM-Rn | SM-Ts | SM-Rn | SM-Ts | SM-Rn | SM-Ts |
| 90.5– 64.5 | 14.4– −84.6 | 94.3–66.4 | 14.0– −85.0 |
68.3– 53.4 | 11.6– −87.4 | 38.45– 38.41 | 8.32– −90.7 |
38.45– 38.41 |
8.32– −90.7 |
| T$\Delta {{S}_{m}}$, кДж/моль, pi ≈ 0.05 // T$\Delta S''$, кДж/моль, pi ≈ 1 | |||||||||
| 28.79 | 15.0 | 27.57 | 14.50 | 20.91 | 12.0 | 11.82 | 2.53 | 12.12 | 2.53 |
| 19.79 | –25.21 | 19.22 | −25.38 | 15.91 | –26.05 | 11.44 | –27.04 | 11.44 | –27.04 |
| $\Delta {{H}_{m}}$, кДж/моль | |||||||||
| –0.054 (–0.065)′ | –0.050 (–0.060)′ | –0.024 (–0.029)′ | –1.25 × 10–6 | –0.0049 (–0.0064)′ | |||||
| $\Delta {{G}_{m}},\frac{{{\text{кДж}}}}{{{\text{моль}}}},{\text{\;}}{{p}_{i}} \approx 0.05~//{\text{\;}}\Delta G''$, кДж/моль, pi ≈ 1 | |||||||||
| –28.84 | –28.77 | –27.62 | –4.44 | –20.93 | –3.66 | –11.84 | –1.49 | –11.92 | –1.50 |
| –20.33 | 25.26 | –19.17 | 25.43 | –15.93 | 26.03 | –11.44 | 27.04 | –11.49 | 27.09 |
* [51] скейлинговые соотношения [S] = 2.16 × 10−3M0.67, [D] = 251 × 10–3M−0.33, [10−7 см2 /с] для проверки расчетных величин df, ${{g}_{{th}}}$ по [η], см3/ г, χ = 1–1.5 × 10−5; ' расчеты проведены по Флори−Хаггинсу [39] и [55] (курсив); '' расчетные текущие значения (курсив), выделенные полужирным шрифтом по M–Ts (при ${{g}_{{th}}}$ > 1 энтропия SM-Ts положительна).
1) фракционированный диоксанлигнин вторичной ксилемы сосны Pinus silvestris “FDLpin− диоксан”, T = 298 K [51];
2) ступенчато растворенный диоксанлигнин ели обыкновенной DLpic (Picea abies) “SDLpic−диоксан”, T = 298 K [50];
3) звездообразные разветвленные полистиролы (линейный, 8- и 20-лучевые) “ArmPS−тетрагидрофуран”, T = 303 K [61];
4) гиперразветвленные полиглицерины “HBPGs− вода” , T = 298 K [61];
5) гиперразветвленные полистиролы “HBPGs− вода”, T = 298 K [62];
6) пиридинсодержащие полифениленовые дендримеры четвертой G4 генерации, состоящие исключительно из фенильных и пиридиновых циклов без гибких фрагментов “PPhD−хлороформ”, T = 298 K (Rh = 4.04 нм, [η] ≅ 9.0 cм3/г) [63].
Из перечисленных полимеров диоксанлигнины FDLpin [51] классифицирутся как случайно-разветвленные структуры со скейлинговым индексом а = 0.26 ± 0.04, что практически совпадает с теоретическим значением для типичных хаотически разветвленных полимеров [51], а диоксанлигнины SDLpic [50, 64] со скейлинговым индексом а = 0.22 ± 0.03 – как случайно-разветвленные, но жесткоцепные полимеры. Значения фрактальной размерности для FDLpin df = 2.50 ± ± 0.08 и SDLpic df = 2.44 ± 0.18 позволяют отнести эти лигнины к классу диффузионно-контролируемой агрегации Виттера–Сандера типа частица−кластер [51].
Модельные звездообразные гиперразветвленные полистиролы (HBPS) [62] с плотностью ветвей f = 15–55 и молярной массой Mbr = (5–50) × × 103 г/моль при сравнении с линейными полистиролами и симметричными 3-, 8-лучевыми звездообразными полистиролами при близких молярных массах этих полимеров демонстрируют заметно меньшие радиус вращения Rh, показатели Марка–Куна–Хаувинка–Сакурады и характеристическую вязкость. По данным авторов [62], HBPS с очень компактной формой и высокой сегментарной плотностью при f ≈ 50 характеризуются Rh, HBPS ~ 5–15 нм, что примерно вдвое меньше соответствующих значений Rh, 10K-LPS для линейных полимеров с той же молярной массой, тогда как для симметричных звезд это соотношение равно 0.8.
Гиперразветвленные полиглицерины HBPGs в водном растворе [61] принимают очень компактную шаровидную конформацию с высоким уровнем гидратации – в среднем 1.7 г воды на 1 г макромолекул.
Дендример PPhD в системе PPhD−хлороформ [63], сохраняющий свою конформацию при изменении температуры, отнесен к классу жестких непротекаемых сфер с крайне низкой плотностью полимера ρ = 0.25 г/см3, для которых выполняется соотношение Эйнштейна [η] = 2.5/ρ.
СРАВНЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА ДЛЯ СИНТЕТИЧЕСКИХ И ПРИРОДНЫХ РАЗВЕТВЛЕННЫХ ПОЛИМЕРОВ
Проведем расчет фрактальной размерности df, факторов ${{g}_{{th}}}$ и ${{g}_{s}}$, энтропий SM-Rn и SM-Ts для сравниваемых систем по общему алгоритму, исходя из молекулярных и гидродинамических характеристик рассматриваемых полимеров по скейлинговым индексам (10), (10а). Например, df и gth = ${{d}_{f}}{\text{/}}D$ рассчитываются по вязкости раствора. По выражениям (8а) и (9а) в редакторе Mahtcad вычислим изменение SM-Rn и SM-Ts во всем диапазоне статистических вероятностей wi ≡ pi (состава полимер−растворитель) от 0 до 1 при N(ε) ≡ N ≅ 100 узлов для лигнинов [50, 51]) и при N ≅ 600 узлов для PPhD, ArmPS, HBPGs, HBPS [61–63].
Если представить мономеры рассматриваемых макромолекул в виде направленных случайных графов [60], то из теории Винера вытекает [83], что при вычислении матриц, построенных по кратчайшим расстояниям между всеми парами характерных точек макромолекул (вершин), топологическую структуру гиперразветвленных полимеров можно описывать суммой этих расстояний с помощью гипериндексов Винера W(s) [82]. Индекс Винера прямо пропорционален радиусу инерции цепи W(N) = $R_{g}^{2}$(N)/${{N}^{2}}$, где N – число вершин гиперразветвленного полимера. Моделируя методом Монте-Карло в кинетическом режиме синтез ряда разветвленных полимеров методом ступенчатой полимеризации, авторы [60] приводят аналитические количественные оценки времени гелеобразования (топологического фазового перехода) и связанной с ним молярной массы, а также рассматривают распределение молекул по размерам, обнаруживая в нем две асимптотические моды со специфическим колебательным поведением молекул. Оказывается, что радиус вращения макромолекул со ступенчатым механизмом роста не зависит от времени, а только от размеров молекулы. Рассматривая методические тонкости теории графов и других популярных моделей, используемых для изучения полимерных систем, авторы [60] особо обращают внимание на нефизический экспоненциальный рост окрестности узла при масштабировании. По их мнению, граф с таким масштабированием не является фракталом с размерностью df и не должен вписываться в евклидово пространство. Вместе с тем, они приходят к неоспоримому выводу, что мультиплексный подход в теории графов дает возможность рассмотреть широкий спектр реальных проблем полимеризации и использовать результаты для оптимизации и проектирования новых материалов. Это тот же самый мультифрактальный подход с его степенными зависимостями, который в настоящее время развивается и применяется в теории и на практике (нанотехнологии).
Нами использованы обобщенные в работе [60] теоретические и смоделированные по методу Монте-Карло зависимости $R_{g}^{2} = f\left( N \right)$ (Приложение 1 ), пригодные, по утверждению авторов, для любых слабо- и гиперразветвленых полимеров, которые можно применить для оценки N ≡ ≡ N(ε) при расчетах SM-Rn и SM-Ts по уравнениям (8а) и (9а). За начальное значение масштаба выбрано ε = $R_{g}^{2}$ для поверхностного D2 или ε = $R_{g}^{3}$ − для объемного D3-масштабирования.
Далее по величине условной начальной энтропии смешения ΔSm (для 5 мол. % полимерного раствора) при выбранной T (K) найдем энтропийный фактор TΔSm.
Затем рассчитаем изменения энтальпии смешения ΔHmix и свободной энергии смешения ΔGmix = ΔHmix − TΔSmix в исследуемых системах с использованием классических уравнений термодинамики растворов полимеров [67]. Вычисление ΔHmix можно провести по уточненному уравнению Флори−Хаггинса [55, 56]
(13)
$\Delta {{H}_{{mix}}} = - RT\left( {\chi p_{{12}}^{0} - \frac{{2{{{(\chi p_{{12}}^{0})}}^{2}}}}{z}} \right),$В табл. 1 и 2 представлены экcпериментальные и расчетные фрактальные характеристики диоксанлигнинов хвойных пород древесины: FDLpin (сосна) и SDLpic (ель) в системах полимер−растворитель при 298 К. В табл. 3 для этих лигнинов приведены расчетные величины ${{g}_{{th}}}$- и ${{g}_{s}}$-факторов, диапазоны энтропий, вычисленных по выражениям (8), (8а) и (9), (9а) в формализме Реньи и Цаллиса. Заметим, что расчеты SM-Rn и SM-Ts по уравнениям (8), (9) и (8а), (9а) приводят к одинаковому результату.
Термодинамические характеристики лигнинов FDLpin и SDLpic в моделях M-Rn и M-Ts имеют принципиальные особенности: свободная энергия смешения в обоих случаях ΔGm < 0, что указывает на совместимость полимеров в данных растворителях при pi ≈ 0.05. Вместе с тем, в модели M-Rn ΔGm гораздо больше по абсолютной величине, чем в модели M-Ts, но с ростом доли полимера в открытой системе лигнин–растворитель в модели M-Ts ΔG изменяет знак на (+), достигая высоких значений ≈27 кДж/моль, так что согласно классическому соотношению dG = dH−TdS любые прямые процессы в системе становятся невозможны. Эту особенность обсудим ниже.
В табл. 3 сравниваются расчетные фрактальные и термодинамические характеристики разветвленных полистиролов различной топологической структуры: линейный разветвленный 19K-LPs, звездообразный 8-лучевой, гиперразветвленный 20K-HBPs [61]; гиперразветвленный полиглицерин четвертой генерации G4 [62]; пиридинсодержащие полифениленовые дендримеры четвертой генерации G4 PPhD [63]. Данные получены из экспериментальных зависимостей характеристической вязкости от молярной массы полимеров с их константами Хаггинса. ΔHm рассчитаны из (13) при z = 12 и по уравнению Флори–Хаггинса $\Delta {{H}_{m}} = - RT\chi {{\varphi }_{1}}{{\varphi }_{2}}$ [39].
Как и для лигнинов (табл. 2), данные табл. 3 содержат принципиальные особенности, связанные с вычислениями термодинамических функций для равновесных (изолированных) и неравновесных (открытых) систем, в которых могут находиться системы полимер–растворитель. Напомним, что оценки TΔSm, ΔHm, ΔGm, ΔG (pi ≈ 1), справедливы только для равновесных условий, т.е. для замкнутых систем.
Как отмечено ранее, в случае степенного гамильтониана распределение Реньи [27] становится степенным, а энтропия Rn(p), как и в термодинамике Гиббса, обладает свойством аддитивности, т.е. экстенсивна: S(W1W2) = S(W1) + S(W2), тогда как энтропия Ts(p) − неэкстенсивна: S(W1W2) ≠ S(W1) + S(W2). Следовательно, оба уравнения M-Rn и M-Ts, так же, как Rn(p) и Ts(p), могут быть использованы при оценке энтропийной составляющей объектов с фрактальными характеристиками: первое для квазиравновесных систем, второе − для существенно неравновесных.
ТЕРМОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ РАЗВЕТВЛЕННЫХ ПОЛИМЕРОВ В РЕАЛЬНЫХ РАСТВОРАХ – ВОЗМОЖНАЯ ИНТЕРПРЕТАЦИЯ
В современной термодинамике для открытых систем с участием “диссипативных структур” школой нобелевского лауреата И.Р. Пригожина разработан особый подход, позволяющий интерпретировать результаты термодинамических расчетов для равновесных и неравновесных состояний, исходя из представлений о локальном термодинамическом равновесии [30]. Согласно этой теории, в большинстве случаев выполняется предположение, что известные равновесные термодинамические соотношения справедливы для всех интенсивных термодинамических переменных (температура, давление, химический потенциал) Т(х, t), p(х, t), μ(х, t) как функций координаты x и времени t, определяемых в элементарном объеме dV, а также плотностей экстенсивных переменных с этими же координатами: s(х, t) − энтропия, g(х, t) − энергия, nk − число молей компонента k в dV. Достаточно рассмотреть соотношение Гиббса dG = TdS − pdV + $\mathop \sum \limits_k {{\mu }_{k}}d{{N}_{k}}$ и переписать его для dV через локальные плотности: Tds = dg + + $\mathop \sum \limits_k {{\mu }_{k}}d{{n}_{k}}$, чтобы убедиться, что второй закон термодинамики должен быть локальным.
Мысленно разделим реальную систему на r частей. Тогда diS = diS1 + diS2 +…+ diSr ≥ 0, где diSk ≥ ≥ 0 − производство энтропии для каждой k-й части системы. Неравенство diSk ≥ 0 справедливо для всех систем. Следовательно, локальное производство плотности энтропии dis/dt ≥ 0. Выражение локальной плотности энтропии в виде ds = = dis + des, где для изолированной системы dis ≥ 0, показывает, что энтропия изолированной системы − dis с внутренними самопроизвольными процессами, контролируемыми внешними процессами с энтропией − des, увеличивается в точном соответствии со вторым законом классической термодинамики. Скорость общего изменения энтропии системы dS/dt равна сумме скорости производства энтропии внутри самой системы diS/dt и скорости обмена энтропией между системой и внешней средой deS/dt. Положительное значение величины deS/dt отвечает увеличению энтропии системы в результате обмена веществом и/или энергией с внешней средой. Отрицательное значение величины deS/dt соответствует ситуации, когда отток положительной энтропии из системы во внешнюю среду за счет оттока из системы теплоты или части вещества превышает приток положительной энтропии извне. Это необходимое условие для реализации внутри системы процессов самоорганизации с образованием фрактальных “диссипативных” структур. Разбиение величины изменения энтропии открытой системы на две составляющие diS и deS указывает на принципиальные различия в термодинамических свойствах изолированных (равновесных) и открытых (неравновесных) систем.
Значение величины deS/dt за счет процессов обмена с внешней средой может быть как положительным, так и отрицательным, поэтому, несмотря на выполнения неравенства diS/dt > 0, общая энтропия открытой системы может как возрастать, так и убывать. Уменьшение энтропии является неустойчивым по Ляпунову процессом [30], т.е. оно не выполняется на бесконечном интервале времени. Данный случай соответствует образованию диссипативных самоорганизованных структур с дальними когерентными связями и реализуется при условии, что изменение энтропии системы станет равным нулю dS/dt = 0, если deS/dt < 0 и |deS/dt| = diS/dt. Это отвечает стационарному состоянию, в котором производство энтропии в системе diS/dt компенсируется оттоком энтропии во внешнюю среду (диссипация энергии), следовательно, общее изменение энтропии системы равно нулю: dS = diS + deS = 0 и dS/dt = = diS/dt + deS/dt = 0.
Попробуем интерпретировать расчетные данные для энтропий SM-Rn и SM-Tsсущественно неравновесных систем в соответствии с изложенным выше.
В условиях диссипации энергии системы полимер–растворитель во внешнюю среду (dS/dt = = 0), полученное расчетом по модели М-Ts отрицательное значение энтропии можно не принимать во внимание. В результате, если рассматривать систему полимер−растворитель как открытую, то знак dG будет определяться знаком энтальпии dH. Вместе с тем, положительные значения энтропии SM-Ts, получаемые при pi ≈ 0, могут быть использованы и интерпретированы как условно равновесные (из-за малых концентраций полимера в растворе и отсутствия в системе дальнодействующих когерентных связей) по классическому соотношению dG = dH−TdS. Как отмечено ранее, при $g{\text{\;}}$> 1 энтропия SM-Ts > 0, т.е. в большей степени определена через более высокие вероятности событий, а следовательно, расчетные значения SM-Ts принимаются во внимание и интерпретируются с позиций поведения открытых систем.
Расчеты энтропии SM-R с любым знаком и оценки TΔSm, ΔGm, проводимые в классическом варианте, следует считать обоснованными. Наблюдаемая для всех рассматриваемых условно открытых систем полимер−растворитель диссипация энергии свидетельствует о возможной самоорганизации с образованием фрактальных, т.е. “диссипативных” структур. По меткому выражению И.Р. Пригожина, “…сильно неравновесные необратимые процессы могут быть источником когерентности, т.е. самим условием образования огромного множества типов структурированного коллективного поведения”.
Из расчета ΔHm и ΔGm (табл. 2 и 3) следует, что конформационное поведение разветвленных полимеров в бинарных системах полимер−растворитель практически определяет термодинамический фактор TΔSm, поскольку вклад ΔHm в свободную энергию (ΔGm < 0) для выбранных систем несущественен (например, для HBPGs он близок к нулю). Это подтверждают и калориметрически измеренные значения ΔHm [67–70].
Таким образом, в равновесных (замкнутых) системах, которые переходят в состояние с минимальной свободной энергией, диссипативные процессы размывают неоднородности и приводят систему к однородному равновесному состоянию. Напротив, неравновесные системы могут развиваться непредсказуемо и переходить в различные конформационные состояния, достигая “упорядоченного состояния” с пространственно-временной организацией [30], в нашем случае, с фрактальной структурой.
ЗАКЛЮЧЕНИЕ
Представлены теоретически обоснованные выражения фактора неидеальности систем $g$, включая простейшее выражение для самоорганизованных структур высокомолекулярных соединений в растворе через фрактальную ${{d}_{f}}~$и евклидову D размерности: g = ${{d}_{f}}$/D, из которого следует, что ключевой характеристикой самоорганизованных структур может выступать их фрактальная размерность, которую можно определить из экспериментальных данных разными способами.
Установлена связь GNF с индексами aη = = $(1 - {{g}_{{th}}}){\text{/}}{{g}_{{th}}}$; ${{b}_{D}} = \frac{1}{{3{{g}_{{th}}}}};{{c}_{S}} = 1 - 1{\text{/}}3{{g}_{{th}}}$, известными из широко применяемой для полуразбавленных растворов полимеров теории скейлинга.
По модифицированным автором выражениям энтропии в формализме Реньи для квазиравновесных и в формализме Цаллиса для существенно неравновесных структур с обобщенным фактором неидеальности систем GNF проведены расчеты термодинамической энтропии на основе экспериментальных данных, полученных спектроскопическим, лазернокорреляционным, седиментационным, вискозиметрическим и другими растворными методами. Алгоритм расчета можно представить следующим образом: скейлинговые индексы ${{a}_{\eta }},~{{b}_{D}},~{{с}_{S}}~$ → фрактальная размерность df → фактор неидеальности систем g → термодинамическая энтропия SM-Rn или SM-Ts → вклады TΔS, ΔH → ΔG.
Результаты расчета для разных по природе разветвленных полимеров с различной топологией, степенью ветвления и функциональностью (диоксанлигнины, полистиролы, полиглицерины, пиридинсодержащие полифениленовые дендримеры) в бинарных системах полимер−растворитель показывают, что основной вклад в свободную энергию ΔG таких систем вносит термодинамический фактор TΔS.
Дана интерпретация результатов расчетов термодинамических функций по модифицированным уравнениям Реньи и Цаллиса соответственно для квазиравновесных и неравновесных открытых систем полимер−растворитель с позиций классической и современной термодинамики диссипативных структур.
В настоящей работе автор основное внимание уделил методологии расчета термодинамических функций по экспериментальным скейлинговым соотношениям, получаемым гидродинамическими методами, и интерпретации полученных результатов. Однако предлагаемый подход с использованием GNF можно распространить на изучение любых коллоидных систем с участием полиэлектролитов, поверхностно-активных веществ и т.д. Резюмируя сказанное выше, добавим что из общего определения GNF следует, что можно не ограничиваться определением $g$ = $~d$f/D для фрактальных объектов, но включать данный фактор в любые уравнения, описывающие поведение только идеальных систем [40, 41]. Это позволит использовать фундаментальную модель, предназначенную для идеальной системы, для построения на ее основе теоретической модели, пригодной с поправками и ограничениями для описания реальной системы [40, 41]. Как указано выше, GNF в форме постоянного множителя либо уравнения любой сложности может отражать произвольные отклонения системы от идеальности в процессе изменения внутренних и внешних параметров. Другими словами, сам GNF может служить объектом моделирования при описании реальных систем и процессов.
Приложение 1 . Аппроксимация зависимостей $R_{g}^{2} = f(N)$ и $N = f(R_{g}^{2})$ для линейных, слабо- и гиперразветвленных полимеров по данным [60] для оценки N при расчете энтропий SM-Rn и SM-Ts с коэффициентом достоверности аппроксимации R2 = 0.95
| Зависимость $R_{g}^{2}$ = f(N) | ||
|---|---|---|
| линейные | слаборазветвленные | гиперразветвленные |
| ${{\langle R_{g}^{2}\rangle }_{l}} = 0.167N{\text{\;}}$ | ${{\langle R_{{\text{g}}}^{2}\rangle }_{{br}}} = 0.475{{N}^{{0.67}}}$ | ${{\langle R_{g}^{2}\rangle }_{{br}}} = 0.394{{N}^{{0.59}}}$ |
| Обратная зависимость $N = f(R_{g}^{2})$ | ||
| линейные | слаборазветвленные | гиперразветвленные |
| $N = 5.99{{\langle R_{{\text{g}}}^{2}\rangle }_{l}}$ | $N = 4.84{{\langle R{{_{g}^{2}}_{{sbr}}}\rangle }^{{1.7}}}$ | $N = 3.03{{\langle R{{_{{\text{g}}}^{2}}_{{hbr}}}\rangle }^{{1.49}}}$ |
Все зависимости оказываются степенными, что является необходимым условием фрактальности. Авторы работ [51] и [60] указывают, что при определении зависимости $\langle R_{g}^{2}\rangle $ = f(s) для разветвленных природных и синтетических полимеров достаточно провести вычисления для N ≅ 100 и N ≅ 400−600 узлов, соответственно. Этот факт можно учитывать при выборе величин текущих значений N ∝ N(ε) для расчета энтропии. Отметим, что фактор разветвленности gbr = $R_{g}^{2}{\text{/}}R_{{g,lin}}^{2}$ с ростом N уменьшается.
Автор выражает искреннюю благодарность рецензентам работы, редакции и редколлегии журнала за внимание, критические замечания и конструктивные предложения по улучшению презентации.
Список литературы
Ge H., Qian H. // Phys. Rev. E. 2010. V. 81. P. 051133.
Esposito M., Van den Broeck C. // Phys. Rev. E. 2010. V. 82. P. 011143.
Ge H. // Phys. Rev. E 2009. V. 80. P. 021137.
Van den Broeck C., Esposito M. // Phys. Rev. E. 2010. V. 82. P. 011144.
Hill T.L. Thermodynamics of Small Systems. New York: Dover, 1994. Pt. I, II.
Abe S., Okamoto Y. // Springer Science & Business Media. Berlin. LNP560. 2001.
Tsallis C. Introduction to Nonextensive Statistical Mechanics. New York: Springer, 2009.
Makarevich N.A. // Proc. of the National Academy of Sciences of Belarus. Chem. Ser. 2021. V. 57. P. 162.
Renyi A. // Acta Math. Acad. Sci. Hung. 1959. V. 10. P. 193.
Peng L., Qian H., Hong L. // Phys. Rev. E. 2020. V. 101. P. 022114.
Rubinstein M., Colby R.H., Sheller U. Polymer Physics. Oxford: Oxford Univ. Press, 2003.
Teraoka I. Polymer Solutions: An Introduction to Physical Properties. New York: Wiley, 2002.
Fischlschweiger M., Enders S. // Thermodynamics Polym. Solutions. 2019. V. 10. P. 311.
Dhar D., Singh Y. // Linear and Branched Polymers on Fractals in Statistics of Linear Polymers in Disordered Media/ Ed by B.K. Chakraborty, Amsterdam: Elsevier, 2005.
Методы компьютерного моделирования для исследования полимеров и биополимеров / Отв. ред. В.А. Иванов, А.Л. Рабинович, А.Р. Хохлов. М.: Книжный дом “ЛИБРОКОМ”, 2009.
Lazzari S., Nicoud L., Jaquet B., Lattuada M., Morbidelli M. // Adv. Colloid Interface Sci. 2016. V. 235. P. 1.
Medina-Castillo A.L. // Macromolecules. 2020. V. 53. P. 5687.
Chremos A., Douglas F.J.// J. Chem. Phys. 2018. V. 149. P. 044904.
Nowicki W., Nowicka G., Dokowicz M., Mańka A. // J. Molec. Modeling. 2012. V. 19. P. 1546.
Lenz D.A., Mladek B.M., Likos C.N., Blaak R. // J. Chem. Phys. 2016. V. 144. P. 204901.
Brillouin L. Scientific Uncertainty and Information. New York; London: Acad. Press, 1964.
Szilard L. // Zeitschrift Phys. 1929. B. 53. S. 840.
Jaynes E.T. // Statistical Physics. Brandeis Lectures. 1963. V. 3. P. 160.
Mandelbrot B.B. The Fractal geometry of nature. New York: Freeman, 1983.
Feder J. Fractals. New York: Plenum Press, 1988.
Климонтович Ю.Л. Статистическая теория открытых систем. М.: Янус, 1995. Т. 1.
Зарипов Р.Г. Принципы неэкстенсивной статистической механики и геометрия мер беспорядка и порядка. Казань: Изд-во Казанского гос. техн. ун-та, 2010.
Зубарев Д.Н., Морозов В.Г., Репке Г. Статистическая механика неравновесных процессов. М.: Физматлит, 2002.
Naimark O.B. // Advances in Multifield Theories for Continua with Substructure. Boston: Birkhuser, 2004. P. 75.
Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. М.: Мир, 2002.
Колесниченко А.В., Маров М.Я. Турбулентность и самоорганизация. Проблемы моделирования космических и природных сред. М.: БИНОМ. Лаборатория знаний, 2014.
Полак Л.С., Михайлов А.С. Самоорганизация в неравновесных физико-химических процессах. М.: Наука, 1975.
Cohen E.G.D. // Physica D. 2004. V. 193. P. 35.
Kullback S., Leibler R.A. // Ann. Math. Statist. 1951. V. 22. P. 79.
Renyi A. Probability Theory. Amsterdam: North-Holland. Univ., 1970.
Tsallis C. // J. Stat. Phys. 1988. V. 52. P. 479.
Башкиров А.Г. // Теорет. и мат. физика. 2006. Т. 149. № 2. С. 299.
Pavlos G.P. // J. Mech. Behav. Mater. 2017. V. 26. № 5–6. P. 139.
Flory P.J. // Disc. Faraday Soc. 1970. V. 49. № 7.
Макаревич Н.А. // Докл. НАН Беларуси. 2016. Т. 60. № 1. С. 94.
Макаревич Н.А. Межфазная граница “газ–жидкость–твердое тело”. Архангельск: Северный (Арктический) федеральный ун-т, 2018.
Maher Patrick // J. Philos. Logic. 2010. V. 39. № 6. P. 593.
Joslin C., Goldman S. // Molec. Phys. 1993. V. 79. № 3. P. 499.
Efimova E.A., Ivanov A.O., Camp P.J. // Phys. Rev. E. 2013. V. 88. № 4. P. 1.
Берлин А.А., Вольфсон С.А., Ениколопян Н.С. Кинетика полимеризационных процессов. М.: Химия, 1978.
Tanford Ch. Physical Chemistry of Macromolecules. New York: Wiley, 1961.
Bertini I., Gutierrez P.J., Sabolo W. // Astron. Astrophys. 2009. V. 504. P. 625.
Цветков В.Н., Эскин В.Е., Френкель С.Я. Структура макромолекул в растворах. М.: Наука, 1964.
Будтов В.П. Физическая химия растворов полимеров. СПб.: Химия, 1992.
Afanas’ev N.I., Fesenko F.V., Vishnyakova F.P., Chaini-kov A.N. // Polymer Science A. 2008. V. 50. № 2. P. 190.
Карманов А.П. Самоорганизация и структурная организация лигнина. Екатеринбург: УрО РАН, 2004.
Karmanov A.P., Kuz’min D.V., Shamshina I.N., Belyaev V.Yu., Kocheva L.S., Matveev D.V., Monakov Yu.B. // Polymer Science A. 2004. V. 46. № 6. P. 613.
Макаревич Н.А.// Изв. вузов. Лесн. журн. 2021. № 2. С. 194.
Макаревич Н.А., Афанасьев Н.И., Монаков Ю.Б. // Высокомолек соед. A. 1998. Т. 40. № 10. P. 1040.
Герасимов В.К. // Высокомолек. соед. А. 1998. Т. 40. № 8. С. 1367.
Чалых А.Е., Герасимов В.К. // Успехи химии. 2004. № 1. С. 63.
Смирнов Б.М. // Успехи физ. наук. 2011. Т. 181. № 7. С. 713.
Fujita H. Polymer Solutions. Amsterdam: Elsevier, 1990.
Muzafarov A.M., Rebrov E.A. // Polymer Science C. 2000. V. 42. № 1. P. 55.
Kharchenko S.B., Kannan R.M., Cernohous J.J., Venkataramani S. // Macromolecules 2003. V. 36. № 2. P. 399.
Lezov A., Gubarev A., Kaiser T., Tobaschus W., Tsvetkov N., Nischang I., Schubert U.S., Frey H., Perevyazko I. // Macromolecules. 2020. V. 53. № 21. P. 9220.
Tsvetkov N.V., Filippov S.K., Kudryavtseva T.M., Ivanova V.O., Shifrina Z.B., Averina M.S., Firsova N.V., Rusanov A.L. // J. Polym. Sci., A. 2006. V. 48. № 4. P. 450.
Tsvetkov V.N., Lavrenko P.N., Bushin S.V. // J. Polym. Sci. A. 1984. V. 22. № 11. P. 3447.
Pavlov G., Frenkel S. // Prog. Colloid Polym. Sci. 1995. V. 99. P. 101.
Михайлов Е.Ф., Власенко С.С. // Успехи физ. наук. 1995. Т. 165. № 3. С. 263.
Чалых А.Е., Герасимов В.К., Горшкова О.В., Стоянова О.В. // Вестн. Казанского технол. ун-та. 2016. Т. 19. № 18. С. 18.
Мищенко К.П., Полторацкий Г.М. Термодинамика и строение водных и неводных растворов электролитов. Л.: Химия, 1976.
Боголицын К.Г., Рябева Н.В., Волкова Н.Н., Вадсе И. // Изв. вузов. Лесн. журн. 1994. № 5–6. С. 109.
Скребец Т.Э., Боголицин К.Г. // Журн. прикл. химии. 2000. Т. 73. № 7. С. 1377.
Смирнова Н.Н., Маркин А.В., Захарова Ю.А., Кучкина Н.В., Русанов А.Л., Шифрина З.Б. // Журн. физ. химии. 2010. Т. 84. № 4. С. 628.
Смирнова Н.Н., Маркин А.В., Захарова Ю.А., Кучкина Н.В., Русанов А.Л., Шифрина З.Б. // Изв. РАН. Сер. хим. 2011. Т. 440. № 1. С. 127.
Hadži E., Ljujic D. XVII Symposium on Condensed Matter Physics – SFKM. Vršac – Serbia. 2007. P. 1.
Sakai V.G. PhD Th. London, 2002.
Dai X., Hou C., Xu Z., Yang Y., Zhu G., Chen P., Huang Z., Yan L.-T.//Entropy 2019. V. 21. P. 186.
Rai D.K., Beaucage G., Ratkanthwar K., Beaucage P., Ramachandran R., Hadjichristidis N. // Phys. Rev. 2016. V. 93. P. 052501.
Deppman A. // Phys. Rev. 2016. V. 93. P. 054001.
Chremos A., Douglas F.J. // J. Chem. Phys. 2018.V. 149. P. 044904.
Колисниченко А.В. Статистическая механика и термодинамика Цаллиса неадитивных систем. Введение в теорию и приложения. М.: ЛЕНАНД, 2019.
Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука,1989.
Grassberger P., Procaccia I. // Physica D. 1984. V. 13. № 1–2. P. 34.
Павлов А.Н., Анищенко В.С. // Успехи физ. наук. 2007. Т. 177. С. 859.
Dobrynin A.A., Entringer R., Gutman I. // Acta Appl. Math. 2001. V. 66. № 3. P. 211.
Gutman I., Furtula B. // Monatsh. Chem. 2003. V. 134. P. 975.
Hawker C.J. // Adv. Polym. Sci. 1999. V. 147. P. 113.
Yates C.R., Hayes W. // Eur. Polym. J. 2004. V. 40. № 7. P. 1257.
Semchikov Yu.D., Bochkarev M.N. // Polymer Science C. 2002. V. 44. № 2. P. 143.
Zamyshlyaeva O.G., Semchikov Yu.D., Kir’yanov K.V., Gasilova E.R., Simonova M.A., Filippov A.P., Kozlov A.V., Shandryuk G.A., Bochkarev M.N. // Polymer Science B. 2011. V. 53. № 8. P. 456.
Korolev G.V., Bubnova M.L. // Polymer Science C. 2007. V. 49. № 4. P. 332.
Potemkin I.I., Palyulin V.V. // Polymer Science A. 2009. V. 51. № 2. P. 123.
Muzafarov A.M., Vasilenko N.G., Tatarinova E.A., Ignat’eva G.M., Myakushev V.M., Obrezkova M.A., Meshkov I.B., Voronina N.V., Novozhilov O.V. // Polymer Science C. 2011. V. 53. № 1. P. 48.
Klimenko N.S., Shevchuk A.V., Vortman M.Ya., Privalko E.G., Shevchenko V.V. // Polymer Science A. 2008. V. 50. № 2. P. 160.
Amirova A.I., Belyaeva E.V., Tarabukina E.B., Filippov A.P. // Polymer Science C. 2010. V. 52. № 7. P. 70.
Иржак В.И // Успехи химии. 2006. Т. 75. № 10. С. 1018.
Dubovitskii V.A., Irzhak V.I. // Polymer Science B. 2011. V. 47. № 1. P. 22.
Иржак В.И. // Успехи химии. 2006. Т. 75. № 10. С. 1018.
Filippov A.P., Belyaeva E.V., Tarabukina E.B., Amirova A.I. // Polymer Science C. 2011. V. 53. № 1. P. 107.
Karmanov A.P., Kocheva L.S., Belyi V.A., Volodin V.V. // Polymer Science A. 2019. V. 61. № 1. C. 53.
Kaniadakis G. // Phys. A. 2001. V. 296. P. 405.
Beck C. // Contemp. Phys. 2009. V. 50. P. 495.
Cleymans J., Worku D. // Eur. Phys. J. A. 2012. V. 48. P. 160.
Bíró G., Barnaföldi G.G., Biró T.S. // Phys. J. G. 2020. V. 47. № 10. P. 105002.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)


