1. На главную
  2. Электронные версии
  3. Высокомолекулярные соединения (серия А)
  4. T. 64, № 6, 2022

Высокомолекулярные соединения (серия А), 2022, T. 64, № 6, стр. 470-480

СТРУКТУРА УГЛЕВОДОРОДНОЙ ЖИДКОСТИ И ТЕЧЕНИЯ КУЭТТА В ЩЕЛЕВЫХ ПОРАХ СО СТЕНКАМИ ИЗ ПИРОФИЛЛИТА

М. А. Логунов a, b, *, А. Г. Калиничев c, В. В. Писарев a, b, d

a Московский физико-технический институт (национальный исследовательский университет)
141701 Долгопрудный, Московской обл., Институтский пер., 9, Россия

b Объединенный институт высоких температур Российской академии наук
125412 Москва, ул. Ижорская, 13, стр. 2, Россия

c Laboratoire SUBATECH (UMR 6457 – IMT-Atlantique, Nantes Université, CNRS/IN2P3)
44307 Nantes, France

d Национальный исследовательский университет “Высшая школа экономики”
101000 Москва, ул. Мясницкая, 20, Россия

* E-mail: mikhail.logunov@phystech.edu

Поступила в редакцию 13.05.2022
После доработки 19.09.2022
Принята к публикации 28.10.2022

Полный текст (PDF)

Аннотация

Методом молекулярной динамики промоделирован процесс течения Куэтта углеводородной жидкости в щелевых порах и исследована динамика упорядочения молекул жидкости в зависимости от плотности жидкости и размера щели. Результаты статистического анализа образующихся областей упорядоченных молекул углеводородной жидкости свидетельствуют о том, что материал стенки и вязкость жидкости влияют на величину таких областей.

ВВЕДЕНИЕ

Углеводородные жидкости представляют интерес для исследования, поскольку входят в состав топлив, масел, смазочных материалов, а также биологических систем. Процессы течения углеводородных жидкостей неизбежно связаны с взаимодействием жидкости и материала стенки, с которым они соприкасаются. Взаимодействие между органическими веществами и глинистыми минералами исследовано многими методами анализа поверхности, такими как инфракрасная спектроскопия с преобразованием Фурье [1–3], сканирующая электронная микроскопия [4–6], рентгеновская фотоэлектронная спектроскопия [7–9] и атомно-силовая микроскопия [9–11], которые дополняют измерения контактного угла [12–14]. Однако ряд вопросов о микроструктуре жидкости в наноразмерных порах до конца не решен, поскольку возможности экспериментальных методов в задаче изучения структуры углеводородной жидкости в процессе течения, как правило, ограничены разрешением в несколько микрометров. Методы численного моделирования, в частности, молекулярная динамика (МД), являются одним из наиболее эффективных инструментов, применяемых для изучения наноразмерных конформационных перестроек и ранних стадий кристаллизации.

В последние десятилетия благодаря бурному развитию суперкомпьютерных технологий методы атомистического моделирования получают в сфере материаловедения все более широкое распространение, в том числе и для получения подробного представления о взаимодействиях между глинистыми минералами и органическими веществами на атомистическом уровне [15–20]. В работе [21] исследованы гидрофобные свойства одного семейства глин без поверхностного заряда, в частности талька и пирофиллита. Показано, что гидрофобные свойства талька и пирофиллита схожи.

Глинистые минералы являются преобладающими компонентами аргиллитов и сланцев, что приводит к обильным микропорам и мезопорам [22]. Таким образом, смачиваемость глинистых поверхностей определяет гидродинамику углеводородсодержащих флюидов, заключенных в этих порах. Кроме того, она определяет герметизирующую способность покрывающих пород и эффективность извлечения сланцевой нефти и газа. В макроскопическом масштабе перенос жидкости удовлетворяет закону Дарси. В пористых средах он обычно описывается уравнением Навье–Стокса при условии, что замкнутая жидкость имеет однородную плотность [23, 24]. Однако флюид, заключенный в нанопорах, сильно взаимодействует со стенками пор (преимущественно глинистыми поверхностями в аргиллитах), что приводит к неоднородности распределения плотности, как показано в работе [23] для воды. Так, вблизи глинистых поверхностей локальная плотность воды сильно отклоняется от плотности воды в объеме. Следовательно, описывать такую замкнутую жидкость как непрерывное состояние с помощью уравнения Навье–Стокса некорректно. Упорядочение n-алканов отмечено в работах [18, 19], однако детального исследования его природы проведено не было. В частности, остается неясным зависимость степени упорядочения от плотности и ширины щелевой поры. В наномасштабе трудно непосредственно наблюдать и измерять смачиваемость поверхности глины в условиях относительно высоких температуры и давления. Классическое моделирование МД является проверенным методом исследования распределения плотности и гидродинамики жидкости, заключенной в нанопорах [23–26].

В литературе имеется большое количество работ, в которых демонстрируются различные подходы к изучению механических свойств углеводородных жидкостей [27–29] и смесей углеводородов [30, 31] в процессе течения. Одним из важных для промышленности механических параметров углеводородных жидкостей является сдвиговая вязкость, исследованию которой посвящено множество работ, в том числе и работ по молекулярной динамике [32–34]. Однако вопрос о структурных перестройках на молекулярном уровне остается открытым.

В настоящей работе в рамках метода классической молекулярной динамики производится попытка продемонстрировать влияние стенок пирофиллита на структуру жидкого додекана в процессе течения Куэтта.

МОДЕЛЬ И МЕТОДИКА МОДЕЛИРОВАНИЯ

Потенциал межчастичного взаимодействия

Молекулярно-динамические расчеты производили с использованием программного пакета LAMMPS [35]. Додекан моделировали с помощью потенциала семейства OPLS-AA [36], аналитическая форма которого представлена ниже.

(1)
$E = {{E}_{{bond}}} + {{E}_{{angle}}} + {{E}_{{dihedral}}} + {{E}_{{nonbond}}}$
(2)
${{E}_{{bond}}} = \sum\limits_{bonds} {{{K}_{r}}{{{(r - {{r}_{0}})}}^{2}}} $
(3)
${{E}_{{angle}}} = \sum\limits_{angles} {{{K}_{\theta }}{{{(\theta - {{\theta }_{0}})}}^{2}}} $
(4)
$\begin{gathered} {{E}_{{dihedral}}} = \sum\limits_{dihedrals} {\frac{{{{V}_{1}}}}{2}\left[ {1 + \cos \left( {\varphi + f1} \right)} \right] + } \\ \, + \frac{{{{V}_{2}}}}{2}\left[ {1 + \cos \left( {2\varphi + f2} \right)} \right] + \frac{{{{V}_{3}}}}{2}\left[ {1 + \cos \left( {3\varphi + f3} \right)} \right] \\ \end{gathered} $
(5)
${{E}_{{ab}}} = \sum\limits_i^a {\sum\limits_j^b {[{{q}_{i}}{{q}_{j}}{{e}^{2}}{\text{/}}{{r}_{{ij}}} + 4{{\varepsilon }_{{ij}}}(\sigma _{{ij}}^{{12}}{\text{/}}r_{{ij}}^{{12}} - \sigma _{{ij}}^{6}{\text{/}}r_{{ij}}^{6})]{{f}_{{ij}}}} } $

Внутримолекулярные невалентные взаимодействия учитывали только для атомов, разделенных тремя или более связями, причем  fij = 0.5 для атомов, разделенных тремя связями, и  fij = 1, если атомы разделены большим количеством связей или находятся в разных молекулах. Для моделирования пирофиллита использовали силовое поле ClayFF [37].

Параметры невалентного взаимодействия стенка–жидкость рассчитывали по правилам среднего геометрического: ${{\varepsilon }_{{ij}}} = \sqrt {{{\varepsilon }_{{ii}}}{{\varepsilon }_{{jj}}}} $, σij = $\sqrt {{{\sigma }_{{ii}}}{{\sigma }_{{jj}}}} $. Коэффициенты взаимодействия ε и σ, а также частичные заряды для атомов в углеводороде получали с помощью сервера LigParGen [38–40]. Значения коэффициентов взаимодействия и зарядов q представлены ниже.

Атом Al Si O1 O2 H1 C H2
ε 1.33e-06 1.84e-06 0.155416 0.155416 0 0.066 0.03
σ 4.27 3.3 3.16552 3.16552 0 3.5 2.5
q 1.575 –1.05 –1.05 –0.95 0.425 – –

МД-расчеты выполняли на вычислительных кластерах Национального исследовательского университета “Высшая школа экономики” и Объединенного института высоких температур Российской академии наук [41, 42].

Генерация расчетной ячейки и параметры МД-расчетов

Пирофиллит (Al2[Si4O10](OH)2) является типичным диоктаэдрическим глинистым минералом типа 2 : 1. Каждый слой пирофиллита состоит из одного октаэдрического листа, зажатого между двумя тетраэдрическими листами [43]. Структуры основаны на элементарной ячейке пирофиллита Al2[Si4O10](OH)2 размером 0.8966 × 0.516 × 0.9347 нм3. Каждый бислой глины содержит 4 × 8 × 2 элементарных ячеек пирофиллита (площадь поперечного сечения 3.5864 × 4.128 нм2). Октаэдрические и тетраэдрические листы соединены между собой мостиковыми атомами кислорода.

Рассматривали три значения плотности додекана, для которых анализировали три различных ширины щелевых пор, образованных стенками пирофиллита. С целью увеличения статистики для каждой плотности и ширины щели было выполнено 12 независимых молекулярно-динамических расчетов. Для нахождения плотности углеводородной жидкости рассчитывали суммарный объем многогранников Вороного Vvoronoi = $\sum\limits_i^N {{{V}_{i}}} $, где Vi – объем многогранника Вороного, построенного на i-м атоме молекулы углеводородной жидкости. Эффективная плотность додекана в поре ${{\rho }_{k}}$ рассчитывали по формуле ρk = $M{\text{/}}{{V}_{{voronoi}}}$, в которой M – полная масса додекана. В качестве эффективной ширины щелевой поры рассматривали величину ${{d}_{{pore}}} = {{V}_{{voronoi}}}{\text{/}}{{L}_{x}}{{L}_{y}}$.

Для ячеек осуществляли единую процедуру генерации и релаксации, включающую в себя несколько шагов.

1. Вначале генерируется ячейка, содержащая одну из стенок щелевой поры, размер которой в 10 раз больше целевой ширины щели.

2. Пустая область расчетной ячейки заполняется молекулами додекана так, что положения центров масс соответствуют позициям в простой кубической решетке с элементарной ячейкой размера 10 × 10 × 10 Å3. Плотность додекана ${{\rho }_{k}}$ регулируется числом создаваемых молекул – заполняется только часть из узлов решетки, попадающих в расчетную ячейку.

3. Следующий шаг – проведение NVT-расчетов с использованием термостата Берендсена. В начале с шагом интегрирования уравнений движения 0.5 фс при температуре Tk + 100 К, где Tk – целевая температура расчетной ячейки, выполняется термостатирование длительностью 250 фс. После шаг интегрирования уравнений движения увеличивается до 1 фс и производится сжатие по оси Oz до величины плотности додекана ${{\rho }_{k}}{\text{/}}1.5$ в течение 200 пс. Затем одновременно осуществляются охлаждение с Tk + 100 K до Tk со скоростью $\dot {T}$ = 1012 К/с и сжатие по оси Oz до величины плотности додекана ${{\rho }_{k}}$ в течение 100 пс. В конце проводится термостатирование при температуре Tk в течение 150 пс.

4. На последнем шаге полученная расчетная ячейка проходила процедуру репликации по Oz, в результате которой ячейка удваивалась. После этого молекулам жидкости присваивали случайные скорости и проводили релаксацию в NVT-ансамбле с использованием термостата Берендсена и шагом интегрирования уравнений движения 1 фс в течение 200 пс.

Моделирование выполняли при температуре Tk = 298.15 К. Плотность додекана при этой температуре и давлениях от 0.1 до 100 МПа лежит в диапазоне 0.746–0.799 г/см3 [44]. Авторы потенциала OPLS-AA заявляют о типичной погрешности воспроизведения плотности жидкостей 0.02 г/см3. Чтобы оценить свойства додекана при давлениях до 100 МПа, в данной работе рассмотрены плотности 0.72, 0.76 и 0.80 г/см3.

В дальнейшем полученные расчетные ячейки (рис. 1а) использовались в молекулярно-динамическом расчете течения Куэтта. Шаг интегрирования уравнений движения составлял 1 фс.

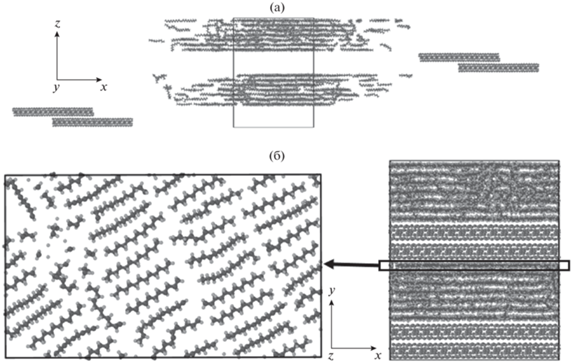
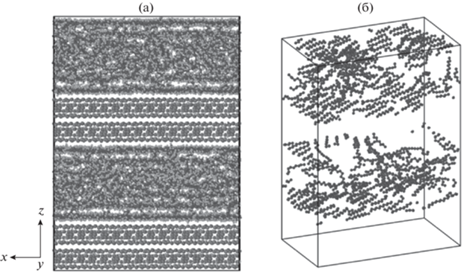
Рис. 1.

Расчетная ячейка додекана при плотности 0.8 г/см3 со стенками пирофиллита (а) и ячейка, в которой показаны только упорядоченные молекулы додекана, в конце моделирования течения Куэтта (б).

Сдвиговое течение осуществляли с помощью предложенного Мюллером-Плате подхода обращенной неравновесной молекулярной динамики (reversed non-equilibrium molecular dynamics – RNEMD) [45]: каждые 10 фс y-компоненты скоростей двух пар атомов кислорода, принадлежащих разным слоям глины, менялись местами. Для перестановок выбирались пары с компонентами скорости $V_{y}^{O}$, ближайшими к 10 м/с и –10 м/с. Такая процедура создает искусственный поток импульса между стенками. В стационарном состоянии этот поток уравновешивается потоком физического импульса через среду между стенками. В случае жидкой среды с нулевой силой сдвига между стенками поток физического импульса вызывается вязкими силами в жидкости по обе стороны от движущихся слоев. В итоге процедура создает два симметричных потока Куэтта, по одному в каждом из слоев жидкости между стенками глины (рис. 2б). Одним из преимуществ такой методики является сохранение полных энергии и импульса моделируемой системы. В работе использовалась реализация метода в команде LAMMPS fix viscosity. При моделировании сдвигового течения температура поддерживалась равной Tk при помощи термостата CSVR (canonical sampling through velocity rescaling – каноническая выборка через масштабирование скоростей). Выбор термостата обусловлен его слабым влиянием на коэффициенты переноса жидкостей [46].

Рис. 2.

Положение молекул додекана и ламелей пирофиллита при течении Куэтта после 13 нс в развернутых координатах (а) и пример упорядоченного слоя додекана в расчетной ячейке вблизи поверхности пирофиллита (б).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Анализ положений молекул додекана в режиме течения Куэтта

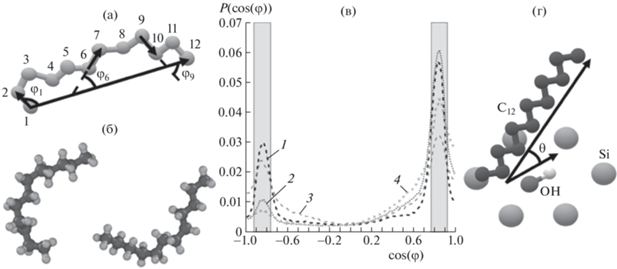
В процессе молекулярно-динамических расчетов для исследования изгибов молекул додекана было построено распределение cos(φi) (рис. 3в), где φi – угол, образованный векторами отдельных последовательных атомов углерода с номерами i и i + 1 молекулы додекана, и вектором, соединяющим концы данной молекулы (рис. 3а). Выделенные области пиков соответствуют φi ∈ [140°, 155°] и φi ∈ [25°, 40°], причем тупых углов в исследуемых системах значительно меньше, чем острых. Наличие пика в области тупых углов указывает на способность молекул додекана совершать перегибы, отраженные на рис. 3б. Конфигурации молекул додекана на рис. 3б были взяты непосредственно из молекулярно-динамических расчетов. В дальнейшем исследовании особый интерес будут представлять более или менее линейные молекулы додекана, которые являются частью упорядоченных областей (рис. 2б). Таким образом, за вектор направления молекулы додекана был принят вектор, образованный концевыми атомами углерода (рис. 3г). Положение молекулы додекана характеризовали углом θ между вектором ее направления и вектором направления гидроксильной группы OH из стенки (рис. 3г). Для удобства исследования полученных результатов в течение молекулярно-динамического расчета для всех молекул додекана был рассчитан косинус угла θ и распределение P(cos(θ)), выражающее долю молекул C12, направленных под углом θ.

Рис. 3.

Наглядное изображение рассчитываемых углов φi (а), примеры изогнутых молекул, возникающих в процессе моделирования (б), а также распределения cos(φi) для разных значений плотности додекана и различных размеров щели перед началом моделирования течения Куэтта (в) и наглядное изображение рассчитываемого в работе угла θ (г). Плотность додекана 0.80 (1, 2) и 0.72 г/см3 (3, 4). Ширина щели 3 (1, 3) и 5 нм (2, 4).

В описанных выше расчетах наблюдалось образование упорядоченных слоев додекана (рис. 1б). Для рассматриваемых систем додекана с пирофиллитом были построены распределения P(cos(θ)) для cosθ ∈ [0.99, 1] (рис. 4, 5). Выбранные значения cosθ отражают факт упорядочения молекул додекана параллельно направлению гидроксильных групп слоя пирофиллита. Полученные зависимости были аппроксимированы формулой

(6)
$P(\cos \theta ) = {{P}_{0}}(1 - A*{{e}^{{ - {\kern 1pt} {\kern 1pt} \frac{t}{\tau }}}}),$
где P0 – предельное значение P(cosθ), связанное с максимально возможным числом молекул додекана, параллельных гидроксильным группам; τ – время, характеризующее начало замедления процесса упорядочения. Рисунок 4 демонстрирует упорядочение додекана с течением времени для щели шириной 3 нм. В случае щелей большей ширины (4 и 5 нм) по-прежнему имеет место эффект упорядочения молекул додекана вдоль направления групп OH в процессе течения Куэтта (рис. 5).

Рис. 4.

Динамика P(cosθ) для cosθ ∈ [0.99, 1] в процессе течения Куэтта для щели шириной 3 нм. Плотность додекана 0.72 (1), 0.76 (2) и 0.80 г/см3 (3).

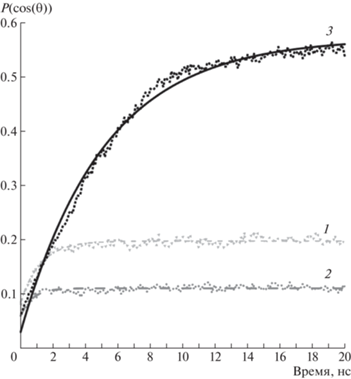
Рис. 5.

Динамика P(cosθ) для cosθ ∈ [0.99, 1] в процессе течения Куэтта. Ширина щели 4 (а) и 5 нм (б). Плотность додекана 0.72 (1), 0.76 (2) и 0.80 г/см3 (3).

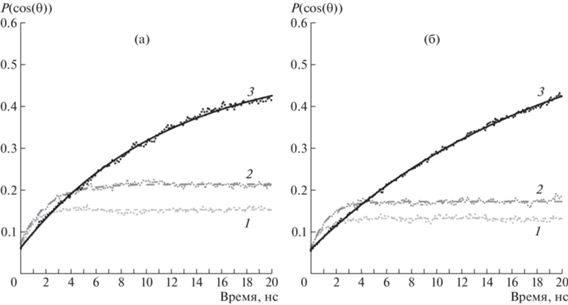
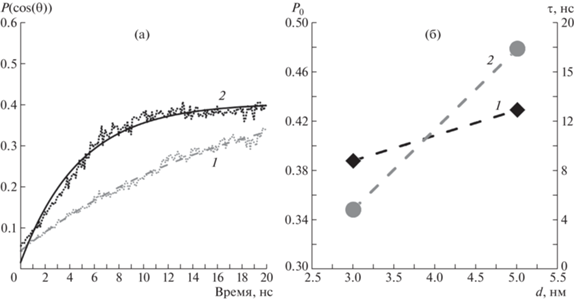
Построив зависимости P0 и τ от плотности додекана (рис. 6а и 6б), можно сделать вывод о том, что в целом чем больше плотность додекана, тем больше значения τ и P0. Для щелей шириной 4 и 5 нм P0 и τ монотонно повышаются с ростом плотности додекана. Однако для щели шириной 3 нм значения параметров P0 и τ при плотности додекана 0.76 г/см3 ниже, чем при плотности 0.72 г/см3. Возникает вопрос, с чем связано подобное поведение молекул додекана.

Рис. 6.

Зависимости P0 (а), τ (б), градиента скорости (в) и эффективной вязкости (г) от плотности додекана при ширине щели 5 (1), 4 (2) и 3 нм (3). Величина τ и градиент скорости даны в логарифмическом масштабе.

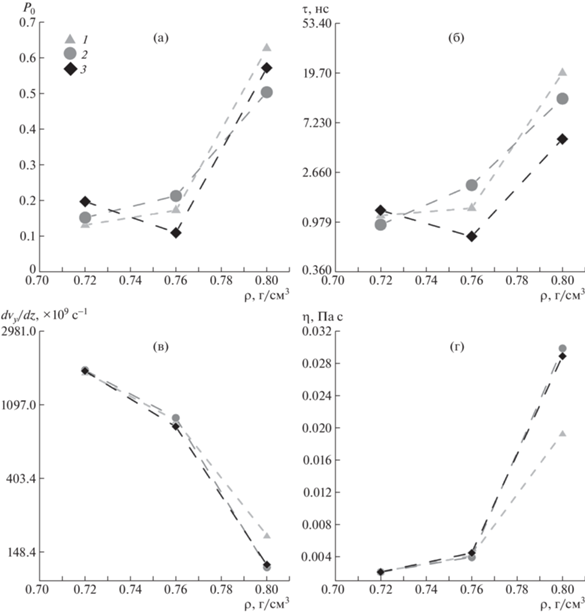
С целью ответа на этот вопрос были построены профили плотности и скоростей додекана между стенками пирофиллита, изображенные на рис. 7. Профили плотности демонстрируют слоистую структуру додекана. Сравнивая профили для плотностей 0.72 и 0.8 г/см3, можно сделать вывод, что при повышении плотности слои становятся более выраженными. Об этом также свидетельствуют значения P0 ≥ 0.5 для плотности 0.8 г/см3 на рис. 6а. Изменения распределения плотности в поре позволяют предположить, что снижение величины P0 при росте плотности от 0.72 до 0.76 г/см3 в порах шириной 3 нм может быть связано с геометрическим фактором. Заметим, что повышение плотности в порах шириной 4 и 5 нм сопровождается увеличением плотности второго адсорбционного слоя с 1.2 до 1.6 г/см3, в порах шириной 3 нм такого не наблюдается. Различие, вероятно, связано с тем, что для формирования плотного и высокоупорядоченного второго адсорбционного слоя требуется больше молекул, чем обеспечивает рост плотности сам по себе, т.е. его образование потребовало бы снижения плотности в центре поры. Таким образом, рост плотности увеличивает количество додекана в системе, но добавленные молекулы не могут сформировать упорядоченные слои, с чем и может быть связано уменьшение полной доли упорядоченных молекул. Этот эффект сильнее всего должен проявляться в порах малой ширины, поскольку увеличение плотности в них приводит к меньшему росту числа молекул на единицу поверхности поры, а необходимое для образования плотных адсорбционных слоев обеднение веществом в центре, наоборот, больше, чем в более широких порах.

Рис. 7.

Профили плотности (1) и скорости (2) додекана при значениях плотности додекана 0.72 (а–в), 0.76 (г–е), 0.80 г/см3 (ж–и) и ширине щели 3 (а, г, ж), 4 (б, д, з), 5 нм (в, е, и).

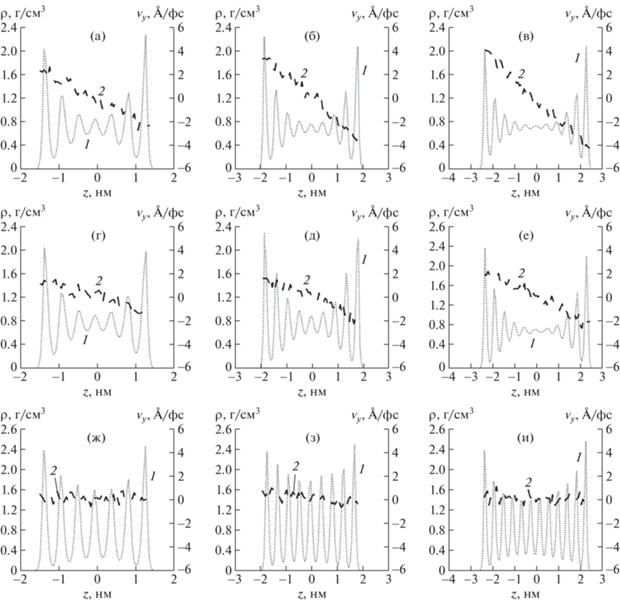
Построенные профили скорости додекана показывают, что при повышении плотности додекана течение постепенно замедляется и при плотности 0.8 г/см3 оно становится слабым. Отсюда следует, что при увеличении своей плотности додекан переходит из текучего состояния в слабо текучее. В результате этого параметр P0 меняется от значений 0.1–0.25 до значений больше или равных 0.5. Другими словами, переход в слабо текучее состояние сопровождается ростом доли наблюдаемых упорядоченных молекул додекана в системе до 50% и выше.

На рис. 6в и 6г представлены зависимости градиента скорости и эффективной вязкости додекана от плотности додекана соответственно. Вязкость рассчитывали по формуле

(7)
$\eta = \frac{{{{\tau }_{{xy}}}}}{{\partial {{v}_{y}}{\text{/}}\partial z}}$

Здесь ${{\sigma }_{{xy}}}$ – сдвиговое напряжение. ${{\sigma }_{{xy}}}$ вычисляли как

(8)
${{\sigma }_{{xy}}} = \frac{{\partial {{p}_{y}}{\text{/}}\partial t}}{{2A}},$

где A – площадь поверхности XY  расчетной ячейки. В результате сдвиговое напряжение ${{\sigma }_{{xy}}}$ оказалось равным 3.59 МПа. По экспериментальным данным [44] увеличение плотности на 0.04 г/см3 повышает вязкость примерно вдвое, что в диапазоне 0.72–0.76 г/см3 согласуется с полученными в ходе расчета величинами эффективной вязкости (рис. 6г). Однако при дальнейшем увеличении плотности наблюдается аномальный рост вязкости.

Упорядочение молекул додекана в процессе релаксации

Для проверки влияния течения на упорядочение молекул додекана были проведены расчеты релаксации молекул додекана в щелевых порах без приложения сдвигового напряжения. Расчеты были выполнены с каноническим термостатом, который использует масштабирование скоростей с гамильтоновой динамикой (CSVR – canonical sampling through velocity rescaling). Характерное время установления температуры было выбрано равным 1 пс. В результате проведенных расчетов были построены зависимости P(cos(θ)) от времени (рис. 8а). Приведенный график показывает, что эффект упорядочения имеет место и без наличия течения. Однако стоит заметить, что значения P0 и τ, полученные в результате релаксации, (рис. 8б) отличаются от таковых при моделировании течения Куэтта. При релаксации без приложения сдвигового напряжения P0 меньше, а τ больше, чем в расчетах с приложенным сдвигом, причем величины P0 различаются почти вдвое. Отсюда можно сделать вывод, что сдвиговое напряжение ускоряет упорядочение молекул углеводородной жидкости, а также позволяет достигнуть большей степени упорядоченности в углеводородной жидкости.

Рис. 8.

Динамика P(cos θ) для cos θ ∈ [0.99, 1] в процессе релаксации додекана плотностью 0.8 г/см3 при ширине щели 5 (1) и 3 нм (2) (a), а также зависимости параметров P0 (1) и τ (2) от ширины щели для плотности додекана ρ = 0.8 г/см3 (б).

ЗАКЛЮЧЕНИЕ

Проведено молекулярно-динамическое моделирование сдвигового течения для н-додекана в щелевых нанопорах со стенками из пирофиллита. Расчеты показывают, что в процессе течения происходит формирование упорядоченных слоев молекул жидкости с переходом в состояние, похожее на жидкий кристалл, при плотностях 0.75–0.8 г/см3, при которых жидкость в объеме имеет разупорядоченную структуру. На упорядочение молекул углеводородной жидкости влияет как ее взаимодействие со стенкой, так и вязкость углеводородной жидкости. Упорядочение молекул додекана происходит в направлении расположения групп OH. При этом эффект упорядочения проявляется и без наличия течения, однако в меньшей степени, что еще раз подтверждает влияние сдвигового напряжения на упорядочение структуры молекул углеводородной жидкости. С повышением плотности углеводородной жидкости степень упорядочения возрастает, а с увеличением расстояния между стенками щели степень упорядочения, наоборот, уменьшается. Вместе с упорядочением наблюдается аномальный рост эффективной вязкости жидкости и переход из состояния течения в слаботекучее состояние при высоком упорядочении. Данные эффекты могут иметь значение для прогнозирования режимов течения в нанопористых средах, таких как сланцевые породы, и при проектировании микроэлектромеханических систем.

Исследование процесса упорядочения и режимов течения проведено в рамках проекта Российского научного фонда 17-79-20391.

Разработка программных средств для анализа МД-траекторий частично поддержана в рамках Программы фундаментальных исследований Национального исследовательского университета “Высшая школа экономики” и государственного задания Объединенного института высоких температур Российской академии наук 075-01056-22-00.

Исследование выполнено с использованием суперкомпьютерных комплексов Национального исследовательского университета “Высшая школа экономики” и Объединенного института высоких температур Российской академии наук.

Список литературы

  1. Bantignies J.L., Cartier dit Moulin C., Dexpert H. // Clays Clay Minerals. 1997. V. 45. № 2. P. 184.

  2. Scholtzová E., Tunega D., Madejová J., Pálková H., Komadel P. // Vibrational Spectroscopy. 2013. V. 66. P. 123.

  3. Xu L., Hu Y., Dong F., Gao Z., Wu H., Wang Z. // Appl. Surface Sci. 2014. T. 321. C. 331.

  4. Lebedeva E.V., Fogden A. // Colloids Surf. A. 2011. V. 380. № 1–3. P. 280.

  5. Lebedeva E.V., Fogden A. // Colloids Surf. A. 2011. V. 377. № 1–3. P. 115.

  6. Fogden A. // Colloids Surf. A. 2012. V. 402. P. 13.

  7. Bantignies J.L., Cartier dit Moulin C., Dexpert H. // Clays Clay Minerals. 1997. V. 45. № 2. P. 184.

  8. Wang S., Liu Q., Tan X., Xu C., Gray M.R. // Energy Fuels. 2013. V. 27. № 5. P. 2465.

  9. Hassenkam T., Mitchell A.C., Pedersen C.S., Skovbjerg L.L., Bovet N., Stipp S.L.S. // Colloids Surf. A. 2012. V. 403. P. 79.

  10. Buckley J.S., Lord D.L. // J. Petroleum Sci. Eng. 2003. V. 39. № 3–4. P. 261.

  11. Kumar K., Dao E., Mohanty K.K. // J. Colloid Interface Sci. 2005. V. 289. № 1. P. 206.

  12. Chau T.T. // Minerals Eng. 2009. T. 22. № 3. C. 213.

  13. Xie X., Morrow N.R., Buckley J.S. // J. Petroleum Sci. Eng. 2002. V. 33. № 1–3. P. 147.

  14. Ghanbari E., Dehghanpour H. // Int. J. Coal Geol. 2015. V. 138. P. 55.

  15. Cygan R.T., Greathouse J.A., Heinz H., Kalinichev A.G. // J. Mater. Chem. 2009. V. 19. № 17. P. 2470.

  16. Greenwell H.C., Jones W., Coveney P.V., Stackhouse S. // J. Mater. Chem. 2006. V. 16. № 8. P. 708.

  17. Anderson R.L., Ratcliffe I., Greenwell H.C., Williams P.A., Cliffe S., Coveney P.V. // Earth-Sci. Revs. 2010. V. 98. № 3–4. P. 201.

  18. Zhang L., Lu X., Liu X., Yang K., Zhou H. // Energy Fuels. 2016. V. 30. № 1. P. 149.

  19. Cao Z., Jiang H., Zeng J., Saibi H., Lu T., Xie X., Zhang Y., Zhou G., Wu K., Guo J. // Chem. Eng. J. 2021. V. 420. P. 127578.

  20. Zhang W., Feng Q., Wang S., Xing X. // J. Mol. Liq. 2019. V. 290. P. 111183.

  21. Rotenberg B., Patel A.J., Chandler D. // J. Am. Chem. Soc. 2011. V. 133. № 50. P. 20521.

  22. Ghanbari E., Dehghanpour H. // Int. J. Coal Geol. 2015. V. 138. P. 55.

  23. Botan A., Rotenberg B., Marry V., Turq P., Noetinger B. // J. Phys. Chem. C. 2011. V. 115. № 32. P. 16109.

  24. Botan A., Marry V., Rotenberg B., Turq P., Noetinger // J. Phys. Chem. C. 2013. V. 117. № 2. P. 978.

  25. Qiao R., Aluru N.R. // J. Chem. Phys. 2003. V. 118. № 10. P. 4692.

  26. Joseph S., Aluru N.R. // Langmuir. 2006. V. 22. № 21. P. 9041.

  27. Wang W., Fan D., Sheng G., Chen Z., Su Y. // Fuel. 2019. V. 256. P. 115737.

  28. Rudkiewicz J.L., Brévart O., Connan J., Montel F. // Org. Geochem. 1994. V. 22. № 3–5. P. 631-IN8.

  29. Debye P., Cleland R.L. // J. Appl. Phys. 1959. V. 30. № 6. P. 843.

  30. Utvik O.H., Rinde T., Valle A. // J. Energy Resour. Technol. 2001. V. 123. № 4. P. 253.

  31. Qiu G., Xu Z., Cai W., Jiang Y. // Appl. Thermal Eng. 2018. V. 140. P. 775.

  32. Kondratyuk N.D., Pisarev V.V. // Fluid Phase Equilibria. 2019. V. 498. P. 151.

  33. Kondratyuk N.D., Pisarev V.V. // Fluid Phase Equilibria. 2021. V. 544. P. 113100.

  34. Kondratyuk N.D., Pisarev V.V., Ewen J.P. // J. Chem. Phys. 2020. V. 153. № 15. P. 154502.

  35. Thompson A.P., Aktulga H.M., Berger R., Bolintineanu D.S., Brown W.M., Crozier P.S., Veld P.J., Kohlmeyer A., Moore S.G., Nguyen T.D., Shan R., Stevens M.J., Tranchida J., Trott C., Plimpton S.J. // Comput. Phys. Commun. 2022. V. 271. P. 108171.

  36. Jorgensen W.L., Maxwell D.S., Tirado-Rives J. // J. Am. Chem. Soc. 1996. V. 118. № 45. P. 11225.

  37. Cygan R.T., Liang J.J., Kalinichev A.G. // J. Phys. Chem. B. 2004. V. 108. № 4. P. 1255.

  38. Jorgensen W.L., Tirado-Rives J. // Proc. Nat. Acad. Sci. 2005. V. 102. № 19. P. 6665.

  39. Dodda L.S., Vilseck J.Z., Tirado-Rives J., Jorgensen W.L. // J. Phys. Chem. B. 2017. V. 121. № 15. P. 3864.

  40. Dodda L.S., Cabeza de Vaca I., Tirado-Rives J., Jorgensen W.L. // Nucleic Acids Res. 2017. V. 45. № W1. P. W331.

  41. Kostenetskiy P.S., Chulkevich R.A., Kozyrev V.I. // J. Phys., Conf. Ser. IOP Publ. 2021. V. 1740. № 1. P. 012050.

  42. Stegailov V., Dlinnova E., Ismagilov T., Khalilov M., Kondratyuk N., Makagon D., Semenov A., Simonov A., Smirnov G., Timofeev A. // Int. J. High Performance Computing Appl. 2019. V. 33. № 3. P. 507.

  43. Szczerba M., Kalinichev A.G., Kowalik M. // Appl. Clay Sci. 2020. V. 188. P. 105497.

  44. Caudwell D.R., Trusler J.P.M., Vesovic V., Wakeham W.A. // Int. J. Thermophys. 2004. V. 25. № 5. P. 1339.

  45. Müller-Plathe F. // Phys. Rev. E. 1999. V. 59. № 5. P. 4894.

  46. Bussi G., Parrinello M. // Comput. Phys. Commun. 2008. V. 179. № 1–3. P. 26.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Высокомолекулярные соединения (серия А)

Архивы выпусков Информация о журнале Отправить рукопись в журнал