Водные ресурсы, 2020, T. 47, № 3, стр. 272-280

Оценка анизотропии проницаемости и скин-эффекта по данным экспресс-откачек из несовершенных скважин

П. Е. Морозов^*

Институт механики и машиностроения – обособленное структурное подразделение ФИЦ “Казанский НЦ РАН”,
420111 Казань, Россия

^* E-mail: morozov@imm.knc.ru

Поступила в редакцию 15.03.2019
После доработки 31.10.2019
Принята к публикации 12.11.2019

DOI: 10.31857/S032105962003013X

Полный текст (PDF)

Аннотация

Получено полуаналитическое и приближенное аналитическое решение задачи экспресс-откачки из несовершенной скважины в напорном или безнапорном анизотропном пласте. Представлено асимптотическое решение задачи экспресс-откачки из несовершенной скважины в безнапорном пласте, в котором, в отличие от полуэмпирического метода Бауэра–Райса, учитывается анизотропия проницаемости и скин-эффект. На основе алгоритма Левенберга‒Марквардта разработан метод определения анизотропии проницаемости и скин-эффекта по данным экспресс-откачек из несовершенных скважин в напорных или безнапорных пластах.

Ключевые слова: несовершенная скважина, анизотропия проницаемости, скин-эффект, экспресс-откачка, вертикальная интерференция.

Экспресс-методы исследования скважин – наиболее быстрые и экономически эффективные методы определения фильтрационных характеристик водоносных горизонтов. Они основаны на резком изменении уровня воды в скважине (с помощью мгновенного подлива или откачки, компрессирования, кратковременного включения насоса и т.д.) и последующей регистрации кривой восстановления уровня (давления). Отличительная особенность экспресс-методов исследования скважин – их непродолжительность по времени и то, что для них не требуются замеры дебита. Получаемые в результате интерпретации таких исследований параметры пласта, как правило, характеризуют ближайшую к скважине зону.

Для определения коэффициента фильтрации по данным экспресс-откачек и наливов широкое распространение получили графоаналитические методы, такие как метод Хворслева (Hvorslev), Бауэра–Райса (Bouwer and Rice), Дагана (Dagan) и др. [14]. Данные методы основаны на модели жесткой фильтрации и различаются способами вычисления фактора формы, зависящего только от анизотропии проницаемости и геометрических параметров фильтра и области дренирования [29]. К недостаткам графоаналитических методов следует отнести невысокую точность определения коэффициента фильтрации, особенно при кольматации фильтра [7, 19, 20].

Впервые аналитическое решение задачи восстановления уровня жидкости в вертикальной скважине после мгновенного подлива получено С.Г. Каменецким [2, 4]. На основе этого решения построены эталонные кривые и предложен экспресс-метод исследования скважин [1, 5]. Позже Х. Купер, Дж. Бредехофт и И. Пападопулос представили аналогичное решение задачи и построили типовые кривые изменения уровня воды в вертикальной скважине [16]. В более общей постановке задача мгновенной откачки из вертикальной скважины рассматривалась Н.И. Гамаюновым и Б.С. Шержуковым в [3, 12], где дополнительно учитывался переток через слабопроницаемую прослойку из горизонта с постоянным напором. Аналитическое решение задачи мгновенной откачки из вертикальной скважины с учетом скин-эффекта и наборы соответствующих типовых кривых представлены в работах [2, 11, 24, 26]. В дальнейшем были получены многие другие аналитические решения задач экспресс-откачек, в частности для вертикальных скважин в слоистых пластах и в пластах с двойной пористостью [14], для несовершенных вертикальных скважин [17, 20, 27], горизонтальных скважин [8, 25] и т.д.

Наряду с очевидными достоинствами, экспресс-методы исследования скважин имеют и свои недостатки. Известно, что экспресс-откачки могут приводить к неоднозначным оценкам параметров водоносного горизонта при исследовании скважин с низкопроницаемым скин-эффектом [7, 14]. Трудновыполнима задача совместной оценки коэффициентов фильтрации, упругоемкости и скин-эффекта по данным одиночной экспресс-откачки без какой-либо априорной информации об этих параметрах [2, 11, 14]. Неопределенность искомых параметров можно уменьшить путем замеров напора в наблюдательных скважинах или пьезометрах, расположенных в непосредственной близости от возмущающей скважины [14]. Экспресс-откачки могут комбинироваться с исследованиями на интерференцию в вертикальном направлении [21]. В этом случае замеры напора проводятся высокоточными датчиками давления в тестируемом и наблюдательном интервалах скважины, изолированных друг от друга надувными пакерами. Последовательные интервальные экспресс-откачки в одиночной скважине на разных глубинах позволяют оценивать неоднородность вертикальной анизотропии проницаемости и упругоемкости по толщине пласта [21].

При решении задач притока к несовершенным скважинам возникают определенные трудности, связанные с заданием смешанных граничных условий на цилиндрической поверхности скважины: в интервале вскрытия задается постоянство напора, а на обсаженной части – условие непротекания. Задачи такого рода со смешанными граничными условиями иногда называются задачами Гильберта и относятся к числу сложных задач математической физики. К примеру, точное решение задачи об установившемся притоке жидкости к несовершенной скважине, полученное М.М. Глоговским, приводит к бесконечной системе уравнений с бесконечным числом неизвестных [6]. Начиная с работы А.Л. Хейна [10] большинство аналитических решений задач нестационарного притока жидкости к несовершенной вертикальной скважине получены на основе предположения о равномерности распределения притока в интервале вскрытия [2, 18]. Модель несовершенной скважины с равномерным распределением притока в интервале вскрытия приводит к неравномерному распределению напора в этом интервале. Более физически обоснованной считается модель бесконечнопроводимой скважины с условием постоянства напора в интервале вскрытия. Часто используется приближенный прием, который заключается в том, что в моделях с равномерным распределением притока в интервале вскрытия рассчитывается средневзешенный напор [17, 20, 27]. В работах [9, 15, 23] задача неустановившегося притока жидкости к несовершенной скважине сводится к системе интегральных уравнений для распределения притока жидкости в интервале вскрытия, которая затем решается числено. Условие постоянства напора в интервале вскрытия, а также ряд других осложняющих факторов, таких как неоднородность пласта, кольматация, наличие свободной поверхности грунтовых вод, могут быть учтены при численном моделировании экспресс-откачек и наливов в несовершенные скважины [7].

ПОЛУАНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ЭКСПРЕСС-ОТКАЧКИ ИЗ НЕСОВЕРШЕННОЙ СКВАЖИНЫ

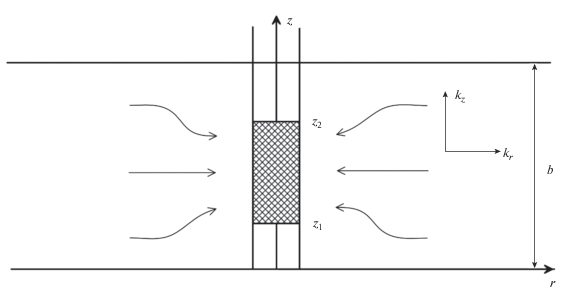
Рассматривается неустановившаяся фильтрация воды в бесконечно простираемом анизотропном пласте после мгновенного изменения уровня в несовершенной скважине на величину s₀ (рис. 1). С течением времени будет происходить повышение (понижение) уровня в скважине s(t) до начального значения за счет притока (оттока) воды с расходом $C\frac{{\partial s}}{{\partial t}}$ ($C = \pi r_{c}^{2}$ ‒ коэффициент влияния объема ствола скважины, r_c ‒ внутренний радиус трубы). Задача состоит в определении функции изменения напора $h\left( {r,z,t} \right)$ в области течения $r > {{r}_{w}}$, $0 \leqslant z \leqslant b$, и функции изменения уровня s(t) в скважине при $t > 0$. В безразмерном виде изменение напора в пласте описывается уравнением пьезопроводности:

(1)

$\frac{1}{{{{r}_{d}}}}\frac{\partial }{{\partial {{r}_{d}}}}\left( {{{r}_{d}}\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right) + \frac{1}{{b_{d}^{2}}}\frac{{{{\partial }^{2}}{{h}_{d}}}}{{\partial z_{d}^{2}}} = \frac{{\partial {{h}_{d}}}}{{\partial {{t}_{d}}}}$

с начальным

(2)

${{h}_{d}}\left( {{{r}_{d}},{{z}_{d}},0} \right) = 0,\,\,\,\,{{s}_{d}}\left( 0 \right) = 1$

и граничными условиями

(3)

${{h}_{d}}\left( {\infty ,{{z}_{d}},{{t}_{d}}} \right) = 0,$

(4)

${{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{z}_{d}}}}} \right|}_{{{{z}_{d}} = 0}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{z}_{d}}}}} \right|}_{{{{z}_{d}} = 1}}} = 0,$

(5)

${{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right|}_{{{{r}_{d}} = 1}}} = 0,\,\,\,\,0 \leqslant {{z}_{d}} < {{z}_{{1d}}},\,\,\,\,{{z}_{{2d}}} < {{z}_{d}} \leqslant 1,$

(6)

$\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {q\left( {{{z}_{d}},{{t}_{d}}} \right)} d{{z}_{d}} = - {{C}_{d}}\frac{{\partial {{s}_{d}}\left( {{{t}_{d}}} \right)}}{{\partial {{t}_{d}}}},$

(7)

${{s}_{d}}\left( {{{t}_{d}}} \right) = {{h}_{d}}\left( {1,{{z}_{d}},{{t}_{d}}} \right) - Sq\left( {{{z}_{d}},{{t}_{d}}} \right),\,\,\,\,{{z}_{{1d}}} \leqslant {{z}_{d}} \leqslant {{z}_{{2d}}},$

где ${{h}_{d}} = \frac{h}{{{{s}_{0}}}}$, ${{s}_{d}} = \frac{s}{{{{s}_{0}}}}$, ${{t}_{d}} = \frac{{{{k}_{r}}t}}{{{{S}_{s}}r_{w}^{2}}}$, ${{r}_{d}} = \frac{r}{{{{r}_{w}}}}$, ${{z}_{d}} = \frac{z}{b}$, ${{b}_{d}} = \frac{b}{{{{r}_{w}}}}\sqrt {\frac{{{{k}_{r}}}}{{{{k}_{z}}}}} $, ${{C}_{d}} = \frac{C}{{2\pi b{{S}_{s}}r_{w}^{2}}}$, $q\left( {{{z}_{d}},{{t}_{d}}} \right) = - {{\left. {\left( {{{r}_{d}}\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right)} \right|}_{{{{r}_{d}} = 1}}}$, h ‒ напор; k_r, k_z ‒ коэффициенты фильтрации в горизонтальном и вертикальном направлении; b ‒ мощность пласта; S_s ‒ упругоемкость; r_w ‒ радиус скважины; S ‒ скин-фактор.

Рис. 1.

Схема несовершенной скважины.

Применяя к (1)‒(7) преобразование Лапласа по времени и конечное косинус-преобразование Фурье по координате z_d [9, 23], получим выражение:

(8)

$\begin{gathered} {{{\bar {h}}}_{d}}\left( {{{r}_{d}},{{z}_{d}},u} \right) = F\left( {{{r}_{d}},u} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)d\xi } + \\ + \,\,2\sum\limits_{m = 1}^\infty {F\left( {{{r}_{d}},{{\lambda }_{m}}} \right)\cos \left( {\pi m{{z}_{d}}} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)\cos \left( {\pi m\xi } \right)d\xi } } , \\ \end{gathered} $

где u ‒ переменная преобразования Лапласа; ${{\lambda }_{m}} = u + \frac{{{{\pi }^{2}}{{m}^{2}}}}{{b_{d}^{2}}}$; $F\left( {x,y} \right) = \frac{{{{K}_{0}}\left( {x\sqrt y } \right)}}{{\sqrt y {{K}_{1}}\left( {\sqrt y } \right)}}$; K₀(x), K₁(x) ‒ модифицированные функции Бесселя второго рода нулевого и первого порядка соответственно.

Изображения изменения уровня и плотности притока воды в интервале вскрытия определяются из решения системы интегральных уравнений:

(9)

$\begin{gathered} {{{\bar {s}}}_{d}} = F\left( {1,u} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)d\xi } + \\ + \,\,2\sum\limits_{m = 1}^\infty {F\left( {1,{{\lambda }_{m}}} \right)\cos \left( {\pi m{{z}_{d}}} \right)\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)\cos \left( {\pi m\xi } \right)d\xi } } + \\ + \,\,S\bar {q}\left( {{{z}_{d}},u} \right), \\ \end{gathered} $

(10)

$\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)} {\kern 1pt} d\xi = {{C}_{d}}\left( {1 - u{{{\bar {s}}}_{d}}} \right).$

Для несовершенной скважины в безнапорном пласте будем считать, что в период проведения теста свободная поверхность остается невозмущенной и фильтр скважины не осушается. Заменив второе граничное условие в (4) на ${{h}_{d}}\left( {{{r}_{d}},1,{{t}_{d}}} \right) = 0$ и применяя к (1)‒(7) преобразование Лапласа по времени и модифицированное конечное синус-преобразование Фурье по координате z_d [23], получим следующую систему интегральных уравнений:

(11)

$\begin{gathered} {{{\bar {s}}}_{d}} = 2\sum\limits_{m = 1}^\infty {F\left( {1,{{\mu }_{m}}} \right)\cos \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{d}}}}{2}} \right)} \times \\ \times \,\,\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)\cos \left( {\frac{{\pi \left( {2m - 1} \right)\xi }}{2}} \right)d\xi } + S\bar {q}\left( {{{z}_{d}},u} \right), \\ \end{gathered} $

(12)

$\int\limits_{{{z}_{{1d}}}}^{{{z}_{{2d}}}} {\bar {q}\left( {\xi ,u} \right)} d\xi = {{C}_{d}}\left( {1 - u{{{\bar {s}}}_{d}}} \right),$

где ${{\mu }_{m}} = u + \frac{{{{\pi }^{2}}{{{\left( {2m - 1} \right)}}^{2}}}}{{4b_{d}^{2}}}$.

Для численного решения систем интегральных уравнений (9), (10) и (11), (12) интервал вскрытия разбивается на сегменты и полагается, что приток воды к каждому сегменту равномерный. В результате получается система линейных алгебраических уравнений для определения изображений по Лапласу изменения напора и притока воды в интервале вскрытия:

(13)

$\left[ {\begin{array}{*{20}{c}} {{{A}_{{11}}} + S}& \cdots &{{{A}_{{1m}}}}&{ - 1} \\ \vdots &{}& \vdots & \vdots \\ {{{A}_{{m1}}}}& \cdots &{{{A}_{{mm}}} + S}&{ - 1} \\ {\Delta {{\zeta }_{1}}}& \cdots &{\Delta {{\zeta }_{m}}}&{{{C}_{d}}u} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\bar {q}}}_{1}}} \\ \vdots \\ {{{{\bar {q}}}_{m}}} \\ {{{{\bar {s}}}_{d}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ \vdots \\ 0 \\ {{{C}_{d}}} \end{array}} \right],$

где ${{A}_{{ij}}} = F\left( {1,u} \right)\Delta {{\zeta }_{i}}$ + $2\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{\pi m}}\sin \left( {\frac{{\pi m\Delta {{\zeta }_{i}}}}{2}} \right)} $ × × $\cos \left( {\pi m{{{\bar {\zeta }}}_{i}}} \right)\cos \left( {\pi m{{{\bar {\zeta }}}_{j}}} \right)$ ‒ для напорного пласта; A_ij = $4\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\mu }_{m}}} \right)}}{{\pi \left( {2m - 1} \right)}}\sin \left( {\frac{{\pi \left( {2m - 1} \right)\Delta {{\zeta }_{i}}}}{4}} \right)} $ × × $\cos \left( {\frac{{\pi \left( {2m - 1} \right){{{\bar {\zeta }}}_{i}}}}{2}} \right)\cos \left( {\frac{{\pi \left( {2m - 1} \right){{{\bar {\zeta }}}_{j}}}}{2}} \right)$ ‒ для безнапорного пласта; $\Delta {{\zeta }_{i}} = {{\zeta }_{i}} - {{\zeta }_{{i - 1}}}$, ${{\bar {\zeta }}_{i}} = {{\left( {{{\zeta }_{i}} + {{\zeta }_{{i - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\zeta }_{i}} + {{\zeta }_{{i - 1}}}} \right)} 2}} \right. \kern-0em} 2}$, $i = 1, \ldots ,m$, ${{z}_{{1d}}} = {{\zeta }_{0}} < {{\zeta }_{0}} < \ldots < {{\zeta }_{m}} = {{z}_{{2d}}}$. Система линейных алгебраических уравнений решается стабилизированным методом бисопряженных градиентов BiCGStab с предобусловливанием. Обратное преобразование Лапласа выполняется численно на основе алгоритма Стефеста (Stehfest) [9].

ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧИ ЭКСПРЕСС-ОТКАЧКИ ИЗ НЕСОВЕРШЕННОЙ СКВАЖИНЫ

Предположим, что распределение притока воды в интервале вскрытия равномерное. Интегрируя уравнения (9) и (11) по z_d с учетом (10), (12), найдем изменение средневзвешенного напора в интервале вскрытия несовершенной скважины:

(14)

${{\bar {s}}_{d}} = \frac{{{{C}_{d}}\left( {u{{{\bar {h}}}_{d}} + \frac{S}{{{{l}_{d}}}}} \right)}}{{1 + u{{C}_{d}}\left( {u{{{\bar {h}}}_{d}} + \frac{S}{{{{l}_{d}}}}} \right)}}.$

Здесь ${{l}_{d}} = {{z}_{{2d}}} - {{z}_{{1d}}}$; ${{\bar {h}}_{d}} = \frac{{F\left( {1,u} \right)}}{u} + \frac{2}{{ul_{d}^{2}}}\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{{{\pi }^{2}}{{m}^{2}}}}} \times $ × ${{\left[ {\sin \left( {\pi m{{z}_{{2d}}}} \right) - \sin \left( {\pi m{{z}_{{1d}}}} \right)} \right]}^{2}}$ ‒ изображение по Лапласу средневзвешенного напора в интервале вскрытия несовершенной скважины, работающей с постоянным расходом в напорном пласте [9]; ${{\bar {h}}_{d}} = \frac{8}{{ul_{d}^{2}}}\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\mu }_{m}}} \right)}}{{{{\pi }^{2}}{{{\left( {2m - 1} \right)}}^{2}}}}} \left[ {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{2d}}}}}{2}} \right)} \right.$ – – ${{\left. {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{1d}}}}}{2}} \right)} \right]}^{2}}$ ‒ для безнапорного пласта. Если несовершенная скважина вскрывает изотропный напорный пласт, то (14) совпадает с решением Д. Догерти и Д. Бабу [17]. Для совершенной вертикальной скважины в напорном пласте (${{z}_{{1d}}} = 0$, ${{z}_{{2d}}} = 1$, l_d = 1) выражение (14) сводится к решению задачи из работ [11, 24], а при S = 0 ‒ к решению С.Г. Каменецкого [4]. Отметим, что в решении З. Хайдера с соавторами [14, 20], известном как “модель KGS” (Kansas Geological Survey), используется модель скин-эффекта конечной толщины. Аналогичная модель скин-эффекта также используется в решении Х. Е с соавторами [27] и в решении Т. Перина и Т. Ли [23].

Исследуем поведение решения (14) для больших значений ${{t}_{d}}$ в случае безнапорного пласта. Применяя к (14) обратное преобразование Лапласа при $u \to 0$, что соответствует ${{t}_{d}} \to \infty $, получим следующее асимптотическое решение задачи мгновенной откачки из несовершенной скважины в безнапорном пласте:

(15)

${{s}_{d}}\left( {{{t}_{d}}} \right) = \exp \left[ { - \frac{{{{t}_{d}}}}{{{{C}_{d}}\left( {{{S}_{p}} + \frac{S}{{{{l}_{d}}}}} \right)}}} \right],$

где ${{S}_{p}} = \frac{2}{{l_{d}^{2}b_{d}^{2}}}\sum\nolimits_{m = 1}^\infty {\frac{{{{K}_{0}}\left( {{{\sigma }_{m}}} \right)}}{{\sigma _{m}^{3}{{K}_{1}}\left( {{{\sigma }_{m}}} \right)}}} \left[ {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{2d}}}}}{2}} \right)} \right.$ – – ${{\left. {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{z}_{{1d}}}}}{2}} \right)} \right]}^{2}}$ ‒ псевдоскин-фактор, ${{\sigma }_{m}} = \frac{{\pi \left( {2m - 1} \right)}}{{2{{b}_{d}}}}$. Суммарный скин-фактор ${{S}_{p}} + \frac{S}{{{{l}_{d}}}}$ в (15) ‒ показатель несовершенства скважины по степени и характеру вскрытия. Следует отметить, что величина псевдоскин-фактора S_p обратно пропорциональна фактору формы несовершенной скважины в безнапорном пласте [29].

Другой известный способ учета скин-эффекта состоит в замене радиуса скважины r_w на приведенный радиус ${{\tilde {r}}_{w}} = {{r}_{w}}\exp \left( { - S} \right)$ [2, 11, 14]. В результате такой замены выражение (15) преобразуется к виду

(16)

${{s}_{d}}\left( {{{{\tilde {t}}}_{d}}} \right) = \exp \left[ { - \frac{{{{{\tilde {t}}}_{d}}}}{{{{{\tilde {C}}}_{d}}{{{\tilde {S}}}_{p}}}}} \right],$

где знак тильда означает, что в безразмерных параметрах радиус скважины r_w заменен на приведенный радиус ${{\tilde {r}}_{w}}$. Расчеты по формулам (15) и (16) показали, что оба способа учета скин-эффекта приводят к одним и тем же результатам.

В отличие от полуэмпирического метода Бауэра‒Райса [13], асимптотическое решение (15) позволяет учитывать анизотропию проницаемости и скин-эффект. В работе В. Злотника [28] с помощью замены радиуса скважины r_w на приведенный радиус $r_{w}^{*} = {{r}_{w}}\sqrt {\frac{{{{k}_{z}}}}{{{{k}_{r}}}}} $ предложена модификация метода Бауэра‒Райса для учета анизотропии проницаемости пласта. Используя аналогию с формулой (15), нетрудно показать, что для учета скин-эффекта в методе Бауэра‒Райса достаточно заменить величину фактора формы P на 1/(1/P + S). Согласно модифицированному методу Бауэра‒Райса и асимптотическому решению (15), график изменения уровня в координатах ln s ‒ t ‒ прямая линия с углом наклона, зависящим от анизотропии проницаемости и скин-эффекта. Этим объясняется тот факт, что применение графоаналитических методов для интерпретации экспресс-откачек из несовершенных скважин без использования априорной информации об анизотропии проницаемости и скин-эффекте может приводить к ошибочным оценкам коэффициента фильтрации [7, 14, 19, 28].

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ИНТЕРВАЛЬНОЙ ЭКСПРЕСС-ОТКАЧКИ ИЗ ВЕРТИКАЛЬНОЙ СКВАЖИНЫ

Рассматривается задача нахождения напора в тестируемом и наблюдательном интервалах скважины (рис. 2) после мгновенного изменения напора в тестируемом интервале на величину s₀. В этом случае постановка задачи (1)‒(7) дополняется граничным условием для наблюдательного интервала

(17)

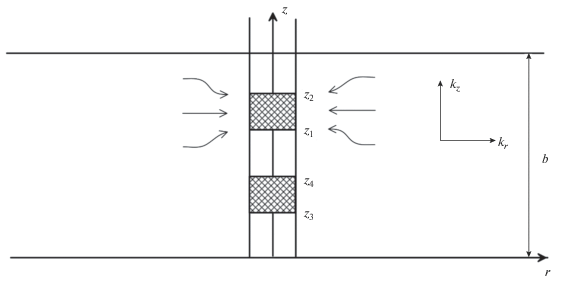
$\begin{gathered} \int\limits_{{{z}_{{3d}}}}^{{{z}_{{4d}}}} {q\left( {{{z}_{d}},{{t}_{d}}} \right)} d{{z}_{d}} = - {{C}_{{2d}}}\frac{{\partial {{s}_{{2d}}}\left( {{{t}_{d}}} \right)}}{{\partial {{t}_{d}}}}, \\ {{s}_{{2d}}}\left( {{{t}_{d}}} \right) = {{h}_{d}}\left( {1,{{z}_{d}},{{t}_{d}}} \right) - {{S}_{2}}q\left( {{{z}_{d}},{{t}_{d}}} \right),\,\,\,\,{{z}_{{3d}}} \leqslant {{z}_{d}} \leqslant {{z}_{{4d}}}, \\ \end{gathered} $

${{C}_{{2d}}} = \frac{{{{C}_{2}}}}{{2\pi b{{S}_{s}}r_{w}^{2}}}$ ‒ безразмерный коэффициент влияния объема наблюдательного интервала, S₂ ‒ скин-фактор наблюдательного интервала.

Рис. 2.

Схема экспресс-исследования скважины на интерференцию в вертикальном направлении (z₁–z₂ ‒ тестируемый, z₃–z₄ ‒ наблюдательный интервалы).

Предположим, что распределение притока воды в тестируемом и наблюдательном интервалах ‒ равномерное. Тогда изображения по Лапласу осредненных напоров по длине интервалов определяются выражениями:

(18)

${{\bar {s}}_{{1d}}} = \frac{{{{U}_{1}}{{I}_{2}} - {{U}_{2}}{{Y}_{2}}}}{{{{I}_{1}}{{I}_{2}} - {{Y}_{2}}{{Y}_{1}}}},\,\,\,\,{{\bar {s}}_{{2d}}} = \frac{{{{U}_{2}}{{I}_{1}} - {{U}_{1}}{{Y}_{1}}}}{{{{I}_{1}}{{I}_{2}} - {{Y}_{2}}{{Y}_{1}}}},$

где ${{I}_{i}} = 1 + {{C}_{{id}}}{{u}^{2}}{{\bar {h}}_{{ii}}} + \frac{{{{S}_{i}}{{C}_{{id}}}u}}{{{{l}_{{id}}}}}$; ${{Y}_{i}} = {{C}_{{id}}}{{u}^{2}}{{\bar {h}}_{{12}}}$; U₂ = = ${{C}_{{1d}}}u{{\bar {h}}_{{12}}}$; ${{U}_{1}} = {{C}_{{1d}}}u{{\bar {h}}_{{11}}} + \frac{{{{S}_{1}}{{C}_{{1d}}}}}{{u{{l}_{{1d}}}}}$; ${{\alpha }_{1}} = {{z}_{{1d}}}$; ${{\beta }_{1}} = {{z}_{{2d}}}$; ${{\alpha }_{2}} = {{z}_{{3d}}}$; ${{\beta }_{2}} = {{z}_{{4d}}}$; ${{\bar {h}}_{{ij}}} = \frac{{F\left( {1,u} \right)}}{u} + \frac{2}{u}$ × $ \times \,\,\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{{{\pi }^{2}}{{m}^{2}}}}{{\Psi }_{i}}} {{\Psi }_{j}}$ ‒ для напорного пласта, $i,j = 1,2$; ${{\bar {h}}_{{ij}}} = \frac{8}{u}\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\mu }_{m}}} \right)}}{{{{\pi }^{2}}{{{\left( {2m - 1} \right)}}^{2}}}}} {{\Omega }_{i}}{{\Omega }_{j}}$ ‒ для безнапорного пласта, $i,j = 1,2$; Ψ_i = $ = \frac{{\sin \left( {\pi m{{\beta }_{i}}} \right) - \sin \left( {\pi m{{\alpha }_{i}}} \right)}}{{{{l}_{{id}}}}}$, ${{\Omega }_{i}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{1}{{{{l}_{{id}}}}}{\kern 1pt} \left[ {\sin {\kern 1pt} \left( {\frac{{\pi {\kern 1pt} \left( {2m - 1} \right){\kern 1pt} {{\beta }_{i}}}}{2}} \right)} \right. - $ – $\left. {\sin \left( {\frac{{\pi \left( {2m - 1} \right){{\alpha }_{i}}}}{2}} \right)} \right]$, ${{l}_{{id}}} = {{\beta }_{i}} - {{\alpha }_{i}}$, $i = 1,2$ (i = 1 ‒ соответствует тестируемому интервалу, i = 2 ‒ наблюдательному интервалу).

Коэффициент влияния объема наблюдательного интервала равен ${{C}_{2}} = {{V}_{2}}{{C}_{w}}{{\rho }_{w}}g$ (V₂ ‒ объем наблюдательного интервала, C_w ‒ сжимаемость воды, ${{\rho }_{w}}$ ‒ плотность воды, g ‒ ускорение свободного падения). Так как величина C₂ мала по сравнению с C₁, то, полагая в (18) ${{C}_{{2d}}} \approx 0$, получим:

(19)

$\begin{gathered} {{{\bar {s}}}_{{1d}}} = \frac{{{{C}_{{1d}}}\left( {u{{{\bar {h}}}_{{11}}} + \frac{{{{S}_{1}}}}{{{{l}_{{1d}}}}}} \right)}}{{1 + u{{C}_{{1d}}}\left( {u{{{\bar {h}}}_{{11}}} + \frac{{{{S}_{1}}}}{{{{l}_{{1d}}}}}} \right)}}, \\ {{{\bar {s}}}_{{2d}}} = \frac{{{{C}_{{1d}}}u{{{\bar {h}}}_{{12}}}}}{{1 + u{{C}_{{1d}}}\left( {u{{{\bar {h}}}_{{11}}} + \frac{{{{S}_{1}}}}{{{{l}_{{1d}}}}}} \right)}}. \\ \end{gathered} $

Видно, что в этом случае выражение для изменения напора в тестируемом интервале совпадает с (14), т.е. наблюдательный интервал не влияет на изменение напора в тестируемом интервале.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

На рис. 3а представлены графики изменения уровня в несовершенной скважине в зависимости от времени, рассчитанные на основе полуаналитического решения (13) (сплошные линии), приближенного аналитического решения (14) (пунктирные линии) и численного решения задачи методом конечных элементов (символы). Расчеты проводились при следующих значениях параметров: s₀ = 3 м, k_r = 5 × 10^–6 м/c, k_z = 10^–6 м/c, S_s = = 10^–5 м^–1, C = 5 × 10^–4 м², S = 0, r_w = 0.1 м, b = = 10 м, z₁ = 4 м, z₂ = 8 м. На рис. 3б представлены кривые изменения уровня, преобразованные с помощью соотношений [22]:

(20)

$\frac{{\partial {{h}_{d}}\left( {{{t}_{d}}} \right)}}{{\partial \ln {{t}_{d}}}} = \frac{{{{t}_{d}}{{s}_{d}}\left( {{{t}_{d}}} \right)}}{{{{C}_{d}}}},\,\,\,\,I\left( {{{s}_{d}}} \right) = \frac{1}{{{{C}_{d}}}}\int\limits_0^{{{t}_{d}}} {{{s}_{d}}\left( \tau \right)d\tau } .$

Рис. 3.

Кривые изменения уровня (а) и преобразованные кривые изменения уровня (б) в несовершенной скважине (1, 3 – напорный, 2, 4 – безнапорный пласты).

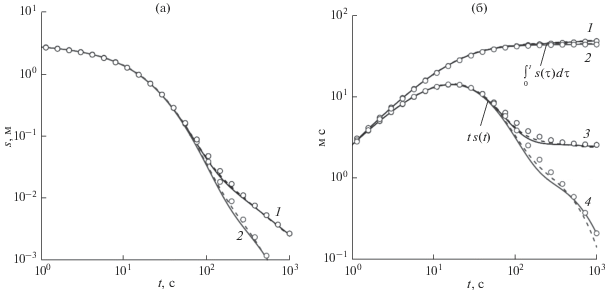
Как видно из рис. 3б, преобразованные кривые изменения уровня в билогарифмических координатах аналогичны типовым кривым откачки и кривым логарифмической производной уровня в скважине, работающей с постоянным дебитом. По единичному наклону преобразованных кривых изменения уровня на малых временах можно диагностировать влияние объема ствола скважины. На больших временах нулевой наклон кривой 3 характеризует радиальный режим течения к несовершенной скважине в напорном пласте, а отрицательный наклон кривой 4 ‒ влияние верхней границы безнапорного пласта.

Решение обратной задачи по определению неизвестных параметров ${{k}_{r}}$, ${{k}_{z}}$ и $S$ строится на основе минимизации функции невязки:

(21)

$J = \mathop \sum \limits_{i = 1}^N {{\left( {{{s}_{{{\text{exp}}}}}\left( {{{t}_{i}}} \right) - {{s}_{{{\text{sim}}}}}\left( {{{t}_{i}}} \right)} \right)}^{2}},$

где ${{s}_{{{\text{exp}}}}}\left( {{{t}_{i}}} \right)$, ${{s}_{{{\text{sim}}}}}\left( {{{t}_{i}}} \right)$ – наблюдаемые и вычисленные значения изменения уровня воды в скважине в моменты времени ${{t}_{i}}$, $i = 1,..,N$. Для минимизации функции невязки (21) используется алгоритм Левенберга–Марквардта.

На рис. 4 представлен пример интерпретации опытных данных экспресс-откачки из несовершенной скважины в безнапорном пласте. Расчеты проводились с использованием следующих исходных данных [14]: s₀ = 0.671 м, C = 1.28 × 10^–2 м², S_s = 2 × 10^–4 м^–1, r_w = 0.125 м, b = 47.87 м, z₁ = 29.58 м, z₂ = 31.1 м. В результате решения обратной задачи получены следующие оценки параметров: k_r = = 3.97 × 10^–5 м/с, k_z = 3.34 × 10^–5 м/с, S = ‒0.49. Следует отметить, что оценки скин-фактора и анизотропии проницаемости чувствительны к упругоемкости пласта. Так, например, при увеличении упругоемкости в два раза получены следующие оценки параметров: k_r = 3.42 × 10^–5 м/с, k_z = = 9.07 × 10^–5 м/с, S = ‒0.28. Оценки коэффициента фильтрации по методу Бауэра‒Райса и по модели KGS составили соответственно 4 × 10^–5 и 4.87 × 10^–5 м/с [14], что хорошо согласуется с результатами расчетов по предложенному методу.

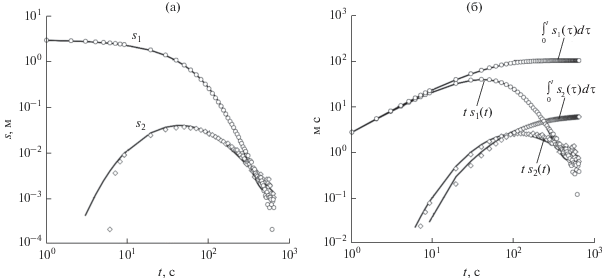
Рис. 4.

Реальные (символами) и вычисленные (сплошные) кривые изменения уровня (а) и преобразованные кривые изменения уровня (б) в несовершенной скважине.

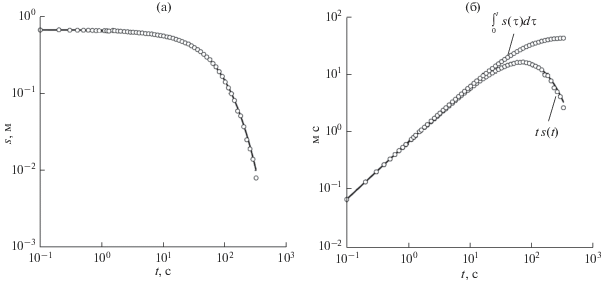
На рис. 5 представлен пример обработки интервальной экспресс-откачки из вертикальной скважины в безнапорном пласте. В расчетах использовались следующие исходные данные [21]: s₀= 2.79 м, C₁= 5 × 10^–4 м², r_w = 0.0254 м, b = 12 м, z₁= 7.4 м, z₂= 8 м, z₃= 6.5 м, z₄= 6.8 м. При решении обратной задачи в качестве целевой функции минимизации бралась сумма среднеквадратических отклонений между наблюдаемыми и вычисленными значениями напора в наблюдательном и тестируемом интервалах. В результате решения обратной задачи получены следующие оценки параметров: k_r = 1.45 × 10^–5 м/с, k_z = 4.16 × 10^–8 м/с, S_s = 3.6 × 10^–5 м^–1, S₁= ‒0.25. Полученные оценки согласуются с результатами интерпретации интервальной экспресс-откачки из работы [21]: k_r = = 2.1 × 10^–5 м/с, k_z = 1.3 × 10^–8 м/с, S_s = 1.1 × 10^–5 м^–1.

Рис. 5.

Реальные (символы) и вычисленные (сплошные) кривые изменения напора (а) и преобразованные кривые изменения напора (б) в тестируемом и наблюдательном интервалах.

ЗАКЛЮЧЕНИЕ

Получено полуаналитическое решение задачи экспресс-откачки из несовершенной скважины в напорном или безнапорном анизотропном пласте с учетом скин-эффекта и условия равномерного распределения напора в интервале вскрытия. С использованием предположения о равномерности распределения притока воды в интервале вскрытия получено приближенное аналитическое решение задачи. Представлено асимптотическое решение задачи экспресс-откачки из несовершенной скважины в безнапорном пласте и показано, что для достоверной оценки коэффициента фильтрации графоаналитическими методами необходима априорная информация об анизотропии проницаемости и скин-эффекте. Получено приближенное аналитическое решение задачи интервальной экспресс-откачки из вертикальной скважины в напорном или безнапорном анизотропном пласте. На основе алгоритма Левенберга‒Марквардта предложен метод определения анизотропии проницаемости и скин-эффекта по данным экспресс-откачек из несовершенных скважин и интервальных экспресс-откачек из вертикальных скважин.

Список литературы

Василевский В.Н., Умрихин И.Д., Каменецкий С.Г., Саитов А.У., Кузьмин В.М. Временное руководство по исследованию скважин “экспресс-методами”. М.: ВНИИ, 1964. 70 с.
Веригин Н.Н., Васильев С.В., Саркисян В.С., Шержуков Б.С. Гидродинамические и физико-химические свойства горных пород. М.: Недра, 1977. 271 с.
Гамаюнов Н.И., Шержуков Б.С. Определение водопроницаемости грунтов в полевых условиях // Инженерно-физический журн. 1961. Т. 4. № 10. С. 71‒78.
Каменецкий С.Г. Две задачи теории фильтрации упругой жидкости в упругой пористой среде // Тр. ВНИИ. Разработка нефтяных месторождений и подземная гидродинамика. М.: Гостоптехиздат, 1959. Вып. 19. С. 134‒145.
Каменецкий С.Г., Саитов А.У. Экспресс-метод исследования пьезометрических непереливающих скважин // Нефтепромысловое дело. 1963. № 8. С. 8–11.
Крылов А.П., Глоговский М.М., Мирчинк М.Ф., Николаевский Н.М., Чарный И.А. Научные основы разработки нефтяных месторождений. М.; Л.: Гостоптехиздат, 1948. 416 с.
Лехов С.М., Лехов М.В. Методы расчета и причины ошибочных результатов экспресс-откачек из скважин // Инженерные изыскания. 2017. № 2. С. 38‒50.
Морозов П.Е. Определение параметров пласта по данным мгновенного изменения давления в горизонтальной скважине // Нефтепромысловое дело. 2018. № 11. С. 36–42.
Морозов П.Е. Полуаналитическое решение задачи нестационарного притока жидкости к несовершенной скважине // Учен. зап. Казан. ун-та. Сер. Физ.-мат. науки. 2017. Т. 159. Кн. 3. С. 340‒353.
Хейн А.Л. Неустановившаяся фильтрация жидкости и газа к скважине с открытым забоем, не полностью вскрывающей пласт // ДАН СССР. 1953. Т. 91. № 3. С. 467‒470.
Шержуков Б.С. Определение сопротивления несовершенных скважин (скин-эффекта) по данным мгновенного налива или откачки и налива с постоянным дебитом // Тр. лаб. инженер. гидрогео-логии. ВНИИ ВОДГЕО. М.: Стройиздат, 1972. Вып. 6. С. 193‒209.
Шержуков Б.С., Гамаюнов Н.И. Методика расчета гидрогеологических параметров водоносных пластов при опробовании их опытной скважиной // Изв. вузов. Геология и разведка. 1964. № 5. С. 105‒111.
Bouwer H., Rice R.C. A slug test for determining hydraulic conductivity of unconfined aquifers with completely or partially penetrating wells // Water Resour. Res. 1976. V. 12. № 3. P. 423‒428.
Butler J.J. Jr. The design, performance, and analysis of slug tests. Boca Raton: Lewis Publishers, 1998. 252 p.
Chang C.C., Chen C.S. An integral transform approach for a mixed boundary problem involving a flowing partially penetrating well with infinitesimal well skin // Water Resour. Res. 2002. V. 38. № 6. P. 1071‒1077.
Cooper H., Bredehoeft J.D., Papadopulos I.S. Response of a finite-diameter well to an instantaneous charge of water // Water Resour. Res. 1967. V. 3. № 1. P. 263‒269.
Dougherty D., Babu D. Flow to a partially penetrating well in a double-porosity reservoir // Water Resour. Res. 1984. V. 20. № 8. P. 1116‒1122.
Hantush M.S. Hydraulics of wells // Advances in Hydroscience / Ed. Chow V.T. N. Y.: Acad. Press, 1964. V. 1. P. 281‒432.
Hyder Z., Butler J.J., Jr. Slug tests in unconfined formations: an assessment of the Bouwer and Rice technique // Ground Water. 1995. V. 33. № 1. P. 16‒22.
Hyder Z., Butler J.J., Jr., McElwee C.D., Liu W. Slug tests in partially penetrating wells // Water Resour. Res. 1994. V. 30. № 11. P. 2945‒2957.
Paradis D., Lefebvre R. Single-well interference slug tests to assess the vertical hydraulic conductivity of unconsolidated aquifers // J. Hydrol. 2013. V. 478. P. 102‒118.
Peres A.M., Onur M., Reynolds A.C. A new analysis procedure for determining aquifer properties from slug test data // Water Resour. Res. 1989. V. 25. № 7. P. 1591‒1602.
Perina T., Lee T.C. General well function for pumping from a confined, leaky, or unconfined aquifer // J. Hydrol. 2006. V. 317. № 3‒4. P. 239‒260.
Ramey H.J., Jr., Agarwal R.G. Annulus unloading rates as influenced by wellbore storage and skin effect // SPE J. 1972. V. 12. № 5. P. 253‒462.
Rushing J.A. A semianalytical model for horizontal well slug testing in confined aquifers. PhD Dissertation. Texas: Texas A&M Univ., 1997. 133 p.
Sageev A. Slug test analysis // Water Resour. Res. 1986. V. 22. № 8. P. 11323-1333.
Yeh H.D., Chen Y.J., Yan S.Y. Semi-analytical solution for a slug test in partially penetrating wells including the effect of finite-thickness skin // Hydrol. Processes. 2008. V. 22. № 18. P. 3741‒3748.
Zlotnik V.A. Interpretation of slug and packer tests in anisotropic aquifers // Ground Water. 1994. V. 32. № 5. P. 761‒766.
Zlotnik V.A., Goss D., Duffield G.M. General steady-state shape factor for a partially penetrating well // Ground Water. 2010. V. 48. № 1. P. 111‒116.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Водные ресурсы

Архивы выпусков Информация о журнале Отправить рукопись в журнал