1. На главную
  2. Электронные версии
  3. Водные ресурсы
  4. T. 48, № 2, 2021

Водные ресурсы, 2021, T. 48, № 2, стр. 135-146

Моделирование быстроразвивающихся паводков на малых реках Северного Кавказа с использованием современных данных автоматизированной гидрометеорологической сети

Е. С. Васильева a, *, П. А. Белякова a, b, А. И. Алексюк a, c, Н. В. Селезнева d, В. В. Беликов a

a Институт водных проблем РАН
119333 Москва, Россия

b Тихоокеанский институт географии ДО РАН
690041 Владивосток, Россия

c МГУ им. М.В. Ломоносова, механико-математический факультет
119991 Москва, Россия

d ГУМРФ им. адм. С.О. Макарова
198035 Санкт-Петербург, Россия

* E-mail: vasilevaes@yandex.ru

Поступила в редакцию 31.01.2020
После доработки 25.09.2020
Принята к публикации 25.09.2020

Полный текст (PDF)

Аннотация

Приведены примеры численного моделирования быстроразвивающихся дождевых паводков в горных районах на основании фактических и прогнозных данных об осадках и сопоставление рассчитанных гидрографов с данными гидрометеорологической сети и расчетами других авторов. Исследования проводились по двум моделям: STREAM 2D CUDA, основанной на численном решении уравнений мелкой воды в двуxмерной (плановой) постановке по оригинальному алгоритму; и KW-GIUH-модели геоморфологического мгновенного единичного гидрографа, основанной на уравнении кинематической волны. Новые в гидрологии научные результаты – прямое численное моделирование уровенных режимов прохождения паводковой волны, а также учет в динамическом режиме аккумуляции части паводкового стока водохранилищами-ловушками. Сделан вывод, что обе модели могут эффективно использоваться для прогнозирования дождевых паводков при наличии надежных данных об осадках.

Ключевые слова: прогнозный расчет, быстроразвивающийся паводок, водосборный бассейн, численное моделирование, водохранилища-ловушки.

ВВЕДЕНИЕ

Катастрофические дождевые паводки проходят на Северном Кавказе регулярно. Наиболее сильными за последние годы были наводнения в 2002 г. в бассейнах рек Кубани, Терека и под Новороссийском; в 2012 г. в Новороссийске, Геленджике и Крымске [1, 3], в 2018 г. в Туапсе и Апшеронском районе Краснодарского края. Такая гидрологическая ситуация требует совершенствования методов прогнозирования экстремальных наводнений и защиты от них.

Экстремальный дождевой паводок в бассейне р. Адагум 6–7 июля 2012 г. привел к катастрофическому затоплению г. Крымска [5], погибло более 150 человек, экономический ущерб составил 20 млрд руб. [8]. Гидрологическая ситуация в бассейне р. Адагум в литературе характеризуется как “быстро развивающийся паводок” [2]. Для изучения этого выдающегося гидрологического события коллективом специалистов под руководством М.В. Болгова в 2013 г. был выполнен комплекс работ по реконструкции паводка [2]. Для расчета стока с водосбора р. Адагум в [2] использован программный комплекс SWMM (модель управления ливневым стоком) [16]. Результаты численного моделирования затопления г. Крымска с учетом детальной городской инфраструктуры изложены в работах [11, 18].

В настоящей работе исследуется возможность применения современных методов численного моделирования формирования паводкового стока в сочетании с фактической и прогнозной гидрометеорологической информацией для прогнозирования динамики быстроразвивающихся паводков в горных и предгорных районах. Проводилось сопоставление результатов расчетов по программам STREAM 2D CUDA и KW-GIUH c данными натурных измерений и расчетов [2]. Впервые совместные расчеты по указанным двум программам были описаны в работе [19] применительно к водосбору р. Дюрсо, но там приведена только косвенная проверка достоверности данных моделирования.

Дополнительно с помощью программного комплекса STREAM 2D CUDA выполнены расчеты водохранилищ-ловушек с высотой плотин до 20 м, которые размещались на водосборе р. Адагум для срезки максимальных расходов. Целью данного исследования была оценка того объема стока, который может быть аккумулирован в водохранилищах-ловушках при прохождении дождевого паводка в бассейне р. Адагум.

МЕТОДЫ ИССЛЕДОВАНИЙ

Расчеты проводились с использованием модели геоморфологического мгновенного единичного гидрографа KW-GIUH [6, 17], основанной на уравнении кинематической волны, и программного комплекса STREAM 2D CUDA [9 ] , основанного на численном решении уравнений мелкой воды в двухмерной (плановой) постановке.

Модель KW-GIUH (одна из моделей типа единичного гидрографа) обобщенно описывает процессы стекания воды по водосбору. Предполагается, что осадки выпадают над водосбором с равномерной интенсивностью, независимо и случайным образом капли дождя попадают в русловую сеть и достигают замыкающего створа по некоторому пути за определенное время. Единичный мгновенный гидрограф обобщает совокупность таких путей в данный момент времени и может быть рассчитан по геоморфологическим характеристикам этого водосбора с применением порядкового подхода. Время добегания по склонам и руслам выражается через модификацию уравнения кинематической волны. Благодаря этому в модели отражена нелинейность стокоформирующих процессов – отклик бассейна на более сильный дождь наступает значительно быстрее, чем на более слабый, а величина пикового расхода паводка возрастает нелинейно с увеличением интенсивности дождя [6, 15]. Временнóй шаг моделирования ≤1 ч. В данном случае временнóй шаг составил 1 ч из-за такой же дискретности исходных данных об осадках.

В последней версии STREAM 2D CUDA реализован оригинальный алгоритм, основанный на точном и единственном решении задачи Римана о распаде произвольного разрыва для уравнений мелкой воды [13, 12 ] и распараллеленный на графическом процессоре NVIDIA с использованием технологии CUDA для ускорения вычислений. Этот алгоритм верифицирован на большом числе тестовых задач и реальных объектов. Расчеты проводятся на нерегулярных сетках треугольно-четырехугольной структуры, покрывающих всю площадь водосбора и адаптированных под русловую сеть. В результате расчетов получаются не только расходы воды в заданных створах (как обычно в гидрологических моделях), но и скорости течения, глубины и отметки водной поверхности в любой точке водосбора. При этом учитывается взаимодействие водного потока с гидротехническими и другими сооружениями, расположенными в расчетной области.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ БЫСТРОРАЗВИВАЮЩИХСЯ ПАВОДКОВ НА ВОДОСБОРЕ р. ЗАПАДНЫЙ ДАГОМЫС

Объектом исследования был водосбор р. Западный Дагомыс, площадь которого составляет 49.0 км2. Максимальная высота на водоразделе составляет 935 м (г. Максимовка).

Исходные данные для моделирования следующие:

высотные отметки HydroSHEDS – скорректированные растры радарной топографической съемки SRTM с разрешением 3 угловых секунды;

часовой ход осадков по данным автоматической метеостанции Солох-аул (37 092) за периоды с 25 по 26 июня 2015 г. и с 23 по 25 октября 2018 г.;

уровни воды с гидропостов (ГП): р. Западный Дагомыс – п. Дагомыс, АГК-159, АГК-186).

Данные об осадках и уровнях воды были предоставлены Специализированным центром по гидрометеорологии и мониторингу окружающей среды Черного и Азовского морей. Уровни воды имели нерегулярный шаг – 2, 4, 8 ч в зависимости от интенсивности изменения уровней воды и были приведены к единой часовой дискретности с привлечением 10-минутных данных региональной автоматизированной системы мониторинга паводковой ситуации на реках Краснодарского края [10]. Проводилось сопоставление измерений по всем доступным данным, определялось время добегания волны между пунктами наблюдений (на р. Западный Дагомыс между АГК-186 сети Эмерсит и ГП Росгидромета время добегания – 30 мин). Для периодов паводков с учетом времени добегания строились регрессионные зависимости, по которым были восстановлены недостающие отметки уровня воды в створах ГП Росгидромета. Восстановление детального хода уровня воды особенно важно для моделирования быстроразвивающихся паводков, когда интенсивность подъема уровней воды достигает 2 м/ч.

Переход от уровней воды к расходам воды проводился с использованием кривой Q(H), построенной по данным срочных наблюдений за конкретный год и результатам нивелировки уровней высоких вод выдающихся паводков.

Построение цифровой модели рельефа водосбора

Цифровая модель водосбора (ЦМР) построена на основе матрицы высот HydroSHEDS (Hydrological data and maps based on Shuttle Elevation Derivatives at multiple Scales), которая, в свою очередь, является гидрографическим продуктом совместного проекта WWF и USGS на основе данных SRTM (Shuttle Radar Topography Mission) с пространственным разрешением 3 угловых секунды. Речная сеть построена с использованием инструментов программного комплекса ArcGIS пакета Spatial Analyst – Hydrology. Принято пороговое значение площади водосбора для образования постоянного водотока для рек Черноморского побережья Кавказа – 0.5 км2, оно обеспечивает близкое соответствие расчетной речной сети водотокам, нанесенным на карты масштаба 1 : 100 000, и сведениям о количестве и суммарной длине притоков, приведенным в Гидрологической изученности [7]. Для модели STREAM 2D CUDA задание порогового значения не требуется, но дополнительно проводилась коррекция рельефа путем понижения отметок на 2 м в руслах рек.

Схематизация водосбора р. Западный Дагомыс

Численная модель STREAM 2D CUDA строилась на всем водосборе р. Западный Дагомыс, включая участок реки после слияния с р. Восточный Дагомыс и прибрежный (до 250 м) участок Черного моря, что диктовалось выбором простого граничного условия на выходной границе модели – уровня моря. Модель KW-GIUH адаптирована для водосбора р. Западный Дагомыс – Дагомыс.

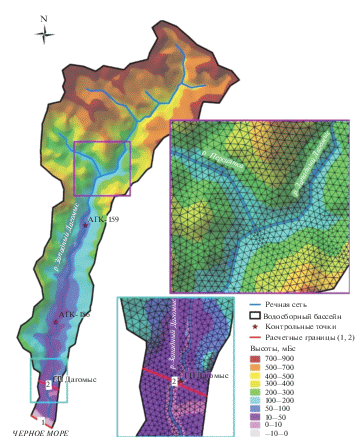
Для модели STREAM 2D CUDA строилась гибридная треугольно-четырехугольная расчетная сетка, адаптированная под плановые очертания речной сети. Вдоль русел рек строилась четырехугольная сетка в одну ячейку поперек русла, остальная область покрывалась треугольной сеткой. Задавались две расчетные границы: 1 – выходная в Черном море, 2 – контрольная в створе ГП р. Западный Дагомыс – Дагомыс. Контрольные точки задавались для трех гидропостов: р. Западный Дагомыс – ГП Дагомыс, АГК-159, АГК-186 (рис. 1).

Рис. 1.

Область моделирования р. Западный Дагомыс и фрагменты расчетной сетки модели STREAM 2D CUDA.

Результаты моделирования паводков 25–26 июня 2015 г. и 23–25 октября 2018 г.

На первом этапе исследований на модели STREAM 2D CUDA проводились расчеты по подбору оптимальных значений коэффициентов шероховатости русла и склонов водосбора р. Западный Дагомыс. Аналогичные расчеты проводились на модели KW-GIUH. Наиболее полное совпадение расчетных и измеренных гидрографов у обеих моделей получено при nрус = 0.03 и nпойм = 0.1 (рис. 2).

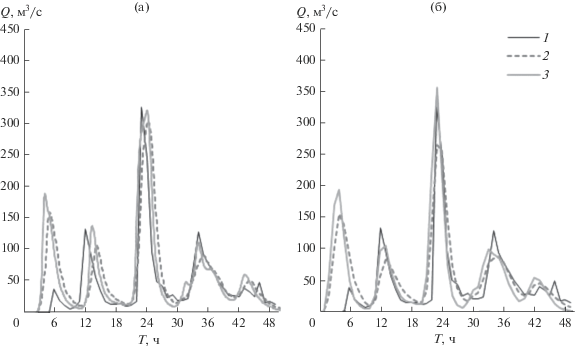
Рис. 2.

Гидрографы расхода по измерениям (1), калибровочным расчетам подбора коэффициентов шероховатости nр = 0.1, nп = 0.2 (2) и nр = 0.03, nп = 0.1 (3): а – модель STREAM 2D CUDA, б – модель KW-GIUH.

На модели STREAM 2D CUDA при калибровке проводилось также сравнение измеренных уровней воды на гидропостах с полученными в ходе расчетов (модель KW-GIUH рассчитывает только расходы воды). На рис. 3 показан ход уровней воды на ГП Западный Дагомыс для паводка 2015 г. и на АГК-159 для паводка 2018 г. Видно, что для ГП АГК-159, расположенного в верхней части водосбора, наилучшее совпадение результатов получено для коэффициента шероховатости в русле 0.1. Тогда как для ГП Западный Дагомыс, расположенного в выходном створе водосбора, лучшее совпадение с натурными данными дает русловая шероховатость, равная 0.03. Такое изменение коэффициента шероховатости по длине русла с уменьшением от верховьев к устью представляется вполне обоснованным, поскольку в верховьях горной реки русло сложено более крупными фракциями, что определяет повышенную относительную шероховатость дна, а следовательно – повышенный коэффициент шероховатости.

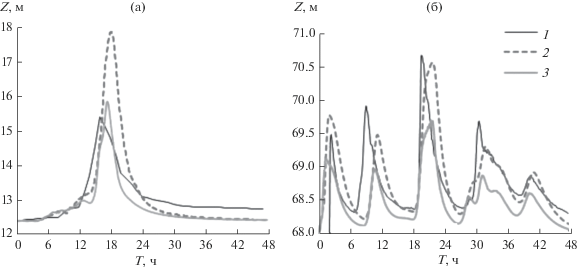
Рис. 3.

Уровни воды на гидропостах: а – ГП “Западный Дагомыс”, июнь 2015 г., б – АГК-159, октябрь 2018 г.; измерения (1), калибровочные расчеты по STREAM 2D CUDA для вариантов шероховатости nр = 0.1, nп = 0.2 (2) и nр = 0.03, nп = 0.1 (3).

На втором этапе исследований при принятых значениях коэффициентов шероховатости проводилось сопоставление моделей STREAM 2D CUDA и KW-GIUH для паводков июня 2015 г. и октября 2018 г. (рис. 4).

Рис. 4.

Сопоставление гидрографов расхода по данным измерений (1) и расчетов по STREAM 2D CUDA (2) и KW-GIUH (3): а – 2015 г., б – 2018 г.

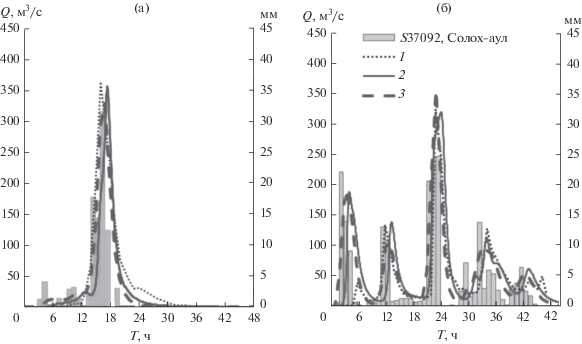
При моделировании дождевого паводка 25 июня 2015 г. (рис. 4а) обе модели – STREAM 2D CUDA и KW-GIUH – показали пиковые значения расходов воды, близкие к максимальному наблюденному (366 м3/с), а именно – 355 и 327 м3/с соответственно. Можно отметить некоторое отставание времени прохождения пика (на 1.5 и 1 ч соответственно) у модельных расчетов относительно фактического времени. Модель STREAM 2D CUDA показывает начало подъема паводка чуть с большей задержкой, чем модель KW-GIUH. Ветвь спада модели описывают схожим образом, быстро срабатывая русловые запасы воды в нижней части графика, тогда как в реальности сток уменьшается не столь интенсивно за счет увеличения запасов воды в бассейновой емкости.

Паводок 24–25 октября на р. Западный Дагомыс (рис. 4б) имел 5 пиков вслед за ходом осадков. Первая волна паводка была сильно завышена обеими моделями по сравнению с натурными данными. Эти расхождения обусловлены неучетом инфильтрации в расчетах, поскольку в начале паводка недонасыщенный влагой грунт интенсивно впитывает осадки, чем замедляет продвижение паводковой волны и ее интенсивность.

Наиболее высокий пик (325 м3/с) пришелся на третью волну из-за усиления интенсивности осадков (>20 мм/ч в течение 3 ч), смоделированный STREAM 2D максимальный расход воды составил 320 м3/с, по модели KW-GIUH – 356 м3/с. Время прохождения пика по модели KW-GIUH совпадает с фактическим (при шаге моделирования 1 ч), по модели STREAM 2D отстает на ~1 ч.

В целом модели удовлетворительно описывают динамику паводка. Разница максимальных расходов наиболее высоких паводков, полученных по обеим моделям, составляет 5–10% по сравнению с данными наблюдений, что лежит в пределах точности оценки самого максимального расхода в полевых условиях. Модель KW-GIUH несколько лучше описывает время прохождения пика, тогда как модель STREAM 2D более точно описывает максимальные расходы и кривую спада.

Прогнозный расчет паводков 24–25 октября 2018 г. моделью KW-GIUH

23 октября 2018 г. был выполнен прогноз паводка на р. Западный Дагомыс по прогностическим осадкам базовой модели Гидрометцентра России COSMO-Ru7, экстраполированным в южную окрестность АМС Солох-Аул. На момент выпуска прогноза для водосбора р. Западный Дагомыс была откалибрована только модель KW-GIUH на паводке 25 июня 2015 г. При шероховатости русла и склонов, равной 0.03 и 0.1, максимальный расход воды (Q = 229 м3/с) ожидался в 19–20 ч 24 октября.

Сравнение сумм прогностических и измеренных осадков на метеостанции Солох-Аул (рис. 5) показало высокую воспроизводимость синоптической ситуации метеорологической моделью COSMO-Ru7. Согласно прогнозу, с 22 ч 23 октября по 23 ч 25 октября ожидалась сумма осадков 132.5–183.8 мм в окрестностях АМС Солох-Аул, фактической слой на АМС составил 208.9 мм.

Рис. 5.

Сопоставление прогностических по модели COSMO-Ru7 (1) и фактических осадков 23–25 октября на АМС Солохаул (2), а также спрогнозированных по модели KW-GIUH расходов воды по прогностическим осадкам (3), расчетных по фактическим осадкам (4) и фактических расходов воды на ГП р. Западный Дагомыс – Дагомыс (5).

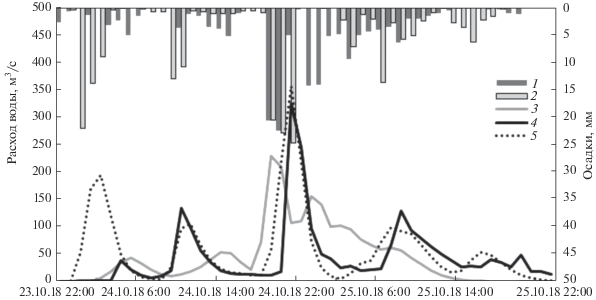
Фактический максимальный расход воды в Дагомысе по результатам нивелировки меток высоких вод был оценен в 325 м3/с. Отметки опасного явления не были превышены, расход воды проходил по краю бровок русла. Прогностический расход KW-GIUH на основе прогностических осадков COSMO-Ru7 занизил максимальный расход на ~30%, что было связано с формой плювиограммы: очень сильные осадки интенсивностью >20 мм/ч прогнозировались в течение 2 ч, тогда как фактически они продолжались 3 ч. Многопиковый характер интенсивности дождя и вызванного им паводка был предсказан верно. Максимальный прогностический расход воды опередил наблюденный на 2 ч.

В случае идеального прогноза интенсивности осадков максимальный расход был бы рассчитан по модели KW-GIUH с завышением на 30 м3/с (Qрасч на рис. 5).

Первый опыт прогноза гидрографа выявил несколько направлений дальнейшего улучшения прогноза: (1) необходимость максимально учитывать все возможные варианты хода осадков на основе полного массива сеточных осадков по основным прогностическим метеорологическим моделям; (2) развитие методов моделирования для рек с отсутствием наблюдений за стоком воды с переносом параметров моделей с изученных на неизученные водосборы; (3) установление зависимостей между накоплением критической суммы осадков и событиями наводнений на реках Кавказа.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ КАТАСТРОФИЧЕСКОГО ПАВОДКА 6–7 ИЮЛЯ 2012 г. НА ВОДОСБОРЕ р. АДАГУМ

Общие сведения. Исходные данные

Другим объектом моделирования был водосбор р. Адагум выше г. Крымска, площадь которого составляет 326 км2. Численная модель строилась на водосбор р. Адагум выше г. Крымска до створа железнодорожного моста, где задавалась выходная граница расчетной области. Моделирование проводилось для “бытовых” условий водосбора и при наличии водохранилищ-ловушек, перехватывающих часть стока.

Исходные данные для моделирования следующие:

высотные отметки HydroSHEDS;

часовой ход осадков на метеостанциях Крымск и Новороссийск за период с 06.07.2012 по 07.07.2012;

предполагаемое местоположение створов 14-ти водохранилищ-ловушек.

В ночь с 6 на 7 июля на метеостанции Новороссийск выпало 275 мм осадков, на метеостанции Крымск было измерено 156 мм. Это максимальные суточные суммы осадков, наблюдавшиеся за всю историю наблюдений на этих пунктах. В связи с большой неравномерностью осадков было решено выполнить расчеты стока с водосбора р. Адагум на основе осредненных данных по обеим метеостанциям.

Формирование цифровой модели рельефа

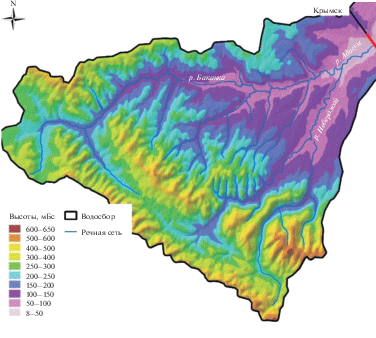
ЦМР водосбора построена на основе матрицы высот HydroSHEDS аналогично водосбору р. Западный Дагомыс. Принятая пороговая величина площади водосбора для образования постоянного водотока для р. Адагум – 1.3 км2. ЦМР водосбора р. Адагум в “бытовых” условиях представлена на рис. 6.

Рис. 6.

ЦМР водосбора р. Адагум.

Для варианта рельефа с водохранилищами-ловушками технология создания ЦМР следующая. По данным HydroSHEDS средствами ArcGIS строилась поверхность TIN, и проводилась локальная корректировка поверхности в створах водохранилищ-ловушек. Отметки гребней плотин назначались следующим образом: на рельефе в месте расположения створа будущей плотины определялись минимальные отметки, и к ним прибавлялась высота плотины, равная 10 и 20 м. Отметки уровня воды в водохранилищах принимались равными отметкам гебней плотин, по этим данным строилась еще одна поверхность TIN уровней воды. Далее выполнялось сопряжение двух поверхностей TIN базового рельефа уровней воды в водохранилищах; таким образом, были получены контуры водохранилищ. Исходные параметры водохранилищ-ловушек приведены в табл. 1. Площади и объемы определены средствами ArcGIS при уровне воды, соответствующем проектным отметкам гребней плотин.

Таблица 1.  

Исходные параметры водохранилищ-ловушек с плотинами высотой 10 и 20 м

Створы Отметки гребня плотин Площади, тыс. м2 Объем, млн м3
плотины высотой 10 м плотины высотой 20 м разница плотины высотой 10 м плотины высотой 20 м разница
1 220 111.12 320.34 209.22 0.50 2.52 2.03
2 190 224.89 468.11 243.22 1.09 4.39 3.30
3 250 23.83 66.05 42.22 0.07 0.43 0.36
4 163 63.27 181.87 118.59 0.22 1.31 1.09
5 166 44.33 172.94 128.61 0.13 1.04 0.90
6 141 81.23 277.08 195.85 0.30 1.81 1.51
7 201 51.98 149.64 97.66 0.18 1.07 0.89
8 172 63.98 177.52 113.54 0.23 1.34 1.11
9 204 14.11 69.06 54.95 0.05 0.37 0.32
10 147 23.38 84.00 60.62 0.06 0.54 0.48
11 195 34.35 95.39 61.04 0.10 0.61 0.51
12 171 85.77 1032.77 946.99 0.28 9.49 9.21
13 143 134.98 353.88 218.90 0.51 2.82 2.31
14 240 14.68 26.88 12.21 0.07 0.19 0.12
Сумма   971.90 3475.53 2503.63 3.79 27.93 24.14

Суммарная площадь водохранилищ-ловушек при проектном уровне, образованных плотинами высотой 10 м, составляет ~0.3% общей площади водосбора, при плотинах высотой 20 м – 1.07%. Проектный объем водохранилищ-ловушек с плотинами высотой 20 м превышает объем водохранилищ с плотинами высотой 10 м более чем в 7 раз.

Схематизация модели STREAM 2D CUDA

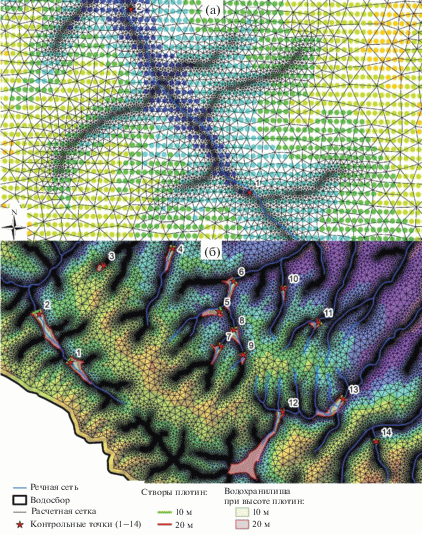
Для существующих условий рельефа (без водохранилищ) и наличия двух вариантов водохранилищ-ловушек строилась единая численная модель. Для ее построения применялась треугольная расчетная сетка нерегулярной структуры, сгущенная к руслам рек, и более редкая – к краям водосбора. Расчетная сетка содержит 214 898 ячеек с длинами сторон от 15 до 250 м. В модели построена одна расчетная граница на выходе в створе железнодорожного моста выше г. Крымска. Назначенные коэффициенты шероховатости по Маннингу – в руслах рек n = 0.03, на пойме n = 0.1 – такие же, как и для водосбора р. Западный Дагомыс. В модели с водохранилищами-ловушками на расчетной области в местах их расположения дополнительно задавались 14 контрольных точек для фиксации расчетных параметров во время счета. Фрагменты расчетной сетки приведены на рис. 7. Данные о рельефе переносились в центры ячеек расчетной сетки методом гармонической (несибсоновской) интерполяции ЦМР [14].

Рис. 7.

Фрагменты расчетной сетки модели STREAM 2D CUDA и ЦМР водосбора р. Адагум для существующих условий рельефа (а) и наличия водохранилищ-ловушек (б).

Результаты расчетов существующих условий рельефа водосбора р. Адагум

Моделирование стока в существующих условиях рельефа водосбора р. Адагум выполнялось на основе плювиограмм с метеостанций Крымск и Новороссийск за период с 06 по 07 июля 2012 г., а также по осредненным осадкам. Осадки распределялись равномерно по всей площади бассейна. Моделируемый временнóй интервал составил 48 ч.

На выходной границе модели (в створе железнодорожного моста) задавалось условие связи расходов и уровней воды: Q = f(H), – оно сформировано приближенно с учетом фактических данных об уровнях воды в створе моста в ходе паводка 2012 г.

По результатам расчетов построены гидрографы расхода в выходном створе модели (створ железнодорожного моста выше г. Крымска). Ниже представлено сопоставление этих гидрографов с расчетами в [2] и расчетами по модели KW-GIUH [6, 17] (рис. 8).

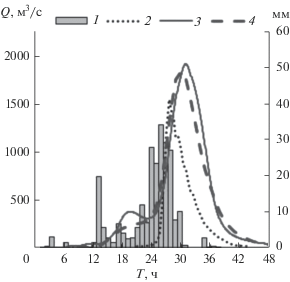
Рис. 8.

Гидрографы расхода с водосборной площади р. Адагум в створе железнодорожного моста, полученные по различным расчетным моделям. 1 – осредненные суммы осадков, 2 – расчет по модели [2], 3 – расчет по модели STREAM 2D, 4 – расчет по модели KW-GIUH.

Анализ результатов расчетов в существующих условиях показал следующее.

Объемы стока за паводок по моделям STREAM 2D и KW-GIUH совпадают (212 мм), а по модели SWMM [2] существенно меньше (91 мм), что, по-видимому, связано с учетом в последней влагопотерь на инфильтрацию в почву. Поскольку перед “пиковыми” осадками сильный дождь шел непрерывно более 12 ч, такие влагопотери представляются завышенными. По оценкам В.Ю. Георгиевского и Ю.Ю. Ткаченко (с. 21 в [4]), выполненныx по расчету водного баланса Варнавинского водохранилища с учетом притока р. Абин, слой стока в бассейне р. Адагум к г. Крымску за 6–7 июля 2012 г. составил 122 мм. Вероятно, слой стока в приведенных расчетах был завышен. В дальнейшем необходим учет потерь осадков за счет задания эффективных осадков для моделей STREAM 2D и KW-GIUH.

Гидрографы расходов и сами максимальные расходы по моделям STREAM 2D и KW-GIUH очень близки (1900 и 1840 м3/с соответственно, но при разных коэффициентах шероховатости), по модели SWMM несколько меньше (1540 м3/с), что объясняется, в частности, существенно меньшим объемом стока.

Время прохождения пика (между 4 и 5 ч ночи 7 июля, или 27 ч от начала расчета) достаточно точно получено моделью SWMM, модель KW-GIUH задерживает пик на 2 ч, модель STREAM 2D задерживает пик на 3 ч. Последний результат может частично объясняться тем, что в модели STREAM 2D учитывается подпор от железнодорожной насыпи, расположенной в замыкающем створе модели, в силу чего происходят аккумуляция части расхода выше створа моста и задержка пика.

Модель SWMM совсем не дает стока в первые 12 ч паводка, когда осадки уже достаточно интенсивные.

Результаты расчетов водохранилищ-ловушек

Поскольку модель кинематической волны не позволяет учитывать влияние подпора и процесс наполнения водохранилищ, расчеты проводились только на модели STREAM 2D CUDA. Рассматривались нерегулируемые плотины высотой 10 и 20 м.

Результаты расчетов для вариантов нерегулируемых плотин высотой 10 и 20 м представлены в табл. 2, объемы водохранилищ вычислены средствами ArcGIS при уровнях воды в водохранилищах, полученных в расчетах. Общий объем накопленной в водохранилищах-ловушках воды при плотинах 20 м почти в 5 раз превышает суммарный объем при плотинах 10 м. Наполнение водохранилищ-ловушек с плотинами высотой 20 м происходит через 30–33 ч от начала расчетного времени или через 6–9 ч после пика дождевых осадков. С плотинами высотой 10 м наполнение водохранилищ-ловушек происходит ранее – уже через 25–26 ч от начала расчетного времени, или через 1–2 ч от пика осадков.

Таблица 2.  

Результаты расчетов для вариантов нерегулируемых плотин высотой 10 и 20 м

Створы Плотины высотой 10 м Плотины высотой 20 м
проектные отметки гребня плотин параметры водохранилищ проектные отметки гребня плотин параметры водохранилищ
уровень воды по расчету объем воды при расчетном уровне уровень воды по расчету объем воды при расчетном уровне
1 210 209.73 0.47 220 216.37 1.53
2 180 177.91 0.68 190 180.57 1.20
3 240 239.81 0.07 250 243.50 0.14
4 153 153.01 0.22 163 162.81 1.28
5 156 155.42 0.11 166 164.23 0.76
6 131 130.50 0.26 141 137.08 0.94
7 191 190.14 0.14 201 199.69 0.89
8 162 161.49 0.21 172 164.28 0.38
9 194 193.99 0.05 204 204.00 0.37
10 137 136.65 0.06 147 146.50 0.50
11 185 184.40 0.09 195 191.85 0.37
12 161 161.07 0.28 171 167.93 6.52
13 133 133.17 0.51 143 138.04 1.38
14 230 229.75 0.06 240 240.00 0.19
Сумма     3.19     16.45

Зависимость максимальных расходов воды в замыкающем створе от суммарного фактического объема водохранилищ (с учетом частичного наполнения некоторых из них) имеет линейный характер (рис. 9). Нулевой объем водохранилищ соответствует бытовым условиям.

Рис. 9.

График зависимости максимальных расходов Q в выходном створе от суммарного объема воды W, аккумулируемого в водохранилищах-ловушках.

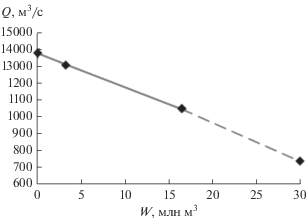
По проведенным расчетам можно сделать вывод о том, что водохранилища-ловушки с высотой плотин 20 м оказались более эффективными в сравнении с плотинами 10 м и могут обеспечить срезку максимального расхода на 30%, но следует более детально проработать этот вопрос о расположении створов плотин, чтобы максимально использовать номинальный объем водохранилищ. Кроме того, необходимо иметь в виду потенциальную опасность прорыва плотин вследствие переполнения водохранилища и размыва сооружения. Такие неоднократные случаи известны в мире, в Краснодарском крае в 2002 г. произошел прорыв плотины в Дюрсо вследствие очень сильных осадков и быстрого переполнения водоема. Гидродинамические условия прорыва были воспроизведены в работе [19] с использованием модели STREAM 2D.

ВЫВОДЫ

Для двух горных водосборов выполнено численное моделирование быстроразвивающихся дождевых паводков с применением модели STREAM 2D CUDA, основанной на численном решении двухмерных уравнений мелкой воды по оригинальному алгоритму, и модели единичного гидрографа KW-GIUH, основанной на уравнении кинематической волны. Получено хорошее совпадение рассчитанных гидрографов между собой и с натурными данными.

В рассмотренных авторами задачах по прогнозным расчетам быстроразвивающихся паводков проявилось некоторое преимущество модели STREAM 2D, которое заключается в возможности расчета по ней не только расходов воды, но и уровней водной поверхности как в заданных створах, так и по площади водосбора, а также в учете подпора от искусственных и естественных препятствий и аккумуляции части расхода в водохранилищах. С другой стороны, модель KW-GIUH оказалась менее чувствительной к точности задания водосборной поверхности и гораздо более быстрой по времени выполнения расчета. Время расчета гидрографа паводка для рассмотренных задач на персональном компьютере составляет ~1 ч для STREAM 2D CUDA и <1 мин для KW-GIUH.

Достаточно близкие к наблюденным результаты моделирования гидрографов показывают, что при наличии оперативных данных об осадках с часовым или более высоким разрешением возможно прогнозирование расходов и уровней воды в требуемых створах с заблаговременностью, равной времени добегания (до нескольких часов в рассматриваемых случаях). При наличии оперативного количественного прогноза осадков проверенного качества возможно прогнозирование расходов и уровней воды быстроразвивающихся паводков с заблаговременностью метеорологического прогноза.

Список литературы

  1. Алексеевский Н.И., Магрицкий Д.В., Колтерманн П.К., Торопов П.А., Школьный Д.И., Белякова П.А. Наводнения на Черноморском побережье Краснодарского края // Вод. ресурсы. 2016. Т. 43. № 1. С. 3–17.

  2. Болгов М.В., Коробкина Е.А., Осипова Н.В. и др. Предотвращение катастрофических паводков и обеспечение безопасности территории Крымского района Краснодарского края. М.: ИВП РАН, 2013. 34 с.

  3. Вишневская И.А., Десинов Л.В., Долгов С.В., Коронкевич Н.И., Шапоренко С.И., Киреева М.Б., Фролова Н.Л., Рец Е.П., Голубчиков С.Н. Географо-гидрологическая оценка наводнений в российском Причерноморье // Изв. РАН. Сер. геогр. 2016. № 1. С. 131–146.

  4. Катастрофический паводок в бассейне р. Адагум 6–7 июля 2012 г. и его причины. 2012. 42 с. [Электронный ресурс] http://meteoweb.ru/biblio/27.pdf

  5. Котляков В.М., Лихачева Э.А., Десинов Л.В., Долгов С.В., Коронкевич Н.И., Маккавеев А.Н., Медведев А.А., Рудаков В.А. Наводнение 6–7 июля 2012 года в городе Крымске // Изв. РАН. Сер. геогр. 2012. № 6. С. 80–88.

  6. Ли К.Т., Чен Н.К., Гарцман Б.И., Бугаец А.Н. Современная версия модели единичного гидрографа и ее применение в Тайване и России // География и природ. ресурсы. 2009. № 1. С. 144–151.

  7. Ресурсы поверхностных вод СССР. Гидрологическая изученность. Т. 9. Закавказье и Дагестан. Вып. 1. Западное Закавказье / Под ред. Т.Н. Джапаридзе. Л.: Гидрометеоиздат, 1964. 225 с.

  8. Рожков А. Заявленный страховщикам ущерб от наводнения на Кубани превысил 1 млрд руб. // Ведомости: газета. 2012. 6 августа. № 145 (3159).

  9. Свид. 2017660266 Российская Федерация. Свидетельство о государственной регистрации программ для ЭВМ. Программный комплекс STREAM 2D CUDA для расчета течений, деформаций дна и переноса загрязнений в открытых потоках с использованием технологий Compute Unified Device Architecture (на графических процессорах NVIDIA) / Алексюк А.И., Беликов В.В. № 2 017 617 252 заявл. 21.07.2017. Опубл. 20.09.2017. Реестр программ для ЭВМ. 1 с.

  10. Ткаченко Ю.Ю., Шержуков Е.Л. Опыт создания систем краткосрочного прогноза угроз гидрологического характера // Вод. хоз-во России: проблемы, технологии, управление. 2014. № 3. С.75–82.

  11. Alekseevskiy N.I., Krylenko I.N., Belikov V.V., Kochetkov V.V., Norin S.V. Numerical Hydrodynamic Modeling of Inundation in Krymsk on 6–7 July 2012 // Power Technology and Engineering. 2014. V. 48. Is. 3. P. 179–186. https://doi.org/10.1007/s10749-014-0505-y

  12. Aleksyuk A.I., Belikov V.V. Simulation of shallow water flows with shoaling areas and bottom discontinuities // Comput. Math. Math. Phys. 2017. V. 57. № 2. P. 318–339.

  13. Aleksyuk A.I., Belikov V.V. The uniqueness of the exact solution of the Riemann problem for the shallow water equations with discontinuous bottom // J. Comp. Phys. 2019. V. 390. P. 232–248. https://doi.org/10.1016/j.jcp.2019.04.001

  14. Belikov V.V., Semenov A.Y. Non-Sibsonian interpolation on arbitrary system of points in Euclidean space and adaptive isolines generation // Appl. Numer. Math. 2000. V. 32. № 4. P. 371–387.

  15. Gonchukov L.V., Bugaets A. N., Gartsman B.I., Lee K.T. Weather Radar Data for Hydrological Modelling: An Application for South of Primorye Region, Russia // Water Resour. 2019. V. 46. Suppl. 2. P. S25–S30.

  16. James W., Huber W.C. User System Models User’s guide to SWMM. 2003. 700 p.

  17. Lee K.T., Yen B.C. Geomorphology and kinematic-wave based hydrograph deviation // J. Hydraul. Eng. 1997. V. 123. P. 73–80.

  18. Norin S.V., Belikov V.V., Aleksyuk A.I. Simulating Flood Waves in Residential Areas // Power Technol. Engineering. 2017. V. 51. № 1. P. 52–57. https://doi.org/10.1007/s10749-017-0782-3

  19. Vasil’eva E.S., Aleksyuk A.I., Belyakova P.A., Fedorova T.A., Belikov V.V. Numerical Modeling of the Behavior of a Destructive Rain Flood on a Mountain River // Water Resour. 2019. V. 46. Suppl. 1. P. 43–55.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Водные ресурсы

Архивы выпусков Информация о журнале Отправить рукопись в журнал