1. На главную
  2. Электронные версии
  3. Водные ресурсы
  4. T. 48, № 5, 2021

Водные ресурсы, 2021, T. 48, № 5, стр. 537-546

Геофильтрация в окрестности вертикальной циркуляционной скважины, обладающей скин-эффектом

П. Е. Морозов *

Институт механики и машиностроения ФИЦ “Казанский научный центр РАН”
420111 Казань, Россия

* E-mail: morozov@imm.knc.ru

Поступила в редакцию 22.01.2020
После доработки 08.02.2021
Принята к публикации 30.03.2021

Полный текст (PDF)

Аннотация

Рассмотрена фильтрация воды в окрестности вертикальной циркуляционной скважины. Представлены решения задач установившегося и неустановившегося притока к вертикальной циркуляционной скважине в анизотропном пласте с учетом влияния скин-эффекта и объемов нагнетательного и откачивающего интервалов. На основе схемы Мятиева–Гиринского получено аналитическое решение задачи установившегося течения воды в окрестности вертикальной циркуляционной скважины в пласте, состоящем из двух проницаемых горизонтальных пропластков, разделенных слабопроницаемым слоем.

Ключевые слова: вертикальная циркуляционная скважина, дипольное опробование, анизотропный пласт, скин-эффект, двухслойный пласт, схема Мятиева–Гиринского.

ВВЕДЕНИЕ

Метод дипольного (дуплетного) опробования скважин ‒ один из эффективных для определения вертикальной проницаемости анизотропных водоносных горизонтов [3, 20]. При дипольном опробовании опытная скважина оборудуется двумя фильтрами, изолированными друг от друга, например с помощью надувных пакеров. Через один фильтр (откачивающий интервал) проводится откачка воды с постоянным расходом, а через другой фильтр (нагнетательный интервал) ‒ закачка с таким же расходом. В результате в окрестности скважины возникает вертикальное циркуляционное течение. По величине изменения напора (давления) в нагнетательном и откачивающем интервалах скважины определяется горизонтальная и вертикальная проницаемость пласта. В других методах интервальных испытаний пласта, используемых для определения анизотропии проницаемости, например при многоуровневых экспресс-откачках и вертикальном гидропрослушивании [2, 12, 14, 21, 24], замеры напора (давления) проводятся в активном и наблюдательном интервалах скважины.

В основе метода дипольного опробования скважин, предложенного в [20], – аналитическое решение задачи неустановившегося притока воды к вертикальной циркуляционной скважине в бесконечном по простиранию анизотропном пласте. Решение задачи получено методом суперпозиции решения Хантуша для откачивающей и нагнетательной несовершенных скважин в анизотропном пласте с перетеканием [8, 20, 23]. Аналогичное решение представлено в работе [34], полученное с использованием преобразования Лапласа и конечного косинус-преобразования Фурье. Аналитическая модель дипольного течения в бесконечном и полубесконечном анизотропных пластах предложена в [39]. В [15] предложен ассиметричный метод дипольного опробования на основе аналитического решения задачи притока к циркуляционной скважине с откачивающим и нагнетательным интервалами разной длины. В [33] предложена приближенная аналитическая модель, описывающая нелинейное течение в напорном анизотропном пласте с вертикальной циркуляционной скважиной.

Метод дипольного опробования в сочетании с индикаторными исследованиями профильно-анизотропных пластов рассмотрен в [3, 7, 31]. В экспериментальной схеме “вертикальный дуплет”, предложенной в работе [3], используются либо две несовершенные скважины с фильтрами, расположенными один над другим, либо одна скважина, в которой создаются два изолированных друг от друга интервала с независимо задаваемыми режимами откачки-нагнетания. Для интерпретации индикаторных экспериментов используется расчетное время перемещения индикаторного фронта вдоль главной (кратчайшей) линии тока, связывающей нагнетательный интервал скважины с откачивающим [3, 7].

Если откачивающий и нагнетательный интервалы скважины имеют равную длину и располагаются симметрично относительно центра напорного анизотропного пласта, то достаточно рассмотреть фильтрацию в верхней или нижней частях пласта с постоянным (нулевым) напором в центральной горизонтальной плоскости. В этом случае получаем эквивалентную задачу откачки из несовершенной скважины с постоянным дебитом в анизотропном пласте с плановыми границами I и II рода, решению которой посвящено большое число работ [4, 6, 8, 11, 13, 38]. Наиболее общее решение данной задачи с учетом равномерного распределения напора по длине фильтра, емкости скважины и скин-эффекта конечной толщины получено в работе [25].

В работах [19, 40] на практических примерах продемонстрировано, что оценки фильтрационных параметров неоднородных пластов, полученные методом дипольного опробования скважин и другими методами, в частности многоуровневыми экспресс-откачками, коррелируются между собой. С целью получения более достоверных оценок фильтрационных параметров в [19] использовано численное моделирование течения в многослойном пласте и нелинейный регрессионный анализ на основе замеров напоров как в циркуляционной скважине, так и в близлежащих пьезометрах.

В [36] на основе численного 2D-моделирования установившегося циркуляционного течения в окрестности вертикальной скважины в слоистом пласте исследовано влияние положения и проводимости слоев на оценку эквивалентной анизотропии пласта. Показано, что один из факторов, существенно искажающий оценку эквивалентной анизотропии, – скин-эффект. Более того, при наличии высокопроницаемой зоны вокруг скважины могут возникнуть утечки и часть потока будет перемещается из одного интервала в другой лишь в этой зоне [20, 26].

Вертикальные циркуляционные скважины нашли применение в методах внутрипластовой очистки загрязненных грунтовых вод [17, 27]. В этих методах вода с помощью насоса откачивается через один фильтр скважины и после очистки закачивается обратно в пласт через другой фильтр. Созданная таким образом вертикальная циркуляция в водоносном горизонте продолжается до тех пор, пока не будут достигнуты цели санации. Кроме этого, вертикальные циркуляционные скважины используются в геотермальных системах отопления и кондиционирования, где теплоносителем служит грунтовая вода [23, 28, 29, 33, 34].

В работе [17] на основе численного 3D-моделирования проведено исследование установившегося течения в окрестности одиночных циркуляционных скважин и рядных систем циркуляционных скважин в условиях взаимодействия с естественным потоком подземных вод. В [18] предложена аналитическая модель стационарного течения воды в системе двух циркуляционных скважин и исследовано влияние дебита и анизотропии проницаемости пласта на зону охвата и величину перетока воды между скважинами. Проблеме 3D-визуализации установившегося течения в окрестности вертикальной циркуляционной скважины при наличии естественного потока подземных вод посвящена работа [35].

В работе автора [22] получено аналитическое решение задачи неустановившегося и установившегося притока жидкости к горизонтальной циркуляционной скважине в анизотропном пласте постоянной мощности. В случае симметричного расположения откачивающего и нагнетательного интервалов относительно центра скважины предложена относительно простая формула для определения продуктивности горизонтальной циркуляционной скважины.

При аналитическом решении задач притока жидкости к несовершенным скважинам возникают определенные трудности, связанные с заданием нелокальных граничных условий или смешанных граничных условий на стенке скважины для учета равномерного распределения напора (давления) в интервале вскрытия [5, 9, 10, 37]. В работах [4, 5, 10, 25] решение таких задач сводится к системе интегральных уравнений для распределения притока в интервале вскрытия, которая затем решается числено.

В настоящей работе получено полуаналитическое решение задачи установившегося и неустановившегося притока воды к вертикальной циркуляционной скважине в анизотропном пласте с учетом скин-эффекта и влияния объемов нагнетательного и откачивающего интервалов. При предположении равномерности притока воды по длине интервалов дано приближенное аналитическое решение задачи. На основе схемы Мятиева–Гиринского получено аналитическое решение задачи установившегося течения воды в окрестности вертикальной циркуляционной скважины в двухслойном пласте со слабопроницаемым прослоем.

ЦИРКУЛЯЦИОННАЯ СКВАЖИНА В АНИЗОТРОПНОМ ПЛАСТЕ

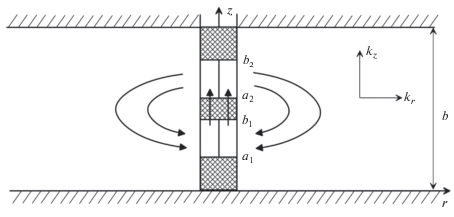
Рассматривается задача притока воды к вертикальной циркуляционной скважине в неограниченном по простиранию анизотропном пласте с непроницаемой кровлей и подошвой (рис. 1). Через нижний откачивающий интервал проводится отбор воды с постоянным дебитом Q, а через верхний нагнетательный интервал ‒ нагнетание воды с постоянным расходом −Q. Полагается, что напор по длине интервалов распределен равномерно. Задача состоит в определении функции изменения напора $h\left( {r,z,t} \right)$ в области течения $r > {{r}_{w}}$, $0 \leqslant z \leqslant b$ и функций изменения уровня si(t) в откачивающем и нагнетательном интервалах скважины при $t > 0$. В безразмерном виде изменение напора в окрестности вертикальной циркуляционной скважины описывается уравнением пьезопроводности:

(1)
$\frac{1}{{{{r}_{d}}}}\frac{\partial }{{\partial {{r}_{d}}}}\left( {{{r}_{d}}\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right) + \frac{1}{{b_{d}^{2}}}\frac{{{{\partial }^{2}}{{h}_{d}}}}{{\partial z_{d}^{2}}} = \frac{{\partial {{h}_{d}}}}{{\partial {{t}_{d}}}}$
с начальным
(2)
${{h}_{d}}\left( {{{r}_{d}},{{z}_{d}},0} \right) = 0$
и граничными условиями
(3)
${{h}_{d}}\left( {\infty ,{{z}_{d}},{{t}_{d}}} \right) = 0,$
(4)
${{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{z}_{d}}}}} \right|}_{{{{z}_{d}} = 0}}} = 0,\,\,\,\,{{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{z}_{d}}}}} \right|}_{{{{z}_{d}} = 1}}} = 0,$
(5)
$\begin{gathered} {{\left. {\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right|}_{{{{r}_{d}} = 1}}} = 0,\,\,\,\,0 \leqslant {{z}_{d}} < {{\alpha }_{1}}, \\ {{\beta }_{1}} < {{z}_{d}} < {{\alpha }_{2}},\,\,\,\,{{\beta }_{2}} < {{z}_{d}} \leqslant 1, \\ \end{gathered} $
(6)
$\int\limits_{{{\alpha }_{i}}}^{{{\beta }_{i}}} {{{q}_{d}}\left( {\xi ,{{t}_{d}}} \right)d\xi } = {{\left( { - 1} \right)}^{{i + 1}}} - {{C}_{{id}}}\frac{{\partial {{h}_{{id}}}\left( {{{t}_{d}}} \right)}}{{\partial {{t}_{d}}}},\,\,\,\,i = 1,2,$
(7)
$\begin{gathered} {{s}_{{id}}}\left( {{{t}_{d}}} \right) = {{h}_{d}}\left( {1,{{z}_{d}},{{t}_{d}}} \right) + {{S}_{i}}{{q}_{d}}\left( {{{z}_{d}},{{t}_{d}}} \right), \\ {{\alpha }_{i}} \leqslant {{z}_{d}} \leqslant {{\beta }_{i}},\,\,\,\,i = 1,2, \\ \end{gathered} $
где ${{h}_{d}} = \frac{{2\pi {{k}_{r}}bh}}{Q}$, ${{s}_{{id}}} = \frac{{2\pi {{k}_{r}}b{{s}_{i}}}}{Q}$, ${{t}_{d}} = \frac{{{{k}_{r}}t}}{{\eta {\kern 1pt} *{\kern 1pt} r_{w}^{2}}}$, ${{r}_{d}} = \frac{r}{{{{r}_{w}}}}$, ${{z}_{d}} = \frac{z}{h}$, ${{b}_{d}} = \frac{b}{{{{r}_{w}}}}\sqrt {\frac{{{{k}_{r}}}}{{{{k}_{z}}}}} $, ${{C}_{{id}}} = \frac{{{{C}_{i}}}}{{2\pi b\eta {\text{*}}r_{w}^{2}}}$, ${{\alpha }_{i}} = \frac{{{{a}_{i}}}}{h}$, ${{\beta }_{i}} = \frac{{{{b}_{i}}}}{h}$, $q\left( {{{z}_{d}},{{t}_{d}}} \right) = - {{\left. {\left( {{{r}_{d}}\frac{{\partial {{h}_{d}}}}{{\partial {{r}_{d}}}}} \right)} \right|}_{{{{r}_{d}} = 1}}}$,

Рис. 1.

Схема вертикальной циркуляционной скважины.

h ‒ напор; kr, kz ‒ коэффициенты фильтрации в горизонтальном и вертикальном направлениях; $\eta {\kern 1pt} *$ ‒ коэффициент упругоемкости породы; b ‒ мощность пласта; rw ‒ радиус скважины; Ci ‒ коэффициент влияния объема i-го интервала; Si ‒ скин-эффект i-го интервала (индекс i = 1 соответствует откачивающему интервалу, i = 2 ‒ нагнетательному интервалу). Коэффициент влияния объема i-го интервала равен ${{C}_{i}} = {{V}_{i}}{{C}_{w}}{{\rho }_{w}}{\text{g\;}}$ (Vi ‒ объем интервала, Cw ‒ эффективная сжимаемость интервала (включает сжимаемость воды, сжимаемость испытательного оборудования), ${{\rho }_{w}}$ ‒ плотность воды, g ‒ ускорение свободного падения) [5, 12]. Скин-эффект Si характеризует дополнительное фильтрационное сопротивление в ближайшей к i-му интервалу зоне пласта [4, 5, 10]. При наличии вокруг i-го интервала кольцевой зоны с отличными фильтрационными свойствами скин-эффект – ${{S}_{i}} = \left[ {\left( {{{{{k}_{r}}} \mathord{\left/ {\vphantom {{{{k}_{r}}} {{{k}_{{si}}}}}} \right. \kern-0em} {{{k}_{{si}}}}}} \right) - 1} \right]\ln \left( {{{{{r}_{{si}}}} \mathord{\left/ {\vphantom {{{{r}_{{si}}}} {{{r}_{w}}}}} \right. \kern-0em} {{{r}_{w}}}}} \right)$, где rsi, ksi ‒ радиус и коэффициент фильтрации скин-зоны [12, 37].

Применяя к (1)‒(7) преобразование Лапласа по времени и конечное косинус-преобразование Фурье по координате zd [4, 5, 10, 25, 37], для безразмерного напора в пласте получим выражение:

(8)
$\begin{gathered} {{{\bar {h}}}_{d}}\left( {{{r}_{d}},{{z}_{d}},u} \right) = \sum\limits_{j = 1}^2 {\left[ {F\left( {{{r}_{d}},u} \right)\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{{\bar {q}}}_{d}}\left( {\xi ,u} \right)d\xi } } \right.} + \\ \left. { + \,\,2\sum\limits_{m = 1}^\infty {F\left( {{{r}_{d}},{{\lambda }_{m}}} \right){\kern 1pt} \cos {\kern 1pt} \left( {\pi m{{z}_{d}}} \right)\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{{\bar {q}}}_{d}}\left( {\xi ,u} \right)\cos \left( {\pi m\xi } \right)d\xi } } } \right], \\ \end{gathered} $
где u ‒ переменная преобразования Лапласа; ${{\lambda }_{m}} = u + {{\left( {\frac{{\pi m}}{{{{b}_{d}}}}} \right)}^{2}}$; $F\left( {x,y} \right) = \frac{{{{K}_{0}}\left( {x\sqrt y } \right)}}{{\sqrt y {{K}_{1}}\left( {\sqrt y } \right)}}$; ${{K}_{0}}\left( x \right)$ и ${{K}_{1}}\left( x \right)$ ‒ модифицированные функции Бесселя второго рода нулевого и первого порядка соответственно.

Приток воды и напор в откачивающем и нагнетательном интервалах скважины определяются из решения системы интегральных уравнений:

(9)
$\begin{gathered} {{{\bar {s}}}_{{id}}} = \sum\limits_{j = 1}^2 {\left[ {F\left( {1,u} \right)\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{{\bar {q}}}_{d}}\left( {\xi ,u} \right)d\xi } } \right.} + \\ \left. { + \,\,2\sum\limits_{m = 1}^\infty {F\left( {1,{{\lambda }_{m}}} \right){\kern 1pt} \cos {\kern 1pt} \left( {\pi m{{z}_{d}}} \right)\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{{\bar {q}}}_{d}}\left( {\xi ,u} \right){\kern 1pt} \cos {\kern 1pt} \left( {\pi m\xi } \right){\kern 1pt} d\xi } } } \right] + \\ + \,\,{{S}_{i}}{{{\bar {q}}}_{d}}\left( {{{z}_{d}},u} \right),\,\,\,\,{{\alpha }_{i}} \leqslant {{z}_{d}} \leqslant {{\beta }_{i}},\,\,\,\,i = 1,2, \\ \end{gathered} $
(10)
$\int\limits_{{{\alpha }_{i}}}^{{{\beta }_{i}}} {{{{\bar {q}}}_{d}}\left( \xi \right)d\xi } = \frac{{{{{\left( { - 1} \right)}}^{{i + 1}}}}}{u} - {{C}_{{id}}}u{{\bar {s}}_{{id}}},\,\,\,\,i = 1,2.$

Система интегральных уравнений (9)–(10) решается численно [4, 5]. Для этого нагнетательный и откачивающий интервалы скважины разбиваются на сегменты и полагается, что приток воды к каждому сегменту равномерный. В результате для определения изображений по Лапласу функций притока и изменения напора в интервалах скважины получаем систему линейных алгебраических уравнений с плотной матрицей. Для ее решения используется стабилизированный метод бисопряженных градиентов BiCGStab с предобусловливанием. Обратное преобразование Лапласа выполняется численно на основе алгоритма Стефеста [30].

Полагая в (9) и (10) $u \to 0$, что соответствует ${{t}_{d}} \to \infty $, после обратного преобразования Лапласа получим систему интегральных уравнений для определения функций притока и напора в интервалах при установившемся режиме течения:

(11)
$\begin{gathered} {{s}_{{id}}} = 2\sum\limits_{j = 1}^2 {\sum\limits_{m = 1}^\infty {\frac{{{{K}_{0}}\left( {{{\gamma }_{m}}} \right)}}{{{{\gamma }_{m}}{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\cos \left( {\pi m{{z}_{d}}} \right)} } \times \\ \times \,\,\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{q}_{d}}\left( \xi \right)\cos \left( {\pi m\xi } \right)d\xi } + {{S}_{i}}{{q}_{d}}\left( {{{z}_{d}}} \right),\,\,\,\,{{\alpha }_{i}} \leqslant {{z}_{d}} \leqslant {{\beta }_{i}}, \\ \end{gathered} $
(12)
$\int\limits_{{{\alpha }_{i}}}^{{{\beta }_{i}}} {{{q}_{d}}\left( \xi \right)d\xi } = {{\left( { - 1} \right)}^{{i + 1}}},\,\,\,\,i = 1,2,$
где ${{\gamma }_{m}} = \frac{{\pi m}}{{{{b}_{d}}}}$. Аналогично из (8) с учетом (12) получим выражения для установившегося поля напора в пласте и компонент скорости фильтрации:

(13)
$\begin{gathered} {{h}_{d}}\left( {{{r}_{d}},{{z}_{d}}} \right) = 2\sum\limits_{j = 1}^2 {\sum\limits_{m = 1}^\infty {\frac{{{{K}_{0}}\left( {{{r}_{d}}{{\gamma }_{m}}} \right)}}{{{{\gamma }_{m}}{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\cos \left( {\pi m{{z}_{d}}} \right) \times } } \\ \times \,\,\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{q}_{d}}\left( \xi \right)\cos \left( {\pi m\xi } \right)d\xi ,} \\ \end{gathered} $
(14)
$\begin{gathered} {{w}_{r}}\left( {{{r}_{d}},{{z}_{d}}} \right) = - \frac{Q}{{\pi {{r}_{w}}b}}\sum\limits_{j = 1}^2 {\sum\limits_{m = 1}^\infty {\frac{{{{K}_{1}}\left( {{{r}_{d}}{{\gamma }_{m}}} \right)}}{{{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\cos \left( {\pi m{{z}_{d}}} \right) \times } } \\ \times \,\,\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{q}_{d}}\left( \xi \right)\cos \left( {\pi m\xi } \right)d\xi } , \\ \end{gathered} $
(15)
$\begin{gathered} {{w}_{z}}\left( {{{r}_{d}},{{z}_{d}}} \right) = - \frac{{Q{{k}_{z}}}}{{{{b}^{2}}{{k}_{r}}}}\sum\limits_{j = 1}^2 {\sum\limits_{m = 1}^\infty {\frac{{m{{K}_{0}}\left( {{{r}_{d}}{{\gamma }_{m}}} \right)}}{{{{\gamma }_{m}}{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\sin \left( {\pi m{{z}_{d}}} \right)} } \times \\ \times \,\,\int\limits_{{{\alpha }_{j}}}^{{{\beta }_{j}}} {{{q}_{d}}\left( \xi \right)\cos \left( {\pi m\xi } \right)d\xi } . \\ \end{gathered} $

Допустим теперь, что распределение притоков по длине откачивающего и нагнетательного интервалов равномерное. Интегрируя (9) по ${{z}_{d}}$ с учетом (10), для средневзвешенных напоров в интервалах скважины получим выражения:

(16)
${{\bar {s}}_{{1d}}} = \frac{{{{U}_{1}}{{I}_{2}} - {{U}_{2}}{{Y}_{1}}}}{{{{I}_{1}}{{I}_{2}} - {{Y}_{2}}{{Y}_{1}}}},\,\,\,\,{{\bar {s}}_{{2d}}} = \frac{{{{U}_{2}}{{I}_{1}} - {{U}_{1}}{{Y}_{2}}}}{{{{I}_{1}}{{I}_{2}} - {{Y}_{2}}{{Y}_{1}}}},$
где ${{I}_{i}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 1 + {{C}_{{id}}}{{u}^{2}}\left( {{{{\bar {h}}}_{{i,i}}} + \frac{{{{S}_{i}}}}{{u{{l}_{i}}}}} \right)$; ${{Y}_{i}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} {{C}_{{id}}}{{u}^{2}}{{\bar {h}}_{{1,2}}}$; Ui = ${{\left( { - 1} \right)}^{{i + 1}}}{\kern 1pt} {\kern 1pt} \times $ $ \times \,\,\left( {{{{\bar {h}}}_{{i,i}}} - {{{\bar {h}}}_{{1,2}}} + \frac{{{{S}_{i}}}}{{u{{l}_{i}}}}} \right)$; ${{l}_{i}} = {{\beta }_{i}} - {{\alpha }_{i}}$; ${{\bar {h}}_{{i,j}}} = \frac{{F\left( {1,u} \right)}}{u} + \frac{2}{u}$ × $ \times \,\,\sum\limits_{m = 1}^\infty {\frac{{F\left( {1,{{\lambda }_{m}}} \right)}}{{{{\pi }^{2}}{{m}^{2}}}}{{\Psi }_{{i,m}}}{{\Psi }_{{j,m}}}} $; ${{\Psi }_{{i,m}}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{\sin \left( {\pi m{{\beta }_{i}}} \right){\kern 1pt} {\kern 1pt} \,\, - {\kern 1pt} {\kern 1pt} \,\,\sin \left( {\pi m{{\alpha }_{i}}} \right)}}{{{{l}_{i}}}}$; $i,j = $ 1, 2. Входящие в (16) выражения ${{\bar {h}}_{{i,i}}}$ определяют средневзвешенные напоры в интервалах без учета влияния их объема и скин-эффекта [4, 5], а ${{\bar {h}}_{{1,2}}} = {{\bar {h}}_{{2,1}}}$ ‒ взаимовлияние откачивающего и нагнетательного интервалов скважины.

Сжимаемость воды, заключенной в откачивающем и нагнетательном интервалах скважины, оказывает влияние на изменение напора в интервалах лишь в малые периоды времени после пуска скважины в работу. Поэтому, полагая в (16) C1 = = C2 = 0, получим

(17)
${{\bar {s}}_{{id}}} = {{\left( { - 1} \right)}^{{i + 1}}}\left( {{{{\bar {h}}}_{{i,i}}} - {{{\bar {h}}}_{{1,2}}} + \frac{{{{S}_{i}}}}{{u{{l}_{i}}}}} \right),\,\,\,\,i = 1,2.$

При установившемся режиме течения средневзвешенные напоры в откачивающем и нагнетательном интервалах скважины определяются выражениями

(18)
${{s}_{{id}}} = {{\left( { - 1} \right)}^{{i + 1}}}\left( {{{S}_{{ip}}} - {{h}_{{1,2}}}} \right),\,\,\,\,i = 1,2,$
где ${{S}_{{ip}}} = {{h}_{{i,i}}} + \frac{{{{S}_{i}}}}{{{{l}_{i}}}}$, ${{h}_{{i,j}}} = 2\sum\nolimits_{m = 1}^\infty {\frac{{F\left( {1,{{\gamma }_{m}}} \right)}}{{{{\pi }^{2}}{{m}^{2}}}}{{\Psi }_{{i,m}}}{{\Psi }_{{j,m}}}} $. Величины ${{S}_{{ip}}}$ имеют простой физический смысл суммарного скин-эффекта для вертикальной скважины с двойным видом несовершенства ‒ как по характеру, так и по степени вскрытия. Следует отметить, что если откачивающая и нагнетательная секции скважины имеют равную длину и симметрично расположены относительно центра пласта, то при отсутствии скин-эффекта (S1 = S2 = 0) получаем ${{s}_{{1d}}} = - {{s}_{{2d}}} = {{s}_{p}}$. Величина ${{s}_{p}}$ обратно пропорциональна фактору формы несовершенной скважины в безнапорном пласте, имеющим толщину 0.5b [4, 38].

При условии равномерного распределения притока воды по длине откачивающего и нагнетательного интервалов скважины выражения (13)‒(15) принимают следующий вид:

(19)
$\begin{gathered} {{h}_{d}}\left( {{{r}_{d}},{{z}_{d}}} \right) = \\ = \frac{2}{\pi }\sum\limits_{m = 1}^\infty {\frac{{{{K}_{0}}\left( {{{r}_{d}}{{\gamma }_{m}}} \right)}}{{{{\gamma }_{m}}m{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\cos \left( {\pi m{{z}_{d}}} \right)\left( {{{\Psi }_{{1,m}}} - {{\Psi }_{{2,m}}}} \right)} , \\ \end{gathered} $
(20)
$\begin{gathered} {{w}_{r}}\left( {{{r}_{d}},{{z}_{d}}} \right) = \\ = - \frac{Q}{{{{\pi }^{2}}{{r}_{w}}b}}\sum\limits_{m = 1}^\infty {\frac{{{{K}_{1}}\left( {{{r}_{d}}{{\gamma }_{m}}} \right)}}{{m{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\cos \left( {\pi m{{z}_{d}}} \right)\left( {{{\Psi }_{{1,m}}} - {{\Psi }_{{2,m}}}} \right)} , \\ \end{gathered} $
(21)
$\begin{gathered} {{w}_{z}}\left( {{{r}_{d}},{{z}_{d}}} \right) = \\ = - \frac{{Q{{k}_{z}}}}{{\pi {{b}^{2}}{{k}_{r}}}}\sum\limits_{m = 1}^\infty {\frac{{{{K}_{0}}\left( {{{r}_{d}}{{\gamma }_{m}}} \right)}}{{{{\gamma }_{m}}{{K}_{1}}\left( {{{\gamma }_{m}}} \right)}}\sin \left( {\pi m{{z}_{d}}} \right)\left( {{{\Psi }_{{1,m}}} - {{\Psi }_{{2,m}}}} \right)} . \\ \end{gathered} $

При равенстве длины интервалов скважины (l1 = l2) и отсутствии скин-эффекта (S1 = S2 = 0) выражения (17)‒(21) совпадают с решением из работы [31]. Если дополнительно предположить, что скважина имеет бесконечно малый радиус, тогда $F\left( {1,{{\gamma }_{m}}} \right)\sim {{K}_{0}}\left( {{{\gamma }_{m}}} \right)$ и выражения (17), (18) сводятся к известному решению задачи для напорного пласта [20, 32].

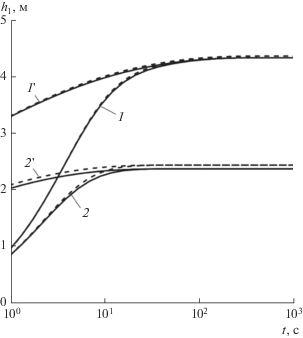
На рис. 2 приведены графики изменения напора в откачивающем интервале скважины, полученные на основе полуаналитического решения (9)‒(10) (сплошные линии) и приближенного аналитического решения (16) (пунктирные линии) при следующих исходных данных: b = 10 м, ${{r}_{w}}$ = 0.1 м, a1 = 2 м, b1 = 4 м, a2 = 8 м, b2 = 10 м, Q = = 10 м3/сут, kr = 1 × 10–5 м/c, $\eta {\kern 1pt} *$ = 1 × 10–4 1/м, С1 = С2 = 1 × 10–4 м2. Кривые 1 ', 2 ' на рис. 2 получены без учета влияния объемов откачивающего и нагнетательного интервалов скважины, т.е. при С1 = С2 = 0 (пунктирная линия 2 ' при S1 = S2 = 0 соответствует решению из работы [31]). Из рис. 2 видно, что анизотропия проницаемости пласта влияет на время выхода на стационарный режим.

Рис. 2.

Кривые изменения напора в откачивающем интервале скважины. Пласты: 1 ‒ анизотропный (kz = 1 × 10–6 м/c, S1 = S2 = 1); 2 ‒ изотропный (kz = = 1 × 10–5 м/c, S1 = S2 = 0); 1' ‒ анизотропный (C1 = = C2 = 0 м2); 2' ‒ изотропный (C1 = C2 = 0 м2).

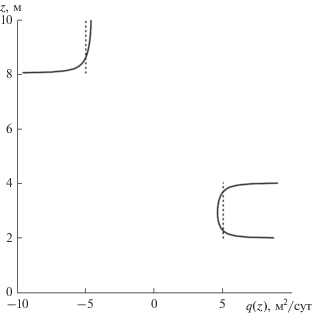
Сплошными линиями на рис. 3 обозначено установившееся распределение притока воды по длине откачивающего и нагнетательного интервалов скважины, полученное на основе решения системы интегральных уравнений (11)‒(12), а пунктирными линиями ‒ равномерное распределение притока. Расчеты показали, что с увеличением скин-эффекта происходит выполаживание профиля притока.

Рис. 3.

Распределение притока воды по длине откачивающего и нагнетательного интервалов скважины.

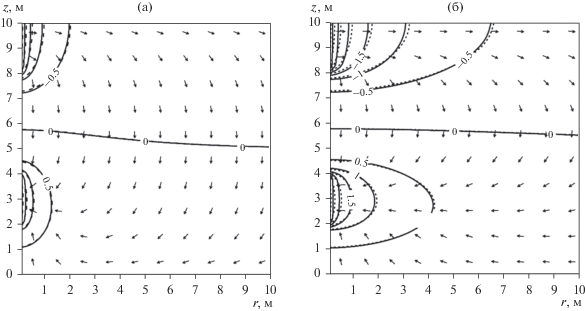
На рис. 4 приведено сопоставление стационарных полей напоров в изотропном и анизотропном пластах, полученных на основе решения интегральных уравнений (11)‒(13) (сплошные линии) и выражения (19) (пунктирные линии). Видно, что модели с равномерным распределением напора и равномерным распределением притока по длине интервалов приводят к практически идентичным картинам течения, за исключением ближайших к интервалам скважины зон пласта. Выражения (8), (13) и (19) могут быть использованы для определения понижения (повышения) напора в пьезометре или наблюдательной скважине, расположенной в окрестности вертикальной циркуляционной скважины.

Рис. 4.

Стационарное поле напоров в изотропном (а) и анизотропном (б) пластах (kr/kz = 10).

ВЕРТИКАЛЬНАЯ ЦИРКУЛЯЦИОННАЯ СКВАЖИНА В СЛОИСТОМ ПЛАСТЕ

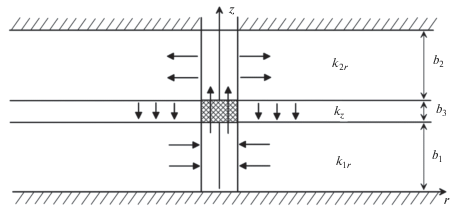
Предположим, что откачивающий и нагнетальный интервалы скважины расположены в разных пропластках, разделенных слабо проницаемым прослоем (рис. 5). Примем схему Мятиева–Гиринского, согласно которой в хорошо проницаемых пропластках пренебрегается вертикальной составляющей скорости фильтрации и течение полагается горизонтальным, а в слабо проницаемом прослое пренебрегается горизонтальной составляющей скорости фильтрации и течение полагается перпендикулярным к направлению напластования [6]. Ограничимся рассмотрением установившегося притока воды к вертикальной циркуляционной скважине в слоистом пласте. Отметим лишь, что решение задачи неустановившегося притока к вертикальной циркуляционной скважине в слоистом пласте легко получается из решения задачи одновременной откачки из двух пластов, разделенных слабопроницаемым прослоем [1, 8, 16]. Для учета скин-эффекта и влияния объемов откачивающего и нагнетательного интервалов скважины можно воспользоваться методом суперпозиции и аналитическим решением задачи раздельной откачки из пропластка двухслойного пласта [14].

Рис. 5.

Схема циркуляционного течения в слоистом пласте.

В безразмерном виде установившееся циркуляционное течение воды в слоистом пласте со слабопроницаемым прослоем описывается системой уравнений

(22)
$\frac{\chi }{{{{r}_{d}}}}\frac{d}{{d{{r}_{d}}}}\left( {{{r}_{d}}\frac{{d{{h}_{{1d}}}}}{{d{{r}_{d}}}}} \right) - \lambda \left( {{{h}_{{1d}}} - {{h}_{{2d}}}} \right) = 0,$
(23)
$\frac{{\left( {1 - \chi } \right)}}{{{{r}_{d}}}}\frac{d}{{d{{r}_{d}}}}\left( {{{r}_{d}}\frac{{d{{h}_{{2d}}}}}{{d{{r}_{d}}}}} \right) - \lambda \left( {{{h}_{{2d}}} - {{h}_{{1d}}}} \right) = 0$
с граничными условиями
(24)
${{h}_{{1d}}}\left( \infty \right) = {{h}_{{2d}}}\left( \infty \right) = 0,$
(25)
${{\left. {\chi \frac{{d{{h}_{{1d}}}}}{{d{{r}_{d}}}}} \right|}_{{{{r}_{d}} = 1}}} = - 1,\,\,\,\,{{\left. {\left( {1 - \chi } \right)\frac{{d{{h}_{{2d}}}}}{{d{{r}_{d}}}}} \right|}_{{{{r}_{d}} = 1}}} = 1,$
(26)
${{s}_{{id}}} = {{\left[ {{{h}_{{id}}} - {{S}_{i}}\frac{{d{{h}_{{id}}}}}{{d{{r}_{d}}}}} \right]}_{{{{r}_{d}} = 1}}},\,\,\,\,i = 1,2,$
где ${{h}_{{id}}} = \frac{{2\pi \left( {{{k}_{{1r}}}{{b}_{1}} + {{k}_{{2r}}}{{b}_{2}}} \right){{h}_{i}}}}{Q}$, ${{s}_{{id}}} = \frac{{2\pi \left( {{{k}_{{1r}}}{{b}_{1}} + {{k}_{{2r}}}{{b}_{2}}} \right){{s}_{i}}}}{Q}$, $\lambda = \frac{{r_{w}^{2}\omega }}{{{{k}_{{1r}}}{{b}_{1}} + {{k}_{{2r}}}{{b}_{2}}}}$, $\chi = \frac{{{{k}_{{1r}}}{{b}_{1}}}}{{{{k}_{{1r}}}{{b}_{1}} + {{k}_{{2r}}}{{b}_{2}}}}$, ${{r}_{d}} = \frac{r}{{{{r}_{w}}}}$, $\omega = \frac{{{{k}_{z}}}}{{{{b}_{3}}}}$; ${{h}_{i}}$ ‒ напор в i-м пропластке; ${{s}_{i}}$ ‒ напор в откачивающем (i = 1) и нагнетательном (i = 2) интервалах скважины; ${{S}_{i}}$ ‒ скин-эффект i-го интервала.

Распределения напоров в пропластках определяются выражениями

(27)
$\begin{gathered} {{h}_{{1d}}}\left( {{{r}_{d}}} \right) = \frac{{{{K}_{0}}(\sqrt \sigma {{r}_{d}})}}{{{{\chi }}\sqrt \sigma {{K}_{1}}(\sqrt \sigma )}}, \\ {{h}_{{2d}}}\left( {{{r}_{d}}} \right) = \frac{{{{K}_{0}}(\sqrt \sigma {{r}_{d}})}}{{\left( {\chi - 1} \right)\sqrt \sigma {{K}_{1}}(\sqrt \sigma )}}, \\ \end{gathered} $
где $\sigma = \frac{\lambda }{{\chi \left( {1 - \chi } \right)}}$.

Напоры в соответственно откачивающем и нагнетательном интервалах скважины выражены так:

(28)
$\begin{gathered} {{s}_{{1d}}} = \frac{1}{\chi }\left( {\frac{{{{K}_{0}}(\sqrt \sigma )}}{{\sqrt \sigma {{K}_{1}}(\sqrt \sigma )}} + {{S}_{1}}} \right), \\ {{s}_{{2d}}} = \frac{1}{{\chi - 1}}\left( {\frac{{{{K}_{0}}(\sqrt \sigma )}}{{\sqrt \sigma {{K}_{1}}(\sqrt \sigma )}} + {{S}_{2}}} \right). \\ \end{gathered} $

Следует отметить, что в частном случае при ${{b}_{1}} = {{b}_{2}}$, ${{k}_{{1r}}} = {{k}_{{2r}}}$ и ${{S}_{1}} = {{S}_{2}} = 0$ выражения (28) совпадают c решением задачи из работы [29].

При условии малости $\sigma $ выражения (28) упрощаются:

(29)
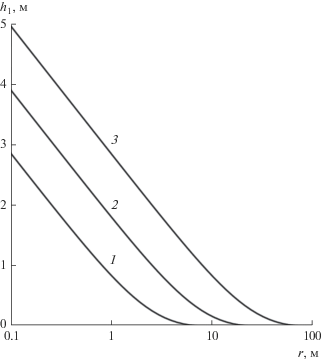
$\begin{gathered} {{s}_{{1d}}} = \frac{1}{\chi }\left( {\ln \frac{2}{{\sqrt \sigma }} - \gamma + {{S}_{1}}} \right), \\ {{s}_{{2d}}} = \frac{1}{{\chi - 1}}\left( {\ln \frac{2}{{\sqrt \sigma }} - \gamma + {{S}_{2}}} \right), \\ \end{gathered} $
где $\gamma \sim 0.5772$ ‒ постоянная Эйлера.

Далее проводится исследование влияния проницаемости прослоя на распределение напора в пропластках двухслойного пласта со следующими параметрами: b1 = b2 = 2 м, b3 = 4 м, ${{r}_{w}}$ = 0.1 м, $Q$ = 10 м3/сут, k1r = k2r = 1 × 10–5 м/с, S1 = S2 = 0. Из рис. 6 видно, что при уменьшении проницаемости прослоя увеличивается область циркуляционного течения. Аналогичным образом на область циркуляционного течения в однородном пласте влияет вертикальная проницаемость (рис. 4).

Рис. 6.

Влияние вертикальной проницаемости на распределение напора в первом пропластке (1 ‒ kz = 10–5 м/с, 2 ‒ 10–6 м/с, 3 ‒ 10–7 м/с).

Предположим, что нагнетательный и откачивающий интервалы скважины примыкают к кровле и подошве анизотропного пласта и имеют равную длину. Тогда, полагая в (29) b1 = b2 = l и k1r = k2r = kr, получим следующие приближенные формулы для определения напора в откачивающем и нагнетательном интервалах скважины:

(30)
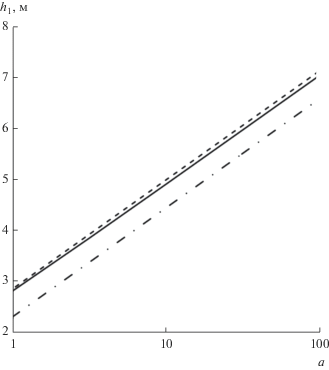
${{s}_{i}} = {{\left( { - 1} \right)}^{{i + 1}}}\frac{Q}{{2\pi {{k}_{r}}l}}\ln \left( {\frac{{a\sqrt {2l\left( {L - l} \right)} }}{{{{e}^{{\gamma - {{S}_{i}}}}}{{r}_{w}}}}} \right),\,\,\,\,i = 1,2,$
где l ‒ длина интервалов; L ‒ расстояние между центрами интервалов; ${{a}^{2}} = \frac{{{{k}_{r}}}}{{{{k}_{z}}}}$ ‒ параметр анизотропии. Из формул (18) и (30) следует, что для симметрично расположенных нагнетательного и откачивающего интервалов циркуляционной скважины ${{s}_{1}} + {{s}_{2}} = \frac{Q}{{2\pi {{k}_{r}}l}}\left( {{{S}_{1}} - {{S}_{2}}} \right)$.

На рис. 7 показанa зависимость напора в откачивающем интервале скважины от параметра анизотропии, рассчитанная по выражению (18), – сплошной линией, а по формуле (30) – пунктирной линией. Для сравнения на рис. 7 штрихпунктирной линией показана аналогичная зависимость, полученная на основе приближенной формулы для дипольного течения в бесконечном анизотропном пласте [8, 39]:

(31)
${{s}_{i}} = {{\left( { - 1} \right)}^{{i + 1}}}\frac{Q}{{2\pi {{k}_{r}}l}}\ln \left( {\frac{{2al\Phi \left( \mu \right)}}{{{{e}^{{1 - {{S}_{i}}}}}{{r}_{w}}}}} \right),\,\,\,\,i = 1,2,$
где $\Phi \left( \mu \right) = {{\left( {\frac{{{{\mu }^{2}}}}{{{{\mu }^{2}} - 1}}} \right)}^{{\frac{\mu }{2}}}}{{\left( {\frac{{\mu - 1}}{{\mu + 1}}} \right)}^{{\frac{1}{2}}}}$, $\mu = \frac{L}{l}$. Отметим, что для учета скин-эффекта радиус скважины в (31) был заменен на эффективный радиус ${{r}_{{{\text{ef}}}}} = {{r}_{w}}{{{\text{e}}}^{{ - {{S}_{i}}}}}$.

Рис. 7.

Влияние параметра анизотропии $a = \sqrt {{{{{k}_{r}}} \mathord{\left/ {\vphantom {{{{k}_{r}}} {{{k}_{z}}}}} \right. \kern-0em} {{{k}_{z}}}}} $ на напор в откачивающем интервале скважины.

Из формул (30) и (31) следует, что при установившемся течении напоры в интервалах циркуляционной скважины линейно зависят от скин-эффекта и логарифма параметра анизотропии. Таким образом, обработка данных дипольного опробования скважин на стационарных режимах без априорной информации о скин-эффекте может привести к неверным оценкам анизотропии проницаемости [36]. Время выхода циркуляционной скважины на стационарный режим работы в большей степени зависит от анизотропии проницаемости, упругой емкости пласта и его толщины [20], чем от скин-эффекта. Поэтому для более достоверной оценки анизотропии проницаемости пласта следует использовать кривые изменения напора в интервалах циркуляционной скважины, включая переходные режимы в начальные моменты времени при пуске или остановке скважины [20].

ЗАКЛЮЧЕНИЕ

Получены полуаналитическое и приближенное аналитическое решения задачи неустановившегося притока воды к вертикальной циркуляционной скважине в анизотропном пласте с учетом скин-эффекта и влияния объемов откачивающего и нагнетательного интервалов скважины. Исследованы установившееся поле напоров в окрестности вертикальной циркуляционной скважины и распределение притока воды по длине откачивающего и нагнетательного интервалов. На основе схемы Мятиева–Гиринского получено решение задачи установившегося течения воды в окрестности вертикальной циркуляционной скважины в двухслойном пласте, разделенном слабо проницаемым прослоем. Показано, что для частных случаев полученные результаты совпадают с известными решениями. Установлена линейная зависимость напоров в откачивающем и нагнетательном интервалах скважины от скин-эффекта и логарифма параметра анизотропии при установившемся режиме течения.

Предложенные в работе аналитические решения могут быть использованы для моделирования течения воды в окрестности вертикальной циркуляционной скважины и для определения фильтрационных параметров водоносного горизонта методом дипольного опробования скважин.

Список литературы

  1. Бабушкин В.Д., Плотников И.И., Чуйко В.М. Методы изучения фильтрационных свойств неоднородных пород. М.: Недра, 1974. 208 с.

  2. Зейбек М. Применение интервальных испытаний пласта и вертикального гидропрослушивания для построения и уточнения моделей различных типов коллекторов // Российская нефтегазовая техническая конференция SPE. М., 2019. С. 1‒14. (SPE-196838-RU)

  3. Мироненко В.А., Румынин В.Г. Опытно-миграционные работы в водоносных пластах. М.: Недра, 1986. 240 с.

  4. Морозов П.Е. Оценка анизотропии проницаемости и скин-эффекта по данным экспресс-откачек из несовершенных скважин // Вод. ресурсы. 2020. Т. 47. № 3. С. 272–280.

  5. Морозов П.Е. Полуаналитическое решение задачи нестационарного притока жидкости к несовершенной скважине // Учен. зап. Казан. ун-та. Сер. Физ.-матем. науки. 2017. Т. 159. Кн. 3. С. 340‒353.

  6. Полубаринова-Кочина П.Я. Теория движения грунтовых вод. М.: Гос. изд-во технико-теоретич. лит., 1952. 676 с.

  7. Румынин В.Г., Атрощенко Ф.Г. Экспериментальные и расчетные модели для оценки параметра скорости вертикальной миграции растворов в профильно-анизотропных пластах // Методы и практика математического моделирования. Белгород, 1982. С. 48–53.

  8. Синдаловский Л.Н. Справочник аналитических решений для интерпретации опытно-фильтрационных опробований. СПб.: Изд-во СПбГУ, 2006. 769 с.

  9. Чарный И.А. Подземная гидрогазодинамика. М.: Гостоптехиздат, 1963. 396 с.

  10. Chang C.C., Chen C.S. An integral transform approach for a mixed boundary problem involving a flowing partially penetrating well with infinitesimal well skin // Water Resour. Res. 2002. V. 38. № 6. P. 1071‒1077.

  11. Boulton N.S., Streltsova T.D. The drawdown near an abstraction well of large diameter under non-steady conditions in an unconfined aquifer // J. Hydrol. 1976. V. 30. № 1/2. P. 29‒46.

  12. Butler J.J.Jr. The design, performance, and analysis of slug tests. 2nd ed. Boca Raton: CRC Press, 2019. 281 p.

  13. Dejam M., Hassanzadeh H., Chen Z. Semi-analytical solutions for a partially penetrated well with wellbore storage and skin effects in a double-porosity system with a gas cap // Transp. Porous. Med. 2013. V. 100. P. 159–192.

  14. Ehlig-Economides C., Ayoub J.A. Vertical interference testing across a low-permeability zone // SPE Form. Eval. 1986. V. 1. № 5. P. 497‒510.

  15. Halihan T., Zlotnik V. Asymmetric dipole-flow test in a fractured carbonate aquifer // Ground Water. 2002. V. 40. № 5. P. 491‒499.

  16. Hantush M.S. Flow to wells in aquifers separated by a semipervious layer // J. Geoph. Res. 1967. V. 72. № 6. P. 1709‒1720.

  17. Herrling B., Stamm J. Numerical results of calculated 3D vertical circulation flows around wells with two screen sections for in situ aquifer remediation // Computational methods in water resources IX. V. 1 / Ed. T.F. Russell. London, 1992. P. 483‒492.

  18. Huang J., Goltz M.M. A three-dimensional analytical model to simulate groundwater flow during operation of recirculating wells // J. Hydrol. 2005. V. 314. № 1‒4. P. 67‒77.

  19. Hvilshøj S., Jensen K.H., Madsen B. Single-well dipole flow tests: parameter estimation and field testing // Ground Water. 2000. V. 38. № 1. P. 53‒62.

  20. Kabala Z.J. The dipole flow test: a new single-borehole test for aquifer characterization // Water Resour. Res. 1993. V. 29. № 1. P. 99‒107.

  21. Kuchuk F., Hollaender F., Onur M. Pressure transient formation and well testing: convolution, deconvolution and nonlinear estimation. V. 57. Developments in petroleum science. Amsterdam: Elsevier, 2010. 389 p.

  22. Morozov P.E. Simulation of the circulating flow in the vicinity of a horizontal well // Physical and mathematical modeling of earth and environment processes (2018). Springer proceedings in earth and environmental sciences. Cham: Springer, 2019. P. 368‒373.

  23. Ni L., Li H., Jiang Y., Yao Y., Ma Z. A model of groundwater seepage and heat transfer for single-well ground source heat pump systems // Appl. Thermal Eng. 2011. V. 31. № 14–15. P. 2622‒2630.

  24. Paradis D., Lefebvre R. Single-well interference slug tests to assess the vertical hydraulic conductivity of unconsolidated aquifers // J. Hydrol. 2013. V. 478. P. 102‒118.

  25. Perina T. General well function for soil vapor extraction // Adv. Water Resour. 2014. V. 66. P. 1‒7.

  26. Peursem D.V., Zlotnik V., Ledder G. Groundwater flow near vertical recirculatory wells: effect of skin on flow geometry and travel times with implications for aquifer remediation // J. Hydrol. 1999. V. 222. № 1–4. P. 109‒ 122.

  27. Philip R.D., Walter G.R. Prediction of flow and hydraulic head for vertical circulation wells // Ground Water. 1992. V. 30. № 5. P. 765‒773.

  28. Rode A., Liesch T., Goldscheider N. Open-loop geothermal heating by combined extraction–injection one-well systems: A feasibility study // Geothermics. 2015. V. 56. P. 110‒118.

  29. Sørensen S., Reffstrup J. Prediction of long-term operational conditions for single-well groundwater heat pump plants // Proc. 27th Intersociety Energy Conversion Engineering Conf. San Diego, CA, USA, 1992. P. 1‒6.

  30. Stehfest H. Numerical inversion of Laplace transform // Commun. ACM. 1970. V. 13. P. 47‒49.

  31. Sutton D.J., Kabala Z.J., Schaad D.E., Ruud N.C. The dipole-flow test with a tracer: a new single-borehole tracer test for aquifer characterization // J. Contam. Hydrol. 2000. V. 44. № 1. P. 71‒101.

  32. Tu K., Wu Q., Simunek J., Chen C., Zhu Ke., Zeng Y., Xu S., Wang Y. An analytical solution of groundwater flow in a confined aquifer with a single-well circulation system // Water Resour. Res. 2020. V. 56. № 7. P. 1‒14.

  33. Tu K., Wu Q., Simunek J., Zhu Ke., Chen C., Zheng W., Zeng Y., Xu S. An approximate analytical solution for non-Darcian flow in a confined aquifer with a single well circulation groundwater heat pump system // Adv. Water Resour. 2020. V. 145. P. 1‒10. (103740)

  34. Tu K., Wu Q., Sun H. A mathematical model and thermal performance analysis of single-well circulation (SWC) coupled ground source heat pump (GSHP) systems // Appl. Thermal Eng. 2019. V. 147. P. 473‒481.

  35. Xia Q., Zhang Q., Xu M., Tang Y., Teng H. Visualizing hydraulic zones of a vertical circulation well in presence of ambient flow // Desal. Water Treatm. 2019. V. 159. P. 151‒160.

  36. Xiang J., Kabala Z.J. Performance of the steady-state dipole flow test in layered aquifers // Hydrol. Processes. 1997. V. 11. № 12. P. 1595‒1605.

  37. Yeh H.-D., Chang Y.-Ch. Recent advances in modeling of well hydraulics // Adv. Water Resour. 2013. V. 51. P. 27‒651.

  38. Zlotnik V., Goss D., Duffield M. General steady-state shape factor for a partially penetrating well // Ground Water. 2010. V. 48. № 1. P. 111‒116.

  39. Zlotnik V., Ledder G. Theory of dipole flow in uniform anisotropic aquifers // Water Resour. Res. 1996. V. 32. № 4. P. 1119‒1128.

  40. Zlotnik V.A., Zurbuchen B.R. Field study of hydraulic conductivity in a heterogeneous aquifer: comparison of single-borehole measurements using different instruments // Water Resour. Res. 2003. V. 39. № 4. P. 1101‒1112.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Водные ресурсы

Архивы выпусков Информация о журнале Отправить рукопись в журнал