Водные ресурсы, 2022, T. 49, № 2, стр. 142-153
Теоретическое и лабораторное моделирование бифуркации топографического вихря на вихревые торы над двухступенчатой осесимметричной возвышенностью
В. Н. Зырянов a, В. М. Егорова a, *
a Институт водных проблем РАН
119333 Москва, Россия
* E-mail: vikchik96@yandex.ru
Поступила в редакцию 19.04.2021
После доработки 16.08.2021
Принята к публикации 09.09.2021
- EDN: FFIKEI
- DOI: 10.31857/S0321059622020183
Аннотация
Первая, теоретическая, часть работы включает в себя математическую постановку задачи обтекания двухступенчатой возвышенности фоновым потоком, а также вывод критерия бифуркации топографического вихря, генерируемого этой возвышенностью. Спектральная задача поиска точек бифуркации решается численно методом обратных итераций. Во второй части представлены результаты лабораторных экспериментов по моделированию топографических вихрей. Основное внимание уделено процессу бифуркации топографического вихря и образованию вторичных тороидальных вихрей над двухступенчатой осесимметричной возвышенностью дна в виде двух коаксиальных сплошных цилиндров разных диаметров, расположенных один на другом. Нижний цилиндр имеет больший диаметр. В качестве входных характеристик в лабораторные эксперименты заложены данные, полученные из численных решений соответствующей спектральной задачи.
ВВЕДЕНИЕ
Впервые распад (бифуркация) топографического вихря на вихревые торы был изучен в работах [2, 22]. Математически проблема свелась к решению спектральной задачи на устойчивость для дифференциального уравнения 6-го порядка. Спектр точек бифуркации находился методом стрельбы [7]. В [2] сформулирована задача для куполообразной горы, аппроксимированной набором двух коаксиальных цилиндров разных диаметров. Показано теоретически, что в кольцевой области над уступом при определенных условиях происходит бифуркация топографического вихря, в результате чего возникают вторичные вихри в виде торов. Такая специфическая конфигурация рельефа дна обнаруживает аналогию с течением Тейлора−Куэтта между двумя вращающимися полыми непроницаемыми цилиндрами [21].
В исследуемом случае роли непроницаемых границ выполняют два цилиндрических слоя Стьюартсона [5, 19], “продолжающие” вверх границы цилиндров вплоть до поверхности бассейна. Таким образом, исследуемый на устойчивость вихрь расположен в кольцевой области между этими двумя вертикальными жидкими слоями.
Развитая в [22] теория применена в [6] для более простой конфигурации дна в виде одного цилиндра. В рассматриваемом случае спектральная задача потребовала более трудоемкого численного метода. Для нахождения спектра собственных значений и собственных функций применялась модификация метода инвариантного погружения (метод уравнений Риккати) [8]. Предложены алгебраические матричные преобразования, которые позволили свести исходную задачу с сингулярными граничными условиями к задаче с регулярными граничными условиями.
Учитывая, что прямых наблюдений за тороидальными течениями над подводными возвышенностями нет, то об их существовании можно судить лишь по численным экспериментам [6, 18, 22]. Еще одним подтверждением может служить описанный в [16] наблюдавшийся хорошо перемешанный вертикальный столб жидкости над подводными горами. Предположительно, вертикальное перемешивание слоя жидкости над подводной возвышенностью может быть вызвано образованием вторичных тороидальных вихрей. Эти соображения послужили мотивацией проведения лабораторных экспериментов.
В работе [13], где анализируются причины резкого повышения биопродуктивности вод над подводными горами, сделан вывод, что вода должна подниматься в центре подводной горы и опускаться по ее краям; т. е. из наблюдений следовало, что вихрь ведет себя как циклон. Это противоречит теории, согласно которой топографический вихрь над возвышенностью всегда имеет антициклоническую завихренность [3, 4, 9, 15, 18].
Объяснение данного несогласования вытекает из теории: в процессе потери устойчивости вихря происходит его разбиение на несколько торов, характеризующихся попеременным направлением вращения [2, 6, 17, 22]. Именно эти тороидальные вихри могут осуществлять необходимый интенсивный подъем вод в центре антициклонического топографического вихря и опускание по его краям.
В настоящей работе кратко излагается теория вторичных тороидальных вихрей, приводятся результаты численных расчетов и лабораторных экспериментов по моделированию вихрей Тейлора [20]. Большое внимание уделяется процессу потери устойчивости топографического вихря над сложной топографией дна с последующим образованием вихревых торов, а также расчету спектра точек бифуркации. Решение спектральной задачи проводится методом обратных итераций. Метод позволяет вычислить спектр и сопоставить данные с расчетами. Результаты эксперимента сравниваются с результатами численных решений спектральной задачи.
Лабораторное моделирование проводилось в лаборатории гидродинамики ИВП РАН на вращающейся установке (рис. 2) с подводной возвышенностью двухступенчатой цилиндрической конфигурации (рис. 1).
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим задачу, в которой подводная возвышенность имеет вид двух коаксиальных сплошных цилиндров с радиусами ${{\tilde {R}}_{1}}$ и ${{\tilde {R}}_{2}}$ и высотами ${{\tilde {h}}_{1}}$ и ${{\tilde {h}}_{2}}$, расположенных один на другом: ${{\tilde {R}}_{1}} < {{\tilde {R}}_{2}}$ (рис. 1).
Рис. 1.
Модельное представление подводной возвышенности в виде двух коаксиальных цилиндров разных радиусов и высот.
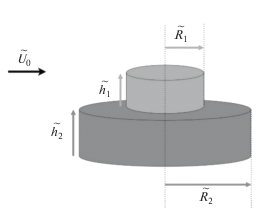
Пусть жидкость натекает на подводное возмущение с постоянной скоростью потока ${{\tilde {U}}_{0}}$, и допустим, что с некоторого момента времени внешнее течение прекращается [2, 22].
Следуя [4, 14], получим радиальное распределение тангенциальной скорости течения ${{{v}}_{0}}\left( r \right)$ в безразмерном виде:
(1)
${{{v}}_{0}}\left( r \right) = - \frac{\sigma }{2}\left\{ \begin{gathered} \left( {{{h}_{1}} + {{h}_{2}}} \right)r,~\,\,\,\,r < {{R}_{1}} \hfill \\ \left( {{{h}_{1}}R_{1}^{2}\frac{1}{r} + {{h}_{2}}r} \right),~\,\,\,\,{{R}_{1}} \leqslant r \leqslant {{R}_{2}} \hfill \\ \left( {{{h}_{1}}R_{1}^{2} + {{h}_{2}}R_{2}^{2}} \right)\frac{1}{r},\,\,\,\,r > {{R}_{2}}, \hfill \\ \end{gathered} \right.$Для кольцевой области наблюдается аналогия с течением Тейлора−Куэтта $\left( {{{{v}}_{0}}\left( r \right) = ar + \frac{b}{r}} \right)$ между двумя вращающимися коаксиальными цилиндрами. В рассматриваемом случае роль таких цилиндров играют жидкие стенки границ кольцевой области, где коэффициенты $a = - \frac{{\sigma {{h}_{2}}}}{2},b = - \frac{{\sigma {{h}_{1}}R_{1}^{2}}}{2}$. Знак минус показывает, что течение в кольцевой области антициклоническое. В теории топографических вихрей предполагается, что число Россби мало, а топографический параметр σ – конечная величина. Малость числа Россби, в частности, характеризует значительное влияние на систему силы Кориолиса [3].
На границах кольцевой области тангенциальная скорость ${{{v}}_{0}}\left( r \right)$ – соответственно ${{{v}}_{0}}\left( {{{R}_{1}}} \right)$ = $ = {{\omega }_{1}}{{R}_{1}},{{{v}}_{0}}\left( {{{R}_{2}}} \right) = {{\omega }_{2}}{{R}_{2}}$. Выражения для скоростей можно записать в виде ${{{v}}_{0}}\left( {{{R}_{1}}} \right) = - \frac{{\sigma \left( {{{h}_{1}} + {{h}_{2}}} \right){{R}_{1}}}}{2},$ ${{{v}}_{0}}\left( {{{R}_{2}}} \right) = - \frac{{\sigma \left( {{{h}_{1}}R_{1}^{2} + {{h}_{2}}R_{2}^{2}} \right)}}{{2{{R}_{2}}}}.$ Отсюда для угловых скоростей имеем
(2)
${{\omega }_{1}} = - \frac{{\sigma \left( {{{h}_{1}} + {{h}_{2}}} \right)}}{2},\,\,\,\,{{\omega }_{2}} = - \frac{{\sigma \left( {{{h}_{1}}R_{1}^{2} + {{h}_{2}}R_{2}^{2}} \right)}}{{2R_{2}^{2}}}.$Для описания движения воспользуемся системой уравнений геофизической гидродинамики для однородной несжимаемой $\left( {{{{\tilde {\rho }}}_{0}} = {\text{const}}} \right)$ жидкости с вязкостью ν (ν – величина размерной кинематической вязкости) в цилиндрической системе координат [11]. Введем следующие допущения: движение жидкости стационарно: $\frac{\partial }{{\partial t}} \to 0,$ имеем приближение f-плоскости. Обезразмерим физические величины: $f = \frac{{{{f}_{0}}}}{{{{f}_{0}}}} = 1$, $U = \frac{{\tilde {U}}}{{{{{\tilde {R}}}_{2}}{{f}_{0}}}}$, $r = \frac{{\tilde {r}}}{{{{{\tilde {R}}}_{2}}}}$, $z = \frac{{\tilde {z}}}{{{{{\tilde {R}}}_{2}}}}$, $\rho = \frac{{{{{\tilde {\rho }}}_{0}}}}{{{{\rho }_{0}}}},$ $P = \frac{{\tilde {P}}}{{{{{\tilde {\rho }}}_{0}}{{{\left( {{{{\tilde {R}}}_{2}}{{f}_{0}}} \right)}}^{2}}}}$ – безразмерное гидродинамическое давление. Учтем, что $\vec {U} = {{\vec {U}}_{0}} + {{\vec {U}}_{1}}$, ${{\vec {U}}_{0}} = \left( {0,{{{v}}_{0}}\left( r \right),0} \right),$ ${{\vec {U}}_{1}}$ = $ = \left( {{{u}_{r}}\left( {r,z} \right),{{u}_{\varphi }}\left( {r,z} \right),{{u}_{z}}\left( {r,z} \right)} \right)$ – малые возмущения скорости.
Функция ${{{v}}_{0}}\left( r \right)$ должна удовлетворять уравнениям вращающейся вязкой однородной жидкости в цилиндрических координатах. Для этого гидродинамическое давление представим как $P\left( {r,z} \right) = {{P}_{0}}\left( r \right) + Ep\left( {r,z} \right)$ и $\frac{{d{{P}_{0}}\left( r \right)}}{{dr}} = \frac{{{v}_{0}^{2}\left( r \right)}}{r} + {{{v}}_{0}}\left( r \right)$; ${\text{Re}} = \frac{{{{{\tilde {R}}}_{2}}{{{\tilde {U}}}_{0}}}}{\nu }$ – число Рейнольдса, $E = \frac{{{{R}_{0}}}}{{{\text{Re}}}} = \frac{\nu }{{{{f}_{0}}\tilde {R}_{2}^{2}}}$ – число Экмана, $p\left( {r,z} \right)$ – малое возмущение давления.
Уравнение для азимутальной компоненты скорости ${{{v}}_{0}}\left( r \right)$ будет удовлетворяться, если выполнено условие $\frac{{{{\partial }^{2}}{{{v}}_{0}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{{v}}_{0}}}}{{\partial r}} - \frac{{{{{v}}_{0}}}}{{{{r}^{2}}}} = 0.$
В результате будем иметь безразмерную систему уравнений [2, 6]:
(3)
$\left\{ \begin{gathered} \frac{1}{r}\frac{{\partial \left( {r{{u}_{r}}} \right)}}{{\partial r}} + \frac{{\partial {{u}_{z}}}}{{\partial z}} = 0 \hfill \\ \frac{1}{E}\left[ {{{u}_{r}}\frac{{\partial {{u}_{r}}}}{{\partial r}} + {{u}_{z}}\frac{{\partial {{u}_{r}}}}{{\partial z}} - \frac{{u_{\varphi }^{2}}}{r} - \left( {\frac{{2{{{v}}_{0}}}}{r} + 1} \right){{u}_{\varphi }}} \right] = - \frac{{\partial p}}{{\partial r}} + \Delta {{u}_{r}} - \frac{{{{u}_{r}}}}{{{{r}^{2}}}}{\text{\;}} \hfill \\ \frac{1}{E}\left[ {{{u}_{r}}\frac{{\partial {{u}_{\varphi }}}}{{\partial r}} + {{u}_{z}}\frac{{\partial {{u}_{\varphi }}}}{{\partial z}} + \frac{{{{u}_{r}}{{u}_{\varphi }}}}{r} + \left( {\frac{{d{{{v}}_{0}}\left( r \right)}}{{dr}} + \frac{{{{{v}}_{{\text{0}}}}}}{r} + 1} \right){{u}_{r}}} \right] = \Delta {{u}_{\varphi }} - \frac{{{{u}_{\varphi }}}}{{{{r}^{2}}}} \hfill \\ \frac{1}{E}\left[ {{{u}_{r}}\frac{{\partial {{u}_{z}}}}{{\partial r}} + ~{{u}_{z}}\frac{{\partial {{u}_{z}}}}{{\partial z}}} \right] = - \frac{{\partial p}}{{\partial z}} + \Delta {{u}_{z}}, \hfill \\ \end{gathered} \right.$СПЕКТРАЛЬНАЯ ЗАДАЧА НА УСТОЙЧИВОСТЬ
Отбрасывая в (3) члены второго порядка малости по возмущениям скорости и давления, получим линеаризованную систему уравнений:
(4)
$\left\{ \begin{gathered} \frac{1}{r}\frac{{\partial \left( {r{{u}_{r}}} \right)}}{{\partial r}} + \frac{{\partial {{u}_{z}}}}{{\partial z}} = 0 \hfill \\ \Delta {{u}_{r}} - \frac{{{{u}_{r}}}}{{{{r}^{2}}}} - \frac{{\partial p}}{{\partial r}} = - \lambda \left( {\frac{{2{{{v}}_{0}}}}{r} + 1} \right){{u}_{\varphi }} \hfill \\ \Delta {{u}_{\varphi }} - \frac{{{{u}_{\varphi }}}}{{{{r}^{2}}}} = \lambda \left( {\frac{{d{{{v}}_{0}}}}{{dr}} + \frac{{{{{v}}_{0}}}}{r} + 1} \right){{u}_{r}} \hfill \\ \Delta {{u}_{z}} - \frac{{\partial p}}{{\partial z}} = 0 \hfill \\ \end{gathered} \right.,$Будем рассматривать множество M дважды непрерывно дифференцируемых векторов $\left\{ {{{{\vec {U}}}_{1}}} \right\}$, определенных в замкнутой кольцевой области $\left\{ {{{r}_{1}} \leqslant r \leqslant {{r}_{2}},~ - \infty < z < + \infty } \right\}$, ${{r}_{1}} = {{R}_{1}},~{{r}_{2}} = {{R}_{2}}.$ Векторы $\left\{ {{{{\vec {U}}}_{1}}} \right\}$ осесимметричные, т. е. ${{u}_{r}},~{{u}_{\varphi }}$ и ${{u}_{z}}$ не зависят от φ и принимают нулевые значения при $r = {{r}_{1}},{{r}_{2}}$; поток через поперечное сечение полости полагается равным нулю, также ${{u}_{r}},~{{u}_{\varphi }}$ – четные функции по z, а ${{u}_{z}}$ – нечетная функция. Следуя работе [12], представим компоненты скорости и давление в следующем виде:
(5)
$\begin{gathered} {{u}_{r}} = u\left( r \right){\text{cos}}\left( {\alpha z} \right),\,\,\,\,{{u}_{\varphi }} = {v}\left( r \right){\text{cos}}\left( {\alpha z} \right), \\ {{u}_{z}} = w\left( r \right){\text{sin}}\left( {\alpha z} \right),\,\,\,\,p = q\left( r \right){\text{cos}}\left( {\alpha z} \right). \\ \end{gathered} $Введем следующие обозначения:
(7)
${\text{g}}\left( r \right) = \frac{{d{{{v}}_{0}}}}{{dr}} + \frac{{{{{v}}_{0}}}}{r} + 1 = 2a + 1 = {\text{const}}.{\text{\;}}$(8)
$\begin{gathered} \left\{ \begin{gathered} (L - {{\alpha }^{2}}){\kern 1pt} u\left( r \right) - \frac{{dq\left( r \right)}}{{dr}} = - \lambda d\left( r \right){v}\left( r \right) \hfill \\ (L - {{\alpha }^{2}}){\kern 1pt} {v}\left( r \right) = \lambda {\text{g}}\left( r \right)u\left( r \right), \hfill \\ \end{gathered} \right. \\ L = \frac{{{{d}^{2}}}}{{d{{r}^{2}}}} + \frac{1}{r}\frac{d}{{dr}} - \frac{1}{{{{r}^{2}}}}. \\ \end{gathered} $Следовательно, при решении системы (8) можно получить вид функций ${{u}_{r}}\left( {r,z} \right),$ ${{u}_{\varphi }}\left( {r,z} \right)$, а также ${{u}_{z}}\left( {r,z} \right)$, $p\left( {r,z} \right)$. Вертикальная скорость ${{u}_{z}}\left( {r,z} \right)$ должна обращаться в нуль на границе бассейна при $z = H$, поэтому $\alpha = k{{\alpha }_{0}},\alpha = \frac{{k\pi }}{H}$, $k \in \mathbb{N}$. Граничные условия на высоте возмущения рельефа дна можно приравнять к граничным условиям (снести) на горизонтальной плоскости $z = 0,$ полагая, что ${{h}_{0}} \ll {{H}_{0}}$.
При этом выполняется тождество:
(9)
$\frac{d}{{dr}}\left[ {\tilde {L}w\left( r \right)} \right] \equiv \left[ {(L - {{\alpha }^{2}}) + \frac{1}{{{{\alpha }^{2}}}}{{{(L - {{\alpha }^{2}})}}^{2}}} \right]u\left( r \right).$(10)
$\left\{ \begin{gathered} {{(L - {{\alpha }^{2}})}^{2}}u\left( r \right) = \lambda {{\alpha }^{2}}d\left( r \right){v}\left( r \right) \hfill \\ (L - {{\alpha }^{2}}){v}\left( r \right) = \lambda g\left( r \right)u\left( r \right). \hfill \\ \end{gathered} \right.$(11)
${{(L - {{\alpha }^{2}})}^{3}}{v}\left( r \right) = {{\lambda }^{2}}{{\alpha }^{2}}d\left( r \right){\text{g}}\left( r \right){v}\left( r \right).$(12)
${v} = L{v} = \frac{d}{{dr}}\left[ {(L - {{\alpha }^{2}}){v}} \right] = 0\,\,\,{\text{при}}\,\,\,r = {{r}_{1}},{{r}_{2}}.$“Если выполнено неравенство
то полученная спектральная задача на собственные значения (11)–(12) для любого фиксированного α, за исключением некоторого счетного множества, имеет положительный и простой спектр собственных значений $\left\{ {{{{\tilde {\lambda }}}_{i}}} \right\}$, причем каждое ${{\tilde {\lambda }}_{i}}$ – точка бифуркации ($\tilde {\lambda } = {{\lambda }^{2}})$”.С учетом (6)–(7) и значений $a = - \frac{{\sigma {{h}_{2}}}}{2},$ $~b = - \frac{{\sigma {{h}_{1}}r_{1}^{2}}}{2}$ для кольцевой области условие (13) для случая рассматриваемой подводной возвышенности примет следующий вид:
(14)
${{h}_{2}} < \frac{1}{\sigma },\,\,\,\,{{h}_{1}} > \frac{{r_{2}^{2}}}{{\sigma r_{1}^{2}}}\left( {1 - \sigma {{h}_{2}}} \right) > 0.$Численная реализация нахождения спектра собственных значений
Следующий этап – численное решение спектральной задачи (11)–(12). Как упоминалось выше, вычисление спектра $\left\{ {{{\lambda }_{i}}} \right\}$ для фиксированного α требуется для расчетов параметров лабораторных экспериментов, моделирующих процесс бифуркации вихря и образования торов. Напомним, что значение λ есть величина, обратная числу Экмана E: $\lambda = \frac{1}{E} = \frac{{{{f}_{0}}\tilde {R}_{2}^{2}}}{\nu }$. Видно, что искомое минимальное значение спектра ${{\lambda }_{{{\text{min}}}}}$ содержит в себе информацию о вязкости жидкости ν, необходимой для проведения экспериментов.
Таким образом, основная цель – вычисление спектра собственных значений спектральной задачи (11)–(12), получение минимального значения ${{\lambda }_{{{\text{min}}}}} = {{\lambda }_{1}}$ и последующее вычисление вязкости ${{\nu }}$ жидкости, требуемой для выполнения критерия бифуркации в лабораторном эксперименте.
Используем метод конечных разностей и представим уравнение (11) в операторном виде:
где $A = \frac{{{{{(L - {{\alpha }^{2}})}}^{3}}}}{{{{\alpha }^{2}}d\left( r \right)g\left( r \right)}}{\text{\;}}$ – дифференциальный оператор 6-го порядка, $\tilde {\lambda } = {{\lambda }^{2}}$ и(16)
$\begin{gathered} d\left( r \right)g\left( r \right) = 4{{a}^{2}} + 4a + 1 + \frac{{4ab}}{{{{r}^{2}}}} + \frac{{2b}}{{{{r}^{2}}}} = C + \frac{D}{{{{r}^{2}}}}, \\ C = 4{{a}^{2}} + 4a + 1,\,\,\,\,D = 4ab + 2b. \\ \end{gathered} $(17)
$\begin{gathered} {{{\text{a}}}_{0}} = \left( { - \frac{{45}}{{{{r}^{6}}}} + \frac{{9{{\alpha }^{2}}}}{{{{r}^{4}}}} - \frac{{3{{\alpha }^{4}}}}{{{{r}^{2}}}} - {{\alpha }^{6}}} \right)T, \\ {{{\text{a}}}_{1}} = \left( {\frac{{45}}{{{{r}^{5}}}} - \frac{{9{{\alpha }^{2}}}}{{{{r}^{3}}}} + \frac{{3{{\alpha }^{4}}}}{r}} \right)T, \\ {{{\text{a}}}_{2}} = \left( { - \frac{{27}}{{{{r}^{4}}}} + \frac{{9{{\alpha }^{2}}}}{{{{r}^{2}}}} + 3{{\alpha }^{4}}} \right)T, \\ {{{\text{a}}}_{3}} = \left( {\frac{{12}}{{{{r}^{3}}}} - \frac{{6{{\alpha }^{2}}}}{r}} \right)T, \\ {{{\text{a}}}_{4}} = \left( { - \frac{6}{{{{r}^{2}}}} - 3{{\alpha }^{2}}} \right)T,\,\,\,\,{{{\text{a}}}_{5}} = \frac{3}{r}T,\,\,\,\,{{{\text{a}}}_{6}} = T. \\ \end{gathered} $Уравнение (15) принимает форму:
(18)
$\mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} 1}^6 {{{\text{a}}}_{k}}\frac{{{{d}^{k}}{{{v}}_{i}}}}{{d{{r}^{k}}}} + {\text{\;}}{{{\text{a}}}_{0}}{{{v}}_{i}} = \tilde {\lambda }{{{v}}_{i}}.{\text{\;}}$Формулы для производных до шестой включительно принимают следующий вид:
(19)
$\begin{gathered} \frac{{d{{{v}}_{i}}}}{{dr}} = \frac{{{{{v}}_{i}} - {{{v}}_{{i - 1}}}}}{{\Delta r}}, \\ ~~\frac{{{{d}^{2}}{{{v}}_{i}}}}{{d{{r}^{2}}}} = \frac{{{{{v}}_{{i + 1}}} - 2{{{v}}_{i}} + {{{v}}_{{i - 1}}}}}{{\Delta {{r}^{2}}}}, \\ \frac{{{{d}^{3}}{{{v}}_{i}}}}{{d{{r}^{3}}}} = \frac{{{{{v}}_{{i + 1}}} - 3{{{v}}_{i}} + 3{{{v}}_{{i - 1}}} - {{{v}}_{{i - 2}}}}}{{\Delta {{r}^{3}}}}, \\ \frac{{{{d}^{4}}{{{v}}_{i}}}}{{d{{r}^{4}}}} = \frac{{{{{v}}_{{i + 2}}} - 4{{{v}}_{{i + 1}}} + 6{{{v}}_{i}} - 4{{{v}}_{{i - 1}}} + {{{v}}_{{i - 2}}}}}{{\Delta {{r}^{4}}}}, \\ \frac{{{{d}^{5}}{{{v}}_{i}}}}{{d{{r}^{5}}}} = \frac{{{{{v}}_{{i + 2}}} - 5{{{v}}_{{i + 1}}} + 10{{{v}}_{i}} - 10{{{v}}_{{i - 1}}} + 5{{{v}}_{{i - 2}}} - {{{v}}_{{i - 3}}}}}{{\Delta {{r}^{5}}}}, \\ \frac{{{{d}^{6}}{{{v}}_{i}}}}{{d{{r}^{6}}}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{{{{v}}_{{i + 3}}} - 6{{{v}}_{{i + 2}}} + 15{{{v}}_{{i + 1}}} - 20{{{v}}_{i}} + 15{{{v}}_{{i - 1}}} - 6{{{v}}_{{i - 2}}} + {{{v}}_{{i - 3}}}}}{{\Delta {{r}^{6}}}}{\kern 1pt} . \\ \end{gathered} $После подстановки (17) и (19) в (18) спектральная задача принимает следующий вид:
(20)
$\begin{gathered} F\left( {{{r}_{i}}} \right){{{v}}_{{i + 3}}} + H\left( {{{r}_{i}}} \right){{{v}}_{{i + 2}}} + I\left( {{{r}_{i}}} \right){{{v}}_{{i + 1}}} + K\left( {{{r}_{i}}} \right){{{v}}_{i}} + \\ + \,\,L\left( {{{r}_{i}}} \right){{{v}}_{{i - 1}}} + M\left( {{{r}_{i}}} \right){{{v}}_{{i - 2}}} + P\left( {{{r}_{i}}} \right){{{v}}_{{i - 3}}} = \tilde {\lambda }{{{v}}_{i}}, \\ \end{gathered} $Перейдем к рассмотрению конечно-разностных представлений граничных условий задачи (12). Данные условия описывают непроницаемость стенок (слои Стьюартсона), “продолжающих” вверх стенки кольцевой области [19].
Аналогичным образом необходимо расписать уравнение (12), записанное в виде
(22)
$\frac{d}{{dr}}\left[ {(L - {{\alpha }^{2}}){v}} \right] = 0\,\,\,{\text{при}}\,\,\,r = {{r}_{1}},{{r}_{{N + 1}}},$Шесть уравнений (21)–(22) будут заполнять три первые и три последние строчки СЛАУ при $r = {{r}_{1}}$ и $r = {{r}_{{N + 1}}}$ соответственно. Таким образом, запись уравнений (21)–(22) в конечных разностях (18) приведет к тому, что получим ненулевые значения при величинах ${{{v}}_{{i - 1}}} = {{{v}}_{0}}$ и ${{{v}}_{{i - 2}}} = {{{v}}_{{ - 1}}}$, выходящих за пределы области при $i = 1$. Такая же ситуация возникает и на второй границе в точке $r = {{r}_{{N + 1}}}$. Ниже, согласно [1, 7], предложен другой вариант записи производных.
Рассмотрим для границы $r = {{r}_{1}}$ формулы восходящей конечной разности, а для границы $r = {{r}_{{N + 1}}}$ – формулы нисходящей конечной разности. Из схемы разложения производных, предложенной в [1], получены следующие формулы:
при $r = {{r}_{1}}$
при $r = {{r}_{{N + 1}}}$
(23)
$\begin{gathered} \frac{{d{{{v}}_{i}}}}{{dr}} = \frac{{{{{v}}_{{i - 2}}} - 4{{{v}}_{{i - 1}}} + 3{{{v}}_{i}}}}{{2\Delta r}}, \\ \frac{{{{d}^{2}}{{{v}}_{i}}}}{{d{{r}^{2}}}} = \frac{{{{{v}}_{{i - 2}}} - 2{{{v}}_{{i - 1}}} + {{{v}}_{i}}}}{{\Delta {{r}^{2}}}}, \\ \frac{{{{d}^{3}}{{{v}}_{i}}}}{{d{{r}^{3}}}} = \frac{{ - {{{v}}_{{i - 3}}} + 3{{{v}}_{{i - 2}}} - 3{{{v}}_{{i - 1}}} + {{{v}}_{i}}}}{{\Delta {{r}^{3}}}}. \\ \end{gathered} $$1){~}{{{v}}_{1}} = 0,$
$\begin{gathered} 2)~{{{v}}_{1}}\left( {\frac{1}{{\Delta {{r}^{2}}}} - \frac{3}{{2{{r}_{1}}\Delta r}} - \frac{1}{{r_{1}^{2}}}} \right) + {{{v}}_{2}}\left( {\frac{{ - 2}}{{\Delta {{r}^{2}}}} + \frac{2}{{{{r}_{1}}\Delta r}}} \right) + \\ + \,\,{{{v}}_{3}}\left( {\frac{1}{{\Delta {{r}^{2}}}} - \frac{1}{{2{{r}_{1}}\Delta r}}} \right) = 0, \\ \end{gathered} $
$\begin{gathered} 3)~{{{v}}_{1}}\left( {\frac{{ - 1}}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{1}}\Delta {{r}^{2}}}} + \frac{3}{{2\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right) + \frac{2}{{r_{1}^{3}}}} \right) + \\ + \,\,{{{v}}_{2}}\left( {\frac{3}{{\Delta {{r}^{3}}}} - \frac{2}{{{{r}_{1}}\Delta {{r}^{2}}}} - \frac{2}{{\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right)} \right) + \\ + \,\,{{{v}}_{3}}\left( {\frac{{ - 3}}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{1}}\Delta {{r}^{2}}}} + \frac{1}{{2\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right)} \right) + {{{v}}_{4}}\left( {\frac{1}{{\Delta {{r}^{3}}}}} \right) = 0. \\ \end{gathered} $
Обозначим коэффициенты при ${{{v}}_{i}}$ следующим образом: ${{\alpha }_{1}} = \frac{1}{{\Delta {{r}^{2}}}} - \frac{3}{{2{{r}_{1}}\Delta r}} - \frac{1}{{r_{1}^{2}}}$, ${{\alpha }_{2}} = \frac{{ - 2}}{{\Delta {{r}^{2}}}} + \frac{2}{{{{r}_{1}}\Delta r}}$, ${{\alpha }_{3}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{1}{{\Delta {{r}^{2}}}} - \frac{1}{{2{{r}_{1}}\Delta r}},{{\beta }_{1}}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{ - 1}}{{\Delta {{r}^{3}}}}{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} \frac{1}{{{{r}_{1}}\Delta {{r}^{2}}}} + \frac{3}{{2\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right) + \frac{2}{{r_{1}^{3}}},$ ${{\beta }_{2}} = \frac{3}{{\Delta {{r}^{3}}}} - \frac{2}{{{{r}_{1}}\Delta {{r}^{2}}}} - \frac{2}{{\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right),\,\,\,\,{{\beta }_{3}} = \frac{{ - 3}}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{1}}\Delta {{r}^{2}}}} + $ $ + \,\,\frac{1}{{2\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right)$, ${{\beta }_{4}} = \frac{1}{{\Delta {{r}^{3}}}}$.
В итоге имеем систему:
(24)
$\left\{ \begin{gathered} {{{v}}_{1}} = 0 \hfill \\ {{{v}}_{1}}{{\alpha }_{1}} + {{{v}}_{2}}{{\alpha }_{2}} + {{{v}}_{3}}{{\alpha }_{3}} = 0 \hfill \\ {{{v}}_{1}}{{\beta }_{1}} + {{{v}}_{2}}{{\beta }_{2}} + {{{v}}_{3}}{{\beta }_{3}} + {{{v}}_{4}}{{\beta }_{4}} = 0. \hfill \\ \end{gathered} \right.$Из (24) видно, что ${{{v}}_{2}}$ и ${{{v}}_{3}}$ легко выражаются через ${{{v}}_{4}}$:
(25)
${{{v}}_{2}} = \frac{{ - {{\alpha }_{3}}}}{{{{\alpha }_{2}}}}\left( {\frac{{{{\beta }_{4}}}}{{\left( {{{\beta }_{2}}\frac{{{{\alpha }_{3}}}}{{{{\alpha }_{2}}}} - {{\beta }_{3}}} \right)}}} \right){{{v}}_{4}} = {{\kappa }_{2}}{{{v}}_{4}},$(26)
${{{v}}_{3}} = \frac{{{{\beta }_{4}}}}{{\left( {{{\beta }_{2}}\frac{{{{\alpha }_{3}}}}{{{{\alpha }_{2}}}} - {{\beta }_{3}}} \right)}}{{{v}}_{4}} = {{\kappa }_{1}}{{{v}}_{4}}.$При $r = {{r}_{{N + 1}}}$:
$1)~{{{v}}_{{N + 1}}} = 0;$
$\begin{gathered} 2)~{{{v}}_{{N + 1}}}\left( {\frac{1}{{\Delta {{r}^{2}}}} + \frac{3}{{2{{r}_{2}}\Delta r}} - \frac{1}{{r_{2}^{2}}}} \right) + {{{v}}_{N}}\left( {\frac{{ - 2}}{{\Delta {{r}^{2}}}} - \frac{2}{{{{r}_{2}}\Delta r}}} \right) + \\ + \,\,{{{v}}_{{N - 1}}}\left( {\frac{1}{{\Delta {{r}^{2}}}} + \frac{1}{{2{{r}_{2}}\Delta r}}} \right) = 0; \\ \end{gathered} $
$\begin{gathered} 3)\,\,{{{v}}_{{N + 1}}}\left( {\frac{1}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{2}}\Delta {{r}^{2}}}} - \frac{3}{{2\Delta r}}\left( {\frac{2}{{r_{2}^{2}}} + {{\alpha }^{2}}} \right) + \frac{2}{{r_{2}^{3}}}} \right) + \\ + \,\,{{{v}}_{N}}\left( {\frac{{ - 3}}{{\Delta {{r}^{3}}}} - \frac{2}{{{{r}_{2}}\Delta {{r}^{2}}}} + \frac{2}{{\Delta r}}\left( {\frac{2}{{r_{2}^{2}}} + {{\alpha }^{2}}} \right)} \right) + \\ + \,\,{{{v}}_{{N - 1}}}\left( {\frac{3}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{2}}\Delta {{r}^{2}}}} - \frac{1}{{2\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right)} \right) + \\ + \,\,{{{v}}_{{N - 2}}}\left( {\frac{{ - 1}}{{\Delta {{r}^{3}}}}} \right) = 0. \\ \end{gathered} $
Аналогичным образом переобозначим коэффициенты при ${{{v}}_{i}}$: ${{\alpha }_{6}} = \frac{1}{{\Delta {{r}^{2}}}} + \frac{3}{{2{{r}_{2}}\Delta r}} - \frac{1}{{r_{2}^{2}}},\,\,{{\alpha }_{5}} = \frac{{ - 2}}{{\Delta {{r}^{2}}}} - \frac{2}{{{{r}_{2}}\Delta r}},\,\,{{\alpha }_{4}} = \frac{1}{{\Delta {{r}^{2}}}} + $ $ + \,\,\frac{1}{{2{{r}_{2}}\Delta r}},$ ${{\beta }_{8}} = \frac{1}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{2}}\Delta {{r}^{2}}}} - \frac{3}{{2\Delta r}}\left( {\frac{2}{{r_{2}^{2}}} + {{\alpha }^{2}}} \right) + \frac{2}{{r_{2}^{3}}}$, ${{\beta }_{7}} = \frac{{ - 3}}{{\Delta {{r}^{3}}}} - \frac{2}{{{{r}_{2}}\Delta {{r}^{2}}}} + \frac{2}{{\Delta r}}\left( {\frac{2}{{r_{2}^{2}}} + {{\alpha }^{2}}} \right),\,\,\,\,{{\beta }_{6}} = \frac{3}{{\Delta {{r}^{3}}}} + \frac{1}{{{{r}_{2}}\Delta {{r}^{2}}}} - $ $ - \,\,\frac{1}{{2\Delta r}}\left( {\frac{2}{{r_{1}^{2}}} + {{\alpha }^{2}}} \right)$, ${{\beta }_{5}} = \frac{{ - 1}}{{\Delta {{r}^{3}}}}$.
В итоге для второй границы имеем систему:
(27)
$\left\{ \begin{gathered} {{{v}}_{{N + 1}}} = 0 \hfill \\ {{{v}}_{{N + 1}}}{{\alpha }_{6}} + {{{v}}_{N}}{{\alpha }_{5}} + {{{v}}_{{N - 1}}}{{\alpha }_{4}} = 0 \hfill \\ {{{v}}_{{N + 1}}}{{\beta }_{8}} + {{{v}}_{N}}{{\beta }_{7}} + {{{v}}_{{N - 1}}}{{\beta }_{6}} + {{{v}}_{{N - 2}}}{{\beta }_{5}} = 0. \hfill \\ \end{gathered} \right.$Из (27) видно, что ${{{v}}_{{N - 1}}}$, ${{{v}}_{N}}$ легко выражаются через ${{{v}}_{{N - 2}}}$:
(28)
${{{v}}_{{N - 1}}} = \frac{{ - {{\alpha }_{5}}}}{{{{\alpha }_{4}}}}\left( {\frac{{{{\beta }_{5}}}}{{\left( {{{\beta }_{6}}\frac{{{{\alpha }_{5}}}}{{{{\alpha }_{4}}}} - {{\beta }_{7}}} \right)}}} \right){{{v}}_{{N - 2}}} = {{\kappa }_{3}}{{{v}}_{{N - 2}}},$(29)
${{{v}}_{N}} = \frac{{{{\beta }_{5}}}}{{\left( {{{\beta }_{6}}\frac{{{{\alpha }_{5}}}}{{{{\alpha }_{4}}}} - {{\beta }_{7}}} \right)}}{{{v}}_{{N - 2}}} = {{\kappa }_{4}}{{{v}}_{{N - 2}}}.$Таким образом, граничные условия (21)–(22), записанные через (25)–(26) и (28)–(29), дают представления о трех первых и трех последних точках рассматриваемой области и позволяют связать все значения ${{{v}}_{i}}~\left( {i = \overline {1,N + 1} } \right)$ в СЛАУ через матрицу $A,\left( {i = \overline {4,N - 2} } \right).$
Учитывая (25)–(26) и (28)–(29), удобно исключить из рассмотрения в СЛАУ три первых и последних столбца матрицы $A$. Подсчет для центральной части (20) проводится начиная со значений $i = 4$.
В итоге имеем систему $A{v} = {{\tilde {\lambda }}_{i}}{v}$, где $A$ — квадратная матрица размера $\left( {N - 5) \times (N - 5} \right)$. Подсчет происходит по $i$: $i = \overline {4,N - 2} $. Приведем пример матрицы А для случая N = 9, ${{r}_{i}} = {{r}_{1}} + \left( {i - 1} \right)\Delta r,~\Delta r = \frac{{\left( {{{r}_{{N + 1}}} - {{r}_{1}}} \right)}}{N}$.
(30)
$A = \left( {\begin{array}{*{20}{c}} {M\left( {{{r}_{4}}} \right){{\kappa }_{2}} + L\left( {{{r}_{4}}} \right){{\kappa }_{1}} + K\left( {{{r}_{4}}} \right)}&{I\left( {{{r}_{4}}} \right)}&{H\left( {{{r}_{4}}} \right)}&{F\left( {{{r}_{4}}} \right)} \\ {P\left( {{{r}_{5}}} \right){{\kappa }_{2}} + M\left( {{{r}_{5}}} \right){{\kappa }_{1}} + L\left( {{{r}_{5}}} \right)}&{K\left( {{{r}_{5}}} \right)}&{I\left( {{{r}_{5}}} \right)}&{H\left( {{{r}_{5}}} \right) + F\left( {{{r}_{5}}} \right){{\kappa }_{3}}} \\ {P\left( {{{r}_{6}}} \right){{\kappa }_{1}} + M\left( {{{r}_{6}}} \right)}&{L\left( {{{r}_{6}}} \right)}&{K\left( {{{r}_{6}}} \right)}&{I\left( {{{r}_{6}}} \right) + H\left( {{{r}_{6}}} \right){{\kappa }_{3}} + F\left( {{{r}_{5}}} \right){{\kappa }_{4}}} \\ {P\left( {{{r}_{7}}} \right)}&{M\left( {{{r}_{7}}} \right)}&{L\left( {{{r}_{7}}} \right)}&{K\left( {{{r}_{7}}} \right) + I\left( {{{r}_{7}}} \right){{\kappa }_{3}} + H\left( {{{r}_{7}}} \right){{\kappa }_{4}}} \end{array}} \right).$Решение (11)–(12) проводилось в среде “Matlab”, СЗ спектральной задачи находились при помощи функции ${\text{eig}}$: $Z = {\text{eig}}\left( A \right)$.
Поиск минимального СЗ методом обратных итераций
Спектральная задача на поиск собственных значений (11)–(12), записанная в виде (20), имеет только вещественные и различные положительные собственные значения ${{\tilde {\lambda }}_{i}}$ [2, 22].
Метод обратных итераций [7] предназначен для вычисления младших (наименьших по модулю) собственных значений ${{\tilde {\lambda }}_{k}}$ и отвечающих им собственных векторов (СВ) $\left\{ {{{{v}}_{k}}} \right\}$. Только небольшая часть младших СЗ матрицы близка к СЗ дифференциального уравнения. Точность остальных СЗ мала. В рассматриваемом случае представляет интерес именно минимальное СЗ – ${{\tilde {\lambda }}_{{{\text{min}}}}}$ матрицы $A$.
Рассмотрим общий принцип метода обратных итераций (обратный степенной метод). Младшие СЗ ищут поочередно, используя алгоритм обратных итераций с переменным сдвигом. Для этого выбирают некоторые начальные приближения СЗ ${{\lambda }^{0}}$ и СВ $\left\{ {{v}_{i}^{0}} \right\}$, по возможности близкие к искомым. Далее находят новое приближение для собственного вектора и собственного значения по следующему алгоритму:
(31)
$(A - {{\lambda }^{{\left( s \right)}}}E){{{v}}^{{\left( {s + 1} \right)}}} = {{{v}}^{{\left( s \right)}}},\,\,\,\,{v} = \left\{ {{{{v}}_{i}}} \right\},$(32)
${{\lambda }^{{\left( {s + 1} \right)}}} = {{\lambda }^{{\left( s \right)}}} + {{({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( s \right)}}})} \mathord{\left/ {\vphantom {{({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( s \right)}}})} {({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( {s + 1} \right)}}})}}} \right. \kern-0em} {({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( {s + 1} \right)}}})}},$Какими бы ни были выбраны начальные приближения ${{\lambda }^{0}}$ и $\left\{ {{v}_{i}^{0}} \right\}$, итерации (31)–(32) всегда сходятся [7].
В программе для поиска минимального СЗ – ${{\tilde {\lambda }}_{{{\text{min}}}}}$ матрицы $A$ в качестве нулевого приближения выбраны единичный вектор $\left\{ {{v}_{i}^{0}} \right\}$ и нулевое СЗ – ${{\lambda }^{0}}$. Такой выбор обусловлен положительными значениями спектра СЗ матрицы. Итерации (31)–(32) принимают следующий вид [10]:
(33)
${{{v}}^{{\left( {s + 1} \right)}}} = B{{{v}}^{{\left( s \right)}}},\,\,\,\,B = {{A}^{{ - 1}}},$(34)
${{\lambda }^{{\left( {s + 1} \right)}}} = {{({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( s \right)}}})} \mathord{\left/ {\vphantom {{({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( s \right)}}})} {({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( {s + 1} \right)}}}).}}} \right. \kern-0em} {({{{v}}^{{\left( {s + 1} \right)}}},{{{v}}^{{\left( {s + 1} \right)}}}).}}$(35)
$({{\lambda }^{{\left( {s + 1} \right)}}} - {\text{\;}}{{\lambda }^{{\left( s \right)}}}) < \varepsilon ,$${{\tilde {\lambda }}_{{{\text{min}}}}}$, полученное методом обратных итераций, и минимальное СЗ, рассчитанное при помощи функции eig, совпадают с большой точностью (табл. 1).
Таблица 1.
Результаты расчетов значений точек бифуркации ${{\tilde {\lambda }}_{{{\text{min}}}}}$, пересчет в вязкость жидкости (Ст – Стоксы) и через процентное содержание глицерина
| Входные данные, [H] = см, [${{\tilde {h}}_{{1,2}}}] = $ см |
α | ${{\tilde {\lambda }}_{{{\text{min}}}}}{\text{\;}}$1, ${\text{eig}}\left( A \right)$ | ${{\tilde {\lambda }}_{{{\text{min}}}}}{\text{\;}}$2, метод обратных итераций | $\lambda = \frac{1}{E}$ | Вязкость ν, Ст | Процентное содержание глицерина, % ($T = 20^\circ {\text{C}})$ |
|---|---|---|---|---|---|---|
| ${{\tilde {h}}_{1}} = 1.5$ | ${{\pi }}$ | 1.551 × ${{10}^{7}}$ | 1.553 × ${{10}^{7}}$ | 3940.4 | 0.015 | 15 |
| ${{\tilde {h}}_{2}} = 0.8$ | $2{{\pi }}$ | 1.254 × ${{10}^{7}}$ | 1.254 × ${{10}^{7}}$ | 3541.2 | 0.016 | 17 |
| $H = 5.8$ | $3{{\pi }}$ | 2.149 × ${{10}^{7}}$ | 2.149 × ${{10}^{7}}$ | 4635.8 | 0.013 | 10 |
| ${{\tilde {h}}_{1}} = 1.8$ | ${{\pi }}$ | 2.691 × ${{10}^{6}}$ | 2.692 × ${{10}^{6}}$ | 1640.6 | 0.035 | 39 |
| ${{\tilde {h}}_{2}} = 1.0$ | $2{{\pi }}$ | 2.174 × ${{10}^{6}}$ | 2.174 × ${{10}^{6}}$ | 1474.4 | 0.039 | 41 |
| $H = 5.5$ | $3{{\pi }}$ | 3.725 × ${{10}^{6}}$ | 3.724 × ${{10}^{6}}$ | 1929.9 | 0.030 | 35 |
| ${{\tilde {h}}_{1}} = 1.2$ | ${{\pi }}$ | 8.501 × ${{10}^{6}}$ | 8.503 × ${{10}^{6}}$ | 2916.0 | 0.027 | 32 |
| ${{\tilde {h}}_{2}} = 0.8$ | $2{{\pi }}$ | 6.870 × ${{10}^{6}}$ | 6.868 × ${{10}^{6}}$ | 2620.6 | 0.030 | 35 |
| $H = 5.0$ | $3{{\pi }}$ | 1.176 × ${{10}^{7}}$ | 1.177 × ${{10}^{7}}$ | 3430.7 | 0.023 | 28 |
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
В основе лабораторной установки – вращающаяся платформа с установленной цилиндрической емкостью высотой 38 см и диаметром 30 см. В фальш-дно емкости встроено возвышение из двух соосных цилиндров разных радиусов ${{\tilde {R}}_{{1,2}}}$ и высот ${{\tilde {h}}_{{1,2}}}$ (рис. 2). Сбоку к платформе крепится видеокамера, веб-камера, источник света и лазер. Видеоизображение передается с веб-камеры через вращающиеся контакты по USB-кабелю на компьютер и записывается.
Платформа приводится в движение с помощью электромотора с импульсным питанием. Управление электромотора осуществляется через программируемый модуль “Arduino Uno”. Обратная связь реализована через систему с датчиком Холла. Под платформой установленo четыре постоянных магнита; когда магнит проходит над датчиком, информация поступает в процессор ATmega328P, где происходят ее обработка и вычисление угловой скорости платформы в режиме онлайн.
Система меняет количество подаваемых на электромотор импульсов и интервалы между ними в соответствии с вычисленным значением угловой скорости. Скорость вращения платформы соответствует заданной с максимальной точностью – до одного/двух оборотов в минуту.
Чтобы избежать влияния кривизны свободной поверхности жидкости на топографический вихрь, сверху над возмущением шальф-дна на штативе помещается прозрачная цилиндрическая пластиковая банка с плоским дном. В результате слой жидкости над “подводной горой” принимает фиксированную толщину ${{H}_{0}}$.
После запуска платформы требуется некоторое время для раскрутки установки и выхода скорости вращения на стационарный режим (рис. 3). Когда жидкость в сосуде уже движется, как твердое тело, подводное возмущение поднимается из фальш-дна со скоростью вытягивания ${{\mathbb{W}}_{0}} = 1\,\,{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$. Этот процесс можно сопоставить с подвижками океанического дна.
Для визуализации движения жидкости и ее записи на видео одновременно с процессом вытягивания из фальш-дна цилиндрических возмущений в область топографического вихря впрыскиваются алюминиевая пудра и марганцовка.
РЕЗУЛЬТАТЫ
Приведем некоторые результаты подсчетов ${{\tilde {\lambda }}_{{{\text{min}}}}}$, полученные в программе для разных конфигураций экспериментального подводного возмущения (подводной горы). Отметим три группы входных данных, использующихся при моделировании рельефа дна в программе:
первая группа: ${{\tilde {h}}_{1}} = 1.5\,\,{\text{см}},\,\,\,\,~{{\tilde {h}}_{2}} = 0.8\,\,{\text{см}},$ $H = 5.8\,\,{\text{см}},{{\tilde {R}}_{1}} = 1.6\,\,{\text{см}},~{{\tilde {R}}_{2}} = 4.3\,\,{\text{см}}$;
вторая группа: ${{\tilde {h}}_{1}} = 1.8\,\,{\text{см}},\,\,\,\,~{{\tilde {h}}_{2}} = 1.0\,\,{\text{см}},$ $H = 5.5\,\,{\text{см}},{{\tilde {R}}_{1}} = 1.6\,\,{\text{см}},~{{\tilde {R}}_{2}} = 4.3\,\,{\text{см}}$;
третья группа: ${{\tilde {h}}_{1}} = 1.2\,\,{\text{см}},\,\,\,\,{{\tilde {h}}_{2}} = 0.8\,\,{\text{см}},$ $H = 5.0\,\,{\text{см}},{{\tilde {R}}_{1}} = 1.6\,\,{\text{см}},~{{\tilde {R}}_{2}} = 4.3\,\,{\text{см}}.$
Скорость вращения лабораторной установки составляет 15 об/мин, что соответствует $\omega = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ рад/с, т. е. ${{f}_{0}} = \pi {\text{\;}}{{{\text{с}}}^{{ - 1}}}$. В таком случае условие возникновения бифуркации (14), записанное в размерном виде, дает следующие допустимые значения скорости потока в кольцевой области над уступом для каждой из групп входных данных:
первая группа: $1.863{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}} < {{\tilde {U}}_{0}} < 2.347{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$;
вторая группа: $2.456{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}} < {{\tilde {U}}_{0}} < 3.068{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$;
третья группа: $2.161{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}} < {{\tilde {U}}_{0}} < 2.610{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$.
С помощью теоремы Стокса (${\text{I}}$) и геометрического соотношения $\frac{{{{{\tilde {U}}}_{0}}}}{{{{{\tilde {R}}}_{2}}}} = \frac{{{{\mathbb{W}}_{0}}}}{{{{H}_{0}}}}$ (II) получены оценки реальных скоростей в центре кольцевой области для каждой из конфигураций:
первая группа: ${{\tilde {U}}_{0}} = 1.983{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{\;}}\left( {\text{I}} \right)$, ${{\tilde {U}}_{0}} = 1.870{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{\;}}\left( {{\text{II}}} \right)$;
вторая группа: ${{\tilde {U}}_{0}} = 2.577{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{\;}}\left( {\text{I}} \right)$, ${{\tilde {U}}_{0}} = 1.153{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{\;}}\left( {{\text{II}}} \right)$;
третья группа: ${{\tilde {U}}_{0}} = 2.137{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{\;}}\left( {\text{I}} \right)$, ${{\tilde {U}}_{0}} = 2.150{\text{\;}}{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{\;}}\left( {{\text{II}}} \right)$.
Первая группа входных данных, при которой достигается наилучшее приближение условия ${{h}_{0}} \ll {{H}_{0}}$, полностью удовлетворяет критерию бифуркации (14). Для такой конфигурации подводного возмущения были получены значения первых точек бифуркации ${{\tilde {\lambda }}_{{{\text{min}}}}}1,2$, которые впоследствии были пересчитаны в требуемые для бифуркации значения вязкости жидкости (табл. 1). Коэффициенты вязкости получились достаточно малыми, достаточно близкими к вязкости воды. Но, к сожалению, требуемую высоту бассейна ${{H}_{0}} = 5.8$ см воспроизвести в лабораторных условиях не удалось.
Таким образом, эксперименты проводились с параметрами установки, соответствующими значениям второй и третьей групп входных данных, с 40 и 30%-м содержаниями глицерина соответственно.
В ходе экспериментов получены следующие результаты.
1. Лабораторное моделирование задачи обтекания подводной горы, проводимое с 30%-м раствором глицерина, позволило зафиксировать формирование цилиндрического столба Тейлора [20] над меньшим из цилиндров (рис. 4). Удалось подтвердить образование вертикальных слоев Стьюартсона над боковыми границами цилиндров, аппроксимирующих подводное возмущение рельефа дна.
Рис. 4.
Кадры видеозаписей экспериментов, демонстрирующие формирование цилиндрического столба Тейлора.

2. В экспериментах с 40%-м раствором глицерина зафиксирован процесс возникновения купольной поверхности формирующегося верхнего вихревого тора (рис. 5).
ЗАКЛЮЧЕНИЕ
Составлена программа численного решения спектральной задачи, описывающей переход к бифуркации топографического вихря в кольцевой области над цилиндрическими подводными возмущениями дна во вращающейся жидкости.
Двумя методами найдены минимальные собственные значения спектра для различных конфигураций подводного возмущения. Показано совпадение обоих решений с большой точностью. По полученным данным рассчитаны величины вязкости жидкости, определяющие развитие неустойчивости в однородной среде, проведены лабораторные эксперименты с различными значениями коэффициентов вязкости жидкости, результаты которых зафиксированы в фото- и видеоматериалax, частично подтверждающиx теоретические оценки.
В связи с несоблюдением строгого стационарного режима, задаваемого через программируемый модуль, а также при очевидных сложностях выполнения критерия бифуркации (14) возможно отклонение от теории вторичных тороидальных вихрей для расчетных коэффициентов вязкости при лабораторном моделировании. Теоретически разбиение топографического вихря на вихревые торы происходит лишь в случае попадания решений в определенные точки бифуркации, что в лабораторном эксперименте затруднено. Данная проблема требует дальнейшего изучения.
Список литературы
Березин И.С., Жидков Н.П. Методы вычислений. М.: ГИФМЛ, 1962. 464 с.
Зырянов В.Н. Вторичные тороидальные вихри Тейлора над возмущениями дна во вращающейся жидкости // ДАН. 2009. Т. 427. № 2. С. 192–198.
Зырянов В.Н. Теория установившихся океанических течений. Л.: Гидрометеоиздат, 1985. 248 с.
Зырянов В.Н. Топографические вихри в динамике морских течений. М.: ИВП РАН, 1995. 240 с.
Зырянов В.Н. Экспериментальные исследования вихревых торов над возмущениями дна во вращающейся однородной жидкости // Процессы в геосредах. 2015. № 2(2). С. 46–55.
Зырянов В.Н., Рыжов Е.А., Кошель К.В. Вихревые торы над возмущениями дна во вращающейся жидкости // ДАН. 2013. Т. 450. № 2. С. 171–175.
Калиткин Н.Н., Альшина Е.А. Численные методы. Численный анализ. М.: Академия, 2013. 295 с.
Кляцкин В.И. Метод погружения в теории распространения волн. М.: Наука, 1986. 256 с.
Козлов В.Ф. Модели топографических вихрей в океане. М.: Наука, 1983. 200 с.
Колобов А.Г. Численные методы линейной алгебры: учебно-методическое пособие // Владивосток: Изд-во ДВФУ, 2008. 36 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Юдович В.И. Вторичные течения и неустойчивость жидкости между вращающимися цилиндрами // ПММ. 1966. Т. 30. № 4. С. 689–698.
Boehlert G.W., Genin A. A review of the effect of seamounts on biological processes // Seamounts, Islands and Atolls. 1987. V. 43. P. 319–334.
Huppert H.E. Some remarks on the initiation of inertial Taylor columns // J. Fluid Mech. 1975. V. 67. P. 397–412.
Huppert H.E., Bryan K. Topographically generated eddies // Deep Sea Res. 1976. V. 23. P. 655–679.
Kitani K., Shimazaki K. On the hydrography of the northern part of the Okhotsk Sea in summer // Bull. Fac. Fish. Hokkaido Univ. 1971. V. 12. P. 231–242.
Koshel K.V., Ryzhov E.A., Zyryanov V.N. Toroidal vortices over isolated topography in geophysical flows // J. Fluid Dyn. Res. 2014. V. 46. № 3. P. 031405–031417.
Sokolovskiy M.A., Verron J. Dynamics of vortex structures in a stratified rotating fluid // Series Atmospheric and Oceanographic Sciences Library. Cham; Heidelberg; N. Y.; Dordrecht; London: Springer, 2014. V. 47. 382 p. https://doi.org/10.1007/978-3-319-00789-2
Stewartson K. On slow transverse motion of a sphere through a rotating fluid // J. Fluid Mech. 1967. V. 30. P. 357–369.
Taylor G.I. Experiments on the motion of solid bodies in rotating fluids // Proc. Roy. Soc. London. 1923. P. 213–218.
Taylor G.I. Stability of a viscous liquid contained between two rotating cylinders // Phil. Trans. Royal Society. 1923. V. A223. № 605–615. P. 289–343.
Zyryanov V.N. Secondary toroidal vortices above seamounts // J. Marine Res. 2011. V. 69. P. 463–481.
Дополнительные материалы отсутствуют.





