1. На главную
  2. Электронные версии
  3. Водные ресурсы
  4. T. 49, № 5, 2022

Водные ресурсы, 2022, T. 49, № 5, стр. 552-567

Мировой опыт численного моделирования динамики потока в устьях рек

А. М. Алабян a, b, *, И. Н. Крыленко a, b, С. В. Лебедева c, d, Е. Д. Панченко a, b

a Московский государственный университет им. М.В. Ломоносова, географический факультет
19991 Москва, Россия

b Институт водных проблем РАН
119333 Москва, Россия

c Северное управление по гидрометеорологии и мониторингу окружающей среды
163020 Архангельск, Россия

d Государственный океанографический институт им. Н.Н. Зубова
119034 Москва, Россия

* E-mail: andrei_alabyan@mail.ru

Поступила в редакцию 30.01.2022
После доработки 12.04.2022
Принята к публикации 12.04.2022

Полный текст (PDF)

Аннотация

Представлены история, математическая основа и обзор современного состояния численного моделирования динамического взаимодействия речных и морских вод в устьевых областях рек. Обобщен обширный и разнообразный опыт отечественных и зарубежных исследователей со второй половины ХХ в. по настоящее время.

Ключевые слова: численное моделирование, устьевая область, гидродинамика, динамическое взаимодействие речных и морских вод, распределение стока по рукавам дельты, неустановившееся течение, система мониторинга устьев рек, программный комплекс.

ВВЕДЕНИЕ

Находясь на географической границе суши и океана, устья рек привлекают внимание как гидрологов, так и океанологов. В технологических аспектах численного моделирования динамического взаимодействия речных и морских вод нашли отражение методические подходы, принятые как в гидрологии суши, так и в океанологии. В то время как “речные” модели исторически развивались от одномерной схематизации потока к двумерной через разложение основных действующих сил на их продольную и поперечную составляющие, модели океана изначально создавались трехмерными, однако для мелководных шельфовых зон допускалось их превращение в двумерные путем интегрирования по глубине. Существенное различие наблюдалось и в параметризации гидравлического сопротивления: в гидрологических моделях основным фактором диссипации энергии считалось трение на поверхности раздела потока и русла, а в океанологических – турбулентная вязкость водной толщи.

Численное моделирование гидродинамических процессов в устьях рек стало развиваться со второй половины ХХ в. практически сразу после начала повсеместного применения электронно-вычислительных машин (ЭВМ, компьютеров) в инженерных расчетах. Этому способствовал уже хорошо сформированный к концу XIX в. математический аппарат, ориентированный на решениe гидрологических, океанологических, гидравлических и гидродинамических задач различной сложности. Благодаря появлению ЭВМ стал возможным синтез инженерного подхода, основанного на работах Шези, Дарси, Вейсбаха и других выдающихся гидравликов конца XVIII – начала XIX вв., с разработками Ньютона, Эйлера, Бернулли, Навье и Стокса в области теоретической гидродинамики, которые воспринимались современниками лишь как красивые математические построения, далекие от практических задач. Предпринятые в “докомпьютерную эпоху” Лагранжем и Сен-Венаном попытки синтеза этих подходов значительно приблизили теоретическую гидромеханику к инженерной речной гидравлике, заложив основу современного видения и описания гидродинамических процессов в устьях рек.

С появлением первых ЭВМ стали развиваться численные методы решения дифференциальных уравнений (методы конечных разностей, конечных элементов, конечных объемов и др.), в основе которых была замена дифференциальных уравнений системами алгебраических. Начавшись в середине XX в. [83], разработка численных методов решения дифференциальных гидродинамических уравнений происходила в 1960-е гг. весьма интенсивными темпами параллельно с совершенствованием вычислительной техники и увеличением ее производительности [20, 28, 36, 111]. В конечном итоге это привело к появлению широкого спектра численных гидродинамических моделей различной степени сложности и детальности, ориентированных на решение разнообразных практических задач в одномерной, двумерной и даже трехмерной схематизации водного потока.

В зависимости от того, является устье приливным или неприливным, а также от пространственных и временны́ х масштабов исследования для практических расчетов могут применяться модели, основанные как на простейшем математическом аппарате, разработанном для квазиравномерных водных потоков (с применением формулы Шези, модулей сопротивления и т. п.), так и на сложных системах нестационарных дифференциальных уравнений (Сен-Венана, Навье–Стокса и др.), аналитическое решение которых до появления численных методов было возможно лишь для частных случаев при существенных упрощениях.

Важным моментом в численном гидродинамическом моделировании стала разработка ведущими мировыми научными центрами специализированных программных продуктов, снабженных дружественным интерфейсом пользователя и ориентированных на выполнение моделирования специалистами, не являющимися разработчиками моделей и компьютерных программ. Наиболее популярные из них в настоящее время наряду с отечественной серией STREAM [7] – нидерландский DELFT [71], датский MIKE [80], французский TELEMAC [76], американские HEC [68] и POM [104]. Большинство этих программных продуктов изначально имело коммерческий характер, однако в последние годы набирает все большую популярность раскрытие пользователям программных кодов гидродинамических моделей через интернет с регистрацией и предоставлением возможности их самостоятельной компиляции.

Предлагаемая статья не претендует на полный охват современных достижений в области численного моделирования динамики потока в устьях рек мира. В ней освящены основные этапы становления численного моделирования и представлен обзор исследований, выполненных в наиболее интересных с точки зрения гидравлики потока или наиболее освоенных устьях рек за последние два-три десятилетия. Эти исследования выполнены с использованием математических моделей разной мерности, детальности схематизации расчетной области, степени разработанности пользовательского интерфейса и пространственно-временны́ х масштабов исследуемых процессов.

ОТ РАСЧЕТНЫХ МЕТОДОВ К ЧИСЛЕННЫМ МОДЕЛЯМ

Из стационарных задач устьевой гидравлики наиболее актуальной исторически считалась задача о распределении расходов воды по дельтовым водотокам. До появления компьютеров задача о распределении стока по рукавам разветвленного русла обычно решалась графоаналитическим методом [24]. Последующая разработка итерационного метода расчета распределения расходов [47] предопределила появление первых численных моделей, ориентированных на решение стационарных гидравлических задач применительно к многорукавным дельтам [11, 27, 35, 40, 46].

Эти модели позиционировались авторами как “расчетные методы” и рассматривались как альтернатива (или же дополнение) к весьма распространенному в середине ХХ в. гидравлическому моделированию [26, 97]. Однако в современном представлении эти расчетные методы, по сути, были именно моделями, ориентированными на предвычисление изменения гидравлического режима многорукавной дельты в результате непосредственного техногенного воздействия на русла водотоков [32] или трансформации гидрологического режима реки [5].

Решение нестационарных задач устьевой гидравлики в то время было связано в основном с исследованием распространения приливных волн и сгонно-нагонных колебаний уровня воды вверх по руслу реки [111]. Именно численное решение дифференциального уравнения в частных производных сначала для неразветвленного русла, а затем и для системы дельтовых рукавов [23] заложило основу современных подходов к моделированию нестационарной гидродинамики приливных устьев сложной морфологии в масштабах времени от синоптического до приливного.

МАТЕМАТИЧЕСКАЯ ОСНОВА ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

При одномерной (1D) схематизации водного потока рассматриваются его характеристики, осредненные по поперечному сечению. Система дифференциальных уравнений, описывающая движение воды в одномерном виде, названа в честь французского математика и инженера Адемара Жан-Клода Барре де Сен-Венана, впервые сформулировавшего и записавшего ее в [114] в следующем виде (некоторые обозначения изменены в соответствии с общепринятыми в настоящее время):

(1)
$ - \frac{{\partial z}}{{\partial x}} = \frac{1}{{\text{g}}}\frac{{\partial u}}{{\partial t}} + \frac{u}{{\text{g}}}~\frac{{\partial u}}{{\partial x}} + \frac{\tau }{{\rho {\text{g}}R}},$
(2)
$\frac{{\partial \left( {u\omega } \right)}}{{\partial x}} + \frac{{\partial \omega }}{{\partial t}} = 0,$
где х – продольная координата вдоль динамической оси потока, направленная вниз по течению; t – время; z – отметка свободной поверхности; u – средняя скорость; ω – площадь поперечного сечения; g – ускорение свободного падения; ρ – плотность воды; τ – касательное напряжение на смоченном периметре потока; R – гидравлический радиус, который может быть принят равным его глубине h для русловых потоков, когда их ширина превосходит глубину на порядок и более.

В системе уравнений Сен-Венана уравнение движения (1) отражает баланс сил тяжести, трения и инерции, действующих на водный поток, а уравнение неразрывности (2) связывает изменения расхода воды $Q~$ = uω с наполнением русла на бесприточном участке.

Левая часть уравнения движения представляет собой уклон водной поверхности I = –$\partial $z/$\partial $x, который также называют “геометрическим уклоном”. Член уравнения движения $\frac{1}{{\text{g}}}\frac{{\partial u}}{{\partial t}}~$ принято называть локальным ускорением, $\frac{u}{{\text{g}}}~\frac{{\partial u}}{{\partial x}}$ – конвективным ускорением, а их вместе – “конвективными членами”. Третий член правой части уравнения (1) представляет собой уклон трения ${{I}_{{{\text{тр}}}}}$ = $\frac{\tau }{{\rho {\text{g}}R}}$, называемый также “гидравлическим уклоном” или “фрикционным членом”. В работе Сен-Венана было принято допущение, что гидравлическое сопротивление при неустановившемся движении воды определяется трением на поверхности раздела между потоком и руслом и принимается равным сопротивлению при равномерном течении с той же средней скоростью в русле, с такими же морфометрическими характеристиками и шероховатостью. Это допущение, довольно спорное с точки зрения современных представлений о диссипации энергии в русловых потоках, продолжает широко использоваться при расчетах. При этом на практике гидравлический уклон в уравнении движения (1) может выражаться исходя из формул инженерной гидравлики (Шези, Шези–Маннинга, Дарси–Вейсбаха и т. п.):

(3)
${{I}_{{{\text{тр}}}}} = \frac{{{{u}^{2}}}}{{{{C}^{2}}R}} = \frac{{{{n}^{2}}{{u}^{2}}}}{{{{R}^{{\frac{4}{3}}}}}} = \frac{{\lambda {{u}^{2}}}}{{8{\text{g}}R}},$
где С – коэффициент Шези; n – коэффициент шероховатости Маннинга; λ − безразмерный коэффициент гидравлического сопротивления, заимствованный из технической гидравлики, где он изначально использовался для расчета потерь напора по формуле Дарси–Вейсбаха, называемой также “первой водопроводной формулой”.

Значения инерционных членов уравнения движения были впоследствии уточнены за счет введения в них “коррективов скорости”, выражающих неравномерность ее распределения в поперечном сечении потока:

(4)
$\alpha = 1 + 3\frac{{\int {\Delta {{u}^{2}}d\omega } }}{{{{u}^{2}}\omega }},$
(5)
${{\alpha }_{0}} = 1 + \frac{{\int {\Delta {{u}^{2}}d\omega } }}{{{{u}^{2}}\omega }},$
где $\alpha $ – корректив кинетической энергии (коэффициент Кориолиса); $~{{\alpha }_{0}}$ – корректив количества движения (коэффициент Буссинеска); Δu – отклонение местной скорости от средней по поперечному сечению. В этом случае локальное ускорение в формуле (1) принимает вид $\frac{{{{\alpha }_{0}}}}{{\text{g}}}\frac{{\partial u}}{{\partial t}}$, а конвективное ускорение – $\frac{{\alpha u}}{{\text{g}}}~\frac{{\partial u}}{{\partial x}}$.

Для устьевых областей в зоне контакта речной и морской воды в правую часть уравнения движения (1) может добавляться “плотностной член” $\frac{h}{{2\rho }}\frac{{\partial \rho }}{{\partial x}}$, обусловленный продольным градиентом плотности воды, зависящей от ее солености и температуры.

В случае, когда в результате приливных и сгонно-нагонных колебаний уровня моря в русле реки возможно формирование реверсивных течений (попеременного движения водных масс из реки в море и обратно), фрикционный член записывается в виде $\frac{{u\left| u \right|}}{{{{C}^{2}}R}}$ (или $\frac{{{{n}^{2}}u\left| u \right|}}{{{{R}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}}}$, или $\frac{{\lambda u\left| u \right|}}{{8{\text{g}}R}}$ в зависимости от способа выражения уклона трения). Таким образом обеспечивается действие силы гидравлического трения в сторону, противоположную направлению течения (скорость и фрикционный член имели бы одинаковые знаки) [43, 46].

С учетом данных преобразований одномерное уравнение движения (1) в системе Сен-Венана для устьевых участков принимает вид, в котором используется в большинстве 1D-моделей:

(6)
$\frac{{{{\alpha }_{0}}}}{{\text{g}}}\frac{{\partial u}}{{\partial t}} + \frac{{\alpha u}}{{\text{g}}}~\frac{{\partial u}}{{\partial x}} + \frac{{u\left| u \right|}}{{{{C}^{2}}R}} + \frac{h}{{2\rho }}\frac{{\partial \rho }}{{\partial x}} + \frac{{\partial z}}{{\partial x}} = 0.$

Переход к двумерным продольно-поперечным (“плановым”, 2D) моделям осуществляется за счет разложения основных действующих сил на продольную и поперечную составляющие в декартовой, криволинейной или полярной системе координат.

Двумерные плановые численные модели базируются на “уравнениях мелкой воды” для двумерного потока (или уравнения Сен-Венана в двумерном виде). В наиболее простой форме (без учета дополнительных внешних сил – Кориолиса, ветрового и волнового воздействия, атмосферного давления и т. п.) система уравнений имеет вид:

(7)
$\begin{gathered} \frac{1}{{\text{g}}}\frac{{\partial {{u}_{x}}}}{{\partial t}} + \frac{{{{u}_{x}}}}{{\text{g}}}\frac{{\partial {{u}_{x}}}}{{\partial x}} + \frac{{{{u}_{y}}}}{{\text{g}}}\frac{{\partial {{u}_{x}}}}{{\partial y}} + \frac{{{{n}^{2}}U{{u}_{x}}}}{{{{h}^{{\frac{4}{3}}}}}} = - \frac{{\partial z}}{{\partial x}}, \\ \frac{1}{{\text{g}}}\frac{{\partial {{u}_{y}}}}{{\partial t}} + \frac{{{{u}_{x}}}}{{\text{g}}}\frac{{\partial {{u}_{y}}}}{{\partial x}} + \frac{{{{u}_{y}}}}{{\text{g}}}\frac{{\partial {{u}_{y}}}}{{\partial y}} + \frac{{{{n}^{2}}U{{u}_{y}}}}{{{{h}^{{\frac{4}{3}}}}}} = - \frac{{\partial z}}{{\partial y}}, \\ \frac{{\partial \left( {{{u}_{x}}h} \right)}}{{\partial x}} + \frac{{\partial \left( {{{u}_{y}}h} \right)}}{{\partial y}} = - \frac{{\partial z}}{{\partial t}},~ \\ \end{gathered} $
где $U = \sqrt {u_{x}^{2} + u_{y}^{2}} $ – модуль скорости течения. Члены $\frac{1}{{\text{g}}}\frac{{\partial {{u}_{x}}}}{{\partial t}}$ и $\frac{1}{{\text{g}}}\frac{{\partial {{u}_{y}}}}{{\partial t}}$ характеризуют локальное ускорение по осям x и y, а $\frac{{{{u}_{x}}}}{{\text{g}}}\frac{{\partial {{u}_{x}}}}{{\partial x}}$, $\frac{{{{u}_{y}}}}{{\text{g}}}\frac{{\partial {{u}_{x}}}}{{\partial y}}$, $\frac{{{{u}_{x}}}}{{\text{g}}}\frac{{\partial {{u}_{y}}}}{{\partial x}}$, $\frac{{{{u}_{y}}}}{{\text{g}}}\frac{{\partial {{u}_{y}}}}{{\partial y}}$ – конвективные ускорения; $~\frac{{{{n}^{2}}U{{u}_{x}}}}{{{{h}^{{\frac{4}{3}}}}}}$ и $\frac{{{{n}^{2}}U{{u}_{y}}}}{{{{h}^{{\frac{4}{3}}}}}}$ – продольный и поперечный уклоны трения (здесь выражены исходя из формулы Шези–Маннинга, но могут использоваться и другие выражения, в том числе с учетом турбулентной вязкости). При этом коэффициент шероховатости n трактуется как показатель гидравлического сопротивления, включающего в себя как трение о дно, так и влияние ледовых явлений, волнения и ветра, а в отдельных случаях – также и турбулентную вязкость. Значение коэффициента шероховатости в разных направлениях (по x и по y) может быть различным, но на практике это учитывается редко.

В устьевой гидродинамике используются и двумерные продольно-вертикальные (“профильные”, 2DH) модели, в которых осреднение выполняется по ширине потока или по области его динамической оси. Такие модели ориентированы главным образом на исследование эстуарной плотностной циркуляции, формирования галоклина и интрузии соленых морских вод в речное русло. Однако в последние годы для решения таких задач все чаще применяются трехмерные модели.

Математическая основа трехмерных моделей (3D) устьевой гидродинамики – система уравнений Навье–Стокса, состоящая из трех уравнений движения, выражающих баланс сил вдоль каждой из координатных осей, и уравнения неразрывности:

(8)
$\begin{gathered} \rho \frac{{d{{{v}}_{x}}}}{{dt}} = \rho {{F}_{x}} - \frac{{\partial p}}{{\partial x}} + {{\mu }_{{\text{т}}}}\Delta , \\ \rho \frac{{d{{{v}}_{y}}}}{{dt}} = \rho {{F}_{y}} - \frac{{\partial p}}{{\partial y}} + {{\mu }_{{\text{т}}}}\Delta {{{v}}_{y}}, \\ \rho \frac{{d{{{v}}_{z}}}}{{dt}} = \rho {{F}_{z}} - \frac{{\partial p}}{{\partial z}} + {{\mu }_{{\text{т}}}}\Delta {{{v}}_{z}}, \\ \frac{{\partial {{{v}}_{x}}}}{{\partial x}} + \frac{{\partial {{{v}}_{y}}}}{{\partial y}} + \frac{{\partial {{{v}}_{z}}}}{{\partial z}} = 0,~ \\ \end{gathered} $
где ${{F}_{x}}$, $~{{F}_{y}}$, ${{F}_{z}}$ – компоненты суммарного воздействия внешних сил, действующих по осям x, y, z декартовой системы координат; $p$ – давление; ${{\mu }_{{\text{т}}}}$ – коэффициент турбулентной вязкости; Δ – оператор Лапласа.

В трехмерных моделях гидравлическое сопротивление (третий член правой части уравнений движения) для внутренних слоев потока задается через турбулентную вязкость, которая (как и шероховатость в двумерных моделях) может сильно отличаться по разным направлениям и зависит от пространственных масштабов расчетной сетки. Для ее определения могут использоваться формулы, заимствованные из полуэмпирической теории турбулентности.

СТРАТЕГИЯ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Корректное решение практических задач устьевой гидравлики методом компьютерного гидродинамического моделирования вне зависимости от мерности и специфики применяемой модели предполагает выполнение следующих этапов.

1. Настройка модели на объект – оцифровка контуров устьевой области или исследуемой ее части, построение расчетной сетки, создание цифровой модели рельефа, подготовка гидрологических данных для задания граничных условий (расходы воды на входных “речных” границах расчетной области и уровни воды на ее выходных “морских” границах).

2. Калибровка модели – подбор ее параметров (коэффициентов шероховатости, параметров турбулентной вязкости и др.) в ходе воспроизведения (“симуляции”) реальной гидрологической ситуации, для которой есть результаты полевых измерений – отметки уровня воды в ключевых точках, скорости течения, распределение расходов воды по рукавам дельты и т. п. В процессе калибровки добиваются максимального совпадения фактических и смоделированных полей характеристик потока.

3. Верификация (валидация) модели – проверка на независимом материале полученных в ходе калибровки параметров модели. Предпочтительно использовать для этой цели аналогичные гидрологические данные, полученные при других уровнях и расходах воды, а для приливных устьев – для другой фазы сизигийно-квадратурного цикла. Степень совпадения измеренных и смоделированных данных в идеале должна быть сопоставима с точностью гидрометрических измерений.

4. Сценарные расчеты – воспроизведение той или иной гидрологической ситуации, для которой нет (или недостаточно) натурных данных. Это могут быть как неизученные соотношения фаз гидрологического режима реки, сгонно-нагонных колебаний уровня моря и сизигийно-квадратурного приливного цикла (в том числе при изменении среднего уровня моря), так и случаи техногенного воздействия на речной поток посредством дноуглубления, строительства струенаправляющих сооружений, перекрытия отдельных рукавов дельты и т. п.

Следует заметить, что выполнение сценарных расчетов на неверифицированных и, тем более, некалиброванных моделях может выполняться лишь для анализа наиболее общих тенденций в изменении характера динамического взаимодействия речных и морских вод при изменении гидрологического режима реки или уровня моря. Использование результатов подобного “моделирования” при решении практических задач может быть допустимым лишь в исключительных случаях, делать это можно с величайшей осторожностью и только при наличии альтернативных методов оценки соответствующих изменений.

СОВРЕМЕННЫЕ ИССЛЕДОВАНИЯ В ОБЛАСТИ МОДЕЛИРОВАНИЯ УСТЬЕВЫХ ОБЛАСТЕЙ В МИРЕ

За последние десятилетия возможности компьютерного гидродинамического моделирования значительно возросли в связи как с развитием вычислительных ресурсов, так и с существенным прогрессом в технологиях натурных измерений, ориентированных на калибровку и верификацию численных моделей.

Рост производительности компьютеров сделал реальным решение трехмерных гидродинамических задач с технической точки зрения. Разработаны, совершенствуются и получили большее распространение программные комплексы для трехмерного гидродинамического моделирования: РОМ [104], Delft3D [71], TELEMAC-3D [76], MIKE3 [80], INMOM [29], STREAM_3D [14] и ряд других. Увеличение компьютерных мощностей дает возможность охватывать все более крупные области без потери детальности воспроизведения рельефа. Время расчета при этом уменьшается соответственно увеличению производительности процессоров, значимый прирост вычислительных ресурсов связан с переходом на распараллеленные расчеты на графическом процессоре NVIDIA с использованием технологии CUDA [7].

В табл. 1 представлены наиболее часто встречающиеся в публикациях программные комплексы, базирующиеся на одномерной, двумерной и трехмерной схематизации потока.

Таблица 1.  

Наиболее распространенные при моделировании динамики потока в устьях программные комплексы

№ Название ПК Схематизация Доступность ПК Место разработки
1 MIKE 1D, 2D, 3D Коммерческий Датский гидравлический институт (DHI – Danish Hydraulic Institute), Дания
2 HEC-RAS 1D, 2D Некоммерческий Инженерный корпус армии США (Army Corps of Engineers, Hydrologic Engineering Center), США
3 STREAM 1D, 2D, 3D Коммерческий Аквариус Аналитик, ИВП РАН, Россия
4 INMOM 3D Некоммерческий ИВМ РАН, Россия
5 LISFLOOD-FP 2D » Бристольский университет (University of Bristol), Великобритания
6 TELEMAC 1D, 2D, 3D » “Electricité de France”, Франция
7 DELFT 2D, 3D » “Deltares”, Нидерланды
8 SOBEK 1D, 2D » То же
9 POM 3D » Университет Принстона (Princeton University)
10 FVCOM 2D, 3D » Массачусетский университет в Дартмуте (University of Massachusetts-Dartmouth), США
11 Hydrodyn-FLOSOFT 2D, 3D Коммерческий “ENVIRON”, Индия
12 CMS 2D Некоммерческий Инженерный корпус армии США (US Army Corps of Engineers), США
13 SisBaHia 2D, 3D » Институт инженерии COPPE/UFRJ, Бразилия
14 SCHISM 1D, 2D, 3D » Орегонский университет медицинских наук (Oregon Health Sciences University), США
15 UnTRIM 2D, 3D » Университет Тренто (Trento University), Италия

Ввиду революционного прорыва в разработке и внедрении новейшего гидрометрического и геодезического оборудования, включая акустические профилографы (ADCP), дифференциальные системы спутникового позиционирования и автоматические регистраторы уровня воды, появилась возможность выполнять гидрологические исследования в устьях на принципиально новом уровне [2, 3, 4, 60, 86, 101, 102, 110]. Применение современных методов измерения уменьшает неопределенность и неточность в задании исходных данных о рельефе, гидрологических характеристиках водотоков, характере распространения приливной волны на взморье или вдоль морского края дельты, расширяет набор данных для задания граничных условий, детальной калибровки и верификации моделей в различных створах.

Можно выделить следующие основные направления современных исследований, связанные с моделированием в устьевых областях, по классу решаемых задач:

1. разработка методов моделирования, тестирование модельных комплексов и их сочетаний на конкретных природных объектах [78, 117, 119], разработка методов калибровки и верификации моделей [77, 103, 116];

2. исследование взаимодействия речного стока и приливных, нагонных волн, моделирование наводнений и других опасных явлений [70, 95, 98, 126];

3. оценка влияния современных и ожидаемых изменений климата на динамику потока в устьях и опасность наводнений [49, 64, 73, 87, 88];

4. мониторинг устьевых процессов, включая динамику потока, транспорт наносов и изменения морфологии устьевых систем [84, 123];

5. решение практических задач: определение оптимальных мест для строительства инженерных сооружений, исследование течений с целью использования приливной энергии, оценка изменения гидродинамического режима в устье под влиянием хозяйственной деятельности [94], обеспечение условий судоходства и работы портовых сооружений [85], исследование интрузии осолоненных вод и ее воздействия на работу водозаборов [16, 99, 115].

Большинство статей последнего десятилетия рассматривают динамику потока во временнóм масштабе от нескольких часов (приливный масштаб времени) до одного месяца (синоптический масштаб).

Исследования, связанные с моделированием гидродинамики устьевых областей, довольно равномерно охватывают Земной шар (рис. 1; табл. 2) и посвящены дельтам, приливным эстуариям и системам фьордов, имеющим важное социально-экономическое значение. В Европе гидродинамическое моделирование широко используется для решения практических задач уже несколько десятилетий и наиболее распространено в Великобритании и Нидерландах [69, 78, 92, 95, 110]. Гидродинамическим моделированием охвачены устьевые области крупнейших рек, таких как Амазонка [60], Янцзы [81, 94], Меконг [64, 117], Нил [62, 100], Конго [67], Ла-Плата [106], Миссисипи [98, 105, 120], Маккензи [108], Святого Лаврентия [101, 102], Колумбия [86]. Наибольшее число отечественных исследований посвящено устьевым областям Северной Двины [37, 39, 40, 49, 63], Волги [1, 18, 19, 52], Оби [10, 21, 51, 53].

Рис. 1.

Устья рек, представленные в публикациях по численному моделированию динамики потока (нумерация объектов соответствует табл. 2).

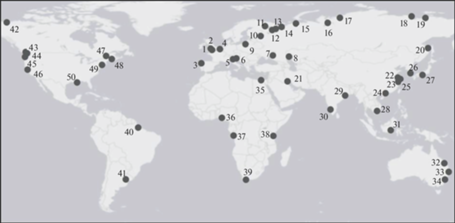
Таблица 2.  

Наиболее значимые устья рек, представленные в публикациях по численному моделированию динамики потока

№ Река Приемный водоем Ссылка № Река Приемный водоем Ссылка
1 Северн Атлантический океан [78, 95] 26 Сумджин (Sumjin) Тихий океан [115]
2 Итчен » [92] 27 Юра (Yura) » [75]
3 Минхо » [82] 28 Меконг Восточно- Вьетнамское море [64, 117]
4 Шельд Северное море [69, 110] 29 Хугли (Hooghly) Бенгальский залив [113]
5 Рецина (Rječina) Адриатическое море [88] 30 Кочин (Cochin) Индийский океан [65]
6 По » [90] 31 Махакам (о. Калимантан) Тихий океан [70]
7 Дон Азовское море [13, 58] 32 Порт-Кертис (Port Curtis) » [74]
8 Волга Каспийское море [1, 18, 19, 52] 33 Брисбэйн (Brisbane) » [93]
9 Преголя, Дейма, Лава Балтийское море [16] 34 Устье Сиднейской гавани Тасманское море [121]
10 Нева » [15] 35 Нил Средиземное море [62, 100]
11 Кереть Белое море [34] 36 Нигер Атлантический океан [72]
12 Онега, Кянда, Тамица » [49, 50] 37 Конго » [67]
13 Северная Двина » [39, 40, 49, 63] 38 Пангани (Pangani) Индийский океан [109]
14 Сёмжа » [48] 39 Бриде (Breede) » [89]
15 Печора Баренцево море [38, 56] 40 Амазонка Атлантический океан [60]
16 Объ, Таз Карское море [10, 51, 53] 41 Ла-Плата » [106]
17 Енисей » [53] 42 Маккензи Северный Ледовитый океан [108]
18 Лена Море Лаптевых [9, 59] 43 Фрейзер Тихий океан [118]
19 Яна » [8] 44 Скагит (Skagit) » [122]
20 Амур Охотское море [14] 45 Колумбия » [86]
21 Карун Персидский залив [61] 46 Сан-Франциско » [96]
22 Янцзы Восточно-Китайское море [81, 94] 47 Святого Лаврентия Атлантический океан [101, 102]
23 Цяньтан (Qiantang) » [124, 125] 48 Салмон Залив Фанди, Атлантический океан [99]
24 Жемчужная река Южно- Китайское море [119, 126] 49 Гудзон » [112]
25 Хайхэ (Haihe) Бохайское море [123] 50 Миссисипи Мексиканский залив [98, 105, 120]

Для некоторых устьев, в частности для дельты Амазонки, моделирование в настоящее время – единственный доступный инструмент для изучения гидродинамического режима, так как охватить всю устьевую область измерениями в различные сезоны года пока еще невозможно. Трехмерная гидродинамическая модель [60] была откалибрована по детальным данным измерений расходов воды с помощью ADCP на репрезентативном участке, включающем в себя два рукава дельты, по которым проходит ~40% речного стока. Данная модель позволила впервые определить вероятные скорости водообмена между устьевым участком и устьевым взморьем в зависимости от условий увлажнения территории и водности реки (сезона года).

В последние десятилетия наибольшее распространение при моделировании устьевых областей получили трехмерные и двумерные модели, при этом в ряде исследований применяется мультимодельный подход, представляющийся авторам как наиболее перспективный. Например, при изучении вероятных изменений гидродинамического режима в дельте Меконга под влиянием глобального потепления [64] была разработана одномерная модель всей дельты и детальная двумерная модель ее участка между протоками Кантхо, Динь Ан и Тран Де, подверженного активному осолонению. Результаты расчетов по одномерной модели использовались при задании граничных условий двумерной модели.

Модели различной мерности были разработаны для оценки рисков наводнений в нижнем течении р. Салмон, впадающей в зал. Фанди [99]. Интегрированная модель 1D–2D PCSWMM использовалась для воспроизведения гидродинамики устьевого участка реки, прорывов дамб и гидравлики поймы; одномерная модель HEC-RAS использовалась для моделирования ледяных заторов; программные комплексы MIKE21 и MIKE3 – для моделирования продвижения и роста амплитуды приливных волн в зал. Фанди, а также для оценки скорости осадконакопления в устье реки. Результаты моделирования позволили количественно оценить последствия паводков различной величины и разработать меры по смягчению их последствий.

Моделирование сложной по морфологии микроприливной устьевой области р. Жемчужной в южной части Китая [119] выполнено на основе комплекса, состоящего из одномерной модели SOBEK и двумерной модели на основе DELFT 3D в однослойном варианте. Одномерная модель снабжает двумерную эстуарную часть величинами входных расходов воды, а двумерная в свою очередь возвращает одномерной модели уровни воды в устьевых створах водотоков.

Для эстуария Святого Лаврентия планируется создание комплексной модели экосистемы в целом, и на данный момент разработана двумерная модель эстуария [101, 102], ставшая связующим звеном между уже существующими двумерной моделью р. Святого Лаврентия (участок Монреаль–Труа-Ривьер) и трехмерной моделью океана.

Для дельты р. Колумбии, гидродинамический режим которой характеризуется сложной эстуарной циркуляцией и формирующейся вследствие этого сильной плотностной стратификацией, была специально разработана трехмерная модель [86], для настройки которой требовались высокоточные данные измерений солености и мутности воды. Такие данные были получены в Северном рукаве дельты с помощью бортового лебедочного профилографа и двух автономных подводных аппаратов в течение двух рейсов, выполненных в 2012 г. в периоды повышенного и пониженного стока.

Для калибровки трехмерной модели устья р. Сан-Франциско [96] использовались данные измерений уровней, скоростей течения и солености воды, выполненных в течение трех лет в 137 пунктах, расположенных на всем протяжении устьевого участка. Благодаря обширному объему данных модель была настроена для большого диапазона величин речного стока и солености воды и использовалась для изучения динамики зоны смешения в различных условиях.

Для отдельных задач разрабатываются новые модельные решения с учетом специфики конкретных устьевых областей. Например, в эстуарии р. Цяньтан при движении приливной волны формируется бор, который плохо воспроизводится в одномерных моделях, основанных на стандартных уравнениях системы Сен-Венана. В связи с этим была специально разработана модель с модифицированным уравнением движения, в которoe добавлен член, искусственно учитывающий приливный эффект [125].

На примере устьевой области Меконга [117] представлена методика для исследования распространения приливной волны по устьевому участку реки, основанная на двумерном моделировании без задания расхода воды на верхней границе.

В некоторых исследованиях, например эстуария Кник Арм – узкого морского залива на Аляске [103], гидродинамическая модель используется для оценки способа задания горизонтальной турбулентной вязкости, параметров шероховатости и точности батиметрических данных на воспроизведение динамики потока.

Для отдельных групп и типов задач проводились попытки обоснования использования тех или иных инструментов оценки качества моделирования. Например, в статье [77] рассматриваются модели объектов со сложными приливо-отливными течениями в многорукавных устьях рек. Авторы приходят к выводу, что окончательное решение о приемлемости или неприемлемости использования созданной модели для тех или иных задач должно приниматься самим исследователем, однако разработка подходящих критериев оценки может упростить его задачу. В Американском обществе гражданских инженеров (ASCE) разработаны стандарты верификации гидродинамических моделей [116], а в Национальной администрации по океану и атмосфере США (NOAA) – стандарты оценки качества прогнозных и расчетных гидродинамических модельных систем [107], которые могут применяться в том числе и для устьев рек.

РОССИЙСКИЙ ОПЫТ МОДЕЛИРОВАНИЯ ГИДРОЛОГИЧЕСКИХ ПРОЦЕССОВ В УСТЬЯХ РЕК

Российские численные модели второй половины ХХ в.

Начиная с 1970-х гг. наряду с физическим моделированием [26] для исследования динамики вод в устьях рек России стали все чаще применяться численные модели. Это направление активно развивалось в Арктическом и антарктическом научно-исследовательском институте (ААНИИ) [33, 51], Институте гидродинамики им. М.А. Лаврентьева Сибирского отделения (ИГ СО) РАН (ранее ИГ СО АН СССР) в Новосибирске [20, 23], институте “Гидропроект им. С.Я. Жука” [42, 45], в Российском государственном гидрометеорологическом университете (РГГМУ, ранее – Ленинградский гидрометеорологический институт – ЛГМУ) [31], в Дальневосточном УГМС [57]. В двумерных моделях часто использовались методические основы численных решений уравнений мелкой воды, изначально разрабатывавшиеся для решения океанологических задач [25, 44].

В результате одномерные и двумерные модели были разработаны для наиболее важных устьевых областей рек Арктического побережья России – Оби [21, 51, 55], Енисея [5, 33], Северной Двины [37], Печоры [56].

Помимо практически ориентированных моделей, разрабатывались модели для абстрактных схематизированных устьевых областей с целью исследования закономерностей неустановившегося движения и распространения прямых и обратных волн при различных параметрах русла, взморья и самих волн [37].

Примером использования численного моделирования для решения конкретной практической задачи того времени была работа [16], где на основе двуслойной модели мелкой воды рассчитываются ветровые нагоны на устьевых участках рек Преголи и Деймы, исследуется возможность попадания соленой морской воды в водозабор г. Калининграда и предлагается стратегия противодействия этому попусками из Правдинских водохранилищ на р. Лаве.

Определенные итоги данного этапа развития методов математического моделирования были подведены в 1986 г. на V Всесоюзном гидрологическом съезде в ходе работы секции “Устья рек”, в которой приняло участие около 80 человек, и 11 из 30 докладов было посвящено численному моделированию динамики потока в устьевых областях [55]. Результаты многочисленных работ подтвердили, что “аппарат, основанный на решении уравнений Сен-Венана, … достаточно надежно описывает как процесс прохождения по устьевой области паводочных и половодных волн, так и распространение вверх по дельтовым водотокам длинных волн приливов и сгонов−нагонов” (Е.П. Котрехов [55], c. 219), при этом “нужны новые, более гибкие, формы концентрации усилий по натурным исследованиям устьевых объектов. Может быть, следует использовать весь парк приборов и судов страны поочередно для каждого объекта” (А.А. Иванова (ААНИИ) [55], c. 225).

В 1990–2000 гг. ввиду ухудшения экономической ситуации в России активность в области разработок численных гидродинамических моделей стала снижаться из-за значительного сокращения финансирования науки. При этом компьютерные мощности и приборная база именно в этот период начали претерпевать существенные изменения – на смену ЭВМ типа БЭСМ и ЕС с перфокартами и магнитными лентами стали приходить персональные компьютеры, что создало предпосылки для дальнейшего развития российских моделей, таких как INMOM [29], STREAM_2D и 3D [17], модели ИГ СО РАН [22], и для более широкого применения зарубежных программных комплексов для российских устьевых областей.

Численные модели XXI в.

В последние два десятилетия исследования охватывают широкий спектр устьевых областей России, включая устья северного побережья Европейской части России [2, 4, 34, 38, 39, 40, 41, 48, 49, 50, 63], Сибири [10, 51, 53], устья Невы [15], Волги [1, 18, 19, 52], Дона [13, 58], Амурского лимана [14] и др.

Значительное количество задач, связанных с исследованиями устьевых областей России, все еще решается на основе одномерного подхода, с использованием как зарубежных программных комплексов (HEC-RAS, MIKE11, SOBEK и др.), так и отечественных разработок. Это связано с наименьшей требовательностью одномерных моделей к данным о рельефе, но существенно ограничивает возможности анализа динамики потока.

В работе [18] показано, при каких условиях на Нижней Волге можно использовать одномерную гидродинамическую модель SOBEK (разработка нидерландской фирмы “Deltares”). Технологический цикл разработки гидродинамической модели дельты р. Волги и Западных подстепных ильменей в программном комплексе MIKE 11 и сравнение гидравлических характеристик для естественных условий и в случае строительства подпорных русловых сооружений представлены в [19].

В предыдущих работах авторов настоящего обзора проанализированы особенности и недостатки применения зарубежных прог-раммных комплексов MIKE11 и HEC-RAS для приливных рек Беломорского бассейна [41, 48, 50]. В ходе данных исследований впервые пo детальным данным натурных измерений с использованием профилографов показана возможность проявления феномена отрицательной турбулентной вязкости и связанного с ним режима гидравлического сопротивления при реверсивном движении водных масс [3, 4], который не учитывается современными программными комплексами.

Из отечественных одномерных моделей наиболее популярна модель ИГ СО РАН [9, 22], ее разработчики сейчас особое внимание уделяют анализу существующих трудностей и поиску новых решений на основе обширного опыта в области математического моделирования нестационарных процессов в системах открытых русел и водоемов.

Из двумерных отечественных моделей наибольшее распространение получила STREAM 2D, последняя версия которой адаптирована для параллельных вычислений на основе новейшего метода численного решения уравнений мелкой воды на неструктурированных треугольно-четырехугольных сетках с использованием алгоритма приближенного решения задачи о распаде гидродинамического разрыва над скачком дна [7]. Наиболее подробно программно-моделирующий комплекс STREAM 2D CUDA и его приложения описаны в монографии [12].

В работе [15] представлена двумерная гидродинамическая модель Невы от ее истока из Ладожского озера до впадения в Финский залив Балтийского моря. Выполняется расчет распределения стока по основным рукавам дельты в зависимости от водности реки и нагонных явлений в заливе.

В статье [13] представлена детальная двумерная модель долины Нижнего Дона от Кочетовского гидроузла до Таганрогского залива для определения зон и глубин затопления поймы при пропуске через гидроузел расходов малой обеспеченности, а также влияния сгонно-нагонных явлений на режим устьевого участка реки. Результаты расчетов использованы при разработке проекта Багаевского гидроузла.

Разработка двумерной модели устьевой области р. Севернaя Двинa на основе программного комплекса STREAM_2D пo натурным данным, полученным с использованием авторской методики организации полевых работ в устьевой области, послужила основой для ряда статей авторов [39, 49, 63] и использовалась для сценарных расчетов гидродинамики устьевой области и оценки зон затопления. В настоящее время данная модель адаптируется для задач мониторинга опасных процессов в устьевой области Северной Двины [40]. Полученный в устье Северной Двины опыт организации полевых работ под задачи разработки двумерной модели устья крупной реки был применен для устьевой области Печоры [2, 38].

На основе стыковки двумерных гидродинамических моделей приливных устьев рек бассейна Белого и Баренцева моря с моделями формирования стока на их водосборах стала возможной оценка влияния климатических изменений на гидродинамический режим устьевых участков рек Северной Двины, Онеги, Печоры при изменениях климата [38, 49].

В течение последних двух десятилетий большее распространение в России получили и наиболее требовательные к исходным данным, сложные по схематизации трехмерные модели устьевых областей. В начале 2000-х гг. в ААНИИ на базе трехмерной модели POM были созданы комплексные модели эстуариев Оби, Таза и Енисея, включающие в себя расчет солености, ледовых процессов с возможностями учета воздействия на водную поверхность ветра и градиентов давления [53, 54]. Горизонтальные размеры ячеек расчетных сеток в этих моделях составляют 4‒5 км, шаг по вертикали – 1 м. Модели откалиброваны и верифицированы на основе экспедиционных данных ААНИИ 1980-х гг. и адаптированы для имитации годового хода полей гидрологических характеристик и устьевых процессов сезонного масштаба в современных условиях.

Прикладные исследования в Обской губе, обусловившие создание ряда моделей данной акватории, в последние годы были связаны с оценкой влияния строительства судоходного канала к порту Сабетта через бар Обской губы на ее термохалинный режим и экологическое состояние [10, 30].

На основе программных комплексов STREAM_2D и STREAM_3D разработаны численные модели Амурского лимана 2D и 3D [14]. На модели 3D продемонстрировано, что плотностная стратификация в мелководном лимане несущественна, и в соответствии с этим расчеты взаимодействия стоковых и приливных течений выполнялись на модели 2D. Моделирование показало, что сток Амура распределяется между северной и южной границами лимана (в сторону Охотского и Японского морей соответственно) в пропорции, близкой к 2 : 1, что хорошо согласуется с натурными данными.

В междисциплинарных работах отечественных исследователей [39, 54] подчеркивается необходимость создания единой автоматизированной системы мониторинга устьевых областей крупных рек России и обозначаются существующие предпосылки и заделы. Ее разработка предлагается на базе комплекса натурных наблюдений и математического моделирования, однако в настоящее время такой системы мониторинга на государственном уровне не существует.

Одним из перспективных направлений развития численных гидродинамических моделей устьевых областей в условиях дефицита натурных данных (главным образом о подводном рельефе) может оказаться решение обратных задач русловой гидравлики [52, 61], когда морфометрические характеристики неизученных участков могут быть восстановлены на основе анализа трансформации там прямых и обратных волн с использованием технологии искусственных нейронных сетей.

ВЫВОДЫ

Устьевые области рек – одни из самых сложных для моделирования типы водных объектов из-за целого комплекса процессов, происходящих на границе река–море, их разномасштабности, трудности организации полевых исследований в этих районах. В последние два десятилетия возможности компьютерного гидродинамического моделирования значительно возросли в связи с развитием вычислительных ресурсов, специализированных программных комплексов и технологий натурных измерений. Активно развиваются численные модели сложных по морфологии устьевых областей большой протяженности, применяется мультимодельный подход.

Основные направления исследований устьевых областей наиболее крупных и важных рек мира активно поддерживаются российскими учеными и включают в себя разработку методов моделирования, исследование взаимодействия речного стока с нагонами и приливными волнами, моделирование наводнений и других опасных явлений, оценку влияния современных и ожидаемых изменений климата на динамику потока в устьях, мониторинг устьевых процессов, решение разнообразных практических задач. В работах российских авторов подчеркивается необходимость создания единой автоматизированной системы мониторинга устьевых областей крупных рек России на базе комплекса натурных наблюдений и математического моделирования.

Список литературы

  1. Алабян А.М., Беликов В.В., Крыленко И.Н., Лебедева С.В. Применение двумерных гидродинамических моделей для решения проблем регулирования русла Нижней Волги в условиях дефицита данных гидрологических изысканий // Инженерные изыскания. 2014. № 2. С. 24–34.

  2. Алабян А.М., Василенко А.Н., Демиденко Н.А., Крыленко И.Н., Панченко Е.Д., Попрядухин А.А. Приливная динамика вод в дельте Печоры в летнюю межень // Вестн. МГУ. Сер. 5, География. 2022. № 1. С. 167–179.

  3. Алабян А.М., Панченко Е.Д. Гидравлическое сопротивление в приливных устьях и феномен “отрицательного трения” в речной гидравлике // Инженерные изыскания. 2017. № 3. С. 24–32.

  4. Алабян А.М., Панченко Е.Д., Алексеева А.А. Особенности динамики вод в приливных устьях малых рек бассейна Белого моря // Вестн. Московского ун-та. Сер. 5, География. 2018. № 4. С. 39–48.

  5. Алабян А.М., Сидорчук А.Ю. Метод расчета переформирования русел рек, разветвленных на рукава при изменении гидрологического режима // Метеорология и гидрология. 1987. № 10. С. 82–87.

  6. Алексюк А.И., Беликов В.В. Моделирование течений мелкой воды с областями обмеления и разрывами дна // Журн. вычисл. математики и мат. физики. 2017. Т. 57. № 2. С. 316–338.

  7. Алексюк А.И., Беликов В.В. Программный комплекс STREAM 2D CUDA для расчета течений, деформаций дна и переноса загрязнений в открытых потоках с использованием технологии CUDA (на графических процессорах NVIDIA). Свид. о регистрации прав на ПО № 2 017 660 266. 2017.

  8. Алешкин С.А., Бабич Д.Б., Михайлов В.Н. Математическая модель распределения расходов воды по рукавам дельты реки Яны // Вестн. Московского ун-та. Сер. 5, География. 2002. № 5. С. 43–49.

  9. Антипова Е.А., Крылова А.И. Численное моделирование речного стока в дельте реки Лены // Сб. докл. Международ. науч. конф. памяти Ю.Б. Виноградова “Грани гидрологии”: Спб., 2018. С. 57–61.

  10. Архипов Б.В., Алабян А.М., Дмитриева А.А., Солбаков В.В., Шапочкин Д.А. Моделирование влияния морского канала к порту Сабетта на гидродинамический режим и соленость Обской губы // Геориск. 2018. 12 (1). С. 46–58.

  11. Байдин С.С. Приближенные способы расчета распределения расходов по рукавам дельты // Тр. ГОИН. 1959. Вып. 45. С. 63–72.

  12. Беликов В.В., Алексюк А.И. Модели мелкой воды в задачах речной гидродинамики. М.: Москва, 2020. 346 с.

  13. Беликов В.В., Борисова Н.М., Алексюк А.И., Румянцев А.Б., Глотко А.В., Шурухин Л.А. Гидравлическое обоснование проекта Багаевского гидроузла с применением численного гидродинамического моделирования // Гидротех. стр-во. 2018. № 5. С. 19–35.

  14. Беликов В.В., Борисова Н.М., Румянцев А.Б., Бугаец А.Н. Численная гидродинамическая модель стоково-приливных течений в Амурском лимане // Сб. науч. труд. Всерос. науч. конф. “Водные ресурсы: новые вызовы и пути решения”. Новочеркасск: Лик, 2017. С 480–485.

  15. Беликов В.В., Зайцев А.А, Зернов А.В. и др. Гидродинамическая модель Невы // Тр. международ. науч.-практ. конф. “Безопасность речных судоходных гидротехнических сооружений”: Спб., 2008. № 1. С. 155–174.

  16. Беликов В.В., Милитеев А.Н. Численная модель морских нагонов в приустьевых участках рек // Науч. тр. КаГУ. Калининград, 1993. С. 15–23.

  17. Беликов В.В., Румянцев А.Б., Кочетков В.В. Программный комплекс для расчета гидротермических режимов и переноса загрязнений в водотоках, водоемах и на шельфе (STREAM_3D). Свид. об официальной регистрации программы для ЭВМ № 2 014 612 186. М., 2014.

  18. Болгов М.В., Красножон Г.Ф., Шаталова К.Ю. Компьютерная гидродинамическая модель Нижней Волги // Водн. ресурсы. 2014. Т. 41. № 1. С. 10–23.

  19. Бубер А.А., Бородычев В.В., Талызов А.А. Разработка гидродинамической модели дельты реки Волги и западных подстепных ильменей // Изв. Нижневолжского агроуниверситетского комплекса: наука и высшее профессиональное образование. 2017. № 2 (46). С. 271–284.

  20. Васильев О.Ф., Шугрин С.М., Притвиц Н.А., Атавин А.А., Гладышев М.Т., Воеводин А.Ф. Применение современных численных методов и цифровых ЭВМ для решения задач гидравлики открытых русел // Гидротех. стр-во. 1965. № 8. С. 44–48.

  21. Виноградова Т.А. Анализ взаимодействия волн половодья с колебаниями уровня моря на закрытых устьевых взморьях сибирских рек // Тр. V Всесоюз. гидрол. съезда. 1990. Т. 9. С. 150‒157.

  22. Воеводин А.Ф., Никифоровская В.С. Об использовании комбинированных математических моделей для исследования нестационарных процессов в системах открытых русел и водоемов // Сб. тез. международ. науч.-практ. конф. “Вторые Виноградовские Чтения. Искусство гидрологии” памяти Ю.Б. Виноградова. СПб., 2015. С. 283–284.

  23. Воеводин А.Ф., Никифоровская В.С., Овчарова А.С. Численные методы решения задачи о неустановившемся движении воды на устьевых участках рек // Тр. ААНИИ. 1983. Т. 378. С. 23–34.

  24. Войнович П.А. К вопросу о распределении расхода по разветвлениям открытого русла // Изв. НИИ гидротехники. 1932. Т. 5. С. 73–105.

  25. Вольцингер Н.E., Пясковский Р.В. Теория мелкой воды. Океанологические задачи и численные методы. Л.: Гидрометеоиздат, 1977. 207 с.

  26. Гиляров Н.П., Иванов В.В. Исследование на моделях режима уровней и течений устьев рек в зоне влияния моря // Тр. ААНИИ. 1963. Т. 254. Вып. 2. С. 155–162.

  27. Гришанин К.В. Гидравлический расчет элементов водного режима в дельтах рек арктической зоны // Тр. ААНИИ. 1967. Т. 278. С. 5–21.

  28. Грушевский М.С. Использование электронной цифровой машины для расчетов неустановившегося движения воды в призматическом русле // Тр. ГГИ. 1962. Вып. 94.

  29. Дианский Н.А., Гусев А.В., Володин Е.М., Залесный В.Б., Багно А.В. Программа для воспроизведения циркуляции Мирового океана и ее климатической изменчивости // Свид. об официальной регистрации прав на ПО № 2 015 612 275. 2015.

  30. Дианский Н.А., Фомин В.В., Грузинов В.М., Кабатченко И.М., Литвиненко Г.И. Оценка влияния подходного канала к порту Сабетта на изменение гидрологических условий Обской губы с помощью численного моделирования // Арктика: экология и экономика. 2015. № 3 (19). С. 18–29.

  31. Доронин Ю.П., Лукьянов С.В. Математическое моделирование взаимодействия морской и речной воды на устьевом взморье с помощью двуслойной модели // Метеорология и гидрология. 1994. № 10. С. 70–77.

  32. Иванов В.В. Гидравлический метод расчета перераспределения стока в дельтах peк (под влиянием водохозяйственных мероприятий) // Тр. II Всесоюз. гидрол. съезда. 1975. Т. 5. С. 388–З98.

  33. Иванов В.В., Котрехов Е.П. Опыт численного моделирования неустановившегося движения в многорукавной дельте реки // Тр. ААНИИ. 1976. Т. 314. С. 16–35.

  34. Ионов В.В., Май Р.И., Смагин Р.Е. Численная гидродинамическая модель приливных явлений в губе Кереть (Кандалакшский залив, Белое море) // Изв. РГО. 2015. Т. 147. № 2. С. 22–37.

  35. Иванов В.В. Метод гидравлического расчета элементов водного режима в дельтах рек // Tp. ААНИИ. 1968. Т. 283. С. 30–63.

  36. Калинин Г.П, Кучмент Л.С. О численных методах решения уравнений Сен-Венана для расчета неустановившегося движения воды в реках // Метеорология и гидрология. 1963. Вып. 6.

  37. Котрехов Е.П., Павлова А.В. К расчету взаимодействия прилива и штормового нагона в дельте Северной Двины // Метеорология и гидрология. 1983. № 3. С. 79–86.

  38. Крыленко И.Н., Алабян А.М., Василенко А.Н., Демиденко Н.А., Панченко Е Д., Попрядухин А.А. Двумерная гидродинамическая модель устьевой области реки Печоры // Тр. X Международ. науч.-практ. конф. “Морские исследования и образование (MARESEDU-2021)”. 2021. Т. 1. С. 321–324.

  39. Лебедева С.В., Алабян А.М., Крыленко И.Н., Федорова Т.А. Наводнения в устье Северной Двины и их моделирование // Геориск. 2015. № 1. С. 18–25.

  40. Лебедева С.В., Одоев Л.С. Роль ледовых явлений в динамике потоков на придельтовом участке Северной Двины // Гидросфера. Опасные процессы и явления. 2020. Т. 2. № 4. С. 330–346. https://doi.org/10.34753/HS.2020.2.4.330

  41. Лебедева С.В., Панченко Е.Д., Аракельянц А.Д. Возможности и ограничения одномерной и двумерной профильной гидродинамических моделей при расчете распространения осолоненных вод в приливных устьевых областях // Сб. докл. международ. науч. конф. памяти Ю.Б. Виноградова “Третьи Виноградовские Чтения. Грани гидрологии”. 2018. С. 754–759.

  42. Ляхтер В.М., Милитеев А.Н. Гидравлические исследования численными методами // Вод. ресурсы. 1981. № 3. С. 60–79.

  43. Мак-Доуэлл Д.М., О’Коннор Б.А. Гидравлика приливных устьев рек. М.: Энергоатомиздат, 1983. 312 с.

  44. Марчук Г.И. Математическое моделирование в проблеме окружающей среды // М.: Наука, 1982. 320 с.

  45. Милитеев А.Н., Соколов Б.И., Школьников С.Я. Математическое моделирование течений на устьевых взморьях неприливных морей с учетом реальных гидрометеорологических условий // Тр. V Всесоюз. гидрол. съезда. Т. 9. 1990. С. 174–181.

  46. Михайлов В.Н. Динамика потока и русла в неприливных устьях рек. М.: Гидрометеоиздат, 1971. 260 с.

  47. Мордухай-Болтовский А.И. Приближенный расчет распределения расходов по рукавам методом повторения // Метеорология и гидрология. 1952. № 6. С. 39–41.

  48. Панченко Е.Д. Моделирование гидродинамических процессов в приливном эстуарии малой реки // Эрозионные, русловые и устьевые процессы (исследования молодых ученых университетов). Сб. стат. по материалам XI семинара молодых ученых вузов, объединяемых советом по проблеме эрозионных, русловых и устьевых процессов. 2016. С. 191–197.

  49. Панченко Е.Д., Алабян А.М., Крыленко И.Н., Лебедева С.В. Моделирование гидродинамических процессов в устьях рек Онеги и Северной Двины при различных сценариях климатических изменений // Тр. IX Международ. науч.-практ. конф. “Морские исследования и образование (MARESEDU- 2020)”. 2020. Т. 2. С. 72–75.

  50. Панченко Е.Д., Льюменс М., Лебедева С.В. Моделирование гидродинамических процессов в приливном устье реки Онеги // Сб. докл. международ. науч. конф. памяти Ю.Б. Виноградова “Четвертые Виноградовские чтения. Гидрология от познания к мировоззрению”. 2020. С. 135–140.

  51. Пискун А.А. Численное моделирование динамики вод в дельте Оби при сгонах–нагонах // Вод. ресурсы. 1987. № 5. С. 129–135.

  52. Романов А.В., Скрибцов П.В., Червоненкис М.А. Решение обратных задач русловой гидравлики с использованием нелинейных математических моделей // Тр. Гидрометцентра РФ. 2013. Вып. 349. С. 142–160.

  53. Третьяков М.В. К моделированию гидрологических процессов в эстуариях с ледовым покровом // Проблемы Арктики и Антарктики. 2008. № 2 (79). С. 67‒74.

  54. Третьяков М.В., Иванов В.В. Состояние и проблемы развития технологий оценки и прогнозирования интрузии морских вод // Тр. ГОИН. 2013. Вып. 214. С. 200‒212.

  55. Труды V Всесоюзного гидрологического съезда. Т. 9. Устья рек. Л.: Гидрометеоиздат, 1990.

  56. Урнышев А.П. Трансформация приливной волны в устье реки Печоры // Новые научные методики. Сыктывкар: Коми НЦ УрО РАН, 1989. 20 с.

  57. Черепок А.А., Бирюков А.А., Бережной В.Т., Любицкий Ю.В. Численное моделирование уровней воды в приливной устьевой области Амура // Тр. V Всесоюз. гидрол. съезда. Т. 9. Устья рек. 1990. С. 201–206.

  58. Чикин А.Л., Клещенков А.В., Чикина Л.Г. Один из подходов к численному исследованию гидрологии дельтовой области Дона // Вод. ресурсы. 2021. Т. 48. № 5. С. 492–499.

  59. Шлычков В.A., Крылова A.И. Численная модель плотностных течений в устьевых областях сибирских рек // Сиб. журн. вычислит. математики. 2014. Т. 17. № 3. С. 305–313.

  60. Abreu C.H.M., Barros M.L.C., Brito D.C., Teixeira M.R., Cunha A.C. Hydrodynamic Modeling and Simulation of Water Residence Time in the Estuary of the Lower Amazon River // Water. 2020. V. 12 (3). 660. https://doi.org/10.3390/w12030660

  61. Adib A., Nasiriyani M. Evaluation of fluvial flow effects on tidal characteristics of tidal rivers by artificial neural networks and genetic algorithm // Int. J. Water. 2016. V. 10 (1). P. 13–27. https://doi.org/10.1504/IJW.2016.073739

  62. Ahmed A.S.M. Numerical model as a tool to investigate coastal problems in Egypt // Tenth Int. Water Technol. Conf. 2006.

  63. Alabyan A.M., Lebedeva S.V. Flow dynamics in large tidal delta of the Northern Dvina River: 2D simulation // J. Hydroinformatics. 2018. V. 20. № 4. P. 798–814. https://doi.org/10.2166/hydro.2018.051

  64. Anh D.T., Hoang L.P., Bui M.D., Rutschmann P. Simulating Future Flows and Salinity Intrusion Using Combined One- and Two-Dimensional Hydrodynamic Modelling—The Case of Hau River, Vietnamese Mekong Delta // Water. 2018. V. 10 (7). 897. https://doi.org/10.3390/w10070897

  65. Balachandran K.K., Reddy G.S., Revichandran C., Srinivas K., Vijayan P.R., Thottam T.J. Modelling of tidal hydrodynamics for a tropical ecosystem with implications for pollutant dispersion (Cochin Estuary, Southwest India) // Ocean Dynamics. 2008. V. 58. P. 259–273. https://doi.org/10.1007/s10236-008-0153-6

  66. Barros M.L.C., Sena M., Mesquita A., Blanco C., Secretan Y. A water flow pattern analysis of Guajará Bay: Amazon Estuary – Brazil // J. Brazilian Society Mechanical Sci. Engineering. 2011. V. 33 (1). P. 79−85. https://doi.org/10.1590/S1678-58782011000100012

  67. Bars Y.L., Vallaeys V., Deleersnijder É. et al. Unstructured-mesh modeling of the Congo river to-sea continuum // Ocean Dynamics. 2016. V. 66. P. 589–603. https://doi.org/10.1007/s10236-016-0939-x

  68. Brunner G.W. CEIWR-HEC. HEC-RAS River Analysis System User’s Manual. Version 5.0. 2016. 960 p.

  69. de Brye B., de Brauwere A., Gourgue O., Kärnä T., Lambrechts J., Comblen R., Deleersnijder E. A finite-element, multi-scale model of the Scheldt tributaries, river, estuary and ROFI // Coastal Engineering. 2010. V. 57 (9). P. 850–863. https://doi.org/10.1016/j.coastaleng.2010.04.001

  70. de Brye B., Schellen S., Sassi M. et al. Preliminary results of a finite-element, multi-scale model of the Mahakam Delta (Indonesia) // Ocean Dynamics. 2011. V. 61. P. 1107–1120. https://doi.org/10.1007/s10236-011-0410-y

  71. Delft Hydraulics. “Delft3D-FLOW User Manual Version 3.14”. Delft, 2007.

  72. Dike C.C., Agunwamba J.C. A study on the effects of tide on sedimentation in estuaries of the Niger delta, Nigeria // J. Urban and Environ. Engineering. 2012. V. 6 (2). P. 86–93.

  73. Du J., Shen J., Zhang Y.J., Ye F., Liu Z., Wang Z. et al. Tidal Response to Sea-Level Rise in Different Types of Estuaries: The Importance of Length, Bathymetry, and Geometry // Geophys. Res. Lett. 2017. V. 45 (1). https://doi.org/10.1002/2017GL075963

  74. Dunn R.J.K., Zigic S., Burling M., Lin H.-H. Hydrodynamic and Sediment Modelling within a Macro Tidal Estuary: Port Curtis Estuary, Australia // J. Mar. Sci. and Engineering. 2015. V. 3. P. 720–744. https://doi.org/10.3390/jmse3030720

  75. Funahashi T., Kasai A., Ueno M., Yamashita Y. Effects of short time variation in the river discharge on the salt wedge intrusion in the Yura Estuary, Japan // J. Water Resour. Protection. 2013. V. 5. P. 343–348. https://doi.org/10.4236/jwarp.2013.53A035

  76. Gifford-Miears C., Leon A.S. TELEMAC-2D tutorial Version: V6P3. The School of Civil and Construction Engineering. Oregon State Univ. 2014.

  77. Gunn K., Stock-Williams C. On validating numerical hydrodynamic models of complex tidal flow // Int. J. Mar. Energy. 2013. № 3. P. e82–e97.

  78. Horritt M.S., Bates P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation // J. Hydrol. 2002. V. 268. P. 87–99.

  79. Howarth J., Palmer M. The Liverpool Bay Coastal Observatory // Ocean Dynamics. 2011. V. 61 (11). P. 1917‒1926.

  80. https://www.mikepoweredbydhi.com/references

  81. Hu K., Ding P., Wang Z., Yang S. A 2D/3D hydrodynamic and sediment transport model for the Yangtze Estuary, China // J. Mar. Systems. 2009. V. 77. P. 114–136. https://doi.org/10.1016/j.jmarsys.2008.11.014

  82. Iglesias I., Avilez-Valente P., Bio A., Bastos L. Modelling the Main Hydrodynamic Patterns in Shallow Water Estuaries: The Minho Case Study // Water. 2019. V. 11 (5). 1040. https://doi.org/10.3390/w11051040

  83. Isaacson E., Stoker J., Troesh A. Numerical solution of flood prediction and river regulation problems // Rep. III. New York Univ. 1956.

  84. Jiang A.W., Ranasinghe R., Cowell P. Contemporary hydrodynamics and morphological change of a microtidal estuary: a numerical modelling study // Ocean Dynamics. 2013. V. 63 (1). P. 21–41. https://doi.org/10.1007/s10236-012-0583-z

  85. Jouanneau N., Sentchev A., Dumas F. Numerical modelling of circulation and dispersion processes in Boulogne-sur-Mer harbour (Eastern English Channel): Sensitivity to physical forcing and harbour design // Deutsche Hydrographische Zeitschrift. 2013. 63 (11–12). P. 1321–1340. https://doi.org/10.1007/s10236-013-0659-4

  86. Kärnäa T., Baptistaa A.M., Lopeza J.E., Turnera P.J., McNeilb C., Sanfordba T.B. Numerical modeling of circulation in high-energy estuaries: A Columbia River estuary benchmark // Ocean Modelling. 2015. V. 88. P. 54–71. doi.org/https://doi.org/10.1016/j.ocemod.2015.01.001

  87. Khojasteh D., Chen S., Felder S., Heimhuber V., Glamore W. Estuarine tidal range dynamics under rising sea levels // PLoS ONE. 2021. V. 16 (9). e0257538. https://doi.org/10.1371/journal.pone.0257538

  88. Krvavica N., Travaš V., Ožanic N. Salt-Wedge Response to Variable River Flow and Sea-Level Rise in the Microtidal Rjecina River Estuary, Croatia // J. Coastal Res. 2017. V. 33 (4). P. 802–814. https://doi.org/10.2112/JCOASTRES-D-16-00053.1

  89. Kupfer S., Santamaria-Aguilar S., van Niekerk L., Lück-Voge M., Vafeidis A.T. Investigating the interaction of waves and river discharge during compound flooding at Breede Estuary, South Africa // Natural Hazards Earth System Sci. 2021. https://doi.org/10.5194/nhess-2021-220

  90. Leupi C., Altinakar M.S., Deville M. Numerical modeling of cohesive sediments dynamics in estuaries: Part I-description of the model and simulations in the Po River Estuary // Int. J. Numerical Methods in Fluids. 2008. V. 57. P. 237–263. https://doi.org/10.1002/fld.1622

  91. Leuven J.R.F.W., Pierik H.J., van der Vegt M., Bouma T.J., Kleinhans M.G. Sea-level-rise-induced threats depend on the size of tide-influenced estuaries worldwide // Nature Climate Change. 2019. V. 9 (12). https://doi.org/10.1038/s41558-019-0608-4

  92. Levasseur A., Shi L., Wells C.N., Purdie D.A., Kelly-Gerreyn B.A. A three-dimensional hydrodynamic model of estuarine circulation with an application to Southampton water, UK // Estuarine Coastal Shelf Sci. 2007. V. 73. P. 753–767.

  93. Liu X., Lim S. Flood inundation modelling for mid-lower Brisbane estuary // River Res. Applications. 2016. https://doi.org/10.1002/rra.3078

  94. Lu. S., Tong C., Lee D.-Y., Zheng J., Shen J., Zhang W., Yan Y. Propagation of tidal waves up in Yangtze Estuary during the dry season // J. Geophys. Res.: Oceans. 2015. V. 120 (9). P. 6445–6473. https://doi.org/10.1002/2014JC010414

  95. Lyddon C., Brown J.M., Leonardi N., Plater A.J. Flood Hazard Assessment for a Hyper-Tidal Estuary as a Function of Tide-Surge-Morphology Interaction // Estuaries and Coasts. 2018. V. 41. P. 1565–1586. https://doi.org/10.1007/s12237-018-0384-9

  96. MacWilliams M.L., Bever A.J., Gross E.S., Ketefian G.S., Kimmerer W.J. Three-Dimensional Modeling of Hydrodynamics and Salinity in the San Francisco Estuary: An Evaluation of Model Accuracy, X2, and the Low–Salinity Zone // San Francisco Estuary Watershed Sci. 2015. V. 13 (1). https://doi.org/10.15447/sfews.2015v13iss1art2

  97. Marion J.A.D. Final model tests of proposed channel improvements in the Fraser River at New Westminster // National Res. Council Canada. Rep. No. MH-18. 1949.

  98. Martyr R.C., Dietrich J.C., Westerink J.J., Kerr P.C. Simulating Hurricane Storm Surge in the Lower Mississippi River under Varying Flow Conditions // J. Hydraulic Engineering. 2012. V. 139 (5). P. 492–501. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000699

  99. Marvin J.T., Wilson A.T. One Dimensional, Two Dimensional and Three Dimensional Hydrodynamic Modeling of a Dyked Coastal River in the Bay of Fundy // J. Water Management Modeling. 2016. V. 25. C404. https://doi.org/10.14796/JWMM.C404

  100. Masria A., Abdelaziz K. Environmentally-Friendly Proposals for Coastal Stability at Rosetta Promontory, Nile Delta // J. Marine Sci. Res. Dev. 2017. V. 7. P. 227. https://doi.org/10.4172/2155-9910.1000227

  101. Matte P., Secretan Y., Morin J. Hydrodynamic Modeling of the St. Lawrence Fluvial Estuary. I: Model Setup, Calibration, and Validation // J. Waterway, Port, Coastal, Ocean Engineering. 2017. V. 143 (5). https://doi.org/10.1061/(asce)ww.1943-5460.0000397

  102. Matte P., Secretan Y., Morin J. Hydrodynamic Modeling of the St. Lawrence Fluvial Estuary. II: Reproduction of Spatial and Temporal Patterns // J. Waterway, Port, Coastal, Ocean Engineering. 2017. V. 143 (5). https://doi.org/10.1061/(asce)ww.1943-5460.0000394

  103. McAlpin T.O., Savant G., Brown G.L., Smith S.J., Chapman R.S. Hydrodynamics of Knik Arm: Modeling Study // J. Waterway, Port, Coastal, Ocean Engineering. 2013. V. 139. № 3. P. 232–245.

  104. Mellor G.L. Users guide for a three-dimensional, primitive equation, numerical ocean model. 2002. 42 p.

  105. Meselhe E.A., Georgiou I., Allison M.A., McCorquodale J.A. Numerical modeling of hydrodynamics and sediment transport in lower Mississippi at a proposed delta building diversion // J. Hydrol. 2012. V. 472–473. P. 340–354. https://doi.org/10.1016/j.jhydrol.2012.09.043

  106. Moreira D., Simionato C.G. Modeling the Suspended Sediment Transport in a Very Wide, Shallow, and Microtidal Estuary, the Río de la Plata, Argentina // J. Advances Modelling Earth Systems. 2019. V. 11 (10). P. 3284−3304. https://doi.org/10.1029/2018MS001605

  107. NOS standards for evaluating operational nowcast and forecast hydrodynamic model systems // US Department of Commerce, National Oceanic and Atmospheric Administration, National Ocean Service, Office of Coast Survey, Coast Survey Development Laboratory. Silver Spring. 2003.

  108. Omstedt A., Carmack E.C., Macdonald R.W. Modeling the seasonal cycle of salinity in the Mackenzie shelf/ estuary // J. Geophys. Res. Oceans. 1994. V. 99 (C5). P. 10 011−10 021. https://doi.org/10.1029/94JC00201

  109. Pamba S., Shaghude Y.W., Muzuka A.N.N. Hydrodynamic Modelling on Transport, Dispersion and Deposition of Suspended Particulate Matter in Pangani Estuary, Tanzania // Estuaries: A Lifeline of Ecosystem Services in the Western Indian Ocean, Estuaries of the World. 2016. https://doi.org/10.1007/978-3-319-25370-1_9

  110. Plancke Y., Stark J., Meire D., Schrijver M. Complex Flow Patterns in the Scheldt Estuary: Field Measurements and Validation of a Hydrodynamic Model // J. Hydraulic Engineering. 2020. V. 146 (7). https://doi.org/10.1061/(ASCE)HY.1943-7900.0001737

  111. Preissmann A., Cunge J.A. Calcul du mascaret sur machine électronique // Intumescences Sosiete Hydrotechnique de France. 1961. № 5. P. 588–596.

  112. Ralston D.K., Geyer W.R., Lerczak J.A. Subtidal salinity and velocity in the Hudson River Estuary: Observations and modelling // J. Phys. Oceanogr. 2008. V. 38. P. 753–770. https://doi.org/10.1175/2007JPO3808.1

  113. Rao Y.R. Modelling of Circulation and Salinity in a Tidal Estuary // J. Coastal Res. 2005. V. 42. P. 363–369.

  114. Saint-Venant A.J.-C.B. Théorie du mouvement non-permanent des eaux avec application aux crues des rivières et a l’introduction des marées dans leur lit // Comptes rendus de l’Acadèmie des Sciences de Paris. 1871. V. 73. P. 148–154, 237–240.

  115. Shaha D.C., Cho Y.-K., Kim T.-W. Effects of river discharge and tide driven sea level variation on saltwater intrusion in Sumjin River estuary: An application of finite-volume coastal ocean model // J. Coastal Res. 2013. V. 29 (2). P. 460–470. https://doi.org/10.2112/JCOASTRES-D-12-00135.1

  116. Standard for Verification and Validation in Computational Fluids and Heat Transfer // The Am. Soc. Mechanical Engineers. ASME V&V 20-2009. N. Y., 2009.

  117. Takagi H., Quan N.H., Anh L.T., Thao N.D., Dang Tri V.P., Anh T. Practical modelling of tidal propagation under fluvial interaction in the Mekong delta // Int. J. River Basin Management. 2019. V. 17. P. 377–387. https://doi.org/10.1080/15715124.2019.1576697

  118. Tsz Yeung Leung A., Stronach J., Matthieu J. Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes // J. Mar. Sci. Engineering. 2018. V. 6 (4). P. 130. https://doi.org/10.3390/jmse60401300

  119. Twigt D.J., De Goede E.D., Zijl F., Schwanenberg D., Chiu A.Y.W. Coupled 1D–3D hydrodynamic modelling, with application to the Pearl River Delta // Ocean Dynamics. 2009. V. 59 (6). P. 1077–1093.

  120. Wang H., Chen Q., Hu K. et al. A Modeling Study of the Impacts of Mississippi River Diversion and Sea-Level Rise on Water Quality of a Deltaic Estuary // Estuaries and Coasts. 2017. V. 40. P. 1028–1054. https://doi.org/10.1007/s12237-016-0197-7

  121. Xiao Z., Wang X.H., Roughan M., Harrison D. Numerical modelling of the Sydney Harbour Estuary, New South Wales: Lateral circulation and asymmetric vertical mixing // Estuarine, Coastal Shelf Sci. 2019. V. 217. P. 132–147. https://doi.org/10.1016/j.ecss.2018.11.004

  122. Yang Z.Q., Khangaonkar T. Modeling tidal circulation and stratification in Skagit River estuary using an unstructured grid ocean model // Ocean Modelling. 2009. V. 28. P. 34–49. https://doi.org/10.1016/j.ocemod.2008.07.004

  123. Yuchuan B., Zhaoyin W., Huanting S. Three-dimensional modelling of sediment transport and the effects of dredging in the Haihe Estuary // Estuarine, Coastal Shelf Sci. 2003. V. 56 (1). P. 175–186. https://doi.org/10.1016/S0272-7714(02)00155-5

  124. Zhang J., Wang R., Guo Y. et al. Modelling study of hydrodynamics in a macro tidal estuary // Maritime Engineering. 2019. V. 172 (2). P. 34–44. https://doi.org/10.1680/jmaen.2018.21

  125. Zhang X., Bao W., Qu S., Yu Z. One-dimensional hydrodynamic model accounting for tidal effect // Hydrol. Res. 2012. V. 43. (1–2). P. 113–122. https://doi.org/10.2166/nh.2011.114

  126. Zheng P., Li M., Wang C. et al. Tide-Surge Interaction in the Pearl River Estuary: A Case Study of Typhoon Hato // Frontiers Mar. Sci. 2019. https://doi.org/10.3389/fmars.2020.00236

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Водные ресурсы

Архивы выпусков Информация о журнале Отправить рукопись в журнал