Водные ресурсы, 2023, T. 50, № 1, стр. 39-52
К вопросу об оценке рисков затопления и защите селитебных территорий, расположенных в поймах рек
В. В. Беликов a, Н. М. Борисова a, *, А. Б. Румянцев a
a Институт водных проблем РАН
119333 Москва, Россия
* E-mail: borisovanm@mail.ru
Поступила в редакцию 11.04.2022
После доработки 11.04.2022
Принята к публикации 03.08.2022
- EDN: EDJSXK
- DOI: 10.31857/S0321059623010042
Аннотация
Обоснована возможность определения вероятного вреда при затоплении селитебных территорий и объектов повышенной опасности, расположенных в поймах рек, в зависимости от глубины затопления. Рассмотрена технология построения кривых вероятности затопления с использованием двумерных гидродинамических моделей (на основе отечественного программного комплекса STREAM 2D CUDA) и данных натурных наблюдений. На примере гидрологических створов на ряде рек показано, что кривые повторяемости затопления могут быть аппроксимированы некими логарифмическими зависимостями. Выведены и обоснованы формулы для определения рисков затопления селитебных территорий и интегральных показателей рисков. Установлено, что в среднем для рассмотренных объектов максимальные риски соответствуют уровням затопления обеспеченностью ~2% и что эффективная инженерная защита селитебных территорий в большинстве случаев должна быть рассчитана на уровни затопления гораздо меньшей обеспеченности.
ВВЕДЕНИЕ
По статистике, наибольший экономический и социальный ущерб из всех стихийных бедствий на Земле приносят наводнения. Известны случаи гибели десятков и даже сотен тысяч людей в результате экстремальных наводнений природного и техногенного (волны прорыва плотин и дамб) генезиса. В России за последние годы прошло несколько разрушительных наводнений: г. Крымск (р. Адагум), 2012 г.; бассейн Амура, 2013 г.; Черноморское побережье Кавказа, 2012, 2018 гг.; г. Тулун (р. Ия), 2019 г. Существующие мероприятия инженерной защиты при этом оказались недостаточными. В связи с этим стоит задача более эффективной защиты селитебных территорий и объектов повышенной опасности от затопления.
В настоящей работе рассматриваются поймы рек с расположенными на них населенными пунктами и объектами повышенной опасности (ОПО) (атомные электростанции, нефтеперерабатывающие и химические предприятия и т. п.); а также польдерные территории, которые затапливаются при прорыве ограждающих их дамб [7].
В соответствии с нормативными требованиями, территории поселений на прибрежных участках должны быть защищены от затопления паводковыми водами, от ветрового нагона воды и подтопления грунтовыми водами – подсыпкой (намывом) или обвалованием. Согласно СП 42.13330.2011 [12], за расчетный горизонт высоких вод следует принимать отметку наивысшего уровня воды повторяемостью один раз в 100 лет – для территорий, застроенных или подлежащих застройке жилыми и общественными зданиями, и один раз в 10 лет – для территорий парков и спортивных сооружений.
Для объектов повышенной опасности (например, атомных электростанций, расположенных в поймах рек) отметка верха горизонтальной промышленной площадки (на которой располагаются все сооружения станции) должна быть не ниже отметки затопления с вероятностью 10–6 1/год, или повторяемостью 1 раз в миллион лет [9].
Близкие к приведенным выше значения допустимых вероятностей затопления приняты и в мировой практике. Между тем научное (и практическое) обоснование этих нормативов отсутствует. В статье предлагается способ определения эффективных уровней инженерной защиты территории, основанный на минимизации рисков затопления. Риск в данном случае определяется стандартным образом как произведение вероятности затопления заданным уровнем воды на величину вероятного вреда (ущерба) при таком затоплении.
При обосновании возможности приближенного определения вероятного вреда при затоплении селитебных территорий и объектов повышенной опасности в поймах рек в зависимости от глубины затопления введены некоторые допущения и в результате получены простые степенные зависимости для величины вероятного вреда, причем показатель степени для ОПО оказывается больше, чем для селитебных территорий.
Технология построения кривых вероятности затопления поймы на основе двумерных гидродинамических моделей излагается с учетом того, что эти кривые строятся не в совсем обычном для классической гидрологии диапазоне величин повторяемости – от нескольких лет до десятков тысяч и миллионов лет. Отметим, что для построения кривых вероятности затопления могут применяться и более простые подходы (одномерные гидродинамические модели, уравнение Шези и пр.), однако в некоторых случаях это может приводить к снижению точности расчетов.
Сочетание аналитической формулы для расчета ущербов в зависимости от глубины затопления и формулы экспоненциального вида для определения вероятности затопления поймы на заданную глубину позволяет вывести формулы для определения рисков затопления селитебных территорий и ОПО, а также интегральных показателей рисков. Анализ последних зависимостей показывает, что эффективная инженерная защита должна быть рассчитана на уровни затопления обеспеченностью <0.1%.
РАСЧЕТ ВЕРОЯТНОГО ВРЕДА ОТ ЗАТОПЛЕНИЯ СЕЛИТЕБНЫХ ТЕРРИТОРИЙ И ОПО В ЗАВИСИМОСТИ ОТ ГЛУБИНЫ
Выполнение расчетов вероятного вреда (в стоимостном выражении) от затопления селитебных территорий природными наводнениями и техногенными паводками (волнами прорыва) в соответствии с имеющимися нормативными документами и методическими указаниями [8] – довольно трудоемкая задача. Для этого, кроме расчетов параметров затопления (зоны затопления, скорости течения, глубины затопления, времени стояния высоких вод), требуются данные о стоимости строений, объектов инфраструктуры, сельхозугодий и пр. Между тем можно показать, что для минимизации рисков затопления путем выбора и реализации защитных мероприятий (подсыпка или обвалование территории до определенной отметки) в ряде случаев конкретная стоимостная оценка вероятного вреда не требуется.
Такой подход к рассматриваемой проблеме позволяет в некоторой степени уйти от сугубо материальных оценок (которые, к тому же, могут сильно меняться во времени), ставя во главу угла вопросы надежности и безопасности защиты селитебных территорий и ОПО от наводнений. Отметим, что это ни в коей мере не исключает возможности расчета стоимостных коэффициентов в соответствии с известными методиками [8] или их модификациями, что необходимо для целей страхования.
Вывод формулы для нормализованного ущерба от затопления селитебной территории
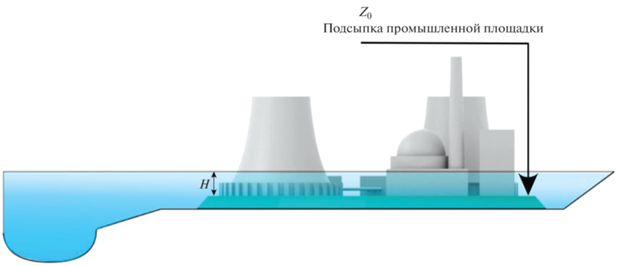
Рассмотрим сначала типичную ситуацию с расположением населенного пункта вдоль водотока частично на плоской пойме, частично на береговом откосе (рис. 1). На самом деле на пойме может быть неровный рельеф (возвышения, впадины), но эти случаи соответствуют рассматриваемой схеме, если рельеф расчленить на отдельные участки.
Предположим, что средняя ширина плоской части поймы по нормали к руслу – B, средний угол наклона берегового откоса к горизонту в ортогональном руслу направлении – α, глубина воды на данной вертикали – h, отметка поймы (или нижняя отметка застроенной территории) – Z0, глубина затопления от этой отметки – H, протяженность населенного пункта вдоль русла – L (рис. 1).
Основные ущербы от затопления в локальной области на местности связаны с двумя определяющими факторами [8] – динамическим и статическим.
1. Динамический фактор характеризуется кинетической энергией столба воды высотой h с единичной площадью основания, которая преобразуется в разрушающий динамический напор при взаимодействии с сооружениями (либо людьми, транспортными средствами и т. п.) и выражается формулой
где ρ – плотность жидкости, v – средняя по глубине скорость на данной вертикали.2. Статический фактор характеризуется глубиной затопления и временем затопления T (временем стояния высоких вод). Определенная глубина затопления может привести к всплытию легких деревянных строений за счет Архимедовой силы даже при незначительных или нулевых скоростях течения, а также может быть причиной гибели людей, порчи интерьеров, мебели, автомобилей, сельхозугодий и пр.
Оба перечисленных фактора приводят как к разрушению или повреждению жилого фонда, промышленных зданий и сооружений, инфраструктурных и сельскохозяйственных объектов, так и к травмам или гибели людей.
Учитывая уравнение Шези
(g – ускорение свободного падения, I – продольный уклон водной поверхности на пойме, λ – коэффициент гидравлического сопротивления поймы), получим из (1), (2) здесь К1 – коэффициент, слабо зависящий от глубины потока в данном месте (через коэффициент гидравлического сопротивления).Далее, предполагая, что время стояния высоких вод в первом приближении пропорционально глубине стояния (чем больше глубина затопления, тем обычно дольше продолжается и само затопление), получим выражение для статического фактора
К2 – коэффициент, не зависящий (или слабо зависящий) от глубины потока в данном месте.Вводя стоимостные коэффициенты А1 и А2 (которые зависят от вида, этажности и стоимости 1 м2 жилья, стоимости объектов инфраструктуры, стоимости сельхозпродукции на затапливаемых территориях, ущерба экологии и т. п.), из (3) и (4) получим выражение для локального (на единицу площади в конкретной точке населенного пункта) ущерба в стоимостном выражении
(5)
${{D}_{{{\text{LOC}}}}} = \left( {{{A}_{1}}{{K}_{1}} + {{A}_{2}}{{K}_{2}}} \right){{h}^{2}} = A{\kern 1pt} '{{h}^{2}},$Подчеркнем, что физическая природа коэффициентов К1, К2 разная, и также принципиально будут различаться стоимостные коэффициенты А1, А2. Например, для многоэтажного железобетонного здания А1 будет близким к нулю, потому что оно паводком не разрушится, а А2 может быть значительным, поскольку высоким уровнем воды будет повреждена отделка здания, интерьеры, мебель, товары в расположенных на первых этажах магазинах и т. п. С другой стороны, для 1–2-этажных деревянных зданий соответствующий динамический напор может привести к сносу их с фундамента и полному разрушению, т. е. в этом случае коэффициент А1 окажется определяющим.
Интегрируя выражение (5) по площади затапливаемой городской территории при максимальной глубине затопления Н с учетом того, что ширина полосы затопления плоской поймы будет равна В, ширина полосы затопления откоса будет, согласно схеме, пропорциональна глубине Н, – получим
(6)
$\begin{gathered} D = \int {A{\kern 1pt} '{{h}^{2}}dS = A{\kern 1pt} 'LB{{H}^{2}} + } \\ + \,\,~~\mathop \smallint \limits_0^H LA{\kern 1pt} '{\text{cot}}\alpha {{h}^{2}}dh = {{C}_{1}}{{H}^{3}} + {{C}_{2}}{{H}^{2}}, \\ \end{gathered} $Таким образом, суммарный ущерб от затопления селитебной территории пропорционален линейной комбинации квадрата и куба максимальной глубины затопления. Обобщенные стоимостные коэффициенты могут быть определены на основе имеющихся нормативных документов по расчету вероятного вреда (например, [8]), а также на основе дополнительных исследований.
Для упрощения дальнейших выкладок запишем формулу (6) в приближенном виде:
здесь $2 \leqslant \gamma \leqslant 3~$, причем значение γ конкретизируется в зависимости от топографии затапливаемой области.Вывод формулы для расчета нормализованного ущерба от затопления ОПО
В случае ОПО в силу их специфики суммарный ущерб будет определяться не степенной, а показательной функцией вида
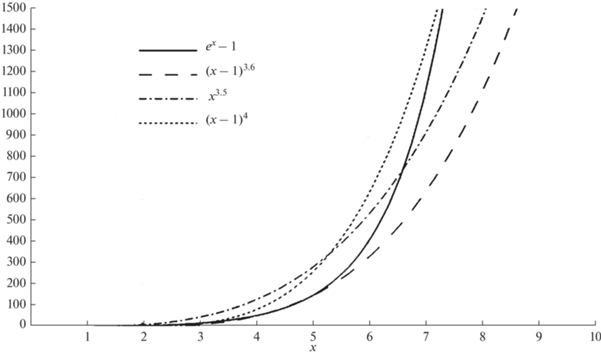
С3 – стоимостной коэффициент; Н – глубина затопления, отсчитываемая не от поверхности поймы, а от горизонтальной плоскости верха промышленной площадки (АЭС, нефтехимического предприятия и т. п.), на которой по проекту в одной отметке расположены все сооружения объекта (рис. 2); d – коэффициент, имеющий размерность длины. Подберем его исходя из условия, чтобы ущерб от затопления промплощадки на каждый последующий метр увеличивался в 10 раз. Тогда d = 0.44 м.Показательная функция в нужном диапазоне изменения (0 < Н/d < 9) может быть с приемлемой для решаемых задач погрешностью аппроксимирована степенными функциями вида (рис. 3):
(9)
$D = {{C}_{3}}{{\left( {\frac{H}{d} - 1} \right)}^{4}}\,\,{\text{или}}\,\,D = {{C}_{3}}{{\left( {\frac{H}{d}} \right)}^{{3.5}}}.$ПОСТРОЕНИЕ КРИВЫХ ВЕРОЯТНОСТИ УРОВНЕЙ ЗАТОПЛЕНИЯ ПОЙМЫ С ИСПОЛЬЗОВАНИЕМ ДВУМЕРНЫХ ГИДРОДИНАМИЧЕСКИХ МОДЕЛЕЙ И ДАННЫХ НАТУРНЫХ НАБЛЮДЕНИЙ
Для оценки рисков затопления необходимо построить кривую связи уровней затопления рассматриваемого объекта на пойме с вероятностью (или повторяемостью) достижения этого уровня. Генезис (причина) затопления может при этом быть различным и складываться из нескольких факторов. Это паводки, наводнения, волны прорыва вышележащих гидроузлов, ветровые нагоны и ветровые волны, волны цунами и т. п. Такая кривая уникальна для каждого объекта и может быть построена на основе данных натурных наблюдений и их экстраполяции, расчетным путем с применением методов математического моделирования (особенно в области малых вероятностей, где наблюдения отсутствуют), а также комбинированным способом.
Для всех анализируемых ниже створов расчеты выполнены с применением программного комплекса STREAM 2D CUDA, основанном на численном решении двумерных уравнений мелкой воды, и его модификаций [2, 3]. Используемые в этой программе алгоритмы уникальные, высокоточные, современные и опубликованы в ведущих мировых научных изданиях [1, 13, 14] и в монографии [4].
Первоначально разработанная методика (технология) построения кривых была применена к объектам повышенной опасности (АЭС Балаковская и Руппур), что было вызвано (ввиду специфики этих объектов) необходимостью рассматривать очень малые вероятности затопления [9, 10]. В работе [6] подробно описана последовательность построения такой кривой для участка р. Ганг (Республика Бангладеш) в районе строительства АЭС Руппур. Объект характеризуется наличием достаточно хороших исходных данных (детальный рельеф местности, актуальная гидрометрическая съемка, столетний ряд гидрологических наблюдений) и широким диапазоном изменения вероятности (повторяемости) затоплений вплоть до 10–9 1/год. Использован как метод экстраполяции данных натурных наблюдений в область малых вероятностей расходов воды, так и метод численного гидродинамического 2D-моделирования с учетом наложения (суперпозиции) нескольких гидрометеорологических явлений редкой повторяемости и с учетом возможного изменения климата. Отличительная особенность этого объекта заключается в том, что расчет кривой вероятностей пришлось проводить с учетом размывов речного дна, сильно влияющего на уровни воды в створе АЭС при пропуске высоких половодий.
Для ряда створов (р. Волга – г. Ярославль [15], р. Волга – г. Балаково [10], 4 створа на Нижнем Дону [5]) при построении кривой вероятностей затопления учитывались параметры волн прорыва вышележащих гидроузлов (не основано на реальной угрозе), которые рассчитаны с применением 2D-гидродинамических моделей протяженных участков долин рек. Отметки затопления в этих случаях обычно выше, чем от естественных паводков, но и вероятности их меньше. Для р. Северная Двина (г. Великий Устюг) кривая вероятности построена с учетом ледовых заторов.
Примеры таких кривых для нескольких створов на крупных реках, построенных с применением численного гидродинамического моделирования на основе работ [5, 6, 10, 15, 16], приведены на рис. 4–6 в полулогарифмических координатах в зависимости от величины повторяемости уровня, обратной вероятности достижения заданного уровня. В области малых вероятностей (≤0.1 1/год), которые интересуют при затоплении поймы, она может быть приближенно аппроксимирована логарифмической функцией. Виды таких функций и параметры аппроксимации приведены в табл. 1 для девяти створов на реках Дон, Волга, Ганг, Северная Двина, Ия. Достаточно хорошую точность аппроксимации обеспечивают функции вида ${{f}_{1}}\left( x \right) = a\sqrt {\ln \left( x \right)} + b$ и ${{f}_{2}}\left( x \right) = a\sqrt[4]{{\ln \left( x \right)}} + b$.
Рис. 4.
Кривая связи уровней воды с повторяемостью достижения этих уровней на в.п. Ростов-на-Дону (Нижний Дон).

Рис. 5.
Кривая связи уровней воды с повторяемостью достижения этих уровней на в.п. Ярославль (р. Волга, Горьковское водохранилище).

Рис. 6.
Кривая связи уровней воды с повторяемостью достижения этих уровней в створе АЭС Руппур на р. Ганг. 1 – экстраполированные данные наблюдений, 2 – результаты моделирования.
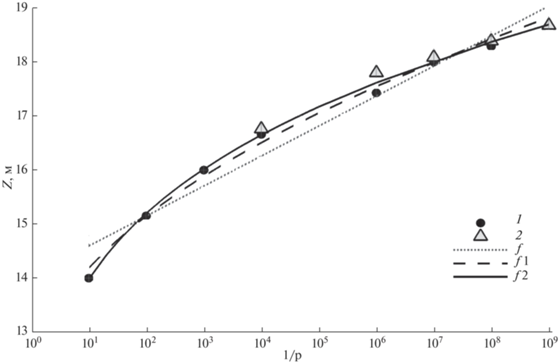
Таблица 1.
Данные по анализируемым створам
| Створы | $f\left( x \right) = a\ln \left( x \right) + b$ | ${{f}_{1}}\left( x \right) = a\sqrt {\ln \left( x \right)} + b$ | ${{f}_{2}}\left( x \right) = a\sqrt[4]{{\ln \left( x \right)}} + b$ |
|---|---|---|---|
| в.п. Ростов на Дону (Нижний Дон) |
a = 0.6375; b = 1.065; | a = 2.664; b = –1.296; | a = 7.229; b = –5.95; |
| SSE = 2.628; R2 = 0.8923 | SSE = 0.8913; R2 = 0.9635 | SSE = 0.4189; R2 = 0.9828 | |
| Багаевский гидроузел НБ (Нижний Дон) | a = 0.7426; b = 2.544; | a = 3.152; b = –0.3061; | a = 8.627; b = –5.917; |
| SSE = 6.121; R2 = 0.8284 | SSE = 2.76; R2 = 0.9226 | SSE = 1.512; R2 = 0.9576 | |
| в.п. Багаевская (Нижний Дон) |
a = 0.7365; b = 2.985; | a = 3.12; b = –0.1711; | a = 8.534; b = –5.374; |
| SSE = 5.945; R2 = 0.8302 | SSE = 2.758; R2 = 0.9212 | SSE = 1.584; R2 = 0.9548 | |
| в.п. Раздорская (Нижний Дон) |
a = 0.9632; b = 4.583; | a = 4.04; b = 0.986; | a = 11; b = –6.127; |
| SSE = 9.341; R2 = 0.8419 | SSE = 4.986; R2 = 0.9156 | SSE = 3.501; R2 = 0.9407 | |
| в.п. Ярославль (р. Волга) |
a = 0.4521; b = 85.87; | a = 2.936; b = 81.34; | a = 10.38; b = 72.3; |
| SSE = 1.273; R2 = 0.9263 | SSE = 0.5228; R2 = 0.9697 | SSE = 0.2558; R2 = 0.9852 | |
| АЭС Руппур (р. Ганг) |
a = 0.241; b = 14.04; | a = 1.528; b = 11.87; | a = 5.223; b = 7.549; |
| SSE = 0.8672; R2 = 0.9552 | SSE = 0.1258; R2 = 0.9935 | SSE = 0.008937; R2 = 0.9995 | |
| АЭС Балаково (р. Волга) |
a = 0.1736; b = 31.26; | a = 1.205; b = 29.44; | a = 4.262; b = 25.82; |
| SSE = 1.336; R2 = 0.8837 | SSE = 0.441; R2 = 0.9616 | SSE = 0.1475; R2 = 0.9872 | |
| в.п. Великий Устюг (р. Северная Двина) |
a = 0.2694; b = 58; | a = 1.418; b = 56.28; | a = 4.528; b = 52.74; |
| SSE = 0.048; R2 = 0.984 | SSE = 0.012; R2 = 0.996 | SSE = 0.002; R2 = 0.9993 | |
| г. Тулун (р. Ия) | a = 1.16; b = 456.5; | a = 5.281; b = 450.9; | a = 15.61; b = 439.5; |
| SSE = 0.123; R2 = 0.9966 | SSE = 0.06751; R2 = 0.9981 | SSE = 0.3108; R2 = 0.9913 |
ОЦЕНКА РИСКОВ ЗАТОПЛЕНИЯ СЕЛИТЕБНЫХ ТЕРРИТОРИЙ И ОБЪЕКТОВ ПОВЫШЕННОЙ ОПАСНОСТИ
При описании методики приближенной теоретической оценки нормализованных рисков затопления как селитебных территорий, так и ОПО под нормализованным риском подразумевается безразмерная величина, равная произведению безразмерного (нормированного) вероятного вреда от затопления территории до определенной отметки на вероятность достижения данной отметки водной поверхности.
Определение нормализованного риска однократного затопления селитебных территорий и объектов повышенной опасности
Запишем вероятность затопления согласно подобранным выше логарифмическим аппроксимациям этих кривых в виде
(10)
$P = {{{\text{e}}}^{{ - {{{\left( {\frac{{z\,{\kern 1pt} - \,{\kern 1pt} b}}{a}} \right)}}^{\beta }}}}},\,\,{\text{где}}\,\,{\text{\;}}1 \leqslant \beta \leqslant 4,\,\,\,\,z \geqslant b.$(11)
$P{\kern 1pt} {\kern 1pt} ' = - \frac{\beta }{a}~{{\left( {\frac{{z - b}}{a}} \right)}^{{\beta {\kern 1pt} - {\kern 1pt} 1}}}{{{\text{e}}}^{{ - {{{\left( {\frac{{z{\kern 1pt} \, - \,{\kern 1pt} b}}{a}} \right)}}^{\beta }}}}}.$Для величины риска затопления с учетом формулы (7) получим
(12)
$R = A~P{{\left( {z - {{z}_{0}}} \right)}^{\gamma }},\,\,\,\,2 \leqslant \gamma \leqslant 4{\text{,}}$(13)
${{\left( {\frac{{z - b}}{a}} \right)}^{{\beta {\kern 1pt} - {\kern 1pt} 1}}}\frac{{\left( {z - {{z}_{0}}} \right)}}{a} = \frac{\gamma }{\beta }.$В формулах (10), (11), (13) примем $\beta = 2$, что, с одной стороны, дает хорошую аппроксимацию кривых вероятности, а с другой стороны – позволяет получить простые аналитические зависимости. Тогда из (13) получается квадратное уравнение
$z - b = H + {{z}_{0}} - b$ подставляем в (14) $\mathop \Rightarrow \limits_{} \frac{{H + {{z}_{0}} - b}}{a}$ $\frac{H}{a} = \frac{\gamma }{2}.$Обозначим $\frac{H}{a} = {{H}_{N}}$ – нормированная глубина затопления, тогда
Обозначив ${{\Delta }_{N}} = \frac{{{{z}_{0}} - b}}{a} \geqslant 0$ (иначе $P\left( {{{z}_{0}}} \right) > 1)$, получим Если ${{\Delta }_{N}} = 0$ (частный случай: ${{z}_{0}} = b$), то ${{H}_{{{{N}_{*}}}}} = \sqrt {\frac{\gamma }{2}} $, здесь нормированная глубина со звездочкой ${{H}_{{{{N}_{*}}}}}$ – корень квадратного уравнения, обозначает глубину затопления, которой соответствует наибольший риск.В общем случае наихудшая (в смысле максимизации риска затопления) нормированная глубина находится по формуле (16) для корней квадратного уравнения (15)
(16)
${{H}_{{{{N}_{*}}}}} = - \frac{{{{\Delta }_{N}}}}{2} + \sqrt {{{{\left( {\frac{{{{\Delta }_{N}}}}{2}} \right)}}^{2}} + \frac{\gamma }{2}} .$(17)
${{R}_{N}} = \frac{R}{{A{{a}^{\gamma }}}} = H_{N}^{\gamma }{{{\text{e}}}^{{ - {{{\left( {{{H}_{N}}{\kern 1pt} + {\kern 1pt} {{\Delta }_{N}}} \right)}}^{\beta }}}}}.$Таблица 2.
Данные по анализируемым створам при $\beta = 2,\gamma = 2.5$
| Створы | а, м | b, м | ${{z}_{0}},\,{\text{м}}$ | ${{\Delta }_{N}}$ | ${{H}_{{{{N}_{*}}}}}$ |
|---|---|---|---|---|---|
| в.п. Ростов на Дону | 2.66 | –1.30 | 2.00 | 1.2372 | 0.66 |
| Багаевский гидроузел НБ | 3.15 | –0.31 | 3.50 | 1.2075 | 0.67 |
| в.п. Багаевская | 3.12 | –0.17 | 4.50 | 1.4971 | 0.60 |
| в.п. Раздорская | 4.04 | 0.99 | 6.00 | 1.2411 | 0.66 |
| в.п. Ярославль | 2.94 | 81.34 | 87.00 | 1.9278 | 0.51 |
| Руппур | 1.53 | 11.87 | 14.00 | 1.3940 | 0.62 |
| Балаково | 1.21 | 29.44 | 31.00 | 1.2946 | 0.64 |
| Великий Устюг | 1.42 | 56.28 | 56.54 | 0.1834 | 1.03 |
| Тулун | 5.28 | 450.90 | 458.00 | 1.3447 | 0.63 |
По данным табл. 2 и по формуле (17) построены графики на рис. 7 для исследуемых створов (за исключением Великого Устюга, график для которого расположен на порядок выше по оси ординат). Видно, что все кривые имеют выраженные максимумы, а при больших ${{H}_{N}}$ быстро убывают до нуля.
Рис. 7.
График ${{R}_{N}}\left( {{{H}_{N}}} \right)$ при $\beta = 2,~\gamma = 2.5$ для исследуемых створов: 1 – Багаевский гидроузел НБ, 2 – в.п. Ростов-на- Дону, 3 – в.п. Раздорская, 4 – Балаково, 5 – Тулун, 6 – Руппур, 7 – в.п. Багаевская, 8 – в.п. Ярославль.

Например, для г. Ростов-на-Дону ${{H}_{{{{N}_{*}}}}}$ = 0.66; это означает, что размерная глубина ${{H}_{*}}$, соответствующая максимальному риску от затопления, равна 0.66 × 2.66 м = 1.76 м над нижней отметкой застроенной поймы Z 0 = 2.0 м БС (табл. 2). Соответственно, опасная (в смысле максимального риска) отметка затопления равна 3.76 м БС, что приблизительно соответствует 2–3%-му затоплению и на 0.7 м ниже отметки 1%-го затопления 4.45 м БС (рис. 4).
Для ст. Раздорской с тем же ${{H}_{{{{N}_{*}}}}}$ = 0.66 размерная глубина ${{H}_{*}}$, соответствующая максимальному риску от затопления, равна 0.66 × 4.04 м = 2.67 м над нижней отметкой застроенной поймы Z0 = = 6.0 м БС (табл. 2). Соответственно, опасная отметка затопления равна 8.7 м БС, что также приблизительно соответствует 2–3%-му затоплению и на 1.0 м ниже отметки 1%-го затопления.
Для г. Тулуна ${{H}_{{{{N}_{*}}}}}$ = 0.63, размерная глубина ${{H}_{*}}$, соответствующая максимальному риску от затопления, равна 0.63 × 5.28 м = 3.33 м над нижней отметкой застроенной поймы Z 0 = 458.0 м БС (табл. 2). Соответственно, опасная отметка затопления равна 461.3 м БС, что также приблизительно соответствует 2–3%-му затоплению и на 0.9 м ниже отметки однопроцентного затопления.
Таким образом, в рассмотренных примерах уровень максимального риска единичного затопления находится в диапазоне отметки затопления 2–3%, а уровень 1%-го затопления – на 0.7–1.0 м выше. Если введем в формулу для вероятности затопления (10) при $\beta = 2$ выражение для наихудшей нормированной глубины (16) и подставим в эту формулу характерные значения $\gamma = 2.5~$ и ${{\Delta }_{N}}~ = 1.3$ (табл. 2), то получим вероятность достижения наихудшей нормированной глубины, равную 0.023, или 2.3%, что хорошо согласуется с приведенным выше диапазоном 2–3%, полученным по натурным данным.
На основе кривой рисков можно планировать мероприятия по защите населенного пункта от затопления. Очевидно, что необходима по крайней мере защита (дамбы обвалования, подсыпка территории при новой застройке) не ниже отметки затопления с максимальным уровнем риска единичного затопления.
Для г. Ростов-на-Дону для снижения риска затопления в 10 раз по сравнению с максимальным необходима защита территории на глубину 4.5 м (на 1.7 нормированной глубины), или до абсолютной отметки 6.5 м БС, что приближается к вероятности затопления 2 × 10–4 1/год (рис. 4). Для ст. Раздорской для снижения риска единичного затопления в 10 раз по сравнению с максимальным необходима защита территории на глубину 6.9 м (на 1.7 нормированной глубины), или до абсолютной отметки 12.9 м БС, что тоже приближается к вероятности затопления 2 × 10–4 1/год. Для г. Тулуна для снижения риска единичного затопления в 10 раз по сравнению с максимальным необходима защита пойменной территории на глубину 9.0 м (на 1.7 нормированной глубины), или до абсолютной отметки 467.0 м БС, что соответствует вероятности затопления 10–4 1/год.
Таким образом, видно, что на разных реках и в разных створах высокая степень защиты селитебных территорий с маленьким риском будет обеспечена при подъеме отметок защитных сооружений на уровень затопления вероятностью порядка 10–3–10–4 1/год, но уж никак не 10–2 1/год, которая принята в настоящее время в Российской Федерации по нормативным документам.
Для ОПО (АЭС Руппур и Балаково) функция риска затопления строилась по тем же формулам с повышенным коэффициентом γ при конкретных значениях коэффициентов, полученных для этих станций. Фактические значения для АЭС Руппур: a = 1.5 м, c = 0.4 м, ${{\Delta }_{N}}~$ = 1.39, ${{H}_{{{{N}_{*}}}}}$ = 0.7, ${{H}_{*}}$ = 1.05 м, 3${{H}_{*}}$ = 3.15 м. Максимум единичного риска для АЭС Руппур наступает при отметке затопления 15.05 мPWD, а уменьшенный в 10 раз риск – при отметке 17.15 мPWD, что соответствует вероятности затопления 2 × 10–6 1/год (рис. 6).
Для Балаковской АЭС имеем ${{H}_{{{{N}_{*}}}}}$ = 0.6, ${{H}_{*}}$ = = 0.72 м, 3${{H}_{*}}$ = 2.16 м. Поэтому максимум риска наступает при отметке затопления 31.72 м БС, а уменьшенный в 10 раз риск – при отметке 33.16 м БС, что на 1 м ниже фактической отметки промплощадки. Таким образом, Балаковская АЭС построена на высоких отметках, надежно обеспечивающих ее защиту от наводнений и волн прорыва.
Построение интегральных кривых рисков затопления при разных значениях параметров
Выше рассмотрены риски единичного затопления, т.е. когда сразу для всей данной территории единовременно вдруг возникла угроза или произошло катастрофическое затопление. Однако если ставить вопрос о долговременной защите какой-то территории от возможного затопления, то необходимо оценить остаточный риск, который возникнет только после того, как критический уровень воды превысит уровень защитных сооружений, а при меньших уровнях никаких рисков не будет, поскольку не будет затоплений селитебных территорий или ОПО (конечно, при условии обеспечения надежности работы этих сооружений).
Для решения этой задачи надо рассчитать нормализованный интегральный риск, который возникает при достижении заданной отметки затопления (совпадающей, по-видимому, с отметкой верха защитных сооружений). В общем случае в соответствии с формулой (17) он выражается величиной интеграла
(18)
${{I}_{{\gamma \Delta }}}\left( x \right) = \mathop \smallint \limits_0^x {{x}^{\gamma }}{{{\text{e}}}^{{ - {{{\left( {\Delta {\kern 1pt} + {\kern 1pt} x} \right)}}^{2}}}}}dx,$Введем обозначения: ${\text{erf}}\left( z \right) = \frac{2}{{\sqrt \pi }}\int_0^z {{{{\text{e}}}^{{ - {{t}^{2}}}}}dt} $ – функция ошибок (интеграл вероятности) – интеграл распределения Гаусса; ${\text{erfс}}\left( z \right) = 1 - {\text{erf}}\left( z \right) = $ $ = \frac{2}{{\sqrt \pi }}\int_z^\infty {{{{\text{e}}}^{{ - {{t}^{2}}}}}dt} $ – дополнительная функция ошибок.
Тогда получаются следующие выражения для интегралов:
при $\gamma = 2$, $\Delta = 0$
${{I}_{{20}}}\left( x \right) = \mathop \smallint \limits_0^x {{x}^{2}}{{{\text{e}}}^{{ - {{x}^{2}}}}}dx$ $ = \frac{1}{4}\left( {\sqrt \pi {\text{\;erf}}\left( x \right) - 2{{{\text{e}}}^{{ - {{x}^{2}}}}}x} \right),$
при $\gamma = 3$, $\Delta = 0$
${{I}_{{30}}}\left( x \right) = \mathop \smallint \limits_0^x {{x}^{3}}{{{\text{e}}}^{{ - {{x}^{2}}}}}dx$ $ = \frac{1}{2} - \frac{1}{2}{{{\text{e}}}^{{ - {{x}^{2}}}}}\left( {{{x}^{2}} + 1} \right)$,
при $\gamma = 4$, $\Delta = 0$
${{I}_{{40}}}\left( x \right) = \mathop \smallint \limits_0^x {{x}^{4}}{{{\text{e}}}^{{ - {{x}^{2}}}}}dx = \frac{3}{8}\sqrt \pi {\text{\;erf}}\left( x \right) - \frac{1}{4}{{e}^{{ - {{x}^{2}}}}}x\left( {2{{x}^{2}} + 3} \right),$
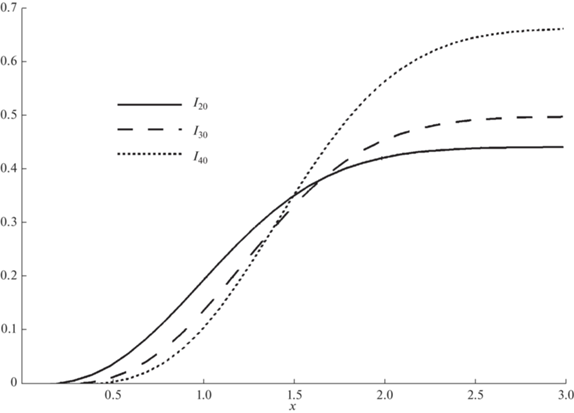
Графики этих функций представлены на рис. 8.
Рис. 8.
Интегральные ненормированные функции распределения нормализованного риска при $\Delta = 0$ и $\gamma = 2$, 3, 4.
Приведем полученные интегралы к нормальному виду, поделив их на соответствующие максимальные значения:
Однако, как видно из табл. 2, значения $\Delta ,$ близкие к нулю, довольно редки, а наиболее часто встречающиеся значения – в диапазоне 1.1–1.5. При этом характерное значение – $\gamma $ = 3 (среднее предельных значений 2 и 4). Выпишем решения интегральных уравнений для этих значений.
Видно, что в этих наиболее характерных случаях x – в диапазоне от 1.5 до 2.0. Графики этих функций приведены на рис. 9.
Рис. 9.
Нормированные интегральные функции распределения нормализованного (безразмерного) риска при $\Delta = 0,~\,\,1,\,\,~2$ и $\gamma = 3.$

Если эти безразмерные глубины, нормированные на параметр а (табл. 1, 2), пересчитать в доли характерных опасных глубин ${{H}_{{{{N}_{*}}}}}$, которые соответствуют максимальным ущербам при одноразовом затоплении, то получим приближенную оценку, согласно которой минимизация рисков на 90% достигается при удвоенной опасной глубине затопления, а минимизация на 99% – при утроенной опасной глубине. Это в некоторой степени напоминает правило 3σ для нормального распределения Гаусса. Напомним, что опасная глубина соответствует вероятности затопления ~2%.
ЗАКЛЮЧЕНИЕ
Разработаны научно-методические основы приближенной теоретической оценки рисков затопления селитебных территорий и объектов повышенной опасности, расположенных в поймах рек. Показано, что при некоторых допущениях величина ущерба от затопления пропорциональна глубине затопления в степени от 2.0 до 3.0 со средним показателем степени 2.5. Для объектов повышенной опасности величина ущерба зависит от глубины затопления не по степенному, а по показательному (экспоненциальному) закону, что связано со спецификой развития аварий на таких объектах. Однако в рассматриваемом диапазоне глубин затопления (до нескольких метров) она может быть аппроксимирована степенной зависимостью с показателем 3.5–4.0, что обеспечивает единую методику расчета.
Для оценки рисков затопления строится кривая связи уровней затопления рассматриваемого объекта с вероятностью достижения этих уровней (кривая вероятности затопления), которая имеет экспоненциальный вид. Плотность распределения рисков затопления получается перемножением зависимости вероятного вреда от глубины затопления на вероятность достижения этой глубины. С иcпользованием натурных данных и результатов математического моделирования построены такие кривые распределения для девяти створов на пяти реках: Волга-2, Нижний Дон-4, Северная Двина-1, Ганг-1, Ия-1.
Интегральная функция распределения нормированного (безразмерного) риска получается путем интегрирования кривой плотности распределения по глубине. На основе кривых рисков затопления и интегральных функций распределения можно планировать мероприятия по защите населенного пункта или объекта повышенной опасности от затопления. На конкретных примерах показано, что уровень воды, соответствующий максимальному риску для данного объекта (опасный уровень), в большинстве случаев довольно близок к уровню 2%-го затопления и что защиты до отметок 1%-го затопления или запрещения строительства в зоне 1%-го затопления недостаточно для надежного обеспечения безопасности селитебных территорий.
Выведено простое правило, согласно которому минимизация рисков на 90% достигается при защите территории до удвоенной опасной глубины затопления, а минимизация на 99% – при утроенной опасной глубине. Защита же территории до уровня 1%-го затопления, как это сейчас принято по нормативам, дает защиту от рисков затопления менее чем на 50% и, по существу, не имеет смысла.
Список литературы
Алексюк А.И., Беликов В.В. Моделирование течений мелкой воды с областями обмеления и разрывами дна // Журн. вычислит. математики и матем. физ. 2017. Т. 57. № 2. С. 316–338.
Алексюк А.И., Беликов В.В. Программный комплекс STREAM 2D CUDA для расчета течений, деформаций дна и переноса загрязнений в открытых потоках с использованием технологии CUDA (на графических процессорах NVIDIA) // Свид. гос. регистрации программы для ЭВМ № 2 017 660 266.
Алексюк А.И., Малахов М.А., Беликов В.В. Решатель задачи Римана для уравнений мелкой воды с разрывным дном // Свид. гос. регистрации программы для ЭВМ № 2 020 660 617. 2020.
Беликов В.В., Алексюк А.И. Модели мелкой воды в задачах речной гидродинамики. М.: РАН, 2020. 346 с. ISBN 978-5-907366-10-7
Беликов В.В., Алексюк А.И., Борисова Н.М., Глотко А.В., Румянцев А.Б. Оценка изменения уровней затопления поймы Нижнего Дона под влиянием хозяйственной деятельности. Ретроспективное гидродинамическое моделирование // Вод. ресурсы. 2022. Т. 49. № 3.
Беликов В.В., Алексюк А.И., Борисова Н.М., Норин С.В., Румянцев А.Б. Об определении отметок промплощадок атомных электростанций, расположенных в поймах рек // Гидротех. стр-во. 2019. № 3. С. 14–24.
Беликов В.В., Норин С.В., Школьников С.Я. О прорыве дамб польдеров // Гидротех. стр-во. № 12. 2014. С. 25–34.
Методика определения размера вреда, который может быть причинен жизни, здоровью физических лиц, имуществу физических и юридических лиц в результате аварии судоходных гидротехнических сооружений. Утверждена Приказом МЧС России и Минтранса России от 02.10.2007. № 528/143.
Рекомендации Росатома. Стандарт организации. Объекты использования атомной энергии. Учет опасных природных процессов и явлений при выборе площадки размещения. АЭС СТО СРО-Г 60542954 00005 -2015.
Румянцев А.Б., Беликов В.В. Оценка рисков воздействия экстремальных гидрометеорологических явлений и техногенных паводков на объекты повышенной опасности // Сб. науч. тр. Всерос. науч. конф. “Научное обеспечение реализации “Водной стратегии Российской Федерации на период до 2020 г.”. Петрозаводск, 2015. Т. 2. С. 38–44.
Румянцев А.Б., Васильева Е.С., Беликов В.В. Интегральный подход к оценке и минимизации рисков затопления селитебных территорий // Сб. науч. тр. Всерос. науч. конф. с международ. участием “Научные проблемы оздоровления Российских рек и пути их решения”. М.: Студия Ф1, 2019. С. 253–258.
СП 42.13330.2011 Градостроительство. Планировка и застройка городских и сельских поселений. Актуализированная редакция СНиП 2.07.01-89*. 2011.
Aleksyuk A.I., Belikov V.V. The uniqueness of the exact solution of the Riemann problem for the shallow water equations with discontinuous bottom // J. Computational Physics. 2019. V. 390. P. 232–248. https://doi.org/10.1016/j.jcp.2019.04.001
Aleksyuk A.I., Malakhov M.A., Belikov V.V. The exact Riemann solver for the shallow water equations with a discontinuous bottom // J. Computational Physics. V. 450. P. 110801. 2022. https://doi.org/10.1016/j.jcp.2021.110801
Belikov V.V., Aleksyuk A.I., Borisova N.M., Vasilieva E.S., Norin S.V., Rumyantsev A.B. Justification of Hydrological Safety Conditions in Residential Areas Using Numerical Modelling // Water Resour. 2018. V. 45. Suppl. 1. P. S39–S49. ISSN 0097-8078. https://doi.org/10.1134/S0097807818050305
Belikov V.V., Borisova N.M., Glotko A.V. Numerical Hydrodynamic 2D-Simulation of the Inundation of Tulun Town on the Iya R. during Flood 2019 // Water Resour. 2021. V. 48. № 5. P. 713–725. https://doi.org/10.1134/S0097807821040023
Дополнительные материалы отсутствуют.