Водные ресурсы, 2023, T. 50, № 2, стр. 163-169

ВВЕДЕНИЕ

Математические исследования движения влаги в ненасыщенной среде связаны с анализом уравнений Ричардса [1, 15]. Соответствующие задачи призваны отвечать на практические вопросы, связанные с восполнением запасов подземных вод, со степенью их защищенности от поступающих с поверхности загрязнений, с потребностями сельского хозяйства. В предлагаемой работе рассматриваются одномерные нестационарные процессы инфильтрации при осциллирующих режимах поступления влаги в ненасыщенный грунт. Исследование проведено методами математического анализа с построением явных решений.

При осциллирующем поступлении влаги в грунт происходит уменьшение амплитуды флуктуаций потока с ростом глубины. Мощность зоны, в которой флуктуации остаются существенными, зависит от фильтрационных параметров грунта и характеристик режима поверхностного питания. Ниже этой зоны поток стабилизируется и приближается к стационарному. Один из основных результатов предлагаемого исследования – вывод эффективной оценки для глубины, начиная с которой флуктуации потока становятся пренебрежимо малыми. Предложенное явное выражение для этой глубины содержит, помимо фильтрационных параметров грунта, основные характеристики режима поступления влаги: частоту колебаний, величину среднего потока и амплитуду флуктуаций водонасыщенности у поверхности.

К стабилизации потока приводят два физических механизма: капиллярная диссипация и нелинейная дисперсия неровностей профиля влажности. Если эти механизмы действуют совместно, то описать в явной форме стабилизацию решений невозможно, так как у уравнений Ричардса нет ни подходящих для рассматриваемой проблемы точных автомодельных решений, ни, тем более, общих выражений, позволяющих найти решение для заданного нестационарного инфильтрационного потока на поверхности грунта. Это делает проблему построения оценок искомой глубины стабилизации нетривиальной.

Когда нелинейность либо капиллярность доминирует, а другим фактором можно пренебречь, исходная задача приобретает удобный для анализа вид. Учет влияния на стабилизацию потока только капиллярных сил приводит к линеаризованной версии уравнений Ричардса. Если же пренебречь капиллярными силами, то понизится порядок этих уравнений. Для этих предельных случаев в работе построены подходящие семейства точных периодических по времени решений, для которых скорости затухания флуктуаций с ростом глубины найдены в явной форме. В общей ситуации, когда оба фактора действуют совместно, для построения оценок мощности нестационарной зоны потока использован метод декомпозиции, предложенный ранее в работе [10], где исследовалась нестационарная инфильтрация при импульсном поступлении влаги в грунт. Этот метод заключается в том, чтобы стабилизирующие эффекты от капиллярной диссипации и нелинейного рассеяния учесть по отдельности, а затем определенным образом сложить.

В предлагаемой работе также исследуется важное свойство осциллирующих режимов инфильтрации, которое заключается в том, что средняя по времени водонасыщенность грунта отличается от той, которая формируется на большой глубине в результате стабилизации потока. В частности, показано, что при естественных предположениях на фильтрационныe параметры грунта среднее влагосодержание в верхней зоне течения, где колебания существенны, меньше, чем на глубине. Математически это свойство аналогично пампинг-эффекту, изучавшемуся в работах [4–6] в связи с некоторыми другими нелинейными геофизическими процессами.

Для процессов инфильтрации при осциллирующих режимах поверхностного питания пампинг-эффект приводит к тому, что типичная скорость частиц влаги в нестационарной зоне течения оказывается выше, чем в соответствующем стационарном потоке. Это обстоятельство может иметь значение для оценок защищенности грунтовых вод от загрязнений, поступающих с поверхности, так как один из определяющих параметров в таких оценках – время добегания загрязняющих примесей до поверхности грунтовых вод.

ПОСТАНОВКА ЗАДАЧИ

Рассматривается одномерная задача об инфильтрации влаги в однородный грунт бесконечной глубины. Требуется определить зависимость водонасыщенности θ и потока влаги q от времени t и глубины z. Предполагается везде далее, что ось z направлена вертикально вниз и значение z = 0 соответствует поверхности грунта. Предполагается также, что инфильтрация безнапорная и всюду в грунте θ < 1. Тогда уравнения Ричардса для искомых функций имеют следующий вид:

m – пористость, K(θ) – коэффициент фазовой проницаемости влаги в ненасыщенном грунте, P ^c(θ) – капиллярное давление, нормированное на удельный вес воды. Для функций P ^c(θ) и K(θ) примем эмпирические выражения Брукса и Кори [1, 12]: где K – коэффициент фильтрации насыщенного грунта; h – размерная константа, определяющая масштаб капиллярных сил; β и γ – некоторые положительные показатели. В дальнейшем важна выпуклость функции K(θ), т. е. β > 1 (наиболее употребительное в гидрогеологии значение – β = 3).

Пусть на поверхности z = 0 задан инфильтрационный поток q(t,0) = R(t) ≥ 0, осциллирующий периодически по времени с некоторым периодом T (необходимо также ограничение R(t) ≤ K, чтобы в грунте не возникало насыщенных зон). Рассмотрим для уравнений (1) задачу об установившихся, т. е. периодических по времени с тем же периодом T, режимах инфильтрации. В этом случае для единственности решения начальных условий не требуется, а при z → +∞ достаточно потребовать ограниченности решений.

Будем обозначать угловыми скобками 〈 〉 среднее значение периодических функций по времени. Из уравнений (1) следует, что среднее значение потока влаги q(t, z) не зависит от глубины и совпадает со средним значением заданной функции R(t):

К этому значению поток q(t, z) стабилизируется при z → +∞, а соответствующее предельное значение водонасыщенности θ₀ определяется соотношением R₀ = K(θ₀) = K$\theta _{0}^{\beta }$. Отметим, что из-за нелинейности задачи среднее значение водонасыщенности 〈θ(·,z)〉 не обязано быть постоянным по глубине и равным этому предельному значению. В исходной задаче в качестве краевого условия на поверхности z = 0 можно задавать не поток q(t, 0), а водонасыщенность θ(t,0), которая на практике проще измеряется. В этом случае, однако, предельные значения θ₀ и R₀, к которым решение стабилизируется при z → +∞, не определяются непосредственно по краевому условию, а вычисляются в результате полного решения задачи.

Разница θ₀ – 〈θ(t, 0)〉 может интерпретироваться как дополнительная влага, закачанная в грунт (или, в зависимости от знака, откачанная из грунта). В работах [4–6] аналогичный пампинг-эффект исследован для нелинейных задач о нестационарных потоках тепла в разные среды.

В качестве иллюстрации на рис. 1 показан численный пример определения профилей водонасыщенности θ(t, z) для установившихся вынужденных колебаний в разные моменты времени внутри одного периода. В этих расчетах принимался период колебаний T = 10 сут, а инфильтрация с поверхности R(t) представляла собой периодическую кусочно-постоянную функцию, принимающую значение R = 0.2 м/сут в течение одних суток и равная 0 в оставшейся части периода. Для остальных параметров задачи принимались значения m = 0.3, K = 0.2 м/сут, р = 0.3 м, β = 3, γ = 1. В этом примере средняя инфильтрация составляет R₀ = 0.02 м/сут, а соответствующая предельная водонасыщенность θ₀ = 0.464.

Выразим зависящую от глубины амплитуду колебаний водонасыщенности θ(t, z) равенством

Из принципа максимума для параболических уравнений следует, что эта функция убывает с глубиной монотонно. Если бы для A(z) было известно явное выражение через параметры задачи, то зону влияния флуктуаций поверхностного питания можно было бы определить неравенством A(z) ≥ ε, в котором ε > 0 – заданное пороговое значение амплитуды, ниже которого колебания можно считать несущественными. К сожалению, задача не допускает явного решения не только в общем случае, но и для частных примеров периодических функций R(t). Ниже для A(z) будут построены некоторые приближенные выражения. Следует отметить, что в практических приложениях точность измерения параметров грунта и особенно – величины поверхностного питания бывает невысока. Более того, предположения об однородности среды и периодичности процесса по времени сильно упрощают реальные ситуации. Поэтому даже точное выражение для A(z), если бы такое существовало, годилось бы только для грубых оценок. Это служит еще одним доводом в пользу поиска приближенных решений задачи.

ЛИНЕЙНАЯ АППРОКСИМАЦИЯ

Рассмотрим периодические решения уравнений (1) с малой амплитудой флуктуаций. Пусть θ = θ₀ + θ′(t, z) и |θ′(t, z)| $ \ll $ θ₀, $\left| {\theta {\kern 1pt} '(t,z)} \right| \ll {{\theta }_{0}}$. В линейном по возмущениям приближении уравнения (1) принимают вид

где mV₀ = dK(θ₀)/dθ = $\beta K_{\theta }^{{\beta {\kern 1pt} - {\kern 1pt} 1}}$, D₀ = D(θ₀) = = K(θ₀)dP  ^c(θ₀)/dθ = γKh$\theta _{0}^{{\beta {\kern 1pt} - {\kern 1pt} \gamma {\kern 1pt} - {\kern 1pt} 1}}$. В силу уравнения (4) среднее 〈θ′(·,z)〉 не зависит от глубины, и без ограничения общности его можно принять равным нулю. Одно из периодических решений уравнения задается выражением в котором a > 0 и t₀ – произвольные константы, ω = 2π/T – циклическая частота колебаний, значения λ > 0 и k зависят от ω и вычисляются подстановкой в уравнение (4). В частности, для λ получается формула Для этого решения амплитуда колебаний (3) выражается формулой A(z) = 2a exp(–λz), а скорость затухания колебаний удовлетворяет равенству

Произвольное периодическое решение линейного уравнения (4) может быть представлено в виде ряда Фурье, в котором слагаемые задаются выражениями, аналогичными (5), с частотами ω, 2ω, 3ω, и т. д. Показатели затухания λ = λ(ω) возрастают с ростом частоты, поэтому на большой глубине основной вклад в решение θ′(t, z) будет вносить первое слагаемое, а остальные будут по сравнению с ним экспоненциально малы. Таким образом, при z → +∞ равенство (6) асимптотически верно описывает скорость затухания колебаний. Более того, этот вывод остается в силе для исходных нелинейных уравнений (1), так как с ростом глубины роль нелинейности уменьшается.

Решения уравнений (1), близкие к равномерному потоку, можно исследовать методом возмущений, раскладывая решение в ряд по степеням амплитуды колебаний: θ = θ₀ + θ′(t, z) + θ′′(t, z) +… . При подстановке этого разложения в уравнения (1) первым приближением является уравнение (4), а для квадратичного по амплитуде слагаемого θ′′(t, z) получаются соотношения

В отличие от линейного приближения θ′(t, z), квадратичная поправка к водонасыщенности θ′′(t, z) содержит не только осциллирующие по времени слагаемые. Для среднего значения 〈θ′′(·, z)〉 из соотношений (7) следует равенство

Если линейная поправка к водонасыщенности θ′(t, z) задана выражением (5), то для 〈θ′′(·, z)〉 из этого равенства следует формула

Лабораторные наблюдения показывают, что для большинства грунтов, смачиваемых водой, коэффициент фазовой проницаемости влаги K(θ) – выпуклая функция, а коэффициент капиллярной диффузивности D(θ) – возрастающая функция водонасыщенности θ [1]. В частности, для соотношений Брукса и Кори (2) эти свойства выполнены, если β > γ + 1. При таком условии выражение (8) – отрицательное. Следовательно, при установившемся осциллирующем режиме инфильтрации средняя по времени водонасыщенность в верхней части грунта меньше, чем в соответствующем равномерном потоке, по крайней мере в случае малых флуктуаций.

Этот вывод остается в силе, если линейная поправка к водонасыщенности θ′(t, z) – периодическая функция времени общего вида и представлена рядом Фурье слагаемых вида (5) с кратными частотами ω, 2ω, 3ω и т. д. В этом случае среднее значение квадратичной поправки 〈θ′′(·, z)〉 равно сумме слагаемых, аналогичных выражению (8), с разными коэффициентами $a$ и соответствующими значениями показателей λ – λ(ω), λ(2ω), λ(3ω) и т. д.

БЕСКАПИЛЛЯРНАЯ АППРОКСИМАЦИЯ

Если действие капиллярных сил в уравнениях Ричардса (1) устремить к нулю, то получится модель фильтрации Грина и Ампта [13]. Эта упрощенная модель фильтрации предложена в статье [16] на основе анализа экспериментов по инфильтрации, приведенного в работе [11]. Математические обоснования предельного перехода от уравнений Ричардса к бескапиллярной модели Грина и Ампта в рамках различных предположений предлагались в работах [7–9, 11], а экспериментальные исследования по определению параметров модели приведены, например, в [14]. При безнапорной инфильтрации бескапиллярное приближение уравнений (1) сводится к простейшему нелинейному уравнению первого порядка (уравнению Римана):

Такое уравнение возникает во многих физических приложениях, связанных с аэродинамикой, сорбционными процессами и др. Свойства и способы построения его решений хорошо известны (например, в [2, 3]). Уравнение (9) может иметь разрывные решения и должно быть дополнено условиями на скачках водонасыщенности. Если закон движения скачка на плоскости (t, z) имеет вид z = z(t) и значения водонасыщенности и потока до и после скачка в момент времени t равны θ₁, q₁ и θ₂, q₂ соответственно, то из закона сохранения массы следует равенство

Для функций K = K(θ) с выпуклым вниз графиком те скачки, для которых θ₂ < θ₁, не являются эволюционными, т. е. не могут образовываться в результате эволюции непрерывного профиля водонасыщенности. Для обеспечения единственности решения задачи такие скачки следует исключить из рассмотрения. Таким образом, условие на скачке (10) должно быть дополнено неравенством θ₂ > θ₁.

Осциллирующие по времени решения бескапиллярного уравнения (9) демонстрируют пампинг-эффект, который выражается неравенством

Это неравенство выполняется для колебаний любой амплитуды. Оно следует из геометрического свойства графиков выпуклых функций и выражает собой тот факт, что центр масс системы материальных точек, распределенных на графике функции q = K(θ), должен лежать выше этого графика. Неравенство 〈θ(·, z)〉 < θ₀ обосновано выше и при наличии капиллярных сил, но только для решений с малыми осцилляциями.

Чтобы исследовать влияние фактора нелинейности на процесс стабилизации потока с ростом глубины, построим семейство точных периодических решений уравнения (9), зависящее от амплитуды флуктуаций водонасыщенности у поверхности. Для этого проведем нормировку переменных следующим образом:

В новых переменных равенства (9) примут следующий вид:

Пусть краевое условие для этих уравнений при x = 0 следующее:

здесь δ(·) обозначает стандартную δ-функцию. Ниже показано, что решение Θ = Θ(τ, x) с периодом 1 по нормированному времени τ при таком краевом условии не ограничено в окрестности точек τ = n, x = 0 полуплоскости x ≥ 0. Чтобы удовлетворить условию θ < 1 в безнапорном потоке, будет использоваться семейство решений Θ = = Θ(τ, x + x₀), зависящее от параметра x₀ > 0. Соответствующее значение нормированного потока Q(τ, x + x₀) на поверхности x = 0 – некоторая ограниченная периодическая функция τ, а не последовательность точечных импульсов. Параметр x₀ определяет амплитуду колебаний у поверхности x = 0 и может быть подобран так, чтобы θ(t, z) ≤ 1.

Качественный вид решения θ(t, z) показан на рис. 2. Профиль нормированной водонасыщенности имеет пилообразную форму и представляет собой последовательность скачков, перемещающихся вниз с непрерывно уменьшающимися скоростью и амплитудой. При x → +∞ решение стабилизируется к равномерному потоку, в котором Θ = Q = 1. Отчасти это поведение решения похоже на численный пример, показанный на рис. 1, где, однако, разрывы профиля водонасыщенности сглажены капиллярной диссипацией.

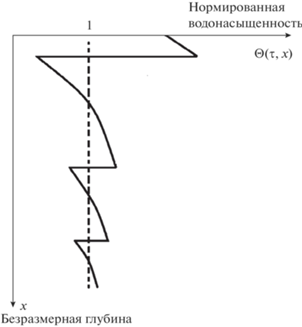
Для любого непрерывного периодического по времени потока R(t), заданного на поверхности, периодическое решение θ(t, z) задачи (9) начиная с некоторой глубины перестает быть непрерывным и распадается на последовательность скачков. Его профиль при этом приобретает пилообразную форму, сходную с показанной на рис. 2. Это происходит из-за нелинейности уравнения (9), приводящей к опрокидыванию тех участков профиля θ(t, z), которые монотонно убывают по глубине z. Таким образом, частное решение Θ = Θ(τ, x) на качественном уровне моделирует общую ситуацию.

Структура решения на полуплоскости x ≥ 0 показана на рис. 3. Если закон движения скачка, выходящего из точки τ = 0, x = 0, имеет вид τ = = S(x), то траектории остальных скачков могут быть получены периодическими сдвигами по нормированному времени τ и задаются уравнениями τ = S(x) + n. Между соседними траекториями функция Θ(τ, x) непрерывна и легко находится методом характеристик. В частности, в области S(x) < τ < S(x) + 1 решение представляет собой центрированную волну Римана и задается выражением

а на оставшуюся часть полуплоскости продолжается по периодичности. Отсюда следует, что

Находить выражение для функции S(x), задающей траектории скачков, удобнее с помощью закона сохранения массы в интегральной форме, а не его дифференциального следствия (10). В результате получается следующее равенство

Используя это явное выражение, можно показать, что S(x) – выпуклая функция нормированной глубины $x$. С ростом глубины траектория τ = = S(x) асимптотически приближается к прямой τ = x/β – 1/2. При этом нормированная скорость скачка dx/dτ = (dS(x)/dx)^–1 убывает с глубиной от +∞ при x = 0 до β при x → +∞.

Из формул (12) и (13) следует важное равенство

Это равенство показывает, что в отсутствие капиллярных сил стабилизация потока с увеличением глубины происходит не экспоненциальным, а степенным образом. Рассматривая вместо случая Θ = Θ(τ, x), ограниченного при x = 0, решение Θ = Θ(τ, x + x₀) и возвращаясь от нормированных переменных к исходным, получим выражения для амплитуды колебаний водонасыщенности (3) и скорости ее затухания

где A₀ обозначает амплитуду флуктуаций вблизи поверхности z = 0.

Сравнение уравнений (6) и (14) для скорости стабилизации показывает, что пороговая амплитуда колебаний – безразмерная величина λ/ϭ. Если A(z) существенно превышает эту величину, то основное влияние на скорость затухания колебаний должен оказывать фактор нелинейности уравнений, а в той зоне течения, где A ⪡ λ/ϭ, должна доминировать капиллярная диссипация. На промежуточном участке, где A ~ λ/ϭ, два фактора действуют совместно. Поскольку и нелинейность, и капиллярная диссипация приводят к затуханию амплитуды (т. е. действуют в одну сторону), то для оценки их совместного действия на этом участке представляется естественным рассматривать их суммарный вклад в скорость стабилизации. Это приводит к уравнению

Решение этого дифференциального уравнения для амплитуды A(z) приводит к формуле

Полученная аппроксимация – не точное следствие исходной задачи (1). Тем не менее оно, по-видимому, может служить инструментом для грубых оценок глубины влияния нестационарности поверхностного питания. Во всяком случае оно дает асимптотически обоснованную оценку амплитуды колебаний в предельных ситуациях доминирования капиллярности над нелинейностью и наоборот.

ЗАКЛЮЧЕНИЕ

При осциллирующем поступлении влаги в грунт происходит уменьшение амплитуды флуктуаций потока с ростом глубины. Это показано на примерах решения задач с периодическими по времени режимами инфильтрации в однородном грунте. Установлено, что к стабилизации потока приводят два физических механизма: капиллярная диссипация и нелинейная дисперсия флуктуаций влажности. Роль каждого из этих факторов исследована с помощью построения подходящих точных решений. Доказано, что капиллярная диссипация приводит к экспоненциальному, а нелинейность – к степенному затуханию амплитуды колебаний с глубиной. Предложена явная формула (15) для оценки глубины, на которой влияние осцилляций становится несущественным. Эта оценка учитывает совместное влияние двух факторов. Найденное для нее выражение включает в себя, помимо фильтрационных параметров грунта, период колебаний, величину среднего потока и амплитуду флуктуаций водонасыщенности у поверхности.

Для осциллирующих периодических режимов инфильтрации аналитически доказано, что среднее по времени водосодержание в верхних слоях грунта оказывается меньше, чем на глубине. В этом состоит проявление пампинг-эффекта, ранее изучавшегося в связи с некоторыми другими физическими процессами. Для инфильтрации влаги в ненасыщенный грунт пампинг-эффект приводит к увеличению типичной скорости движения жидких частиц в осциллирующем потоке по сравнению с соответствующим стационарным.